Molecular Population Genetics of the SRK and SCR Self-Incompatibility Genes in the Wild Plant Species Brassica cretica (Brassicaceae)

Abstract

Self-incompatibility (SI) in plants is a classic example of a trait evolving under strong frequency-dependent selection. As a consequence, population genetic theory predicts that the S locus, which controls SI, should maintain numerous alleles, display a high level of nucleotide diversity, and, in structured populations, show a lower level of among-population differentiation compared to neutral loci. Population-level investigations of DNA sequence variation at the S locus have recently been carried out in the genus Arabidopsis, largely confirming results from theoretical models of S-locus evolutionary dynamics, but no comparable studies have been done in wild Brassica species. In this study, we sequenced parts of the S-locus genes SRK and SCR, two tightly linked genes that are directly involved in the determination of SI specificity in samples from four natural populations of the wild species Brassica cretica. The amount and distribution of nucleotide diversity, as well as the frequency spectrum of putative functional haplotypes, observed at the S locus in B. cretica fit very well with expectations from theoretical models, providing strong evidence for frequency-dependent selection acting on the S locus in a wild Brassica species.

HOMOMORPHIC self-incompatibility (SI) is a pollen–pistil interaction mechanism that inhibits self-fertilization and is found in a number of higher plant families (De Nettancourt 2001). In the majority of cases, SI is genetically controlled by a single locus, the S locus, which may contain several different genes (Silva and Goring 2001). Members of the Brassicaceae family have a sporophytic SI system, which means that the SI specificity of the haploid pollen is determined by the S-locus genotype of the diploid parent (Hiscock and McInnis 2003). In sporophytic SI systems, there are often complex patterns of dominance among different S alleles; in Brassica, for example, two major dominance classes have been found with class I alleles being dominant over class II alleles in pollen and codominant in the stigma (Nasrallah et al. 1991).

Two genes have been identified as essential for determination of incompatibility mating types in the Brassicaceae: S-receptor kinase (SRK; Stein et al. 1991) and S locus protein 11/S locus cystein rich protein (SP11/SCR, hereafter referred to as SCR; Schopfer et al. 1999; Suzuki et al. 1999). The female determinant, SRK, is expressed in the stigma as a transmembrane receptor kinase, which recognizes the gene product of SCR (the male determinant) located on the pollen surface. Recognition of self-SCR by SRK receptors leads to haplotype-specific rejection of self-pollen (Kachroo et al. 2001). The SRK and SCR genes are typically inherited as a single unit (Casselman et al. 2000), as recombination between the two determinant genes would disrupt the SI response (Uyenoyama and Newbigin 2000). Indeed, population-based studies in Arabidopsis have found evidence for the near absence of historical recombination between SRK and SCR (Kamau and Charlesworth 2005; Charlesworth et al. 2006; Hagenblad et al. 2006). Because of the tight linkage among S-locus genes, S alleles are usually referred to as haplotypes (Boyes and Nasrallah 1993).

SI is arguably the best-known example of a trait subject to frequency-dependent selection. Population genetics theory makes a number of specific predictions about loci under strong frequency-dependent selection, e.g., the S locus. First, S loci should maintain a large number of alleles or haplotypes since individuals carrying rare S haplotypes have more mating opportunities (Wright 1939; Schierup 1998). Second, the S locus is also expected to show elevated levels of nucleotide diversity, resulting from long coalescence times as different functional haplotypes are retained in a population over extended periods of time (Vekemans and Slatkin 1994; Schierup et al. 1998). Third, in subdivided populations, a lower level of population differentiation is expected at the S locus compared to neutral loci because frequency-dependent selection will elevate within-population heterozygosity at the S locus and also because immigrant S haplotypes with novel specificities will be favored, thereby increasing the effective migration rate (Schierup et al. 2000). Finally, due to the requirement of matching pistil and pollen specificities, recombination at the S locus should be suppressed (Awadalla and Charlesworth 1999). While these predictions are not, in a qualitative sense, expected to be sensitive to dominance, the occurrence of a dominance hierarchy among S-locus haplotypes, as in sporophytic SI, will lead to more complicated population dynamics where S-haplotype equilibrium frequencies depend on the particular system of dominance relationships among haplotypes (Sampson 1974; Schierup et al. 1997; Vekemans et al. 1998; Uyenoyama 2000; Billiard et al. 2007).

Despite the fact that cultivated Brassica species such as Brassica oleracea and Brassica rapa have provided the bulk of today's knowledge about the molecular genetics of sporophytic SI (Nasrallah 2000; Takayama et al. 2001; Takayama and Isogai 2005), studies of natural S-locus DNA sequence variation in the Brassicaceae have almost exclusively focused on Arabidopsis species. While these studies have largely confirmed theoretical predictions about the diversity at the S locus [i.e., higher frequencies of recessive alleles (Mable et al. 2003; Schierup et al. 2006); lower population structure relative to neutral loci (Kamau et al. 2007; Ruggiero et al. 2008; see also Glémin et al. 2005); high among-haplotype and low within-haplotype diversity (Charlesworth et al. 2003a); and low historical rates of recombination (Kamau and Charlesworth 2005; Charlesworth et al. 2006; Hagenblad et al. 2006; Kamau et al. 2007)], it has not been clear to what extent these results also hold for wild Brassica species because the pattern of dominance between S haplotypes is not the same in Arabidopsis and Brassica (Prigoda et al. 2005). We are aware of only two studies of S-locus diversity in wild or naturalized Brassica species (Nou et al. 1993; Glémin et al. 2005), but neither of these studies has provided any DNA sequence data. Moreover, the sequence data that are available from Brassica crops (Fobis-Loisy et al. 2004; Fujimoto et al. 2006) may not be representative of wild Brassica species due to their history of domestication and artificial selection.

Here, we present the first study of DNA sequence data from both SRK and SCR in a sample from four natural populations of the wild species Brassica cretica. Our main aims are (i) to determine whether the amount and structure of genetic diversity at the S locus in B. cretica is consistent with current population genetics theory of the S locus and (ii) to investigate whether there are indications of historical recombination at the S locus in B. cretica.

MATERIALS AND METHODS

Study species:

B. cretica (2n = 18) is a wild perennial plant species belonging to the Brassicaceae family. It is a member of a group of allied Brassica species, including wild and cultivated B. oleracea (cabbage), all of which have the same basic type of genome (the Brassica C genome; Harberd 1972; Kianian and Quiros 1992; von Bothmer et al. 1995). B. cretica is found in the eastern Mediterranean region, mainly on Crete and the surrounding Aegean islands, where it grows in isolated populations in cliff systems and ravines (Snogerup et al. 1990). Populations on Crete show a high degree of genetic differentiation for a wide range of morphological and molecular characters (Widén et al. 2002; Edh et al. 2007), indicating a long history of genetic drift and low levels of gene flow among populations. B. cretica is self-incompatible, but individuals capable of setting seed after enforced self-pollination have been found in some of the studied populations (Rao et al. 2002a,b). Outcrossing nevertheless appears to be the dominant mating system in B. cretica as genotype frequencies within populations generally conform to Hardy–Weinberg expectations (Widén et al. 2002).

Plant material and DNA extraction:

Seeds from 29 to 43 maternal plants were collected in the field from each of four B. cretica populations on Crete (Gonies, Miliaradon, Moni Kapsa, and Topolia; Figure 1; see Widén et al. 2002 for exact coordinates) and grown in a greenhouse at Lund University. The original sample was regenerated by crossing one individual from each field-collected maternal family with a randomly chosen but distinct non-sib pollen donor from the same population. The final sample included a single offspring from each such cross. By ensuring that each individual transmits exactly two gametes (i.e., that the variance in offspring number is zero) and by avoiding selfing, this crossing scheme maximizes the effective population size of the field-collected material (Crow and Denniston 1988). In this study, we used 10 randomly chosen offspring individuals from each of the four populations. Approximately 100 mg leaf tissue was used for whole-genome DNA extraction with a DNeasy plant mini kit (Qiagen) according to the manufacturer's instructions.

Figure 1.—

Map of Crete showing the locations of the four B. cretica populations used in this study.

PCR amplification and sequencing:

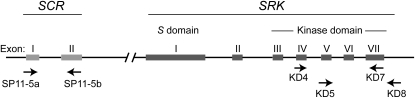
Approximately 1200 bp of the SRK kinase domain (exons 4–7) were amplified using primers specific for each of the two dominance classes (Park et al. 2002; Table 1; Figure 2). Separate amplification reactions were performed for each dominance class. The SRK kinase domain was chosen for amplification in this study to avoid cross-amplification of the SLG gene, which is very similar to the S domain of SRK (Stein et al. 1991). For SCR, primers SP11-5a and SP11-5b (Table 1; Figure 2) were designed from the S15 (class II) haplotype in B. oleracea (Shiba et al. 2004). These primers amplified ∼300 bp, including part of SCR exon 1 and most of exon 2 in B. cretica individuals having at least one class II haplotype at SRK. Despite several attempts to amplify fragments from class I haplotypes of the B. cretica SCR gene using primers designed from publicly available Brassica class I haplotype sequences, the large variability of the 3′-end of exon 2 together with, most likely, the very long distance between the two short exons in class I haplotypes, made it impossible to obtain amplification products from SCR class I haplotypes in B. cretica. The SRK amplification reactions contained 1.5 mm MgCl₂, 0.25 mm dNTP, 1.5 μm of each primer, and 0.3 units AmpliTaq Gold DNA polymerase (Applied Biosystems) in a 20-μl reaction volume. The cycling scheme included 95° for 8 min, 30 cycles of 94° for 1 min, 56° for 2 min, 72° for 2 min, and, finally, 72° for 7 min. For SCR, a 2-mm MgCl₂ concentration was used; otherwise, conditions were identical to the SRK amplification.

TABLE 1.

Primers used for amplification of the SRK and SCR genes

Name	Gene	Dominance class	Sequence (5′–3′)	Position	Reference
KD5	SRK	Class I	TGG AAG GAG AGA TTC GAC ATT AC	Exon 5	Park et al. (2002)
KD8	SRK	Class I	GCT TTC ATA TTA CCG GGC ATC GAT GA	Upstream exon 7	Park et al. (2002)
KD4	SRK	Class II	GAG GGC GAG AAG ATC TTA ATT	Exon 4	Park et al. (2002)
KD7	SRK	Class II	AAG AC(GT) ATC ATA TTA CCG AGC	Exon 7	Park et al. (2002)
SP11-5a	SCR	Class II	ATA CAC TAC TTG TGT TTC ATA TTT T	Exon 1	This study
SP11-5b	SCR	Class II	TGC AAC AGT AGC AAG TAA TCC	Exon 2	This study

Figure 2.—

Overview of the Brassicaceae SRK and SCR genes. Arrows indicate the positions of the primers used for amplification from B. cretica.

For SRK, PCR products from individuals having both class I and class II haplotypes (I/II heterozygotes) were sequenced directly whereas PCR products from individuals with either only class I or only class II alleles (apparent I/I or II/II homozygotes) were cloned in the pGEM-T vector system (Promega), and six clones per fragment were sequenced. In both cases, sequencing was done in both directions using the original PCR primers (Table 1). For SCR, all PCR products were cloned as described for SRK. Between two and six clones were sequenced in one direction using the SP11-5a primer. Sequencing was carried out at the SweGene Centre for Genomic Ecology, Lund University, Sweden.

The SCR and SRK sequences were assembled separately for each individual and edited in SeqMan (Lasergene6, DNAstar). Variable sites represented by at least two clones were considered true polymorphisms. Separate alignments for SCR and SRK were done with the ClustalW algorithm (Thompson et al. 1994) using BioEdit version 7.0.5.3 (Hall 1999). Manual adjustments were performed when required. Previously published S-locus sequences (supplemental Table 1) were included as reference sequences in the alignment to identify reading frames and intron–exon boundaries in the B. cretica genes.

Estimation of haplotype number:

The number of haplotypes and individual haplotype frequencies for each of the SRK and SCR genes were first computed directly from sequence data by defining identical sequences as a single haplotype. This procedure is likely to overestimate the number of functionally distinct haplotypes, since we can expect some segregating variation within functional haplotype lineages. Crossing experiments are the only means by which S-haplotype compatibility, and thereby functional identity, can be unequivocally determined. Exhaustive cross-compatibility information may, however, be impractical to produce even in samples of moderate size and especially when plants often take several years to reach reproductive maturity, as in B. cretica. In lieu of crossing data, we may nevertheless obtain a tentative estimate of the number of functionally distinct haplotypes by examining the distribution of the number of nucleotide differences per site (π) among all pairs of molecularly distinct haplotypes. Since haplotype copies carrying different SI specificities will have much longer coalescence times than copies with the same specificity, we expect a bimodal distribution of π (Vekemans and Slatkin 1994), with most haplotype pairs displaying either few or many nucleotide differences. We thus made an attempt to assign haplotypes initially identified on the basis of sequence identity to a smaller number of putative functional haplotypes according to sequence similarity by considering two haplotypes as belonging to the same functional type if their degree of sequence divergence was below a cutoff point located in the valley between the two modes of the observed distribution. Assignment was performed separately for each of two phylogenetically distinct subsets of SRK class I sequences (denoted class Ia and class Ib; Edh et al. 2009, accompanying article in this issue) for SRK class II sequences and for SCR class II sequences. From here on, we will refer to haplotypes defined by sequence identity as “haplotypes” and to putative functional haplotypes defined by sequence similarity as “functional haplotypes.”

Descriptive population genetics:

In all analyses, 80 SRK and 31 class II SCR haplotype copies were included in the B. cretica data set unless otherwise reported. As measures of genetic diversity, we computed the proportion of segregating sites (K) and the average number of nucleotide differences per site (π). For between-species comparisons, we calculated within-species π at synonymous (π_S) and nonsynonymous (π_N) sites of the SRK kinase domain for B. cretica and for B. rapa, B. oleracea, Raphanus sativus, and Arabidopsis lyrata using publicly available sequence data from the latter species (supplemental Table 1). The relative level of differentiation at SRK and SCR, respectively, among the four B. cretica populations was quantified by an overall F_ST (Wright 1951) using full haplotype data and the F_ST estimator of Hudson et al. (1992). All calculations of descriptive population genetics statistics were made in the DnaSP 4.10 computer program (Rozas et al. 2003).

Tests of frequency-dependent selection:

Two tests were performed to find evidence of frequency-dependent selection at the B. cretica S locus. First, Tajima's D statistic (Tajima 1989), which measures the deviation of the mutation frequency spectrum from a standard neutral model, was calculated for the total sample. As the samples originate from genetically differentiated subpopulations, the statistical significance of the hypothesis that D = 0 was evaluated by comparing the observed value to a null distribution of D derived from 1000 coalescence simulations of an island model using θ = 4Nμ estimated from the proportion of segregating sites (Watterson 1975) in the data and a migration rate of N_m = 0.315 (calculated from nuclear microsatellite data; Edh et al. 2007). Simulations were performed in the ms computer program (Hudson 2002). As a second test for selection, equilibrium frequencies of B. cretica functional haplotypes under frequency-dependent selection via male fitness (FDS_m; Wright 1939) and via both male and female fitness (FDS_m/f; “fecundity selection” sensu Vekemans et al. 1998) were derived under a Brassica-type dominance scheme (i.e., where class I haplotypes are dominant over class II haplotypes in pollen, but codominant in the stigma) using the general model of sporophytic SI developed by Billiard et al. (2007) and implemented in the NESSI software (Billiard 2008). Haplotype equilibrium frequencies were computed for each population separately and tested against observed frequencies by a likelihood-ratio test (Billiard et al. 2007).

Tests of recombination at the S locus:

Two methods were employed to find evidence of recombination within each of the two genes: First, all pairs of sites in which each site segregated for two nucleotides were searched for the presence of all four possible gametic configurations of nucleotides (the four-gamete test; Hudson and Kaplan 1985). Under the infinite-sites model, if all four configurations are found at a pair of sites, recombination must have occurred between the two sites. Second, the Pearson correlation coefficient, r, between the strength of linkage disequilibrium (LD) and nucleotide distance among pairs of polymorphic sites was calculated. Recombination is expected to lead to a negative correlation between LD and distance; i.e., LD should be stronger between sites closer together (Awadalla and Charlesworth 1999). LD was quantified by the r² statistic (Hill and Robertson 1968), and the probability that the correlation between LD and distance is r ≥ 0 (i.e., the test is one tailed) was evaluated by a Mantel test (e.g., Sokal and Rohlf 1995) with 1000 random permutations.

RESULTS

In the gene regions sequenced in this study, 67% of ∼1200 bp of the SRK kinase domain and 73% of ∼300 bp of the SCR gene composed the coding regions. For SRK, PCR products were obtained from all 40 individuals in the sample. For 8 individuals, only a single sequence type was found among the cloned amplification products; these individuals were considered homozygous. Three of the 8 SRK homozygotes were class I homoygotes. Formation of class I homozygotes should generally not be possible as class I haplotypes are dominant; however, some class I haplotypes in B. cretica show weak rejection and class I homozygote offspring can be found in crosses made under greenhouse conditions (Edh et al. 2008). For SCR, an amplification product was observed in all 23 individuals possessing one or two class II SRK haplotypes whereas no product was found in class I SRK homozygotes, as expected. A single class II SCR sequence type was found among the cloned amplification products from the 5 individuals assumed to be homozygous for a class II SRK sequence and also from those individuals that were class I/II SRK heterozygotes. When defining haplotypes by sequence identity, we found a total of 46 different SRK haplotypes and 6 different SCR class II haplotypes among the 40 individuals (Table 2). For the SRK gene, the number of distinct haplotypes in the total sample was considerably higher among class I haplotypes than among class II haplotypes (32 and 14 haplotypes, respectively; Table 2). The lower number of class II SCR haplotypes (6) compared to class II SRK haplotypes (14) is likely due to the shorter sequence length analyzed for the SCR gene.

TABLE 2.

Diversity at the SRK and SCR genes in B. cretica

Gene	Haplotype class	Population	Na	Nfb	Pc	Pfd	Ke	πf
SRK	All	All	46	21	0.022	0.046	0.111	0.187
		Gonies	14	10	0.071	0.100	0.140	0.178
		Miliaradon	12	9	0.083	0.100	0.122	0.148
		Moni Kapsa	13	8	0.077	0.111	0.115	0.166
		Topolia	11	9	0.091	0.111	0.121	0.169
SRK	Class I	All	32	18	0.019	0.032	0.098	0.090
		Gonies	10	8	0.075	0.100	0.090	0.100
		Miliaradon	10	7	0.085	0.106	0.075	0.087
		Moni Kapsa	6	5	0.058	0.093	0.082	0.083
		Topolia	7	7	0.064	0.064	0.089	0.090
SRK	Class II	All	14	3	0.028	0.129	0.011	0.016
		Gonies	4	2	0.050	0.100	0.015	0.018
		Miliaradon	2	2	0.075	0.075	0.023	0.023
		Moni Kapsa	7	3	0.093	0.217	0.012	0.018
		Topolia	4	2	0.138	0.275	0.013	0.016
SCR	Class II	All	6	3	0.065	0.129	0.058	0.091
		Gonies	3	2	0.067	0.100	0.091	0.112
		Miliaradon	2	2	0.075	0.075	0.095	0.094
		Moni Kapsa	3	3	0.217	0.217	0.073	0.110
		Topolia	2	2	0.275	0.275	0.050	0.064

^aNumber of haplotypes.

^bNumber of putative functional haplotypes.

^cAverage haplotype frequency.

^dAverage frequency of putative functional haplotypes.

^eProportion of segregating sites.

^fAverage number of pairwise nucleotide differences per site.

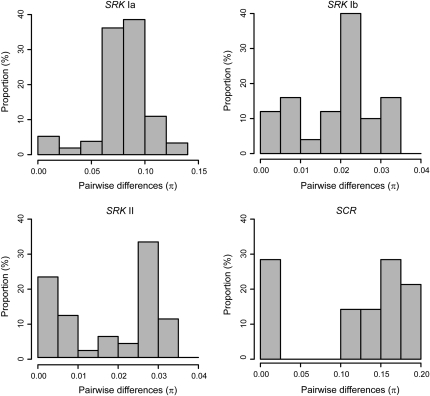
The number of nucleotide differences per site (π) among all pairs of haplotypes showed a bimodal distribution for each of the SRK class Ia, class Ib, and class II haplotypes, as well as for the SCR class II haplotypes (Figure 3). Defining π_l as the lower limit for π between different functional haplotypes—and using post-hoc values of π_l = 0.030, 0.010, 0.014, and 0.100 for the SRK classes Ia, Ib, and II and the SCR class II haplotypes, respectively—the number of putative functional haplotypes was inferred to be 14 for SRK class Ia, 4 for SRK class Ib, and 3 each for SRK class II and SCR class II. This gives a total of 21 functional haplotypes of which 18 were class I and 3 were class II (Table 2). Of all SRK and SCR haplotypes, 93% (43/46) and 67% (4/6), respectively, were restricted to a single population. The corresponding proportions for the functional haplotypes were 67% (14/21) for SRK and 33% (1/3) for SCR. The proportion of private haplotypes was higher for SRK class I (97% of all haplotypes and 72% of the functional haplotypes) than for class II haplotypes (86 and 33%, respectively).

Figure 3.—

Observed distribution of the number of nucleotide differences per site (π) among all pairs of molecularly distinct B. cretica haplotypes for each of the major groups of the SRK gene (classes Ia, Ib, and II) and for the SCR gene (class II haplotypes only). See Edh et al. (2009) for definition of class Ia and Ib haplotypes.

For all haplotypes, as well as for the functional haplotypes, SRK class I haplotypes had a lower average frequency compared to SRK class II haplotypes in the total data set (Table 2). Exceptions from the overall frequency distribution of class I and class II S haplotypes were found in two of the individual populations (Table 2). In the Gonies and Miliaradon populations, the average frequency of molecularly distinct haplotypes was higher for SRK class I haplotypes than for class II haplotypes (Table 2). In the Miliaradon population, functional haplotypes also had a higher average frequency among SRK class I haplotypes than among class II haplotypes whereas the frequencies of functional haplotypes were equal in the Gonies population (Table 2).

In the total sample, K and π for SRK were 0.111 and 0.187, respectively (Table 2). Overall, SRK class I haplotypes were more diverse than class II haplotypes with an almost 10-fold difference in K and a >5-fold difference in π between the two classes (Table 2). For the SCR gene, K and π were 0.058 and 0.091, respectively, among the class II haplotypes (Table 2). Diversity differences among populations were generally small (Table 2). Synonymous diversity (π_S) at the studied region of the SRK kinase domain of B. cretica was nearly three times higher than nonsynonymous diversity (π_N), a pattern that was similar in B. oleracea, B. rapa, R. sativus, and A. lyrata (Table 3). The degree of population differentiation was low for both S-locus genes with overall F_ST values of 0.145 for SRK and 0.075 for class II haplotypes of SCR.

TABLE 3.

Diversity at the SRK kinase domain in wild and cultivated Brassicaceae species

Species	No. of haplotypesa	πb	πSc	πNd
B. cretica	21e	0.138	0.267	0.088
B. oleracea	31	0.118	0.217	0.089
B. rapa	29	0.150	0.308	0.104
R. sativus	18	0.112	0.165	0.082
A. lyrata	12	0.205	0.448	0.085
A. halleri	22f	0.251	0.529	0.153

^aThe number of haplotypes used for comparison in this study; the total number of haplotypes identified in the different species may be higher.

^bAverage number of pairwise differences per site for all sites.

^cAverage number of pairwise differences per site for synonymous sites.

^dAverage number of pairwise differences per site for nonsynonymous sites.

^ePutative functional haplotypes.

^fData are from Castric and Vekemans (2007).

We found positive values of Tajima's D for both SRK (D = 2.348) and SCR (D = 2.218). The D-values were significantly positive (P < 0.05) both compared to a standard β-distribution (Tajima 1989) and compared to the null distribution simulated under a model of strong population structure (the upper limit of the 95% confidence interval for D was 2.118 for SRK and 1.755 for SCR). Observed frequencies of functional haplotypes did not deviate significantly from the expected equilibrium frequencies derived under two models of frequency-dependent selection (FDS_m and FDS_m/f) in any of the four populations (Table 4).

TABLE 4.

Observed and expected frequencies of putative functional S-locus haplotypes in four B. cretica populations under two models of frequency-dependent selection

	Population
Gonies			Miliaradon			Moni Kapsa			Topolia
Haplotypea	Obs	FDSm	FDSm/f	Obs	FDSm	FDSm/f	Obs	FDSm	FDSm/f	Obs	FDSm	FDSm/f
I-1	0.050	0.080	0.074	0.100	0.080	0.074	0.050	0.106	0.097	0.015	0.089	0.082
I-2										0.050	0.089	0.082
I-3	0.050	0.080	0.074							0.050	0.089	0.082
I-4										0.050	0.089	0.082
I-5	0.150	0.080	0.074
I-6	0.050	0.080	0.074
I-7				0.100	0.080	0.074
I-8				0.050	0.080	0.074
I-9	0.150	0.080	0.074
I-10				0.100	0.080	0.074
I-11							0.050	0.106	0.097
I-12										0.050	0.089	0.0882
I-13	0.15	0.080	0.074	0.200	0.080	0.074
I-14				0.100	0.080	0.074
I-15										0.050	0.089	0.082
I-16							0.050	0.106	0.097
I-17	0.050	0.080	0.074	0.100	0.080	0.074	0.100	0.106	0.097	0.050	0.089	0.082
I-18	0.150	0.150	0.074	0.100	0.080	0.074	0.100	0.106	0.097
II-1	0.100	0.180	0.203	0.100	0.180	0.203	0.250	0.157	0.172	0.150	0.190	0.213
II-2	0.100	0.180	0.203	0.050	0.180	0.203	0.250	0.157	0.172	0.400	0.190	0.213
II-3							0.150	0.157	0.172
Likelihood ratio		6.622	8.015		6.829	8.605		4.111	2.965		6.796	5.664
P-value		0.676	0.533		0.655	0.474		0.767	0.888		0.559	0.684

FDS_m and FDS_m/f give the expected equilibrium frequency for each haplotype under a model of frequency-dependent selection through male function (FDS_m) or through male and female functions (FDS_m/f); see Billiard et al. (2007) for details.

^aEach putative functional haplotype corresponds to a single or to a small number of closely related, molecularly distinct haplotypes; see materials and methods. Prefixes I and II denote class I and class II haplotypes, respectively. Obs, observed.

Recombination was detected by the four-gamete test among 20 pairs of sites at the SRK gene. However, for 14 of those pairs, three of the gametes were found among class I haplotypes whereas the fourth gamete could be found only among the class II haplotypes. Statistically significant levels of LD, judged by Fisher's exact test and corrected for multiple comparisons, were found among 21.4% (2682/12,561) and 41.5% (529/1275) of the total number of pairs of polymorphic sites for the SRK and the SCR class II data set, respectively. No significantly negative correlation was found between the level of LD for a pair of sites and the distance between the sites for either SRK (r = −0.015, P = 0.315) or SCR (r = 0.093, P = 0.987).

DISCUSSION

Identification of functional haplotypes—validity of the indirect approach:

In the absence of information from crossing experiments, we have relied on an indirect method, based on the distribution of the number of pairwise nucleotide differences per site (π) among all haplotypes, to infer the number of functionally distinct haplotypes in B. cretica. For each of the SRK class Ia, Ib, and II haplotypes, as well as for the SCR class II haplotypes, the distribution of π is bimodal with a certain proportion of haplotype pairs showing relatively little divergence, implying that they belong to the same functional type, and a larger proportion of more divergent haplotypes presumably corresponding to different functional types (Figure 3). While we have no experimental validation of our method for identifying functional haplotypes in B. cretica, the observation of a bimodal distribution of π fits very well both with theoretical expectations (Vekemans and Slatkin 1994; Schierup et al. 2000) and with empirical data from S-locus haplotypes with known recognition specificities (Awadalla and Charlesworth 1999; Kusaba et al. 2000; Miege et al. 2001; Charlesworth et al. 2003a; Sato et al. 2003; Takebayashi et al. 2003). Nevertheless, our method has at least two sources of bias: On the one hand, as restricted migration is expected to increase divergence within functional haplotypic groups (Schierup et al. 2000), observed intermediate divergence values (Figure 3) might represent functionally similar haplotype pairs in which the two members were sampled from different B. cretica populations. This might, in a strongly subdivided species such as B. cretica, lead to an overestimate of the true number of functionally different haplotypes. On the other hand, if some pairs of haplotypes have different recognition specificities despite showing a relatively high sequence similarity, as has been found in interspecific pairs of class II haplotypes in Brassica (Sato et al. 2006), we would rather underestimate the number of functional haplotypes. We cannot at present determine the precise extent to which these sources of bias have influenced the estimated number of functionally different haplotypes in the B. cretica sample, but we did not find any overrepresentation of cross-population haplotype pairs among pairs with intermediate divergence values for any of the four haplotype groups, a finding that suggests that our estimate, if anything, is too low rather than too high.

S-locus diversity in B. cretica:

Several features of the amount and structure of genetic diversity at the B. cretica S locus are in good agreement with theoretical models of S-locus population dynamics. First of all, we find a large number of haplotypes and very high levels of diversity at both SRK and SCR (Tables 2 and 3). High haplotype diversity is a distinct feature of the S locus in self-incompatible plant species (Lawrence 2000), and our findings are in line with previous results obtained from wild Brassica species: In two wild B. rapa populations, Nou et al. (1993) found 30 functionally distinct S haplotypes among 76 individuals. Comparatively fewer S haplotypes were reported from the wild Brassica insularis, in which Glémin et al. (2005) found only 24 haplotypes among 273 individuals from five natural populations. That study, however, was based on biochemical identification of S-locus haplotypes, a procedure which, as pointed out by the authors, left a relatively large number of haplotypes undetected and most likely underestimated the true number of haplotypes in B. insularis (Glémin et al. 2005).

While high S-locus haplotype and sequence diversity levels strongly indicate the action of frequency-dependent selection, this conclusion depends on comparisons with diversity levels at unlinked, neutral loci. Nevertheless, the sequence diversity estimates obtained from the B. cretica S-locus genes are nearly two orders of magnitude higher than the average level of diversity found genomewide in typical plant species (Zhang and Hewitt 2003). For SRK, the actual target of selection, however, is located outside the kinase domain in the region of the gene coding for the extracellular S domain, which is directly involved in pollen recognition (Kachroo et al. 2001). In the case of SCR, there are indications that selection may act on the entire coding region (Takebayashi et al. 2003). At any rate, the generally low rate of recombination at the S locus means that selection will affect synonymous polymorphisms in the region as a whole (e.g., Kamau and Charlesworth 2005; Castric and Vekemans 2007; Takuno et al. 2007). In fact, we find that the synonymous diversity level at the B. cretica SRK kinase domain (π_S = 0.267; Table 3) is comparable to, and even exceeds, the synonymous diversity found at the hypervariable region of the S domain in B. oleracea (π_S = 0.219; Sato et al. 2002). Further evidence for frequency-dependent selection at the B. cretica S locus comes from the positive values of Tajima's D for both SRK and SCR. In general, D becomes larger than zero under balancing (including frequency-dependent) selection and/or population subdivision. Differentiation at neutral genetic marker loci among B. cretica populations is, as mentioned above, extremely high for an outcrossing species, indicating pronounced population subdivision. Nevertheless, coalescent simulations showed that D for both S-locus genes in the B. cretica sample remained significantly larger than zero even when the effect of population subdivision was accounted for.

In this context, it is noteworthy that previous studies have found that levels of molecular diversity at the S locus is higher in Arabidopsis than in Brassica (Schierup et al. 2001; Charlesworth et al. 2003b; Castric and Vekemans 2007). Because S-locus sequence data, until now, have been available only from cultivated Brassica species, it would appear tempting to blame the lower diversity observed in Brassica on a bottleneck induced by domestication. However, as shown here, S-locus diversity in the wild B. cretica is at the same level as that in B. oleracea and B. rapa (and in R. sativus), and lower than that in A. lyrata or Arabidopsis halleri (Tables 2 and 3). Similar conclusions were reached in a phylogenetic study of the SRK and SCR genes in Brassica (Edh et al. 2009). Little is known about the history of domestication in Brassica, but it has been proposed that gene flow between wild and cultivated forms has occurred (von Bothmer et al. 1995). Thus, even though there are indications of a bottleneck in the Brassica lineage (Castric and Vekemans 2007), it most likely predates domestication of the cultivated species.

A second finding consistent with theoretical prediction concerns population differentiation at the S locus in B. cretica, which, with F_ST = 0.145 for SRK and F_ST = 0.075 for SCR class II, is strikingly low compared to the extraordinary degree of population differentiation observed at neutral loci in this species (F_ST = 0.600 and 0.617 for allozymes and microsatellites, respectively, calculated among the populations included in this study from Widén et al. 2002 and Edh et al. 2007). Similar results were obtained by Glémin et al. (2005) who found a lower population structure at the S locus than at microsatellite loci and a relatively high number of private haplotypes among Corsican populations of the wild B. insularis and by Kamau et al. (2007) and Ruggiero et al. (2008) who detected a significant decrease in F_ST at markers close to the S locus in A. lyrata and A. halleri, respectively. A lower S-locus population structure compared to neutral loci is expected to result from elevated heterozygosity within subpopulations and/or a higher effective migration rate for S haplotypes (Schierup et al. 2000). In B. cretica, the relatively high proportion of private functional haplotypes suggests that S-locus migration among the four B. cretica populations is limited, a conclusion supported by the near absence of gene flow observed among Cretan populations of B. cretica (Edh et al. 2007). Moreover, like Glémin et al. (2005), we found fewer private functional haplotypes among the SRK class II haplotypes (33%) than among the class I haplotypes (72%). The opposite situation would, in fact, be expected if effective migration is increased due to the selective advantage conferred to a new specificity when entering a population, since recessive haplotypes are “sheltered” and thus more prone to be lost by drift, whereas dominant haplotypes are always exposed to selection (Schierup et al. 2000). However, it must be kept in mind that the limited within-population sample sizes, together with the relatively low frequencies of class I alleles, may produce an upward bias in the estimated proportion of private haplotypes in this study.

Class I and II haplotypes in B. cretica:

Theoretical models approximating the dominance scheme in Brassica generally predict a situation with fewer recessive haplotypes at high frequency and a larger number of dominant haplotypes at lower frequencies (Schierup et al. 1997; Vekemans et al. 1998; Uyenoyama 2000; Billiard et al. 2007). Assuming that dominance relationships in B. cretica conform to the Brassica scheme, the data from B. cretica SRK support these expectations: Among the four B. cretica populations, class I haplotypes were more numerous and had a lower average frequency compared to class II haplotypes (Table 2). Similar findings have been reported from the wild B. insularis, in which 18 class I and only 2 class II haplotypes were found (Glémin et al. 2005), as well as from cultivars of B. oleracea (Ockendon 1982; Ruffio-Châble et al. 1999). More explicit tests of haplotype frequencies (Billiard et al. 2007) revealed that, under the assumption of equilibrium, observed frequencies of class I and class II haplotypes in each of the four B. cretica populations conformed to frequencies expected under frequency-dependent selection (Table 4): Both a classical model with frequency-dependent selection acting only through the male function (the FDS_m model; Wright 1939), and a more elaborate model where selection acts both through male and female functions (the FDS_m/f model; Vekemans et al. 1998), could explain the observed haplotype frequencies in the B. cretica populations (Table 4).

One of the B. cretica populations (Miliaradon) showed a deviation from the expected pattern of a lower average frequency of class I haplotypes compared to class II haplotypes (Table 2). Recognizing that this may be an effect of limited sample size, factors other than frequency-dependent selection can influence equilibrium S-haplotype frequencies in natural populations. For example, uneven segregation can cause certain haplotypes to attain an equilibrium frequency higher than expected from their level of dominance, as has been observed in natural populations of A. lyrata (Bechsgaard et al. 2004; Schierup et al. 2006). Significant S-locus segregation distortion has also been detected in B. cretica (Edh et al. 2008); in that study, however, it was found that a recessive class II haplotype showed preferential transmission over class I haplotypes in class I/II heterozygotes. Thus, there is currently no evidence that the higher average frequency of dominant class I haplotypes observed in the Miliaradon population has been caused by a selective advantage conferred to class I haplotypes by uneven segregation. A second possibility is that dominance relationships in B. cretica differ from that generally observed in Brassica. For example, in Sinapis, a genus closely related to Brassica, the dominance hierarchy is not the same as in Brassica (Stevens and Kay 1989). Even though this possibility cannot be excluded, the very close relationship between B. oleracea and the Mediterranean wild Brassica species, manifest by their near complete interfertility (Snogerup et al. 1990), makes it most likely that dominance relationships in B. cretica are similar to those in B. oleracea. Furthermore, the frequencies of the two “deviant” putatively functional class II haplotypes in the Miliaradon population did not differ significantly from the respective expected equilibrium frequencies derived according to Billiard et al. (2007) under a Brassica-type dominance scheme (data not shown; see also below). Hence, the lower-than-expected frequency of functional class II haplotypes in this particular population is presumably due to sampling error and/or genetic drift.

An interesting observation concerns the presence of two, and in one case three, functional class II haplotypes in each of the four B. cretica populations (Table 2). Similar results have been obtained from the wild B. insularis in which four of five populations examined harbored two distinct class II haplotypes (Glémin et al. 2005; however, whether the B. insularis haplotypes have different functional specificities is not clear). Under a Brassica dominance scheme, theoretical models predict that the most recessive class (i.e., class II) cannot simultaneously maintain exactly two haplotypes in a deterministic setting, since even the slightest perturbation causes the loss of one of the haplotypes (Uyenoyama 2000). However, Billiard et al. (2007) showed that coexistence of two haplotypes in the most recessive class is possible when there is selection on female fecundity, i.e., when a limited supply of compatible mates reduces the total seed set (Vekemans et al. 1998). Such selection, for example, may arise when individual density or pollinator activity is low, conditions that seem typical of many B. cretica populations (A. Ceplitis, personal observation).

A final note should be made on the possibility that the two pylogenetically distinct groups of class I haplotypes, classes Ia and Ib, constitute two distinct dominance classes. There is some evidence that class Ia haplotypes might be dominant to class Ib haplotypes (see Edh et al. 2009). Moreover, in the sample as a whole, class Ia haplotypes were more numerous than class Ib haplotypes (14 vs. 4), but had a lower average frequency (0.030 vs. 0.047), a situation that would be expected if class Ib haplotypes had a level of dominance intermediate between class Ia and II haplotypes. We therefore tested a model, again with the method of Billiard et al. (2007), with three dominance classes, assuming codominance in the stigma and a class Ia > class Ib >class II dominance hierarchy in the pollen. Observed haplotype frequencies, in fact, did fit expected frequencies under this dominance scheme, for both the FDS_m and the FDS_m/f models. For each model, however, likelihood differences between a two-class and three-class dominance scheme were small and insignificant. Thus, even though there are some indications that class Ia and Ib haplotypes form two separate dominance classes, this issue cannot be resolved with the data currently available (see Edh et al. 2009 for further discussion).

Recombination at the S locus in B. cretica:

Several lines of evidence indicate a very low level of recombination at the S locus in B. cretica: First, we were able to amplify class II SCR haplotypes only in individuals having at least one class II SRK haplotype. This suggests that each class II SCR haplotype is part of the same S haplotype as a class II SRK haplotype. Individuals who shared a certain SRK haplotype did indeed also share a common SCR haplotype. Similar observations from A. lyrata involving shared haplotypes at the SRK and the linked Aly8 locus have been taken as evidence for the absence of recombination in the S-locus region of that species (Hagenblad et al. 2006). More explicit tests of recombination at the B. cretica S locus lead to similar conclusions. Thus, even though all four possible gametic configurations were initially found among 20 pairs of sites in the B. cretica SRK gene, indicating several recombination events, a closer examination revealed that 14 of these site pairs had three of the gamete types among the class I haplotypes with the fourth type found among the class II haplotypes. Considering the extensive molecular divergence between haplotypes from dominance classes I and II in Brassica, it is likely that multiple substitutions have occurred at these sites, mimicking the effect of recombination. Indeed, multiple substitutions occur at ∼18% of all sites in the part of B. cretica SRK studied here. Six pairs of sites may thus represent true recombination events in the SRK data set. The four-gamete test revealed no incidence of recombination at the SCR gene. Also, the level of LD did not decrease with distance in either SRK or SCR as would have been expected in the presence of recombination. By contrast, in a study of sequence variation at the Brassica SLG gene, which is also located at the S locus, Awadalla and Charlesworth (1999) found a statistically significant decline of LD with distance. The SLG gene, however, is not directly involved in the SI response (Cabrillac et al. 1999; Kusaba et al. 2001; Silva et al. 2001), and it is possible that recombination can happen within the SLG gene without disrupting the match between female and male specificities. Takuno et al. (2007) found phylogenetic evidence for recombination at the kinase domain of SRK and at other S-locus genes outside SCR and the SRK S domain of B. oleracea and B. rapa. A phylogenetic analysis of sequence data from the SRK kinase domain and SCR in B. cretica detected a weak signal of a potential recombination event between these two regions (Edh et al. 2009). Together, these observations suggest that recombination at the S locus, if it happens, affects regions not directly involved in the determination of SI specificity.

Conclusions:

In the S-locus sequence data collected from four natural populations of the wild plant species B. cretica, we found many of the signatures expected from a genomic region under frequency-dependent selection: a high level of diversity with a significantly positive Tajima's D, a weak population structure compared to neutral markers, and a limited incidence of recombination at the SRK and SCR genes. Furthermore, even though we could infer the number of functional S haplotypes only by an indirect method, the haplotype frequency data indicate that frequency-dependent selection is the main selective force and that other factors, such as unequal segregation, are likely to play only a minor role in affecting the S-haplotype frequencies in the four investigated B. cretica populations.