Reaction mechanism of the ε subunit of E. coli DNA polymerase III: Insights into active site metal coordination and catalytically significant residues

Abstract

The 28kDa ε subunit of Escherichia coli DNA polymerase III is the exonucleotidic proofreader responsible for editing polymerase insertion errors. Here, we study the mechanism by which ε carries out the exonuclease activity. We performed quantum mechanics/molecular mechanics calculations on the N–terminal domain containing the exonuclease activity. Both the free–ε and a complex, ε bound to a θ homolog (HOT), were studied. For the ε–HOT complex, Mg²⁺ or Mn²⁺ were investigated as the essential divalent metal cofactors, while only Mg²⁺ was used for free–ε. In all calculations, a water molecule bound to the catalytic metal acts as the nucleophile for the hydrolysis of the phosphate bond. Initially, a direct proton transfer to H162 is observed. Subsequently, the nucleophilic attack takes place, followed by a second proton transfer to E14. Our results show that the reaction catalyzed with Mn²⁺ is faster than with Mg²⁺, in agreement with experiment. In addition, the ε–HOT complex shows a slightly lower energy barrier compared to free–ε. In all cases the catalytic metal is observed to be penta–coordinated. Charge and frontier orbital analyses suggest that charge transfer may stabilize the penta–coordination. Energy decomposition analysis to study the contribution of each residue to catalysis suggests that there are several important residues. Among these, H98, D103, D129 and D146 have been implicated in catalysis by mutagenesis studies. Some of these residues were found to be structurally conserved on human TREX1, the exonuclease domains from E. coli DNA–Pol I, and the DNA polymerase of bacteriophage RB69.

Introduction

The fidelity of DNA replication remains a subject of considerable interest because of its relevance to a large part of biology.¹ Studies of DNA replication of Escherichia coli (E. coli) suggest that the in vivo substitution error rate for the replication machinery is around 10⁻¹⁰.² The high rate of fidelity is obtained by at least three activities that operate serially: base selection, exonucleolytic proofreading and postreplicative mismatch repair. Of these three, the exonucleolytic proofreading activity has been reported to have an error discrimination in the range of 40–400 fold.²

The replication of DNA in E. coli is performed by DNA polymerase III holoenzyme (Pol III). This is a large protein complex that contains 10 distinct subunits.³ In this complex there are two catalytic cores composed of three subunits named α, ε and θ, bound in this linear order. The ε subunit has been shown to be responsible for the proofreading exonuclease activity in Pol III. ⁴

The exonuclease activity removes newly incorporated nucleotides, preferentially excising incorrect nucleotides.⁵ The 186 residue N–terminal domain of ε (ε 186) has been shown to contain the exonuclease active site.⁶ The reaction catalyzed by ε is proposed to involve either one⁷ or two divalent metal ions.⁸ For the two metal mechanism, the catalytic metal (Me1), is proposed to facilitate the formation of an attacking hydroxide ion. This hydroxide performs a nucleophilic attack on the α phosphate of the nucleotide base to be excised. The second metal is termed the nucleotide binding metal (Me2). Recent experimental studies have shown that the reaction of ε in vitro is faster with Mn²⁺ than with Mg²⁺.⁸

Association of ε with θ has been proposed to promote exonuclease activity.^9,10 In addition, it has recently been shown that a homolog of theta (HOT) from bacteriophage P1 can substitute for θ and has been proposed to stabilize ε.^11,12 On the other hand, experimental studies on free–ε, free–ε 186 and ε 186–θ with 5′–p–nitrophenyl ester of TMP (pNP–TMP) suggest that there is only a minor change in k_cat and K_m between free–ε 186 and the ε 186–θ complex for this substrate.⁸

Recently, the X–ray crystal structures of free–ε 186 and ε 186–HOT have been reported.^13,14 These structures show that the active site is composed of three residues, D12, E14 and D167, that bind to two divalent metals (Mn²⁺). In addition, H162 hydrogen bonds to a water that is coordinated to the catalytic metal. Based on structural and experimental data, Hamdan et al. ⁸ have proposed a mechanism for the exonuclease activity of ε (see Figure 1). In this mechanism H162 deprotonates the nucleophilic water coordinated to the catalytic metal, which attacks the α phosphate. Based on the coordination of the catalytic metal, they suggest that E14 could also serve as a proton acceptor from the nucleophilic water. These authors also point out that the coordination sphere of the catalytic metal only contains 5 ligands.¹³

Figure 1.

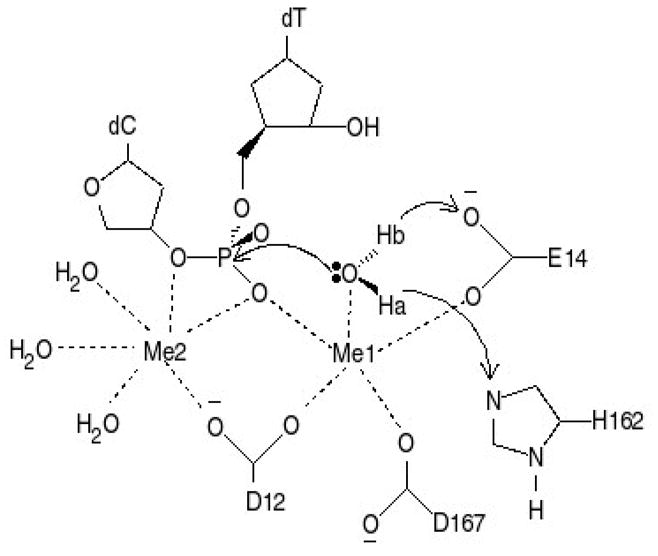
Proposed reaction mechanism for ε.⁸ Catalytic metal is labeled Me1 and nucleotide binding metal is labeled Me2. The coordination sphere for the metals is denoted with dashed lines. Ha is abstracted first, followed by the nucleophilic attack and subsequent transfer of Hb.

We have previously investigated the mechanism of human DNA polymerase γ with Mg²⁺ and Mn²⁺ using QM/MM calculations.¹⁵ Here, we employ the reported ε 186–HOT structure¹⁴ as the starting point for molecular dynamics (MD)^16–18 and QM/MM^19–24 calculations to further our theoretical investigation of the mechanisms of the replication machinery. The catalytic mechanism of ε 186 is studied with three sets of calculations: ε 186–HOT with either Mg²⁺ or Mn²⁺ as the divalent cation to investigate possible differences in mechanisms based on metals, their coordination, and metal preference. The third comprises free–ε 186 with Mg²⁺ to investigate the role of HOT on the reaction. The penta–coordination observed in the X–ray crystal structure is maintained in our calculations during catalysis for all three structures. Additionally, energy decomposition analysis to determine the role of residues from the MM environment suggests several amino acids around the active site have a catalytic effect. Some of these residues are shown to be structurally conserved with other exonucleases.

Methods

The initial structure for all calculations was taken from a recent X–ray crystal structure of the ε 186–HOT complex with Mn²⁺ in the active site.¹⁴ There are two molecules of ε 186 in the asymmetric unit. The relevant one for the present study has a disordered loop just before the catalytically important H162 is located. This loop was modeled based on a previous structure reported by Hamdan et al.¹³ The chosen substrate for the reaction is a ss–DNA trinucleotide (dA–dC–dT). This is based on experiments by Miller and Perrino in which they showed that at least three nucleotides are required to achieve the maximum excision rate.²⁵ The substrate was docked in the active site using the position of the TMP from the X–ray crystal structure as a guide. Hydrogens and solvation water box were added using the XLEaP program in AMBER9.²⁶ For this step, the active site metals were replaced by Mg²⁺ ions. The resulting systems were minimized and equilibrated using molecular dynamics (MD) simulations for 2 ns using the PMEMD module in AMBER9.²⁶ In the original crystal structure only 5 ligands are observed coordinating the catalytic metal, therefore, a harmonic constraint was included during the equilibration to maintain this coordination (see main text and supplementary information for details).

After equilibration, the final configuration was modified by retaining all atoms in the protein and all water molecules within 30 Å of the catalytic metal. This resulted in a total of 18158 atoms for the ε 186–HOT system. In all cases the QM subsystem was chosen to include both active site metals, side chains of D12, E14, H162, D167, the middle dC nucleotide (excluding C5′ and the phosphate group), a part of the dT nucleotide (phosphate bond and C5′) and five water molecules that complete the coordination spheres of the metals, for a total of 82 QM atoms including 6 boundary atoms (Cα of D12, D167 H162 and E14; C5′ of dC and C4′ of dT).

In the case of the ε 186–HOT system, two sets of calculations were performed with either Mg2+ or Mn²⁺ as active site metals. For the free–ε 186 system, only Mg²⁺ was considered. For the system with Mn²⁺ as the catalytic metal, all calculations were performed assuming a high spin state with all d electrons on both Mn atoms unpaired (see Supplementary Information). ^27–29 The QM subsystem was treated at the B3LYP level^30,31 with a combined basis set where the 6–31G* basis was used for all reactive atoms: OD1 from E14, Nε from H162, O in one of the waters coordinating the nucleotide binding metal, O in the nucleophilic water and both Mg²⁺. For the O3′, O5′ and P atoms (involved in the phosphate bond breaking and forming) the 6–31+G* basis was used. All other (non–reactive) QM atoms were represented with 3–21G. The Mn²⁺ atoms were treated with the LANL2DZ pseudopotential. The remaining atoms were included in the MM subsystem and treated with the parm99 force field.²⁶ We have previously used these methods to study DNA polymerase λ and have observed that the combined basis sets give similar results to those calculated with unmixed (larger) basis sets.¹⁵ After the QM/MM optimization of the ε 186–HOT(Mg²⁺), the free–ε 186 system was prepared by replacing HOT with solvent and re–equilibrating. This resulted in a total of 18043 atoms for free–ε 186.

The product structures for all systems (ε 186–HOT Mg²⁺, Mn²⁺ and free–ε 186 Mg²⁺) were produced in silico from the reactant structure and subjected to QM/MM optimization. Path optimizations were performed following a procedure used previously for the study of the reaction mechanism of DNA polymerase λ.¹⁵ The optimized end–points were employed for the reaction path calculation with the quadratic string method (QSM).³² This is a “chain–of–replica” method where the path is represented by a discrete number of structures.^22,33–36 In this method the intermediate structures are obtained by a linear interpolation between the end points and all structures are optimized to the minimum energy path simultaneously. This results in a highly efficient and unbiased optimization of the path. The initial QSM paths consist of 10 points including end–points and were iteratively optimized with constrained MM optimization.^36–38 After the initial paths were converged, the highest energy points were optimized to the closest TS with the quadratic synchronous transit (QST3) method.^39,40 Following the TS optimization the paths between the critical points were calculated with either QSM or reaction coordinate driving (RCD) (see supplementary materials).

All MD simulations were carried out with the AMBER9 suite of programs.²⁶ QM/MM calculations were carried out with modified versions of Gaussian03 and TINKER.^41,42 The QM/MM optimizations were performed with an iterative method.^43,44 using the pseudobond model for all boundary atoms.^45,46 All QM calculations were performed using an effective Hamiltonian (electrostatic embedding).^43,44

Results and Discussion

Initial structure determination

MD simulations were performed for both ε 186–HOT and free–ε 186 with Mg²⁺. As mentioned above, the X–ray crystal structures show that the catalytic metal is penta–coordinated, with E14 forming a single bond to the metal and a hydrogen bond to the nucleophilic water. Initially, the systems were unconstrained during the MD simulations. However, this results in a distortion of the active site because E14 forms a second bond to the catalytic Mg (chelating orientation) and loses the hydrogen bond to the water molecule. This results in an increased inter–metal distance. The binding of the substrate is disrupted. The resulting structure contains a differently penta–coordinated catalytic metal that is not conducive to chemistry. This change in coordination may be due to limitations in the classical force field.

A further attempt to regain the hexa–coordination involved considering the carbonyl backbone oxygen from T8 as the sixth ligand. This atom is located approximately 3.5 Å from the catalytic metal in the X–ray structure. However, after MD this atom increases the inter–metal distance to around 4 Å. Furthermore, its inclusion in the coordination shell would involve the displacement of other axial ligands. This would possibly disrupt the orientation of the substrate or the position of E14 resulting in a structure not conducive to catalysis. One last possibility would be for a water molecule to occupy the place of the carbonyl. However, although the carbonyl backbone from T8 moves slightly away, there is still not enough room for a water molecule to fill a sixth coordination. Therefore, in order to retain a catalytically competent structure, the MD equilibrations were repeated including a constraint to enforce the single bond of E14 to the catalytic metal.

Subsequently, QM/MM optimizations were carried out with all constraints removed, based on the equilibrated systems. The final rmsd of the backbone atoms between the X–ray and optimized structures are 0.4, 0.6 and 0.8 Å for the ε 186–HOT(Mg²⁺), ε 186–HOT(Mn²⁺) and free–ε 186 respectively. The rmsd of all heavy atoms in the active site between the X–ray and the optimized systems is 0.2 Å for the ε 186–HOT structures and 0.1 Å for free–ε 186.

The QM/MM optimizations do not contain any constraints. In all cases, the five ligands around the catalytic metals were observed to be maintained after the optimizations (see Figure 2 and Table S1 in supplementary materials for coordination distances). The final calculated structures are consistent with the penta–coordinated structures observed experimentally.^13,14 The observed geometry for the catalytic metals is distorted trigonal bipyramidal with angles around 110–120° for the axial and around 170° for the equatorial ligands. This is not unexpected for the Mn²⁺ system since Mn²⁺ is known to support this type of coordination, however, this is not common for Mg²⁺. To investigate whether the Mg²⁺ structures are indeed penta–coordinated, the unconstrained MD structure of ε 186–HOT (with E14 chelating the catalytic metal) was used for QM/MM optimizations. Three optimizations were performed with different MM environments (taken from different snapshots of the MD simulation) for the reactant and product structures and in all cases the optimized structures reverted to the single E14–Mg²⁺(catalytic) bond.

Figure 2.

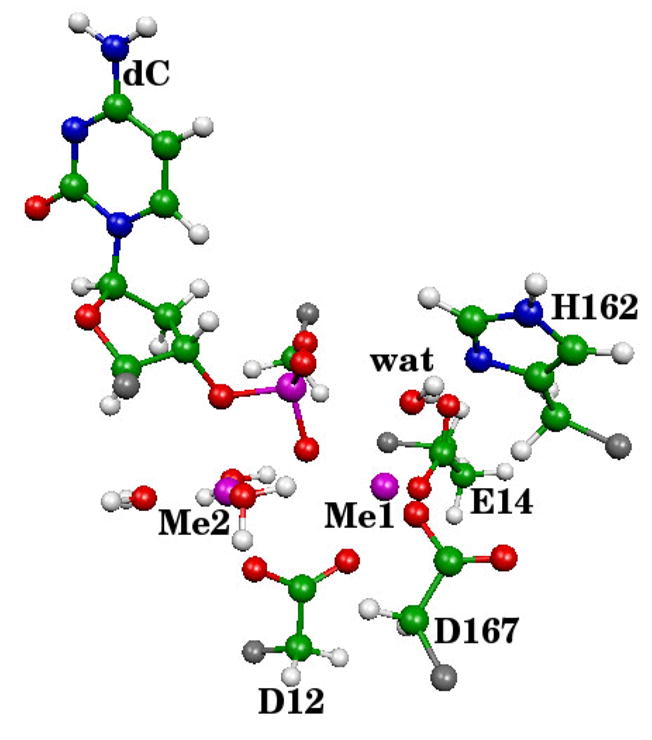
Atoms included in the QM region. Note, that most of the dT nucleotide is not present. Nucleophilic water is labeled “wat” and pseudobonds are shown in grey.

Analysis of the charges on the metals and the location of the highest occupied molecular orbital (HOMO) helps understand the observed penta–coordination for the Mg–containing structures. A significant charge transfer to the metals is observed, with charges of 1.3 and 1.5 for the catalytic and nucleotide binding metals respectively, calculated with Merz–Kollman fitting.⁴⁷ These charges are approximately 0.2–0.4 units less positive than charges calculated by the same procedure for the equivalent metals (both hexa–coordinated) in our previous study of DNA polymerase λ.¹⁵ In addition, as seen in Figure 3, the HOMO is centered almost exclusively on the catalytic metal, D12, D167, H162 and the nucleophilic water. This is also observed for free–ε 186 (results not shown). Furthermore, cluster calculations on penta– and hexa–hydrated Mg²⁺ give charges close to 2+ on the ion. Taken together, this suggests that the HOMO could provide a channel that enables the catalytic metal to attract charge density from the ligands. This charge transfer helps stabilize the unusual coordination sphere.

Figure 3.

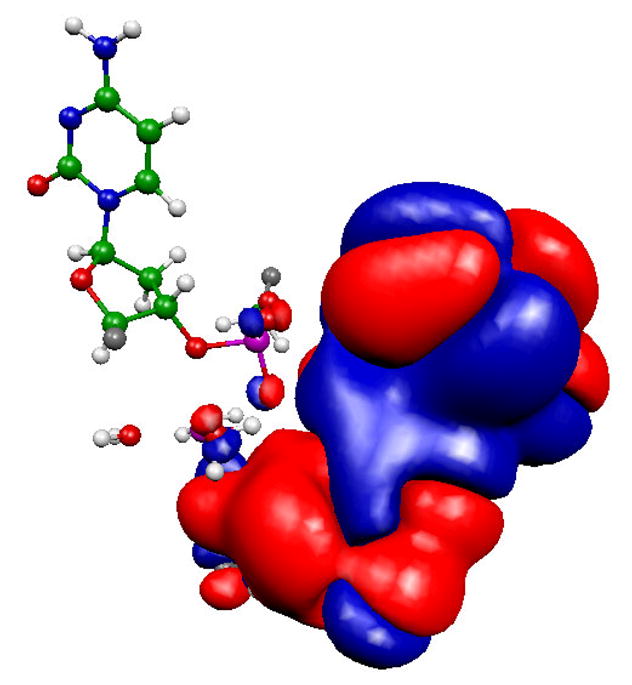
HOMO for the optimized ε 186–HOT (Mg²⁺) reactant structure (QM subsystem only), cutoff = 10⁻³ au. Orbital colors denote sign of the respective lobe (red = positive). Note that the orientation is the same as in Figure 2.

Furthermore, penta–coordinated Mg is not exclusive to ε. This coordination has been reported in inorganic compounds^48,49 and other enzymes such as the Klenow fragment of DNA polymerase I,⁵⁰ ribonuclease H (RNaseH),^51,52 GTPase Ffh⁵³ and tryptophanyl–tRNA synthetase.^54–56 Additionally, in a recent simulation of the related RNAseH reaction mechanism this coordination has also been reported.⁵⁷ Interestingly, in the case of RNAseH, the penta–coordinated Mg²⁺ is the nucleotide binding and not the catalytic ion.^51,52,57 These observations, together with our results, point to a penta–coordinated metal regardless of whether there is a Mn or Mg in the active site. Note that this only corresponds to the catalytic step, and the octahedral geometry could be restored after catalysis or nucleotide release.

Catalytic mechanism

Based on the optimized structures, the corresponding product structures were generated for all three systems. These structures were employed for the reaction path optimizations as explained in the methods section. In the case of the initial guess for the product (see Methods section), only the transfer of the proton to H162 and nucleophilic attack were initially considered. Interestingly however, the second proton transfered spontaneously to E14 during the optimization procedure to give a lower energy structure.

Figure 4 shows the superposition of the critical points along the reaction path for the ε 186–HOT with Mg²⁺ and Mn²⁺ (similar superpositions for free–ε 186 are given in the supplementary materials). As can be observed, the reactant structures for both metals are very similar. In all cases, the reaction begins by an initial proton transfer from the nucleophilic water to H162 to form the nucleophilic hydroxyl. Subsequently, the phosphodiester is attacked by the hydroxyl forming a pentavalent phosphorane transition state (TS) structure resulting in an inversion of configuration at the P atom (see ). Finally, after the phosphate bond has been broken, a second proton transfer takes place to E14.

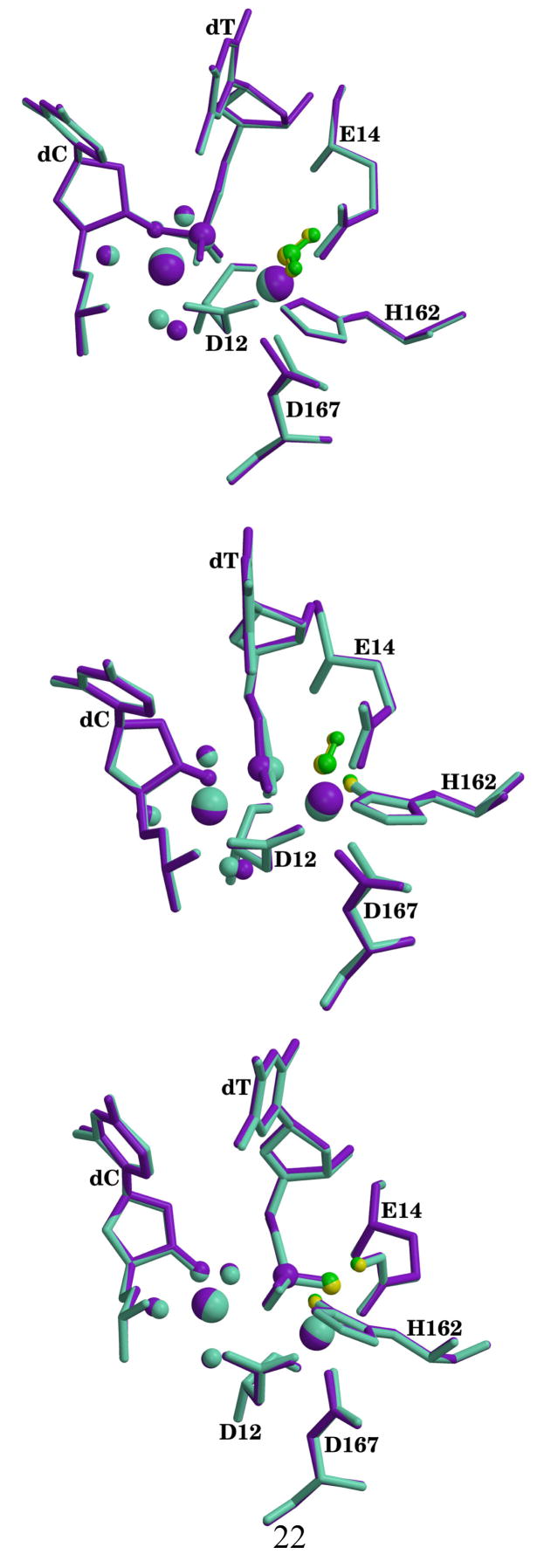
Figure 4.

Superposition of active sites for the calculated reactants (top), transition states (middle) and products (bottom) from the ε 186–HOT structures. Mg²⁺ structure is shown in aquamarine with nucleophilic water in yellow and Mn²⁺ structure is shown in purple with nucleophilic water in green. The nucleophilic waters are shown in ball and sticks while divalent metals are rendered as large spheres. Electrophilic phosphate, O3′ on dC and waters coordinating the nucleotide binding metal are shown as spheres. Hydrogen atoms except for the ones on the nucleophilic waters have been omitted for clarity.

This reaction mechanism is consistent with the proposal by Hamdan et al.⁸ Note that the second proton transfer proposed by Hamdan et al. and observed in the present work only occurs in the second leg of the reaction after the phosphate bond has been broken. Additionally, the configuration inversion has been observed experimentally for the analogous reaction catalyzed by RNaseH.⁵⁸

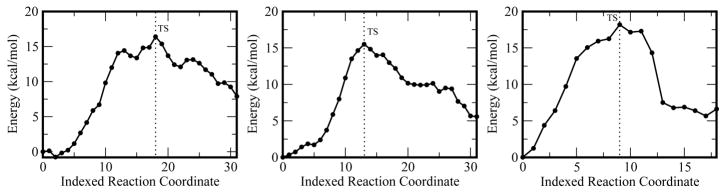
The reaction profiles in Figure 5 show that the reactions for all systems (including both metals) proceed in an approximately similar manner. In the case of ε 186–HOT(Mg²⁺) two shoulders are observed flanking the TS, these correspond to the proton transfers. However, the putative intermediates are not stable structures along the potential energy surface (PES). This is due to the fact that when these structures were optimized they returned either to the reactant or product minima. In the case of ε 186–HOT(Mn²⁺) and free–ε 186 only one TS is observed. In all cases the TS structures were optimized with QST3 and a single imaginary frequency was obtained. The calculated reaction barriers are 16.4, 15.4 and 18.2 kcal/mol for the ε 186–HOT(Mg²⁺), ε 186–HOT(Mn²⁺ ), and free–ε 186(Mg²⁺) catalyzed reactions respectively.

Figure 5.

Calculated reaction paths for the ε –186–HOT Mg²⁺(left), ε 186–HOT Mn²⁺ (middle) and free–ε 186 Mg²⁺ (right) catalyzed reactions.

Experimental results for free–ε 186 have been reported for the hydrolysis of 5′–p–nitrophenyl ester of TMP (pNP–TMP) with both Mg²⁺ and Mn²⁺.⁸ The experimental k_cat of 19 min⁻¹ and 293 min⁻¹ for Mg²⁺ and Mn²⁺ correspond to barriers of 13.5 and 11.9 kcal/mol respectively. The rate constant for ε 186–θ (Mn²⁺) has been reported in the same work to be 215 min⁻¹, corresponding to a barrier of 12.1 kcal/mol. Furthermore, pre–steady state kinetic results for the degradation of a 10–mer single stranded DNA (ss–DNA) with Mg²⁺ by ε give a k_cat of 280 s⁻¹ which corresponds to a barrier of 14.4 kcal/mol.²⁵ These barriers are obtained via the transition state formula (TST) $k_{\mathit{cat}}=\frac{k_{b}T}{h}\mathit{exp}\left(-\frac{\mathrm{\Delta }{G}^{‡}}{RT}\right)$.⁵⁹ In addition, these barriers assume that the free energy of activation ΔG^‡ corresponds to the energy barrier.

Experimental estimates for the energy barriers point to a lower value for Mn²⁺ compared to Mg²⁺ in the free–ε case.⁸ This is similar to the results obtained for the ε 186–HOT complex in our calculations, which show a slight preference of Mn²⁺ over Mg²⁺. Note that the experimental substrate is different from our simulations which may account for some of the differences. Additionally, as pointed out by Hamdan et al.,⁸ p–nitrophenol is a stronger acid than the 3′–OH group of a nucleotide chain and the breaking of the phosphate bond should be easier. Indeed, experimental results for pNP–TMP and ss–DNA (dT₁₀) show that the barrier for the former is around 1 kcal/mol lower than the latter.^8,25 Moreover, our calculated barriers correspond to potential energies and provide an upper bound to the corresponding free energy barriers.^44,60 Therefore, it is possible that a free energy calculation would lower the value of the barriers closer to the experimental estimate.

Our results suggest that the presence of HOT lowers the energy barrier by ≈2 kcal/mol. On the other hand, experimental results have reported that the addition of θ to ε have little measurable effect on the exonuclease activity.¹⁰ Also, free–ε 186 has been shown to have a slightly lower energy barrier (0.2 kcal/mol) than ε 186–θ with pNP–TMP and Mn²⁺.⁸ Again, this discrepancy could be a result of the difference in substrates, as pNP–TMP is a better leaving group than the O3′ of a nucleotide chain.

Another possible mechanism involves a hydroxyl ion bound to the catalytic metal instead of a water molecule. For this case, when the reactant structure with the hydroxide ion was optimized the structure immediately turned to the product. That is, the reaction immediately takes place in ε without a stable reactant structure (results not shown). Therefore, based on these results this reaction scheme is not viable for ε. This is not surprising considering what is observed in Figs. and, where the transition state corresponds to the hydroxyl ion already performing the nucleophilic attack. In contrast De Vivo et al. have shown that the hydroxyl mechanism is much lower in energy for RNaseH.⁵⁷ In addition, as mentioned above, their structures show that the nucleotide binding metal is the penta–coordinated one not the catalytic one as in the case of ε.

Finally, as observed in, although the main chemical step has taken place, the calculated products in the reaction mechanism are 5–7 kcal/mol higher than the reactants. One possible reason for this difference is the fact that the O3′ on the dC is not protonated immediately after the breaking of the phosphate bond. To investigate whether this is one of the reasons for the higher energy, a second product with a deprotonated H162 and protonated dC–O3′ was optimized for ε 186–HOT(Mg²⁺) and free–ε 186(Mg²⁺). Indeed, the relative energy of these products is found to be around 2 kcal/mol for ε 186–HOT(Mg²⁺) and -1 kcal/mol for free–ε 186.

There are several possible mechanisms to transfer a proton to the O3′ including transfer from solvent,⁵⁷ from H162 or from E14. Two such mechanisms were tested to investigate possible paths. Both mechanisms involve the transfer of the proton located on H162 that was originally on the nucleophilic water. The only direct way to transfer this proton to the O3′ is through an oxygen on the phosphate of the excised nucleotide (dT). In both cases the calculated barriers are over 30 kcal/mol, which rule out these paths (see supplementary materials).

Residue analysis

Further insights into the catalytic mechanism of ε can be obtained by understanding the role of individual residues in catalysis. This can be achieved by decomposing the non–bonded inter-molecular interaction energy between the MM environment and the QM region into contributions per residue.^61,62 This “breakdown” is only obtained in an approximate manner and therefore, is only qualitative. In this analysis the differences in interaction energies are calculated between individual residues and the QM subsystem when the system goes from reactant to TS. A negative contribution refers to a stabilizing contribution to the TS and the opposite applies to a positive one. We consider a residue to provide a significant contribution to (de)stabilization if the interaction is greater than 1 kcal/mol, see supplementary materials for details.

Figure 6 shows the residues that have a significant effect on catalysis for all three systems investigated. The Coulomb and Van der Waals decomposition analyses show that most of the stabilization is provided by the enzyme with some contribution from the solvent (see supplementary materials). In all cases the non–bonded interactions are electrostatic with no significant contributions from the Van der Waals component.

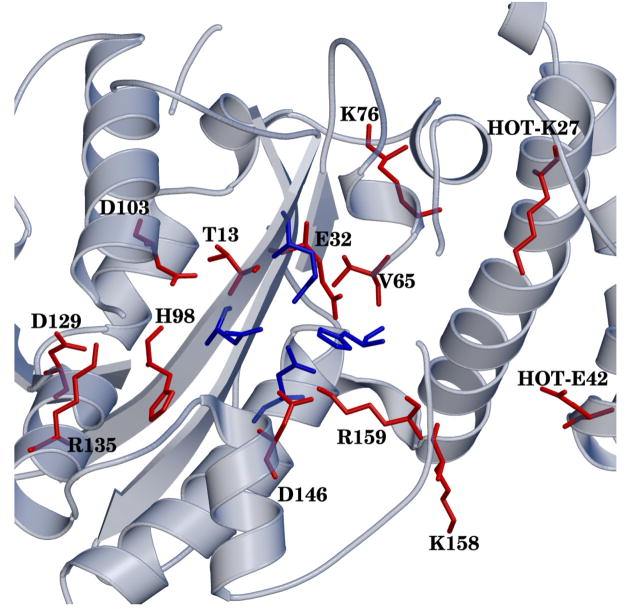
Figure 6.

Positions of residues (red) that have a significant (de)stabilization to the TS during catalysis for any of the three systems. Metal binding residues and H162 are shown in blue. Hydrogens have been omitted for clarity.

In particular, the residues that contribute to catalysis in all systems include V65, H98, D103, D129, D146 and R159. In addition, for the ε 166–HOT(Mg²⁺ system two residues from HOT are observed to have significant effects: K27 and E42. Overall the effect of the enzyme environment is stabilizing. In the case of HOT, the overall effect is slightly stabilizing when all contributions from HOT are taken into account.

Of the residues observed from the decomposition, H98, D103, D129 and D146 have been studied experimentally. H98 has been shown to be a moderate dominant mutator and is well conserved among gram–negative and gram–positive organisms.⁶³ This residue shows a stabilizing contribution in all systems of over −1:5 kcal/mol. D146 is reported to be a weak mutator,⁶⁴ this residue is observed to have a destabilizing contribution in our results. The last two aspartates, D103 and D129 show strong mutator effects.⁶⁴ In our analysis, these two residues provide large stabilizations to the TS, around −5 and −2 kcal/mol for D103 and D129 respectively. To our knowledge, none of the remaining residues from the decomposition analysis have been studied experimentally and could be targets for mutagenesis studies.

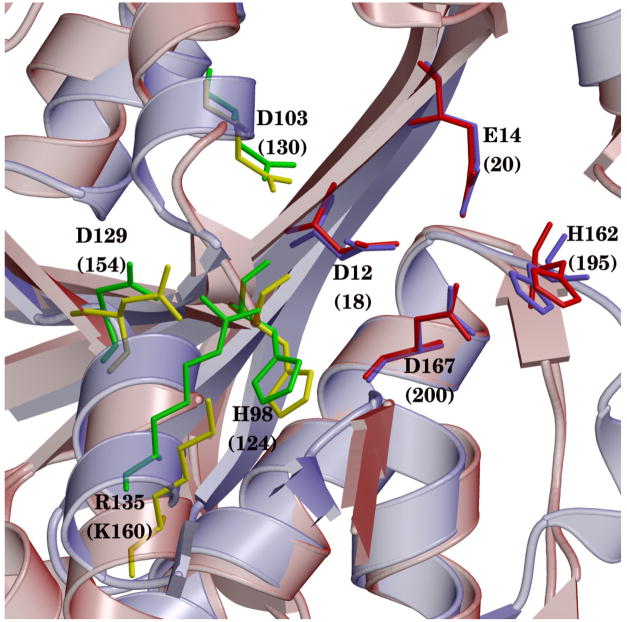
Finally, three structural alignments have been carried out to further understand the catalytic role of these residues. The alignments compare the X–ray structure of ε with a monomer of human TREX1 (see Figure 7),⁶⁵ the exonuclease domain (Klenow fragment) of DNA polymerase I from E. coli⁶⁶ and the exonuclease domain of the DNA polymerase from bacteriophage RB69⁶⁷ (see Figs. S9 and S10 in supplementary materials). In all cases, the sequence homology is very low (below 30%), therefore, the structural alignments were performed by superposing the "DED" catalytic triad in the active site cores. Previous studies have shown that both DNA and RNA exonucleases have a conserved “DEDD” domain

Figure 7.

Structural alignment comparing residues obtained from the decomposition analysis in ε 186–HOT (light blue) superposed with the exonuclease domain (red) of TREX1 (red). Residues from energy decomposition for ε 186–HOT are shown in green; structurally homologous residues for TREX1 are shown in yellow. Metal binding residues (and H162) for ε 186–HOT are shown in light blue; structurally homologous residues for TREX1 are shown in red.

As can be seen from Figs. 7, S9 and S10, there are several residues in the alignments that appear structurally conserved among the exonucleases. In particular, two homologous aspartates are conserved both in structure and position between all three exonucleases. These residues are D103 and D129 in ε which correspond to D130 and D154 in TREX1; D424 and D441 in the Klenow fragment; and D222 and D272 in RB69. This is a striking similarity taking into account that these residues are located in the “second” shell around the active site and also the low sequence homology among the exonuclease domains. D103 appears to be conserved among exoribonuclease superfamilies based on sequence alignments and is part of the “DEDD” domain.⁷⁰ As mentioned above, alteration of D103 and D129 have been reported to show strong mutator effects experimentally in ε.⁶⁴ Furthermore, D222 in RB69, equivalent to D103 in ε, has been shown to be catalytically important.⁷⁶ In this case, the mutation of D222 to Ala in RB69 produces a reduction in catalytic activity.

Conclusions

The reaction mechanism for the E. coli exonuclease domain of Pol-III, the ε subunit, has been determined by means of QM/MM calculations. Three systems were investigated; ε 186–HOT with Mg²⁺ or Mn²⁺ and free–ε 186 with Mg²⁺. In all cases a water molecule bound to the catalytic metal acts as the nucleophile for the hydrolysis of the nucleotide. This water is activated by the catalytic metal, which is found to be penta–coordinated. This coordination results in a polarization of the water molecule that promotes the required deprotonation. Initially, a proton from this water is transferred to H162, followed by the phosphate bond breaking. A second proton transfer to E14 is observed on the downward (second) leg of the reaction. A single transition state is obtained for all systems which corresponds to the phosphate bond breaking step. This mechanism is consistent with a previously proposed schemes. Our results suggest that ε is slightly more active with Mn²⁺ than with Mg²⁺ in qualitative agreement with experiment. A slightly lower activation barrier for ε 186–HOT compared with free–ε 186 is observed in our calculations. However, experiments with pNP–TMP point to free–ε having a slightly lower barrier.

To explain individual residue contributions to catalysis, an energy decomposition analysis was carried out using the minimized reactant and transition state coordinates. This analysis suggests that there are several residues that can have a significant influence on the TS barrier. Among the residues highlighted from the energy decomposition analysis, H98, D103, D129 and D146 have been studied experimentally in ε and shown to influence catalysis. The remaining residues could be potentially interesting targets for mutagenesis experiments. Structural superposition with the related TREX1 and exonuclease domains of Klenow fragment and RB69 shows that several residues implicated in the catalysis by energy decomposition analysis surrounding the active site are structurally conserved among these exonucleases. In particular, D103 and D129, which are strong mutators in ε when altered, are structurally conserved among ε, TREX1 and the exonuclease domains of Klenow and RB69.

Supplementary Material

1_si_001. Supporting Information Available.

Detailed methods for initial structure, QM/MM structure optimization and path optimization are given, as well as metal coordination distances for critical points, free–ε structures, 2nd step QSM paths residue analysis for all residues and waters, structural alignments for Klenow and RB69 and complete citation for references.^41,73,74 This material is available free of charge via the internet at http://pubs.acs.org.