Effect of Synaptic Connectivity on Long-Range Synchronization of Fast Cortical Oscillations

Abstract

Cortical gamma oscillations in the 20- to 80-Hz range are associated with attentiveness and sensory perception and have strong connections to both cognitive processing and temporal binding of sensory stimuli. These gamma oscillations become synchronized within a few milliseconds over distances spanning a few millimeters in spite of synaptic delays. In this study using in vivo recordings and large-scale cortical network models, we reveal a critical role played by the network geometry in achieving precise long-range synchronization in the gamma frequency band. Our results indicate that the presence of many independent synaptic pathways in a two-dimensional network facilitate precise phase synchronization of fast gamma band oscillations with nearly zero phase delays between remote network sites. These findings predict a common mechanism of precise oscillatory synchronization in neuronal networks.

INTRODUCTION

The waking state of the brain is characterized by a low correlation of spike discharges across neighboring neurons (Noda and Adey 1970) and the predominance of frequencies in the beta (15–30 Hz) and gamma (30–80 Hz) ranges (Bressler 1990; Freeman 1991). Studies have indicated that cortical gamma activity is associated with attentiveness (Bouyer et al. 1981; Rougeul-Buser et al. 1975), focused arousal (Sheer 1989), sensory perception (Gray et al. 1989), working memory (Axmacher et al. 2007), and movement (Murthy and Fetz 1992; Pfurtscheller and Neuper 1992). It has been proposed that synchronization in the gamma frequency range is related to cognitive processing and to the temporal binding of sensory stimuli (Joliot et al. 1994; Llinas and Ribary 1993; Singer and Gray 1995). Gamma oscillations can also become synchronized between neighboring cortical sites during deep anesthesia, natural slow-wave, and REM sleep (Steriade et al. 1996a,b).

Gamma oscillations induced by visual stimuli become synchronized over distances of a few millimeters with nearly zero phase lag (Gray et al. 1989). Precise long-range synchronization in the gamma (20–80 Hz) frequency range was found between primary and associational visual cortices (Engel et al. 1991; Frien et al. 1994), between prefrontal and parietal cortical areas (Desmedt and Tomberg 1994), and between the cortex and the thalamus (Steriade et al. 1996b). Synchronized gamma band activity has been observed in the visual cortex of anesthetized cats (Eckhorn et al. 1988; Gray et al. 1989; Steriade et al. 1996a,b), and awake monkeys (Eckhorn et al. 1993; Kreiter and Singer 1992). These results support the hypothesis that gamma synchronization plays a role in the binding of spatially distributed features and inter-area cooperation (Gray et al. 1989). However, the limited speed of spike propagation along axonal collaterals (e.g., 0.15–0.55 m/s for pyramidal cells) (Murakoshi et al. 1993), in addition to synaptic delays, leads to the question: what are the mechanisms that can provide precise long-range synchronization of gamma activity? Based on simulations of conductance-based network models organized in 1D structures, it has been proposed that interneuron spike doublets are critical for the long-range synchrony of gamma oscillations in the hippocampal CA1 region (Traub et al. 1996b). In other studies, the synchrony of gamma oscillations was simulated using models with random and sparse (Brunel and Wang 2003) or all-to-all connectivity (Borgers et al. 2005).

The cerebral cortex is a three-dimensional structure. Ideally a cortical network model should simulate this structure by explicitly modeling lateral two-dimensional connectivity as well as cortical depth (layer structure). However, a majority of computational studies, including those dealing with neural oscillations and synchrony, simulate the cortex in only one dimension. In this study, we report how the network geometry and connectivity can critically influence the synchronization properties of fast cortical oscillations. Using in vivo recordings from anesthetized cats, we show the existence of precise gamma range synchronization in isolated cortical slabs (Timofeev et al. 2000), thus excluding extracortical mechanisms of synchronization. Based on large-scale cortical network simulations, we show how the existence of many independent synaptic pathways between remote sites in a two-dimensional network facilitates precise long-range synchronization of cortical gamma oscillations. Although explicit representation of cortical depth may be lacking, our model includes lateral connectivity in two dimensions. Using this model, we show that neuronal synchrony and oscillations cannot be properly described using a 1D approach.

METHODS

In vivo recordings

Multi-site field potential recordings were performed on slabs and surrounding tissue in four cats anesthetized with ketamine-xylazine (intramuscular injection of 10–15 mg/kg ketamine and 2–3 mg/kg xylazine). Additional doses of anesthesia were administrated when the electroencephalograph (EEG) showed changes toward activating patterns. The slabs were prepared as described in Timofeev et al. (2000). Monopolar field potential recordings were performed with a tungsten electrode (1 MΩ inserted to a depth of 1 mm) with neck muscles referenced. All recordings were obtained within 3–10 h from the isolation of the slab. Ten to 15 active periods were analyzed in each of four cats. Electrographic activities were amplified (×1,000), band-pass filtered (0.1–1,000 Hz), and digitally stored using a Vision data-acquisition system (Nicolet, WI). Analysis of the recorded activity was done with IgorPro software (Lake Oswego, OR). All experimental procedures used in this study were performed in accordance with the Canadian guidelines for animal care and were approved by the Committee for Animal Care of Laval University.

Network model

We studied two-layer, one- and two-dimensional network models of up to 640 × 640 (409,600 total) excitatory pyramidal (PY) neurons and 320 × 320 (102,400 total) inhibitory interneurons (INs). The ratio of PY neurons to INs was kept at 4:1. Each neuron in the network received synaptic inputs from all the neurons of given type located within a certain radius. This set of presynaptic neurons formed a synaptic footprint. We also tested models with different PY to IN ratios (e.g., equal number of PY and IN neurons), and we found the network dynamics to be qualitatively similar as long as the individual synapses were scaled to keep the total inhibitory drive to PY neurons unchanged. The radius of the synaptic footprint was 8 for neurons with AMPA-mediated PY-PY synapses [∼200 presynaptic neurons in 2-dimensional (2D) model with circular connectivity], 8 for neurons with AMPA mediated PY-IN synapses (∼200 presynaptic neurons in 2D model with circular connectivity) and 4 for neurons with GABA_A-mediated IN-PY synapses (∼50 presynaptic neurons in 2D model with circular connectivity). We have also tested models with a larger synaptic footprint (up to ∼1,200 excitatory and ∼300 inhibitory inputs in 2D model) and with different footprints of excitatory and inhibitory connections. No difference was found in the model dynamics, provided the individual synaptic connections were scaled to keep the total synaptic input the same.

Individual neuron models

To allow for a detailed analysis of oscillatory dynamics in large-scale network simulations, we used a reduced neuron model described by difference equations (map) (Bazhenov et al. 2005; Rulkov 2002; Rulkov et al. 2004). The model is described by the following equations:

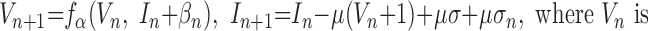the membrane voltage, I_n is a slow dynamical variable describing the effects of slow conductances, and n is a discrete time step (∼0.5 ms). Slow temporal evolution of I_n was achieved by using small values of the parameter μ ≪ 1. Input variables β_n and σ_n were used to incorporate external current I_n^ext (e.g., synaptic input): β_n = β^eI_n^ext, σ_n = σ^eI_n^ext. The nonlinearity f_α(V, I) was designed in the form of a piece-wise continuous function

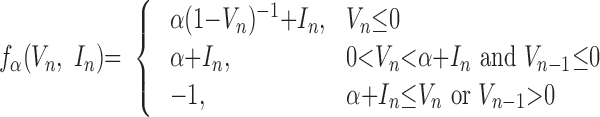To convert the dimensionless “membrane potential” V to the physiological membrane potential V_ph, the following equation was applied: V_ph = V*50–15 [mV].

This model, despite its intrinsic low dimensionality, produces a rich repertoire of dynamics and is able to mimic the dynamics of Hodgkin-Huxley type neurons both at the single-cell level and in the context of network dynamics (Bazhenov et al. 2005; Rulkov et al. 2004). Two different cell types were implemented: a fast spiking neuron for inhibitory INs and a regular spiking neuron for excitatory PY neurons. To simulate a regular-spiking neuron, the model parameters were set at α = 3.65, σ = 0.09, μ = 0.0005, β^e = 0.03, σ^e = 1. The model parameter σ sets the resting potential of the neuron and, therefore, its state with respect to spiking threshold. The neuron was silent for σ < 0.085. For σ = 0.09, the isolated model neuron spiked at a low frequency of 6–7 Hz. When σ was increased to σ = 0.17 to model the effect of external depolarizing input, the firing frequency increased to ∼20 Hz (Fig. 1A). To ensure variability of the resting potentials across a population of neurons, σ was picked randomly from a uniform distribution with 0.1% variability.

FIG. 1.

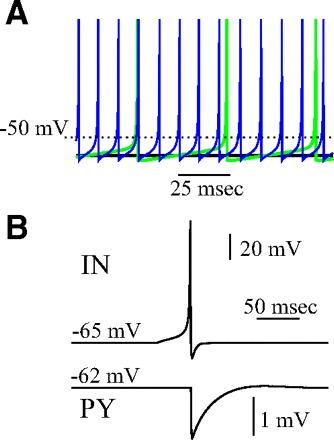
Model properties. A: steady-state response pattern of excitatory (PY) neuron for 3 different levels of the resting potential. Black, σ = 0.06; green, σ = 0.09; blue, σ = 0.17. B: inhibitory postsynaptic potential (IPSP) in the postsynaptic PY neuron (bottom) triggered by a spike in presynaptic interneuron (IN) (top).

In response to a rectangular pulse, a fast-spiking neuron fires without spike frequency adaptation, but it shows a noticeable hyperpolarization induced by each spike. To capture this hyperpolarization effect, the slow subsystem in the model used for a regular-spiking neuron (see preceding text) was substituted with an equation for the hyperpolarizing current I_n^hp generated by the action of each spike as follows

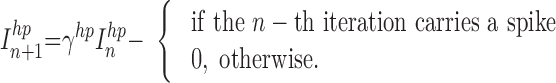The parameter, γ^hp, controls the duration, τ^hp ∼ (1 − γ^hp)⁻¹, and the parameter, g^hp, controls the amplitude of the hyperpolarization current. The model of the fast spiking neuron in this study can be described by the following equation V_n+1 = f(V_n, I^rest + β^hpI_n^hp + β^eI_n^ext), where I^rest is a constant defining the resting state of the model, and I_n^hp is a new slow variable. These equations with parameter values α = 3.8, I^rest = −2.9, β^hp = 0.5, γ^hp = 0.6, g^hp = 0.1, β^e = 0.1, were used to describe the dynamics of fast spiking INs.

To model synaptic interconnections, we used conventional first-order kinetic models of synaptic conductances rewritten in the form of difference equations

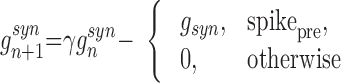and the synaptic current computed as

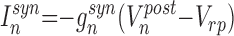where g_syn is the strength of synaptic coupling, and indices pre and post stand for the pre- and postsynaptic variables, respectively. The first condition, spike_pre, is satisfied when presynaptic spikes are generated. Parameter γ controls the relaxation rate of synaptic conductance after a presynaptic spike is received (0 ≤ γ < 1). Parameter V_rp defines the reversal potential and, therefore the type of synapse: excitatory (V_rp = 0) or inhibitory (V_rp = −1.1). A single inhibitory postsynaptic potential (IPSP) produced in a postsynaptic excitatory cell by a spike in a presynaptic IN is shown in Fig. 1B. To model a synaptic delay, the implementation of condition spike_pre may be delayed from the moment of the presynaptic spike generation by the number of iterations corresponding to the delay time.

Synaptic weights of individual synapses were always scaled by the number of synapses to allow a direct comparison between one- and 2D network models. Maximal conductances (in dimensionless units) (see Rulkov et al. 2004) denoting the total excitation and inhibition received by a given cell were selected from the following range: GABA_A (IN–PY) = 0–0.0025, AMPA (PY–IN) = 0–0.005, and AMPA (PY–PY) = 0–0.0001. There is no simple way to associate these dimensionless units with maximal synaptic conductances measured experimentally. However, the range of values we used corresponded to the physiological range [e.g., IPSP size in the excitatory neuron was ∼2 mV for GABA_A (IN–PY) = 0.007, Fig. 1B]. An external DC input of constant amplitude was applied to all PY neurons within a selected region to trigger network gamma oscillations. In some simulations, to test the stability of the synchronized states, these external stimuli were applied to different neurons at different times (with different delays that were drawn from a uniform distribution [0, 50 ms]).

Frequency analysis

To characterize the changes in network oscillation frequency, we calculated the power spectrum of the “field potential” (averaged activity) generated by the membrane potentials of individual PY and IN cells and plotted them as a function of network parameters. The frequency of network oscillations was evaluated as the frequency of peak harmonics in the field potential power spectrum.

Cross-correlation analysis

To characterize the synchrony of gamma oscillations, the local field potentials were calculated by averaging the activity of all PY neurons within N × N [for 2-dimensional (2D) network] or N × 1 [for 1-dimensional (1D) network] groups covering the entire population of neurons receiving external input. Cross-correlations were calculated for all pairs of field potentials as

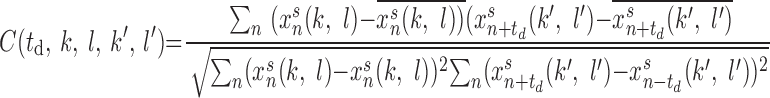where (k, l) and (k′, l′) are the indices of cells located at the center of each group, x_n^s(k, l) is local field potential at site (k, l), 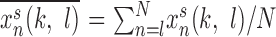, and N is the number of data points of x_n^s used for the analysis. The distribution of time lags to the main peak of the cross-correlation function was plotted for different parameter values. To study the role of network geometry, the normalized probability density distribution of time lags to the main peak of the cross-correlation function was plotted for each network size on a logarithmic scale.

RESULTS

Gamma oscillation during active cortical states in vivo

To exclude extracortical mechanisms of long-range gamma synchronization, we analyzed spontaneous activity in vivo in small, surgically isolated islands of neocortex (slabs) (Timofeev et al. 2000). Neuronal activity in slabs consisted of brief active periods separated by long periods of silence (≤60 s in duration). Each active period (reminiscent of UP states) (Steriade et al. 1993; Wilson and Kawaguchi 1996) appeared spontaneously, lasted a few hundred milliseconds, and appeared as fast neuronal oscillations in the beta-gamma frequency range superimposed over large depolarizing potentials. The synchronization properties of these states were studied using multi-electrode field potential recordings from isolated slabs (Fig. 2A). Two observations became evident from our analysis: 1) in all four recorded animals, the onset of an active state propagates from the initiation site such that the entire network becomes involved in the oscillation within 50–70 ms (58 ± 3 ms, Fig. 2, B and C, top). The initiation site was never found to be <2 mm from the border of the slab. 2) Fast network oscillations that occurred during the active state did not propagate and were synchronized across the slab (Fig. 2, B and C, bottom). During individual cycles, the maximum of the cross-correlation function could be delayed by 1–2 ms. When electrode 5 was used as a reference (Fig. 2) in all four slabs, the maximum delays never exceeded 2 ms with 0.27 ± 0.67 ms between electrodes 5 and 8 (distance 4.5 mm) and 0.22 ± 0.53 ms between electrodes 5 and 3 (distance 3.0 mm). The first finding clearly demonstrates that synaptic delays substantially limit the propagation velocity of activity onset within the slab. It takes ≥50 ms for an active state initiated near the center of the network to reach its boundaries (Fig. 2C, top). However, synaptic delays did not affect the synchronization of fast cortical oscillations (Fig. 2C, bottom). These results are in agreement with previous findings of precise synchronization of gamma activity (Desmedt and Tomberg 1994; Eckhorn et al. 1988, 1993; Engel et al. 1991; Frien et al. 1994; Gray et al. 1989; Kreiter and Singer 1992) and raise a fundamental question: how is long-range gamma synchrony maintained in spite of the presence of synaptic delays and limited axonal propagation speed?

FIG. 2.

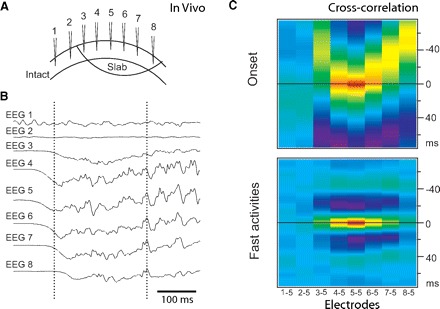
Fast gamma oscillation in vivo. Patterns of activity onset and synchronization during active states in a neocortical slab 6 × 10 mm. A: the position of recording electrodes. Distance between electrodes ∼1.5 mm. B: the active state started from around electrode 5 (see left vertical line) and propagated to other electrodes. C, top: cross-correlation of the onset of active states (electrode 5 is the reference, analyzed fragments from −100 to +100 ms of electrode 5 half-amplitude). Bottom: cross-correlation during active states (electrode 5 is the reference, analyzed fragments from +200 to +400 ms of electrode 5 half-amplitude). Note the absence of correlation between activities in the slab (electrodes 3–8) and outside the slab (electrodes 1 and 2).

Fast gamma oscillations in the network model

To study long-range cortical synchronization, we constructed a cortical network model including layers of excitatory PY neurons (regular spiking type, representing a layer of PY neurons) and inhibitory INs (fast-spiking type, representing local INs; Fig. 3A). Only IN-PY and PY-IN connections were included in this particular network model. However, PY-PY connections were introduced in other simulations (Fig. 4Ai). Neuronal dynamics was simulated using reduced models implemented with difference equations (Bazhenov et al. 2005; Rulkov 2002; Rulkov et al. 2004). This approach allowed for efficient large-scale simulations, while still preserving realistic firing patterns (Rulkov et al. 2004) and intrinsic resonance properties (Bazhenov et al. 2005) of different types of neurons. The synaptic connection between any two interconnected neurons was modeled with a single synapse. Therefore the maximal strength of a synapse (synaptic weight) in the model characterized the number of synaptic contacts between two neurons. In the cortex, synaptic connections involved in a feedback inhibitory loop (PY-IN-PY) occur with much higher probability than synaptic connections between excitatory neurons (PY-PY) (Yoshimura and Callaway 2005). Therefore in our model, lateral excitatory connections between PY neurons were implemented with lower strength (see methods) than those responsible for feedback inhibition (Thomson and Morris 2002; Thomson et al. 2002). A time delay between presynaptic action potentials and the postsynaptic response was introduced to all synapses in the model to simulate both synaptic and conduction delays. Long-range PY-PY connections have not been included in our model to ensure that any two remote network sites are separated by multiple synaptic connections and therefore multiple delays.

FIG. 3.

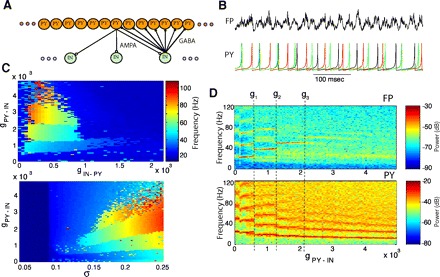
Effect of synaptic coupling on fast network model oscillations. A: structure of synaptic connectivity in a cortical network model including 512 PY neurons and 128 INs. AMPA, excitatory synapses; GABA, inhibitory synapses. B: field potential (top) and representative PY neurons (bottom) during gamma oscillations. C, top: frequency of field potential oscillations is plotted as a function of inhibitory feedback: excitatory PY → IN and inhibitory IN → PY coupling. Bottom: frequency of field potential oscillations is plotted as a function of excitatory PY → IN coupling and resting potential (σ): σ = 0.09 corresponds to the onset of spiking; σ = 0.17 corresponds to ∼20-Hz sustained firing rate. D: spectrograms representing the power spectrum of the field (top) and PY (bottom) oscillations as a function of PY → IN coupling for a fixed value of IN → PY coupling (g = 0.0007).

FIG. 4.

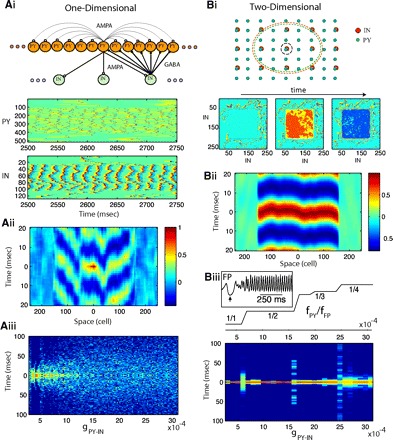
Synchrony of oscillations in 1- and 2-dimensional (2D) network models. Group of PY neurons [with indexes (107,406) for 1D or (107,406) × (107,406) for 2D] was entrained to gamma oscillations by DC input. A: 1D model: 512 PY neurons and 128 INs. Ai, top: connectivity structure. Bottom: spatiotemporal patterns of activity in a 1D network (g_IN-PY = 0.0007, g_PY-IN = 0.0015). Spikes are shown in red; dark blue indicates hyperpolarization. Aii: cross-correlation of the local field potential (averaged over 20 PY neurons) between the center of the network and remote sites. Aiii: time lags to the main peak of the cross-correlation function between local field potentials in different spatial locations (see methods) plotted for various strengths of PY-IN coupling. Color indicates number of time lags within 1 ms bins (dark blue indicates no lags). B: 2D model: 512 × 512 PY neurons and 256 × 256 INs. Bi, top: connectivity structure. Red and green dashed circuits illustrate radii of PY-IN and IN-PY connectivity for a single PY and IN neurons (shown with black circuit). Bottom: snapshots of activity in the IN population during global coherent gamma oscillation at times t₀, t₀+5 ms, t₀+8 ms. Bii: cross-correlation of the local field potential (averaged over 20 × 20 PY neurons) between the center of the network and remote sites along the x axis. Biii, top: the staircase structure of resonance modes (f_PY/f_FP ) is shown as a function of PY-IN coupling. Bottom: same as in Fig. 3Aiii but for a 2D network. Inset: field potential oscillations near the onset of DC input (↑).

In the absence of synaptic coupling, the neurons in the model were depolarized above the spiking threshold and fired randomly. To study the effect of synaptic feedback inhibition on the network synchronization properties, the local (within a footprint, see methods) excitatory (AMPA-type) connections from PY neurons to INs and inhibitory (GABA_A–type) connections from INs to PY neurons were introduced in a 1D network model (chain of neurons). As a result, the network activity became synchronized, with manifested effect of ∼40-Hz mean field oscillations (Fig. 3B). A sufficient level of depolarization was required so the neurons could maintain gamma range network oscillations. The mean field (i.e., field potential; FP), was estimated as the average of the membrane potential across all PY neurons in the network (see Assisi et al. 2007; Bazhenov et al. 2001; Hill and Tononi 2005 for a similar approach). In some experiments, we convolved all the spikes with an exponentially decaying kernel, thereby effectively replacing each spike by the exponent function with time constant of the synapse prior to averaging to explicitly simulate the contribution of synaptic currents to the field potential. Both approaches produced similar results when the synchrony of oscillations was analyzed.

Different oscillatory states as a function of synaptic coupling

The network activity was characterized by the frequency of the highest peak in the power spectrum of the mean field oscillations (Fig. 3C, top). We found that for a wide range of synaptic weights, the network displayed fast gamma (20–80 Hz range) oscillations; however, the frequency of oscillations and the dynamic behavior of the network was altered as a function of the synaptic strength. In the model, an increase of excitatory PY-IN coupling (g_PY-IN) was followed by a step-like increase in the frequency of mean field oscillations (f_FP) and concurrent decreases of individual PY frequency (f_PY) for certain values of PY-IN coupling–bifurcation points (g_i; Fig. 3D). As a result, the frequency ratio, f_PY/f_FP, characterizing the network oscillatory state changed at each bifurcation point: g₁: 1/1 → 1/2; g₂: 1/2 → 1/3;…; g_n: 1/n → 1/(n + 1). Furthermore, gamma range network oscillations were only observed when the neurons were depolarized sufficiently to sustain spiking activity (Fig. 3C, bottom). Only transient network dynamics were found for σ ≤ 0.085. For σ ∈ [0.09, 0.14], the network displayed low-frequency asynchronous firing at 5–15 Hz. When σ was increased beyond σ = 0.17, the firing frequency of individual neurons increased to up to 15–20 Hz and the network oscillations became synchronized. The level of depolarization also affected conductance values at the bifurcation points, g_i. In agreement with experimental data, INs were locked to the field and the frequency of IN's oscillations was equal to the frequency of mean field activity (Traub et al. 2000).

The model oscillations, characterized by f_FP = f_PY (g_PY-IN < g₁), is reminiscent of transient gamma oscillations that can be induced by tetanic stimulation of the hippocampal slices (Traub et al. 1996b; Whittington et al. 1997). An increase of PY-IN coupling in our model transformed the network to an oscillatory mode with f_FP ≫ f_PY that is similar to persistent gamma activity found in CA3 (Fisahn et al. 1998) and the neocortex (Buhl et al. 1998). These results are in agreement with previous studies (Traub et al. 1996b, 1997) and suggest that input from GABAergic INs is critical for creating oscillations in the gamma-beta frequency range and that the balance between excitatory (PY-IN) and inhibitory (IN-PY) coupling controls the frequency of oscillations and the resonance mode (f_PY/f_FP ratio).

Synchronization properties of gamma oscillations

To study large-scale synchronization properties of gamma oscillations, we considered the same synaptically coupled network with all PY neurons being depolarized just near the spiking threshold (σ ≅ 0.09). This initiated background activity in the network with all PY cells firing randomly across the population with a mean frequency in the 4- to 8-Hz range. In the spatial domain, this activity was manifested by random local waves of excitation moving through the network. Thus in these experiments, we simulated background network activity (effect of cholinergic activation) as opposed to the silent background state found in our experiments with a slab (Fig. 2). We can speculate that our model was designed to simulate the background state of the activated cortical network in vivo in the absence of sensory stimulation (Noda and Adey 1970; Tsodyks et al. 1999; Volgushev et al. 2006). To model effect of the sensory input, a subpopulation of neurons in the network was depolarized by external current. In some simulations, depolarization was induced by changing the parameter σ (controlling resting potential) from σ ≅ 0.09 to σ ≅ 0.17. This depolarization involved 50–80% of the total population of neurons. Neurons receiving depolarizing inputs (PY_i,j, IN_i,j) were located in the middle of the network (i₀ ≤ i ≤ i_max −i₀, j₀ ≤ j ≤ j_max − j₀); different patterns were tested to ensure that our results do not depend on a specific stimulus. A random background network state that was set before the stimulation guaranteed random initial conditions at the stimulus onset. In some cases, stimuli to different neurons were applied at different times (with delays that were drawn from the uniform distribution [0, 50 ms]). This further ensured that network synchronization properties of fast oscillations were not influenced by the onset of the external input. In addition to PY→IN and IN→PY coupling, low-probability excitatory connections were introduced between PY neurons (Thomson and Morris 2002; Thomson et al. 2002; Yoshimura and Callaway 2005). Each synapse in the model included a 1-ms “hard-coded” synaptic delay. However, the actual time delay between the presynaptic and evoked postsynaptic spikes in any of two coupled neurons was substantially larger as it included the time required to depolarize the membrane of the postsynaptic cell to its spiking threshold.

Depolarization of PY neurons led to a firing rate increase up to 15–20 Hz. The area where firing rate increased remained localized in space (as opposed to spreading over the entire network), which potentially allowed many external stimuli to be processed in parallel. Note that in simulations using a network model where the neurons are relatively hyperpolarized, the background state was silent and the same stimulus could trigger waves of activity propagating through the entire network [as observed in the experiment with slabs (Fig. 2)]. During active background states, shunting inhibition (Borg-Graham et al. 1998; Hirsch et al. 1998) and an activity-dependent increase of failures in synaptic transmission (Crochet et al. 2005) significantly reduce the effectiveness of single-axon excitatory postsynaptic potentials (EPSPs), thus diminishing activity propagation and, therefore preventing the cortical network from overexcitation.

In the area of depolarization, the frequency of field potential oscillations and the network resonance mode were determined by synaptic coupling as described in the preceding text (Fig. 3C). However, despite the presence of ∼45-Hz field oscillations, the synchrony of PY firing across the network was weak in this 1D network model (Fig. 4A). Different groups of cells fired with different phase delays relative to the peak of field oscillations, thereby creating a nonuniform distribution of PY activity (Fig. 4A, i and ii). The distribution of the time delays corresponding to the peak of the cross-correlation function between pairs of local field potentials measured at different network sites was plotted against the strength of PY-IN coupling (Fig. 4Aiii). Each time delay characterizes a phase shift between oscillations in two remote network sites; a sharp distribution of such delays centered at zero would indicate global synchronization. The width of this distribution increased rapidly for increasing values of PY-IN coupling. Thus this network failed to display precise global spatial synchrony of PY cell activity within the range of network gamma oscillations. This disagreement between 1D model simulations and experimental data are not unique to our study and various strategies have been proposed to address this problem (see, e.g., Traub et al. 1996b). One difference, however, is obvious between these models and the biological networks in vivo (including a cortical slab). The model we considered is 1D in the spatial domain and therefore lacks many important spatial properties found in biological systems.

Nearly perfect synchronization in 2D network model

To evaluate the effect of the network geometry on the synchrony of oscillations, we extended our model into the second spatial dimension without changing any other network property. The strength of individual synapses was rescaled to keep the total synaptic input per cell unchanged. The transition from a 1D network to a 2D network model dramatically increased the precision of synchrony across the population of neurons (Fig. 4B). In the 2D model, the local field potential oscillations at different network sites were synchronized with <5-ms delay (Fig. 4B, i and ii), while the propagation of activity between remote sites mediated by synaptic coupling required >50 ms (estimation based on individual synaptic delays and network size). An artificially induced increase in the synaptic delay for each synapse from 1 to 2 ms did not disturb the precision of long-range synchronization. To test the stability of synchronized oscillations, the input to the different neurons was applied at different times selected randomly from the uniform distribution [0, 50 ms]. The inset in Fig. 4Biii depicts a time of <150 ms (after all cells were depolarized) to achieve global synchrony. When depolarizing input was applied simultaneously to all neurons, synchronized network oscillations were achieved within the first few cycles of gamma oscillations. In this regime of global synchronization, the spike times of PY neurons were mediated by nearly synchronized spiking across all INs. Similar to the 1D model, when the strength of PY-IN coupling was increased, the distribution of time delays between oscillations in remote sites displayed sharp increases at each bifurcation point. However, in the 2D model, the range of synaptic couplings corresponding to the asynchronous firing was very narrow and oscillations became synchronized again as the network achieved a new resonance state (Fig. 4Biii).

Network dynamics near transition points between different oscillatory states

Analysis of the network dynamics in transition from one oscillatory state (resonance mode) f_FP = nf_PY (e.g., f_PY/f_FP = 1/2, Fig. 4Biii) to the next f_FP = (n + 1)f_PY (e.g., f_PY/f_FP = 1/3, Fig. 4Biii), revealed that two oscillatory states could appear simultaneously (Fig. 5). In this case, the network displayed a complex activity pattern consisting of several embedded populations of neurons oscillating independently (Fig. 5, A–C). The exact spatial pattern for each population depended on the initial state. The boundaries between groups of neurons oscillating in different states evolved very slowly in time. Interestingly, the size of these populations far exceeded the radius of its synaptic footprint. Again, a cross-correlation analysis revealed precise phase synchronization of oscillations between remote sites within a given subpopulation of neurons (Fig. 5D). Spatially separated subpopulations displaying the same type of oscillations (such as groups 1 and 2 in Fig. 5B) were also synchronized. The presence of several groups of neurons oscillating independently explained a sharp increase in the width of the time delay distribution of each transient state (for each bifurcation point; Fig. 4Biii). However, when the value of the coupling strength was shifted away from the bifurcation point, one of these two oscillatory states waned, thus converging to a homogeneous network oscillation.

FIG. 5.

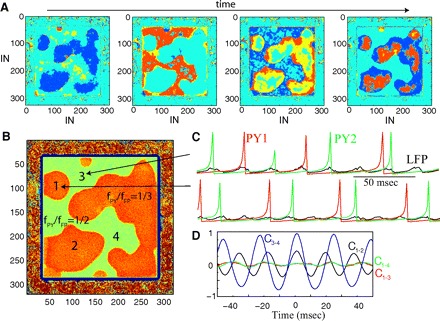
Two-dimensional network dynamics at the transition between 2 resonance states. A: representative snapshots of network activity at 4 different times illustrated with IN population. Network size: 640 × 640 PY neurons and 320 × 320 INs. B: spatial distribution of the resonance modes computed as the ratio of the total number of IN spikes to the total number of PY spikes in each network site during a given time interval. Orange (green) area indicates f_PY/f_FP = 1/3 (f_PY/f_FP = 1/2) resonance mode, respectively. Note that the population of neurons in f_PY/f_FP = 1/3 mode (orange area) is broken into several disjointed sets. C: examples of oscillations in 2 network sites (1 and 3 in B) belonging to different resonance areas (black indicats field potential; green and red indicates PY neurons). D: cross-correlation of the field oscillations among 4 network sites indicated in B. The synchrony was high between sites 3 and 4 (C_3–4, the same population); moderate between sites 1 and 2 (C_1–2, disjoint populations of the same type); low between 1 and 3 or 1 and 4 (C_1–3, C_1–4, populations oscillating in different resonance modes).

Mechanism for long-range synchronization of gamma activity

We further investigated different network models that can explain mechanisms behind precise long-range synchronization found in our simulations with 2D cortical networks.

NETWORK WITH CROSS-LIKE CONNECTIVITY PATTERN.

To explore the reasons behind the dramatic improvement of synchrony in the transition from 1D to 2D network models, we designed a 2D network using a cross-like connectivity pattern (Fig. 6A). While such a connectivity pattern is definitely a deviation from realistic biological structure, it allowed us to analyze 2D models where the number of presynaptic neurons is comparable with that in a 1D model. By reducing the size of the footprint along the y axis, we could model the transition from a 2D geometry to a 1D network. Individual synaptic weights were scaled by the number of synapses per cell to keep the total synaptic input constant for all network topologies. To test the effects of the network boundaries on the network synchronization, the area depolarized by the input to entrain gamma oscillations was set asymmetrically. This area included all PY neurons in the y dimension and only the central group of neurons (with indexes [30, 226]) in the x dimension (Fig. 6B). Periodic boundary conditions were used along the y dimension [neurons at the network boundary (y = 0) were connected to neurons at the other boundary (y = y_max) using the same pattern of synaptic connectivity as in the rest of the network]. Input to the different neurons was applied with varying delays selected from a uniform distribution [0, 50 ms]. The 1D model derived from a 2D network displayed a low level of synchrony similar to that in the original 1D model (Fig. 4A). However, the synchrony of oscillations in a 2D network with full cross-like connectivity (Fig. 6B) was close to the original 2D model implemented with a circular connectivity pattern (compare with Fig. 4B) except near the boundaries where the network activity displayed propagation. The spiking was synchronized within <5-ms delays across the entire population of neurons (Fig. 6B, right). Thus even though the network allows wave propagation with a velocity limited by synaptic delays, its dynamics was dominated by highly synchronized oscillations.

FIG. 6.

Effect of network connectivity structure on gamma range synchronization. A: “cross-like” connectivity structure in a 2D network. B: oscillations in the network with cross-like connectivity: 512 × 512 PY neurons and 256 × 256 INs. Left: snapshots of spiking activity in the IN population. Right: cross-correlation of the field potential oscillations (averaged over 10 × 10 PY neurons) between the center of the network and remote sites along the x axis as a function of the distance between the sites. C: multiple independent pathways with different synaptic lengths connect any 2 sites in a 2D network. Circles illustrate the synaptic connectivity of INs (red dots). Dashed lines illustrate different pathways connecting 2 selected INs (black dots).

The existence of synchrony in the model with a cross-like connectivity pattern shows that the effect of averaging across a larger presynaptic population in the 2D model with a circular synaptic footprint is, in itself, not sufficient to explain its higher synchrony compared with the 1D model. Rather we propose that 2D network models with circular or cross-like connectivity structure support multiple synaptic pathways (polysynaptic chains) connecting any two network sites and engage different INs. In a 1D network, there is only one way to connect any two remote points; therefore a spike delay (or advance) in any neuron (or small group of neurons) will disrupt precise synchronization between the distal ends of the 1D network and may even initiate a traveling wave. Indeed the activity in a 1D network was dominated by local traveling waves diminishing synchronization of PY firing (Fig. 4Ai). In the 1D network, the synchrony could be possibly improved if more than one IN spike is produced at each cycle; those additional spikes may “simulate” effect of complementary (though not quite independent) IN subpopulations. This may explain why IN spike doublets are important for the long-range synchrony of gamma oscillations in models of the hippocampal CA1 region (Traub et al. 1996b).

In a 2D network, a similar delay (or advance) of spiking in a local group of INs will produce a negligible effect on the other parts of the network because it would only influence a small fraction of many synaptic pathways connecting any two network sites (Fig. 6C). Under these conditions, a group of INs spiking at differing times from the rest of the population will be aligned during subsequent cycles of gamma activity by the feedback action of other neurons. Only when phase delays along all the pathways in a particular direction happen to match each other can a 2D network become engaged in global dynamics with a stable phase difference between oscillations at remote network sites. Examples of such active states include plane (or spiral) waves of neuronal activity traveling along the entire network. This behavior occurs in a network with cross-like connectivity near the boundaries of the depolarized area on the sides of the network.

NETWORK WITH A VARIABLE GEOMETRY.

To test our hypothesis that the existence of independent synaptic pathways is critical for long-range synchronization, we varied the network size in the y dimension (along the y axis, Fig. 7). All other network properties, including the number of synapses per cell and the total synaptic conductance per cell, remained unchanged and identical to the model shown in Fig. 6B. We expected that as the network size along the y axis decreased, the number of independent pathways connecting remote network sites would also decrease. In the limiting case, only one pathway going through a 1D chain of neurons along the x axis would remain. Indeed the synchrony of gamma activity remained high in our model until the size of the network in the y-dimension became less than approximately two synaptic footprints (16 PY neurons). The synchrony degraded to the level of a 1D model for the networks of size less than one footprint (Fig. 7C). The variety of synaptic pathways between remote sites was lost for such a narrow network and it started to behave as a 1D system. For each of these network models, regardless of the size along the y dimension, the field potential oscillated at ∼40 Hz, indicating that network oscillatory state remained unchanged (Fig. 7D).

FIG. 7.

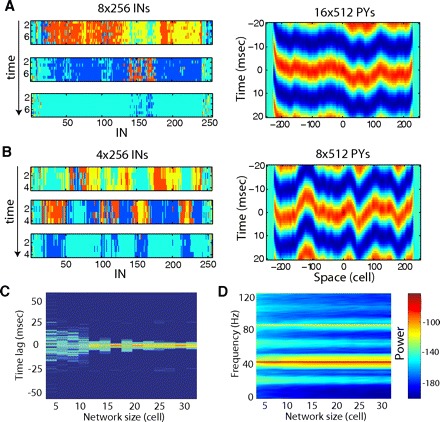
Effect of network dimensionality on gamma range synchronization. A: oscillations in the 16 × 512 PYs (8 × 256 INs) network model. Snapshots of IN activity as 3 different times (left) and cross-correlation of field potentials along x axis (right). B: oscillations in the 8 × 512 PYs (4 × 256 INs) network model. C: normalized probability density distribution of time lags to the main peak of the cross-correlation function between local field potentials at different spatial locations as a function of the network size along the y dimension. Logarithmic scale. Results are averaged across 15 independent trials with randomly selected initial conditions. Note disappearance of the isolated peak for the network of size <1 footprint (8 PY neurons). D: spectrogram of the local field potential [averaged across all neurons within (150,350) × (1, N) area, where N is number of PY neurons along y axis] as a function of the network's size along the y-dimension. Logarithmic scale (dB). E, left: cross-correlation of field potentials along x axis in 2D model with radius of the synaptic footprint 4 for PY-PY and PY-IN synapses (total 47 and 48 neurons, respectively) and 2 for IN-PY synapses (total 13 neurons). Right: cross-correlation of field potentials along the chain of neurons in 1D model with radius of the synaptic footprint 24 for PY-PY and PY-IN synapses (total 47 and 48 neurons, respectively) and 6 for IN-PY synapses (total 13 neurons). Not only is delay to the peak of cross-correlation function larger in 1D model but also the amplitude of the correlation function is significantly reduced in 1D model.

This study also showed that the difference in the synchronization properties between 1D and 2D models cannot be explained by the difference in the strength of individual synapses in 1D and 2D networks (in all our models the synaptic weights are normalized by the number of synapses per cell to keep the system in the same oscillatory state regardless of its geometry). In all simulations shown in Fig. 7, the total number of synapses per cell, and thus the individual synaptic weights, remained unchanged. Nevertheless synchronization of gamma oscillations changed dramatically as a function of the network geometry (size of the network in y dimension). To further confirm that an increase in the number of synapses per cell in a 1D model does not recover synchrony, we simulated a model with a larger synaptic footprint (±24 neurons for PY-PY, PY-IN coupling and ±6 neurons for IN-PY coupling). This was compared with a 2D network with a circular footprint and the same number of presynaptic units per cell (48 PYs and 13 INs). Despite the reduced footprint (compared with previous 2D simulations), the synchrony of oscillations remained high in this 2D model (Fig. 7E, left). In contrast, in the 1D model, the synchrony of gamma band oscillations was significantly reduced (Fig. 7E, right).

NETWORK WITH ALL-TO-ALL CONNECTIVITY ALONG ONE DIMENSION.

We also tested a network model with cross-like connectivity where the radius of connections extended over the entire network along one spatial dimension—the x axis (Fig. 8A, right). To allow a comparison with a 2D network with a circular connectivity pattern (Fig. 8A, left), we kept the number of synapses per cell and the total synaptic conductance per cell identical between the two models. The power spectrum of field oscillations in both models displayed a main peak at ∼40 Hz (Fig. 8D). Despite the presence of synaptic delays, oscillations were synchronized in the 2D model with circular connectivity (Fig. 8, B and C, left). Perfect synchronization in this direction was displayed at the network where the radius of connections extended over the entire network along the x axis. However, the synchrony along the y direction was lost (Fig. 8, B and C, right). To quantify the difference between oscillations in these networks, we calculated time delays (phase shift) between oscillations in remote sites of the network and then plotted the distribution of these delays for two different network configurations (Fig. 8E). As before, a distribution with only zero delays would represent a perfectly synchronized network. For a 2D network with circular connectivity, most of the delays were within the range of a few milliseconds (Fig. 8E, green line). For the network with all-to all connections along the x axis, the distribution of time delays was wide, with many delays >20 ms (Fig. 8E, blue line), indicating a significant phase shift between oscillations in remote network sites. Due to the perfect synchrony of oscillations along the x axis, all the neurons behaved identically in this direction such that a spike delay or advance in any neuron was mirrored precisely in all the neurons along the x axis. In this quasi-1D model any perturbation will disrupt precise synchronization between the sides of the network, thus affecting network behavior.

FIG. 8.

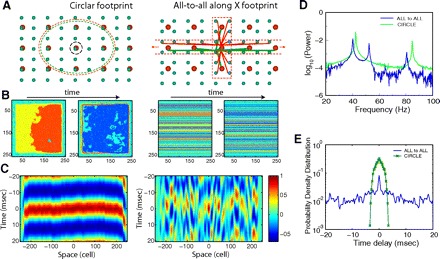
Effect of connectivity patterns on the network synchronization. A: connectivity structure for 2 different networks, 512 × 512 PY neurons and 256 × 256 INs. Left: circular footprint. The radius of the synaptic footprint: 18 for neurons with AMPA mediated PY-PY synapses, 18 for neurons with AMPA-mediated PY-IN synapses and 9 for neurons with GABA_A-mediated IN-PY synapses. Right: cross-like footprint with all-to-all connections along the x axis. B: snapshots of activity in the IN population. C: cross-correlation of the field potential oscillations between the center of the network and remote sites along the y axis as a function of the distance between the sites. D: power spectra of field potential oscillations. For both networks, the main peak was at ∼40 Hz with subharmonics at ∼80 Hz. Network with all-to-all connections along the x-axis also showed a 2nd peak at ∼50 Hz. Logarithmic scale. E: normalized probability density distribution of time lags to the peak of the cross-correlation function between local field potentials at different spatial locations. Logarithmic scale.

DISCUSSION

Mechanisms and properties of cortical gamma oscillations

Fast neural oscillations in the 20- to 80-Hz range are associated with attentiveness (Rougeul-Buser et al. 1975), sensory perception (Gray et al. 1989), and movement (Murthy and Fetz 1992; Pfurtscheller and Neuper 1992), and show a strong relation to both cognitive processing and temporal binding of sensory stimuli (Llinas and Ribary 1993; Singer and Gray 1995). These oscillations are found in different brain systems, including the cerebral cortex, hippocampus, and olfactory bulb. Gamma activity can exist in transient and persistent forms. Transient gamma oscillations can be induced by tetanic stimulation of the hippocampus, lasting hundreds of milliseconds (Traub et al. 1996b; Whittington et al. 1997); both fast-spiking INs and PY cells fire at the population frequency. Persistent gamma activity is found in CA3 (Fisahn et al. 1998) and neocortex (Buhl et al. 1998); this form of gamma can be induced by bath application of carbachol or kainate and last from minutes to hours. During persistent gamma activity, INs fire at every cycle or every two cycle, whereas PY cells fire at much lower frequencies. It was suggested that GABAergic interactions in isolated IN networks might also lead to network oscillation in the gamma frequency range (Traub et al. 1996a; Wang and Buzsaki 1996).

At least two nonexclusive basic mechanisms have been proposed to explain the origin of beta-gamma oscillations. One of these emphasizes the extracortical origin of activities, while the other emphasizes intracortical activity. Transient feed-forward synchronization to high-frequency peripheral (retinal, lemniscal or cerebellar) oscillations (Castelo-Branco et al. 1998; Timofeev and Steriade 1997) could impose the peripheral fast activities onto the thalamocortical system. Intracortical mechanisms include several possibilities. The first depends on the intrinsic property of fast rhythmic-bursting (FRB) neurons (Calvin and Sypert 1976; Gray and McCormick 1996; Steriade et al. 1998) to fire fast spike-bursts at frequencies in the 20- to 60-Hz range. Synchronized activity in a population of FRB neurons could, in principle, drive network oscillations in gamma frequency range. The second intracortical mechanism of gamma activity generation depends on the activity of inhibitory INs as described both in vitro and in computational models (Borgers and Kopell 2003; Lytton and Sejnowski 1991; Traub et al. 1996b, 1997–1999). Transitions between gamma and beta oscillations were simulated by alternating excitatory coupling between PY neurons and by changes in K⁺ conductances (Kopell et al. 2000; Traub et al. 1999). Last, the role of gap junctions between axons of PY cells in generating gamma oscillation was proposed (Traub et al. 2000). In this model, spontaneous spiking activity in PY cell axons was critical for persistent gamma oscillations. A transition from the asynchronous network state to persistent gamma oscillations, triggered by an increase in the excitability of PY neurons, was later described in a simplified network model with all-to-all connectivity (Borgers et al. 2005).

Synchronization properties of gamma oscillations

Cortical gamma oscillations may become synchronized within a few milliseconds over distances of up to a few millimeters (Gray et al. 1989). It remains a mystery how long-range synchronization of gamma (20–80 Hz) activity is achieved in systems with a limited speed of spike propagation along axonal collaterals and synaptic delays. In this study using in vivo recordings and large-scale cortical network models, we reveal a critical role played by the network geometry in achieving precise long-range synchronization in the gamma frequency band. In agreement with previous studies (Borgers and Kopell 2003; Lytton and Sejnowski 1991; Traub et al. 1996b, 1997–1999), gamma oscillations in our model were mediated by feedback inhibition from local GABAergic INs. The strength of the excitatory input from PY neurons to inhibitory INs defines the synchronization mode. A weak excitatory input requires cooperative activity in many PY cells to trigger IN spikes. Therefore many PY cells spike at each cycle of gamma oscillations as observed during transient gamma oscillations (Traub et al. 1996b; Whittington et al. 1997). Increasing the strength of excitatory coupling between PY cells and INs reduces the size of the PY cell population required to spike together to maintain IN activity. This leads to another mode when each PY cell spikes only once over many cycles—a regime that is reminiscent of persistent gamma activity (Buhl et al. 1998; Fisahn et al. 1998).

One of the most surprising findings, however, was the dramatic difference in the synchronization properties of gamma oscillations produced by 1D and 2D networks of neurons. In a 1D system (a chain of neurons), a relatively small (compared with the network size) synaptic footprint and synaptic delays created a poorly synchronized oscillatory state characterized by localized waves of gamma activity; a phase shift between local field oscillations in remote network sites achieved tens of milliseconds. When this network was extended to the second dimension, a highly synchronized network state was established although the synaptic connectivity remained localized. Variations of the system size revealed a critical point—when the network size became less than one synaptic footprint in one spatial dimension, the highly synchronized network state disappeared. We concluded that the presence of multiple pathways that connect any two remote sites of a 2D network model provide stability against the onset of local phase distortions—the same distortions that can effectively destroy long-range synchrony in a 1D system.

These results are obtained using a simplified model of the cortical network that contained only two classes of neurons described using reduced models. To define a direct and complete link between the reduced model parameters and the physiological properties of a biological neuron is rather difficult. Therefore as with any simplified model, some specific patterns of the network behavior may depend on the model design. To ensure that our main results are generic, we tested different network models and found that the connectivity patterns and the size of the synaptic footprint only produced a minor effect on the network synchronization properties. The synchrony sustained synaptic delays up to 3–4 ms reducing gradually as the synaptic delays further increased. The synchrony also remained after we included inhibitory connections between INs (IN-IN) with the same maximal strength as IN-PY connections. Finally, we tested the effect of synaptic depression in lateral excitatory connections between PY neurons and found no significant difference on the dynamics of synchronization. Thus our main prediction, that the network dimensionality plays a critical role in network synchronization, can be generalized beyond the specific class of models that we used in this study. While our results may seem less surprising from an experimental perspective, a majority of existing computer models utilize a 1D geometry that, as shown here, may be insufficient to capture important properties of complex brain dynamics.

These theoretical results were observed in in vivo recordings from an isolated cortical slab. In a slab, the transition to an active network state was characterized by wave propagation, suggesting the predominance of local synaptic connectivity. On the other hand, fast gamma range oscillations observed during the active state were perfectly synchronized. Due to the slab shape and size (∼8–10 mm long and 5–6 mm wide), 2D connectivity structure was preserved in this preparation and was responsible for synchronization of gamma range activity. Our study predicts that neural structures that are relatively homogeneous in the 2D plane, with local synaptic connectivity (as seen in many cortical areas), are able to display large-scale synchronous oscillations despite the limited speed of spike propagation along axonal collaterals and synaptic delays.

Role of network topology for synchronization

Recently studies of the role of the network topology in the onset and persistence of synchrony have become an area of significant interest (Restrepo et al. 2004a,b). Previous modeling studies (Lago-Fernandez et al. 2000) show that in a network of Hodgkin-Huxley neurons, a random topology of the network facilitated the onset of synchronization. In small-world networks (Watts and Strogatz 1998), the onset of synchronization was fast and led to coherent oscillations. Both random and small-world networks contain long-range connections that promote long-range and global synchrony. As was shown in Masuda and Aihara (2004), neurons tended to form local clusters with precise synchronization in regular lattices while staying globally asynchronous. As the regular lattice is randomly rewired to form a small-world network, the cooperation of global connections and the effect of local clustering forces synchrony among remote neuronal groups receiving coherent inputs (Masuda and Aihara 2004). The role of connectivity in the randomly rewired networks in formation of large-scale synchronization were considered as possible mechanisms mediating synchronization during seizures (Percha et al. 2005). The present study demonstrates that even in the absence of long-range connections, precise long-range synchronization of network oscillations can be achieved in a large population of neurons organized in the form of a 2D spatial structure.

Conclusion

Stimulus-evoked neuronal oscillations have been found in a variety of neuronal systems (Adrian 1950; Gray et al. 1989; Hubel and Wiesel 1965). Numerous theoretical studies have explored mechanisms and synchronization properties of neuronal oscillations. However, to date, a majority of these studies have explored network models with only one spatial dimension and local spatial connectivity or scale-free (all-to-all connected) networks. Our study suggests that using network models with two spatial dimensions is critical in capturing important synchronization properties of real biological systems. An intrinsic property of 2D networks [i.e., a large number of independent pathways (synaptic chains) connecting any 2 network sites] dramatically increases the stability and precision of global synchrony in 2D network models in comparison to their 1D counterparts. In a more general sense, in 2D networks the stability of a spatially homogeneous solution is maintained over a much broader range of network parameters compared with a 1D system. In contrast to 1D network models, this region of stability in 2D networks overlaps with the parameter regime (network states) where gamma oscillations exist, thus guaranteeing precise long-range synchronization of fast gamma range activity as observed experimentally.

GRANTS

This work was supported by National Institutes of Health grants to M. Bazhenov and to M. Bazhenov and I. Timofeev and funding from Canadian Institutes of Health Research and Natural Science and Engineering Research Council of Canada to I. Timofeev. I. Timofeev is a Canadian Institutes of Health Research scholar.