Network-level molecular evolutionary analysis of the insulin/TOR signal transduction pathway across 12 Drosophila genomes

Abstract

Biological function is based on complex networks consisting of large numbers of interacting molecules. The evolutionary properties of molecular networks and, in particular, the impact of network architecture on the sequence evolution of its individual components are, nonetheless, still poorly understood. Here, we conducted a fine-scale network-level molecular evolutionary analysis of the insulin/TOR pathway across 12 species of Drosophila. We found that the insulin/TOR pathway components are completely conserved across these species and that two genes located at major network branch points show evidence for positive selection. Remarkably, we detected a gradient in the strength of purifying selection along the pathway, increasing from the upstream to the downstream genes. We also found that physically interacting proteins tend to have more similar levels of selective constraint, even though this feature might represent a byproduct of the correlation between selective constraint and the pathway position. Our results clearly indicate that the levels of functional constraint do depend on the position of the proteins in the pathway and, consequently, the architecture of the pathway constrains gene sequence evolution.

Biological function is based on complex networks consisting of large numbers of molecules. Indeed, genes do not act in isolation but interact in molecular pathways. The evolutionary dynamics of biochemical networks is, moreover, a fundamental issue in systems biology. Establishing the patterns of genetic variation across networks and the impact of natural selection on such variability can provide important insights into the evolutionary forces acting in network evolution. Most evolutionary studies, however, have focused on individual genes or gene families; consequently, the properties and mechanisms underlying network evolution remain largely unknown.

A central question in biological network evolution concerns the role of topology in the evolution of individual network components and, in particular, the effect of the position of an element in the network on the strength of positive and purifying selection. Whole-genome analysis has shown that better connected network elements (e.g., hubs) tend to be more functionally constrained (Fraser et al. 2002; Hahn and Kern 2005; Lemos et al. 2005; Vitkup et al. 2006) and that physically interacting elements tend to exhibit similar levels of selective constraint (Fraser et al. 2002; Lemos et al. 2005). The position of an element in a network, therefore, clearly affects its evolutionary fate. Nevertheless, little research has addressed this question on well-characterized molecular pathways, showing that elements located at network branch points tend to evolve adaptively (Eanes 1999; Flowers et al. 2007). Moreover, the upstream elements in some biochemical pathways are more constrained than those in downstream positions (Rausher et al. 1999; Lu and Rausher 2003; Riley et al. 2003). This kind of selective constraint gradient along the upstream/downstream axis has been explained by the hierarchical organization of these pathways; namely, mutations in upstream genes would generate greater pleiotropic effects than those in genes at the downstream part of the pathway, being therefore more likely to have a deleterious effect.

Biochemical pathways can be classified into three categories: metabolic; transcriptional regulatory; and signal transduction (or signaling) pathways. Signaling pathways transduce signals (such as hormones acting as ligands of extracellular receptors) from outside to inside the cell. The ligand–receptor interaction triggers a cascade of biochemical reactions (often through protein phosphorylation and dephosphorylation). The transduced signal ultimately activates the effector elements of the pathway, which are responsible for mediating the response.

The insulin/TOR (IT) signal transduction pathway plays a central role in many critical biological processes in animals, including organism growth, anabolic metabolism, cell survival, fertility, and lifespan determination (Goberdhan and Wilson 2003; Oldham and Hafen 2003). Both the network topology and the molecular functions of its components have been well characterized in different organisms, including Drosophila melanogaster (Supplemental Fig. S1), and are highly conserved across metazoans.

Current knowledge of IT signaling in D. melanogaster, with the recent addition of the complete genome sequences for 12 species of the same genus, offers the possibility of conducting a fine-scale evolutionary analysis of a signal transduction pathway. Here, we have studied the molecular evolution of the IT signaling pathway genes of 12 Drosophila species within a network-level framework.

Results

Identification of insulin/TOR pathway genes in Drosophila genomes

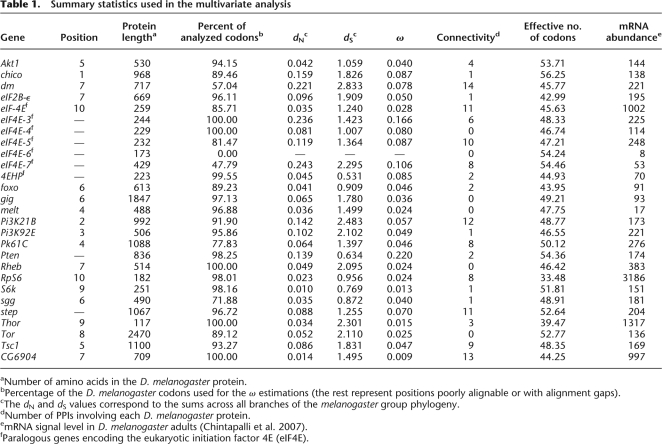
We identified a total of 315 putative orthologs of the 27 D. melanogaster IT signaling pathway genes (Table 1) in 11 Drosophila genomes. Therefore, we analyzed 342 DNA sequences (Supplemental Table S2). Since current genomic projects include many unsequenced regions, this should be considered as the minimum number of actual genes. Additionally, recent gene duplication events are difficult to identify given the low divergence between the resulting paralogous copies, which might have been treated as a single copy during genome assembly. Some of the identified sequences are incomplete (they are located in partially sequenced regions), and seven of them reveal some pseudogenization footprint (frameshifts, premature stop codons, or indels; Supplemental Table S2).

Table 1.

Summary statistics used in the multivariate analysis

^aNumber of amino acids in the D. melanogaster protein.

^bPercentage of the D. melanogaster codons used for the ω estimations (the rest represent positions poorly alignable or with alignment gaps).

^cThe d_N and d_S values correspond to the sums across all branches of the melanogaster group phylogeny.

^dNumber of PPIs involving each D. melanogaster protein.

^emRNA signal level in D. melanogaster adults (Chintapalli et al. 2007).

^fParalogous genes encoding the eukaryotic initiation factor 4E (eIF4E).

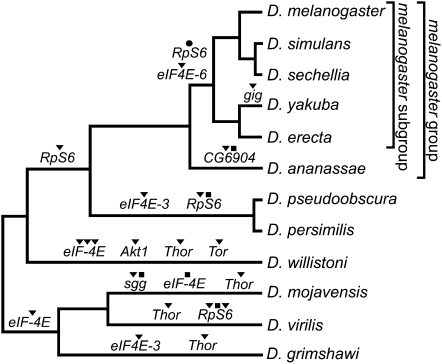
All the IT pathway genes studied have orthologs in all 12 genomes, except eIF4E-6, which is present only in the melanogaster subgroup of Drosophila. The D. melanogaster eIF4E-6 and 4EHP genes, which belong to a seven-member paralogous group (Table 1), may be either nonfunctional or negative IT signaling regulators (Hernandez et al. 2005). Current results, therefore, suggest that the IT signaling pathway is well conserved across available Drosophila genomes. Seventeen IT pathway genes have a 1:1 orthology relationship, while the remaining 10 genes underwent a number of duplication and/or loss events (20 duplications, 1 loss, and 5 pseudogenization events; Fig. 1).

Figure 1.

Gene duplication (▼), loss (●), and pseudogenization (■) events detected in the IT pathway across the Drosophila phylogeny.

Synonymous and nonsynonymous divergence along the IT pathway

We inferred the impact of natural selection on the IT pathway genes of the D. melanogaster group from the nonsynonymous (d_N) to synonymous (d_S) substitution rate ratio (ω = d_N/d_S). The values of ω range from 0.009 for CG6904 to 0.220 for Pten (Table 1). We detected the footprint of positive selection in the eIF2B-ε, Akt1, and Tor genes by comparing the M7 and M8 models (the M7 model assumes a discrete beta distribution for ω [0 ≤ ω ≤ 1], whereas the M8 model adds an extra class of sites [ω > 1]; Supplemental Table S3). The test is only significant for eIF2B-ε and Akt1 at a false discovery rate (FDR) of 5%.

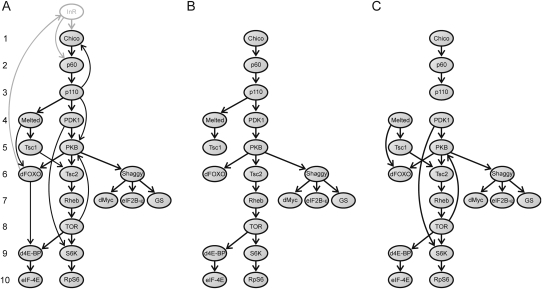
To study the relationship between the ω values and the architecture of the IT signaling pathway, we evaluated whether: (1) physically interacting elements within the IT pathway have more similar ω values, and (2) the ω values are affected by the position of the elements in the pathway. The first analysis revealed that physically interacting IT pathway proteins (Fig. 2C) tend to evolve at more similar rates: The average absolute difference between the ω values of the physically interacting elements in the IT pathway (X_ω = 0.015) is significantly lower than expected from a network with the same elements and the same number of interactions assigned at random (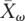 = 0.023, P = 0.010). To establish which ω component is the main contributor to this trend, we conducted the analysis for d_N and d_S independently. The results of the Monte Carlo test showed that the nonsynonymous changes are the main contributors to the tendency (X_N = 0.031, P = 0.004; X_S = 0.591, P = 0.164).

Figure 2.

Graphs used in the network-level analysis. (A) Directed graph (G graph) representing the interactions across the D. melanogaster IT pathway elements. Arrows (arcs) indicate the direction of signal transduction. Numbers on the left represent the position of the elements in the pathway. (B) Graph T is a directed spanning tree of G used to compute the position of each element in the IT pathway (i.e., the number of signal transduction steps required to transduce the signal from InR to the downstream elements of the pathway). This graph was obtained by removing some arcs from G (according to specific biochemical criteria). We eliminated the three arcs involving feedback loops (activation of Chico by PIP₃, which is synthesized by p110; activation of InR by the transcription factor dFOXO; phosphorylation of PKB by TOR). Furthermore, if a particular node is reached by different paths (d4E-BP, dFOXO, PKB, S6K, and Tsc2) we considered only one of them. For dFOXO, PKB, and S6K, we chose the longest path, since each of the paths allows the transduction of one necessary but not sufficient signal for the activation/inhibition of these proteins (i.e., the elements need to receive all the signals for activation/inhibition). Indeed, the recruitment of dFOXO to the cell membrane by Melt is a prior step to the phosphorylation (and consequent inhibition) of dFOXO by PKB (the Akt1 product). In the same way, the recruitment of PKB to the cell membrane through its interaction with PIP₃ (synthesized by p110) is also a prior step to the phosphorylation of PKB by PDK1 (the Pk61C product). S6K needs to be phosphorylated by both PDK1 and TOR for full activation (Chou and Blenis 1995; Dufner and Thomas 1999; Avruch et al. 2001). d4E-BP (the Thor encoded protein) is an inhibitor of the pathway activated by its transcription factor dFOXO and inhibited by the TOR kinase. Given that only the second interaction activates the pathway, we eliminated the first from the analysis. (C) Graph S is a subgraph of G that includes only the direct physical PPIs between the elements of the IT pathway.

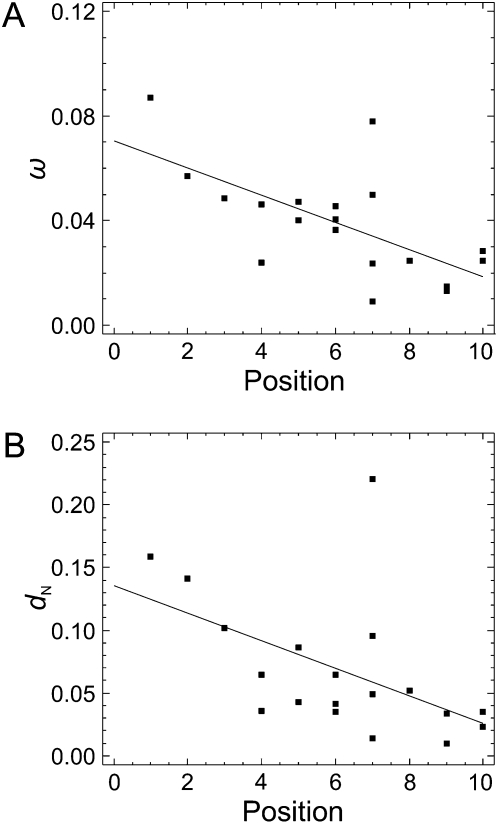
We found a significant negative correlation between ω estimates for IT pathway genes and their position in the pathway (computed as the number of steps required to transduce the signal from InR to the other elements; Fig. 2) (Spearman's rank correlation coefficient, ρ = −0.607; P = 0.006; Fig. 3A). This result suggests that the topology of the IT pathway influences the distribution of selective constraint along it. More specifically, the downstream elements (Fig. 2) have higher levels of selective constraint than the upstream elements. When this analysis was conducted separately for d_N and d_S, we again found that nonsynonymous changes are the main contributors to the tendency (d_N: ρ = −0.622, P = 0.004, Fig. 3B; d_S: ρ = –0.165, P = 0.499).

Figure 3.

Correlation between the position of the elements in the IT pathway and the ω (A) and d_N (B) estimates. Continuous lines represent regression lines.

We considered whether the correlation between ω and pathway position was a general trend in the phylogeny or—on the contrary—whether it might be attributable to some specific lineage. To establish this, we analyzed each of the nine lineages (the six external and the three internal branches of the melanogaster group phylogeny) separately using the ω values estimated under the free-ratio model (FR). This test is only significant for the D. yakuba (ρ = –0.524, P = 0.021), D. erecta (ρ = –0.511, P = 0.025), and D. ananassae (ρ = –0.729, P = 0.0004) lineages. Even though this correlation is not significant in the six remaining lineages, the ρ statistic is also negative in five of them. We also applied a specific two-ratio branch model to estimate the ω ratios in two groups: one including the D. yakuba, D. erecta, and D. ananassae lineages, and the other comprised of the six remaining lineages. The correlation is significant in the two groups (ρ = –0.669, P = 0.002; ρ = –0.455, P = 0.050; respectively), indicating that the negative correlation between the ω values and the position of the elements in the pathway is a phylogeny-wide trend and not caused by any lineage-specific pattern.

The estimates of ω used in the previous analyses were obtained from nucleotide sequence data clearly alignable across the six species of the melanogaster group. Since removing the most divergent regions might bias the results, we reanalyzed the data using the noncurated data set (the direct output of the ProbCons alignment software). This analysis does not change the main conclusion, namely, that ω correlates negatively with the position of the elements in the pathway (ρ = –0.559, P = 0.013). Another putative source of bias is the use of an inadequate codon frequency model (the ω values reported here were estimated using the F3×4 codon frequency model; Goldman and Yang 1994). However, the correlation was significant independently of the codon frequency model used to estimate ω (Fequal, F1×4, or F61).

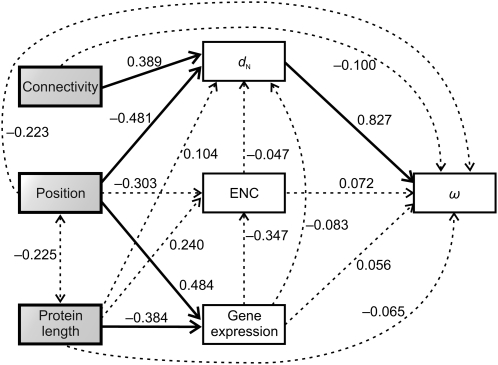
Finally, as the selective constraint of a given gene is known to correlate with different factors, including gene expression level, codon bias, protein length, and connectivity (number of protein–protein interactions [PPIs]), we considered whether these factors could account for the correlation between ω and the position of the elements in the pathway. We found that (1) expression level, codon bias, and protein length show a significant correlation with the position of the elements in the pathway (ρ = 0.484, P = 0.036 for expression level; ρ = –0.497, P = 0.030 for codon bias, measured as the effective number of codons [ENC]; ρ = –0.480, P = 0.037 for protein length; Supplemental Fig. S2B–D), whereas connectivity does not (ρ = 0.083, P = 0.734; Supplemental Fig. S2A), and (2) these factors do not correlate with ω (ρ = –0.213, P = 0.381 for expression level; ρ = 0.207, P = 0.395 for ENC; ρ = 0.354, P = 0.137 for protein length; ρ = 0.213, P = 0.380 for connectivity; Supplemental Fig. S2E–H). Since expression level, codon bias, and protein length are intercorrelated, some of the observed correlations might actually result from indirect rather than from direct effects. We used path analysis to better characterize the relationships among these factors, connectivity, d_N, ω, and the position in the pathway. This joint analysis (Fig. 4) shows that (1) the d_N values are clearly affected by the position of the elements in the pathway (standardized path coefficient, β = –0.481; P = 0.035), even after removing the effects of putatively relevant factors (gene expression level, codon bias, and protein length); (2) connectivity and d_N are positively associated after factoring out the effects of all other variables (β = 0.389, P = 0.027); and (3) apart from d_N, only the gene expression level is significantly influenced by the pathway position (β = 0.484; P = 0.006). The multiple regression model explains 44.4% of the d_N variability. Path analysis using two other causal models (considering gene expression and protein length as exogenous and endogenous variables, respectively) yielded similar results.

Figure 4.

Path analysis used to characterize the relationships among element positions in the IT pathway, nonsynonymous divergence (d_N), d_N/d_S ratio (ω), gene expression level, codon bias (measured by the ENC), protein length, and connectivity. Pathway position, protein length, and connectivity were treated as exogenous variables (those with no explicit causes in the model), while the rest were treated as endogenous variables (those caused by one or more variables in the model). The causal dependencies between variables assumed in the model are represented by single-headed arrows. Correlations between exogenous variables are represented by double-headed arrows. The numbers on the arrows represent the standardized path coefficients (β). Solid and broken lines represent significant and nonsignificant relationships, respectively.

Discussion

Distribution of IT pathway genes across Drosophila genomes

Our analysis shows that the IT pathway genes underwent 20 gene duplications, one loss, and five pseudogenization events throughout the evolution of the 12 Drosophila species (Fig. 1). Nevertheless, all the IT pathway genes have representatives in the 12 Drosophila species; the only exception is the eIF4E-6 gene, which may be a nonfunctional paralog of the eIF4E multigene family (Hernandez et al. 2005). The existence of nearly all the genes in all the surveyed species, together with the relatively high selective constraint levels (ω < 0.25), suggests that the IT pathway is functional across all these species.

It has been suggested that proteins that interact with each other tend to show similar phylogenetic patterns of gene duplication and loss, owing to coordinated evolution (Fryxell 1996). Noticeably, we found that some genes encoding physically interacting proteins underwent gene duplication in the same lineages (Akt1, Tor, Thor, and eIF-4E in the D. willistoni lineage; eIF4E-3 and Thor in the D. grimshawi lineage) (Fig. 1). Nevertheless, the null hypothesis of random accumulation of gene duplications across the branches of the phylogeny could not be rejected (Monte Carlo simulation test; P = 0.190).

Impact of positive selection

We found that eIF2B-ε, Akt1, and Tor genes show the footprint of positive selection (only eIF2B-ε and Akt1 after controlling for the FDR). It has been suggested that elements located at branch points of metabolic pathways exert a greater flux control and, therefore, may tend to evolve under positive selection (Eanes 1999; Flowers et al. 2007). If this is so, it should also be true for signal transduction pathways. Interestingly, both PKB and TOR (the encoded products of Akt1 and Tor, respectively) locate at major network branch points (Fig. 2). Upon activation by insulin, p110 catalyzes the synthesis of the membrane lipid PIP₃, which acts as a docking site for a number of pleckstrin homology domain-containing proteins, including PKB. Consistent with the flux control hypothesis, the Akt1 codons identified as evolving under positive selection are located in the pleckstrin homology domain. Furthermore, since TOR phosphorylates multiple IT pathway elements, it also locates at a major branch point of the IT pathway.

Selective constraints along the IT pathway

We found that physically interacting elements of the IT pathway tend to have more similar ω and d_N values (P < 0.010). This pattern, already observed in interactomic-level analyses, has been attributed to the coevolution of amino acids involved in protein interactions (Fraser et al. 2002; Lemos et al. 2005). In our study, however, this pattern might be a byproduct of the current correlation between selective constraint and the pathway position. In fact, after factoring out this effect, the association between ω (and d_N) values of physically interacting elements is no longer significant (X_ω = 0.013, P = 0.105; X_N = 0.030, P = 0.057), although close to the critical value.

Remarkably, our study reveals a robust positive correlation between the position of the elements in the pathway and functional constraint levels. Although both ω and d_N estimates exhibit a statistically significant correlation with the pathway position (P < 0.006), results of the path analysis (Fig. 4) clearly indicate that nonsynonymous divergence (d_N) would be the main responsible. A number of factors might underlie the detected correlation between selective constraints and pathway position. First, it has been suggested that regulatory genes tend to evolve faster than structural genes (Tucker and Lundrigan 1993; Whitfield et al. 1993; Purugganan and Wessler 1994; Gaut and Doebley 1997; Rausher et al. 1999), and the structural genes (eIF-4E, RpS6, eIF2B-ε, and CG6904) in the IT pathway are located downstream. Thus, the observed correlation might be a byproduct of this downstream location of the structural genes. However, the correlation between the position of the elements in the pathway and selective constraint remains significant even after removing these genes from the analysis (ρ = –0.691, P = 0.004 for ω; ρ = –0.594, P = 0.034 for d_N). Second, four IT pathway genes (chico, melt, Pk61C, and Akt1) that encode proteins with a pleckstrin homology domain are located in the upstream part of the pathway; therefore, relaxed purifying selection in this domain might explain the observed correlation along the pathway. However, the elimination of these genes from the analysis does not affect the results (ρ = –0.620, P = 0.014 for ω; ρ = –0.652, P = 0.008 for d_N). Finally, throughout our study we consider that the TOR pathway locates downstream of the insulin pathway. Some experimental studies have questioned this and place some elements of the TOR pathway (Tsc1, Tsc2, Rheb, and TOR) on a route parallel to the insulin pathway (Oldham et al. 2000; Gao et al. 2002; Radimerski et al. 2002; Dong and Pan 2004). Again, the observed correlation remains significant after removing these four elements from the analysis (ρ = –0.581, P = 0.023 for ω; ρ = –0.683, P = 0.005 for d_N).

Thus, our results suggest that the structure of the IT pathway constrains the sequence evolution of its components. However, it is not clear what the biological explanation is for the polarity in the strength of purifying selection along the pathway. Diverse factors might affect selective constraints in molecular pathways. For instance, interactomic-level analyses have revealed a negative correlation between evolutionary rate and connectivity (Fraser et al. 2002; Hahn and Kern 2005; Lemos et al. 2005). In contrast, our path analysis uncovered a positive association between d_N and connectivity. Hence, a polarity in the element's connectivity along the pathway might explain the correlation between selective constraint and the pathway position. However, no significant correlation was detected between connectivity (Table 1) and pathway position (Supplemental Fig. S2A); therefore, the connectivity pattern would not explain the correlation between selective constraints and the position of the elements in the pathway. Results based on interactomic data, however, should be taken with caution since current D. melanogaster interactomic data is incomplete and unreliable.

Gene expression level, expression breadth (the number of different tissues in which a gene is expressed), codon usage bias, and the length of the encoded proteins can also affect selective constraints. In fact, genes with higher expression levels, higher codon bias, or shorter encoded proteins tend to be more constrained (Duret and Mouchiroud 1999; Pal et al. 2001; Rocha and Danchin 2004; Subramanian and Kumar 2004; Wright et al. 2004; Lemos et al. 2005; Drummond et al. 2006; Ingvarsson 2007). As all IT pathway genes seem to be expressed in all body tissues and structures (Chintapalli et al. 2007), expression breadth cannot account for the pathway polarity of the ω values. A putative higher translation rate of downstream IT pathway genes might justify the observed correlation between ω and the position of the elements in the pathway. In fact, given the signal-amplifying kinetic behavior of the insulin pathway—at least in mammals (Sedaghat et al. 2002), a higher protein abundance is expected in downstream IT pathway elements. On the other hand, shorter protein lengths at the downstream IT pathway part might also generate the observed selective constraint polarity. Interestingly, we detected (1) a positive correlation between the position of the elements in the pathway and both expression level and codon bias (Supplemental Fig. S2B,C) and (2) a negative correlation between protein length and the position of the elements in the pathway (Supplemental Fig. S2D). Namely, downstream IT pathway genes encode shorter and more actively translated proteins. In this pathway, however, none of these factors correlate with ω or d_N (Supplemental Fig. S2F–H). Consequently, these would not be the main factors responsible for the correlation between ω and the position of the elements in the IT pathway. It is conceivable that some coupled effect emerging from codon bias, expression level, and protein length might generate the selective constraint polarity, even though these factors do not correlate with ω or d_N separately. However, path analysis confirms that the relationship between selective constraint and the position of the elements in the pathway is significant even after factoring out the effects of gene expression level, codon bias, protein length, and connectivity (Fig. 4). Consequently, other biological factors are needed to explain the purifying selection polarity along the IT pathway.

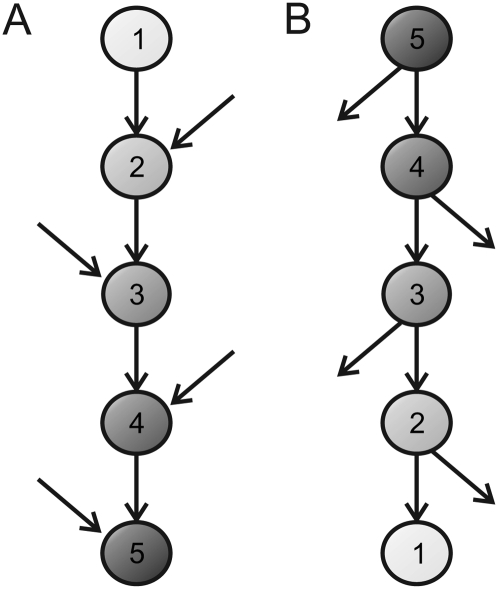
The number of molecular pathways in which a gene is involved may affect its functional constraint levels; for instance, highly pleiotropic genes are expected to be more constrained (Waxman and Peck 1998). Therefore, the distribution of the strength of purifying selection along the upstream/downstream axis of a pathway may be affected by its particular pattern of interconnections with other pathways. A signal transduction pathway receiving signaling inputs from a number of pathways (i.e., with multiple inputs and a single output) is expected to be more constrained at the downstream part given that the downstream elements would be involved in a greater number of pathways (Fig. 5A). Conversely, a network with a branching topology including multiple outputs along the pathway will exhibit the opposite trend in its selective constraint pattern (Fig. 5B). Hence, the balance between the biological relevance of the signaling inputs and outputs might generate a selective constraint polarity along the pathway.

Figure 5.

Schematic representation of the selective constraint levels expected along two hypothetical signaling pathways with different connection patterns. (A) Pathway receiving multiple signaling inputs along the pathway and with a single output. In this scenario, selective constraint levels will be higher at the downstream part, since the elements are progressively involved in a greater number of pathways. (B) Pathway with multiple outputs along the pathway (i.e., with multiple branching points able to transmit information to other pathways). In this scenario, the selective constraint levels will be higher for the upstream elements. The more constrained elements (nodes) are darker. The numbers in the nodes represent the number of pathways in which each element is involved.

The correlation between functional constraint levels and the position of the elements in the IT pathway might, therefore, be explained by its information flux pattern; in particular, on the basis of the predominance of inputs over outputs along the pathway (in terms of biological relevance). Indeed, even though the IT pathway connection patterns for Drosophila are far from being fully known, it does receive inputs from other pathways (Supplemental Table S4). However, some IT pathway elements also transduce signals to other pathways (i.e., there is not just one single output signal) (Supplemental Table S4). Moreover, the biological impact (in terms of fitness) of the interrelations of the IT pathway with these other routes cannot be easily evaluated; therefore, it is difficult to determine whether the effects of signaling inputs overweigh those of the outputs.

Rausher et al. (1999) have shown that the selective constraint levels in the plant anthocyanin biosynthetic pathway also correlate with the position of the elements in the pathway. However, the correlation has the opposite sense to that observed in the IT pathway (i.e., upstream anthocyanin biosynthetic pathway elements are more constrained than those in the downstream part). In this case, the upstream elements are located above major branch points and are consequently involved in the biosynthesis of a greater number of compounds, whereas the downstream genes only affect anthocyanins biosynthesis. The pathway, therefore, has more outputs than inputs (Fig. 5B). Polarity in the selective constraint along the anthocyanin pathway was explained by the involvement of upstream elements in a greater number of biochemical routes (Rausher et al. 1999).

The sensitivity of the overall pathway function to the kinetic properties of a given element will also affect selective constraint levels. If genetic variation in the kinetic properties strongly affects the pathway function, the element should be more constrained than if the system works with relative independence from these properties. Therefore, the selective constraint of a protein would be determined not only by its kinetic properties, but also by its position in the pathway and the properties of the interconnected pathway elements. Along these lines, a theoretical analysis conducted in the Ras signaling pathway (Nijhout et al. 2003) predicted that the pathway output would be more sensitive to the upstream enzymes, which therefore should be more constrained. This prediction was supported by DNA polymorphism analysis (Riley et al. 2003). Applying this sensitivity analysis to the IT signaling pathway would probably provide valuable insights into the major biological processes that determine the selective constraints along the pathway.

In summary, even though the biological processes underlying the polarity in the selective constraint levels along the IT pathway remain unclear, our results provide strong evidence that the pathway architecture constrains the molecular evolution of its components. Further work studying the patterns of molecular evolution in pathways encompassing a wide range of topologies and analyzing the biological impact of the interconnection patterns is required to fully understand how network topology constrains the evolution of its components.

Methods

Identification of IT signaling pathway genes in Drosophila genomes

The protein coding sequences (CDS) of the IT pathway genes in the D. melanogaster genome (release 5.1) (Adams et al. 2000) were retrieved from the FlyBase database (Crosby et al. 2007). Orthologous sequences of these genes in the 11 additional Drosophila species with completely sequenced genomes (D. simulans, D. sechellia, D. yakuba, D. erecta, D. ananassae, D. pseudoobscura, D. persimilis, D. willistoni, D. mojavensis, D. virilis, and D. grimshawi) were obtained from the Assembly, Alignment and Annotation site (http://rana.lbl.gov/drosophila; CAF1 release; Clark et al. 2007). For those genes with multiple splicing isoforms we chose the variant encoding the longest protein among those shared across the 12 species (Supplemental Table S1).

To obtain a bona fide set of genomic orthologous sequences, we curated available preliminary gene annotations and orthologous relationships (GLEAN-R and fuzzy reciprocal BLAST data sets, respectively; Clark et al. 2007). For this purpose, we discarded erroneous automatic orthology assignations; merged those groups of adjacent gene predictions actually corresponding to different regions of a single gene; and annotated coding regions that were unannotated in the original GLEAN-R data set. Putative premature stop codons and frameshift mutations were confirmed by analyzing the genomic trace archives (raw DNA sequence data); these features were discarded if there was at least one sequencing trace without the disrupting mutations. D. simulans sequences with incomplete information were curated using DNA sequence data information from the population genomics project for this species (DPGP Simulans Syntenic Assembly version 2; Begun et al. 2007).

To identify putative unannotated genes, we conducted a two-round search for each orthologous group. First, for each D. melanogaster protein we performed a TBLASTN search against all other 11 genomes. Second, each hit (E-value ≤ 10⁻⁵) was in silico translated and used as a query for searching the D. melanogaster genome. If the best hit in this second round corresponded to the original D. melanogaster gene, the sequence was considered an orthologous sequence.

We checked whether identified duplicated genes were artifactual (i.e., attributable to sequencing errors and the consequent erroneous assembly). For this purpose, we used Fisher's exact test to contrast whether the relative number of nucleotide differences between duplicates was similar for silent and nonsynonymous positions. Copies with significantly different ratios were considered to be true paralogs. For the remaining cases, we checked the quality of either the genomic sequences or the trace archives at the mismatch positions, discarding those sequences with poor quality (phred score < 20).

We confirmed the orthologous/paralogous relationships of the different eIF4E genes in the 12 Drosophila species by analyzing the topology of the protein gene tree. Orthologous relationships of highly incomplete sequences were established by colinearity conservation analysis.

Phylogenetic reconstruction

We generated a multiple sequence alignment (MSA) of the amino acid sequences of each orthologous group using the software ProbCons 1.11 (Do et al. 2005). This MSA was used to guide the alignment of the CDS. The resulting CDS alignments were manually improved using the software BioEdit 7.0.5.2. Unreliably aligned regions were removed with Gblocks 0.91b (Castresana 2000) using the default protein alignment parameters.

For each orthologous group, we conducted a bayesian phylogenetic reconstruction using the software MrBayes 3.1.2 (Ronquist and Huelsenbeck 2003), applying the nucleotide substitution model that best fits the data according to the Akaike information criterion. The FindModel program (http://hcv.lanl.gov/content/sequence/findmodel/findmodel.html or http://www.hiv.lanl.gov/content/sequence/findmodel/findmodel.html; an implementation of the MODELTEST software; Posada and Crandall 1998 ) was used for model selection. When the best-fitting model was the HKY+Γ (not implemented in MrBayes), we used the GTR+Γ model (i.e., the next most complex model implemented in MrBayes). All analyses were conducted allowing for a proportion of sites to be invariable (I). The eIF4E protein phylogenetic tree was reconstructed by bayesian inference using the Whelan-Goldman model of amino acid evolution (Whelan and Goldman 2001).

Codon-based analysis

We evaluated the impact of natural selection by estimating nonsynonymous (d_N) and synonymous (d_S) divergence, and their ratio (ω = d_N/d_S) using the program codeml from the PAML 3.15 package (Yang 1997). We restricted this analysis to the six melanogaster group species (D. melanogaster, D. simulans, D. sechellia, D. yakuba, D. erecta, and D. ananassae) to avoid saturation at synonymous sites, which could bias the d_S estimates and therefore the ω values, and also because of the impossibility of obtaining reliable alignments for all 12 species. We used MSAs based on 1:1 ortholog sets. In the two cases in which there were more than one gene copy in a given species (i.e., co-orthologs), we used the gene with the most complete sequence or the one without any pseudogenization features (stop codons or frameshift mutations). Only clearly alignable regions of the MSAs were used.

The M0 model (the simplest model, which assumes a single ω value for all lineages and sites) was used for most analyses. We also applied the FR model (which assumes that each lineage has a different ω value) and a specific two-ratio model (assuming two different ω values across the phylogeny). To determine whether some codon positions evolve under positive selection, we compared the M1a and M2a models (Wong et al. 2004) and also the M7 and M8 models (Yang et al. 2000) using the likelihood ratio test (Whelan and Goldman 1999). The FDR associated with multiple testing was controlled at q = 0.05 (Benjamini and Hochberg 1995). The Bayes Empirical Bayes approach (Yang et al. 2005) was used to identify the codons evolving under positive selection (posterior probability ≥ 95%).

Given the differences between gene trees and the species tree concerning the phylogenetic position of the D. erecta and the D. yakuba lineages (Pollard et al. 2006), for each orthologous group we used the topology (from the three competing alternatives) that best fits the data according to the M0 model. We conducted all likelihood estimations using three different ω starting values (0.1, 1, and 2) to overcome the problem of multiple local optima. All these analyses were conducted using the F3×4 codon frequency model (Goldman and Yang 1994).

Network-level analysis

We coded the structure of the IT pathway into a directed graph (termed G, Fig. 2A) with nodes and arcs representing genes/proteins and signaling (activation/inhibition) interactions, respectively. We restricted the analyses to the intracellular part of the pathway. Elements that do not directly interact with any other element in the graph (PTEN) or which have an unclear position in the pathway (Step; Fuss et al. 2006) were not included in G. Additionally, to avoid using redundant information, we considered only one of the seven genes encoding the eIF4E isoforms: the gene with the highest mRNA abundance in D. melanogaster (eIF-4E; Chintapalli et al. 2007; Hernandez et al. 2005). In total, the resulting G graph has 19 nodes connected by 25 arcs. Twenty of these interactions are physical—direct PPIs, four are metabolic (p110 catalyzes the synthesis of the membrane phospholipid PIP₃, which recruits Chico, Melted, PDK1, and PKB proteins to the cell membrane), and the other involves the activation of the Thor gene by the dFOXO transcription factor.

We generated two subgraphs of G (termed S and T) by removing some arcs. The S graph contains only the 20 physical PPIs (Fig. 2C) and was used to contrast whether levels of selective constraint and patterns of gene duplication are more similar for physically interacting proteins. T is a directed spanning tree of G obtained according to biochemical criteria; in this graph, Chico is in the root (upstream) while the effectors of the pathway are downstream (Fig. 2B). This graph was used to establish the position of the elements in the pathway, defined as the number of steps required to transduce the signal from InR to the other elements (the maximum number of steps was 10).

To establish whether physically interacting proteins in the IT signaling pathway exhibit similar levels of selective constraint, we applied the Monte Carlo method described in Fraser et al. (2002) to the S graph. For the analysis we used the X statistic, defined as

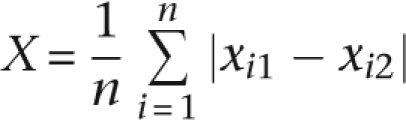where x_i1 and x_i2 are the evolutionary parameters (either d_N, d_S, or ω; the analysis was conducted separately for the three parameters) of the two genes encoding interacting proteins (1 and 2) at pair i, and n is the total number of interacting protein pairs (20 for the IT pathway). The statistical significance of X was determined by generating 100,000 randomizations of S. Each randomization had the same 19 nodes as S, and the same number of arcs (n = 20). Each arc was generated by randomly choosing two distinct nodes from S. To factor out the effect of the correlation between the pathway position and selective constraint, we conducted a modification of this Monte Carlo test. After fitting a linear model to the data (i.e., obtaining the regression equation relating the pathway position and either ω or d_N), we used the residuals of the linear model to obtain the X statistic value (i.e., for each gene we used as evolutionary parameter the difference between the observed and predicted selective constraint—ω or d_N—values).

We carried out an additional Monte Carlo test to determine whether the genes encoding physically interacting proteins tend to duplicate in the same phylogenetic branch. We used as statistic the number of gene pairs encoding physically interacting proteins that duplicated in the same phylogenetic branch. The statistical significance was evaluated on the basis of 100,000 replicates. In each replicate we incorporated 20 duplication events (sampled with replacement from that observed in our data; Fig. 1) across the 22 branches of the phylogenetic tree. Each duplication event was incorporated into a given branch with a probability proportional to its branch length. For the analysis we used the Drosophila tree topology and branch lengths reported in Russo et al. (1995).

Multivariate analysis

We performed a multivariate analysis considering d_N, ω, the pathway position, and some parameters influencing purifying selection levels (expression level, codon bias, protein length, and connectivity). First, we evaluated whether these parameters correlated using Spearman's rank correlation coefficient (ρ). Later, we analyzed the data using path analysis, an extension of multiple regression analysis that allows decomposing the regression coefficients into their direct and indirect components by considering an underlying user-defined causal model, and to assess the statistical significance of the relevant direct components. This analysis was conducted using the Amos 6.0 software.

Connectivity was estimated as the number of PPIs involving each D. melanogaster IT pathway protein. Putative PPIs dealing with these proteins were obtained from Giot et al. (2003). mRNA abundance in the D. melanogaster adult body of each gene was obtained from the FlyAtlas database (Chintapalli et al. 2007). These data were log-transformed for the path analysis to improve normality. The codon usage bias of each orthologous group was measured as the median of ENC (Wright 1990) of the six melanogaster group species. ENC values of each sequence were obtained using the DnaSP 4.20.1 software (Rozas et al. 2003).