Structural Insight into RNA Hairpin Folding Intermediates

Abstract

Hairpins are a ubiquitous secondary structure motif in RNA molecules. Despite their simple structure, there is some debate over whether they fold in a two-state or multi-state manner. We have studied the folding of a small tetraloop hairpin using a serial version of replica exchange molecular dynamics on a distributed computing environment. On the basis of these simulations, we have identified a number of intermediates that are consistent with experimental results. We also find that folding is not simply the reverse of high-temperature unfolding and suggest that this may be a general feature of biomolecular folding.

RNA hairpins are one of the most common secondary structure motifs, appearing in most every large RNA structure.^1–3 In addition to serving as nucleation sites for RNA folding,(4) they may also guide RNA folding by forming tertiary contacts^5,6 and serve as recognition sites for RNA binding proteins.(7) They are potential drug targets,(8) terminate transcription,(4) and influence translation through their role as aptamer domains in riboswitches.(9) Despite the great variety of functions they may serve, hairpins are one of the simplest RNA motifs, requiring only monovalent ions to fold. Thus, understanding the folding of small RNA hairpins is both a critical first step in understanding the folding of larger RNA molecules(8) and amenable to computer simulation.^10–12

RNA hairpins consist of a primarily Watson−Crick base-paired stem capped with a loop of unpaired or non-Watson−Crick base-paired nucleotides. Tetraloops, such as the GCAA tetraloop (5′-GGGCGCAAGCCU-3′) examined in this work and shown in Figure 1, have four such bases in their loop. This particular structure was chosen due to its predominance in the ribosome.(3)

Figure 1.

(A) NMR structure of the GCAA tetraloop. (B) Contact map for the native state. Bases are numbered from 5′ to 3′, and native base-pair contacts (dotted lines) are numbered 1−4.

Despite their simple structure, there is some controversy over whether these hairpins fold in a two-state or multi-state manner. The two-state hypothesis for nucleic acid hairpins is primarily based on thermodynamic measurements. For example, Ansari et al. found similar sigmoidal melting curves when they monitored all the base-pairing interactions or a subset of fluorescently labeled nucleotides.(13) The multi-state hypothesis is based on kinetic measurements, such as FCS and T-jump experiments. For example, Jung et al. found discrepancies between equilibrium distributions from FCS and melting experiments.(14) More recently, Ma et al. found evidence of melting in T-jump experiments starting at temperatures above the melting temperature (T_M), indicating that the supposed unfolded state in melting experiments is not completely unstructured.^15,16 These authors went on to propose an intermediate state in which the ends of the hairpin are in contact but the base-pairing and base-stacking interactions in the stem are not yet formed.

To investigate if there is, in fact, an intermediate and, if so, what its structure is, we have run serial replica exchange molecular dynamics (SREMD)^17,18 simulations of the GCAA tetraloop depicted in Figure 1. Due to the heterogeneity of the loop,^19,20 we have defined the native state as any conformation with all four stem base-pair contacts formed, numbered as shown in Figure 1B. We refer to these base-pair contacts as native contacts. Two nucleotides are considered to be contacting if any two atoms, one from each nucleotide, fall within 3 Å of each other. Thus, a structure can be well described by a contact map—a bit string specifying which residues are in contact.

Previously, Sorin et al. studied the folding of this system using constant temperature molecular dynamics (MD) and explicit solvent.(10) While these studies provided valuable insight into the folding of RNA hairpins, only 19 folding events were observed within the thousands of simulations run. We have applied SREMD on the Folding@home infrastructure to obtain better sampling and, therefore, greater insight into RNA folding.

SREMD is a serial version of replica exchange molecular dynamics (REMD),^21,22 which induces the system to perform a random walk in temperature space such that broad sampling is achieved at high temperature and detailed exploration of free energy minima is achieved at low temperature. In REMD, multiple simulations are run, each at a different temperature. A random walk in temperature space is achieved by periodically attempting to swap the conformations at two neighboring temperatures. The probability of accepting a swap is

where P(i→j) is the probability of transitioning from temperature i (T_i) to temperature j (T_j), β_i is 1/(kT_i), and U_i is the potential energy of the conformation at T_i. Thus, the detailed balance condition is satisfied. SREMD allows any number of asynchronous simulations to be run, making it more suitable for distributed computing than standard REMD.(18) This is accomplished by providing each simulation with the potential energy distribution function (PEDF) for each temperature. SREMD uses the same criteria for swapping temperatures as REMD except that the energy of the current conformation is compared to an energy randomly drawn from the neighboring temperature’s PEDF rather than the energy from a parallel simulation. The simulation parameters are described in detail in the Supporting Information (SI).

We ran 2800 SREMD simulations with an aggregate simulation time of 54.6 μs starting from the NMR structure (PDB code 1ZIH) in the explicit solvent.(2) Even with this amount of simulation, reversible folding was not achieved and we cannot claim to be at equilibrium.(24) However, we did observe 760 trajectories with a complete unfolding event and 550 trajectories with a complete refolding event. Thus, we have sufficient data to define the dominant states in the folding and unfolding pathways, though we cannot give their relative probabilities. While SREMD will not give any kinetic information directly, an analysis of the relevant thermodynamic states can yield information about the states along the folding and unfolding pathways and their hypothesized connectivity.

An unfolding event is defined as the set of conformations between the first point with no contacts between any two residues on opposite sides of the stem and the first preceding point with four native contacts. A refolding event is defined as the set of conformations between the first point with no contacts between any two residues on opposite sides of the stem and the first subsequent point where the number of native contacts is four.

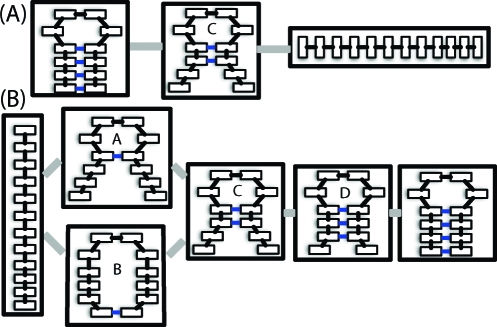
We used Mapper,^25,26 a topological data analysis algorithm, to identify the dominant states in the folding and unfolding pathways. For example, to understand unfolding, we applied the Mapper technique to conformations from unfolding events, where the conformations were represented by contact maps. The Mapper clustering technique works as follows: First, the similarity between each pair of conformations was determined using the Hamming distance metric. The data set of interest was then divided into overlapping subsets based on the density of configurations around each conformation, allowing efficient identification of intermediate states with low populations as well as folded/unfolded states with high populations. Single-linkage clustering was carried out in each subset, facilitating the identification of nonconvex clusters. Finally, a graph was generated that represents the connectivity between clusters in different density levels based on their degree of overlap. Though this connectivity is based on structural similarity rather than kinetic connectivity, it was found to be consistent with our SREMD pathways.(25) More details are provided in the SI.

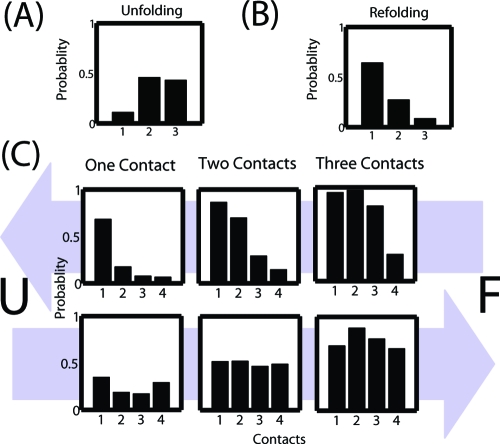
In SREMD, replicas visiting high temperatures lead to rapid unfolding. To better understand this unfolding process, we first calculated the probability of having one, two, or three native contacts during unfolding as shown in Figure 2A. These data indicate that there is substantial breathing, with one or two base pairs being broken and re-formed, but that complete unfolding quickly follows the breakage of three native contacts. Further insight is provided by Figure 2C, where we show the probability of each native contact given that a certain number of native contacts are present. Apparently, unfolding has a single dominant pathway characterized by unzipping from the end. This result is confirmed by Mapper, as shown in Figure 3.

Figure 2.

Probability of a given number of native contacts during (A) unfolding and (B) refolding. (C) Probability of each contact when a given number of contacts are present during unfolding and refolding, with the arrows representing the direction of movement between the unfolded state (U) and the folded state (F).

Figure 3.

Contact maps representing the cluster centers from independent clustering of the unfolding (A) and refolding data (B). The gray lines represent the connectivity of the states. The blue lines represent native contacts with a probability of 0.6 or greater within the cluster. Intermediate structures are labeled A−D.

Figure 2B shows that there is often a single contact present during refolding but adding subsequent base pairs becomes progressively less likely. Thus, there are many nucleation events consisting of the formation of a single native contact, but few proceed to the folded state. Figure 2C again shows the probability of each contact given that a certain number of contacts are present. When a single native contact is present, it is most likely between the closing base pair or the two ends, native contacts 1 and 4, respectively. The higher probability of native contact 1 is probably due to the close special proximity of the two participating residues imposed by their close proximity in the sequence. The higher probability of native contact 4 may be explained by the lack of steric hindrance relative to the other native contacts. Once two or three native contacts are formed, each is more or less equally probable, which is consistent with numerous models.

The results from Mapper shown in Figure 3 give more insight. The first step is the formation of either the closing base pair or the end base pair. This is followed by the formation of native contacts 1 and 2, and subsequent folding is dominated by zipping. Presumably, the formation of the end base pair facilitates the formation of native contacts 1 and 2 by reducing the conformational space that needs to be searched, as predicted by Ma et al.(15) The fact that the end base pair does not appear in the center of the cluster with two native contacts does not mean it breaks as folding proceeds, just that it does not occur frequently within the cluster. This is consistent with the fact that about four times as many refolding events occur through the pathway starting with the formation of native contact 1 as go through the pathway starting with the formation of native contact 4. Once again, we note these relative probabilities are not necessarily expected to be found in experimental studies due to the random walk in temperature space our simulations undergo. However, these are expected to be the two dominant pathways.

The two folding pathways observed here are consistent with the zipping and compaction mechanisms observed by Sorin et al.(10) as well as experimental work pointing to the presence of multiple folding pathways.^8,27 Furthermore, these results support the hypothesis that the folding pathway of RNA hairpins has at least three states. In particular, the collapsed structure with a single native contact between the end base pair is consistent with the intermediate structure proposed by Ma et al.(15) However, the other states along the folding pathway with one, two, or three native contacts formed may also contribute to the experimental signal. Full-atom structures for each of these intermediates are shown in Figure 4. Reptation (defined as the sliding of the two strands of the stem relative to one another) is not one of the dominant folding pathways, in agreement with results for small β-hairpins.(28) Thus, it appears that misfolded states must unfold before refolding properly, although we cannot discount the possibility that they may contribute to folding on longer timescales than our simulations reach. Results from the unfolding analysis using Mapper lend further support to this hypothesis. They include small clusters of reptated structures between the folded and intermediate states (data not shown), consistent with the idea that misfolding serves as an off-pathway trap that slows the overall folding process.^8,13,16,28

Figure 4.

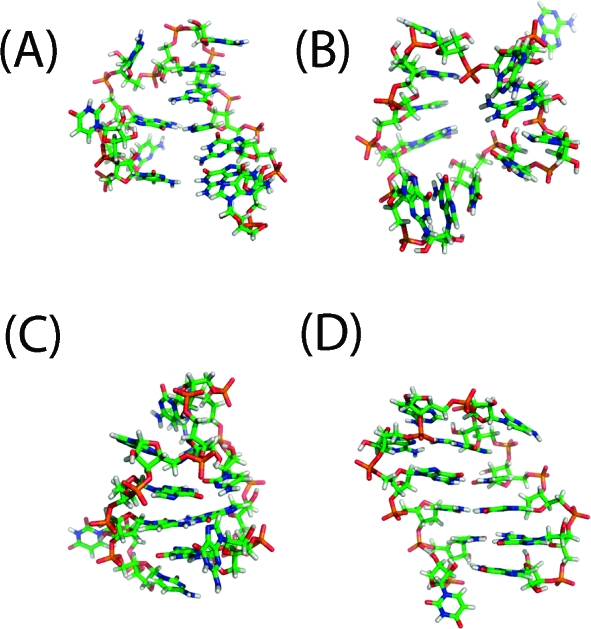
Representative full-atom structures for the intermediate states with labels (A−D) corresponding to the labels A−D in Figure 3.

Another result of this work is that low-temperature folding and high-temperature unfolding follow different pathways. We propose that this may be a general feature of hairpin folding, due to the intrinsic similarities in the thermodynamic forces which stabilize their structure. Furthermore, the amount of sampling we have achieved and the fact that we have still not reached convergence calls into question the results of shorter REMD studies. Such simulations will be dominated by nonequilibrium unfolding, which as we show here does not necessarily provide any insight into folding. Applying measures of convergence, such as reversible folding or agreement between simulations with different starting states, is critical for validating such studies.

The results presented here support recent work indicating that the folding of even the smallest of RNA motifs is quite complex. We have identified a number of folding intermediates consistent with experimental observations. We also found multiple highly populated folding pathways but only a single dominant unfolding pathway. Significant sampling was necessary to gain any statistics on folding, indicating that shorter simulations are dominated by unfolding, which differs from the folding pathway in this system. In future works, we intend to determine the sequence dependence of intermediate states and folding kinetics. We will also perform further constant temperature simulations to confirm that the pathways observed in our SREMD simulations are indeed biologically relevant. Such work will provide more insight into whether or not folding and high-temperature unfolding differ for biomolecules in general.

Supporting Information Available

SREMD method, simulation details, Mapper, PEDFs, and melting curves. This material is available free of charge via the Internet at http://pubs.acs.org.

Funding Statement

National Institutes of Health, United States