Determining the lifetime density function using a continuous approach

Abstract

Objective

To apply a continuous hazard function approach to calculate the lifetime density function (LDF) at any age, and to compare the life expectancies derived from the LDF with those obtained with standard life table (SLT) methods.

Methods

Age‐specific mortality rates were modeled through a continuous hazard function. To construct the cumulative hazard function, appropriate integration limits were considered as continuous random variables. The LDF at any age was defined on the basis of the elemental relationships with the cumulative hazard function. Life expectancies were calculated for a particular set of mortality data using the SLT approach and the expectancy of the LDF defined.

Applications and comparisons

The proposed approach was applied using mortality data from the 2001 census of Catalonia (Spain). A Gompertz function was used to model the observed age‐specific mortality rates, which fitted the observed data closely. The LDF and the life expectancy, median and standard deviation of the LDF were derived using mathematical software. All differences, in percentages, between the life expectancies obtained from the two methods were 1.1% or less.

Conclusions

The LDF gives a wider interpretation of life duration, by extending a deterministic value like life expectancy to a fully informative measure like the LDF.

Life expectancy is a widely used measure in epidemiology that provides a point estimation of the expected remaining lifetime of an individual at a given age.¹,²,³,⁴,⁵,⁶ It is commonly calculated with standard life table (SLT) methods, usually given for discrete time intervals.²,⁴,⁷ The existing variability in life duration contrasts with life expectancy, which does not truly represent the wide range of possible lifetime values.³ The lifetime density function (LDF) is a highly informative measure for studying mortality and life duration, but it cannot be derived directly from age‐specific mortality rates.⁶ A continuous interpretation of lifetime, and consequently of life expectancy, can be performed using a continuous form of the hazard function and treating age conveniently as a continuous variable. The objective of this analysis was to apply a continuous hazard function approach for the calculation of the LDF at any age, and to compare the life expectancies derived from the LDF with those obtained with SLT methods.

Methods

Basis of the method

We will refer to time as a continuous random variable and not as a discrete time interval, in which the future lifetime expresses the amount of time to be lived after a particular age. The probability density function of lifetime given by f(x)  =  µ(x)S(x) is derived on the basis of the relationship between the hazard function µ(x) and the survival function given by S(x)  =  exp(–H(x)). These three functions are equivalent in the sense that any two may be derived from the third.²,⁶,⁸,⁹,¹⁰ In the expression of the survival function; H(x) denotes the cumulative hazard function, which is equivalent to the area under the hazard function µ(x). The area under the hazard function was defined by taking the corresponding integration limits ranging from x, current age of an individual, to x + y_x, age at death or quantity of time lived from birth to death, where X and Y_x are non‐negative continuous random variables.

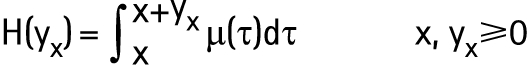The calculated area will give the risk of dying at a given age x up to a particular future time y_x. Substituting the terms in the expression of the probability density function given by f(x)  =  µ(x)S(x) the following expression is obtained:

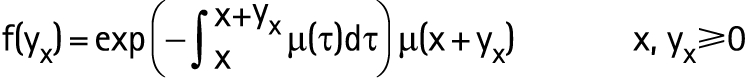Where µ(τ) denotes a continuous form of the hazard function. The hazard is a rate and thus it is non‐negative and has no upper bound. Under some circumstances, the observed mortality rate can be modeled as a parametric continuous hazard function if proper time units and death as the event of interest are considered.

The LDF cannot be defined solely by its mean and variance because it does not follow a symmetric pattern. Solving equation 2 provides important information in the interpretation of life duration, allowing any statistical measure usually obtained from a density function to be calculated.

Validation

A specific case was developed. The setting was Catalonia (Spain). Population data of the last census of Catalonia in 2001 and the number of deceased in 2001 were obtained from the Institute of Statistics (Institut d'Estadística de Catalunya; IDESCAT). The calculated mortality rates were modeled through a Gompertz function using the Levenberg–Marquardt non‐linear iterative least‐squares method.¹¹,¹²,¹³,¹⁴,¹⁵ Separate models were adjusted for men and women. The Gompertz function was the curve that best fitted our observed data.¹¹,¹²,¹³,¹⁴,¹⁶,¹⁷,¹⁸,¹⁹,²⁰

To compare SLT calculations and the approach proposed, life expectancies were calculated by applying both methods to the population and mortality data from Catalonia described above. The differences between the life expectancies predicted by the two approaches were calculated.

Applications and comparisons

Representation of the observed mortality rates and the modeled Gompertz hazard function showed that the estimated function almost overlaps with the observed mortality rates for both men and women (data not shown).

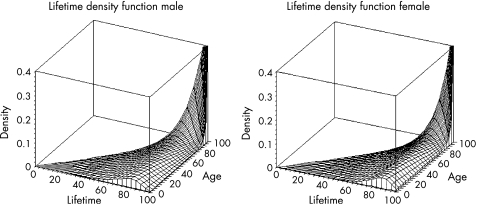
The lifetime probability density functions at any current age are represented in fig 1 and show a great asymmetry, being left skewed and with a flattened slope for ages under 50 years for men and 60 years for women. As age increases over these values, the density becomes more right skewed and leptokurtic.

Figure 1 Density function of life duration for men and women. Mortality data from Catalunya 2001.

Table 1 compares the life expectancies obtained with the approach proposed with those obtained from the SLT method. Life expectancies were calculated for all age values between one and 100 but, for reasons of space, only ages at five‐year intervals are presented in the table; however, the results refer to all the data. All differences were 1.1% or less. For women, the largest difference was found in the middle‐age range (approximately 55–65 years), in which a maximum difference of 0.90 (84.51 versus 85.41) more years for the age of 58 years was estimated with the SLT method. This difference diminished gradually as younger and older ages were considered. For males the largest differences were found in the youngest age groups (1–15 years of age) and in those approximately 60 years of age. A maximum difference of 0.70 (77.62 versus 76.92) more years was estimated by the proposed approach for infants aged one year, and a difference of 0.53 (81.47 versus 82.00) more years was estimated by the life tables for people aged 65 years.

Table 1 Life expectancy (age at death) from standard life table calculations.

Age (years)	Males					Females
	Life table	Lifetime density function			% Difference in life expectancy	Life table	Lifetime density function			% Difference in life expectancy
	Life expectancy	Life expectancy	Median age at death	Lifetime SD		Life expectancy	Life expectancy	Median age at death	Lifetime SD
5	77.00	77.63	79.68	12.56	0.82	83.75	83.70	85.41	10.39	0.05
10	77.06	77.64	79.69	12.52	0.76	83.79	83.71	85.41	10.38	0.10
15	77.11	77.67	79.69	12.45	0.72	83.83	83.71	85.41	10.37	0.14
20	77.30	77.71	79.70	12.36	0.53	83.92	83.72	85.41	10.35	0.25
25	77.54	77.77	79.72	12.24	0.30	84.00	83.73	85.41	10.31	0.32
30	77.74	77.86	79.74	12.06	0.15	84.10	83.75	85.42	10.26	0.42
35	78.00	77.99	79.78	11.83	0.01	84.23	83.78	85.43	10.19	0.53
40	78.30	78.19	79.85	11.51	0.13	84.38	83.83	85.44	10.07	0.65
45	78.72	78.49	79.97	11.09	0.30	84.58	83.92	85.47	9.89	0.77
50	79.23	78.91	80.15	10.56	0.41	84.83	84.07	85.51	9.64	0.90
55	79.95	79.51	80.46	9.90	0.56	85.16	84.31	85.60	9.28	1.00
60	80.82	80.34	80.94	9.10	0.60	85.56	84.68	85.76	8.80	1.03
65	82.00	81.48	81.69	8.16	0.64	86.09	85.25	86.04	8.15	0.97
70	83.42	82.98	82.82	7.12	0.52	86.84	86.11	86.54	7.34	0.84
75	85.23	84.91	84.46	6.00	0.37	87.84	87.34	87.39	6.37	0.57
80	87.49	87.32	86.68	4.87	0.19	89.30	89.06	88.77	5.28	0.27
85	90.33	90.23	89.54	3.79	0.11	91.45	91.34	90.83	4.15	0.12
90	93.70	93.60	92.97	2.82	0.10	94.33	94.21	93.65	3.07	0.12
95	97.74	97.41	96.90	2.01	0.34	98.05	97.66	97.17	2.12	0.40

Life expectancy (age at death), median and standard deviation (SD) from the lifetime density function, and percentage difference in life expectancy between standard life table calculations and the continuous lifetime calculation proposed. Data from Catalonia, 2001.

What this paper adds

The study of mortality is of great interest for epidemiologists, demographers and statisticians. Calculation of the lifetime distribution function at any age using a continuous approach gives useful information for the interpretation of mortality and life duration beyond the usual life expectancy calculated through standard life tables.

As the present study concerns asymmetric forms of the density function, calculation of the median and standard deviation of the distribution was especially relevant and is included in table 1. Median values were higher than mean values for ages less than 60 years for men and under 75 years for women, reflecting the left skewness of the distribution for these ages. For ages over these values the opposite relationship was found but was less pronounced. Standard deviations were larger in males than in females for ages under 65 years, for ages over 65 years women had larger standard deviations. The large standard deviations obtained show the great variability involved with human mortality and life duration.

Policy implications

The applied procedure, which is based on age‐specific mortality rates, gives the opportunity to study life duration more accurately, because all the information about the distribution of lifetime is contained in its density function. Obtaining density functions is essential in several statistical methods such as Bayesian analysis or simulation.

Discussion

Life expectancies obtained from the LDF were valid as they were similar to those calculated using SLT methods. The applied method allows the characterisation of the lifetime distribution, which seems essential on account of the level of uncertainty found in life expectancy.⁶ The LDF was shown to be non‐symmetric and to have different shapes depending on the current age considered. In addition to its utility in the interpretation of mortality, the LDF might be of great interest in situations in which a priori distributions are needed, such as Bayesian statistics or stochastic processes. A poorly estimated hazard function would, however, lead to biased estimations.²,¹⁰,²¹

In conclusion, the LDF provides a wider interpretation of life duration by extending a deterministic point estimation such as life expectancy to a totally informative measure like the density function of lifetime values.

Abbreviations

LDF - lifetime density function

SLT - standard life table