Computation by oscillations: Implications of experimental data for theoretical models of grid cells

Abstract

Recordings in awake, behaving animals demonstrate that cells in medial entorhinal cortex show ‘grid cell’ firing activity when a rat explores an open environment. Intracellular recording in slices from different positions along the dorsal to ventral axis show differences in intrinsic properties such as subthreshold membrane potential oscillations (MPO), resonant frequency and the presence of the hyperpolarization activated cation current (h-current). The differences in intrinsic properties correlate with differences in grid cell spatial scale along the dorsal-ventral axis of medial entorhinal cortex. Two sets of computational models have been proposed to explain the grid cell firing phenomena: oscillatory interference models and attractor dynamic models. Both types of computational models are briefly reviewed and cellular experimental evidence is interpreted and presented in the context of both models. The oscillatory interference model has variations that include an additive model and a multiplicative model. Experimental data on the voltage-dependence of oscillations presented here supports the additive model. The additive model also simulates data from ventral neurons showing large spacing between grid firing fields within the limits of observed MPO frequencies. The interactions of h-current with synaptic modification suggests that the difference in intrinsic properties could also contribute to differences in grid cell properties due to attractor dynamics along the dorsal to ventral axis of medial entorhinal cortex. Mechanisms of oscillatory interference and attractor dynamics may make complementary contributions to the properties of grid cell firing in entorhinal cortex.

Introduction

The entorhinal cortex regulates the flow of information to and from the hippocampus, subiculum, and cortical regions such as postrhinal and perirhinal cortex (Witter et al., 1989; Burwell, 2000), suggesting a unique role for entorhinal cortex in memory and spatial processing (Parron and Save, 2004; Steffenach et al., 2005). Behavioral research indicates that cells in the medial entorhinal cortex (mEC), called ‘grid cells’, fire in spatially specific locations, which repeat at regular intervals (Fyhn et al., 2004; Sargolini et al., 2006; Moser and Moser, 2008). The pattern of spiking activity forms a hexagonal grid of firing and the spacing and field size of the spiking changes along the dorsal-ventral axis of mEC (Sargolini et al., 2006). Grid cell firing remains stable over several days or weeks in a familiar environment (Fyhn et al., 2004; Hafting et al., 2005) however, environmental changes such as external cue rotation (Hafting et al., 2005), complete darkness (Hafting et al., 2005), or a change in the size of a familiar environment (Barry et al., 2007) and lesions of the hippocampus (Fyhn et al., 2004) can cause the grid cell firing pattern to drift or change in field size and spacing, suggesting that grid cells rely on information about the environment to form functional fields.

Neurons in several distinct layers (I-VI) of medial entorhinal cortex show grid cell firing properties, with the highest density of grid cells located in layer II of the dorsal portion of mEC (Sargolini et al., 2006). The deeper layers (III, V, VI) of mEC show a higher proportion of head direction cells and conjunctive head direction and grid cells (Sargolini et al., 2006). The deeper layers of mEC project to layer II and provide head direction information in combination with head direction input directly from the dorsal presubiculum (Caballero-Bleda and Witter, 1993; Kohler, 1985; van Groen and Wyss, 1990). In addition to changes in grid cell firing properties along the dorsal-ventral axis of mEC, layer II cells also show dorsal-ventral changes in several intrinsic cellular properties (Giocomo et al., 2007; Giocomo and Hasselmo, submitted).

Intracellular data in entorhinal cortex

Layer II stellate cells in mEC develop rhythmic voltage oscillations at theta frequency (Klink and Alonso, 1997) near firing threshold (Alonso and Klink, 1993). Research suggests that interactions between two ionic conductances, the persistent sodium current (I_NaP) and the hyperpolarization activated inward rectifying current (I_h), cause subthreshold membrane potential oscillations in layer II neurons (Dickson et al., 2000; Fransen et al., 2004; Giocomo and Hasselmo, submitted). In vitro slice physiology research has demonstrated that in layer II mEC neurons the intrinsic properties, such as subthreshold oscillation and resonant frequency, change along the dorsal-ventral axis (Giocomo et al., 2007). Changes in the temporal frequency dynamics of cells in layer II correlate with the spatial changes in grid cell periodicity (Giocomo et al., 2007; Hasselmo et al., 2007) and may depend on a systematic change in the kinetics of I(h) (Giocomo and Hasselmo, submitted). Recent work indicates that the time constant of I(h) changes from fast to slow from dorsal to ventral entorhinal cortex (Giocomo and Hasselmo., submitted) and a biophysical computational model supports for a role of I(h) time constant kinetics in accounting for the different dorsal-ventral subthreshold oscillation frequencies observed (Heys et al., 2008). While changes in the temporal frequency dynamics of layer II neurons correlate with changes in the periodicity of grid cells, no causal experimental evidence yet exists to support this relationship. It remains unclear if the frequency dynamics themselves play a key role in grid cell periodicity (Burgess et al., 2007; Hasselmo et al., 2007) or if the dorsal-ventral temporal changes merely reflect a graded change in ion channel kinetics (Giocomo and Hasselmo, submitted), which play an alternate, different role in grid cell periodicity by impacting network dynamics (e.g. long-term potentiation) (Fuhs and Touretzky, 2006; McNaughton et al., 2006).

Computational Models of Grid Cell Formation

Several computational models of grid cell formation in the entorhinal cortex have been developed (Blair et al., 2006; Burgess et al., 2007; Fuhs and Touretzky, 2006; McNaughton et al., 2006; O'Keefe and Burgess, 2005). Computational models of grid cell formation include two types, oscillatory interference models (Burgess et al., 2007; Hasselmo et al., 2007) and attractor-dynamic models (Fuhs and Touretzky, 2006; McNaughton et al., 2006). Oscillatory interference models assume that modulation of interacting oscillatory dynamics by the speed and direction of the rat can result in a spatially dependent spiking pattern rather than a temporally dependent spiking pattern. The second type of model utilizes attractor dynamics and assumes specific patterns of synaptic interactions contribute to forming grid cell firing properties. While oscillatory interference models may rely on the temporal dynamics which change from dorsal to ventral (i.e. subthreshold oscillations and resonant frequency), attractor dynamic models could also depend more on h-current kinetics, which can influence synaptic plasticity and the spiking behavior of the neuron.

Methods

Slice Physiology

Previous publications describe the slice technique in detail (Giocomo et al., 2007). Briefly, the brain was removed under cold artificial cerebrospinal fluid (ACSF concentrations in millimolar: NaCl[126.0], KCl[3], MgSO₄[2], Dextrose[10.0], NaHCO₃[26.0], NaH₂PO₄[1.25], CaCl₂[2]) after anesthetization and rapid decapitation of a rat aged 17-24 days. The Institutional Animal Care and Use Committee at Boston University approved all experimental techniques. Under cold ACSF, 400-micron thick slices were placed in individual holding chambers and the depth of the last slice taken was measured, at 2 mm lateral from the midline and −4 mm Bregma. Patch pipettes (3-7 MΩ) were pulled from 10 cm borosilicate glass capillary tubes (Sutter Instrument) and filled with (in mM): K-gluconate[120], HEPES[10], EGTA[0.2], KCl[20], MgCl[2], diTrisPhCr[7], Na₂ATP[4] and TrisGTP[0.3] (pH adjusted to 7.3 with KOH). Whole-cell patch clamp recordings were amplified by a Multiclamp 700B. Capacitance neutralization and bridge balance were applied accordingly, and current clamp data was filtered at 10kHz and digitized with a Digidata 1440 at a sampling frequency of 20 kHz (50 μs). The liquid junction potential was estimated between 5 and 6 mV, membrane potential values reported here do not contain this correction. Dorsal cells are defined as cells located 3.8 – 4.9 mm from the dorsal surface of the brain (the postrhinal border occurs at approximately 3.8 mm from the dorsal surface according to Paxinos and Watson), ventral cells are defined as cells located 5.0 – 7.0 mm from the dorsal surface of the brain.

Analysis and statistics

Clampfit 10.0, MATLAB and Excel were used for data analysis. Overall, the data did not show a Gaussian distribution and the Kolmogorov-Smirnov test function ‘kstest2’ in MATLAB was used to test differences between two data samples (e.g. dorsal versus ventral). P-values less than .05 were considered significant. Regression lines were constructed using the least-squares method in Microsoft Excel and r values are reported.

To determine the dominant frequency of membrane potential oscillations, an automated script in MATLAB analyzed segments of membrane potential recorded near firing threshold (−55 mV, −50 mV, −45 mV and −40 mV). Three second long windows which overlapped by 1.5 seconds were zero centered and autocorrelations were performed using MATLAB's xcorr function. Data windows containing spikes were automatically removed. The inverse of the interval from the central peak to the first side peak determined the frequency of the autocorrelation and the three frequencies with the highest difference between the amplitudes of the side peak and trough were averaged.

To examine the increase in firing frequency to a constant current input, negative or positive current was used to hold the cell at −60 mV in current clamp. Depolarizing current steps (1.5 - 2.5 seconds in duration) were applied successively and the number of spikes counted. The amplitude of the current level which resulted in the first action potential was used to normalize the amplitude of each successive current step. Spikes per second was calculated and plotted relative to the normalized current amplitude.

To determine the peak-to-peak interval, a different automated script in MATLAB analyzed the same data segments. After applying a Butterworth filter between 0 and 15 Hz, an automated peak detection function (peakdetect) in MATLAB determined the peak-to-peak interval (in seconds) for oscillations at a membrane potential of approximately −50 mV.

Computational Simulations

The oscillatory interference model (Burgess et al., 2007) was simulated here using MATLAB. The MATLAB scripts were adapted from the scripts originally written by Michael Hasselmo (Giocomo et al., 2007; Hasselmo et al., 2007) and Eric Zilli (Giocomo et al., 2007). The long-linear track (18 m) was added as an environmental feature and utilized the random walk described in Hasselmo et al., 2007. For simulations of noise, the dendritic frequency was multiplied by a predetermined noise factor (.001, .002 or .003).

Results

Oscillatory interference models of Grid Cell Formation

Oscillatory interference models utilize the idea that two interacting oscillations of slightly different frequencies result in a constructive and destructive interference pattern that, when a threshold is applied, results in a periodic spiking pattern (Burgess et al., 2007; O'Keefe and Burgess, 2005). This model grew out of earlier models of theta phase precession (O'Keefe and Recce, 1993; Lengyel et al., 2003). The oscillatory model proposed by Burgess and O'Keefe (2005) relates experimental research demonstrating the change in the frequency of subthreshold oscillations to the spatial periodicity change in grid cells along the dorsal-ventral axis of medial entorhinal cortex (Burgess et al., 2007; Giocomo et al., 2007; Hasselmo et al., 2007). In the model, a baseline frequency interacts with changes in frequency induced by input from head direction cells modulated by the speed and direction of movement, allowing the resulting interference pattern to provide a mechanism for updating the internal representation of location, which corresponds to the integration of velocity necessary for path integration (McNaughton et al., 2006). A higher frequency of intrinsic subthreshold oscillations, as found in dorsal entorhinal cortex, shortens the distance between firing fields and supports the prediction by McNaughton and colleagues that a systematic variation in gain of a movement-speed signal could underlie differences in grid cell spacing (Maurer et al., 2005; McNaughton et al., 2006). Head direction cells in other layers of entorhinal cortex (Sargolini et al., 2006) as well as those in other structures (Sharp et al., 2001a; Sharp et al., 2001b; Taube and Bassett, 2003) could provide the speed modulated input based on head direction.

Subthreshold membrane potential oscillations

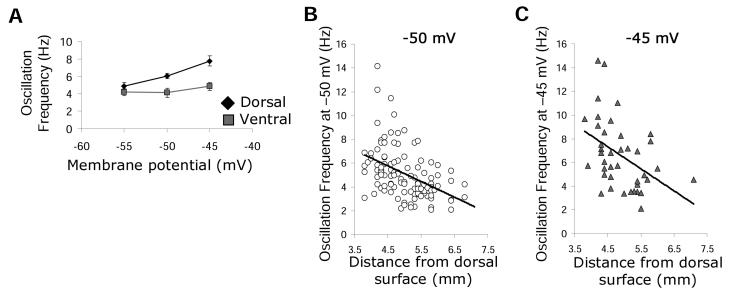
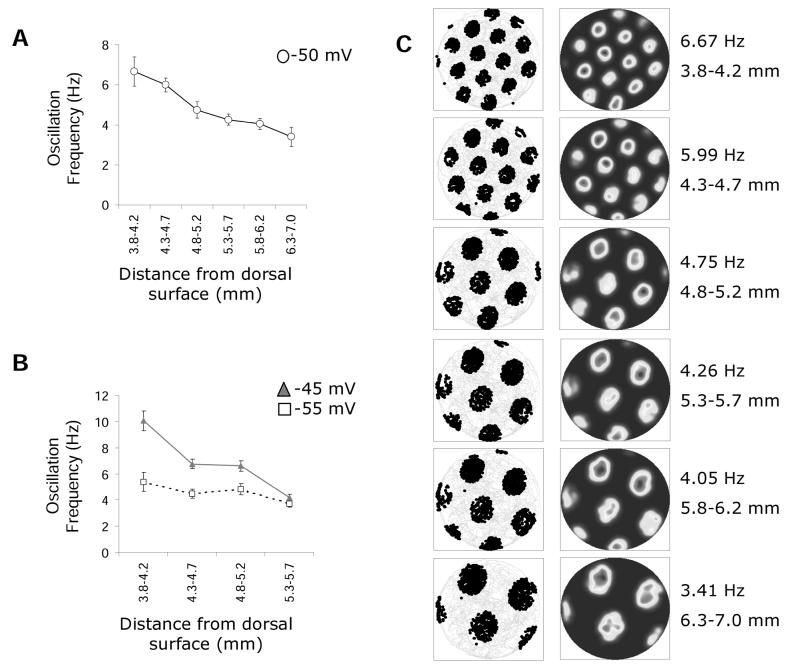
The frequency of subthreshold oscillations changes from dorsal (defined as 3.8-4.9 mm from the dorsal surface of the brain) to ventral (defined as 5.0 – 7.0 mm from the dorsal surface of the brain) medial entorhinal cortex (Giocomo and Hasselmo, submitted; Giocomo et al., 2007). Based on a collection of 137 stellate cells (Giocomo and Hasselmo, submitted; Giocomo et al., 2007) the mean frequency of subthreshold oscillations is higher in dorsal versus ventral entorhinal at an approximate membrane potential of −50 mV (mean Hz ± SEM; dorsal = 6.06 ± .30 and n = 56; ventral = 4.13 ± .18 and n = 59) and −45 mV (mean Hz ± SEM; dorsal = 7.76 ± .58 and n = 25; ventral = 4.87 ± .45 and n = 16) (Figure 1A). The change from high frequency in dorsal cells to low frequency in ventral cells occurs systematically at an approximate membrane potential of −50 mV (r = .44; slope = −1.32) and −45 mV (r = .43, slope = −1.86) (Figure 1B and 1C). When the mean oscillation frequency is binned into anatomical sections 400 microns thick, a decrease in the mean frequency is clearly observed from dorsal to ventral medial entorhinal cortex from 6.67 ± .74 Hz at the most dorsal region of 3.8 to 4.2 mm from the dorsal surface to 4.05 ± .28 at the more ventral region of 5.8 to 6.2 mm from the dorsal surface (Figure 2A). At the very ventral pole (6.3-7.0 mm from the dorsal surface, binned together due to a smaller sample size) the oscillation frequency decreases to 3.41 ± .48 Hz. The same decrease in frequency is observed for oscillations at an approximate membrane potential of −45 mV (5.8 to 7.0 not shown due to a small sample size). However, at an approximate membrane potential of −55 mV, the frequency does not change from dorsal to ventral mEC (mean Hz ± SEM; all dorsal = 5.31 ± .43 and n = 35; all ventral = 4.45 ± .34 and n = 23) (Figure 1A, 2B). Combined, the frequency change in dorsal to ventral near firing threshold indicates that the mechanism for the change in oscillations plays a crucial and selective role when the cell is more depolarized. Simulations of the Burgess model (Burgess et al., 2007; Hasselmo et al., 2007) demonstrates that the experimentally determined oscillation frequencies, binned into anatomical sections, results in grid cell firing with increasing larger field size and spacing along the dorsal-ventral axis (Figure 2C).

Figure 1.

Frequency of subthreshold oscillations across a population of 137 cells in medial entorhinal cortex. A. The mean subthreshold oscillation frequency in dorsal cells shows a significantly larger increase in frequency with voltage compared to a smaller slope of increase in ventral cells. B-C. The frequency of cells decreases systematically from dorsal to ventral at approximate membrane potentials of −50 mV (B) and −45 mV (C).

Figure 2.

Oscillation frequency decreases systematically from dorsal to ventral. A-B. The average subthreshold oscillation frequency is plotted for each anatomical bin at a membrane potential of approximately −50 mV (A), −45 mV (B) and −55 mV (B). C. Simulations of the oscillatory model using the average frequency from each anatomical bin shown in part A. The field size and spacing of the grid decreases as the frequency of the subthreshold membrane oscillation decreases. Left: Trajectory plotted in gray and spikes in black. Right: Smoothed plot of the firing rate data shown on the left.

Changes in frequency with depolarization

The oscillatory interference model proposed by Burgess et al., 2007 and analyzed by Hasselmo et al., 2007, requires a change in the frequency of subthreshold membrane potential oscillations dependent on changes in the membrane potential (depolarization or hyperpolarization). The model assumes that depolarization, relative to the baseline membrane potential, will result in an increase in the frequency of the subthreshold membrane potential oscillation. Based on oscillatory data collected from the combined set of 137 stellate cells, the frequency of subthreshold oscillations shows a substantially larger slope of change in dorsal cells than ventral cells from an approximate membrane potential around −50 mV to −45 mV (mean change in frequency ± SEM; dorsal = 1.70 and n = 59; ventral = .75 and n = 62). The larger slope of change in dorsal cells also appears in the change from an approximate membrane potential of −55 mV to an approximate membrane potential of −50 mV (mean change in frequency ± SEM; dorsal = .75 and n = 65; ventral = −.32 and n = 64).

Additional analysis on a subset of cells that oscillated at multiple membrane voltages (n = 66) indicated that the change in subthreshold oscillation frequency depends on the baseline frequency of the cell at −55 mV or −50 mV. Neurons with very high frequency oscillations at −55 mV decrease slightly in frequency with depolarization to −50 mV (r = .59; slope = −.65) while neurons with lower frequency oscillations at −55 mV increase in frequency with depolarization to −50 mV (r = .59; slope = −.65). The same trend occurs when comparing oscillation frequency at −50 mV with the more depolarized value of −45 mV (r = .42; slope = −.41). Ignoring the direction of frequency change (increase or slight decrease with depolarization) dorsal cells show significantly more voltage dependent change, as determined by the Kolmogorov-Smirnov test, in the frequency of subthreshold oscillations compared to ventral cells at a change from −55 mV to −50 mV (mean absolute frequency change ± SEM; dorsal = 1.98 ± .41 Hz and n = 23; ventral = 1.34 ± .26 Hz and n = 18; k = .37, p = .006) and at a change from −50 mV to −45 mV (mean absolute frequency change ± SEM; dorsal = 2.67 ± .40 Hz and n = 22; ventral = 1.54 ± .40 Hz and n = 13; k = .46, p = .0008).

Computational simulations using the Burgess model of the frequency change in subthreshold oscillations indicate that either a positive or negative change in the frequency of the oscillation is sufficient for generating grid cell firing patterns, as long as the changes are linear and consistent in direction.

Spiking frequency to current input

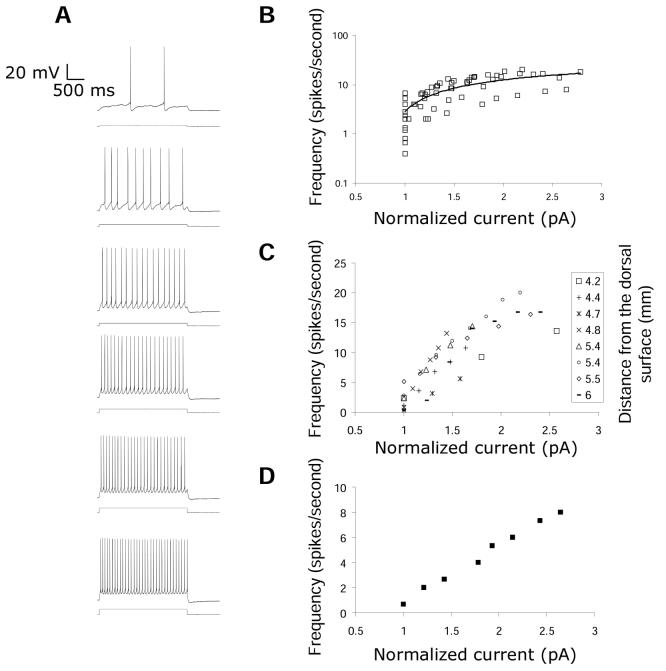
Oscillating stellate cells do not tend to spike near the frequency of their corresponding membrane potential oscillations or resonant frequency. Instead, in response to a constant depolarizing current injection, stellate cells tend to increase their firing frequency with each successive increase in current amplitude. Figure 3A shows a typical example of a stellate cell's response to slowly increasing amplitudes of current injection. Overall, both dorsal and ventral cells show a similar increase in firing frequency in response to current input (Figure 3B) and Figure 3C shows the firing frequency for eight different cells along the dorsal-ventral axis as the current input increases. These f-I curves suggest that membrane potential oscillations alone cannot directly determine spiking frequency (Burgess, 2008), but instead may need to interact with other neurons with stable baseline spiking frequencies, such as persistent firing neurons (Hasselmo, 2008).

Figure 3.

Effect of steady current injection on spiking frequency of stellate cells. A. Firing frequency of a single stellate cell at successively higher current amplitude steps 2.5 seconds long in duration. B. Frequency of spiking (spikes per second) relative to the normalized injected current amplitude for 15 stellate cells. C. Frequency of spiking relative to the normalized injected current shown for 8 individual cells along the dorsal-ventral axis. Legend lists the distance of each cell from the dorsal surface (mm). D. Example of a single stellate cell's spiking frequency relative to normalized injected current.

Simulations of grid cells

The multiplicative version of the Burgess oscillatory interference model (Burgess et al., 2007; Hasselmo et al., 2007; Burgess, 2008) was used in previous simulations to demonstrate that lower subthreshold oscillation frequencies resulted in grids with larger field size and spacing (Giocomo et al., 2007; Hasselmo et al., 2007). However, in the multiplicative model, the lowest experimentally observed mean membrane potential oscillation frequency of 3.41 Hz does not result in grids with firing fields and spacing as large as those observed in unit recording data from the most ventral pole of medial entorhinal cortex (Solstad et al., 2007; Brun et al., 2008).

The Burgess oscillatory interference model (Burgess et al., 2007; Burgess, 2008) was used in previous simulations to relate intracellular data to grid cell data (Giocomo et al., 2007; Hasselmo et al., 2007). These previous simulations used the multiplicative version of the model as follows:

$$g\left(t\right)={[\prod _{\theta }\cos \left(2\pi f\left(z\right)t\right)+(\cos 2\pi (f\left(z\right)t+f\left(z\right)B_H{\int }_0^{t}v\left(\tau \right)•h_{\theta }d\tau )+{\phi }_{\theta })]}_H$$

Where g(t) is the firing of the grid cell over time, with spiking determined by the threshold of a Heaviside step function []_H on the right side of the equation. The equation takes the product Π over dendrites receiving input from different head direction cells with preference angles θ. For each individual dendrite, the equation has two oscillations (soma and dendrite) with an initial phase difference φ_θ. In the absence of head direction input, these oscillations have the same baseline frequency f(z). In the multiplicative model, this baseline frequency f(z) stays the same over time but differs dependent on the dorsal to ventral anatomical location z of the neuron. The frequency of the dendritic oscillation is shifted by depolarization caused by speed modulated head direction cells. This depolarization is represented by the dot product of the velocity v and the unit vector h_θ representing head direction cell responses with different preferred head directions θ. Because the frequency shift is cumulative, the depolarization is integrated from starting time 0 until current time t. The depolarization by head direction is scaled by the constant B_H that is the same at all anatomical locations. For the multiplicative model, we assume that the experimental recording of membrane potential oscillation frequency f_e samples the change in frequency across all dendrites, with depolarization of membrane potential V_m replacing head direction input: f_e=f(z)+f(z)B_HV_m. This relationship is plotted in Figure 4E.

Figure 4.

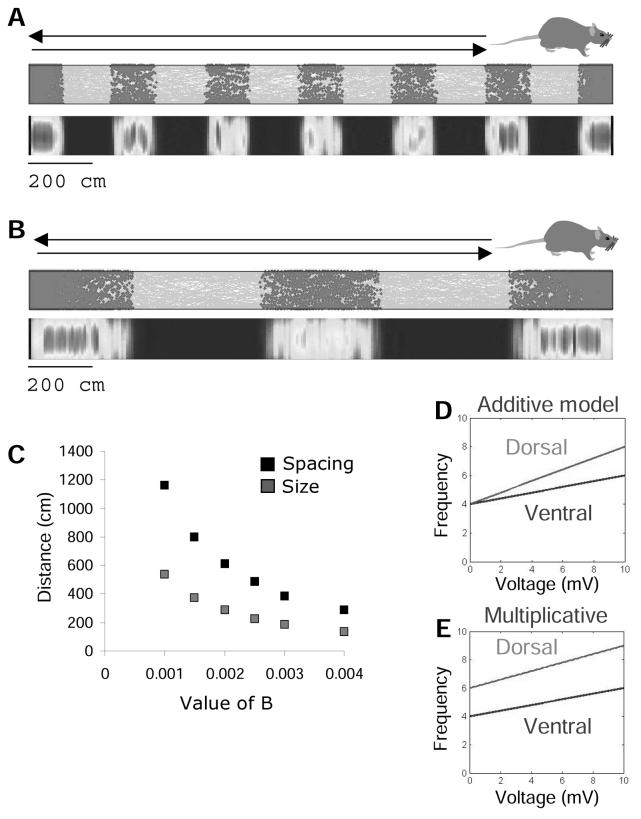
Changes in the voltage-dependence of oscillations corresponds to changing the B parameter. A. Simulation of the oscillatory model with a virtual rat running on an 18 m linear track. The B value was set to .004. B. Simulations of the oscillatory model on an 18 m linear track with the B value set to 0.0015, resulting in larger field size and spacing of the grid firing fields. C. Variations in the B parameter result in different field size and spacing of grid firing fields. Large B values result in smaller field size and spacing while smaller B values result in larger field size and spacing. D-E. Frequency changes with voltage associated with the additive model (D) and multiplicative model (E).

In this multiplicative model, the influence of a rat's velocity on frequency of the dendritic oscillation was scaled by the frequency of the soma oscillation and a constant value (B_H = .00385) derived from the relationship between the in vivo unit recording data (field size and spacing G of grid cell firing) and the in vitro slice physiology data (frequency f of subthreshold oscillations). For a review of how B_H is derived, see Hasselmo et al., 2007. This gave grid cell spacing according to the equation $G=2∕\sqrt{3}f\left(z\right)B_H$, or in simpler form G = H / f , where H is approximately 300 cmHz over all locations z. For a grid spacing G=600 cm, this would require a frequency of f(z)=0.5 Hz, which is below the range of observed membrane potential oscillation frequencies.

However, the originally proposed oscillatory interference model (Burgess et al., 2007) is referred to as an additive model, because the relationship of oscillation frequency to the depolarization (caused by speed-modulated head direction) does not depend on the baseline frequency, but only on the parameter B(z). Thus, the additive model takes the form:

$$g\left(t\right)={[\prod _{\theta }\cos \left(2\pi \mathit{ft}\right)+(\cos 2\pi (\mathit{ft}+B\left(z\right){\int }_0^{t}v\left(\tau \right)•h_{\theta }d\tau )+{\phi }_{\theta })]}_H$$

The main difference from the multiplicative model is that the change in oscillation frequency caused by depolarization (due to speed-modulated head direction) does not depend on baseline frequency. Instead, f(z)B is replaced by the parameter B(z) that reflects the slope of the frequency/voltage relationship found in neurons at different anatomical locations z. The units of B(z) in the model are cycles/cm, which multiplied by running speed in cm/sec becomes frequency in cycles/sec. For the additive model, the frequency recorded experimentally willbe f_e=f+B(z)V_m, as plotted in Figure 4D, and the baseline frequency f will not depend on anatomical location, consistent with Fig. 2B. The additive model in Fig. 4D more closely matches the experimental data in Figure 1A.

Thus, in the additive model, the change in spatial scaling along the dorsal to ventral axis requires a change in the parameter B(z) dependent on location z along the dorsal-ventral axis, resulting in a higher value of B(z) in dorsal compared to ventral entorhinal cortex. Simulations using the Burgess model tested the effect of the B(z) value on field size and spacing while a virtual rat randomly explored a long linear track (18 m in length, 10 cm in width). All simulations used the same baseline frequency value of f=4 Hz, consistent with the approximate baseline frequency observed at −55 mV for all dorsal to ventral positions (Figure 1A and Fig. 2B).

Figure 4A demonstrates how a smaller B(z) value of .004 results in larger field size and spacing (288 cm) of the grid firing. Reducing the B(z) value to 0.0015 results in even larger field size and spacing (770 cm) of the grid (Figure 4B). Figure 4C illustrates the field size and field spacing of the grid cell firing as a function of the value of B(z), which reflects the relationship obtained from the model $G=2∕\sqrt{3}B\left(z\right)$ The increase in the field size and spacing relative to the decrease in the value of B(z) results from a smaller difference between the soma and dendritic oscillation frequency, causing the oscillations to take a longer distance to transition in and out of phase relative to each other. The additive model has the advantage that very large spacing can be obtained within the range of observed oscillation frequencies. Oscillation frequency in these simulations did not go below the baseline frequency of 4 Hz. In addition, the voltage-dependence of the additive model, shown in Figure 4D matches the experimentally demonstrated voltage-dependence in Figure 1A better than the voltage-dependence of the multiplicative model shown in Figure 4E.

Oscillation Consistency

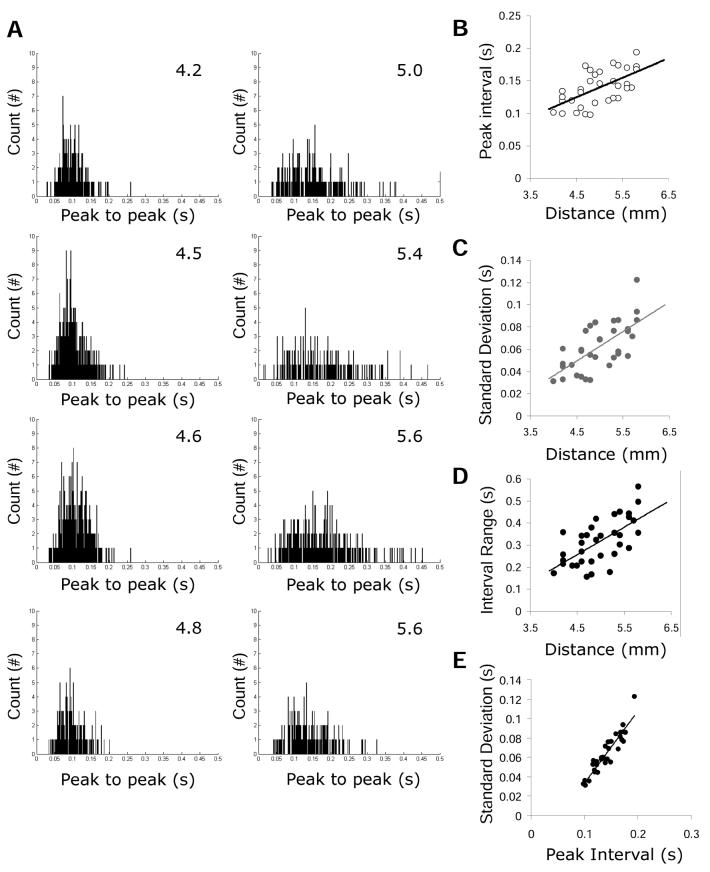
The oscillatory interference models proposed predict that any single intrinsic oscillation should show phase consistency over time when the level of input is constant. A selection of 35 stellate cells along the dorsal-ventral axis were analyzed for consistency of oscillation period. The average number of oscillation cycles analyzed was 191 ± 16 cycles. Figure 5A illustrates examples of the peak-to-peak intervals measuring oscillation period in four dorsal cells and four ventral cells. The average peak-to-peak interval was higher in dorsal (Peak to peak interval ± SEM; .126 ± .006 s and n = 18) compared to ventral (Peak to peak interval ± SEM; .151 ± .006 s and n = 17; p = .007 and k = .543) using this technique (Figure 5B). The phase consistency varied along the dorsal to ventral axis, with dorsal cells showing a more consistent phase compared to ventral cells, based on statistical measurements using the Kolmogorov-Smirnov test. The average standard deviation (Standard deviation of peak-to-peak interval ± SEM; .062 ± .004 s and n = 35) was significantly higher in ventral (Standard deviation of peak-to-peak interval ± SEM; .074 ± .005 s and n = 17) compared to dorsal cells (Standard deviation of peak-to-peak interval ± SEM; .0513 ± .005 s and n = 18; p = .023 and k = .48) (Figure 5C). The average range of the peak-to-peak interval (Range of peak-to-peak interval ± SEM; .315 ± .017, n = 35) was significantly higher in ventral (Mean range ± SEM; .370 ± .025 s and n = 17) compared to dorsal cells (Mean range ± SEM; .267 ± .019 s and n = 18; p = .046and k = .441) (Figure 5D). Overall, the ventral cells showed more variance in their oscillation consistency. Plotting the standard deviation relative to the peak-to-peak interval (Figure 5E) demonstrates the close correlation between an increase in the peak-to-peak interval time and an increase in the variance of the oscillation consistency (r = .94, slope = .75). The positive correlation between the peak-to-peak interval (time) and the standard deviation of the interval is reminiscent of the Weber Law, in which the variance of error increases in constant proportion with the original stimulus value (Chater and Brown, 2008; Weber, 1996).

Figure 5.

Variance of oscillation period along the dorsal to ventral axis. . A. Histograms of the distribution of oscillation period in four dorsal (left) and four ventral (right) cells. B. The oscillation period increases from dorsal to ventral mEC. C. The standard deviation of the oscillation period increases from dorsal to ventral mEC. D. The range of the oscillation period increases from dorsal to ventral mEC. E. Example of the Weber law. The standard deviation of the oscillation period is linearly related to the average interval length.

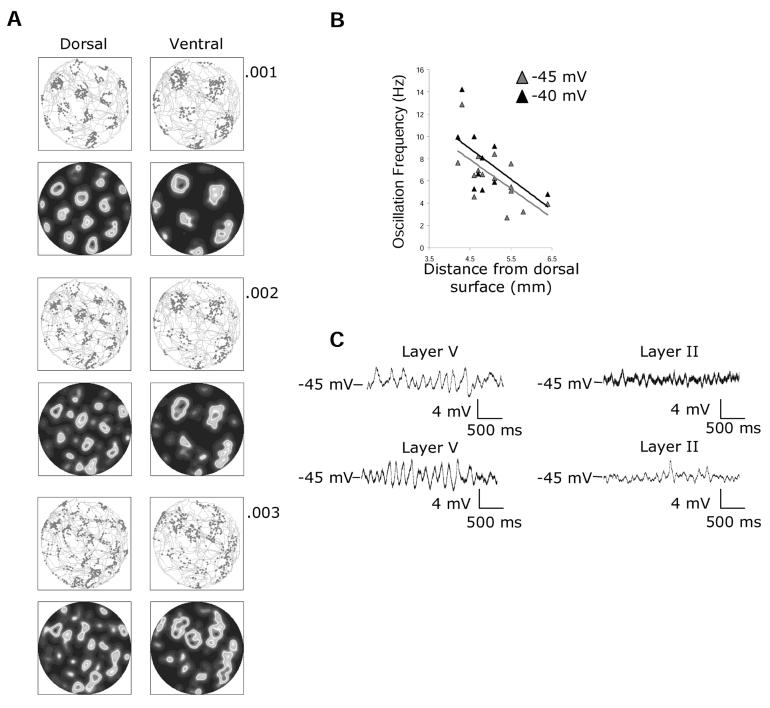
To investigate the effects of noise on the oscillatory model, a noise factor was introduced to the simulation. Noise was added to the dendritic oscillation frequency with a uniformly distributed random number between 0 and 1 scaled by a noise factor of 0.001, 0.002 or 0.003. The noise factor added to the dendritic oscillation frequency at each step caused the grid cell formation to drift over time (Figure 6A). A very small noise factor of .001 (top of Figure 6A) left the grid intact but even small increases in noise (.003 at the bottom of Figure 6A) resulted in a complete loss of the grid structure. The effect of noise on the grid cell firing output suggests that the recorded soma oscillations may reflect interference between dendritic and soma frequencies, resulting in a less consistent oscillation pattern in experimental data. To overcome this problem in the model, external input from place cells would need to constantly re-update the relative phases of the interference pattern. The noise also resulted in a decrease in the firing frequency of the grid cells by 22-41% in simulations of dorsal cells and 19-28% in simulations of ventral cells, consistent with the decrease in firing frequency of grid cells observed with muscimol inactivation of the hippocampus (Hafting et al., 2008), perhaps resulting from the loss of an updating mechanism from place cells. However, it is also possible that the phase response to a highly variable input pattern is less noisy than the response to a steady input, similar to the greater consistency of spiking response to variable current injection versus steady input (Mainen and Sejnowski, 1995). The research presented here and previous work (Giocomo et al., 2007; Giocomo and Hasselmo, submitted) primarily studies the effects of steady current injection on frequency of oscillations and spiking behavior and does not investigate the role of synaptic influences on frequency and phase of oscillations.

Figure 6.

A. Effects of noise in the oscillatory model. As the noise levels in the model are increased, the firing of the simulated grid cell becomes less consistent and loses its grid pattern of spatial periodicity. B. Layer V cells show higher frequency membrane oscillations in dorsal compared to ventral portions of medial entorhinal cortex at a membrane potential of −45 mV and −40 mV. C. Qualitative differences between m-current (layer V) and h-current (layer II) dependent subthreshold oscillations. Two different layer V cells (left; top 4.2 mm from dorsal surface, bottom 4.7 mm from the dorsal surface) show higher amplitude oscillations compared to two different layer II cells (right; top 4.4 mm from dorsal surface, bottom 4.6 mm from dorsal surface).

Oscillations in other layers and brain regions

The oscillatory model predicts that grids might exist in any region which contains cells that have voltage dependent, intrinsically generated oscillations near firing threshold and receive structured head direction inputs. Subthreshold oscillations in layer II medial entorhinal cells are not blocked in the presence of the M-current blocker XE991, suggesting that the M-current does not play a role in generating subthreshold oscillations in stellate cells (Giocomo and Hasselmo, submitted; Yoshida and Alonso, 2007). However in layer V of mEC, cells show subthreshold oscillations dependent on the M-current rather than the H-current (Yoshida and Alonso, 2007). Whole-cell patch clamp recordings of layer V cells along the dorsal-ventral axis of medial entorhinal cortex indicate that dorsal oscillating layer V cells show higher frequency oscillations at a membrane potential of −45 mV (slope = −2.61, r = .63) and −40 mV (slope = −2.75, r = .57) compared to more ventral oscillating layer V cells (Figure 6B). However, the two types of oscillations (M-current dependent layer V oscillations and h-current dependent layer II oscillations) appear to differ qualitatively. Layer V oscillations (M-current dependent) tend to have a higher amplitude compared to layer II oscillations (h-current dependent) and appear at more depolarized potentials compared to layer II oscillations (Figure 6C). Oscillatory activity dependent on the M-current may contribute to grid cell formation in the deeper layers of mEC (layer V) (Sargolini et al., 2006).

Layer III pyramidal neurons do not generate subthreshold oscillations. Grid cells exist in layer III but show conjunctive grid and head direction responses (Sargolini et al., 2006) and make up a smaller percentage of recorded cellular activity compared to layer II. The absence of subthreshold oscillations, within the context of the oscillatory model, suggests that layer III grid cells either reflect interconnectivity with layer II or are formed by another process (Blair et al., 2006). The absence of phase precession and theta modulation of firing in layer III, compared to layer II (Hafting et al., 2008), may offer evidence that layer III grid cell activity reflects activity in other cell layers.

Discussion

Attractor Dynamic Models

Computational models utilizing attractor dynamics can obtain grid cell firing pattern due to the spread of activity along the recurrent synaptic weights in the network population. While the head-direction system (Taube et al., 1990a; Taube et al., 1990b) has been modeled using one-dimensional continuous attractors (McNaughton et al., 1991; Touretzky and Redish, 1996; Zhang, 1996) modeling the spatial navigation system for path integration requires multi-dimensional continuous attractors (McNaughton et al., 1996; Redish and Touretzky, 1997; Samsonovich and McNaughton, 1997; Tsodyks and Sejnowski, 1995). The attractor network models of grid cell firing utilize a synaptic matrix where excitation and inhibition from a simulated neuron differs as a function of the distance from the position of the neuron on a neural sheet (e.g. Mexican-hat connectivity). To model the grid cell phenomena, attractor based models (McNaughton et al., 2007; Fuhs & Touretzky, 2006) use two populations of interconnected cells; one population provides information about the direction and speed of the animal's trajectory, which induces a bump of activity due to attractor dynamics in the second population and shifts the bump to neighboring cells in the appropriate direction as the animal moves through the environment. In entorhinal cortex, McNaughton et al., (2006) proposes that the deeper layers of mEC, which contains information about the rat's movement (Sargolini et al., 2006), serve as the input layer while the superficial layers of mEC, which contain more spatial information (Sargolini et al., 2006), serve as the attractor based spatial output of the system. Multiple repeating fields, such as the grid cell firing fields, are attained either as a result of periodic connectivity in a cell array with a torus- like topology (McNaughton et al., 2006) or radial changes in synaptic connectivity (Fuhs and Touretzky, 2006). Dorsal to ventral changes in spacing result from the assumption that the velocity input to the ventral portion of medial entorhinal cortex has a lower gain compared to the dorsal medial entorhinal cortex (McNaughton et al., 2006). In this framework, the change in grid field size is determined either by the single parameter of velocity modulation or separately by changing the spatial wavelength of the Mexican-hat connectivity (Fuhs and Touretzky, 2006). The regulation of field size and spacing by separate parameters in the attractor models differs from the oscillatory interference model in which field size and spacing are simultaneously determined by changes in one parameter (either f or B). In addition, attractor dynamic models can only represent a finite number of discrete spatial scales while the oscillatory interference model can express a continuous increase in spatial scale along the dorsal-ventral axis. The presence of discrete spatial scales is consistent with discrete values of spacing in experimental data (Barry et al., 2007).

The hyperpolarization activated cation current

Both types of models of grid cell firing indicate that specific properties of membrane channels could underlie the change in grid cell properties along the dorsal to ventral axis of entorhinal cortex. The membrane potential oscillations discussed earlier depend on the hyperpolarization activated inward current (I_h) (Dickson et al., 2000; Fransen et al., 2004), which has been observed in several other cortical regions including the hippocampus (Magee, 1998) and the cerebellum (Raman and Bean, 1999). Activated by hyperpolarization, the I(h) channel conducts both Na+ and K+ ions (Pape, 1996) and is also referred to as the HCN channel (hyperpolarization activated cAMP-regulated cation channel). Four different mammalian genes which encode HCN channels have been cloned (HCN1-4) (Baruscotti et al., 2005; Biel et al., 2002; Robinson and Siegelbaum, 2003), and immunohistochemical staining indicates a high level of the subunit HCN1 and moderate levels of the subunit HCN2 in medial entorhinal cortex (Notomi and Shigemoto, 2004). H-current channels cloned in oocytes with different subunit compositions show different activation kinetics both in their time constants and steady-state activation curves (Chen et al., 2001), which could affect the characteristics of membrane potential oscillations, as well as other properties shown to differ along the dorsal-ventral axis of mEC such as ‘sag’ and resonant frequency (Giocomo et al., 2007). Homomeric HCN1 channels have very fast activation and deactivation time constants, activate at a depolarized membrane potential and have only moderate modulation by intracellular cAMP. Homomeric HCN2 channels have very slow activation and deactivation time constants, activate at more hyperpolarized membrane potential and have strong modulation by intracellular cAMP. Heteromultimeric HCN1/HCN2 channels show properties in between the homomeric channels with the exception that they activate at membrane potentials similar to the HCN1 homomeric channels (Chen et al., 2001). A gradient in the relative expression of HCN1 to HCN2 subunits along the dorsal-ventral axis could provide a potential molecular mechanism for the dorsal-ventral differences in stellate cell kinetics, which map to changes in grid cell spatial periodicity. Recent work indicates that the time constant of I(h) changes from fast to slow from dorsal to ventral entorhinal cortex (Giocomo and Hasselmo, submitted) and the change in subthreshold oscillation frequency may be due to a change in the relative ratio of I(h) subunits with fast kinetics (HCN1) to subunits with slower kinetics (HCN2).

The frequency of membrane potential oscillations and the spatial properties of grid cells could also be influenced by neuromodulatory influences on intracellular second-messenger pathways. In addition the encoded HCN protein, similar to a voltage-gated potassium (K) channel, consists of six transmembrane segments including a pore-forming region (Biel et al., 2002; Santoro and Tibbs, 1999), and a cytosoloic NH2 and COOH termini. A cyclic-nucleotide binding-domain (CNBD) is located on the COOH temini (Chen et al., 2001; Santoro et al., 1997) which mediates the response of HCN channels to cAMP levels. Levels of cAMP can subsequently modulate the activation kinetics of HCN channels to different degrees, another potential molecular mechanism underlying the dorsal-ventral change in stellate cell biophysical properties (Ludwig et al., 1998; Santoro et al., 1998; Seifert et al., 1999). Several other substances can also cause changes in the kinetics of HCN channels, which could also affect the dorsal-ventral changes observed in stellate cells. Increasing the level of PI(4,5)P2 shifts the activation curve of homomeric HCN2 channels to more depolarized membrane potentials while also slowing down the deactivation time constant (Pian et al., 2007). Activation of different neuromodulatory receptors, such as M1 receptors and bradykinin receptors, can increase the activation of PLC and cause the depolarizing shift in the activation curve of homomeric HCN2 channels as well as heteromultimeric HCN1/HCN2 channels, while simultaneously slowing down the time constant of deactivation at −70 mV (Pian et a., 2007). The slowing of the deactivation time constant suggests a possible mechanism for the decrease in the frequency of subthreshold oscillations observed in the presence of the cholinergic agonist carbachol (Klink and Alonso, 1997b), suggesting that cholinergic manipulation of entorhinal cortex could affect grid cell periodicity.

Genetic manipulations could be used to analyze the role of specific membrane channels in grid cell properties. In stellate cells, the kinetics of the h-current resemble those of heteromultimeric HCN1/HCN2 channels (Chen et al., 2001). Research in HCN1 knockout mice suggests that HCN1 channels, in stellate cells, dominate the membrane conductance at resting potential, decrease the input resistance of the cell, suppress low frequency components of the resonant frequency and subthreshold oscillations, and promote recovery of spike afterhyperpolarization (Nolan et al., 2007). In addition, stellate cells often fire action potentials in clusters (Klink and Alonso, 1997b) and knockout of HCN1 decreases the spike frequency within a cluster and increases the time between clusters (the intracluster spike frequency) (Nolan et al., 2007). HCN1 knockout mice also show more coherence in the theta oscillation, recorded from behaving mice, suggesting that knocking down high frequency intrinsic oscillations may result in a more coherent field oscillation in the theta frequency range (Nolan et al., 2004). These knockout mice also show enhanced short-term and long-term memory on the hidden platform Morris Water Maze task, most likely due to the enhancement of long-term potentiation in the hippocampus observed with HCN1 knockout (Nolan et al., 2004). Knockout of HCN1 results in numerous changes in the biophysical properties of stellate cells, which suggests that the kinetics of the h-current could play a role in dorsal-ventral changes observed in the biophysical characteristics of layer II stellate cells (Giocomo et al., 2007) and possibly play a key role in grid cell formation or dorsal-ventral change in spatial periodicity.

Relationship between I(h) and attractor dynamic based models

Changes in the intrinsic properties of layer II mEC neurons could also apply to attractor-dynamic models of grid cell formation (McNaughton et al., 2006; Fuhs and Touretzky, 2006). Attractor based models assume that a dorsal-ventral difference in gain of velocity results in the change in grid cell field spacing and field size. As presented earlier (Figure 1A), the voltage dependent frequency change of subthreshold membrane oscillations is higher in dorsal compared to ventral entorhinal cortex. The larger sensitivity of dorsal cells to membrane potential depolarization could reflect that velocity input has a larger gain (amplification) in the dorsal region compared to the ventral region of medial entorhinal cortex. In the oscillatory interference model, this change in gain corresponds to the change in the value of the B parameter, as discussed earlier.

Attractor-dynamic models can change the field size of the grids by assuming a change in the spatial wavelength of connectivity (or a change in the spatial wavelength of the Mexican-hat connectivity). Changes in traditional Hebbian long-term potentiation and long-term depression during development could result in an increase or decrease in the spatial wavelength. The h-current, which shows changes in its kinetics along the dorsal-ventral axis, has been shown to interact with both long-term potentiation and long-term depression in the hippocampus (Brager and Johnston, 2007; Fan et al., 2005; Nolan et al., 2004). In the hippocampus, long-term potentiation causes an increase in I(h) and a subsequent decrease in excitability while long-term depression causes a decrease in I(h) and a subsequent increase in excitability (Fan et al., 2005; Brager and Johnston, 2007). Knockout of the HCN1 subunit causes enhanced long-term potentiation in the hippocampus (Nolan et al., 2004), potentially by suppressing calcium spikes in the distal dendrites of pyramidal cells (Tsay et al., 2007a). A higher ratio of HCN1 to HCN2 during development (e.g. dorsal mEC), could contribute to the building of a network with more constrained connectivity. Thus, as an alternative hypothesis, the differences in subthreshold oscillation frequency (Giocomo et al., 2007) that reflect dorsal-ventral differences in the kinetics of the h-current may be complemented by dorsal-ventral h-current differences that contribute to cortical plasticity during development, resulting in different spatial wavelengths of connectivity along the dorsal-ventral axis of mEC, and resulting in differences in grid cell size based on attractor dynamics.

HCN1 and spatial learning

HCN1 knockout mice show enhanced learning in the fixed platform version of the Morris Water maze (Nolan et al., 2004). Interestingly, this enhanced learning appears immediately only if the mice are primed for 15 seconds on the location of the platform. When the mice are not primed the enhanced learning takes several sessions to develop (Nolan et al., 2004).

Within the context of the models presented here, the loss of HCN1 subunits should not result in the complete absence of grid cell firing fields. However, the spacing of the grids should increase and the difference in their spacing from dorsal to ventral should be absent with the loss of HCN1 subunits, as depletions of HCN1 subunits influence the HCN channel time constant (Chen et al., 2001) and subsequently reduce the frequency of dorsal membrane potential oscillations, increasing the size and field spacing of the grids. Once the knockout mouse knows the location of the platform, then a single set of larger grids should still allow the animal to navigate successfully, with less interference, through the environment. Perhaps not surprisingly, these animals also show enhanced theta rhythmicity. Loss of the higher frequency intrinsic oscillations would suggest that the theta rhythm observed in the absence of HCN1 would have more coherence, as the oscillatory activity from dorsal to ventral would remain more consistent.

Conclusions

The analysis of intracellular recording data on entorhinal cortex reported here has implications for models of entorhinal grid cell firing properties. In particular, the voltage-dependence of oscillations supports the additive version of the oscillatory interference model, in contrast to the multiplicative version. The additive version also allows a wider range of large grid cell spacing without requiring low oscillation frequencies outside of the experimentally demonstrated range. The variance of the oscillation period provides a serious issue for the oscillatory interference model that must be accounted for by mechanisms such as the reset of grid cell phase by place cell input (Burgess et al. 2007). Finally, the interaction of h current with synaptic modification provides a potential mechanism by which differences in h current could contribute to differences in size of grid cell firing fields via changes in attractor dynamics along the dorsal to ventral axis of medial entorhinal cortex.