Mechanism of Increased BK Channel Activation from a Channel Mutation that Causes Epilepsy

Abstract

Concerted depolarization and Ca²⁺ rise during neuronal action potentials activate large-conductance Ca²⁺- and voltage-dependent K⁺ (BK) channels, whose robust K⁺ currents increase the rate of action potential repolarization. Gain-of-function BK channels in mouse knockout of the inhibitory β4 subunit and in a human mutation (α_D434G) have been linked to epilepsy. Here, we investigate mechanisms underlying the gain-of-function effects of the equivalent mouse mutation (α_D369G), its modulation by the β4 subunit, and potential consequences of the mutation on BK currents during action potentials. Kinetic analysis in the context of the Horrigan-Aldrich allosteric gating model revealed that changes in intrinsic and Ca²⁺-dependent gating largely account for the gain-of-function effects. D369G causes a greater than twofold increase in the closed-to-open equilibrium constant (6.6e⁻⁷→1.65e⁻⁶) and an approximate twofold decrease in Ca²⁺-dissociation constants (closed channel: 11.3→5.2 µM; open channel: 0.92→0.54 µM). The β4 subunit inhibits mutant channels through a slowing of activation kinetics. In physiological recording solutions, we established the Ca²⁺ dependence of current recruitment during action potential–shaped stimuli. D369G and β4 have opposing effects on BK current recruitment, where D369G reduces and β4 increases K_1/2 (K_1/2 μM: α_WT 13.7, α_D369G 6.3, α_WT/β4 24.8, and α_D369G/β4 15.0). Collectively, our results suggest that the D369G enhancement of intrinsic gating and Ca²⁺ binding underlies greater contributions of BK current in the sharpening of action potentials for both α and α/β4 channels.

INTRODUCTION

Large-conductance Ca²⁺- and voltage-activated K⁺ (BK) channels open in response to additive effects of Ca²⁺ and voltage to contribute to action potential repolarization in neurons. It is generally assumed that outward K⁺ currents through BK channels repolarize the cell and reduce excitability (Faber and Sah, 2003). However, in some neurons, the sharpening of action potentials due to increased BK channel activation has been found to facilitate high frequency firing (Brenner et al., 2005; Gu et al., 2007).

The observation that increased BK channel activation increases excitability in some neurons may explain the otherwise paradoxical finding that a human BK potassium channel gain-of-function mutation (D434G) is associated with epilepsy (Du et al., 2005). The D434G mutation resides in the RCK1 domain, a putative Ca²⁺-binding domain within the pore-forming α subunit (Jiang et al., 2001, Bao et al., 2002, Zeng et al., 2005). In heterologous expression systems, the D434G mutation speeds channel activation, increases steady-state open probabilities, and results in Ca²⁺-dependent G-V shifts consistent with increased Ca²⁺ sensitivity (Du et al., 2005; Diez-Sampedro et al., 2006).

In the context of the Horrigan-Aldrich (HA) model (Horrigan and Aldrich, 2002), BK channel gating is determined by three equilibria: a central “closed-to-open” step (also called intrinsic gating [L]), voltage sensor activation (J), and Ca²⁺ binding (K). These are coupled through allosteric interactions between them (C, D, E, respectively; see Table I). Changes in closed-to-open equilibrium can alter the apparent Ca²⁺ sensitivity of G-V relations (Wang and Brenner, 2006). In addition, increased “Ca²⁺ sensitivity” could arise through either changes in Ca²⁺ affinity (i.e., binding) or allosteric coupling between Ca²⁺ binding and gating.

TABLE I.

HA Model Gating Parameters (Horrigan and Aldrich, 2002)

L	C-O equilibrium constant (unliganded channel, resting voltage sensors).
	L=L0 exp(zLV/kT)
	L0, zL The zero voltage value of L and its partial charge, respectively.
J	R-A equilibrium constant (closed, unliganded channel).
	J = J0 exp(zJV/kT)
	J0, zJ The zero voltage value of J and its partial charge, respectively.
K	Equilibrium constant for Ca2+ binding (closed channel, resting voltage sensors).
	K=[Ca2+] / KC
	KC Ca2+ dissociation constant (closed channel, resting voltage-sensors).
C	Allosteric factor describing interaction between channel opening and Ca2+ binding.
	C = KC / KO
	KO Ca2+ dissociation constant (open channel, resting voltage-sensors).
D	Allosteric factor describing interaction between channel opening and voltage sensor activation.
	D = exp [-zJ (Vho-Vhc)/kT]
	VhO, VhC Half-activating voltage of QC and QO, respectively
	QC, QO Steady-state gating charge distribution for closed or open channels.
E	Allosteric factor describing interaction between Ca2+ binding and voltage-sensor activation.

In addition, it was observed that the inhibitory effect of β4 is lost in the D434G mutant channels (Diez-Sampedro et al., 2006).This is quite surprising because β subunit interaction domains have not previously been mapped to this region (RCK1 domain) of the channel (Wallner et al., 1996; Qian et al., 2002; Morrow et al., 2006). Further, this implies that the D434G epilepsy phenotype may partly result from a loss of modulation by β4.

Here, we seek to gain a better understanding of the effects of D434G mutation by using the equivalent mutation in the mouse BK channel (D369G). Guided by the HA allosteric gating model for BK channels (Horrigan and Aldrich, 2002), we used recording conditions to identify specific gating parameters altered by the mutation. We further reexamined effects of the mutation on BK channels coassembled with the inhibitory β4 subunit using conventional voltage step protocols as well as action potential–shaped stimuli to understand potential functional consequences. These studies reveal that the D369G mutation promotes channel activation by increasing both intrinsic gating and Ca²⁺ affinities. Although the mutation does not qualitatively perturb β4 inhibitory effects on activation kinetics, we did find that BK/β4 channels containing D369G show greater relative current during action potential–type stimuli. This may have important implications in understanding the D434G epileptic phenotype in humans.

MATERIALS AND METHODS

Patch Clamp Recording of HEK Cells

Experiments were performed with the mouse α subunit cDNA expression vector in pcDNA3 (GenBank accession no. MMU09383) and mouse β4 in the vector pcDNA3.1Hygro(+) (Invitrogen). The D369G mutation, originally described in the human gene (D434G in human) (Du et al., 2005), was introduced in the mouse α subunit cDNA using the Quick-Change Mutagenesis kit (Agilent Technologies) and verified by sequencing. The human α subunit wild-type cDNA (GenBank accession no. NM002247) and D434G mutant cDNAs were cloned in pCDNA 3.1. Expression constructs were transfected at a ratio of 1:10 α to β4 subunit using 2–3 µg of total DNA and 10 µl of lipofectamine reagent per 35-mm dish of HEK293 cells. After 5 h of incubation, the cells were re-plated on German glass coverslips (Bioindustrial Products) and analyzed by electrophysiology for the next 1–3 d. Green fluorescent protein expression from cotransfection (0.2 µg) of the EGFP-N1 vector (Clontech Laboratories, Inc.) was used to identify channel-expressing cells.

Macropatch recordings were made using the excised inside-out patch clamp configuration. Experiments were performed at 22°C. Data were sampled at 10- to 30-µs intervals and low-pass filtered at 8.4 kHz using the EPC8 four-pole bessel filter (HEKA). Data were analyzed without further filtering. Leak currents were subtracted after the test pulse using P/5 negative pulses from a holding potential of −120 mV. Patch pipettes (borosilicate glass; Sutter Instrument Co.) were coated with Sticky Wax (Kerr Corp.) and fire polished to ∼1.5–3-MΩ resistance.

The “symmetrical” external recording solution (electrode solution for Figs. 1–6) was composed of the following (in mM): 20 HEPES, 140 KMeSO₃, 2 KCl, and 2 MgCl₂, pH 7.2. The “physiological” external recording solution (electrode solution for Figs. 7 and 8) was composed of the following (in mM): 10 HEPES, 145 NaCl, 5 KCl, 1 MgCl₂, and 2 CaCl₂, pH 7.2. Internal solutions were composed of a pH 7.2 solution of the following (in mM): 20 HEPES, 140 KMeSO₃, and 2 KCl. Intracellular Ca²⁺ was buffered with 5 mM EGTA (0.073 and 0.006 µM), HEDTA (2.1 and 0.363 µM) or NTA (41 µM), and free [Ca²⁺] was measured using a Ca²⁺-sensitive electrode (Orion Research, Inc.). In low Ca²⁺ solutions (0.073 and 0.006 µM), Ba²⁺ was chelated with 40 µM (+)-18-crown-6-tetracarboxylic acid (Cox et al., 1997).

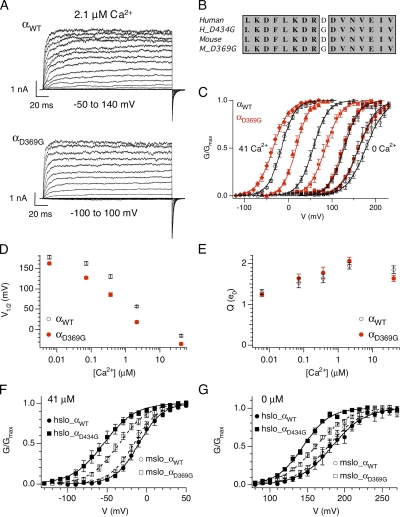
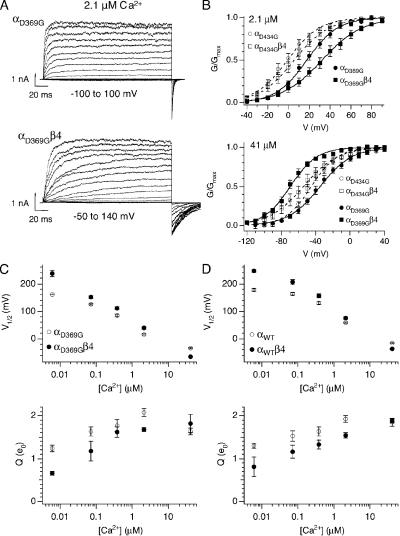
Figure 1.

D369G shifts mslo steady-state G-V relation to hyperpolarizing membrane potentials. (A) A family of currents from wild-type (top) or D369G mutant (bottom) BK channels composed of only the pore forming α subunits. Recorded in 2.1 μM Ca²⁺, currents were evoked in response to 200-ms depolarizations at the indicated membrane potentials. (B) Alignment of amino acid sequence flanking the lysine (D) to glycine (G) epilepsy mutation. (C) Mean G-V relations at different Ca²⁺ for α_WT and α_D369G. Each point represents mean data from 5 to 26 experiments. Solid curves represent fits to the Boltzmann function. (D) Mean V_1/2 and (E) mean effective gating charge (Q) values plotted as a function of Ca²⁺. Error bars represent SEM. (F) D434G shifts G-V to more negative membrane potentials at 41 µM Ca²⁺ compared to D369G (hslo_α_WT: n = 9; hslo_α_D434G: n = 10; mslo_α_WT: n = 19; mslo_α_D369G: n = 18). (G) D434G shifts G-V to more negative membrane potentials at nominal Ca²⁺ compared to D369G (hslo_α_WT: n = 5; hslo_α_D434G: n = 5; mslo_α_WT: n = 12; mslo_α_D369G: n = 14). Symbols represent mean G/G_max data, curves represent fits to the Boltzmann function, and error bars represent SEM.

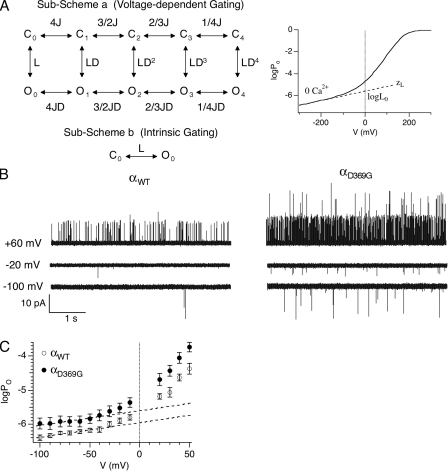
Figure 2.

D369G decreases the energetic barrier for channel to open. (A; left) According to the dual-allosteric mechanism (Horrigan et al., 1999; Horrigan and Aldrich, 2002), BK channel transitions between closed (C) and open (O) conformation is allosterically regulated by the state of four independent and identical voltage sensors. Sub-Scheme a represents BK channel’s gating scheme at 0 Ca²⁺. The channel resides in either the open or closed conformation, with 0–4 voltage sensors in the activated state. The equilibrium between C-O transitions is allosterically regulated by the states of the voltage sensors. Sub-Scheme b represents BK channel’s gating scheme at 0 Ca²⁺ and very negative voltages. With all voltage sensors in the resting state, the channel resides in one of two conformations, C₀ and O₀. The equilibrium between the C₀-O₀ transition is described by L, the intrinsic equilibrium for channel opening in the absence of Ca²⁺ and voltage sensor activation. (Right) This illustrates how two components of L (L₀ and z_L) can be estimated by logPo-V data at 0 Ca²⁺ and negative voltages. The curve represents simulated logPo versus voltage curve in nominally 0 Ca²⁺. The gating parameters used for simulation are as follows: L₀ = 2.5 × 10⁻⁶, z_L = 0.25 e₀, z_J = 0.54e₀, Vh_C = 173 mV, and Vh_O = 25 mV. Dashed line represents fit for logPo-V at limiting slope using Eq. 4. L₀ and z_L can be derived from the fit (Horrigan and Aldrich, 2002). (B) Single-channel BK currents recorded in nominally 0 [Ca²⁺] at the indicated voltages. α_WT and α_D369G data were obtained from patches containing estimated 64 and 317 channels, respectively. All traces were filtered at 5 kHz. (C) D369G increases L₀. Mean logPo plotted as a function of voltage in nominally 0 Ca²⁺ (α_WT: n = 5–13; α_D369G: n = 6–11). Error bars represent SEM. L₀ was estimated by linear fits (dashed lines) of logPo-V relations between −100 to −50 mV using Eq. 1. z_L value was set as 0.25 e₀.

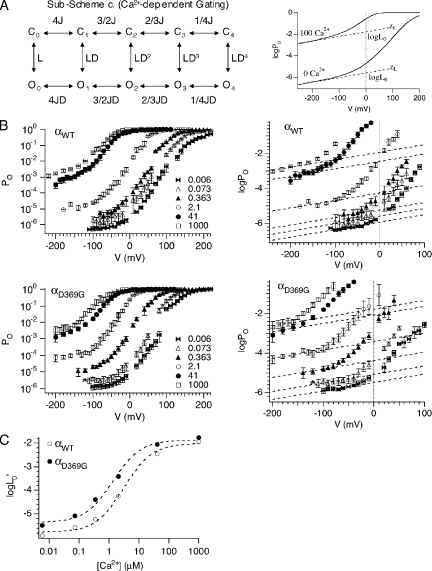
Figure 3.

D369G increases channel’s Ca²⁺-binding affinities. (A; left) According to the dual-allosteric mechanism (Horrigan and Aldrich, 2002), BK channel transitions between closed (C) and open (O) conformation are allosterically regulated by the state of four independent and identical Ca²⁺-binding sites. Sub-Scheme c represents BK channel’s gating scheme at very negative voltages, where voltage sensors remain in the resting states. The channel resides in either closed or open conformations, with 0–4 Ca²⁺-binding sites occupied. The equilibrium between the C-O transitions is allosterically regulated by the states of the Ca²⁺-binding sites. In the absence of voltage sensor activation, voltage dependence of the C-O transition is entirely dependent on z_L. (Right) This illustrates how logL₀′ can be estimated by logPo-V data at high Ca²⁺ and very negative voltages. Curves are simulated logPo-V curves in nominally 0 Ca²⁺ and 100 μM Ca²⁺ according to Sub-Scheme c. The gating parameters used for simulation are as follows: L₀ = 2.5 × 10⁻⁶, z_L = 0.25 e₀, z_J = 0.54 e₀, Vh_C = 173 mV, Vh_O = 25 mV, K_C = 13.9 µM, and K_O = 1.4 µM. Dashed lines represent fits for logPo-V at limiting slopes using Eq. 8. L₀′ and z_L can be derived from the fits (Horrigan and Aldrich, 2002). (B) Symbols represent averaged logPo-V relations at various Ca²⁺. Error bars represent SEM. Dashed lines are fits for mean logPo-V at limiting slope using Eq. 2 and z_L of 0.25 e₀. (C) Open and closed symbols are logL₀′ versus Ca²⁺ for α_WT and α_D369G BK channels, respectively. Curves represent fits of logL₀′-Ca²⁺ using Eq. 3.

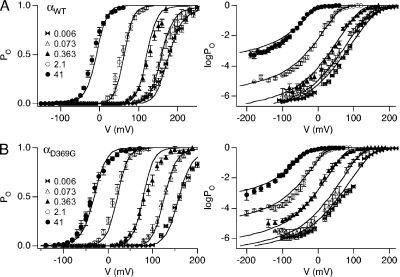
Figure 4.

Changes in Ca²⁺ affinities and intrinsic gating are sufficient to account for changes between α_WT (A) and α_D369G (B). Fits (curve and gating parameters listed in Table II) are compared with average P_O-V and logPo-V data (symbols).

Figure 5.

Ca²-dependent effects of β4 on mutant BK channel G-V. (A) A family of currents from α_D369G BK channels composed of either the pore forming alone (top) or with the β4 auxiliary subunits (bottom). Recorded in 2.1 µM Ca²⁺, currents were evoked in response to 200-ms depolarizations. (B, top) Effect of β4 on mslo and hslo mutant G-V relations at 2.1 µM Ca²⁺ (hslo_α_D434G: n = 7; hslo_α_D434G β4: n = 9; mslo_α_D369G: n = 22; mslo_α_D369G β4: n = 32). (B, bottom) Effect of β4 on mslo and hslo mutant G-V relations at 41 µM Ca²⁺ (hslo_α_D434G: n = 10; hslo_α_D434G β4: n = 11; mslo_α_D369G: n = 18; mslo_α_D369G β4: n = 15). Symbols represent mean G/G_max data, curves represent fits to the Boltzmann function, and error bars represent SEM. (C) Effects of β4 on steady-state gating of mutant channels. Mean V_1/2 (top) and mean effective gating charge (Q) values (bottom) plotted as a function of Ca²⁺. Error bars represent SEM. (D) Effects of β4 on steady-state gating of wild-type channels. Mean V_1/2 (top) and mean effective gating charge (Q) values (bottom) plotted as a function of Ca²⁺. Error bars represent SEM.

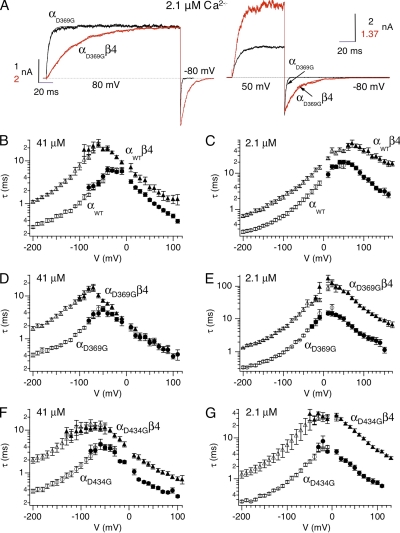
Figure 6.

Effects of β4 on D369G BK channel gating kinetics. (A; left) Compare activation kinetics. α_D369G and α_D369Gβ4 currents at 2.1 µM Ca²⁺. Patches were held at −80 mV and stepped to +80 mV for 200 ms. Superimposed on the current traces are the single-exponential fits to the activation time courses (α_D369G: τ = 4.7 ms; α_D369Gβ4: τ = 40.3 ms). (Right) Compare deactivation kinetics. α_D369G and α_D369Gβ4 currents at 2.1 µM Ca²⁺. Channels were activated at +50 mV before membrane was stepped to −80 mV for 100 ms. Superimposed on the current traces are the single-exponential fits to the deactivation time courses (α_D369G: τ = 1.1ms; α_D369Gβ4: τ = 11.7 ms). (B) Comparison of α_WT and α_WTβ4 channel kinetics at 41 µM Ca²⁺ (α_WT activation: n = 8–26; α_WT deactivation: n = 12; α_WTβ4 activation: n = 13–35; α_WTβ4 deactivation: n = 16–21). (C) Comparison of α_WT and α_WTβ4 channel kinetics at 2.1 µM Ca²⁺ (α_WT activation: n = 17; α_WT deactivation: n = 6–30; α_WTβ4 activation: n = 7–22; α_WTβ4 deactivation: n = 11–12). (D) Comparison of α_D369G and α_D369Gβ4 channel kinetics at 41 µM Ca²⁺ (α_D369G activation: n = 5–18; α_D369G deactivation: n = 13–14; α_D369Gβ4 activation: n = 5–16; α_D369Gβ4 deactivation: n = 13). (E) Comparison of α_D369G and α_D369Gβ4 channel kinetics at 2.1 µM Ca²⁺ (α_D369G activation: n = 5–23; α_D369G deactivation: n = 13–19; α_D369Gβ4 activation: n = 6–34; α_D369Gβ4 deactivation: n = 8–20). (F) Comparison of α_D434G and α_D434Gβ4 channel kinetics at 41 µM Ca²⁺ (α_D434G activation: n = 11; α_D434G deactivation: n = 7; α_D434Gβ4 activation: n = 11; α_D434Gβ4 deactivation: n = 10). (G) Comparison of α_D434G and α_D434Gβ4 channel kinetics at 2.1 µM Ca²⁺ (α_D434G activation: n = 7; α_D434G deactivation: n = 5; α_D434Gβ4 activation: n = 9; α_D434Gβ4 deactivation: n = 9). Filled symbols represent measurements obtained from tail currents (deactivation time constant), and empty symbols represent measurements obtained from activation time constant.

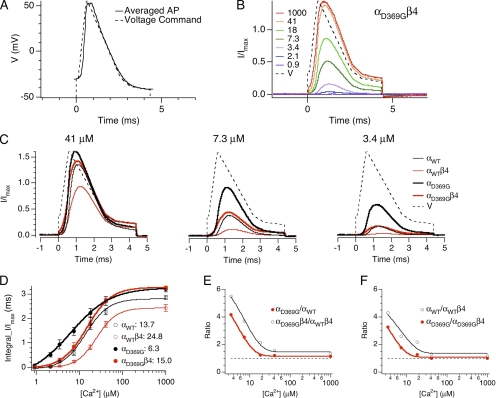
Figure 7.

Ca²⁺-dependent effects of the mutation on BK channel recruitment by spike-shaped depolarization. (A) Voltage command of the spike-shaped depolarization (dashed line) approximating average DG granule cell action potentials (trace). (B) Representative patch showing α_D369Gβ4 current evoked by spike depolarization and various intracellular Ca²⁺. (C) Average BK current for different channels at 41 µM Ca²⁺ (α_WT: n = 19; α_WTβ4: n = 16; α_D369G: n = 22; α_D369Gβ4: n = 18), 7.3 µM Ca²⁺ (α_WT: n = 10; α_WTβ4: n = 11; α_D369G: n = 16; α_D369Gβ4: n = 9), and 3.4 µM Ca²⁺ (α_WT: n = 9; α_WTβ4: n = 8; α_D369G: n = 12; α_D369Gβ4: n = 7). Currents in B and C were normalized to maximal current size obtained from 0 mV tail current (0 mV) at saturating (1 mM) Ca²⁺. (D) Average current integral as a function of intracellular Ca²⁺ concentration. Error bars represent SEM. Curves represent fits to Hill equations (α_WT: K_1/2 = 13.7, n = 1.6; α_WTβ4: K_1/2 = 24.8, n = 1.9; α_D369G: K_1/2 = 6.3, n = 0.9; α_D369Gβ4: K_1/2 = 15.0, n = 1.5). (E) Fold increase in current resulting from the D369G mutation measured from ratio values (from D) of α_D369G/α_WT (red) and α_D369Gβ4/ α_WTβ4 (green). (F) Fold increase in current resulting from channels lacking β4 measured from ratio values (from D) of α/α_WTβ4 (green) and α_D369G/α_D369Gβ4 (blue).

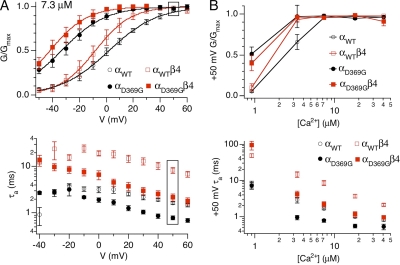
Figure 8.

Ca²⁺-dependent effects of the mutation on BK channel gating in “physiological” solutions. (A; top) Average G-V relationship at 7.3 µM Ca²⁺ (α_WT: n = 18; α_WTβ4: n = 10; α_D369G: n = 8; α_D369Gβ4: n = 10). (Bottom) Average activation time constants at 7.3 µM Ca²⁺ (α_WT: n = 15; α_WTβ4: n = 10; α_D369G: n = 8; α_D369Gβ4: n = 9). Boxed regions indicate values at +50 mV. (B; top) G/G_max versus Ca²⁺ concentration at +50 mV. (Bottom) Average activation time constants at +50 mV as a function of Ca²⁺ concentration.

Analysis of Macroscopic Currents

G-V relationships were obtained using a test pulse followed by a step to a post test voltage to measure instantaneous tail current 200 microseconds after the test pulse. For symmetrical Ca²⁺, +60 mV was used for 0.073 and 0.006 µM Ca²⁺ and −80 mV was used for higher Ca²⁺. For physiological external solutions, 0 mV was used. In experiments where G_max was not reached, G_max values at higher [Ca²⁺] from the same patch was used. G/G_max-V data were fit with the Boltzmann function, G/G_max = 1/(1 + e^{ZF(V_1/2−V)/RT}), where V is the test potential, V_1/2 is the membrane potential at half-maximal conductance, Q is the effective gating charge, and F, R, and T are constants.

For action potential–shaped stimuli, we used the physiological pipette solution described above. The action potential stimulus waveforms were ramp voltage steps designed to simulate action potentials from wild-type dentate gyrus (DG) granule neurons during 105-pA current injections (Brenner et al., 2005). Prepulse is −80 mV for 100 msec, followed by a 0.1-msec step to a threshold voltage of −30 mV. Action potential rise is from −30 to +57 mV over 0.5 msec. Repolarization is in three phases: from +57 to −28 mV over 2 msec, −28 to −38 mV for 0.56 msec, and −38 to −42 mV in 1.2 msec. To subtract capacitance and leak currents, a P/5 leak subtraction protocol was used from a holding potential of −120 mV. The action potential currents were normalized to maximal current in the same patch measured from the tail current (0 mV) after a maximal activating 40-msec square wave stimulus in 1 mM of internal calcium concentration.

Single-Channel Analysis

Single-channel opening events were obtained from patches containing one to hundreds of channels. Recordings are of 20 s to hundreds of seconds long. Analysis was performed using TAC and TACFIT programs (Bruxton Corporation). NP_O was determined using either all-point amplitude histogram or by event detection using a 50% amplitude criteria. The probability (P_k) of occupying each open level (k) gave rise to NP_O: 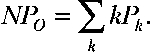. P_O was then determined by normalizing NP_O values by channel number (N). N was obtained from the instantaneous tail current amplitude during maximal opening at saturating [Ca²⁺] divided by the single-channel current for each channel at the tail voltage.

RESULTS

D369G Increases BK Channel Opening

A mouse BK channel mutation (α_D369G) equivalent to α_D434G in humans (Fig. 1 B) was generated and transiently expressed in HEK 293 cells. Ionic currents were recorded using excised inside-out patches to allow control of [Ca²⁺] at the cytoplasmic side of the membrane. Fig. 1 A shows representative BK currents in response to test voltage steps in 2.1 µM of internal Ca²⁺. Tail current amplitudes (G at −80 mV) were normalized to maximum tail current (G_max at −80 mV) to generate average G-V (G/G_max-V) relationships. Relative to α_WT, G-V relationships are consistently shifted to negative potentials for α_D369G (Fig. 1 C). Plots of V_1/2 (voltage at half-maximal G/G_max) versus Ca²⁺ demonstrate more dramatic shifts at intermediate Ca²⁺ (between 0.073 and 2.1 µM) and smaller shifts at low (nominal) and high Ca²⁺ (41 µM; Fig. 1 D; values are listed in Table II). The D369G mutation, however, does not significantly alter the slope or the equivalent gating charge (Q) of the G-V relationship (Fig. 1 E and Table II).

TABLE II.

G-V Parameters

Ca2+ (μM)	αWT			αD369G			αWTβ4			αD369Gβ4
	V1/2 (mV)	Q (e0)	n	V1/2 (mV)	Q (e0)	n	V1/2 (mV)	Q (e0)	n	V1/2 (mV)	Q (e0)	n
0.006	177.6 ± 4.0	1.30 ± 0.06	12	161.5 ± 2.5	1.23 ± 0.05	14	246.1 ± 3.8	0.81 ± 0.23	4	237.2 ± 12.2	0.66 ± 0.05	9
0.073	162.5 ± 5.2	1.53 ± 0.12	13	126.2 ± 3.0	1.63 ± 0.11	9	206.4 ± 9.7	1.16 ± 0.16	6	150.9 ± 3.74	1.34 ± 0.13	9
0.363	130.2 ± 3.8	1.63 ± 0.11	15	85.6 ± 4.3	1.77 ± 0.14	16	155.8 ± 6.2	1.33 ± 0.10	19	111.0 ± 3.8	1.84 ± 0.12	10
2.1	57.3 ± 3.1	1.93 ± 0.08	26	16.2 ± 3.1	2.06 ± 0.09	22	74.5 ± 5.6	1.54 ± 0.06	19	40.2 ± 3.6	1.62 ± 0.05	32
41	−15.7 ± 2.5	1.85 ± 0.09	19	−34.3 ± 3.6	1.63 ± 0.08	18	−36.9 ± 2.8	1.88 ± 0.04	38	−65.6 ± 2.7	1.77 ± 0.13	15

The values shown are Boltzmann-fit parameters. They indicate mean ± sem.

Effects of D369G on V_1/2 and Q are qualitatively similar to previous descriptions of the equivalent human D434G mutation (Du et al., 2005; Diez-Sampedro et al., 2006), confirming that D369G is a gain-of-function mutation. We directly compared effects of the mutation on human (hslo) and mouse (mslo) channels at 41 and 0 µM Ca²⁺. Although effects were qualitatively similar, D434G produced larger G-V shifts on hslo than D369G did on mslo. At 41 µM Ca²⁺, ΔV_1/2 for hslo and mslo are ∼−35 and −20 mV, respectively (Fig. 1 F). At 0 Ca²⁺, ΔV_1/2 for hslo and mslo are ∼−36 and −16 mV, respectively (Fig. 1 G). Whereas the size of G-V shift at 41 µM Ca²⁺ is comparable to previous results on the hslo mutant channel (Du et al., 2005; Diez-Sampedro et al., 2006), negative shift at 0 Ca²⁺ was not observed previously (Diez-Sampedro et al., 2006).

Increased Intrinsic Gating and Ca²⁺-binding Affinities Underlie Increased Channel Opening of the D369G Mutation

To better understand how the D369G mutation alters BK channel gating, we used recording conditions that isolate the effects on intrinsic gating from Ca²⁺- and voltage-dependent gating. Fig. 2 A illustrates how intrinsic gating (closed-to-open transition in the absence of Ca²⁺ binding and voltage sensor activation) can be examined. At 0 Ca²⁺, we observe gating of primarily unliganded channels (i.e., with 0 Ca²⁺ bound). In the context of the HA model, these reside in 1 of 10 states: closed or open, with 0–4 voltage sensors activated (Fig. 2 A, Sub-Scheme a) (Horrigan and Aldrich, 2002). At 0 Ca²⁺ and very negative membrane potentials (i.e., toward the “limiting slope” of the G-V curve, where voltage sensors are not activated), channels reside primarily in either C₀ or O₀ (Fig. 2 A, Sub-Scheme b) (Horrigan and Aldrich, 2002). LogP_O at the limiting slope is only weakly voltage dependent, reflecting the weak voltage dependence of closed-to-open transition. Fitting the limiting slope phase of logPo-V relations (Fig. 2 A, right panel) by

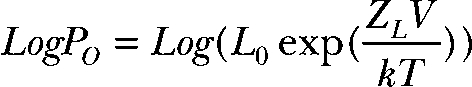(1)

provides an estimate of intrinsic gating (L₀) and the weak voltage dependence due to the closed-to-open transition (Z_L) (Horrigan and Aldrich, 2002). Fig. 2 B shows representative currents recorded at 0 Ca²⁺ for estimation of these parameters. Although these membrane patches contain tens to hundreds of channels, only single-channel openings were observed under these conditions. There is a striking drop in the voltage dependence of Po below −20 mV, which likely reflects relaxation of voltage sensors (and thus “intrinsic” gating). This is reflected in the average logP_O-V relationships that show a similar limiting slope voltage dependence (Z_L, dashed line) in both α_WT and α_D369G channels (Fig. 2 C). However, α_D369G has an increased logPo relative to α_WT in this portion of the curve, indicating an increased intrinsic gating (Fig. 2 C). Fitting of the logP_O-V relationship at the limiting slope (using Eq. 1) estimates a greater than twofold increase in intrinsic gating equilibrium constant for α_D369G over α_WT (2.49 ± 0.08e⁻⁶ vs. 1.12 ± 0.02e⁻⁶, respectively; see Table III). This could contribute to the leftward G-V shift for α_D369G seen in nominal Ca²⁺ (Fig. 1 C). In addition, the observation that logPo deflects from the limiting slope at similar voltages (∼−30 mV; Fig. 1 C) for α_WT and α_D369G suggests that open-channel voltage sensors are not altered by the D369G mutation (Wang and Brenner, 2006).

TABLE III.

Gating Parameters Based on Limiting Slope logP₀

	αWT	αD369G
L0	1.12 ± 0.02e−6	2.49 ± 0.08e−6
KC (μM)	8.7 ± 0.8	3.8 ± 1.0
KO (μM)	1.0 ± 0.2	0.5 ± 0.1
C	8.7 ± 0.8	7.5 ± 0.8

To understand how the mutation might affect Ca²⁺ sensitivity, we recorded current at very negative voltages, but over a range of Ca²⁺ (Fig. 3, A and B). At very negative voltages where voltage sensors are not activated, the channel resides in 1 of 10 states: closed or open, with 0–4 subunits bound to Ca²⁺ (Fig. 3 A, Sub-Scheme c). The limiting slope logP_O-V was fitted using

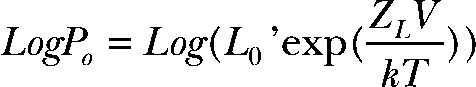(2)

to obtain an estimate of channel open probability at a corresponding Ca²⁺ in the absence of voltage sensor activation (Horrigan and Aldrich, 2002). The limiting slope P_O’s at 0 mV (L₀’) were plotted as a function of Ca²⁺ concentration and fitted using

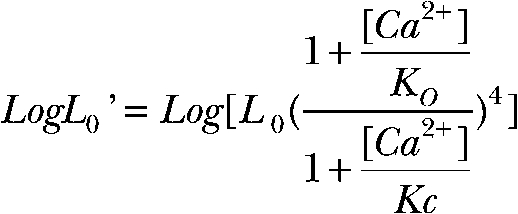(3)

to estimate open- and closed-channel Ca²⁺-binding affinity of K_O and K_C, respectively, and coupling between Ca²⁺ binding and gating (C = K_C/K_O) (Horrigan and Aldrich, 2002). For the α_D369G channels, the log(L₀’) versus [Ca²⁺] curve is shifted to lower Ca²⁺ concentrations compared with α_WT channels, with a small decrease in the slope (Fig. 3 C). Fitting of the data using Eq. 3 indicates that the D369G mutation does not alter the coupling between Ca²⁺ binding and gating (C_D369G = 7.5 ± 0.8; C_WT = 8.7 ± 0.8), but increases apparent Ca²⁺-binding affinities of both the closed (K_{C_D369G} = 3.8 ± 1.0 µM; K_{C_WT} = 8.7 ± 0.8 µM) and open channels (K_{O_D369G} = 0.5 ± 0.1 µM; K_{O_WT} = 1.0 ± 0.2 µM; 2.3- and twofold, respectively; see Table III). In summary, the major effects of the D369G mutation are increases in apparent Ca²⁺-binding affinities and intrinsic gating, both of which contribute to higher P_O.

To determine whether changes in intrinsic gating (L₀) and Ca²⁺ affinities (K_C and K_O) are sufficient to account for differences between α_WT to α_D369G, we simultaneously fitted P_O and log(Po)--V data (Fig. 4) using the allosteric gating model. The voltage-dependent parameters were fixed at α_WT values to determine if changes in other parameters are sufficient to fit the data. The resulting parameters are very similar to those obtained from the above measurements (Table IV) and fit the data reasonably well (Fig. 4, A and B). There is a predicted 2.5-fold increase in L₀ and a 2.2- and 1.7-fold increase in closed- (1/K_C) and open-channel (1/K_O) Ca²⁺-binding affinity, respectively. These results indicate that changes in these parameters can largely account for the increased channel openings observed in the α_D369G mutant channels.

TABLE IV.

Gating Parameters Based on P_O and logP_O

	αWT		αD369G
L0	6.6e−7 ± 3e−8		1.65e−6 ± 3e−8
KC (μM)	11.3 ± 0.2		5.2 ± 0.1
KO (μM)	0.92 ± 0.02		0.54 ± 0.01
E	4.9 ± 0.2		7.6 ± 0.2
zL (e0)		0.25
zJ (e0)		0.58
VhC (mV)		181.7
VhO (mV)		14.8

β4 Modulation of Steady-state and Kinetic Properties of D369G Channels

A previous study indicated that the BK channel’s accessory β4 subunit has little effect on the V_1/2 of human D434G channels (Diez-Sampedro et al., 2006). This raised the possibility that D369G perturbs co-assembly or functional interactions with the β4 subunit. In addition, it suggests that the D369G mutation may cause more severe defects in β4-expressing neurons, where β4 otherwise inhibits channel opening. We tested these ideas by coexpressing α_WT or α_D369G with or without β4 (Fig. 5 A). We observed that coexpression of the β4 subunit resulted in shifted G-V relations in D369G mutant channels (Fig. 5 B and Table II), indicating that β4 does indeed modulate steady-state gating of the mutant. Similar to wild-type channels (Fig. 5 D, top), β4 causes a negative G-V shift at high Ca²⁺ (41 µM Ca²⁺) and positive G-V shifts at lower Ca²⁺ concentrations (<2.1 µM Ca²⁺; Fig. 5 C, top) (Wang et al., 2006). Also, β4 reduces the equivalent gating charge (slope of G-V relation) of D369G channels (Fig. 5 C, bottom), similar to wild-type channels (Fig. 5 D, bottom) (Wang et al., 2006).

The effects of β4 on the gating kinetics of α_D369G channels are also similar to its effects on α_WT. At 2.1 µM, step depolarization from −80 to +80 mV activates α_D369G/β4 channels visibly slower compared with α_D369G channels (Fig. 6 A, left). Similarly, α_D369G/β4 channels deactivate more slowly compared with α_D369G channels (Fig. 6 A, right). At 41 and 2.1 µM Ca²⁺, we observed qualitatively similar effects of β4 on α_WT and α_D369G channel–gating kinetics (Fig. 6, B–E); β4 coexpression results in slowed activation kinetics, and this effect is greater at lower Ca²⁺ compared with higher Ca²⁺ (Fig. 6, B–E, filled symbols).

β4 shift of both mouse α_WT and α_D369G V_1/2 is in contrast with a previous study showing that β4 affects V_1/2 of human α_WT, but not the equivalent human mutation (α_D434G) (Diez-Sampedro et al., 2006). In the previous study, α and β4 were transfected in a low ratio (3:1 ratio; Diez-Sampedro et al., 2006), raising the possibility that β4 was not saturated for D434G channels. Here, we transfected D434G and β4 in a 1:10 ratio to examine the effects of β4 on hslo D434G channels (Fig. 5 B). The effects of β4 on D434G G-V relations at 41 and 2.1 µM Ca²⁺ are small, similar to the previous observation (Diez-Sampedro et al., 2006). However, the β4 subunit does interact with human α_D434G channels as suggested by the dramatic slowing of activation and deactivation kinetics (Fig. 6, F and G). In summary, these results indicate that effects of β4 on steady-state opening of the epilepsy gain-of-function mutation are larger for mslo compared with hslo. However, activation kinetics of mslo and hslo mutant channels are dramatically slowed by β4, suggesting that recruitment of both channels during action potentials would be reduced by β4.

The D369G Mutation Alters the Ca²⁺ Dependence of BK Currents during Action Potential–shaped Voltage Commands

Recruitment of BK channel current during an action potential depends critically on the time course of channel opening as a function of membrane voltage and Ca²⁺. To consider the relative current activation during action potentials, we used voltage commands designed to mimic those of action potentials measured in neurons (hippocampus DG granule cells, where the β4 subunit is expressed) (Brenner et al., 2005). The recordings were conducted using physiological ionic concentrations of K⁺ and Na⁺ to mimic a physiological K⁺-driving force and to account for possible effects of these ionic conditions on channel activation.

Fig. 7 A shows the command voltage (dashed line) superimposed on an averaged action potential waveform (trace) from wild-type (α/β4) DG granule neurons (Brenner et al., 2005). Representative recordings from a single α_D369G/β4 patch at various internal Ca²⁺ is shown in Fig. 7 B. BK currents were activated with a small delay after the voltage command. The normalized BK currents show a graded increase with increasing Ca²⁺. Fig. 7 C shows averaged BK currents at the indicated Ca²⁺ where BK current sizes follow the trend: α_D369G > α_D369G/β4 ≈ α_WT > α_WT/β4. As predicted by the gating kinetics in Fig. 6, β4 inhibition of both α_WT (thin red vs. thin black) and α_D369G (thick red vs. thick black) current recruitment is much greater at low than at higher Ca²⁺ concentration (Fig. 7 C). The increase of current activation by the D369G mutation in the presence (thick vs. thin red) or absence (thick vs. thin black) of β4 subunits is also greater at lower [Ca²⁺] (Fig. 7 C).

Summary data across a broad range of Ca²⁺ for different channels is plotted in Fig. 7 D. D369G and the β4 subunit have opposing effects on current recruited during action potential stimuli. β4 shifts the dose–response of both mutant and wild type so that higher Ca²⁺ is required to recruit BK current, whereas the D369G mutation shifts the dose–response of α and α_/β4 channels toward lower Ca²⁺. Indeed, there is a roughly twofold increase in apparent K_1/2 for D369G channels and a twofold decrease in apparent K_1/2 for β4-containing wild-type channels (Fig. 7 D). Interestingly, the effect of the D369G mutation is to shift α_D369G/β4 channels to a dose–response overlapping α_WT channels lacking the β4 subunit. In addition, α_D369G channels have a higher maximal current integral at saturating Ca²⁺ (Fig. 7 D). The relative effects of the D369G mutation and β4 are quantified by comparing relative ratio of current recruitment as a function of the D369G mutation (Fig. 7 E) or as a function of the β4 subunit (Fig. 7 F). The results clearly indicate that the effect of D369G and β4 are most dramatic at low Ca²⁺ and are Ca²⁺ independent at Ca²⁺ >18 µM. For example, there is an approximately four- to sixfold increase in BK current with the D369G mutation (Fig. 7 E) and an approximately three- to fourfold reduction of BK current with β4 subunit (Fig. 7 F) at 3.4 µM Ca²⁺. At lower Ca²⁺, the current recruited is too small for estimation of fold changes.

Analysis of the G-V and τ_a-V relations (with the physiological ionic conditions used in the experiments above) indicates that activation kinetics determine the relative current recruitment during action potential stimuli. For example, at 7.3 µM Ca²⁺, steady-state open probability is maximal for all channels at the peak action potential voltage of +50 mV (boxed in Fig. 8 A, top). Rather, the relative activation taus at +50 mV (boxed in Fig. 8 A, bottom) correlate well with the current recruitment during the action potential stimulus (Fig. 7 F). Thus, β4-mediated slowing of activation (8.1 ± 1.2 msec) effectively precludes α_WT channel opening during the relatively short action potential time window. In contrast, β4 slows α_D369G to time constants (2.9 ± 0.4 msec) that allow significant BK channel activation. This is consistent across Ca²⁺ concentrations, which show high steady-state conductance at +50 mV for either α_WT or α_D369G channels, with or without β4 (Ca²⁺ > 0.9 µM; Fig. 8 B). Nevertheless, α_D369G, which displayed the fastest gating kinetics, showed the largest action potential–evoked BK currents (Fig. 8 B). α_D369G/β4 and α_WT channels have intermediate activation rates and current recruitment. Finally, the slowest gating α_WT/β4 has the least current recruitment.

DISCUSSION

In the context of the HA allosteric gating model, our analysis suggest that mslo D369G is a gain-of-function mutation affecting two aspects of gating. It favors opening independently of Ca²⁺ and voltage sensor activation, with an approximate twofold increase of the closed-to-open equilibrium constant (L₀). It increases the channel’s Ca²⁺ sensitivity by an approximate twofold increase of the Ca²⁺-binding equilibrium constant (K). Given that D369 is located in RCK1, a putative Ca²⁺-sensing domain (Zeng et al., 2005), it was not surprising to see that the mutation affects Ca²⁺ binding. The D369G mutation does not greatly alter the allosteric interaction between channel opening and Ca²⁺ binding (C), nor voltage-dependent gating.

Similar gating effects may be shared by the hslo (D434G) mutation. Changes in G-V slopes were not observed in the mutation (Du et al., 2005; Diez-Sampedro et al., 2006). In addition, the mutation does not alter Mg²⁺ facilitation of opening (Diez-Sampedro et al., 2006), which is highly dependent on voltage sensor activation (Yang et al., 2007; Horrigan and Ma, 2008). These observations suggest that D434G has little effects on voltage-dependent gating. Negative G-V shift by the mutation in 0 Ca²⁺ was observed in our study, suggesting that D434G increases channels’ closed-to-open equilibrium constant. Finally, consistent with the possibility that D434G alters Ca²⁺ binding instead of coupling, shifts of G-V by D434G are greater at intermediate Ca²⁺ compared with nominal and saturating Ca²⁺ (Du et al., 2005; Diez-Sampedro et al., 2006).

One difference between studies was that the 0 Ca²⁺ G-V shift by hslo D434G mutation was not previously observed (Diez-Sampedro et al., 2006). A possible explanation is that the previous study may have overestimated G/G_max for the wild-type channels, with +210 mV being the maximum voltage step. In our study, the wild-type channel reaches G_max at around +270 mV, and G/G_max at +210 mV is estimated to be 0.77 (Fig. 1 G). Consistent with this possibility, V_1/2 values for D434G channels are similar between the two studies (∼+150 mV), but our V_1/2 estimate for wild-type channels (∼+180 mV) is higher.

Our study observed some differences in β4 effects between the human and mouse mutant channels. Interestingly, although β4 affects wild-type and D369G mslo G-V relations in a similar manner, it only weakly affected mutant hslo G-V relations (consistent with previous observations; Diez-Sampedro et al., 2006). Whereas β4 slows the activation of both hslo D434G and mslo D369G at low Ca²⁺, at high Ca²⁺ (41 µM) β4 slows the activation of D434G (threefold), but not mslo D369G. As a consequence, one may expect that β4 reduces recruitment of the D434G mutation more than that of D369G at high Ca²⁺. These findings suggest that at some Ca²⁺, β4 may have differing effects on human versus mouse neurons containing the epilepsy mutation.

BK channels have very depolarized G-V relations in the absence of Ca²⁺ and require micromolar Ca²⁺ to open at physiological membrane potentials (i.e., neuronal voltages between −100 to +60 mV) (Cui et al., 1997). BK channels are often colocalized with Ca²⁺ sources such as voltage-dependent Ca²⁺ channels, ryanodine receptors, and NMDA receptors (Davies et al., 1996; Marrion and Tavalin, 1998; Prakriya and Lingle, 2000; Isaacson and Murphy, 2001; Parsons et al., 2002; Berkefeld et al., 2006; Berkefeld and Fakler, 2008). Using the short time window of action potential–like voltage commands reveals the relatively high Ca²⁺ concentrations required to activate BK channels during neuronal action potential firing. Little BK current is observed below 2.1 and 3.4 µM Ca²⁺, with K_1/2 of 13.7 and 24.8 µM, respectively, for wild-type BK/α and BK/αβ4 channels. These high μM Ca²⁺ concentrations suggest that neuronal BK channels are especially suited to respond to high local Ca²⁺ rises; much greater than global Ca²⁺ generally attains (Fakler and Adelman, 2008).

Our Ca²⁺ dose–response curves may also provide some footing for estimation of local Ca²⁺ that BK channels sense in neurons. Previous studies in DG granule neurons indicate that β4 reduces BK channel activation during the action potential, whereas knockout of β4 allows greater BK channel contribution to action potential repolarization (Brenner, et al., 2005). The Ca²⁺ dose–response curves (Fig. 7 D) suggest that β4 inhibition most effectively occurs at Ca²⁺ below 41 µM during action potential–type stimuli. This is somewhat lower than the estimated 40–50 µM of calcium nanodomain that BK channels experience during action potentials of DG neurons (Muller et al., 2007). The discrepancies may be due to the fact that we used constant buffered Ca²⁺ to activate BK channels in our experiments, whereas neuronal BK channels experience dynamic changes of Ca²⁺ in response to voltage-dependent Ca²⁺ channel activation and deactivation during an action potential. Thus, in neurons, BK channels may sense somewhat larger peak calcium increases but over a more transient time course. In addition, the BK channel and cellular environment may be different between neurons and HEK cells due to differences in BK channel phosphorylation state, alternative splicing, or redox status. In other ways, however, experiments performed in HEK cells provide certain advantages. Analyzing isolated macroscopic BK currents in excised patches takes into account both changes in G-V relationship and gating kinetics during action potential–type stimuli, without the requirement for imperfect pharmacological inhibitors or mathematical modeling of action potential currents.

By slowing the BK channel’s activation rate beyond the time scale of action potentials (i.e., >5 msec), our study shows that β4 effectively limits BK channel recruitment at low and moderate Ca²⁺ (∼3.4–18 µM). In DG neurons from β4 knockout mice, increased BK channel activation sharpens the repolarization phase of the action potentials. The resulting briefer action potential may reduce both activation of voltage-dependent Ca²⁺ channels during the action potential (Lo et al., 2001), as well as recruitment of Ca²⁺-activated SK-type channels that act to limit firing frequency; these effects likely contribute to high frequency neuronal firing and epilepsy (Brenner et al., 2005). Opposing b4 effects, D369G facilitates BK channel opening by lowering K_1/2 to 6.3 and 15.0 µM for α and α/β4 channels, respectively. The D369G enhancement of Ca²⁺ affinity appears to reduce the slow-gating β4 brake on BK channel activation in a similar manner as high calcium’s effect on α_WT/β4 channels. Increased DG firing in D434G humans may contribute to epilepsy, similar to the mouse β4 knockout (Brenner et al., 2005). However, increased BK channel activity associated with increased neuronal excitability may not be limited to hippocampal DG neurons. A previous study has shown that a maladaptive gain-of-function of BK channels underlies elevated firing of neocortical pyramidal neurons in a picrotoxin-induced spontaneous seizure mouse model (Shruti et al., 2008). It will certainly be interesting to establish a causal relationship between BK channel gain-of-function and epilepsy by generating a tissue-specific knockin mouse model of the D369G mutation.