Actin filament dynamics are dominated by rapid growth and severing activity in the Arabidopsis cortical array

Abstract

Metazoan cells harness the power of actin dynamics to create cytoskeletal arrays that stimulate protrusions and drive intracellular organelle movements. In plant cells, the actin cytoskeleton is understood to participate in cell elongation; however, a detailed description and molecular mechanism(s) underpinning filament nucleation, growth, and turnover are lacking. Here, we use variable-angle epifluorescence microscopy (VAEM) to examine the organization and dynamics of the cortical cytoskeleton in growing and nongrowing epidermal cells. One population of filaments in the cortical array, which most likely represent single actin filaments, is randomly oriented and highly dynamic. These filaments grow at rates of 1.7 µm/s, but are generally short-lived. Instead of depolymerization at their ends, actin filaments are disassembled by severing activity. Remodeling of the cortical actin array also features filament buckling and straightening events. These observations indicate a mechanism inconsistent with treadmilling. Instead, cortical actin filament dynamics resemble the stochastic dynamics of an in vitro biomimetic system for actin assembly.

Introduction

The actin cytoskeleton of plants plays an integral yet poorly understood role during cell morphogenesis and elongation. The most compelling data link actin filament cables and networks with organelle motility and/or positioning, vesicle trafficking to the vacuole, and vacuolar morphogenesis (for reviews see Wada and Suetsugu, 2004; Holweg, 2007; Sheahan et al., 2007; Yoneda et al., 2007). Nevertheless, many popular models postulate that the cortical array of actin filaments regulates exocytic vesicle delivery or fusion (for reviews see Smith and Oppenheimer, 2005; Hussey et al., 2006). Unfortunately, there is scant information correlating actin organization or dynamics with sites of secretion or expansion in plant cells undergoing diffuse growth.

The organization and function of actin filament arrays depend not only on the properties of actin itself, but upon a plethora of accessory proteins. Advances in the characterization of actin-binding proteins from plants reveal important differences between the activities of plant and mammalian/yeast proteins (Staiger and Blanchoin, 2006). However, connecting these insights with an understanding of the dynamic properties of actin arrays in vivo has lagged. In part, this limitation is due to the lack of a functional actin–fluorescent fusion protein (FFP) for decorating filament arrays and monitoring dynamics in real time. Similar to the situation in budding yeast, actin-binding domain–FFP reporters have partially alleviated this limitation. Because its interaction with actin filaments appears least detrimental to cells, the second actin-binding domain from Arabidopsis FIMBRIN1 (fABD2) is currently the reporter of choice for live-cell imaging (Ketelaar et al., 2004b; Sheahan et al., 2004; Voigt et al., 2005; Wang et al., 2008). Even with this reporter, a clear picture of the behavior of actin filaments within complex arrays, arrived at through high temporal and spatial resolution microscopy, is lacking. The most common imaging technique, laser scanning confocal microscopy, suffers from slow acquisition times and therefore poses problems when monitoring events that occur on timescales of seconds. Spinning disk confocal microscopy and variable-angle epifluorescence microscopy (VAEM) offer two alternatives for rapid imaging of live cells. Recent studies of cytoskeleton dynamics and vesicle trafficking demonstrate the utility of VAEM for examining dynamic events in the cortical cytoplasm of plant cells (Fujimoto et al., 2007; Konopka and Bednarek, 2008a,b; Konopka et al., 2008).

Epidermal cells in hypocotyls from etiolated Arabidopsis seedlings provide a good model system for exploring the role of the cytoskeleton during cell elongation and cell wall deposition (Ehrhardt and Shaw, 2006; Lucas and Shaw, 2008). For example, cortical microtubules translocate using a form of dynamic instability called “hybrid treadmilling,” can be severed, and display angle-dependent changes in behavior upon contacting other microtubules (Mathur et al., 2003; Shaw et al., 2003; Dixit and Cyr, 2004; Chan et al., 2007; Wightman and Turner, 2007). In addition, simultaneous imaging of multiple FFPs reveals the importance of cortical microtubule organization to tracking of cellulose synthase complexes in the plasma membrane (Paredez et al., 2006). A few studies hint at similarly complex dynamics in the cortical actin network of hypocotyl epidermal cells (Kwok and Hanson, 2004; Sheahan et al., 2004; Higaki et al., 2007; Holweg, 2007; Wang et al., 2008); however, a full view of actin filament organization and turnover remains to be captured. Nevertheless, pharmacological and genetic analyses indicate a role for the actin cytoskeleton during cell expansion of hypocotyls.

In nonplant cells, cytoskeletal arrays often comprise networks of short actin filaments beyond the diffraction-limited resolution of light microscopy. A classical example is the dendritic network of filaments that drives lamellipodium protrusion at the leading edge of motile cells. At the ultrastructural level, these arrays consist of a dense, branched network of filaments that are ∼100 nm long (Svitkina and Borisy, 1999). Consequently, fluorescent-speckle microscopy is often used to analyze the average behavior of filaments within these dense arrays (Waterman-Storer et al., 1998; Waterman-Storer and Danuser, 2002). The translocation of actin speckles at velocities of 0.5 µm/min in newt lung epithelial cells (Ponti et al., 2004) and 2.5 µm/min in Drosophila S2 cells (Iwasa and Mullins, 2007) is inferred to correlate with actin-monomer assembly rates onto the barbed ends of filaments. A recent study of cytokinesis in the fission yeast used time-lapse spinning-disk confocal microscopy to reveal actin dynamics during contractile ring formation (Vavylonis et al., 2008). Actin filaments were observed to interconnect nodes and facilitate myosin-dependent clustering of the nodes into higher-order structures by a “search-capture and pull” mechanism. Dynamic behavior of the filaments includes fast growth (0.2 µm/s) and stochastic destruction by severing and shrinkage. This latter study, along with a biomimetic system allowing actin filament formation in the presence of formin and ADF/cofilin (Michelot et al., 2007), suggests that actin arrays can display features and organizational principles more consistent with “stochastic dynamics” than filament treadmilling.

We used time-lapse VAEM to examine the dynamics of the cortical actin array in hypocotyl epidermal cells from Arabidopsis seedlings to gain new insight into the molecular mechanisms that control actin organization. We observed complex and dynamic behavior of individual actin filaments and thick filament bundles. Cortical actin filaments were arrayed into randomly oriented networks that reorganized continuously. In part, reorganization was due to actin filament buckling and straightening events. Most individual actin filaments were typically short lived (<30 s), a condition maintained by balancing high growth rates (1.7 µm/s) with severing activity. The apparent growth rate was reduced in a dose-dependent manner by treatments with the monomer-sequestering agent, Latrunculin B (LatB). We believe remodeling of cortical arrays results from growth at actin filament barbed ends (enabled by a large pool of assembly-competent monomers) counteracted by the disappearance of filaments due to severing. Surprisingly, the growth rate and severing frequency of filaments in nongrowing epidermal cells are not markedly changed compared with elongating cells. To our knowledge, this is the first quantitative analysis of actin filament turnover in the cortical cytoplasm of plant cells. The dynamics observed are inconsistent with an actin filament treadmilling mechanism. Similar to a biomimetic system for actin turnover and generation of higher-order structures in vitro (Michelot et al., 2007), the term “stochastic dynamics” best describes the behavior of actin filaments in live plant cells.

Results

Cortical cytoskeleton dynamics can be observed by time-lapse VAEM

To examine cortical cytoskeleton dynamics we adjusted our total internal reflection fluorescence microscope for variable-angle epifluorescence illumination. VAEM delivers better signal-to-noise ratios than wide-field microscopy. Here, we used time-lapse VAEM to analyze the behavior of cortical cytoskeletal arrays in the epidermal cells of dark-grown Arabidopsis seedlings. We used transgenic lines expressing GFP-fABD2 to image actin filaments (Sheahan et al., 2004) and EYFP-TUB5 or GFP-EB1 expressing plants to visualize microtubules and microtubule plus ends, respectively (Mathur et al., 2003; Shaw et al., 2003). For most experimental observations, we imaged epidermal cells from the top third of the hypocotyl, adjacent to the hook region, in plants harvested 3–5 d after germination. These epidermal cells are undergoing rapid expansion along the axis of hypocotyl elongation (Gendreau et al., 1997; Fig. S1 B, available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Notably, the GFP-fABD2 line we selected has modest levels of reporter expression and does not hinder growth of hypocotyls (Fig. S1 A) or epidermal cell elongation (Fig. S1 B).

We found that the organization and dynamics of cortical microtubules visualized by time-lapse VAEM were similar to those reported by others using spinning disk confocal microscopy in the same cell type (Shaw et al., 2003; Paredez et al., 2006; Chan et al., 2007). Microtubule arrays oriented transversely along the long axis of the cell, although discordant microtubules and bundles of microtubules were also observed (Fig. S2 A, available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Microtubules exhibited “hybrid treadmilling” and plus-end behavior was observed to alternate between periods of growth and catastrophic disassembly (Fig. S2 D). As a simple measure of microtubule dynamics, we recorded rates of growth at plus ends. The mean plus-end elongation rate (±SD) for EYFP-TUB5–decorated microtubules was 5.2 ± 1.3 µm/min (n = 52), a value slightly higher than that reported by Shaw and coworkers (3.7 ± 1.9 µm/min; Shaw et al., 2003). We also used the bright, comet-like structures generated by GFP-EB1 to monitor microtubule plus-end dynamics (Fig. S2 B; Video 1, available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Transverse microtubules had a mean plus-end elongation rate of 2.8 ± 0.9 µm/min (n = 58), significantly slower than that derived from EYFP-TUB5, but consistent with previous reports using EB1-FFPs (Mathur et al., 2003; Dixit et al., 2006; Chan et al., 2007). Collectively, cortical microtubule arrays in the epidermal cells of etiolated hypocotyls showed a coordinate, predominantly transverse orientation with respect to the cell's long axis, with individual microtubules exhibiting dynamic instability at plus-ends and growth rates of 3–5 µm/min. Importantly, we could document differences in microtubule behavior, like the difference in plus-end elongation rate between EYFP-TUB5 and GFP-EB1 expressing lines, validating the use of VAEM for detailed analysis of cortical cytoskeletal dynamics. The VAEM approach itself does not appear to alter microtubule dynamics relative to previous reports. Moreover, no appreciable photodamage occurs, even when cells are imaged over 5–10 min (see Videos 1–3), providing further confidence that VAEM reports cytoskeletal dynamics faithfully. We therefore used identical settings for VAEM angle, laser power, image acquisition time, and total illumination to image actin filaments in the cortical array noninvasively.

In contrast to the orderly and predictable behavior of cortical microtubules, actin filaments visualized with GFP-fABD2 were extremely dynamic, producing a randomly organized and continuously rearranging cortical array (Videos 2 and 3, available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Overlaying two consecutive images separated by 3 s revealed mostly randomly oriented and convoluted actin filaments that changed positions, in addition to a few rigid and static actin filaments (Fig. S2 C, bottom). A montage and time-lapse video of another representative cell, with individual frames captured at ∼3-s intervals for a period of >5 min, reveals further aspects of actin filament behavior (Fig. 1; Video 2). Actin filaments that we identified as being single (see below) were oriented at a wide range of angles with respect to the cell's long axis, whereas stiffer, straighter filament bundles or cables were mostly oriented longitudinally. Actin filaments typically had a convoluted appearance that changed from frame to frame, indicating extensive buckling and straightening. New actin filaments appeared randomly and elongated rapidly from one end. Most individual filaments could rarely be tracked for >30 s with disappearance a consequence of severing activity. We detail the quantification of these and other aspects of cortical actin filament dynamics in the following sections.

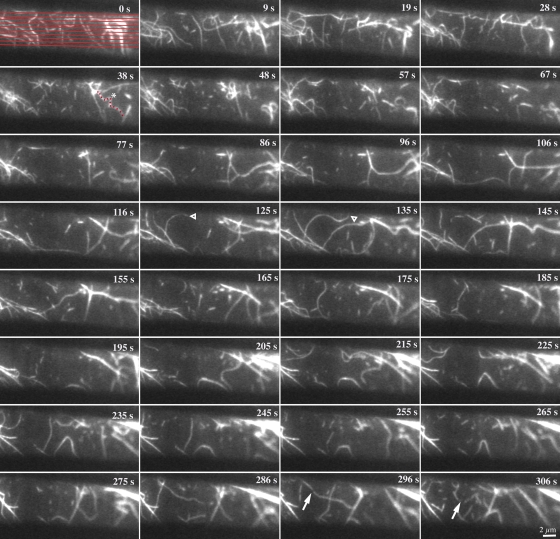
Figure 1.

The cortical actin array is remodeled continuously. Representative epidermal cell from a 5-d-old, dark-grown hypocotyl expressing GFP-fABD2 was observed with time-lapse VAEM. Successive images were made at ∼3-s intervals and every third image is depicted. Actin filament behaviors such as rapid growth (open arrowheads), buckling and straightening (red dots and asterisk), and severing activity (arrows) are marked. Collectively, this dynamic actin behavior resulted in rather short filament lifetimes (<30 s) and constant remodeling of the cortical array. Time points indicate the elapsed time from start of video sequence. See also Video 2 (available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1) for the full time-lapse series. Bar, 2 µm.

Actin filament elongation rates are fast

To correlate the nature of an actin-based structure with its average pixel intensity, we computer-generated multiple lines that scanned the entire surface of the observed field of view throughout a full time-lapse series (e.g., Fig. 1). After background subtraction, we were able to generate the full range of pixel intensities corresponding to different populations of cortical actin-based structures for growing (Fig. S3 A, available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1) and nongrowing cells (Fig. S3 B). The majority of pixels in the field of view had intensities below 1800 arbitrary units (a.u.). A direct comparison of these values with those generated by individual, hand-selection revealed that the faintest actin filaments had average pixel intensities of ∼1000 a.u., but the intensity varied substantially along their length (Fig. S3 C). As shown in a representative example of filament growth after severing, the newly elongated region has an average intensity similar to the mother filament, but varies by more than 500 a.u. along its length (Fig. 2 C). Importantly, where two actin filaments crossed, the pixel intensity nearly doubled (Fig. 2 C, arrow).

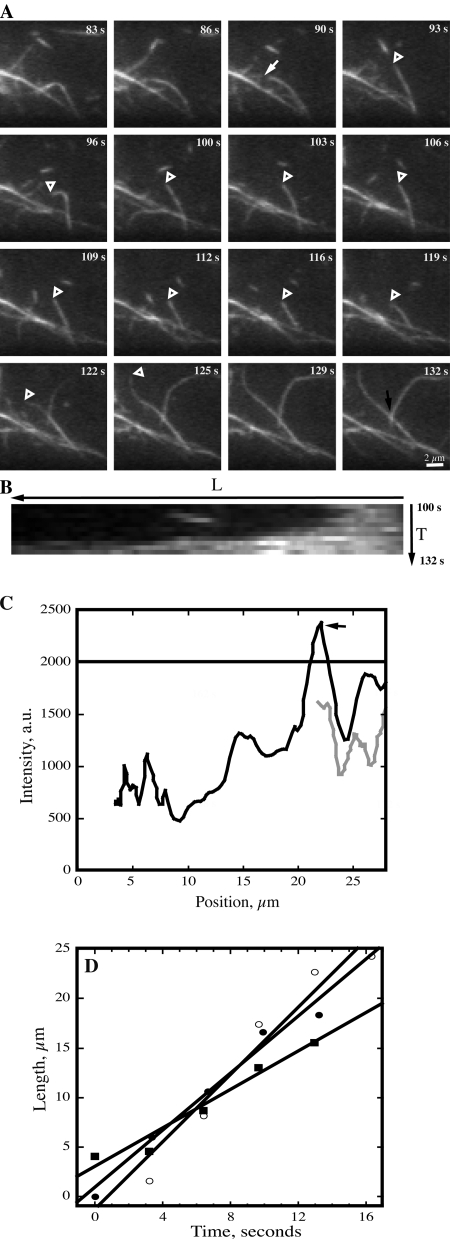
Figure 2.

Actin filaments elongate rapidly. (A) An actin filament is tracked during successive images collected at ∼3-s intervals. It undergoes a breakage event at t = 90 s (arrow) and the newly created filament end (open arrowhead) remains stationary or shrinks slightly during the next 30 s. At t = 116 s, the filament end (open arrowhead) begins to grow and extends out of the field of view at t = 129 s. The average rate of growth for this filament, determined as shown in D, was 0.97 µm/s. A second filament, first appearing at t = 116 s, grows upward and toward the right at a rate of 1.7 µm/s. See Video 4 (available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Bar, 2 µm. (B) Kymograph of the filament highlighted in A. The filament origin or base is at the right and the elongation extends toward the left. (C) Plot of pixel intensity as a function of position along the filament shown in A. The traces show two different time points: gray line, 100 s; black line, 132 s. Filament origin is plotted at the right and growth occurs toward the left. A black arrow marks the location where this filament crosses over another filament (see also Fig. 2 A; 132 s), resulting in a doubling of fluorescence intensity. The solid black line at 2000 represents the upper limit of pixel intensity for an individual actin filament, as determined with the analyses shown in Fig. S3. (D) Actin filament length as a function of time for several representative filaments is plotted and a line of best fit used to estimate rate of elongation. Closed squares, filament marked with open arrowheads in A; open circles, second filament growing upward and toward right in A; closed circles, example filament from a different time-lapse series.

Differences in actin-based structures were also revealed by comparing numerous filamentous elements from multiple cells and hypocotyls. Two populations of actin-based structures were identifiable based on a combination of average pixel intensity, average length, convolution (Table I), and stochastic dynamics (see below). 3A plot of average pixel intensities revealed that the population of faintest structures has a Gaussian distribution with an average value of ∼1100 (Fig. S3 D). Actin filament bundles or cables were significantly brighter and longer (Table I; Fig. S3 D) and had longer lifetimes (not depicted) than the more dynamic single actin filaments. These large actin-based structures were also stiffer, straighter, and mostly longitudinally oriented in the cytoplasm (Fig. 1; Table I). For the subsequent analyses, we considered any actin-based structure with an average pixel intensity <2000 as a single actin filament.

Table I.

Comparison of fluorescence intensity, length, and convolutedness of thick vs. thin actin-based structures

Measurement	Thick structures	Thin structures
Mean intensity	8130 ± 282a	1102 ± 122
Length (µm)	34.5 ± 1.14	17.6 ± 0.7
Convolutednessb	1.1 ± 0.01	2.3 ± 0.6
n; actin-based structures	131	141

^aValues given are means ± SEM.

^bConvolutedness is a dimensionless descriptor of filament shape, defined as the ratio of traced filament length to the length of the longest side of a bounding rectangle encompassing the same filament.

To better understand the dynamic properties of single actin filaments, we tracked >80 filaments from first appearance to complete disappearance in growing epidermal cells. Actin filaments elongated at fast rates, which could occur from the ends of a preexisting fragment (Fig. 2 A; Video 4, available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1), de novo in the cytoplasm, or from the side of an existing actin filament (Fig. 2 A). Of 52 actin filaments tracked for elongation, 13 (25%) formed de novo or from an indeterminate origin; 22 (42%) grew from the end of a preexisting fragment or recently severed filament; and 17 (33%) originated from the side of a mother filament or bundle (Table II). Plots of individual actin filament length as a function of time produced a linear trend (see Fig. 2, B and D) and the mean R-value for the entire dataset was 0.96 ± 0.03. From such plots we determined a mean growth rate of 1.7 ± 0.7 µm/s (Table II). This elongation rate is 20-fold faster than plus-end growth of cortical microtubules.

Table II.

Comparison of actin-dynamic parameters from control and inhibitor-treated epidermal cells

	Control: Growing cells	Nongrowing cells	100 nM LatB	20 or 50 mM BDM
Elongation rate; µm/s	1.7 ± 0.7 (52)a	1.6 ± 0.8 (57)ND	0.6 ± 0.2 (51)**	1.4 ± 0.5 (34)*
Severing frequency; breaks/µm/s	0.011 ± 0.009 (50)	0.014 ± 0.011 (47)ND	0.02 ± 0.02 (40)*	0.004 ± 0.005 (30)**
Max. filament length; µm	14.8 ± 6.4 (78)	10.3 ± 4.4 (61)**	4.4 ± 1.6 (57)**	9.5 ± 5.2 (51)**
Filament origin; % de novo/end/side	25/42/33 (52)	33/40/26 (57)	29/55/16 (51)	18/53/29 (34)
Re-growth of severed end; %	4.4 (362 ends)	2.1 (290 ends)	7.7 (154 ends)	2.5 (122 ends)
Convolutedness	1.6 ± 0.4 (87)	1.6 ± 0.4 (48)ND	1.2 ± 0.2 (54)**	1.5 ± 0.3 (40)ND
Rate of change of convolutedness; s−1	0.08 ± 0.07 (87)	0.05 ± 0.03 (48)*	0.03 ± 0.01 (54)**	0.02 ± 0.03 (40)**

^ND, Not significantly different from control value by Student's t test; P value >0.05.

*, Significantly different from control value by Student's t test; P value ≤0.02.

**, Significantly different from control value by Student's t test; P value <0.0001.

^aValues given are means ± SD, with (n) = number of filaments in parentheses. See text for details of experimental treatment and measurement.

Filament turnover is mediated by severing activity

Lifetimes of most individual actin filaments were <30 s—a phenomenon mediated by severing or fragmentation rather than depolymerization. Nevertheless, a few actin filaments were observed to shrink over time and this usually happened at the end opposite to where growth had occurred or was ongoing. The average shrinkage rate of 0.3 ± 0.3 µm/s (n = 9) was almost an order of magnitude slower than growth and we never observed complete disassembly by this mechanism. Instead, most newly formed actin filaments disappeared because severing activity fragmented them into small pieces that subsequently moved from the field of view (Fig. 3; Video 5, available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). The apparent severing frequency, defined as the number of severing events per length of filament as a function of time, was 0.011 ± 0.009 breaks/µm/s (n = 50 filaments; Table II). Importantly, breakage of actin filaments is unlikely to result from irradiation damage because imaging of filaments in vitro with the same laser settings and TIRF optics does not cause appreciable breakage (unpublished data).

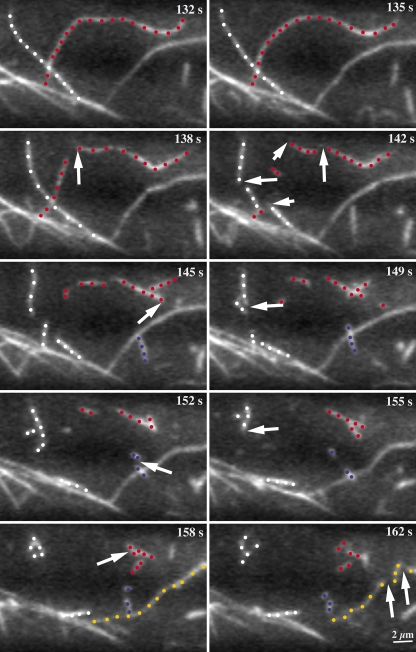
Figure 3.

Actin filaments are destroyed by severing activity. A long actin filament (red dots), previously shown during its elongation phase in Fig. 2 A, is fragmented into many short pieces. At t = 135 s, the filament was 25.4 µm in length. During the next 20–30 s multiple severing events, some of which are marked by arrows, generate numerous small fragments from the mother filament. Most fragments quickly disappear from the field of view. The apparent severing frequency was seven breaks over 25.4 µm of original filament length during a 23-s period, or 0.012 breaks/µm/s. Three other actin filaments in this field of view (white, blue, and yellow dots) were also eliminated or shortened by fragmentation (arrows). See also Video 5 (available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Time points indicate elapsed time from start of video sequence. Bar, 2 µm.

If a break in an actin filament creates a free barbed end, it should elongate immediately at a rate of 1.7 µm/s. However, this was observed only infrequently, suggesting a modification of barbed ends. Newly created actin filament barbed ends occasionally resumed growth within 5–15 s after severing (e.g., Fig. 2 A). Of 181 severing events assessed, which created 362 new filament ends, only 16 (4.4%) were observed to resume growth. Only one or two of these events appeared to show immediate regrowth after severing (e.g., Fig. 4 B; Video 7, available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Thus, most severed ends appear to be capped at the same time as, or shortly after, severing.

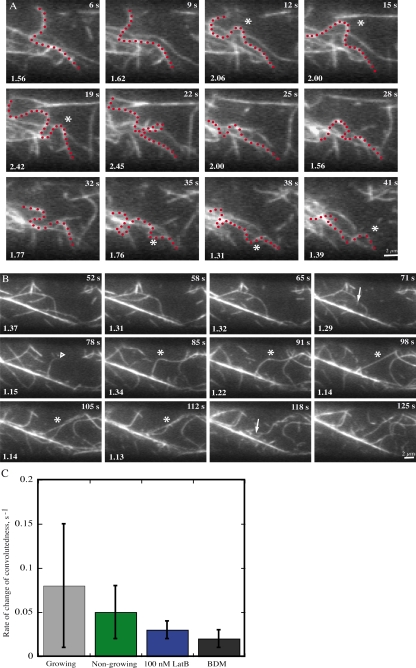
Figure 4.

Buckling and straightening are prominent actin filament behaviors. (A) A representative filament (asterisk) that undergoes continuous undulations and buckling is shown. The highlighted filament (red dots) almost completely changes shape between some consecutive frames. A measure of filament buckling, convolutedness, was applied to this example and the value is given on each frame at bottom left. The average convolutedness (±SEM) for this filament was 1.8 ± 0.4. Time points indicate elapsed time from start of video sequence. See also Video 6 (available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Bar, 2 µm. (B) A long, convoluted actin filament (asterisk) exhibits many aspects of dynamic behavior. Changes to convolutedness in the first three frames, precede a breakage event at 71 s (arrow). The newly created end (open arrowhead) immediately begins elongating at the rate of 1.2 µm/s. Between t = 91 s and t = 98 s, the filament straightens and the convolutedness value approaches one. Subsequently, numerous fragmentation events destroy the mother filament completely so that it is unrecognizable by t = 125 s. Values marked on the frame represent measure of convolutedness for the filament of interest and the average value (±SEM) was 1.2 ± 0.1. Time points indicate elapsed time from start of video sequence. See also Video 7 (available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Bar, 2 µm. (C) The average rate of change in convolutedness for different cell types and inhibitor treatments. Compared with the elongating epidermal cells from 3–5-d-old hypocotyls, both nongrowing cells and cells treated with latrunculin B or BDM showed a significant (P < 0.002) reduction in the rate of change of convolutedness. Data are presented as mean ± SD.

Actin filaments slide along other filaments

The ends of actin filaments were quite dynamic, but entire filaments also changed shape and translocated in the cortical cytoplasm. The only cytoskeletal structures that were relatively static, albeit not immobile, were the large actin bundles (Videos 2 and 3). Actin filaments were typically convoluted, appearing to buckle and contort in time-lapse (Fig. 4 A; Video 6). Buckling could be observed when a filament slid along another actin filament or bundle, but also in the absence of any direct association with other filaments. Actin filaments also underwent straightening events, suggesting a high level of tension along the filament. As an example, Fig. 4 B (asterisk; and Video 7) shows a convoluted filament that straightens within one frame, an interval of only 3 s.

We assessed actin filament buckling and straightening by measuring a dimensionless descriptor of shape (Table II). We define “convolutedness” as the ratio of traced filament length to the longest length of a bounding rectangle defined by the actin filament. Thus, linear actin filaments have a convolutedness value of one. Values increase according to the amount of convolution in the filament. As an example, values of convolutedness are given in Fig. 4 A and B for filaments undergoing buckling and straightening behaviors, respectively.

Nongrowing epidermal cells also show stochastic dynamics

To test whether actin filament dynamics correlate with the growth status of epidermal cells, we made similar measurements on nongrowing cells. Etiolated hypocotyls exhibit a temporal and spatial gradient of growth that begins in cells at the base and moves upward to the hook region (Gendreau et al., 1997). Here, we examined filament dynamics in epidermal cells at the base of 11-d-old dark-grown hypocotyls that have ceased growing along the major axis of hypocotyl elongation (Fig. S1 C). The cortical cytoskeleton of nongrowing cells was comprised of a similar array of actin filaments and actin cables (Fig. S3 B), but was somewhat less densely populated (Video 8, available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Individual actin filaments had apparent elongation rates of 1.6 ± 0.8 µm/s (n = 57), not significantly different from the growing epidermal cells (Table II). The severing frequency was also similar between the two cell types (Table II). However, the maximum length of actin filaments, achieved at the end of growth phase or before severing, was markedly shorter in nongrowing cells (10.3 µm) compared with growing cells (14.8 µm). Finally, although the average convolutedness value was the same, the rate of change in this parameter was significantly lower in nongrowing cells (P = 0.002; Table II, Fig. 4 C). Thus, filament growth rates and severing frequency are not different in growing versus nongrowing epidermal cells, whereas filament density, length, and waving/buckling activity are reduced in nongrowing cells.

Latrunculin B reduces the apparent filament elongation rate

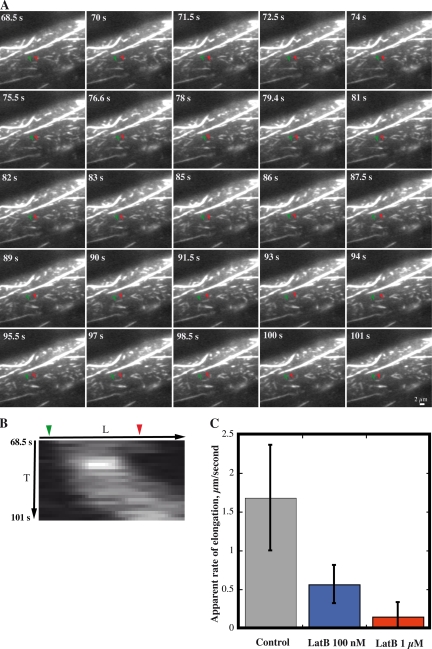
Latrunculin B (LatB) binds tightly to plant monomeric actin (K_d = 74 nM) and reduces polymeric actin levels in live cells (Gibbon et al., 1999). Here, we used LatB to test whether filament growth rates were dependent on the available monomer concentration. Growing epidermal cells were treated with either 100-nm or 1-µM LatB and imaged by VAEM within 2–10 min. After several minutes, 1 µM LatB reduced the dynamics and overall length of actin filaments (Fig. 5 A; Video 9, available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). Individual actin filaments became short fragments with reduced stochastic dynamics (Fig. 5 B). Filament growth and severing still occurred; however, the elongation rate was just 0.15 ± 0.2 µm/s (n = 47; Fig. 5 C). Lower concentrations of LatB (100 nM) still had significant effects on stochastic dynamics (Table II). Elongation rates in the presence of 100 nM LatB were 0.6 ± 0.2 µm/s (n = 51), nearly threefold less than in control cells (Table II; Fig. 5 C). Surprisingly, severing frequency was slightly elevated in the presence of 100 nM LatB (Table II). The combination of lower growth rates and constant severing activity resulted in a net reduction of average filament length. In control cells, the maximum length of growing filaments was 14.8 ± 6.4 µm (n = 78), whereas this value was reduced to 4.4 ± 1.6 µm (n = 57) and 2.4 ± 1.5 µm (n = 49) in cells treated with 100-nM or 1-µM LatB, respectively.

Figure 5.

Latrunculin treatment reduces the filament elongation rate in a dose-dependent manner. (A) Representative cell treated with 1 µM LatB has numerous, short filaments or fragments as well as several large cables. Actin filaments or fragments grow rather slowly, if at all. Time points indicate elapsed time from start of video sequence. Bar, 2 µm. See Video 9 for full time-lapse series (available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1). (B) Kymograph of the single filament marked in A. This short filament undergoes slow elongation and rapid shrinkage events. (C) Plot of average rate (±SD) of filament elongation in control and LatB-treated cells. Treatments with 100 nM and 1 µM LatB for 1–10 min significantly reduce the rate of filament elongation (P < 0.0001).

Although the main effect of LatB treatment is a dose-dependent reduction in elongation rates and a consequent shortening of the actin filaments over time, there were additional impacts in that filament convolutedness and the rate of change in convolutedness were reduced compared with control cells (Table II). This might be an indirect effect of filament shortening, if the forces that cause buckling and tension depend upon filament length or alternately, indicate that forces generated by actin polymerization contribute to buckling.

A presumptive myosin inhibitor reduces filament dynamics

To gain insight into the potential involvement of myosin in the observed dynamic parameters, we used 2,3-butanedione monoxime (BDM). BDM is an antagonist of mammalian myosin II ATPase (Ostap, 2002), inhibits at least one class of plant myosin in vitro (Tominaga et al., 2000; Funaki et al., 2004), and at millimolar concentrations perturbs cytoplasmic streaming and organelle movements in planta (Nebenführ et al., 1999; Holweg et al., 2003; Higaki et al., 2006).

We treated hypocotyls with 20- or 50-mM BDM and imaged cells within 30 min. The example in Video 10 (available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1) shows that several aspects of filament dynamics were markedly reduced by BDM treatment. Interestingly, BDM did not affect average convolutedness of filaments, but did reduce the rate of change of convolutedness fourfold (Table II). Collectively, these results provide evidence that myosin-dependent forces drive filament buckling and straightening, either directly or indirectly. To verify that BDM affects myosin specifically and not other aspects of filament dynamics, we also measured growth rates and severing frequency. The elongation rate in the presence of BDM, 1.4 ± 0.5 µm/s (n = 34), was slightly but significantly reduced compared with control cells (P = 0.02; Table II). Further, the apparent severing efficiency in the presence of BDM, with a mean value of 0.004 ± 0.005 breaks/µm/s (n = 30), was reduced by more than half compared with the controls (P < 0.001; Table II). Thus, BDM has a substantially greater effect on the buckling and straightening of actin filaments than it does on the stochastic dynamics of actin filaments.

Discussion

Here, we report the first examination of actin filament dynamics in living plant cells at high spatial and temporal resolution using time-lapse VAEM. Based on actin filament properties in motile animal cells and yeasts, we expected to find modest elongation rates, polarized organization of arrays and/or filament treadmilling. Instead, our results reveal a dynamic, complex, and stochastic behavior of actin filaments, resembling in many ways a biomimetic system of actin assembly (Michelot et al., 2007). New actin filaments originate from the side of existing filaments or bundles, de novo in the cortical cytoplasm or from fragmented filament ends. Elongation rates are high, 1.7 µm/s, and capable of generating filaments that span the cell diameter within 10–20 s. Despite high assembly rates, most filaments are rather short lived. Disappearance of actin filaments is not mediated by depolymerization at their ends, but rather by severing activity. Finally, actin filaments exhibit buckling and straightening events, indicative of filament–filament sliding and/or tension along a filament. Qualitatively similar actin dynamics in dividing fission yeast cells were reported recently (Vavylonis et al., 2008). For example, actin filament lifetimes were <20 s, and filament buckling and severing were observed. Detailed consideration of these stochastic actin dynamics and knowledge of the biochemical activities of actin-binding proteins can be combined to generate testable models that describe the molecular control of actin turnover in plant cells.

Given the prominent buckling behavior of many actin filaments, there exists a possibility that what is reported as elongation might actually represent intact filaments moving into the VAEM plane. This is unlikely, however, for the following reasons: First, movement of an actin filament into the VAEM plane would not be expected to give a good linear fit to a plot of filament length versus time. Second, more than 40% of filaments originate unambiguously from a preexisting fragment or elongate from a severed filament end (e.g., Figs. 2 A, 4 B) and the elongation rates are independent of filament origin. Third, the complementary behavior of filaments shrinking by a smooth and uniform movement is rare. Fourth, inhibition of myosin activity with BDM, and thus filament buckling, has a negligible effect on elongation rate (Table II). Finally, the actin monomer-sequestering agent, LatB, inhibits filament elongation rates (Fig. 5 C) and the maximal length of filaments (Table II) in a dose-dependent manner. Thus, we believe that 1.7 µm/s reflects the polymerization rate at actin filament ends, presumably the barbed ends.

Individual actin filaments in Arabidopsis epidermal cells grow at rates 10 to 100× faster than the actin filaments in fission yeast or in the dendritic actin array at the leading edge of motile metazoan cells (Ponti et al., 2004; Vavylonis et al., 2008). The high growth rate is consistent with a sizable pool of assembly-competent actin monomers or profilin–actin in vivo (Pollard et al., 2000; Staiger and Blanchoin, 2006). Assuming that elongation occurs exclusively at filament barbed ends; that the association rate constant from monomer assembly is the same as that for ATP-loaded rabbit skeletal muscle α-actin (k₊ = 11.6 µM²¹ s²¹; Pollard, 1986); and that one micrometer of actin filament comprises 370 subunits (Pollard et al., 2000), then at a rate of 1.7 µm/s or 629 subunits/s we estimate the actin monomer concentration at ∼50 µM using the equation: [G-actin] = rate/k₊. This seems reasonable for plant cells, where pollen maintains a 100–200-µM pool of monomeric actin (Gibbon et al., 1999; Snowman et al., 2002). If this pool of actin is buffered with profilin, known to be present in amounts at least equimolar to the total actin (Chaudhry et al., 2007), then actin filament nucleation and elongation from pointed ends will be suppressed (for review see Staiger and Blanchoin, 2006). The plant profilin–actin complex can, however, add onto barbed ends and elongate actin filaments in vitro (Michelot et al., 2005). If nucleation is suppressed by abundant profilin in plant cells, then mechanisms to generate new actin filaments or filament ends in such cells are necessary (Staiger and Blanchoin, 2006; Blanchoin and Staiger, 2008).

Like the stochastic dynamics of an in vitro biomimetic system (Michelot et al., 2007), shrinkage of actin filaments in the cortical array of epidermal cells is not due to depolymerization, but rather filament severing. Quantifying severing activity gives an average value of 0.01 breaks per micrometer of actin filament every second (Table II). In other words, a filament that is 10 µm long will suffer on average six breaks per minute before disappearing from the field of view. Biochemically, this severing activity could be the result of ADF/cofilin or villin/gelsolin proteins. Both classes of protein are present in Arabidopsis cells (Klahre et al., 2000; Dong et al., 2001; Huang et al., 2005; Chaudhry et al., 2007), and both sever actin filaments in vitro (Xiang et al., 2007; unpublished data). ADF/cofilin is responsible for switching from a simple barbed-end growth mechanism to stochastic dynamics in vitro (Michelot et al., 2007). Therefore, either villin/gelsolin and ADF/cofilin could be responsible for the severing activity observed in epidermal cells. How the fragments generated by severing are recycled into the polymerizable actin pool is difficult to analyze, as these small filaments typically move quickly from the field of view. However, several mechanisms can be envisioned to regenerate the monomer pool; the fragments might be disassembled by further severing or they could depolymerize monomer-by-monomer from either end of the filament.

The behavior of actin filament ends that remain in the field of view may give additional clues about the proteins responsible for severing. If a breakage event creates a free barbed end, that end should assemble from the pool of polymerizable subunits at an average rate of 1.7 µm/s. Newly created filament barbed ends occasionally resume growing within 5–15 s after severing (e.g., Fig. 2 A), but of 181 severing events observed (362 new ends) only 16 (4.4%) resumed growth. Only one or two of these filament ends underwent immediate regrowth after severing (e.g., Fig. 4 B). The failure of the majority of newly created ends to grow suggests villin/gelsolin activity. Villin/gelsolin caps barbed ends after severing, whereas ADF/cofilin does not. It has been proposed that actin-interacting protein1 (AIP1) caps the ends of filaments and thereby promotes the activity of ADF/cofilin (Okada et al., 2002); however, such biochemical activity for plant AIP1 has not yet been demonstrated directly (Allwood et al., 2002; Ketelaar et al., 2004a).

Another possibility is that heterodimeric capping protein (CP) rapidly binds and caps the ends of filaments severed by ADF/cofilin. Arabidopsis CP binds filament barbed ends with high affinity (K_d ∼10–20 nM) and prevents subunit addition (Huang et al., 2003). Assuming a cellular concentration for AtCP of ∼1 µM, similar to that in yeast and mammalian cells (Pollard et al., 2000), then the association rate constant (k₊) of 0.07 µM⁻¹ s⁻¹ (Huang et al., 2006) and half-life of 10 s predict that filament barbed ends will grow by ∼17 µm before they are capped. As noted above, this was not the case for most severing events we observed.

In addition to the stochastic dynamics of rapid polymerization and severing, actin filaments are constantly being rearranged in the cortical cytoplasm. A prevalent observation was of filament buckling or “waving” (Fig. 4 A). Actin filaments also rapidly straightened, appearing to be under tension (Fig. 4 B). Both of these changes in shape were reduced by the putative myosin inhibitor, BDM (Fig. 4 C). Other aspects of filament dynamics, like the site of filament origin, elongation rate and severing frequency were affected only modestly by BDM (Table II) and could be an indirect result of myosin inhibition. For example, the ability to visualize a breakpoint likely requires myosin-driven movement or lateral translocation of the fragment away from the mother filament. Thus, severing events might be underscored in the presence of BDM. Alternatively, filament fragmentation could require the cooperative action of a severing protein and myosin-dependent tensile forces on the filament backbone. Finally, the mode of action of BDM remains controversial and the possibility for off-target interactions is not excluded (McCurdy, 1999; Tominaga et al., 2000).

An important unanswered question is how the dynamic behavior of the cortical actin array relates to its function during cell expansion. Simple models linking stochastic dynamics of the cortical actin network to secretory vesicle trafficking or sites of exocytosis are difficult to imagine. Moreoever, both growing and nongrowing epidermal cells have quantitatively similar filament elongation rates and apparent severing frequencies (Table II). The only notable differences are a reduction in overall filament density and length, and a decreased rate of change in convolutedness, for nongrowing cells. Thus, a direct role for cortical actin arrays during cell expansion and wall deposition may be over-estimated. Alternatively, cortical actin remodeling might represent a surveillance mechanism that expends energy to be ready to respond to biotic and abiotic stress. Fungal and oomycete pathogens elicit a rapid response that involves the actin cytoskeleton to recruit defense machinery at the site of attack (Hardham et al., 2007; Hückelhoven, 2007). The stochastic dynamics of actin filaments would permit a cell to change the architecture of its cytoskeletal array within seconds, by locally down-regulating severing activity, stabilizing filaments, or enhancing filament uncapping.

In summary, our findings support a model whereby actin turnover is ruled by stochastic dynamics rather than filament treadmilling. This stochastic behavior has two major components: (1) rapid polymerization from a large pool of polymerizable actin; and (2) destruction by severing activity of the aged portions of filaments. We predict several conserved actin-binding proteins, including profilin, ADF/cofilin, and villin will play major roles in this model. Reverse-genetic strategies in Arabidopsis will allow these models to be tested in the future. The combination of genetic approaches and imaging of actin filament dynamics by VAEM make epidermal cells from the hypocotyl an excellent system for further exploration of cortical cytoskeleton function.

Materials and methods

Chemicals

All chemicals were purchased from Sigma-Aldrich unless stated otherwise. BDM was prepared freshly in water. LatB (Calbiochem) was dissolved in ethanol and stored as a 5-mM stock solution at −20°C.

Plant material

Arabidopsis thaliana Col-O expressing GFP-fABD2 was as described previously (Sheahan et al., 2004), whereas seed for plants expressing EYFP-TUB5 (Shaw et al., 2003) and GFP-EB1 (Mathur et al., 2003) were donated by J. Sedbrook (Illinois State University, Normal, IL) and J. Mathur (University of Guelph, Ontario, Canada), respectively. Seed was surface sterilized and stratified at 4°C on agar plates containing 0.5X Murashige and Skoog medium fortified with 1% sucrose (Sheahan et al., 2004). After exposing stratified seed for 4 h with white light, seedlings were grown in the dark for 3–5 d at 21°C before use in experiments with elongating epidermal cells. Nongrowing epidermal cells were visualized on etiolated hypocotyls at 11 d post-germination. When BDM or LatB were applied, the appropriate concentration of drug was added during mounting and the hypocotyls imaged within 2 min but no longer than 30 min post-treatment. Controls for LatB treatments included 0.02% (vol/vol) ethanol.

Variable-angle epifluorescence microscopy (VAEM)

Imaging the cortical cytoplasm of epidermal cells was essentially as described by Konopka and Bednarek (2008a,b), albeit using a different manufacturer's instrument. Variable-angle epifluorescence illumination was achieved using a total internal reflection fluorescence (TIRF) illuminator mounted on an IX-71 microscope equipped with a 60X 1.45 NA TIRFM PlanApo objective (Olympus). After focusing on the first visible actin filaments (or microtubules) at the periphery of a cell, the angle of laser illumination was adjusted for maximal contrast and signal-to-noise ratio. We estimate the depth of focal plane at 0.5–1 µm in VAEM mode. Illumination was from a 100-mW argon ion laser (Melles Griot Photonics) attenuated to 20% power with neutral density filters and shuttered between consecutive exposures. The 488-nm laser line was filtered through a triple-wavelength filter and dichroic mirror set (488–543-633TB; Omega Optical) and GFP emission from the specimen captured with a 512 × 512 electron-multiplying CCD camera (ORCA-EM C9100-12; Hamamatsu Photonics). Typical exposure times were ∼200 ms with an electronic gain of 200. The VAEM system was operated with IPLabs software (version 3.9.4; Scanalytics Inc.) running on a Macintosh G5 computer.

Quantitative analyses

Time-lapse series of 100 images were collected at 1–3.5-s intervals in IPLabs and a table of elapsed time between each frame recorded. Minimal contrast enhancement or changes to the black level were applied to the entire stack to improve image quality for analysis and display. For some purposes, cropped regions and subsets of the time-lapse images were converted to 3 or 10 frames per second (fps) QuickTime movies, without compression, using IPLabs. Regions of interest were also transferred to MetaMorph (version 6.2r6; MDS Analytical Technologies) for preparing montages of still images. Figures were composed with Adobe Illustrator CS3. The range of individual pixel intensities for different epidermal cells was computer generated with multiple line-scans over the field of view using MetaMorph. The intensity of the different actin-based structures was determined over time after subtraction of the background intensity. To measure actin assembly rates, filament origin, and severing frequency, actin filaments were tracked manually through the time-lapse stack of images. For growing epidermal cells, nongrowing cells and hypocotyls treated with BDM or LatB, 40–100 filaments from at least 5 different cells in 3 or more hypocotyls were selected. For example, 87 filaments from 12 elongating cells in 5 different hypocotyls were tracked, and an overlapping set of filaments was used for elongation rate and severing frequency measurements. Actin filament length was measured using the “length” tool in IPLabs and a conversion factor of one pixel = 0.267 µm. Only filaments that could be tracked over at least four successive frames were quantified. Assembly rates were determined by plotting filament length versus time and the data fit with a linear function in Kaleidagraph (version 4.0, Synergy Software), with rate taken as the slope from the line of best fit. Plus-end elongation rates for microtubules in epidermal cells expressing EYFP-TUB5 or GFP-EB1 were determined in a similar manner. Filament severing frequency was estimated by measuring the maximal length of an actin filament and then monitoring breaks along the filament over time. If a filament had a break before it finished growing or disappeared, the length was taken as its maximum theoretical length between point of origin and endpoint of growth. Filament fragments of greater than one micrometer were tracked for as long as practical to monitor additional breakage events. Apparent severing frequency was calculated as the number of breaks per length of original mother filament per unit time (breaks/µm/s). To quantify filament buckling, image sequences were imported into ImageJ (version 1.37; http://rsb.info.nih.gov/ij). A freehand line was traced over the filament of interest before using the “measure” function to evaluate filament length, bounding rectangle, and mean fluorescence intensity along the filament (see Table I). “Convolutedness” was calculated as the ratio of filament freehand length to the longest side of the bounding rectangle (averaged over the image series; ≥10 frames) and change in convolutedness from the average of differences in convolutedness between consecutive frames. Values were tested for significance with a two-tailed Student's t-test.

Online supplemental material

Fig. S1: Hypocotyls and epidermal cells expressing GFP-fABD2 grow similarly to those from wild-type seedlings. Fig. S2: VAEM is useful for documenting the organization and dynamics of the cortical cytoskeleton. Fig. S3: Analysis of pixel intensities for actin filaments and actin-based structures in the cortical array. Video 1: Time-lapse series of microtubule plus-end dynamics as visualized by GFP-EB1 expression. Video 2: Full time-lapse sequence of actin dynamics as reported by GFP-fABD2 expression. Video 3: Another example of full time-lapse series for actin dynamics. Video 4: Filament elongation from a severed end. Video 5: Severing activity destroys actin filaments. Video 6: Buckling or waving of an actin filament. Video 7: Actin filament tension/straightening. Video 8: Nongrowing cells also show stochastic dynamics. Video 9: Latrunculin reduces the elongation rate and length of actin filaments. Video 10: BDM treatment dampens actin cytoskeleton dynamics. Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.200806185/DC1.