RICHEST ‐ a web server for richness estimation in biological data

Abstract

Richness is defined as the number of distinct species or classes in a sample or population. Although richness estimation is an important practice, it requires mathematical and computational methods that are challenging to understand and implement. We have developed a web server, RICHness ESTimator (RICHEST), which implements three non-parametric statistical methods for richness estimation. Its user-friendly web interface allows users to analyze and compare their data conveniently over the web.

Availability

A web server hosting RICHEST is accessible at http://richest.cgb.indiana.edu/cgi-bin/index.cgi and the software is freely available for local installations.

Background

Characterizing biological diversity has been a longstanding interest among biologists. In particular, estimating species richness (i.e., the number of distinct plant, animal or microbial species) is important for understanding the structure of specific environmental niches. Because it is impractical to exhaustively survey entire ecosystems, such estimates must often be inferred from sampling, e.g., giventhe number of unique species identified from an initial random sample, how many new species are expected in an additional sample? It is not trivial to perform such estimations. First, it is still an active research area for statisticians to develop robust estimation methods. Biologists do not always have time to follow the latest statistical breakthroughs. Second, methods published by statisticians are not always implemented into convenientcomputer programs for biologists. Biologists are left with mathematical formulations that may be prohibitively complicated to use with their data. We have developed a web-based server, RICHness ESTimator (RICHEST),which implements sophisticated statistical methods for richness estimation. The intuitive web interface guidesusers to upload their data and easily perform their analyses.

Methodology

Implementation

We have identified three non‐parametric richness estimation methods: (i) a non‐parametric Bayesian method described by Lijoi et al. [1]; (ii) a Poisson non‐parametric maximum‐likelihood (PNPML) method, similar to Wang et al. [2]; paired with the rarefaction methodology [3]; and (iii) the Good‐Toumlin estimator [4]. We have chosen to focus on non‐parametric methods because they eliminate the need for assumptions about the underlying distribution. However, despite the elegant mathematics published in the Bayesian method, no computer program accompanies the publication. The computational instructions obtained directly from the authors (personal communication) are difficult to follow without significant computational expertise. For the PNPML method, Wang et al. [2] have already implemented it into a user‐friendly web‐based tool called ESTstat. However, the focus of the ESTstat web server is for analyzing EST data although users can also apply it for general species richness estimation. Other existing tools for richness estimation such as EstimateS [5] are desktop applications instead of web‐based servers.

To bridge the gap between the published statistical methods and the biologists wishing to apply the methods to their data, we have implemented all three methods in RICHEST using the R program for statistical computing. For the Bayesian method, the estimates are achieved by optimizing Pitman's sampling formula with respect to two parameters of a Poisson‐Dirichlet distribution. In our implementation, we have taken advantage of the smoothness of the function of Pitman's sampling formula to apply the Nelder‐Mead optimization technique [6]. The implementation of the PNPML method is similar to that of ESTstat [2], except that it does not implement a penalty function to constrain the population richness parameter. Instead, a user can specify some estimate of the richness of the population and use the method to estimate the richness of subsequent samples. When such information is not scientifically available, one strategy for using the PNPML method is to set the population richness estimate parameter to the Chao lower bound, which is automatically calculated by RICHEST when the data is loaded. The PNPML method uses an expectation‐maximization algorithm [7] to estimate the maximum‐likelihood species abundance distribution based on the non‐parametric Poisson mixture model, and it uses this estimated distribution to generate sample richness estimates by rarefaction. Finally, the classic Good‐Toulmin estimator was implemented as described in [4]. The web interface of RICHEST (Figure 1) is implemented with the Perl programming language.

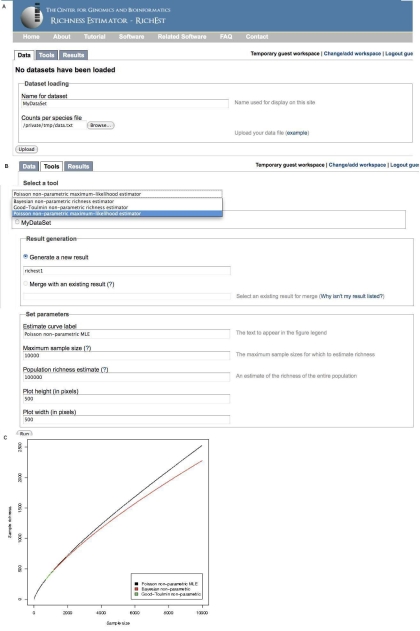
Figure 1.

Screenshots of the RICHEST program outlining key features of the application. The RICHEST web interface consists of three tabs, named Data, Tools, and Results that divide the analysis process into three stages as described below. Users are encouraged to follow the tutorial at the project web site to demonstrate the step‐by‐step usage of the program. (A) Loading data: The Data tab allows the user to load tab‐delimited data files. Users may also upload multiple datasets before running any estimation procedures. (B) Selecting tools: The tools tab allows the user to select and run our integrated richness estimation programs. The tab prompts the user to select which data to use as input, which method to use for estimation, and which options to use for that method. (C) Viewing results: RICHEST outputs a hyperlink to a tab‐delimited table and the corresponding graph representing the estimated sample richness curve which gives the richness estimates as a function of the cumulative sample size.

Validation

We have validated the RICHEST tool by applying it to several data sets. Here, we describe a published microbial data set compiled by Schloss and Handelsman [8], in which total 690 16S rRNA sequences were extracted from the Sargasso Sea metagenome sequencing project [9] and clustered into 114 different microbial species based on sequence similarity. To validate the methods that we have integrated in RICHEST, we used a subset of the 16S rRNA sequences to predict richness of the whole microbial sample. For example, we randomly selected some 16S rRNA sequences and counted the number of microbial species in this subset; then we used the three methods to estimate the total number of predicted microbial species in all 690 16S rRNA sequences. That is, we asked whether our predictions would be close to what Schloss and Handelsman observed (i.e., 114 microbial species in total). Table 1 (under supplementary material) shows that our predictions are consistent with their observations. Our result also confirms the prediction by Lijoi et al that the Good‐Toulmin estimator provides reliable estimates for the species richness of an additional sample only if its size is not too large.