Abstract
Synthetic biology aims to the design or redesign of biological systems. In particular, one possible goal could be the rewiring of the transcription regulation network by exchanging the endogenous promoters. To achieve this objective, we have adapted current methods to the inference of a model based on ordinary differential equations that is able to predict the network response after a major change in its topology. Our procedure utilizes microarray data for training. We have experimentally validated our inferred global regulatory model in Escherichia coli by predicting transcriptomic profiles under new perturbations. We have also tested our methodology in silico by providing accurate predictions of the underlying networks from expression data generated with artificial genomes. In addition, we have shown the predictive power of our methodology by obtaining the gene profile in experimental redesigns of the E. coli genome, where rewiring the transcriptional network by means of knockouts of master regulators or by upregulating transcription factors controlled by different promoters. Our approach is compatible with most network inference methods, allowing to explore computationally future genome-wide redesign experiments in synthetic biology.
INTRODUCTION
Molecular regulations govern the cell response under environmental (extracellular) or genetic (intracellular) perturbations. The elucidation of these regulations with computational techniques will allow analyzing the cell behavior (1), since modeling in biology has boosted the understanding of the cell mechanisms by means of systemic approaches (2). On the other hand, the design of new transcriptional networks requires a quantitative description of the transcription regulation. Thanks to the new developments in the inference from transcriptomic data, now it is possible to reconstruct the regulatory network with enough accuracy to predict the gene expression profile in presence of heterologous networks. We propose a procedure that, by extending a recent methodology, could be used to redesign transcriptional networks.
The continuous developments on genome sequencing and annotation allow us to design microarrays and to identify the genes and transcription factors (TFs) of an organism. The development of the microarray technology has provided high-throughput genomic measurements, where cells are subjected to several conditions or stresses to measure their gene expression profiles (3). Large-scale cell models, such as metabolic, transcription or protein networks, are distilled from high-throughput genomic data, which poses one of the most challenging problems in biology. The construction of a deterministic model would allow the prediction of the cell response under different stimuli (4).
To redesign the transcriptional regulation network, we need a quantitative model able to predict the gene dynamics. We propose to characterize such model by using microarray data with a known transcriptional network inference method. We first infer the network topology and we later estimate the corresponding kinetic parameters. For the last decade, there has been an enormous effort in the improvement of techniques aimed at the inference of the connectivity of the transcription network. Clustering approaches (5–9) have been used to obtain information of regulatory networks but with low accuracy (10). Information-theoretic inference provides more accurate networks (11–15) even from reduced expression datasets. A local significance calculation has been very fruitful to capture the network topology (14). On the other hand, Bayesian methods (16–19) give networks with high precision but low proportion of true recovered interactions (they introduce few regulations with high confidence). Moreover, such methods have a higher computational cost. Herein, we propose the construction of predictable genome models in a standard format from a regulatory scaffold captured by using probabilistic methods. Other approaches, instead, optimized directly the corresponding kinetic parameters for a linear regulatory model (20,21). In addition, recent algorithms (22,23) applied sparse logistic regression (24) for gene selection in order to avoid overfitting.
METHODS
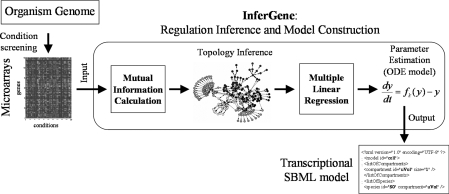
We aim to the development of a methodology able to in silico evolve a genome for having a predefined transcriptional profile. For this, we require to construct a predictive genome model of transcription, based on ordinary differential equations (ODEs), to account for global redesigns of the cellular regulatory map. Using such models we could study the evolution of gene regulations as a consequence of the environmental stimuli. To construct this we have to use as input microarray data properly normalized (Figure 1). In general, transcription involves protein–DNA interactions, but microarray data gives the genetic expression by quantifying the amount of mRNA. Thus, inferring just from transcriptomic profiles could introduce some inaccuracies due to, for instance, protein–protein interactions of TFs (25,26). Furthermore, some environmental stresses (e.g. heat shock) can alter globally protein expression. However, in this work we neglect these effects for simplicity, assuming that the mRNA amount is proportional to the protein expression and that it is function of the TFs only. In addition, as the precise kinetic model of transcription regulation is not known for any organism, we have generated in silico genomes having random regulatory maps with scale-free topology (27). We have applied our methodology against synthetic transcriptomic profiles. We will only assume a previous knowledge of the list of all genes and TFs obtained from genome annotation [e.g. RegulonDB (28) for Escherichia coli]. Eventually, we can consider the genomic organization in operons (especially in case of bacteria). Such operons can be known a priori or inferred from the same microarray data. Our approach consists of two nested steps. First, we obtain the topology of the network (i.e. which TF regulates which gene or operon) by using an information theory-based approach. We store in a matrix the likelihood of the mutual information (MI) among all the TFs and operons (29–31), computed as the z-scores from the distribution of MI using the transcriptomic expressions for all the perturbing conditions (14). Then, using a suitable threshold, we infer the TFs regulating a given operon. Subsequently, for each operon we perform a multiple linear regression against the corresponding TFs to recover the model kinetic parameters (32). To infer cooperative regulations, we create a set of artificial TFs whose expression profiles are obtained in a combinatorial way as the product of two TF profiles (with the aim of conserving linearity in the formalism). This model is subsequently exported into a SBML file (33), which could be visualized using Cytoscape (34). We have measured the performance of our algorithm by using synthetic transcriptomic data from artificially generated networks.
Figure 1.
Scheme to infer the regulatory network of an organism. Our inference algorithm uses microarray data and prior knowledge about operons and TFs to predict the full transcriptional regulatory map. It consists of two nested steps: (i) inference of the topology using MI; and (ii) the estimation of the kinetic parameters via multiple linear regressions (Figure S1). We export the constructed model in SBML format (33). We apply our methodology to infer the E. coli genome model by using the M3D compendium versus 3 (41) and a list of TFs and operons from RegulonDB (28).
Mathematical model
We describe the genetic regulations using a linear model for the mRNA dynamics. Here, we use as input data mRNA expression profiles in steady state derived from transcriptional perturbations. As transcriptomic data is normalized and usually represented in logarithmic scale, we have considered log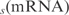 as variables (where s can be 2 or 10). Therefore, the mRNA dynamics from gene yi is given by
as variables (where s can be 2 or 10). Therefore, the mRNA dynamics from gene yi is given by
| 1 |
where ai is the basal synthesis rate, 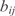 the transcription regulatory coefficient of TF j,
the transcription regulatory coefficient of TF j, 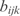 the cooperative transcription regulatory coefficient of TFs j and k acting on the promoter controlling the gene i and δi the degradation rate. We set
the cooperative transcription regulatory coefficient of TFs j and k acting on the promoter controlling the gene i and δi the degradation rate. We set 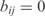 and
and 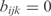 when j and j, k are not TFs regulating the gene i. We assume that all the genes of an operon have the same expression value. We also consider that two regulators could act in a cooperative way (i.e. synergistic inductions and cooperative repressions). We do not consider cooperation between more than two TFs.
when j and j, k are not TFs regulating the gene i. We assume that all the genes of an operon have the same expression value. We also consider that two regulators could act in a cooperative way (i.e. synergistic inductions and cooperative repressions). We do not consider cooperation between more than two TFs.
Here, we use expression values in steady state. Nevertheless, it could be also possible to extend our approach to the use of time series to enrich the experimental input (35). Hence, in the steady state we can write
| 2 |
where we have defined 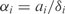 ,
, 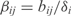 and
and 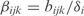 . Notice that the resulting parameters are referred to the intensity scale of the microarray technology. We use a time scale such that the mRNA degradation constant is δ = 1. To use a realistic mRNA degradation constant, it would require translating the Affymetrix (36) data to concentration units.
. Notice that the resulting parameters are referred to the intensity scale of the microarray technology. We use a time scale such that the mRNA degradation constant is δ = 1. To use a realistic mRNA degradation constant, it would require translating the Affymetrix (36) data to concentration units.
Using network inference to obtain a kinetic model
To obtain a kinetic model suitable for redesign, we take advantage of recent methods aimed to infer the topology of the global regulatory map. In particular, we have chosen one of the best performing methods, the CLR (14), although other methodologies providing a transcriptional map, such as sparse Bayesian methods (19) could also be used. Our approach consists of using multiple regressions to fit the kinetic parameters of a continuous model of the transcription regulation. The approach for large-scale transcription inference is based on measuring the influence between the expression levels of TFs and operons across a large set of conditions. Here, we use MI to estimate the correlation between a TF t and an operon p by using 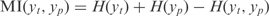 , where H is the entropy of a variable. It is defined as
, where H is the entropy of a variable. It is defined as 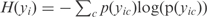 , where
, where 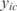 is the expression value of gene i in the condition c, and
is the expression value of gene i in the condition c, and 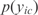 the probability to reach that value. The MI is always a positive magnitude. Joint normal distributions are generated with independent variables
the probability to reach that value. The MI is always a positive magnitude. Joint normal distributions are generated with independent variables 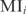 and
and 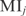 (values for gene i and TF j, in row i and column j). Thus, the MI matrix is converted into Z matrix where
(values for gene i and TF j, in row i and column j). Thus, the MI matrix is converted into Z matrix where 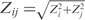 and Zi and Zj are the z-scores of
and Zi and Zj are the z-scores of 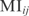 from the marginal distributions. According to this matrix, we obtain the genomic interactions.
from the marginal distributions. According to this matrix, we obtain the genomic interactions.
For completeness, we have developed an algorithm (InferOpe) to infer operons from microarray data. Since two genes from one operon share the same mRNA molecule, we would expect that their transcriptomic profiles would be similar. Our operon prediction is based on the use of co-expression patterns (37), assuming that two genes, i and j, belong to the same operon if they are highly correlated. We evaluate this by using the Pearson correlation coefficient (we assume correlation if 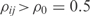 ). Moreover, we impose that the angle (
). Moreover, we impose that the angle (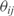 ) of such correlation should be around
) of such correlation should be around 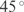 {i.e.
{i.e. 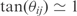 ], where the relationship with
], where the relationship with 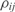 is given by
is given by 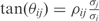 .
.
For each operon we compute the kinetic parameters for the TFs regulating its promoter. The experimental value of one operon is computed as the average of the expressions of all genes belonging to that operon (i.e. 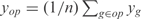 , where n is the number of genes of the corresponding operon). To estimate the model parameters αi,
, where n is the number of genes of the corresponding operon). To estimate the model parameters αi, 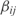 and
and 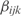 we use multiple linear regression (32), which is the result of a minimization problem (least squares) defined by
we use multiple linear regression (32), which is the result of a minimization problem (least squares) defined by
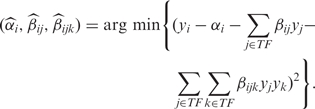 |
3 |
We assume that the variability in the experimental conditions and the complexity of the natural regulation is high enough to prevent linear correlations between TFs, which would produce identifiability problems in the regression parameters. Even in such a case, our model is a valid solution although there could be alternative models. We have used the LINPACK libraries (38) to calculate the solution.
Our procedures are implemented in C++, and they run on any UNIX environment. The InferGene software, a tutorial, the corresponding files and some examples are available upon request. The software consists of different functional modules to compute first the network topology and then the corresponding kinetic parameters (see Supplementary Figure S1). Below we present the procedure implemented in InferGene:
Represent the microarray data organized in matrix form, for instance, genes in rows and conditions in columns.
Obtain the list of TFs for the given organism.
Ensure that the microarray matrix contains the expression profiles for all TFs.
Add new rows corresponding to the combinations of two TFs obtained as the product of them (i.e.
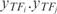 are the new TF profiles).
are the new TF profiles).In case of bacteria, have a file containing the list of operons with the corresponding genes. Otherwise, run InferOpe, our algorithm to infer clustered genes based on co-expression patterns. To maintain the same scheme in all cellular contexts, we can dispose one gene per operon in case of eukaryotes.
Compute the MI among all the TFs and operons by using the CLR algorithm (14).
Compute the z-score among all the TFs and operons from the MI distributions by using the CLR algorithm.
Infer the TFs regulating a given operon, single and cooperative interactions, according to a given threshold depending on the desired precision. The threshold for cooperative regulations is taken higher than for single ones (2-fold for the reported calculations, although it can be modified straightforwardly) to avoid overfitting in the computation of the combinatorial interactions. See Supplementary Data for cut-off threshold selection.
For each operon, estimate the kinetic parameters for its regulating TFs by using multiple linear regressions (obtaining single and synergistic interactions). Eventually, remove regulations with low strength.
Construct a SBML file containing the ODE-based model using the inferred topology and the estimated kinetic parameters.
Prediction of transcriptomic profiles
To compute the performance of our algorithm, we defined a reference network taking those genes with known transcriptional regulation. In addition, the TFs that were present in our reference set regulating genes outside the reference set were also removed when determining the performance of the algorithm. Then, only the interactions among the genes present in that reference set were evaluated to compute the algorithm efficiency. All known interactions cataloged in RegulonDB version 4 (28) were used to construct the reference network in E. coli. However, we are still far from a complete understanding of the transcriptional regulation network of E. coli. Therefore, we designed in silico genomes with predefined regulations to validate the performance of our algorithm. For that, we did not consider: (i) operons with self-regulations; (ii) operons with constitutive promoters; and (iii) operons containing only TFs.
We calculated two types of efficiencies (precision rate and sensitivity) to compare the inferred network with the reference network. We defined precision rate as the fraction of predicted interactions that are correct 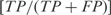 , and sensitivity as the fraction of all known interactions that are discovered by the algorithm
, and sensitivity as the fraction of all known interactions that are discovered by the algorithm 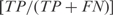 , where
, where 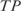 is the number of true positives,
is the number of true positives, 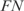 the number of false negatives and
the number of false negatives and 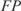 the number of false positives (39,40).
the number of false positives (39,40).
Designing genomes and expression data
In order to evaluate the suitability of our procedure to redesign the transcription regulation, we will analyze our ability to infer the kinetic parameters. Since they are not known for any organism, this lead us to the development of a Generator of Artificial Genomes (GAG) to in silico create expression profiles (Figure S2). To construct such genomes, we specify the number of genes and TFs (this last is usually taken one order of magnitude less than the number of genes), and eventually the ratio between inducers and repressors (we have used 2/3). We can also specify the degree of connectivity to obtain scale-free networks [we have considered a probability distribution 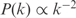 where k is the number of regulators of an operon], and the law for clustering distribution [we have assumed
where k is the number of regulators of an operon], and the law for clustering distribution [we have assumed 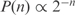 where n is the number of genes per operon]. To generate synthetic microarray data, we first obtain the steady state of the system [
where n is the number of genes per operon]. To generate synthetic microarray data, we first obtain the steady state of the system [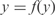 , since
, since 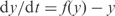 with an arbitrary degradation rate of 1] without taking into account cooperations between different regulators (i.e.
with an arbitrary degradation rate of 1] without taking into account cooperations between different regulators (i.e. 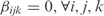 ) as an approximate solution of the system (Equation 2). In fact, as the gene expressions (y) are only functions of the TFs (
) as an approximate solution of the system (Equation 2). In fact, as the gene expressions (y) are only functions of the TFs (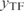 ), we can write the system as
), we can write the system as 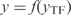 . Subsequently, we generate a new condition by randomly choosing a set of TFs with given size optimized for the inference (Figure S4) and perturbing their steady state values, while maintaining constant the other TF expressions. The perturbations over/under-express the TFs to a
. Subsequently, we generate a new condition by randomly choosing a set of TFs with given size optimized for the inference (Figure S4) and perturbing their steady state values, while maintaining constant the other TF expressions. The perturbations over/under-express the TFs to a 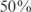 , relative to their steady states. Hence, this perturbed value (
, relative to their steady states. Hence, this perturbed value (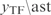 ) is used to recalculate the gene expressions by applying the model
) is used to recalculate the gene expressions by applying the model 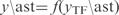 . Although this could be extended to more complicated conditions, where different gene categories are altered, the conditions based on TF perturbations are more revealing. Furthermore, to generate more realistic data we have added random fluctuations (which would simulate noisy data) in the expression values. We have studied the efficiency (precision rate and sensitivity) of our algorithm for different noise levels. In Figure S5 (see Supplementary Data) we show that InferGene maintains high efficiency up to 10% of noise amplitude.
. Although this could be extended to more complicated conditions, where different gene categories are altered, the conditions based on TF perturbations are more revealing. Furthermore, to generate more realistic data we have added random fluctuations (which would simulate noisy data) in the expression values. We have studied the efficiency (precision rate and sensitivity) of our algorithm for different noise levels. In Figure S5 (see Supplementary Data) we show that InferGene maintains high efficiency up to 10% of noise amplitude.
RESULTS
Genome-wide quantitative model of E. coli
In the present study, we have applied inference methodologies recently used to obtain models suitable for genome redesign. We have considered the E. coli genome, which contains 4345 nonredundant genes, of which 328 are putative TFs. The genome is organized into 3333 operons, 2447 containing single genes and 886 polycistronic units. The reference regulatory set has been constructed according to RegulonDB (28). For the inference procedure, we have used public microarray data (41) from Affymetrix normalized using RMA (42). This is a microarray compendium containing 189 experiments. From this dataset, 20 experiments were excluded in order to later predict expression profiles from unbiased data. The inferred network contains 525 regulatory interactions (z-score 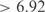 ) and 566 combinatorial influences (z-score
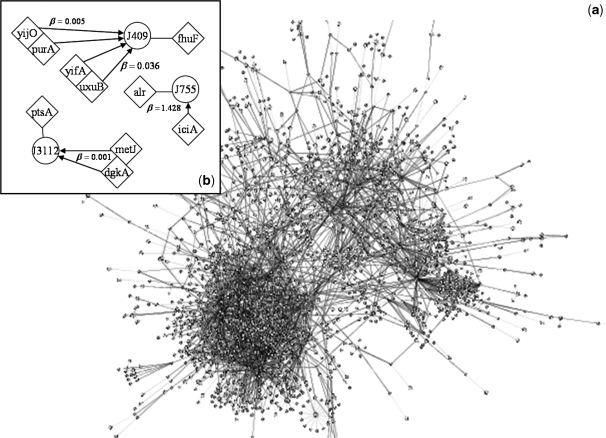
) and 566 combinatorial influences (z-score 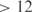 ). InferGene predicts 3982 genes to be controlled by constitutive promoters. In Figure 2a, a we plot the inferred transcriptional regulatory network of E. coli visualized using Cytoscape, having 75% of precision rate and 5% of sensitivity for single regulations, comparing with the regulations present in RegulonDB. Indeed there is a trade-off between sensitivity and precision, and the requirement of a high precision rate (such as 75%) gives very low sensitivities around 5% for E. coli (14). Notice that even a perfect algorithm (100% precision), where there are no false positives, could reach very low sensitivities if it is too conservative and suggest much fewer interactions than the ones in the reference set.
). InferGene predicts 3982 genes to be controlled by constitutive promoters. In Figure 2a, a we plot the inferred transcriptional regulatory network of E. coli visualized using Cytoscape, having 75% of precision rate and 5% of sensitivity for single regulations, comparing with the regulations present in RegulonDB. Indeed there is a trade-off between sensitivity and precision, and the requirement of a high precision rate (such as 75%) gives very low sensitivities around 5% for E. coli (14). Notice that even a perfect algorithm (100% precision), where there are no false positives, could reach very low sensitivities if it is too conservative and suggest much fewer interactions than the ones in the reference set.
Figure 2.
Inferred regulatory network of E. coli visualized using Cytoscape (34) thanks to the SBML import. (a) Full transcriptional regulatory network by InferGene with 75% of precision rate and 5% of sensitivity for single regulations (z-score > 6.92). Genes are indicated as rhombus and transcription reactions as circles. Arrows mean regulations and lines connect reactions with the corresponding gene products. We represent synergistic TFs regulations by drawing together several rhombus. The strength of each regulation can be found in the SBML model (provided in the Supplementary Data). (b) Example of an E. coli subnetwork involving genes related with the cell structure and transport (one of the best predicted biological functions, see also Figure S9). The TF 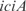 was selected by InferGene as the most likely regulator of the
was selected by InferGene as the most likely regulator of the 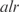 operon from the set of all (328) candidates. On the other hand, the TFs
operon from the set of all (328) candidates. On the other hand, the TFs 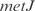 and
and 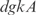 synergistically regulate the
synergistically regulate the 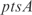 operon. Also InferGene proposes a combinatorial regulation of the
operon. Also InferGene proposes a combinatorial regulation of the 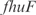 operon: (
operon: (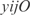 AND
AND 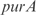 ) OR (
) OR (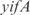 AND
AND 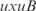 ).
).
To analyze those results in a biological context, we have used the EcoCyc (43) classification to group genes by biological functions and to rank those groups according to their level of prediction (see Supplementary Figure S9). We have scored each biological function as 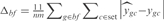 , where n is number of genes involved in the biological function, m the number of the new conditions of the set (m = 20),
, where n is number of genes involved in the biological function, m the number of the new conditions of the set (m = 20), 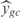 the predicted expression and
the predicted expression and 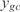 the measured expression. The best predicted functions are involved in the metabolism, such as biosynthesis of lipoprotein, carnitine, glycolate and glycoprotein, or functions related with information transfer such as rRNA and stable RNA, ATP binding, DNA and DNA degradation. In addition, we have observed two significant correlations between the number of constitutively expressed genes and the error in expression
the measured expression. The best predicted functions are involved in the metabolism, such as biosynthesis of lipoprotein, carnitine, glycolate and glycoprotein, or functions related with information transfer such as rRNA and stable RNA, ATP binding, DNA and DNA degradation. In addition, we have observed two significant correlations between the number of constitutively expressed genes and the error in expression 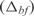 . These genes are from biological functions involved in the location of gene products and the cell processes (see in Supplementary Figure S9). On the other hand, in Figure 2b, we show an example of such groups, where the
. These genes are from biological functions involved in the location of gene products and the cell processes (see in Supplementary Figure S9). On the other hand, in Figure 2b, we show an example of such groups, where the 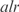 operon, involved in metabolism of alanine biosynthesis, is regulated by
operon, involved in metabolism of alanine biosynthesis, is regulated by 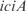 with a strength of
with a strength of 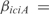 1.428, according to InferGene. InferGene also predicts the regulation for the
1.428, according to InferGene. InferGene also predicts the regulation for the 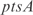 operon, involved in the cell structure of
operon, involved in the cell structure of 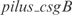 , where
, where 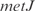 and
and 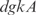 act synergistically with
act synergistically with 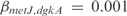 . For the
. For the 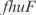 operon, involved in transport, InferGene proposes the combinatorial regulation (
operon, involved in transport, InferGene proposes the combinatorial regulation (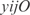 AND
AND 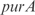 ) OR (
) OR (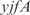 AND
AND 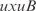 ), with
), with 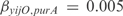 and
and 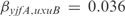 . Notice that these regulations are not found in RegulonDB, but are obtained as the best experiment-fitting regulators.
. Notice that these regulations are not found in RegulonDB, but are obtained as the best experiment-fitting regulators.
Furthermore, we provide in the Supplementary Data a list of the E. coli promoters classified according to their inferred regulation. An analysis of the prediction of the promoter regulation shows (see Supplementary Figure S10) that the promoters which are regulated by two TFs are better predicted. In addition, the algorithm can be used to account for nontranscriptional regulations (20). In the Supplementary Data, we have applied this to the well-known SOS pathway. There we show that an effective model of gene–gene interactions can improve the prediction over the pure transcriptional one (see Figures S23–S25).
Designing genomes and validating their transcription profiles
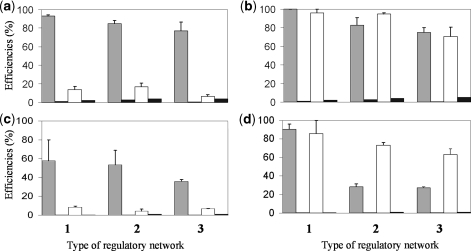
We have constructed several genomes in silico using GAG and we have compared the predefined regulations in our models with the regulations inferred by InferGene. We have constructed three types of transcription networks according to the mode of regulation of its constituent operons: (i) networks with promoters regulated by at most one TF; (ii) networks with promoters that can be regulated by more than one TF; and (iii) networks with promoters that can be combinatorially regulated including synergistic effects. We have computed the precision rate and sensitivity (see Methods section) to quantify the efficiency of InferGene. In Figure 3, we show the evaluation of the inference for different types of genome networks. InferGene, which at this stage relies on CLR, predicts the 85.4% (sensitivity) of the possible interactions although only the 15.7% (precision rate) of them are correct for a genome of 500 genes using 100 conditions (Figure 3a). However, if the number of conditions increases to 250, the precision rate reaches values around the 90% (see Figure 3b). The same trend occurs with larger genomes as we can see from Figures 3c and d, where we have worked with genomes of 5000 genes with 300 and 600 conditions, respectively. Thus, we improve 6-fold the precision rate, maintaining a given level of sensitivity, when increasing the number of conditions 2.5-fold. Therefore, the efficiency of algorithm has a nonlinear behavior regarding the number of conditions used for training. We have also extended the inference capabilities of CLR to cooperative interactions. Our results show that we need a minimum set of microarray experiments to infer a transcriptional regulatory network with high precision rate for a given sensitivity. Furthermore, genomes with only promoters regulated by at most one TF reached higher values of precision rate and sensitivity.
Figure 3.
InferGene performance. Evaluation of sensitivity (gray) and precision rate (white) together with a random inference (black) of the transcriptional regulatory network. We used several types of synthetic genomes with different topological and parametrical properties generated by GAG. We constructed three types of genomes: (i) all promoters are regulated by at most one TF; (ii) the promoters that can be regulated by more than one TF; and (iii) promoters with combinatorial regulations including synergistic effects. Genomes for (a,b) had 500 genes and 50 TFs, and for (c,d) 5000 genes and 200 TFs. The number of conditions was in (a) 100, (b) 250, (c) 300 and (d) 600. Deviations in precision rates and sensitivities were calculated using three different genomes for each type. The z-score threshold used was in (a) 0.5, (b) 1, (c) 3 and (d) 7.
We have analyzed the predictive power of InferGene by calculating a score based on the error made on predicting the expression levels 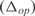 , and other score based on the error made on the prediction of the model parameters
, and other score based on the error made on the prediction of the model parameters 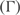 . We define
. We define 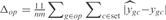 , where
, where 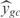 is the predicted expression profile,
is the predicted expression profile, 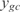 is the experimental value, n is the number of operons that are correctly inferred according to RegulonDB and m is the number of conditions that were not used in the training set (m = 20). We also define
is the experimental value, n is the number of operons that are correctly inferred according to RegulonDB and m is the number of conditions that were not used in the training set (m = 20). We also define 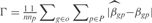 , where np is number of parameters we use to model the kinetics of the operon expression,
, where np is number of parameters we use to model the kinetics of the operon expression, 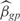 are the estimated model parameters and
are the estimated model parameters and 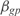 are the model parameters from GAG. To perform such analysis, we have generated a network using the GAG algorithm with 500 genes across 250 conditions (see Supplementary Figure S11). The median for
are the model parameters from GAG. To perform such analysis, we have generated a network using the GAG algorithm with 500 genes across 250 conditions (see Supplementary Figure S11). The median for 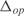 was 0.009, and for Γ was around 0.01. Moreover, we have validated the estimated parameters by performing linear regressions with the predefined kinetic models and obtaining correlations (Pearson coefficients) above 0.90 (see Supplementary Figure S3).
was 0.009, and for Γ was around 0.01. Moreover, we have validated the estimated parameters by performing linear regressions with the predefined kinetic models and obtaining correlations (Pearson coefficients) above 0.90 (see Supplementary Figure S3).
Prediction of wild-type E. coli trancriptomic profiles
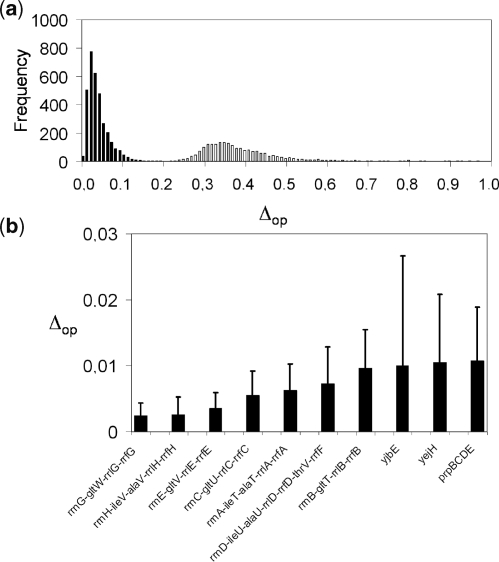
Before proceeding to change the regulation of E. coli, we have calculated the ability of the inferred model to predict the steady state expression levels of the E. coli genes. For that, we have used the model together with the expression levels of all the TFs for each experimental condition to compute the global expression profile. Afterwards, we have compared the predicted expression values with the corresponding measurements, obtaining 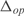 . We have also determined the predictive power of the inferred model on the 20 experimental conditions excluded from training dataset. The distribution of
. We have also determined the predictive power of the inferred model on the 20 experimental conditions excluded from training dataset. The distribution of 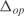 for the 3333 operons of E. coli is shown in Figure 4a (black bars). The mean of this distribution is 0.048. White bars represent a model with random parameters for the inferred topology. In Figure 4b, we show the prediction for the best inferred operons. It is interesting to note that the genes from these operons are involved in functions related with information transfer (RNA related, such as transcription related, tRNA, rRNA or stable RNA; and protein related such as translation), regulation, location of gene products (cytoplasm and
for the 3333 operons of E. coli is shown in Figure 4a (black bars). The mean of this distribution is 0.048. White bars represent a model with random parameters for the inferred topology. In Figure 4b, we show the prediction for the best inferred operons. It is interesting to note that the genes from these operons are involved in functions related with information transfer (RNA related, such as transcription related, tRNA, rRNA or stable RNA; and protein related such as translation), regulation, location of gene products (cytoplasm and  ) and cell processes (adaptation and defense survival).
) and cell processes (adaptation and defense survival).
Figure 4.
(a) Histogram of the expression error on the transcriptomic profile for each operon (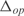 ). In black, model with parameters from linear regression; in white, model with random parameters (for a fixed inferred topology). (b) We show the mean of
). In black, model with parameters from linear regression; in white, model with random parameters (for a fixed inferred topology). (b) We show the mean of 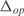 with the corresponding standard deviations for the best predicted operons. We measured the predictive power under the 20 conditions of the testing set.
with the corresponding standard deviations for the best predicted operons. We measured the predictive power under the 20 conditions of the testing set.
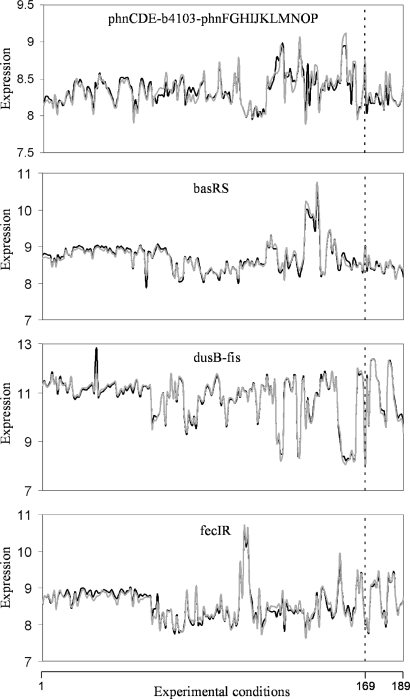
In Figure 5, we plot the predicted profiles with lowest 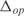 against the experimental profiles across all conditions (189 experiments, 169 conditions from the training set and 20 new conditions for prediction). We also perform a K-fold cross-validation (we consider nine partitions, see Figures S13 and S14) to ensure that our results do not depend on the selection of the testing set. In the Supplementary Data, we provide the best predicted profiles for the distinct types of promoters. In addition, we have analyzed the profile prediction to evaluate the best predicted conditions (see Figure S12). We have found that the conditions upregulating genes
against the experimental profiles across all conditions (189 experiments, 169 conditions from the training set and 20 new conditions for prediction). We also perform a K-fold cross-validation (we consider nine partitions, see Figures S13 and S14) to ensure that our results do not depend on the selection of the testing set. In the Supplementary Data, we provide the best predicted profiles for the distinct types of promoters. In addition, we have analyzed the profile prediction to evaluate the best predicted conditions (see Figure S12). We have found that the conditions upregulating genes 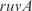 ,
, 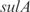 ,
, 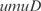 ,
, 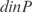 ,
, 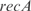 ,
, 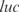 ,
, 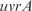 ,
, 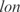 ,
, 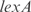 and
and 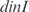 are better predicted, and the experiments with plasmids pPROEx-CAT, pET3d and T7 controllable have higher error (see more details in the Supplementary Data).
are better predicted, and the experiments with plasmids pPROEx-CAT, pET3d and T7 controllable have higher error (see more details in the Supplementary Data).
Figure 5.
Prediction of expression profiles in E. coli. Each plot shows the experimental profile (gray line), and the profile predicted by our model (black line). The last 20 experiments, separated by a dashed line, correspond to conditions that were not included in the training dataset with which we inferred the kinetic model.
Redesign of the global transcription regulation
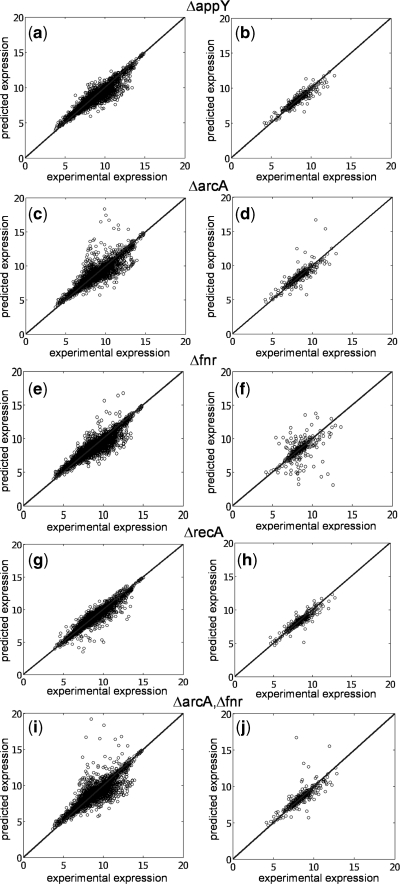
Finally, we have used our model to predict the expression profile under knockouts of TFs (conditions from the training set). This is a first step toward changing the transcription regulation. For that, we have solved the system of equations in steady state by removing the corresponding transcription regulation. For simplicity, here we have neglected the combinatorial terms to work with a linear model and recalculated the kinetic parameters. To account for experimentally reported interactions, we have incorporated into the model regulations between pairs of TFs according to RegulonDB. In Figure 6, we plot the predicted versus the experimental profiles for the knockouts of the TFs 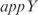 ,
, 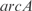 ,
, 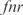 and
and 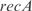 . In the Supplementary Data we also show predictions for the knockouts of the TFs
. In the Supplementary Data we also show predictions for the knockouts of the TFs 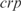 ,
, 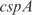 ,
, 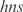 ,
, 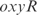 ,
, 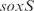 and a double knockout of
and a double knockout of 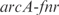 . We show how the model is able to capture the whole transcriptomic expression due to a perturbation in the TF network (the relative expression errors, in average for all genes, are shown in Figure 6 caption). Therefore, the model quantitatively accounts for a global regulatory redesign, especially in case of knockouts of master regulators.
. We show how the model is able to capture the whole transcriptomic expression due to a perturbation in the TF network (the relative expression errors, in average for all genes, are shown in Figure 6 caption). Therefore, the model quantitatively accounts for a global regulatory redesign, especially in case of knockouts of master regulators.
Figure 6.
Prediction of expression profiles in E. coli from single knockouts of the TFs 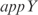 ,
, 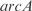 ,
, 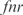 and
and 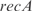 , and a double knockout of the TFs
, and a double knockout of the TFs 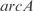 and
and 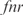 . In (a, c, e, g, i) whole transcriptome, in (b, d, f, h, j) TFs profile. The relative expression error (
. In (a, c, e, g, i) whole transcriptome, in (b, d, f, h, j) TFs profile. The relative expression error (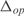 ) is 4% in (a), 4% in (b), 5% in (c), 5% in (d), 5% in (e), 5% in (f), 4% in (g), 4% in (h), 6% in (i) and 5% in (j). Experimental data is obtained from (41).
) is 4% in (a), 4% in (b), 5% in (c), 5% in (d), 5% in (e), 5% in (f), 4% in (g), 4% in (h), 6% in (i) and 5% in (j). Experimental data is obtained from (41).
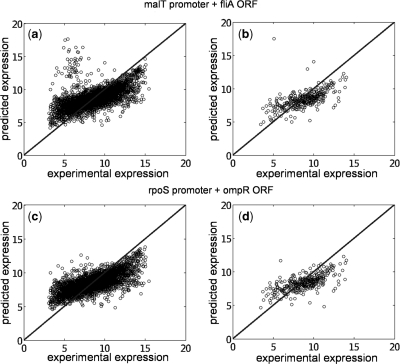
Moreover, we have applied our procedure to the modification of the global transcription regulation by adding new regulations into the genomic network. This was done experimentally by Isolan et al. (44), where they overexpressed plasmids pairing together wild-type promoters with ORFs coding for TF that were master regulators. We used our procedure to predict the gene expression of such transcriptional perturbation for the particular case where the 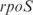 and
and 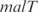 promoters are disposed together with the ORFs
promoters are disposed together with the ORFs 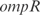 and
and 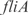 , respectively (see Figure 7, relative expression errors are shown in the caption).
, respectively (see Figure 7, relative expression errors are shown in the caption).
Figure 7.
Prediction of expression profiles in E. coli from transcriptional perturbations rewiring the wild-type regulatory map putting together in a high-copy plasmid the 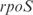 and
and 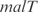 promoters with the ORFs of
promoters with the ORFs of 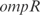 and
and 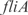 , respectively. In (a,c) whole transcriptome, in (b,d) TFs profile. The relative expression error (
, respectively. In (a,c) whole transcriptome, in (b,d) TFs profile. The relative expression error (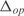 ) is 18% in (a), 16% in (b), 19% in (c) and 16% in (d). Experimental data is obtained from (44).
) is 18% in (a), 16% in (b), 19% in (c) and 16% in (d). Experimental data is obtained from (44).
DISCUSSION
We have discussed a methodology to create quantitative models for transcription regulation aimed to future genome redesign projects. We have shown how we could use recent methodologies to infer the global topology of transcription regulation to produce the kinetic model able for genome redesign. We have successfully applied the inferred model to predict the transcriptomic response of E. coli under experimental conditions not included in the training set. The prediction has in average an error of 1–5% relative to the experimental value (average computed across all conditions). Furthermore, we have predicted the gene expression under knockouts of TFs and genetic rewirings (44) by solving a perturbed model, showing the predictive power of the inference procedure. Such perturbations change the regulatory map of the cell, but more complex redesigns, even a whole transcription refactorization, could be in silico explored by using our model. Our algorithm provides a global deterministic kinetic model of genetic regulations using microarray data. We show how to use this kinetic model to make predictions (23). Thus, our approach constitutes an important step toward the large-scale design of cell behaviors by providing models which are validated using in silico genomes and experimental transcription data. In this direction, we have accounted for simple transcription rewirings (44) by obtaining the gene expressions using computational methods. Such models can be used in the future to rewire the regulation of organisms without affecting their physiological behavior.
The algorithm reaches high efficiencies at the topology and kinetic level, based on the CLR algorithm (14) to infer the network together with an extension to include cooperations in combinatorial promoters. However, it could use other approaches such as Bayesian methods (19). In addition, the generation of synthetic data from specified genome models has been essential to analyze the performance and limitations of InferGene. Indeed, we have shown how the precision rate is drastically improved, from 10–20% to 80–90%, by just doubling the number of perturbations in artificial genomes. Moreover, the error in the prediction of the expression value for correctly predicted regulations is of the order of magnitude of the standard errors on measured expression data, and the estimated parameters highly correlate with the predefined ones (correlation coefficient >0.9). The inaccuracies in our prediction could be rationalized by the lack of modeling of many dynamic variables of the cell (e.g. proteins or metabolites) or nontranscriptional regulations (e.g. protein–protein or RNAi), since these variables are not experimentally measured using microarrays. Furthermore, future works could consider confidence intervals on the model parameters to analyze the stochasticity in expression data. We provide the inferred model in a standard format, as it is SBML (33), which can be used for further applications. In addition, we have used genome annotation to identify the best predicted biological functions.
Our approach can take advantage from additional sources of information. For instance, it can incorporate in the inferred model experimentally validated interactions (e.g. from functional genomics measurements or sequence analysis) as a regulatory background. In addition, the knowledge on the genome sequence can help in the inference procedure, by providing information about operon structure, identification of TFs and their regulations (28,45,46). The prior knowledge about regulation provides a topology that can be added into the model and can be used to predict new interactions with high fidelity (47). The methodology can also be applied to account for nontranscriptional interactions. In the Supplementary Data, we use the well known SOS pathway to show that an effective model of gene–gene interactions can improve the prediction over the pure transcriptional one. Furthermore, the algorithm can be expanded in a straightforward way to input expression data from time series.
The identification of regulations is a high time-consuming activity. The running time scales with the number of genes and the square of the number of conditions. Nonetheless, the parameter estimation is a quick process (relative to the previous). For instance, in E. coli there are 4345 genes (strain K-12) clustered in 3333 operons, and 328 TFs and 53 628 pairs of TFs (28). The whole inference process took 6 h accomplished on a computer Pentium M 2.00 GHz and 1 GB RAM (time resources for parameter estimation are neglected as they are around 2 min). However, all simulations can be run in parallel allowing the reduction of the execution time (<5 min on a simple cluster). In this way, distributed computing provides the necessary resources to apply our methodology to infer the regulations of much larger genomes. Our methodology provides a simple and fast way to obtain a quantitative global model of transcriptional regulation even for large networks. The incorporation of sparse Bayesian regression methods (19) provides a promising extension for further works. Such methods would provide better inference but increasing the computational cost.
The construction of genome-scale models is clearly a valuable step toward the understanding of the cellular behavior (4), but it is also of interest for the emerging field of synthetic biology, where functional genetic circuits are engineered into cells dealing to minimize the impact on the host (48). Hence, InferGene provides an accurate model to predict the changes in the biological processes when perturbing the cell. In addition, this model can be applied to discover molecular targets of heterologous compounds (20,21).
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Spanish Ministry of Education and Science (ref. TIN 2006-12860); Structural Funds of the European Regional Development Fund; EU grants BioModularH2 (FP6-NEST contract 043340) and EMERGENCE (FP6-NEST contract 043338); ATIGE Genopole/UEVE and the MIT-France grants; Graduate fellowship from the Conselleria d'E;ducacio de la Generalitat Valenciana (ref. BFPI 2007/160 to G.R.) and an EMBO Short-term fellowship (ref. ASTF-343.00-2007 to G.R.). HPC-Europa programme. Funding for open access charge: EU grant BioModularH2 FP6-NEST-043340.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We are indebted with M. Elati for his careful reading of the article and his comments. We also acknowledge the anonymous reviewers for their suggestions.
REFERENCES
- 1.Lee T, Rinaldi N, Robert F, Odom D, Bar-Joseph Z, Gerber G, Hannett N, Harbison C, Thompson C, Simon I, et al. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science. 2002;298:799–804. doi: 10.1126/science.1075090. [DOI] [PubMed] [Google Scholar]
- 2.deJong H. Modeling and simulation of genetic regulatory systems: a literature review. J. Comp. Biol. 2002;9:67–103. doi: 10.1089/10665270252833208. [DOI] [PubMed] [Google Scholar]
- 3.Hughes T, Marton M, Jones A, Roberts C, Stoughton R, Armour C, Bennett H, Coffey E, Dai H, He Y, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- 4.Covert MW, Knight EM, Reed JL, Herrgard MJ, Palsson BO. Integrating high-throughput and computational data elucidates bacterial networks. Nature. 2004;429:92–96. doi: 10.1038/nature02456. [DOI] [PubMed] [Google Scholar]
- 5.Eisen M, Spellman P, Brown P, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl Acad. Sci. USA. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ben-Dor A, Shamir R, Yakhini Z. Clustering gene expression patterns. J. Comput. Biol. 1999;6:281–297. doi: 10.1089/106652799318274. [DOI] [PubMed] [Google Scholar]
- 7.Alon U, Barkai N, Notterman D, Gish K, Ybarra S, Mack D, Levine A. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc. Natl Acad. Sci. USA. 1999;96:6745–6750. doi: 10.1073/pnas.96.12.6745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dhaeseleer P, Liang S, Somogyi R. Genetic network inference: from co-expression clustering to reverse engineering. Bioinformatics. 2000;16:707–726. doi: 10.1093/bioinformatics/16.8.707. [DOI] [PubMed] [Google Scholar]
- 9.Ihmels J, Friedlander G, Bergmann S, Sarig O, Ziv Y, Barkai N. Revealing modular organization in the yeast transcriptional network. Nat. Genet. 2002;31:370–377. doi: 10.1038/ng941. [DOI] [PubMed] [Google Scholar]
- 10.Bansal M, Belcastro V, Ambesi-Impiombato A, diBernardo D. How to infer gene networks from expression profiles. Mol. Syst. Biol. 2007;3:78. doi: 10.1038/msb4100120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Butte A, Kohane I. Mutual information relevance networks: functional genomic clustering using pairwise entropymeasurements. Pac. Symp. Biocomp. 2000;5:415–426. doi: 10.1142/9789814447331_0040. [DOI] [PubMed] [Google Scholar]
- 12.Basso K, Margolin AA, Stolovitzky G, Klein U, Dalla-Favera R, Califano A. Reverse engineering of regulatory networks in human B cells. Nat. Genet. 2005;37:382–390. doi: 10.1038/ng1532. [DOI] [PubMed] [Google Scholar]
- 13.Margollin A, Nemenman I, Basso K, Wiggins C, Stolovitzky G, dellaFavera R, Califano A. ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics. 2006;7:S7. doi: 10.1186/1471-2105-7-S1-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Faith J, Hayete B, Thaden J, Mogno I, Wierzbowski J, Cottarel G, Kasif S, Collins J, Gardner T. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. Plos Biol. 2007;5:e8. doi: 10.1371/journal.pbio.0050008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Meyer PE, Kontos K, Lafitte F, Bontempi G. Information-theoretic inference of large transcriptional regulatory networks. EURASIP J. Bioinf. Syst. Biol. 2007;2007:79879. doi: 10.1155/2007/79879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yu J, Smith V, Wang P, Hartemink A, Jarvis E. Advances to bayesian network inference for generating causal networks from observational biological data. Bioinformatics. 2004;20:3594–3603. doi: 10.1093/bioinformatics/bth448. [DOI] [PubMed] [Google Scholar]
- 17.Husmeier D. Sensitivity and specificity of inferring genetic regulatory interactions from microarray experiments with dynamic Bayesian networks. Bioinformatics. 2003;19:2271–2282. doi: 10.1093/bioinformatics/btg313. [DOI] [PubMed] [Google Scholar]
- 18.Fujita A, Sato JR, Garay-Malpartida HM, Yamaguchi R, Miyano S, Sogayar MC, Ferreira CE. Modeling gene expression regulatory networks with the sparse vector autoregressive model. BMC Syst. Biol. 2007;1:39. doi: 10.1186/1752-0509-1-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Steinke F, Seeger M, Tsuda K. Experimental design for efficient identification of gene regulatory networks using sparse Bayesian models. BMC Syst. Biol. 2007;1:51. doi: 10.1186/1752-0509-1-51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gardner T, diBernardo D, Lorenz D, Collins J. Inferring genetic networks and identifying compound mode of action via expression profiles. Science. 2003;301:102–105. doi: 10.1126/science.1081900. [DOI] [PubMed] [Google Scholar]
- 21.diBernardo D, Thompson M, Gardner T, Chobot S, Eastwood E, Wojtovich A, Elliott S, Schaus S, Collins J. Chemogenomic profiling on a genome-wide scale using reverse-engineered gene networks. Nat. Biotechnol. 2005;3:377–383. doi: 10.1038/nbt1075. [DOI] [PubMed] [Google Scholar]
- 22.Shevade S, Keerthi S. A simple and efficient algorithm for gene selection using sparse logistic regression. Bioinformatics. 2003;19:2246–2253. doi: 10.1093/bioinformatics/btg308. [DOI] [PubMed] [Google Scholar]
- 23.Bonneau R, Reiss D, Shannon P, Facciotti M, Hood L, Baliga N, Thorsson V. The inferelator: an algorithm for learning parsimonious regulatory networks from systems-biology data sets de novo. Genome Biol. 2006;7:R36. doi: 10.1186/gb-2006-7-5-r36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tibshirani R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B. 1996;58:267–288. [Google Scholar]
- 25.Behrens J, vonKries J, Khl M, Bruhn L, Wedlich D, Grosschedl R, Birchmeier W. Functional interaction of bold β-catenin with the transcription factor LEF-1. Nature. 1996;328:638–642. doi: 10.1038/382638a0. [DOI] [PubMed] [Google Scholar]
- 26.Stewart V, Bledsoe P. Fnr-, NarP- and Narl-dependent regulation of transcription initiation from the Haemophilus influenzae Rd napF (Periplasmic Nitrate Reductase) promoter in Escherichia coli K-12. J. Bacteriol. 2005;187:6928–6935. doi: 10.1128/JB.187.20.6928-6935.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Long J, Roth M. Synthetic microarray data generation with RANGE and NEMO. Bioinformatics. 2008;24:132–134. doi: 10.1093/bioinformatics/btm529. [DOI] [PubMed] [Google Scholar]
- 28.Salgado H, Gama-Castro S, Peralta-Gil M, Diaz-Peredo E, Sanchez-Solano F, Santos-Zavaleta A, Martinez-Flores I, Jimenez-Jacinto V, Bonavides-Martinez C, Segura-Salazar J, et al. Regu-lonDB (version 5.0): Escherichia coli K-12 transcriptional regulatory network, operon organization, and growth conditions. Nucleic Acids Res. 2006;34:D394. doi: 10.1093/nar/gkj156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gray R. Entropy and Information Theory. New York, NY, USA: Springer-Verlag; 1990. [Google Scholar]
- 30.Steuer R, Kurths J, Daub CO, Weise J, Selbig J. The mutual information: detecting and evaluating dependencies between variables. Bioinformatics. 2002;18:S231–S240. doi: 10.1093/bioinformatics/18.suppl_2.s231. [DOI] [PubMed] [Google Scholar]
- 31.Daub C, Steuer R, Selbig J, Kloska S. Estimating mutual information using B-spline functions – an improved similarity measure for analysing gene expression data. BMC Bioinformatics. 2004;5:118. doi: 10.1186/1471-2105-5-118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cohen JPC, West S, Aiken L. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences. Hillsdale, NJ, USA: Lawrence Erlbaum Associates; 2003. [Google Scholar]
- 33.Hucka M, Bolouri H, Finney A, Sauro H, Doyle JKH, Arkin A, Bornstein B, Bray D, Cornish-Bowden A, Cuellar A, et al. The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics. 2003;19:524–531. doi: 10.1093/bioinformatics/btg015. [DOI] [PubMed] [Google Scholar]
- 34.Shannon P, Markiel A, Ozier O, Baliga N, Wang J, Ramage D, Amin N, Schwikowski B, Ideker T. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13:2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bar-Joseph Z. Analyzing time series gene expression data. Bioinformatics. 2004;20:2493–2503. doi: 10.1093/bioinformatics/bth283. [DOI] [PubMed] [Google Scholar]
- 36.Affymetrix. Affymetrix Microarray Suite User Guide, version 4. Santa Clara, CA, USA: Affymetrix; 1999. [Google Scholar]
- 37.Sabatti C, Rohlin L, Oh M, Liao J. Co-expression pattern from DNA microarray experiments as a tool for operon prediction. Nucleic Acids Res. 2002;30:2886–2893. doi: 10.1093/nar/gkf388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dongarra J, Bunch J, Moler C, Stewart P. LINPACK User's Guide. Philadelphia, PA, USA: SIAM; 1979. [Google Scholar]
- 39.Altman D, Bland J. Statistics notes: diagnostic tests 1: sensitivity and specificity. Br. Med. J. 1994;308:1552. doi: 10.1136/bmj.308.6943.1552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Altman D, Bland J. Statistics notes: diagnostic tests 2: predictive values. Br. Med. J. 1994;309:102. doi: 10.1136/bmj.309.6947.102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Faith J, Driscoll M, Fusaro V, Cosgrove E, Hayete B, Juhn F, Schneider S, Gardner T. Many microbe microarrays database: uniformly normalized Affymetrix compendia with structured experimental metadata. Nucleic Acids Res. 2008;36:D866–D870. doi: 10.1093/nar/gkm815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Irizarry R, Hobbs B, Collin F, Beazer-Barclay Y, Antonellis K, Scherf U, Speed T. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics. 2003;4:249–264. doi: 10.1093/biostatistics/4.2.249. [DOI] [PubMed] [Google Scholar]
- 43.Karp P, Riley M, Saier M, Paulsen I, Collado-Vides J, Paley S, Pellegrini-Toole A, Bonavides C, Gama-Castro S. The EcoCyc DataBase. Nucleic Acids Res. 2002;30:56–58. doi: 10.1093/nar/30.1.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Isalan M, Lemerle C, Michalodimitrakis K, Horn C, Beltrao P, Raineri E, Garriga-Canut M, Serrano L. Evolvability and hierarchy in rewired bacterial gene networks. Nature. 2008;452:840–845. doi: 10.1038/nature06847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Price M, Huang K, Alm E, Arkin A. A novel method for accurate operon predictions in all sequenced prokaryotes. Nucleic Acids Res. 2005;33:880–892. doi: 10.1093/nar/gki232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Reiss D, Baliga N, Bonneau R. Integrated biclustering of heterogeneous genome-wide datasets for the inference of global regulatory networks. BMC Bioinformatics. 2006;7:280. doi: 10.1186/1471-2105-7-280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mordelet F, Vert J-P. SIRENE: supervised inference of regulatory networks. Bioinformatics. 2008;24:i76–i82. doi: 10.1093/bioinformatics/btn273. [DOI] [PubMed] [Google Scholar]
- 48.Sprinzak D, Elowitz M. Reconstruction of genetic circuits. Nature. 2005;438:443–448. doi: 10.1038/nature04335. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.