The advantages of linear information processing for cerebellar computation

Abstract

Purkinje cells can encode the strength of parallel fiber inputs in their firing by using 2 fundamentally different mechanisms, either as pauses or as linear increases in firing rate. It is not clear which of these 2 encoding mechanisms is used by the cerebellum. We used the pattern-recognition capacity of Purkinje cells based on the Marr–Albus–Ito theory of cerebellar learning to evaluate the suitability of the linear algorithm for cerebellar information processing. Here, we demonstrate the simplicity and versatility of pattern recognition in Purkinje cells linearly encoding the strength of parallel fiber inputs in their firing rate. In contrast to encoding patterns with pauses, Purkinje cells using the linear algorithm could recognize a large number of both synchronous and asynchronous input patterns in the presence or absence of inhibitory synaptic transmission. Under all conditions, the number of patterns recognized by Purkinje cells using the linear algorithm was greater than that achieved by encoding information in pauses. Linear encoding of information also allows neurons of deep cerebellar nuclei to use a simple averaging mechanism to significantly increase the computational capacity of the cerebellum. We propose that the virtues of the linear encoding mechanism make it well suited for cerebellar computation.

Purkinje cells receive >150,000 parallel fiber synaptic inputs (1) that provide them with a vast and broad spectrum of information. These inputs are integrated with the spontaneous activity of Purkinje cells to provide the sole output of the computational circuitry of the cerebellar cortex. The mechanism by which this information is encoded by Purkinje cells is fundamental to theories of cerebellar computation. It has been recently demonstrated that Purkinje cells can encode this information by using 2 different mechanisms (2), either as pauses in their activity (3) or as linear increases in their firing rate (4) (see also Fig. 1B). Although, in principle, cerebellar computation can be based on either of these 2 encoding schemes, it is unlikely that they are used concurrently because they require fundamentally different decoding mechanisms. It has not been established whether either of these 2 mechanisms is used by the cerebellum, nor is it even known how they directly compare in their ability to encode information.

Fig. 1.

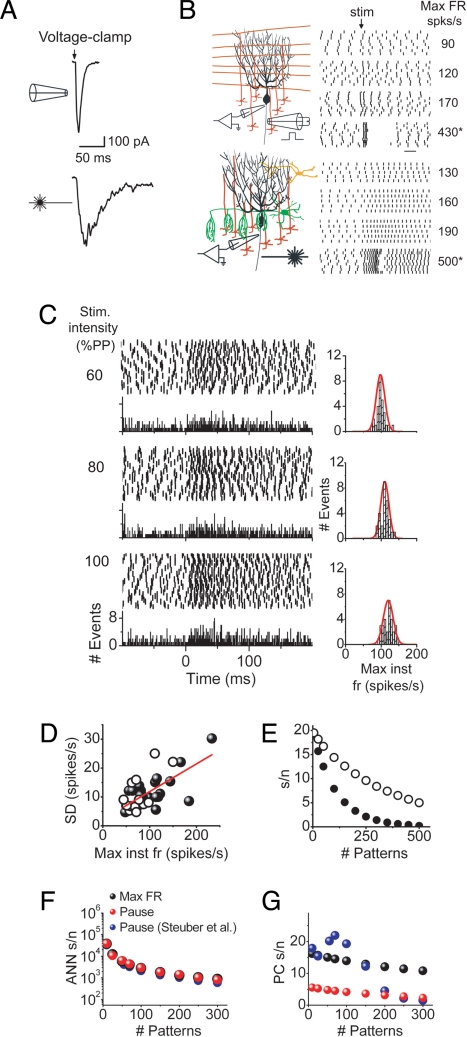
Pattern recognition capacity of Purkinje cells using the linear computational algorithm. The reproducibility with which Purkinje cells encode the strength of the same parallel fiber input in their maximum firing rate was determined by repeatedly stimulating the same patch of granule cells and measuring the maximum instantaneous firing rate after stimulus. Granule cells were activated synchronously by electrical stimulation or asynchronously by photoreleasing glutamate by using a 1-ms pulse of UV light. (A) In contrast to the fast kinetics of Purkinje cell EPSCs obtained from synchronous activation of granule cells by electrical stimulation, photorelease of glutamate activated granule cells asynchronously and resulted in corresponding EPSCs that had a slow time course and noisy appearance. (B) Raster plots showing that increasing the strength of stimulation resulted in correspondingly higher maximum firing rate responses with either synchronous or asynchronous activation of parallel fiber inputs. Vertical bars indicate the time of occurrence of each action potential. Strong stimulation intensities produced responses that consisted of an initial high frequency burst, followed by a pause (asterisks), although with asynchronous activation of inputs, it was not always possible to generate a burst–pause response. (C) Raster plots of the response of a Purkinje cell to 50 repeated presentations of the same asynchronous stimulus. Granule cells were stimulated every 30 s, and the intensity of the UV photolysis light was adjusted to 1 of 3 different strengths that were chosen to be below that which resulted in a burst–pause response. Below each raster plot, the associated population histogram is shown. The histograms to the right of each raster plot show the resulting maximum instantaneous firing rate distribution after stimulus. Each distribution was fit well by a Gaussian function (red line). (D) The scatter plot of the standard deviations of the maximum firing rates after stimulus determined from a number of experiments similar to that described above. Open symbols correspond to standard deviations obtained when latterly positioned patches of granule cells were activated, whereas the filled symbols correspond to activation of patches of granule cells immediately underneath the target Purkinje cell. (E) The experimentally determined standard deviations were implemented in an artificial neural network to estimate the s/n of Purkinje cells by using the linear computational algorithm in distinguishing learned patterns from novel ones. The s/n decreased as the number of patterns that had to be learned increased. Filled circles correspond to estimates where it was assumed that each parallel fiber synapse releases neurotransmitter only once. The open circles correspond to estimates for which paired pulse facilitation at the parallel fiber to Purkinje cell synapse was taken into consideration. (F) The pattern recognition capacities of 3 different ANNs were compared for synchronous parallel fiber inputs and with synaptic inhibition blocked. Black symbols corresponds to the ANN described in the present study assuming that Purkinje cells encode information in their maximum firing rate. Red symbols reflect the performance of the same ANN when it was assumed that Purkinje cells encode information in pauses. Blue symbols represent the performance of the ANN implemented by Steuber et al. (3) that also used pauses to encode input patterns. (G) Comparison of the pattern recognition capacity of a Purkinje cell based on the ANNs described in F. Blue symbols are taken from Steuber et al. (3). Black and red symbols correspond to present study assuming that Purkinje cells encode information in their maximum firing rate (black symbols) or in pauses (red symbols).

Pattern recognition was proposed in a pair of seminal papers by Marr and Albus (5, 6) to be the mechanism by which cerebellar Purkinje cells learn motor tasks. Based on this theory, the more patterns the cerebellum recognizes, the higher its computational power and ability to fine-tune and learn motor tasks. Numerous attempts have been made to estimate the pattern recognition capacity of Purkinje cells (3, 5–8), and recently it has been used to evaluate the suitability of an encoding mechanism in cerebellar computation (3).

A recent evaluation of a detailed Purkinje cell model suggested that optimal pattern recognition capacity is obtained if Purkinje cells encode information by using pauses (3). However, encoding with pauses requires a specialized decoding mechanism such as rebound firing by neurons of the deep cerebellar nuclei, the physiological prevalence of which is under considerable debate (9). In contrast to encoding with pauses, the linear algorithm is independent of the pattern or location of synaptic input and holds even under conditions of input asynchrony and intact inhibition (4). Thus, given the simplicity of encoding/decoding with the linear algorithm, as was done for pauses, we examined its suitability for cerebellar information processing by examining its utility in pattern recognition.

We developed an artificial neural network based on the linear algorithm and combined it with experimental data that estimated Purkinje cell response variability to examine the pattern recognition capacity of Purkinje cells (P-ANN) [see supporting information (SI) Text]. The pattern recognition capacity was estimated under conditions of synchronous and asynchronous parallel fiber synaptic input and in the presence and absence of inhibitory synaptic transmission. The relevant parameters for the P-ANN were experimentally obtained in acutely prepared rat cerebellar slices. We found that under all conditions, use of the linear algorithm enabled Purkinje cells to recognize a large number of input patterns. Moreover, compared with estimates of storage capacity when information was encoded as pauses, the capabilities of linear algorithm-based pattern recognition were always superior. In addition to its compatibility with the rate and pattern of Purkinje cell activity observed in vivo, the linear algorithm of Purkinje cells allows deep cerebellar nuclei (DCN) neurons to use a simple averaging mechanism to increase the pattern recognition capacity of the system. Given its simplicity, versatility, and computational power, we propose that the linear algorithm is suited for cerebellar information processing.

Results

High Pattern Recognition Capacity with Asynchronous Inputs.

The pattern recognition capacity of Purkinje cells depends on the mechanism and reproducibility with which they encode patterns of comparable strength, the number of parallel fiber inputs forming a pattern, and the extent to which these synapses can be modified (SI Text and Fig. S1). We first experimentally evaluated the reproducibility with which various synaptic input patterns of comparable strength are encoded in the maximum firing rate of a Purkinje cell by measuring its response variability when inputs were repeatedly activated in acutely prepared rat cerebellar slices. We restricted our analysis to inputs strengths that increased Purkinje cell firing rates to a maximum of ≈250 spikes per second (Fig. 1B), a range comparable with those observed during performance of motor tasks in vivo (10–13). To remain as close to physiological conditions as possible, inhibitory synaptic transmission was left intact. The background activity of interneurons combined with any remaining parallel fiber activity in the acutely prepared slice preparation resulted in irregular firing of Purkinje cells such that they had a relatively high interspike interval coefficient of variation (14).

As has previously been shown in vivo, brief, discrete sensory stimuli in rats result in the asynchronous activity of patches of granule cells (15–19). The axons of these granule cells, parallel fibers, provide Purkinje cells with asynchronous inputs dispersed throughout their dendritic tree. We reproduced this asynchronous, dispersed pattern of input by photoreleasing glutamate onto a patch of granule cells (4). The stimulated patch of granule cells was chosen to be either directly beneath the target Purkinje cell or >100 μm lateral to it. There were no differences between the data obtained with stimulation at these 2 different locations.

To estimate response variability, we measured the maximum instantaneous firing rate of a spontaneously firing Purkinje cell in response to a large number of repeated photolytic stimulations. Up to a maximum firing rate of ≈250 spikes per second, this parameter is a good measure of the strength of granule cell synaptic input because it is linearly and directly correlated with the number of extra spikes after stimulus and also with the average firing rate after stimulus (4). With this method of stimulation, from trial to trial, photorelease of glutamate at the same location results in the activation of different combinations of granule cells. This is because, depending on their membrane potential before photolysis, different granule cells are brought to threshold by glutamate in each trial. Furthermore, the cells that reach threshold fire different numbers of action potentials and with varying delays. In addition, because of synaptic failure, activation of a granule cell does not necessarily imply that it will release neurotransmitter. Therefore, from trial to trial, the repeated photorelease of glutamate at the same location in the granule cell layer will result in randomly dispersed, asynchronous input to the dendrites of the target Purkinje cell (4). As expected from asynchronous activation of granule cells, this method of stimulation produced an excitatory postsynaptic current (EPSC) in voltage-clamped Purkinje cells that had a relatively slow time to peak (20 ms) and a slow, noisy decay to baseline (Fig. 1A), resembling the time course of activation of granule cells in vivo (15–19).

For every Purkinje cell, the maximum firing rate response to 3 different strengths of stimulation were experimentally determined in acutely prepared rat cerebellar slices. At all stimulation strengths and in every cell tested, the resulting maximum firing rate distributions resembled Gaussian functions that permitted the use of their standard deviations as a measure of response variability (Fig. 1C). The standard deviation of the response was positively correlated with the strength of stimulation (n = 38 from 8 cells, Fig. 1D). Standard deviations obtained from stimulating a patch of granule cells immediately underneath a Purkinje cell were comparable with those estimated by activating lateral patches of granule cells (Fig. 1D). These standard deviations may be an overestimate of the response variability because, even though photorelease of glutamate on average is likely to activate the same number of granule cells, it is unlikely that it will activate exactly the same number in each trial. Reassuringly, our experimentally determined standard deviations are in remarkable agreement with those measured in Purkinje cells in response to repeated smooth eye pursuit trials in awake trained macaques (13). Moreover, reanalysis of a limited set of our own data available from a separate study showed that these standard deviations were also similar to those obtained in vivo in which granule cells were repeatedly activated in the absence of inhibition in mice.

We next determined the number of parallel fiber inputs that constitute a pattern. It is reasonable to postulate that Purkinje cells optimally use their linear dynamic range and thus that an unlearned pattern increases the firing rate of a Purkinje cell to ≈250 spikes per second. With this assumption, the number of inputs that constitute a pattern will be that which increases the firing of a Purkinje cell from its average spontaneous rate of ≈50 spikes (14, 20) to ≈250 spikes per second. With inhibition intact, and if each synaptic input releases neurotransmitter only once, this number corresponds to release from 650 asynchronously activated inputs (SI Text and Fig. S2).

To estimate the pattern recognition capacity of Purkinje cells, we combined the experimentally obtained Purkinje cell response variability measured in acutely prepared rat cerebellar slices as detailed above with an artificial neural network representing a Purkinje cell in the cerebellar cortex (P-ANN). The P-ANN not only incorporated our experimentally determined response variability and pattern size, but also was based on the linear algorithm. To allow for direct comparison with the recent study that examined the efficacy of pauses in pattern recognition, the connectivity and learning rule of the P-ANN used here were modeled after their artificial neural network (3, 21) and simulated a Purkinje cell receiving 150,000 independent parallel fiber inputs (see SI Text for details). Each pattern was created by randomly selecting 650 inputs from the entire pool of 150,000 inputs. The response of the P-ANN was a linear function of the strength of its input. Six hundred fifty novel inputs increased the firing rate of the P-ANN by 200 spikes per second.

The Marr–Albus–Ito theory of cerebellar learning postulates that selective modification of the strength of parallel fiber synaptic inputs (LTD) by a climbing fiber acting as an instructor enables Purkinje cells to recognize groups (patterns) of parallel fibers relaying contextual information related to intended motor tasks. In our P-ANN, learning occurred by a process mimicking long-term depression (LTD) of the parallel fiber to Purkinje cell synapses, resulting in a 50% decrease in the strength of all inputs constituting a learned pattern (22–24).

We used the P-ANN to evaluate the capacity of a Purkinje cell in pattern recognition by altering the number of patterns it had to learn and quantifying its ability to distinguish between learned and novel patterns. As detailed in SI Text, to quantify the latter, we calculated the resulting signal-to-noise ratio (s/n) of the maximum firing rate of a Purkinje cell in response to learned patterns as compared with novel ones by using:

where μ_l and μ_n are the means, and σ_l and σ_n are the standard deviations of the learned and novel maximum firing rate distributions (3, 25, 26).

Fig. 1E quantitatively shows the remarkable utility of the linear computational algorithm of Purkinje cells in bestowing a large capacity for pattern recognition under physiological conditions. As can be noted, by using the linear algorithm, a Purkinje cell can recognize >25 patterns with a s/n of 15 and ≈70 patterns with a s/n of 10 (Fig. 1E, filled circles).

The considerable pattern recognition capacity of Purkinje cells using the linear algorithm described above was based on parameters obtained experimentally in acutely prepared cerebellar slices under physiological experimental conditions where inhibitory synaptic transmission was intact and parallel fiber inputs were asynchronously activated. The analysis presented here was designed to examine the range of parallel fiber inputs that increased the firing rate of Purkinje cells to those typically seen during performance of a motor task. However, it has been shown that very strong synchronous parallel fiber inputs cause Purkinje cells to depolarize to extents that produce brief high-frequency bursts followed by pauses that encode the strength of the input (ref. 3 and Fig. 1B). We found that with asynchronous parallel fiber stimulation and with inhibition intact, it was not possible to obtain such a burst–pause response. Thus, we were not able to estimate the pattern recognition capacity of Purkinje cells, assuming that they encode information in pauses under these conditions. With inhibition blocked, it was possible to get burst–pause responses with asynchronous inputs (Fig. 1B). However, durations of these bursts were long, and those of the pauses were short and variable such that, under these conditions by using our P-ANN, the estimated pattern recognition capacity of Purkinje cells encoding information as pauses was marginal (see SI Text). In agreement with our observations, a recent study based on a biophysical model of a Purkinje cell (in which the pauses are much more reproducible) found that with asynchronous inputs, the pattern recognition capacity of Purkinje cells using pauses to encode information was severely limited (3). In fact, when inputs are delivered asynchronously, this encoding mechanism does not recognize any patterns with a s/n >10 (3). Asynchronous activation of parallel fibers over 10- or 25-ms time windows alone degrade the s/n for the recognition of 75 patterns to ≈5 and ≈2, respectively (3).

Impact of Facilitation at the Parallel Fiber Synapse on Pattern Recognition.

In response to a discrete input in vivo (18, 19), and with our method of granule cell stimulation, a granule cell is likely to release neurotransmitter more than once. If one takes into consideration the significant paired-pulse facilitation observed at parallel fiber synapses (27) and adjusts the number of inputs accordingly, then release from only 185 parallel fiber inputs is needed to drive a Purkinje cell to ≈250 spikes per second (SI Text and Fig. S2). This reduction in the number of inputs per pattern dramatically increases the pattern recognition capacity of a Purkinje cell such that ≈75 patterns can be recognized with a s/n of 15 and >200 patterns with a s/n of 10 (Fig. 1E, open circles). These estimates are more likely to represent what occurs in vivo than those made assuming that each synapse releases neurotransmitter only once.

Pattern Recognition with Synchronous Inputs.

The pattern recognition capacity of Purkinje cells using pauses to encode patterns is considerably improved in the absence of inhibition and when inputs are assumed to be synchronous (3). Although what is commonly observed in vivo is asynchronous granule cell activity (15–19), there may be conditions in which granule cells provide synchronous input. Thus, we wondered whether the use of the linear algorithm enabled Purkinje cells to recognize a large number of patterns when their inputs were synchronously activated and how the capacity of Purkinje cells using the linear algorithm compared with those using pauses to encode information under similar conditions. To estimate this, we experimentally determined the response variability of Purkinje cells after repeated synchronous activations of granule cells by using electrical stimulation and confirmed that a standard LTD protocol significantly reduced the maximum firing rate response (SI Text and Fig. S3). We then estimated that in the absence of inhibitory synaptic transmission, synchronous release of neurotransmitter from only 70 inputs is sufficient to increase the firing rate by 200 spikes per second (SI Text and Fig. S2). Because of the smaller number of inputs in a pattern, a Purkinje cell could recognize more learned synchronous input patterns (>350 with a s/n of 10) than asynchronous ones (Fig. 1 E and G).

To allow for direct comparison for pattern recognition capacity when information is encoded in pauses rather than in firing rate, we adapted our P-ANN to encode information as pauses (SI Text). We found that the pattern recognition capacity of the ANN component of the P-ANN was comparable when information was encoded as pauses rather than as increases in firing rate (Fig. 1F). However, the pattern recognition capacity of Purkinje cells using pauses was appreciably lower than when they encoded information in increases in their firing rate (Fig. 1G). In fact, using a pause-based encoding mechanism, Purkinje cells recognized a single learned pattern with a s/n of only ≈6. This estimate is in close agreement with an experimentally determined s/n of 5.6 for discrimination between pauses produced by parallel fiber inputs before and after induction of LTD under comparable conditions (3).

We also compared our results with those of Steuber et al. (3), which assumed information was encoded as pauses and was based on a biophysical model of a Purkinje cell. Because our ANN was modeled after theirs, the performance of both ANNs was comparable (Fig. 1F). However, the pattern recognition capacity of the biophysical Purkinje cell model was higher than that estimated for encoding with pauses here (Fig. 1G). This is mainly because, in their study, from trial to trial, the pause duration of their biophysical Purkinje cell model was much less variable than pause durations seen in Purkinje cells in acutely prepared cerebellar slices (3). Nonetheless, when compared with their estimates, the pattern recognition capacity using the linear firing rate algorithm outperformed by >2-fold (Fig. 1G) that of encoding with pauses under comparable conditions (3). In fact, under all conditions examined, the use of the linear algorithm to encode patterns is as good as or better than the use of pauses.

A Simple Mechanism to Increase s/n.

A limitation of the Marr–Albus pattern recognition scheme is that learning large numbers of patterns invariably adds significant noise and reduces the accuracy of decoding (see SI Text). However, it has recently been reported that the cerebellum introduces little noise to motor signals (13). Thus, the cerebellum must implement a mechanism to minimize the noise inherently associated with decoding large numbers of patterns. As delineated below, an advantage of the use of the linear algorithm by Purkinje cells is that the cerebellum can use a simple averaging mechanism to reduce noise and improve its pattern recognition capacity.

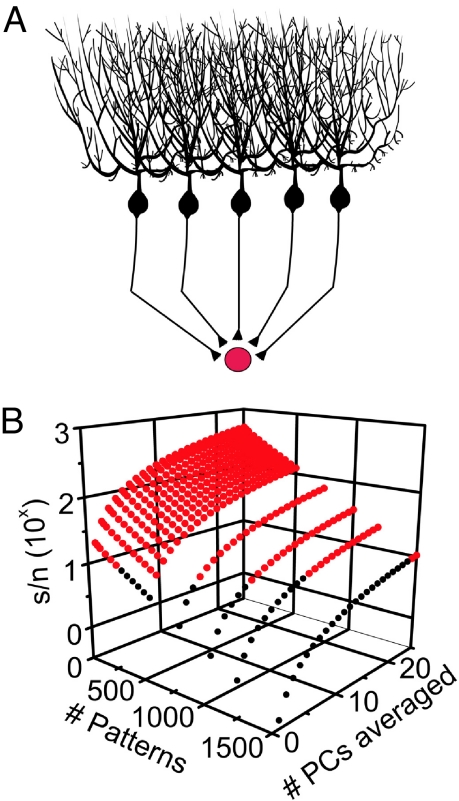
The majority of Purkinje cells within the cerebellum converge onto neurons of the deep cerebellar nuclei (DCN) via synapses specialized for the transmission of their high-frequency signals (28). In turn, neurons of the DCN further process and relay this information out of the cerebellum. One form of processing that individual DCN neurons are ideally suited to perform is that of averaging the information from the tens to hundreds of Purkinje cells estimated to converge onto them (29, 30). By linearly summing synaptic inputs from multiple Purkinje cells, individual DCN neurons can, in principle, reduce the standard deviation of the signals encoded in Purkinje cell firing. With this method of averaging, the extent to which the noise is reduced is proportional to the number of converging Purkinje cells that have learned the same parallel fiber input patterns and the extent to which the noise in different Purkinje cells is uncorrelated (Fig. 2). As can be noted in Fig. 2, the remarkable consequence of this simple averaging is that the s/n of the pattern recognition capacity of this system for a specific pattern increases by the number of Purkinje cells averaged (see SI Text and Fig. S4 for an extensive discussion). Thus, as many as 1,000 patterns can be recognized by a single DCN neuron with a s/n of ≈10 if as few as 7 Purkinje cells are averaged. The simplicity of this averaging algorithm is due to the linearity with which Purkinje cells encode the strength of learned and unlearned patterns and the ease with which pattern recognition can subsequently be accomplished by DCN neurons.

Fig. 2.

Averaging significantly improves the pattern recognition capacity of the cerebellum. (A) The signal-to-noise ratio of the pattern recognition capacity of the cerebellum was estimated as a function of the number of patterns to be learned, assuming that DCN neurons average information from a number of Purkinje cells, each of which have learned the same patterns. (B) Averaging reduced the standard deviation of learned and novel Purkinje cell maximum firing distributions by $\sqrt{N}$, resulting in a N-fold improvement in the signal-to-noise ratio. Red circles denote signal-to-noise ratios ≥10.

Discussion

In principle, Purkinje cells can encode information by using 2 fundamentally different mechanisms: strong parallel fiber inputs as pauses and weaker inputs in firing rate. It is not known whether either of these 2 mechanisms is implemented by the cerebellum, although, within the context of Marr–Albus–Ito theory, it has been suggested that encoding information as pauses is optimal for pattern recognition. We sought to assess the suitability of encoding information by using the linear algorithm and to compare its pattern recognition capacity with that achieved when encoding with pauses. Under all conditions examined, with the linear algorithm, a Purkinje cell had a significantly higher capacity for recognizing patterns than when it used pauses to encode inputs. As shown above and discussed in detail below, the simplicity, versatility, and computational power of linearly encoding the strength of parallel fiber inputs in the firing rate of Purkinje cells endows it with several advantages for cerebellar computation.

Superior Pattern Recognition Capacity of the Linear Algorithm.

Based mainly on its anatomy and perceived function, Marr and Albus proposed that cerebellar motor learning occurs by adjusting the strength of parallel fiber synaptic inputs onto Purkinje cells (5, 6). More than a decade later, plasticity at the parallel fiber-to-Purkinje cell synapse was experimentally demonstrated by Ito and colleagues in vivo (22, 23). According to the Marr–Albus–Ito theory of cerebellar function, the proficiency of the cerebellum in coordinating movement is limited by the number of input patterns that it learns to recognize (5, 6).

The pattern recognition capacity of Purkinje cells has been evaluated when using various learning rules, connectivity patterns, and information-encoding mechanisms (3, 5–8). Steuber et al. (3) combined an artificial neural network based on the Marr–Albus–Ito learning rule with a detailed biophysical model of a Purkinje cell to examine the pattern recognition capabilities of Purkinje cells using pauses to encode information. To similarly explore the utility of linearly encoding information in the firing rate, we generated a comparable artificial neuronal network incorporating the linear algorithm. Furthermore, rather than estimating the relevant parameters from a biophysical model in silico as done by Steuber et al., we experimentally determined them in Purkinje cells in cerebellar slices. Remarkably, the use of the linear algorithm to encode input patterns endowed Purkinje cells with a high pattern recognition capacity that, under all conditions examined, was greater than that achieved with pauses.

Compatibility with Spontaneous Firing of Purkinje Cells.

Use of the linear algorithm of Purkinje cells to encode patterns also endows the system with numerous features compatible with the known physiological properties of the cerebellum. Purkinje cells in vivo are spontaneously active. Underlying this spontaneous activity is an input-independent intrinsic pace-making mechanism that drives Purkinje cells to fire at an average firing rate of ≈50 spikes per second (14, 20, 31, 32). In vivo, the activity in parallel fibers and interneurons strongly modulates this intrinsic firing over a wide range. The presence of an intrinsically driven pace making is incompatible with most pattern recognition theories (5, 7, 8), and the recent study using pauses to encode patterns did not incorporate it because the biophysical model used did not support it. Instead, this study found that the accuracy of pattern recognition strongly depended on the spontaneous activity of Purkinje cells that was artificially generated by background parallel fiber input (3). In contrast, however, pattern recognition based on encoding the relative strength of parallel fiber inputs in the maximum firing rate of Purkinje cells easily incorporates Purkinje cell pace making as long as the maximum firing rate does not exceed ≈250 spikes per second.

Compatibility with Patterns of Purkinje Cell Activity in Vivo.

If the cerebellum utilizes pattern recognition as proposed by the Marr–Albus–Ito hypothesis, then as patterns of parallel fiber input representing learned and unlearned contexts are presented to a Purkinje cell, its firing rate should change to represent values associated with learned and unlearned patterns. The linear algorithm predicts that Purkinje cell firing rates should reach a maximum of ≈250 spikes per second. This is in close agreement with Purkinje cell activity observed during the performance of motor tasks in vivo (10–13). In contrast, the use of pauses to encode patterns would dictate that a pattern of parallel fiber input, whether learned or unlearned, is represented by pauses of ≈40- to 80-ms duration (3). Because these pauses are the consequence of a hyperpolarization after a very large parallel fiber-induced depolarization, each of these pauses must be preceded by at least 1 interspike interval corresponding to a firing rate >250 spikes per second (3). This predicted burst–pause activity pattern is not only inconsistent with that seen in vivo (10–13, 33) but also, as previously noted by Steuber et al. (3), significantly limits the maximum processing speed of the cerebellar circuitry.

Encoding Asynchronous Parallel Fiber Input Patterns.

We find that, similar to that seen when patterns are encoded as pauses (3), synchronous inputs result in higher pattern recognition capacity. However, there is good evidence to suggest that parallel fiber inputs to Purkinje cells arrive asynchronously in vivo (15–19). Although the ability of Purkinje cells to recognize asynchronous patterns significantly degrades when encoding information as pauses, the linear algorithm remains remarkably proficient. The ability of Purkinje cells to recognize large numbers of synchronous and asynchronous input patterns when using the linear algorithm highlights the diversity of function of this encoding mechanism and, thus, its potential utility in cerebellar computation.

Beyond the Marr–Albus–Ito Theory.

The pioneering work of Marr and Albus and the subsequent experimental demonstration of LTD has made the Marr–Albus–Ito theory of motor learning one of the most prominent theories for cerebellar function. Nonetheless, recent advances in our understanding of the cerebellar circuitry suggest that numerous additional factors are likely to contribute to cerebellar motor learning. There is good evidence to suggest, for example, that synaptic connections made by interneurons and even Purkinje cells are plastic and contribute to motor learning (34–38). Moreover, during performance of motor tasks such as smooth eye pursuit (39) or alternate wrist movements (33), the firing rate of a Purkinje cell is smoothly modulated both below and above its resting spontaneous rate, suggesting that Purkinje cells can also encode information in decreases in firing rate. In this study, we purposefully restricted our analysis to the classic Marr–Albus–Ito theory to allow direct comparison with a similarly focused study that examined the efficacy of encoding the strength of parallel fiber input patterns as pauses (3). A cursory consideration suggests that the linear algorithm can easily incorporate bidirectional signaling by Purkinje cells. Nonetheless, there is no doubt that in future studies, analysis of computational capabilities of the linear algorithm and encoding information as pauses need to be extended to incorporate additional sites of plasticity and the active role that cortical interneurons play in cerebellar information processing.

Linear Algorithm and Averaging.

As noted by Eccles (40), the anatomy of the cerebellum suggests that the convergence of several Purkinje cells to a single DCN neuron can be used as an averaging mechanism to increase s/n and ensure the reliability of cerebellar computations. Use of the linear algorithm allows for implementation of such an averaging mechanism to increase the pattern recognition capacity of the cerebellum. Whether this method of averaging improves pattern recognition capacity critically depends on the functional connectivity of the cerebellum and remains to be established. For example, the effectiveness of this DCN averaging requires the convergence of Purkinje cells whose noise is not fully correlated and that also have learned the same patterns. These converging Purkinje cells should not only receive the same information but also must have learned to recognize the same patterns for a given motor task. Thus, the limiting factor is likely to be the number of Purkinje cells that receive the same instructor signal from a climbing fiber. Because of electrical coupling in the inferior olive (41), several climbing fibers may convey the same information, and, moreover, a single climbing fiber contacts ≈10 Purkinje cells (42). Thus, given that even the convergence of 2 Purkinje cells can, in principle, double the s/n, it seems quite likely that averaging is used by the cerebellum.

Implementation of the linear computational algorithm affords individual Purkinje cells a high capacity for pattern recognition and makes predictions that are consistent with many features of Purkinje cell function observed in vivo. Moreover, linearity allows for a simple, yet extremely powerful, mechanism to use the highly conserved anatomical circuitry of the cerebellum to significantly improve the pattern recognition capacity of the system.

Materials and Methods

Slice Preparation.

Experiments were carried out in accordance with the guidelines and recommendations set by Albert Einstein College of Medicine. Wistar rats of the age 12–25 days were anesthetized with halothane and decapitated. Three-hundred-micron-thick sagittal or 400-μm-thick coronal slices were made from the cerebellar vermis by using a modified Oxford vibratome. Slices were kept at room temperature until use (1–4 h) in a solution containing 125 mM NaCl, 2.5 mM KCl, 26 mM NaHCO₃, 1.25 mM NaH₂PO₄, 1 mM MgCl₂, 2 mM CaCl₂, and 10 mM glucose (pH 7.4) when gassed with 5% CO₂/95% O₂.

Electrophysiological Recordings.

Slices were placed in a recording chamber on the stage of an upright Olympus microscope, and Purkinje cells were visualized by using a 40× water-immersion objective (N.A. 0.8) with infrared optics. The slices were constantly superfused at a rate of 1.5 mL/min. When noted, the solution contained 100 μM picrotoxin (Sigma) and 1 μM CGP 55845 (Tocris) to block GABA_A and GABA_B receptors. The temperature of the bathing solution was adjusted to 35 ± 1 °C.

Extracellular recordings were made from single Purkinje cells by using a home-made differential amplifier and glass pipette electrodes. Whole-cell recordings were performed with an Optopatch amplifier (Cairn Research) with electrodes pulled from borosilicate glass with a resistance of 1–3 MΩ when filled with internal solution containing 120 mM cesium gluconate, 10 mM CsF, 20 mM CsCl, 10 mM EGTA, 10 mM Hepes, and 3 mM MgATP (pH 7.4) with CsOH. This intracellular solution also contained 2 mM QX-314 to block voltage-gated sodium channels. EPSCs were recorded in Purkinje cells whole-cell voltage-clamped at −60 mV.

Extracellular data were sampled at 10 kHz, and whole-cell data were sampled at 20 kHz by using a National Instruments analog-to-digital converter (PCI-MIO-16XE-10) and acquired and analyzed by using custom software written in LabView (National Instruments).

Granule Cell Stimulation.

To estimate response variability, granule cells were activated synchronously by electrical stimulation and asynchronously by glutamate photolysis. Electrical stimulation was done by using 200-μs current pulses applied with an electrode placed within the granule cell layer by using a constant current stimulator (Digitimer).

To asynchronously activate granule cells, a patch of granule cells was activated by local photorelease of glutamate. MNI-caged l-glutamate (1 mM; Tocris) was added to the bathing solution and recirculated to allow preequilibration with the slice. The energy source for glutamate photolysis was a multiline UV Coherent Innova 300C Krypton ion laser. An accusto-optical modulator (NEOS) was used to gate (1 ms) and regulate the intensity of the UV pulse. The laser light was transmitted to the microscope via a fiber optic cable, collimated, and positioned via a pair of galvos (Cambridge Technology) driven by the data-acquisition software. The laser light was focused to form a 40-μm-diameter spot in the granule cell layer.

With both electrical and photolytic activation of granule cells, the maximum instantaneous firing rate after stimulus was calculated as the inverse of the briefest interspike interval after stimulus. Unless otherwise noted, the data are presented as mean ± SEM.