Weak, strong, and coherent regimes of Fröhlich condensation and their applications to terahertz medicine and quantum consciousness

Abstract

In 1968, Fröhlich showed that a driven set of oscillators can condense with nearly all of the supplied energy activating the vibrational mode of lowest frequency. This is a remarkable property usually compared with Bose–Einstein condensation, superconductivity, lasing, and other unique phenomena involving macroscopic quantum coherence. However, despite intense research, no unambiguous example has been documented. We determine the most likely experimental signatures of Fröhlich condensation and show that they are significant features remote from the extraordinary properties normally envisaged. Fröhlich condensates are classified into 3 types: weak condensates in which profound effects on chemical kinetics are possible, strong condensates in which an extremely large amount of energy is channeled into 1 vibrational mode, and coherent condensates in which this energy is placed in a single quantum state. Coherent condensates are shown to involve extremely large energies, to not be produced by the Wu–Austin dynamical Hamiltonian that provides the simplest depiction of Fröhlich condensates formed using mechanically supplied energy, and to be extremely fragile. They are inaccessible in a biological environment. Hence the Penrose–Hameroff orchestrated objective-reduction model and related theories for cognitive function that embody coherent Fröhlich condensation as an essential element are untenable. Weak condensates, however, may have profound effects on chemical and enzyme kinetics, and may be produced from biochemical energy or from radio frequency, microwave, or terahertz radiation. Pokorný's observed 8.085-MHz microtubulin resonance is identified as a possible candidate, with microwave reactors (green chemistry) and terahertz medicine appearing as other feasible sources.

In 1968, Fröhlich showed how a driven collection of vibrational oscillators could achieve a highly ordered nonequilibrium state that has some properties reminiscent of Bose–Einstein condensation (1–3). Specifically, this Fröhlich condensate has nearly all of its vibrational energy concentrated in just one of its collective motions, the motion of lowest frequency. Such a condensation would have a profound influence on the dynamical properties of the system, and there has been considerable interest in finding applications in physics (4, 5), biology (6–20), and medicine (21–26). Indeed, other phenomena that give rise to similar collective properties of a system such as lasing, superconductivity, and Bose–Einstein condensation are of great importance.

Fröhlich condensation has even been postulated to play a central role in cognitive function within the Penrose–Hameroff orchestrated objective reduction (Orch OR) (27, 28) and related (29, 30) proposals. These controversial (31) proposals evoke Fröhlich condensation to maintain coherent quantum dynamics within microtubules inside cells on a physiologically relevant time scale (at least microseconds), enabling them to function as cellular quantum computing elements. In nerve cells, these elements are then presumed to interact with the electrochemical operation of the cells, leading to cognitive function. This is significant as Penrose has argued that linear (or, more generally, nonexponential) computational elements such as electrochemical-only neural networks are fundamentally incapable of cognition (32), undermining the basis for our current understanding of intelligence.

Despite intense interest, the 40 years subsequent to Fröhlich's proposal have produced no unambiguous identification of a Fröhlich condensate. The most substantial efforts have come from Pokorný (14, 15) who, interestingly, also considered microtubules. A range of other experimental detections of some of the key signatures of Fröhlich condensates have also been reported (5, 11, 17–20) or predicted (12, 13). Pokorný's work concerns the interaction of MHz radio-frequency radiation with biological systems, and many other suggested occurrences of Fröhlich condensates also involve either adverse or medicinal effects of microwave or terahertz radiation (9, 11, 14–26).

Here, we investigate the basic properties of Fröhlich condensates, considering their robustness to parameter variations, the effective temperature at which they form, limitations of the basic assumptions, and the Wu–Austin physical model for their production (33–35). We classify solutions to the Fröhlich model into 3 distinct types: weak condensates, strong incoherent condensates, and strong coherent condensates, with each expected to arise in different circumstances and produce profound but greatly varying observable effects. These results lead us to postulate chemical and biochemical scenarios in which effects of condensation could be observed and assess the likelihood of it occurring in microtubules in a way that could provide a mechanism for the operation of Orch OR.

Results

Weak and Strong Fröhlich Condensates.

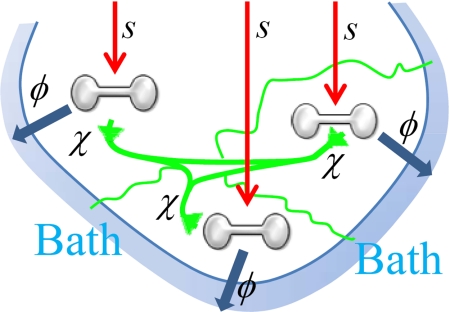
Fröhlich's model is depicted in Fig. 1. The system of interest is taken to consist of a number Z of coupled oscillators whose collective motions occur at frequencies ω_i (for i = 1 to Z) in a band of finite width at average frequency ω₀. The model does not consider the form of the dispersion of these frequencies, but an important property is the lowest frequency ω₁. These collective motions are each fed energy at the rate of s per unit time, whereas 2-body “collisions” with surrounding bath states dissipate this energy at a rate specified by a parameter φ (the rate of energy gain at 0 K) and 3-body interactions involving 2 system states and the bath redistribute the energy among the oscillators at a rate specified by parameter χ. Fröhlich's expressions for these processes are described in detail in SI Appendix in terms of occupation numbers n_i depicting the average number of quanta of excitation of collective mode i and the bath temperature T; they arise purely from the detailed balance requirement that equilibrium is established whenever s = 0, with the average number of quanta in each mode given by the Planck distribution function

depicting a canonical energy distribution. Such an energy distribution is a requirement of most models for chemical reaction kinetics, e.g., the Arrhenius equation and transition-state theory.

Fig. 1.

Fröhlich's model for a driven system of Z = 3 oscillators connected to a thermal bath. Red- energy input into each system oscillator at rate s, blue- energy losses to the bath with a rate proportional to φ, and green- energy redistributions within the system at a rate proportional to χ.

Fröhlich solved this model to obtain the steady-state in the classical high-temperature limit kT ≫ ℏω_i, showing that (i) the total number of vibrational quanta N = Σ_{i = 1}^Zn_i increases dramatically above that in thermal equilibrium with the bath, N^T = Σ_{i = 1}^Zn_i^T, by

where ω̄ is slightly larger than the lowest frequency ω₁, and (ii) that nearly all of these quanta activate the lowest-frequency mode. These 2 properties depict strong Fröhlich condensates. Another condition required for condensation that is not widely discussed is Nχ > φ. Even though the 3-body exchange rate χ is expected to be much less than the 2-body relaxation rate φ, because N grows very large, this condition generally holds. The formation of the condensate is thus insensitive to χ and is instead controlled by the ratios s/φ and kT/ℏω₁. At χ = 0, however, the condensate does not form although the number of quanta in the system, N^{χ = 0}, can still increase dramatically as a result of the directed energy transduction, producing a nonequilibrium energy distribution:

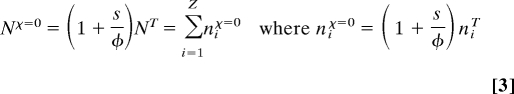In the classical high-temperature limit this distribution is in fact that which would be produced if the temperature of the system oscillators was (1 + s/φ)T.

In general, Fröhlich's model is described in terms of the dimensionless parameters s/φ and χ/φ, the number of oscillators Z, and the mode frequency distribution relative to the bath temperature. Here, we represent the frequency distribution through the dimensionless parameters ℏω₀/kT and ω₁/ω₀, using 3 functional forms for the dispersion: linear, cosine (e.g., as would be generated from a linear arrangement of local oscillators connected by only nearest-neighbor coupling in a tight-binding model), and Gaussian (e.g., as would be generated by inhomogeneous broadening). We evaluate numerically the [unconditionally attainable (36)] steady-state solution to Fröhlich's model as a function of these parameters over a wide range from MHz oscillators to high-frequency stretching motions (see SI Appendix) with key features highlighted in Fig. 2. Fröhlich's supposition that condensation is insensitive to the form of the frequency dispersion is verified, with most properties converging to the infinite-mode limit by only Z = 25. Fig. 2 shows the condensation index

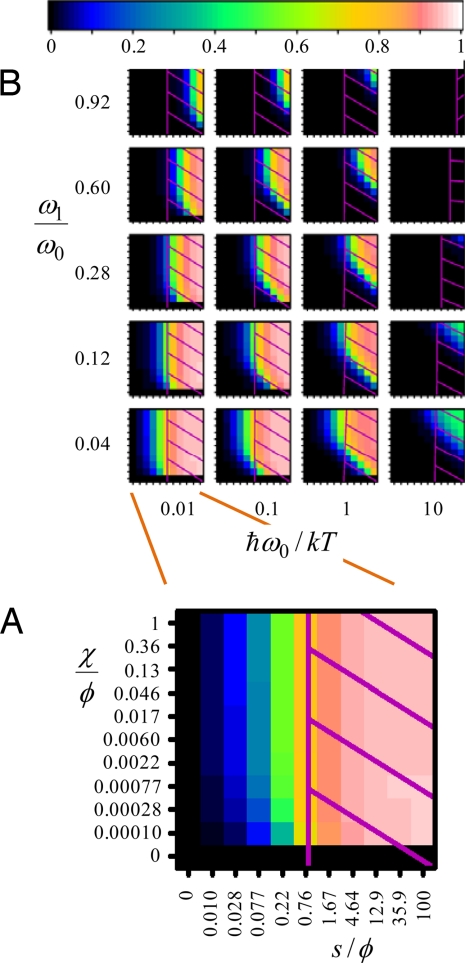
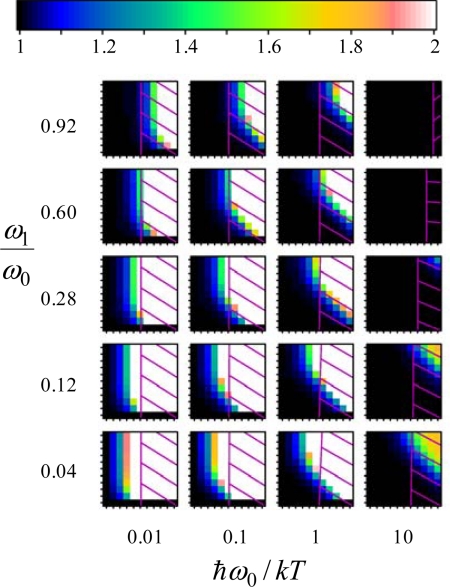
giving the fraction of the total vibrational quanta of the system that are present in the lowest-frequency mode, above that present in the hot noncondensate produced at χ = 0. The condensation index goes to zero as either s or χ goes to zero (no condensate) and approaches a value just below unity when the condensate is fully formed (the strong condensate limit). Strong condensation requires high s/φ, high bath temperature to vibration-frequency ratio ℏω₀/kT, and very wide bands (low ω₁/ω₀) (see Eq. 2) and produces a novel state of matter. However, even low values of the condensation index would give rise to significant deviations from the simple energy distribution of Eq. 3 expected for an ensemble of uncoupled equally driven oscillators, an aspect of the condensation phenomenon generally overlooked. Such systems we refer to as “weak condensates.” To depict them we show in Fig. 3 (and in detail in SI Appendix) the enhancement factor n₁/n₁^{χ = 0}, the ratio of the number of quanta in the lowest-frequency mode to that expected for the steady state in which the supplied energy is equally dispersed among all vibrational modes. Highly nonequilibrium behavior can arise over a wide range of parameter space, including regions with s/φ < 1 provided that bandwidth is wide (i.e., ω₁/ω₀ is small).

Fig. 2.

Regions in which strong Fröhlich condensates can be observed. For linear dispersion and Z = 25 modes, the condensation index η is colored in plots as a function of the ratio of the energy input to the bath relaxation, s/φ, and the ratio of the rate of energy redistribution to bath relaxation, χ/φ. (A) single plot at a band-Center vibration frequency to temperature ratio of ℏω₀/kT = 0.1 and band-narrowness parameter ω₁/ω₀ = 0.04 extracted from B. (B) All results. Superimposed on each plot is a hatched region indicating system temperature T_S/T > 5/3 (500 K if the bath temperature is T = 300 K); such regions are certainly not accessible in a biological environment.

Fig. 3.

Regions in which at least weak Fröhlich condensates can be observed. For linear dispersion and Z = 25 modes, the condensation-induced enhancement factor n₁/n₁^{χ = 0}, depicting the ratio of the number of quanta in the lowest-frequency mode to that expected if the source energy is evenly dispersed, is shown as a grid of plots akin to those in Fig. 2. For each plot, the abscissa is the ratio of the energy input to the bath relaxation, s/φ, whereas the ordinate is the ratio of the rate of energy redistribution to bath relaxation, χ/φ. White regions indicate regions with n1/n₁^{χ = 0}; much lower values should give experimentally observable effects. Superimposed on each plot is a hatched region indicating biologically inaccessible regions with system temperature T_S/T > 5/3 (500 K if the bath temperature is T = 300 K).

As the flow of energy through the system causes its internal energy to rise, and as physical processes not envisaged in the Fröhlich model become important at high energies, we introduce an effective temperature T_S (see SI Appendix) as a guide as to whether or not any particular application of the model is physically realistic. Indeed, the calculated heating can be extreme (12), with some values exceeding T_S/T = 100 (i.e., T_S > 30,000 K for a room temperature bath). Temperatures of this order serve primarily to indicate shortcomings in possible applications of the model. In a biological environment, a temperature of 500 K in the system modes exceeds all realistic expectations, and we take this limit as a generous indication of the validity of the condensation predictions. In Figs. 2 and 3 the regions in which T_S exceeds 500 K for T = 300 K are highlighted, indicating that weak condensates are biologically feasible but strong condensates are not.

Coherent Motion Within Strong Fröhlich Condensates.

Although strong Fröhlich condensation delivers most of the vibrational energy into a single mode, it does not in itself ensure coherent vibrational motion. In fact, the theory describes only the average incoherent energy in the mode, not the way that this energy is distributed among the quantum states of the mode or the temporal fluctuations of the instantaneous energy about its average. Fröhlich condensation is a classical process, described semiclassically using the Planck quantization condition (Eq. 1). In SI Appendix we show that Fröhlich condensation also arises within classical statistical mechanics, indicating that neither quantization of energy nor quantum coherence are essential aspects of the model. Although the Fröhlich condensate is often likened to the Bose–Einstein condensate, a coherent macroscopic quantum state in which all particles have the same quantum number, the differences are profound.

It is, of course, possible that Fröhlich condensates do show coherent motion, but analysis of such effects requires first the introduction of a physical model for the energy source, flow, and sink. The generality of Fröhlich's arguments implies that many possible physical models could develop condensates, with e.g., variants including mechanical (thermal or nonthermal) energy and radiative energy sources. Indeed, a range of physical models have been proposed and shown to support condensation (12–15, 33–35, 37–41), mostly based on the original mechanical Hamiltonian proposed by Wu and Austin (33–35). Because the Wu–Austin model is directly relevant to the Orch OR proposal, we consider whether or not it is likely to support coherent Fröhlich condensates.

Wu and Austin (33–35) proposed a dynamical model containing the Z system modes connected to harmonic baths representing the energy input source and the surrounding thermal-relaxation bath. For Z_B relaxation-bath modes k of frequency Ω_k and Z_I input modes l of frequency Ω′_l, their Hamiltonian is

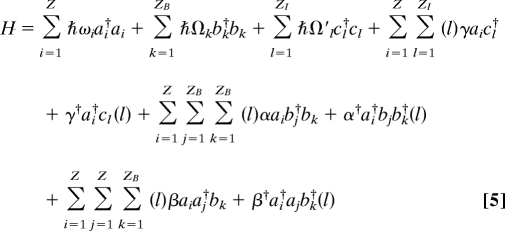where a_i, b_k, and c_l are creation operators for the system, bath, and input oscillators, respectively. Further, they assumed that unspecified processes maintain the bath and input oscillators in equilibrium canonical distributions at temperatures T and T_I, respectively. We implement these constraints using Nose-Hoover thermostats (42) with time constants of 0.1 ps each. Only linear frequency dispersion among Z = 25 source oscillators is considered, whereas a uniform spectral distribution of the bath and input oscillators is assumed, choosing Z_B = 430 bath modes and Z_I = 200 input modes; as demonstrated in SI Appendix, all simple properties of the [quantum (43, 44)] dynamics are converged to the infinite-mode limit using these numbers of oscillators.

The primary parameters in the Wu–Austin Hamiltonian are the couplings α, β, and γ; as shown in SI Appendix and refs. 33–35, these may be related to mode-specific Fröhlich-like parameters s_i, φ_i, and χ_i. A key feature found in the simulations is that the rates of energy flow s_i and φ_i are surpassed in significance by the rate of phase decoherence associated with the dynamics. This occurs as, during each period of system-oscillator motion, the bath and energy input sources transfer large amounts of energy into and out of the system, with the net energy transfer being quite small (see SI Appendix, Figs. S9 and S10).

The Wu–Austin Hamiltonian also has the undesired property of having no finite ground state (38). This is a general property of all cubic potentials as for high-enough energies nonphysical transition states are reached that lead to dissociation. It is a particular concern for Fröhlich condensates as condensation drives the system to very high energy and thus by necessity accesses the nonphysical regions of the potential-energy surface. In dynamics calculations such unphysical trajectories are easy to detect and exclude from analysis. Although variants of the Wu–Austin Hamiltonian have been derived that embody quartic terms that make the ground-state finite (39), they obscure the nonphysical regions, converting them into hard-to-detect alternative local minima. Hence we choose to remain with the basic Wu–Austin Hamiltonian.

Exploratory studies using the Wu–Austin Hamiltonian indicate that it indeed depicts all of the key properties of Fröhlich condensation. A range of results are presented in SI Appendix and in Fig. 4 depicting strong Fröhlich condensates in the wide-band low-frequency limit (ω₁/ω₀ = 0.12, ℏω₀/kT = 1/15), the narrow-band low-frequency limit (ω₁/ω₀ = 0.76, ℏω₀/kT = 1/15), and the narrow-band high-frequency limit (ω₁/ω₀ = 0.94, ℏω₀/kT = 1.46). The low-temperature simulations pertain to the extensive studies of Pokorný (14, 15) on the possibility of Fröhlich condensation in the MHz region and to studies of the effects of GHZ and THz radiation in biology (9, 11, 14–25), whereas the high-temperature simulations pertain directly to the extensive studies of Mesquita et al. (12, 13) on the possibility of Fröhlich condensation in protein amide-I vibrations. Together, these provide a rough guide to the dynamics of strong condensates over the whole parameter space of the Wu–Austin model.

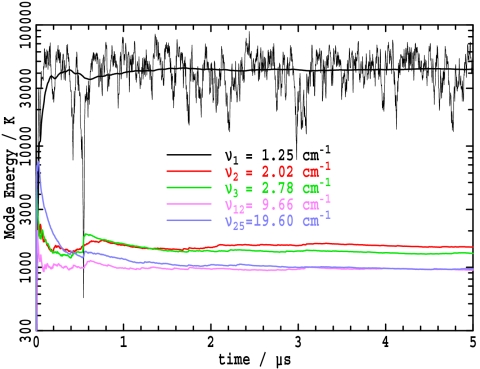
Fig. 4.

Dynamics of the Wu–Austin Hamiltonian in the wide-band low-frequency limit (ω₁/ω₀ = 0.12, ℏω₀/kT = 1/15), showing the change in the average kinetic energy in modes 1 (the mode undergoing Fröhlich condensation), 2, 3, 12, and 25 for Z = 25 system oscillators; the instantaneous kinetic energy in mode 1 is also shown (thin line). Other parameters are: linear frequency dispersion, Z_B = 430 bath modes at T = 300 K (hence ω₀ = 10.425 cm⁻¹, ω₁ = 1.251 cm⁻¹), Z_I = 200 source modes at T_I = 96,000 K, α/k = 150 μK, β/k = 150 μK, γ/k = 750 μK.

Fig. 4 shows the dynamics of formation of the Fröhlich condensate among Z = 25 oscillators initially at equilibrium with the bath at T = 300 K in the wide-band, high-temperature limit. The condensate forms after 20 ns of dynamics and maintains its qualities throughout the remaining ≈5 μs duration of the trajectory. More than 90% of the vibrational quanta reside in the lowest mode, identifying this system as being in the strong-condensate limit; mode 2 has the next greatest occupancy, with the occupancy slowly decreasing with increasing frequency, as has been predicted for other Fröhlich condensates (13). Although the average energy in mode 1 quickly approaches a limiting value in accordance with Fröhlich's predictions (1), the instantaneous energy in mode 1, also shown in Fig. 4, fluctuates rapidly. Fröhlich condensation is thus seen not to be associated with highly stable coherent oscillations. Nevertheless, it is possible that coherence is maintained over times too short to be apparent in this figure that are indeed large compared with the intrinsic coherence lifetime of an analogous noncondensing system. However, quantum dynamics analysis of this trajectory reveals that the coherence lifetime remains very short indeed (femtosecond time scale only), being much shorter than a single vibrational period.

Fourier transformation of the energy fluctuations shows that they are dominated by white noise spanning the MHz region, increasing significantly <5 MHz. As shown in detail in SI Appendix, Fig. S13, for condensates in the low temperature limit, these fluctuations become extremely large, and the time required to form the condensate increases to become of the microsecond time scale. The simulations of the condensate proposed by Mesquita et al. (12, 13) in protein amide-I vibrations at 300 cm⁻¹ (10 THz) showed extremely large 400 kHz fluctuations in the strongly formed condensate.

Across the whole of the parameter space, we thus see that the Wu–Austin Hamiltonian does not lead to coherent Fröhlich condensates. Alternatively, using a modified Wu–Austin Hamiltonian in which the mechanical microscopic energy source is replaced with general macroscopic energy flow, Mesquita et al. (12, 13) have shown that enhanced lifetimes for coherent excitations are possible. It is conceivable that such a situation could be physically manifested if the energy source was radiation rather than thermal energy. Based on their results, we explore in SI Appendix the likelihood of finding a coherent Fröhlich condensate. For the cosine dispersion appropriate for a linear chain of coupled oscillators as envisaged in the Orch OR proposal, the competing effects result in a minimum system temperature for coherence of 1,560 K for ≈19 ≤ Z ≤ 46 oscillators. This is not possible in any biological environment. Indeed, in the low-temperature limit originally considered by Mesquita et al. pertinent to Fröhlich condensates involving protein amide-I vibrations, our simulations (SI Appendix, Fig. S13) indicate that the condensing mode attains an energy corresponding to a temperature of order 10⁵ to 10⁷ K!

Discussion

Fröhlich Condensation and the Orch OR Proposal.

Fröhlich condensation, driven by the hydrolysis of GTP to GDP by tubulin, is evoked within the Penrose–Hameroff Orch OR proposal (27, 28) for quantum consciousness to provide long-time quantum coherence of vibrational motions in a noisy environment that would normally be expected to dephase coherent motion extremely rapidly (31, 45). Because the energy is expected to flow mechanically after the hydrolysis reaction, the Wu–Austin Hamiltonian should provide a realistic description of the process. Because we find that the Wu–Austin model does not lead to coherent Fröhlich condensates in any region of its parameter space, Orch OR could not exploit this effect to achieve the required coherent motion.

Despite this analysis, it could be envisaged that some other dynamical Hamiltonian could deliver a coherent Fröhlich condensate as envisaged by Orch OR. Such a condensate would have properties similar to the one produced by Mesquita et al. (12, 13) using a phenomenologically represented energy source. For such a condensate at ω₁ = 300 cm⁻¹ in the low-temperature limit originally studied, coherence requires a pumping power per oscillator of s = 2 × 10⁴ kcal·mol⁻¹·ps⁻¹. This implies that a power of ≈10² kcal·mol⁻¹·ps⁻¹ is required to drive the low-frequency protein modes (46) evoked in the Orch OR proposal (27, 28). Orch OR using these modes thus requires, e.g., the energy equivalent to the formation of a C–C bond per oscillator every picosecond. This is extremely unrealistic. Hence the energy being fed into the system oscillators envisaged is unlikely to exceed the relaxation rate (s ≪ φ) with the effective s corresponding to only a small fraction of the total chemical power. Because of the high input powers and system temperatures required, in general it will not be possible to generate coherent Fröhlich condensates in biochemically powered systems, as is required by Orch OR.

Realizable Manifestations of Fröhlich Condensation.

Although coherent Fröhlich condensates are not biologically feasible, weak incoherent condensates within individual proteins may still be significant. Fröhlich's original motivation (3) was to explain the action of enzymes in terms of coherent excitation of vibrational modes. However, coherence is not essential as any energy redistribution could enhance enzymatic action (47). Fig. 3 shows how weak condensation can lead to a significant deviation from the simple steady-state expected when biochemical processes provide energy to an enzyme.

The majority of claims of observation of Fröhlich condensates in biological environments have indeed involved observed minor enhancements to black-body radiation levels or unexpected dependences of some process to microwave or terahertz radiation (9, 11, 14–25). In the most developed of these hypotheses, Pokorný (14) has documented enhancements of a factor of ≈5 in the radiation at 8.085 MHz in microtubules and estimated values for key parameters (14, 15) that we express using Fröhlich's notation as s/k = 100 Ks⁻¹ and φ/k = 20 Ks⁻¹ so that s/φ = 5. In Pokorný's analysis, s is derived as the maximum possible rate of energy supply whereas φ is obtained on assumptions of slip boundary conditions and ignores many relaxation processes. The observed enhancement of just a factor of 5 is consistent with a weak Fröhlich condensate, however, and from Fig. S1G in SI Appendix, we see that a value of s/φ = 0.1 is all that is required to produce the observed effect, provided that the oscillator band is sufficiently wide. Another significant issue pertaining to whether or not a Fröhlich condensate could form as envisaged is the time required for formation, given that the lifetime of microtubules is from seconds to hours (48). Because Pokorný's maximum possible energy flow rate s is ≈9 orders of magnitude less than the values used in our simulations, and as we found condensates forming on the 10- to 1,000-ns time scale, sufficient time could indeed be available.

Outside a biological environment, strong or even coherent Fröhlich condensation could occur when a high power optical or other external energy source is directly coupled to a set of oscillators, for example in a microwave reactor or through the application of high-power terahertz radiation for medical use (9, 23–26). These scenarios could easily produce the large s/φ ratios necessary for condensation, concentrating energy within specific parts of a system even in the presence of a low-temperature bath. Coherent condensates are not required, and even low condensation indices of say η ≈0.1 would have profound consequences for processes coupled to specific vibrational modes such as the rates of chemical reactions. Indeed, microwave reactors are increasingly used to control chemical reactions under mild conditions in green chemistry. In such cases significant nonthermal energy, as manifest through N^χ=0 (Eq. 3), becomes available to the system, and in favorable cases Fröhlich condensation could focus this energy into just a single vibrational mode.

Conclusions

Historically, attempts to identify Fröhlich condensation have focused on anticipated novel states of matter in which a large amount of energy is coherently channeled into a specific vibrational mode of a complex (biological) system. We show that no mechanical source of energy can produce such a condensate, and that although intense radiation could facilitate its formation, the energies required preclude its production in biological media. The most likely sources of coherent condensates are in microwave reactors and in systems exposed to intense terahertz radiation. Strong Fröhlich condensates in which there is an extreme amount of energy incoherently activating the lowest-frequency mode of the system are easier to produce and could be feasible to produce using mechanical energy sources, but still they remain unlikely in a biological environment. Coherent condensates could be detected from the intense coherent light emission that they must generate, whereas strong condensates could be identified through broadband emission at frequencies ranging from the system oscillator frequency down to at least 6 orders of magnitude lower. However, we find that experimental manifestations of Fröhlich condensation are most likely to be observed via the effects of weak condensates. Weak condensates embody the enhanced nonequilibrium energy in all of the system modes associated with the energy flow from the input source to the surroundings. Further, enhancement of small but very significant factors of the lowest-frequency mode can occur. Because chemical reaction rates vary exponentially with the energy in the lowest mode, these effects can produce dramatic changes compared with scenarios in which the input energy gets randomly distributed. Although one possible example of weak condensation has been detailed by Pokorný (14, 15), many other possibilities associated arising from the interaction of radiation with biological system also exist (9, 11, 16–25). The possible role of Fröhlich condensation in chemical kinetics remains largely unexplored, however.

Materials and Methods

The computational methods used are described in detail in SI Appendix, including numerical evaluation of the solutions to Fröhlich's model evaluated over its full parameter space and numerical evaluation of the semiclassical quantum dynamics of the Wu–Austin Hamiltonian for some paradigm examples.