Collapse transition in proteins

Abstract

The coil–globule transition, a tenet of the physics of polymers, has been identified in recent years as an important unresolved aspect of the initial stages of the folding of proteins. We describe the basics of the collapse transition, starting with homopolymers and continuing with proteins. Studies of denatured-state collapse under equilibrium are then presented. An emphasis is placed on single-molecule fluorescence experiments, which are particularly useful for measuring properties of the denatured state even under conditions of coexistence with the folded state. Attempts to understand the dynamics of collapse, both theoretically and experimentally, are then described. Only an upper limit for the rate of collapse has been obtained so far. Improvements in experimental and theoretical methodology are likely to continue to push our understanding of the importance of the denatured-state thermodynamics and dynamics for protein folding in the coming years.

1. Introduction—the denatured state of proteins and its role as the “initial condition” for folding

Proteins are heteropolymers made of twenty different monomer types. Their self-assembly into well-ordered 3-D structures has fascinated biochemists and physical chemists since the seminal experiments of Anfinsen.¹ Much progress has been made in recent years in understanding the mechanism of protein folding, both theoretically^2,3 and experimentally.^4,5 The simplest model for folding takes into account only two states, the denatured state and the folded state. Many small proteins have been shown to obey this minimal model.⁶ During the folding process a protein molecule has to overcome a free energy barrier, fleetingly populating the transition state. The energetic balance between the folded and denatured states may be tuned by varying the temperature or by changing the concentration of osmolytes or chemical denaturants in solution.⁷

It has become clear that in order to decipher folding it is essential to understand not only the folded state and the transition state ensemble, but also the “initial state” for the process, namely, the distribution of structures in the denatured state. However, while it is now possible to determine the 3-D structure of a folded protein with relative ease, using either X-ray crystallography or NMR spectroscopy, there is no simple way to determine the structure of a denatured protein. The modern science of protein folding views the denatured state as an ensemble of microstates sampled quickly by unfolded protein molecules. While the denatured state of proteins has been described for many years as being similar to a random coil-like polymer, it is now understood that unfolded protein molecules may not be entirely devoid of any internal structure. In fact, recent experiments suggest that under relatively mild denaturing conditions proteins may possess some residual structure, including transiently-formed secondary structure elements.⁸ However, as will be discussed below, the denatured state is perhaps more akin in its equilibrium and dynamic properties to a homopolymer than to a folded protein.⁹ Thus, concepts from polymer physics can be fruitfully used to describe many properties of denatured proteins. Here, we will focus on the phase transition that a denatured protein undergoes as solution conditions are changed from ‘good’ (or denaturing) to ‘poor’ (or folding-promoting). This phase transition, known in polymer science as the coil-globule (or collapse) transition, is in many cases the first step in the protein folding process. While early theoretical studies¹⁰ established an intimate link between the collapse and folding temperatures of proteins and their folding efficiency, methods for experimentally characterizing and measuring the collapse transition in denatured proteins have only appeared in recent years.

We will start our excursion into the collapse transition in the denatured state of proteins (or its inverse, the expansion transition) by discussing equilibrium properties in section 2. We will briefly review the coil-globule (CG) transition as it is manifested in homopolymers, where it has been studied for many years, and will then discuss possible ways by which homopolymer theory can be extended to heteropolymers. Measurements of the CG transition of proteins will subsequently be described and the results analyzed within a simple theoretical framework that suggests some level of universality of the process. Section 3 is devoted to the dynamics of protein collapse, starting with a theoretical analysis and continuing with a review of experimental work attempting to measure the time-dependence of collapse. A brief discussion of the connection between collapse and secondary structure formation in section 4 will be followed by some concluding words. This perspective is not intended as an extensive review of the field. Rather, we chose to focus on issues which we felt can be used to develop a well-rounded view of collapse. We therefore apologize for any omission or incomplete description of relevant studies.

2. Equilibrium

a The coil, the globule and in-between

A polymer in a good solvent (in which interactions between monomers and solvent molecules are more favorable than between monomers) adopts an expanded random coil (RC) conformation.¹¹ The ideal, volume-free RC obeys Gaussian statistics, which dictate that its end-to-end distance, as well as its radius of gyration, R_g, scales as N^1/2, where N is the number of monomers. However, a real polymer, whose chain segments cannot cross each other, behaves as a self-avoiding walk (SAW), with R_g ∝ N^ν, and ν = 3/5 in 3-D space (or more accurately 0.588¹²). The N^3/5 scaling has been shown to hold for denatured proteins. Indeed, a fit to a series of R_g values of proteins which were strongly-denatured either in guanidinium chloride (GdmCl) or urea (i.e. under ‘good’ solvent conditions), obtained by small-angle X-ray scattering (SAXS, see section 2d below), gave the relation R_g ≈ a_DN^{0.59 13} where a_D ≈ 2 Å.

The hydrodynamic radius (or Stokes radius) of a polymer, R_h, is defined as the radius of a sphere which has the same diffusion coefficient. R_h of a SAW shows, according to the Zimm theory of polymer dynamics, the same scaling with N as R_g, that is R_h ∝ N^3/5.¹⁴ However, the theory predicts that the R_h of a polymer in a good solvent is smaller than its R_g, obeying the ratio R_g/R_h ≈ 1.5. There are several methods to measure the hydrodynamic radii of proteins. Among these are size-exclusion chromatography, dynamic light scattering, fluorescence correlation spectroscopy and pulse field gradient NMR spectroscopy. Using the values of R_h for proteins at 6M GdmCl and 6 M urea,¹⁵ Uversky has found that R_h ≈ 2.3 Å∙N^0.55 in GdmCl, and R_h ≈ 2.6 Å ∙N^0.52 in urea. R_h values obtained from pulse field gradient NMR studies of proteins show a rather similar dependence on length, R_h ≈ 2.2 Å ∙N^0.57.¹⁶ It is not clear why the above-mentioned theoretical relation between R_g and R_h (R_g/R_h ≈ 1.5) is not obeyed. A recent study of protein L using single-molecule fluorescence methods¹⁷ yielded values for both R_g and R_h in the fully denatured state (see sections 2d and e), and the ratio between them was found to be smaller than 1.2, also less than the expected theoretical value for a SAW.

In a poor solvent (monomer-monomer interactions are more favorable than these between monomers and the solvent) a polymer collapses to a compact globular structure, with R_h ∝ N^1/3. A simple geometric calculation shows that for a spherical globule = $R_{\mathrm{g}}/R_{\mathrm{h}}=\sqrt{3/5}$. This relation was shown to hold in the case of collapsed homopolymers (see e.g. ref. ¹⁸). For proteins it is usually maintained when one compares R_g to R_h calculated from crystal structures using a program such as Hydropro.¹⁹ However, diffusion measurements of globular proteins show that their hydrodynamic radii are typically larger than calculated, leading to a ratio R_g/R_h that is smaller than the theoretical prediction.²⁰ This result is attributed to the role of the solvation shell (a layer of weakly-bound water molecules) which exists around folded proteins. It is possible that solvating water molecules increase the effective R_h of unfolded proteins as well, which might explain the lower-than-expected experimental value of R_g/R_h. Note however that, as the Zimm theory of polymer dynamics shows, hydrodynamic interactions between polymer segments already induce a coordinated diffusion of the polymer and the water entrapped between its segments (this is the so-called non-draining regime²¹). Thus the solvation water molecules are already included in the calculation of the hydrodynamic properties of polymers or denatured proteins based on the Zimm theory.

The coil and globule regimes discussed above are the two end points of the collapse transition. Obviously, it is of high interest to have a theory that spans these two regimes and correctly predicts the thermodynamics of protein collapse. The following sections discuss the theory of the CG transition in polymers and show how it can be applied to analyze experimental data on the equilibrium collapse of denatured proteins.

b Homopolymer collapse

The CG transition of a polymer chain is driven by the balance of two factors, the net attractive (or repulsive) interaction between monomers and the chain’s conformational entropy.¹⁴ As the quality of solvent is tuned from ‘good’ to ‘poor’, e.g. by reducing the temperature, the free energy of interaction between the monomers becomes more attractive relative to the interaction energy of monomers with the solvent molecules. As a result, the monomers segregate from the solvent, causing an overall contraction of the polymer. However, chain contraction leads to a loss of conformational entropy, as the conformational space available to the polymer becomes more restricted. The balance between net monomer–monomer interaction and chain entropy determines the expansion of the polymer, whose size can be parameterized by α² = R_g²/R_g,0 ² with R_g,0 being the dimension of the ideal chain. This simple description of the process is at the heart of theories for the CG transition. Starting with Flory,²² many theoretical treatments employed the chain dimension as the order parameter for the process^14,23 (for a discussion of other approaches see ref. 24).

The free energy of interaction can be written as an expansion in a power series of the number density of monomers, n = N/V, where V is the volume of a polymer molecule:

$$F_{\text{int}}=nVT(nB+n^{2}C+\dots ).$$ (1)

Here T is the temperature, and B and C are virial coefficients. The second virial coefficient, B, is given by

$$B(T)={\displaystyle \int \{1-\text{exp[}-u(r)/T]\}}{\mathrm{d}}^{3}r,$$ (2)

where u(r) is the microscopic interaction energy. The Flory elastic (or conformational) entropy is

$$F_{\text{el}}(\alpha )/T=3/2{\alpha }^2-2\text{ln}\alpha .$$ (3)

Minimizing the sum of F_int and F_el with respect to α leads to the famous Flory result

$${\alpha }^5-{\alpha }^3=const·N^{1/2}B.$$ (4)

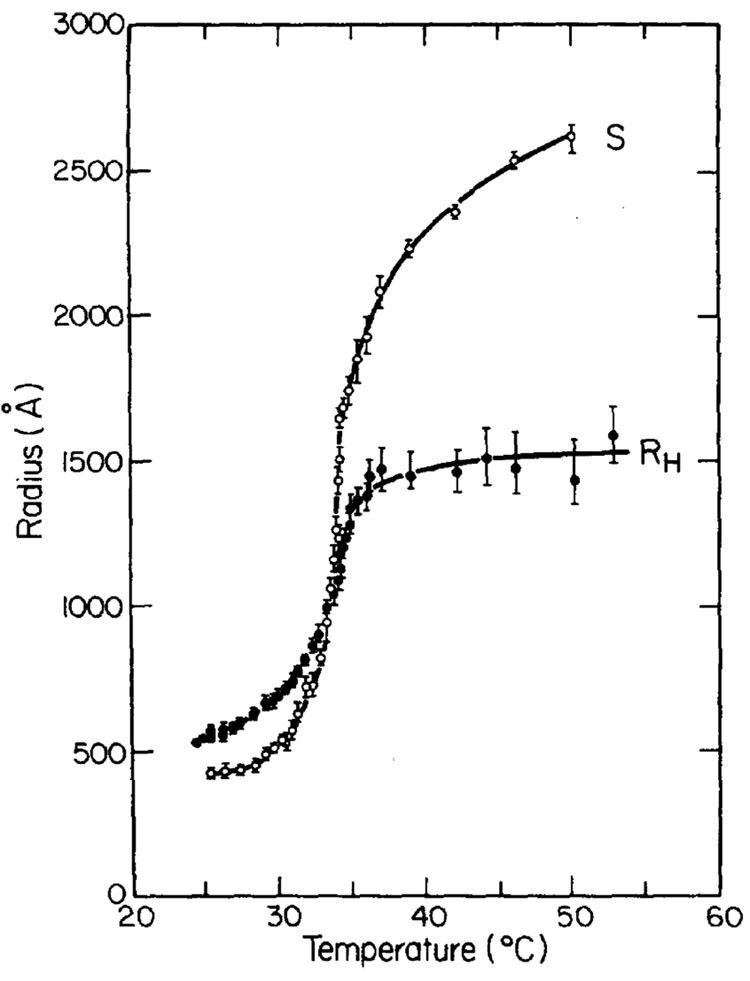
This equation does not reproduce well experimental results, but it can be ameliorated by more elaborate treatments of the statistics of the polymer. Such an extension of the Flory approach, due to Sanchez,²⁵ was used by Tanaka and coworkers to fit the results of their pioneering observation of the CG transition in polystyrene chains¹⁸ (Fig. 1). We will get back to the Sanchez theory below.

Fig. 1.

Temperature dependence of the radius of gyration (here labeled S), and the hydrodynamic radius, R_H, of a homopolymer (polystyrene, Mw = 2.6 × 10⁷). Reused with permission from ref. 18.Copyright 1980, American Institute of Physics.

At the temperature in which the second virial coefficient B equals zero (traditionally called the θ point), α equals 1—the chain has the dimensions of the ideal polymer chain. It can be shown¹⁴ that in the vicinity of the θ point there is a thermodynamic phase transition between coil and globule, which is second order in flexible polymers, and can be first order in stiff polymers.²⁶

c Protein collapse—what’s the difference?

Since proteins are evolved heteropolymers, there are additional factors that need to be taken into account when describing their collapse transition. While it is in principle necessary to deal with all twenty amino acids and their interactions, it suffices for the sake of the current discussion to group them in two groups-hydrophobic and hydrophilic. The folding transition is at least partially driven by the need to bury hydrophobic amino acids within the interior of the protein. It is likely that the collapse transition in a poor solvent is driven by a similar requirement, which imposes specific structural constraints on the collapsed state. The term ‘hydrophobic collapse’ has been used extensively to describe the burial of hydrophobic amino-acid side chains as the driving force for folding. Here we will reserve this term to the coil-globule transition driven by hydrophobic interactions. How can the theory of homopolymer coil-globule transition be modified to take into account the hydrophobic collapse in heteropolymers?

Dill and coworkers²⁷ approached this problem within the framework of their effort to develop a theory for protein folding.²⁸ They built the properties of the protein into the mean-field monomer–monomer interaction energy appearing in theories such as Flory’s and Sanchez’s.²⁵ An expression was written for the interaction energy in terms of the free energies of transfer of hydrophobic amino acids from water into denaturant solutions, as originally measured by Nozaki and Tanford.^29,30 The distribution of amino acids between the surface of the protein and its core was explicitly taken into account. This rather simple approach was good enough to obtain satisfactory correlations between calculated and experimental values of the free energy change with denaturant concentration.

Several studies used random heteropolymer models to describe the phase diagram of proteins, including the collapsed state. Pande et al.³¹ applied a random energy model to show that in some cases the transition to the frozen (folded) state may be coupled to the collapse transition, making it first-order, in contrast to the second-order collapse transition usually associated with homopolymers. Camacho and Thirumalai were among the first to propose a correlation between the collapse and folding temperatures,¹⁰ based on lattice simulations and scaling arguments. The consequence of this finding is that optimal folding occurs near a tricritical point that naturally explains the marginal stability of folded proteins.³²

A drastically different view of hydrophobicity-driven collapse was promoted in recent work by Chandler and coworkers.^33,34 They propose that the hydrophobic collapse is driven by evaporation of water molecules from the vicinity of hydrophobic groups, with the formation of a vapor bubble around the developing core being the rate-limiting step for the process, and making it a first-order transition. Casting aside the relevance of the drying transition in amphiphilic sequences, experimental work described in the coming section suggests that the collapse in denatured proteins is a second-order transition, rather than a first-order one.

d Experimental observation of protein collapse

A major problem in studying the equilibrium collapse of a denatured protein is that this transition may overlap with the folding transition. In other words, there is a range of parameters (temperature or denaturant concentration, [C]) in which the folded state coexists with the denatured state, and it is therefore difficult to directly measure the size of the denatured protein. For that reason, equilibrium studies of collapse using standard ensemble method (to be described below) are limited to the parameter range in which the fraction of folded protein is very low. Single-molecule experiments are particularly useful here, since they usually allow the separation of the folded and denatured states, thus enabling the study of the collapse transition over a much broader range of parameters. While some types of experiments may provide indirect indications for conformational changes in the denatured state (such as changes in the fluorescence of intrinsic fluorophores), we focus here on experiments that directly provide structural information on the collapse transition.

Small-angle X-ray and neutron scattering methods are classical techniques for studying the size of proteins. SAXS³⁵ has been used more frequently than the related small-angle neutron scattering.³⁷ Typically, the size of scattering objects (molecules) is extracted from scattered intensity at very small angles, using the so-called Guinier plot. Scattering at slightly larger angles provides the pair distribution function, which measures the distribution of pair-wise distances within the protein,³⁵ and therefore contains information about its shape. Small-angle scattering experiments are performed at rather high protein concentrations, and therefore usually require some verification that concentration effects do not distort the results. However, these methods provide a route for an accurate determination of protein size parameters over a broad range of conditions.

Regan and coworkers used SAXS to study the GdmCl denaturation of surface mutants of the B1 domain of streptococcal Protein G,³⁷ over a rather small range of [C] (up to 2.5 M). They found evidence for a collapse transition in the denatured state of one of the mutants, but a second mutant did not show collapse. No collapse was detected in a study of protein L by Baker and coworkers.³⁸ These authors studied both the equilibrium size-dependence of protein L on GdmCl as well as the kinetics of folding. The inability to detect denatured-state dimension changes in the equilibrium experiment is surprising in view of two recent single-molecule fluorescence experiments on protein L (to be discussed again below), that show a very clear collapse transition of the protein.^17,39 It is possible that this result is due to the rather low contrast for X-ray scattering in high-concentration GdmCl solutions. Sosnick and coworkers also obtained a ‘negative’ result when looking for GdmCl- or temperature-driven expansion in fully reduced ribonuclease A, finding that the radius of gyration of the protein remained essentially constant over the whole range of conditions studied.⁴⁰ The reduction of disulfide bonds of this protein rendered it denatured, which facilitated the study. However, the experiments were conducted at pH 2.5, where the protein carries a net charge of +18, and it is possible that in this state the protein is fully expanded due to electrostatic repulsion. A recent SAXS study of dihydrofolate reductase⁴¹ showed clear evidence for collapse in equilibrium measurements of the protein’s size. Observations of collapse by time-resolved SAXS will be discussed in section 3b.

Fluorescence resonance energy transfer (FRET) spectroscopy has emerged as a very powerful tool for studying the coil-globule transition in denatured proteins. FRET spectroscopy makes use of the sensitivity of the energy transfer efficiency to the distance between two fluorescent probes in order to extract information about intramolecular distances, their distribution and dynamics.^42,43 It was shown many years ago that distance distributions can be extracted from time-resolved FRET experiments.⁴⁴ This method has been used extensively to study protein folding.⁴⁵ Udgaonkar and coworkers⁴⁶ utilized time-resolved FRET to obtain distance distributions between two labeled sites on the protein barstar under a range of conditions, and found bimodal distributions, the two peaks of which could be attributed to native-like and unfolded-like forms of the protein. In both forms the mean distance between the probes changed continuously with the concentration of denaturant (either urea or GdmCl).

Single-molecule FRET (smFRET) experiments offer the possibility of obtaining histograms of FRET efficiencies and separating the populations of different states directly. In particular, changes in the dimensions of the denatured state of proteins under conditions that favor the native state can be directly monitored. Thus, smFRET is uniquely poised to follow the CG transition. In smFRET experiments, proteins are labeled with two fluorescent probes, donor and acceptor. They can then be measured in dilute solution as they diffuse through a focused laser beam. Alternatively, they can be immobilized near a surface, so as to allow an extended observation time on each molecule. For more details on smFRET experiments in relation to folding see recent reviews. ^43,47 In the free-diffusion experiment, a passage of a protein molecule through the laser beam leads to a burst of emitted photons detected in two channels, one for the donor and one for the acceptor. FRET efficiency is calculated for each of these bursts and a histogram of the frequency of occurrence of FRET efficiency values is constructed. In the case of two-state proteins, only two peaks appear in such a histogram. One of these peaks is attributed to the folded molecules, and usually does not shift (or only barely shifts) when the experimental conditions (typically [C]) are changed. The other peak is due to the denatured state ensemble, and changes in its position with [C] can be attributed to the CG transition.

Eaton and coworkers⁴⁸ reported the first observation of the equilibrium collapse of a protein in the denatured state based on smFRET experiments. Studying a double-labeled mutant of the cold shock protein from Thermotoga maritima, they noted a shift in the position of the denatured state peak in smFRET histograms to higher values of FRET efficiency as the [C] was lowered, indicating a gradual collapse of the unfolded chain. Several additional observations of the equilibrium collapse transition in denatured proteins by smFRET have been subsequently published,^{17,39,49–54} and these are listed in Table 1. In the next section we discuss the analysis of these data using the theory of the CG transition. We note that Nienhaus and co-workers have analyzed their results on ribonuclease H using a more specialized model in which the denatured state is described by a continuum of substates.⁵⁰

Table 1.

Denaturant-induced collapse observed by smFRET experiments

Protein	Na	Labeling positionsb	Rg,0Mc/Å	Rg,Dc/Å	Reference
ACBP	86	17, 86	—	—	49
Barstar	90	12, 89	18.2	31.6	83
CI2	64	1, 53	—	—	49
CspTm	67	2, 67	22.5	32.4	39, 48, 53
CspTm	66	1, 66	20.4	30.2	36
Im9	86	23, 81	22.8	36.9	51
Protein L	64	1, 64	17.1	28.9	17, 39
Protein L	65	1, 65	19.8	30.3	36
Protein A	60	10, 59	—	—	54
RNaseH	155	3, 135	24.8	50.4	50
SUP35	253d	21, 121	—	—	52

^aNumber of residues.

^bAs reported in original references.

^cThe radii of gyration of the unfolded proteins under native conditions (R_g,0M), and in highly denaturing conditions (R_g,D, calculated for 6 M GdmCl or 8 M urea) were calculated for some of the proteins in the table. The calculation was based on the modified Sanchez theory (see eqn (6) and following text), and extrapolation of ε values extracted from experimental data, as in Fig. 3.

^dThe first 123 amino acids form an unstructured region.

e Analysis using theory and general properties

In order to gain some further understanding of the CG transition, we recently employed a modification of the mean-field theory of Sanchez²⁵ to analyze smFRET data on protein L.¹⁷ The Sanchez theory yields a generalization of eqn (4) which reproduces better the form of experimental results,¹⁸ especially below the θ point. It was found that the expansion of the denatured protein L spanned the whole range of [C] studied, from 1 M GdmCl up to 7 M GdmCl. Using the Sanchez theory, the mean net interaction energy per monomer (a value related to the second virial coefficient of eqn (2)) was calculated from each R_g value, and was found to be attractive over the whole range of [C]. Naturally, as [C] decreased this net interaction energy increased, driving the collapse of the denatured protein.

Here we generalize the approach used in reference¹⁷ to study the CG transition in several of the proteins for which published smFRET data are available (Table 1). FRET efficiency values, measured in single-molecule experiments performed over a range of [C], should first be converted into distance values. The denatured-state FRET efficiency distribution does not directly provide the distribution of the end-to-end distance. Recent experiments^55,56,80 suggest that the end-to-end distance dynamics for a denatured protein of the size of protein L are on the microsecond, or even nanosecond time scale, while the smFRET data is averaged over millisecond fluorescence bursts. It is therefore reasonable to take the mean FRET efficiency of the denatured-state distribution as an average over the end-to-end distance distribution, P(R_ee), of the protein:

$$\langle E\rangle ={\displaystyle \int P}(R_{\text{ee}})/(1+R_{\text{ee}}^6)/R_0^6)\mathrm{d}{R}_{\text{ee}}$$ (5)

Here R₀ is the Förster radius for energy transfer. Instead of using idealized distribution functions (such as a Gaussian function), it is advantageous to derive an expression for P(R_ee) that directly related to the expansion process.

The Sanchez theory²⁵ describes the continuous expansion of P(R_g), the probability distribution function of R_g, by the following expression

$$P(R_{\mathrm{g}})=P_0(R_{\mathrm{g}})\text{exp}(-N·q(\varphi ,\epsilon )/k_{\mathrm{B}}T).$$ (6)

Here P₀(R_g) is the Flory–Fisk empirical distribution for the radius of gyration of an ideal chain,⁵⁷ which is weighted by the expansion free energy per monomer:

$$q(\varphi ,\epsilon )=-\frac{1}{2}\varphi \epsilon +k_{\mathrm{B}}T\frac{1-\varphi }{\varphi }\text{ln}(1-\varphi )$$ (7)

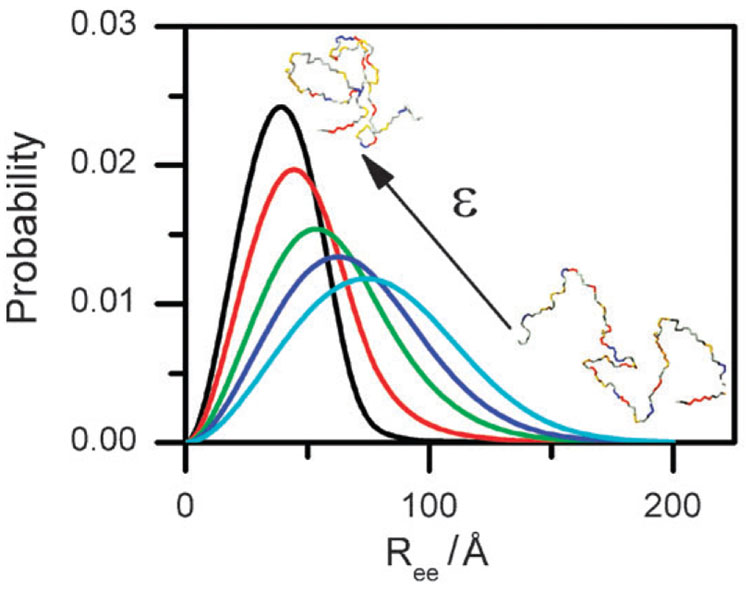
In this expression φ is the volume fraction of the chain (we write φ ≡ R_g,N ³/R_g ³ where _Rg,N is the radius of gyration of the fully-compact native state), and ε is the mean-field interaction energy of a monomer within the maximally-collapsed chain, which depends on [C]. The first term in eqn (6) shows that monomer–monomer attraction (ε > 0) favors compaction of the chain, while the second term is the entropy arising from excluded volume interactions. Using a physically-motivated approximation, P(R_g) can be mapped into P(R_ee). Fig. 2 shows how P(R_ee) depends on the value of ε, hence on [C]. At low values of ε the chain is expanded and the distribution is very broad. As ε increases, the chain contracts and the distribution becomes much narrower. The expression for P(R_ee) can be used to match experimental FRET efficiencies using eqn (5), a procedure leading to a value of ε for each experimental point (Ziv and Haran, submitted).

Fig. 2.

The end-to-end distribution P (R_ee) for different values of the interaction energy ε, calculated as described in text following eqn (6) for a protein of 64 amino acids. Arrow indicates direction of growth of ε. As ε increases, the average distance shortens and the distribution becomes narrower. Sample chain configurations at low ε and high ε are shown as insets. P (R_ee) can be used to calculate average FRET efficiency as a function of ε using eqn (5).

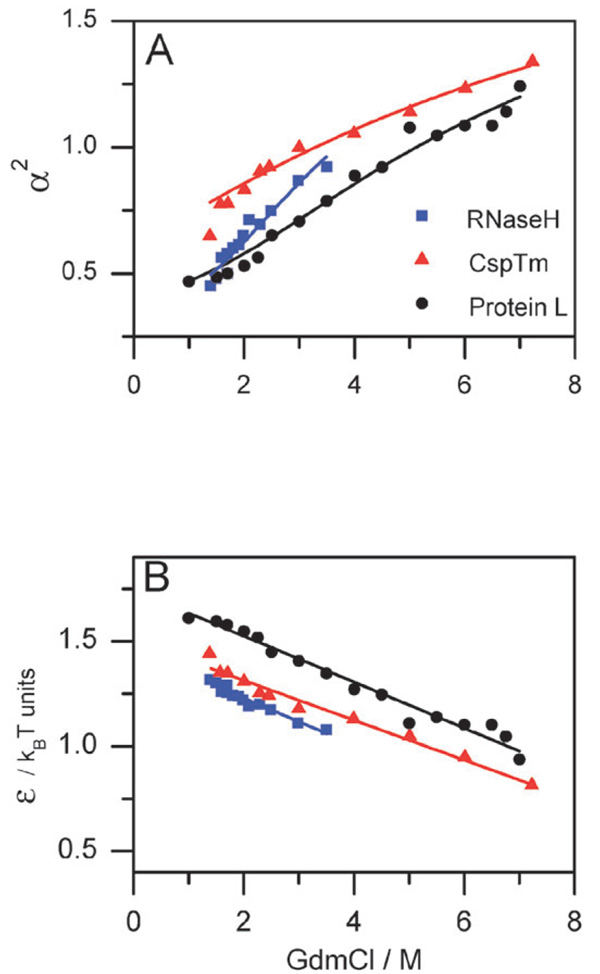
From Fig. 3A, which shows the expansion factor α² = R_g ²/R_g,0² calculated for 3 different proteins, we see that there is a continuous expansion of the denatured state over the whole range of denaturant concentrations. Furthermore, some proteins (e.g. CspTm and protein L) span across the CG transition point (defined as the point where α² = 1), which necessitates the use of Sanchez theory as most other models do not traverse smoothly the two regimes, expanded and collapsed. An extrapolation of the size of these denatured proteins to 0 M denaturant shows that the denatured-state size under these conditions is only ~30% larger than that of the folded state. Fig. 3B shows ε, the mean-field interaction energy for the same proteins of Fig. 3A. The interaction energy is positive (i.e. attractive) at all denaturant values, and decreases linearly for high [C]. Interestingly, the slopes of ε of different proteins seem to be similar, suggesting a universal behavior.

Fig. 3.

Analysis of the CG transition in 3 different proteins using the modified Sanchez theory described in the text. FRET efficiency values measured in single-molecule experiments were matched to calculated values obtained from eqn (5) by varying the interaction energy ε. These values were subsequently used (with eqn (6) and eqn (7)) to calculate other average quantities. (A) The expansion factor, α² = R_g ²/R_g,0², as a function of denaturant concentration. (B) The interaction energy ε as a function of denaturant concentration. Symbols are calculated from experimental points (see references to original papers in Table 1). A linear fit of ε, shown in (B), is used to calculate the solid lines in (A), indicating that a linear model captures the essential features of the collapse process.

The modified Sanchez theory can also be used to calculate the free energy difference for collapse (Ziv and Haran, submitted), as well as other therymodynamic functions, from experimental data. This kind of calculation opens the way to a comparison of the energetics of the collapse and folding transitions.

An important observation in all smFRET experiments is that the shift of the denatured-state distribution as [C] is lowered is continuous, implying a similarly continuous collapse of the denatured protein. This stands in contrast to the folding transition of the protein, which involves coexistence of two populations, folded and denatured. This observation strongly suggests that the expansion/collapse transition is second-order in nature, as is usually observed for the CG transition of flexible polymers.¹⁴

3. Collapse dynamics

a Theoretical considerations

As discussed in the previous section, at sufficiently high temperatures or equivalent high denaturant concentrations ([C]) a polypeptide chain behaves as a SAW, while at low temperatures or [C] proteins are compact. Using ideas from polymer theory we can anticipate general scenarios for this CG transition. The expansion at high values of [C] occurs because such environment is a good solvent whereas in the absence of denaturants water is a poor solvent. For a homopolymer the CG transition occurs at [C] = C_θ, below which the polymer is a compact globule.⁵⁸

The kinetics of globule formation in homopolymers can be described by imagining a concentration quench from [C] > C_θ to [C] = C_Q < C_θ. In this case, the transition from a SAW to a compact globule is thought to occur in two distinct stages. In the initial stage, locally compact conformations form on a length scale ξ/a ≈ [C_θ–C_Q]/C_θ, resulting in pearl-necklace like structures with the size of each pearl being on the order of ξ (a being the size of a monomer). At longer times, the pearls coalesce by incorporating additional monomers, leading to a globule with dimensions R_g ∝ N^1/3. The two-stage globule formation, proposed originally by de Gennes,⁵⁹ has been extended by others and observed in several computer simulations. The dependence of the time scales of the two stages on N has also been obtained theoretically and by scaling-type arguments.^60,61 It should be emphasized that these considerations hold well only for N »1, and due to large-scale fluctuations the behavior for finite N can be different.

The native structure of proteins is unique and compact, which implies that among the exponentially large number of compact structures⁶² the one with the lowest free energy is preferred due to specific favorable intramolecular interactions. As a result at [C] ~ C_f (where C_f, the folding concentration, is typically <C_θ) transition to native state occurs. In contrast to globule formation in homopolymers, one can anticipate different scenarios for compact structure formation in proteins depending on σ = (C_θ − C_f)/C_θ. If σ is small then the collapse, which occurs on a time scale τ_c, is specific in the sense that the ensemble of collapsed structures does not contain a large number of non-native contacts.⁶³ As a consequence, the rearrangement of such structures to the native conformation occurs relatively fast. In this scenario 1 < τ_f/τ_c < 10, where τ_f is the folding time. In contrast, if σ is not too small then a spectrum of collapsed structures can form. A fraction χ of the ensemble of compact structures contains only a small fraction of non-native contacts, while the remaining (1 − χ) have a large number of non-native contacts. From a kinetic perspective, the probability of observing specific collapse is χ. Molecules behaving in this manner traverse the complex energy landscape in a manner that is similar to the sequences with small σ (‘fast track’). The fraction (1 – χ) of molecules form compact structures on time scale τ_c with a large number of incorrect contacts which anneal to form the native structure with a time constant τ_s. Both simulations (see below) and experiments show that τ_s/τ_c > 100 (‘slow track’). The fraction χ increases continuously with decreasing σ.

The physical picture that proteins can undergo specific or non-specific collapse depending on σ, can be illustrated using lattice models. In the simplest lattice model each residue is represented as a site, confined to the vertices of a three dimensional cubic lattice. We constructed the native structure as maximally compact, occupying a volume (4 × 4 × 3)a³ where a is the lattice spacing. The energy of a configuration is taken to be

$$H={\displaystyle \sum _{i<j}{\epsilon }_{ij}{\delta }_{r_{ij,a}}}$$ (8)

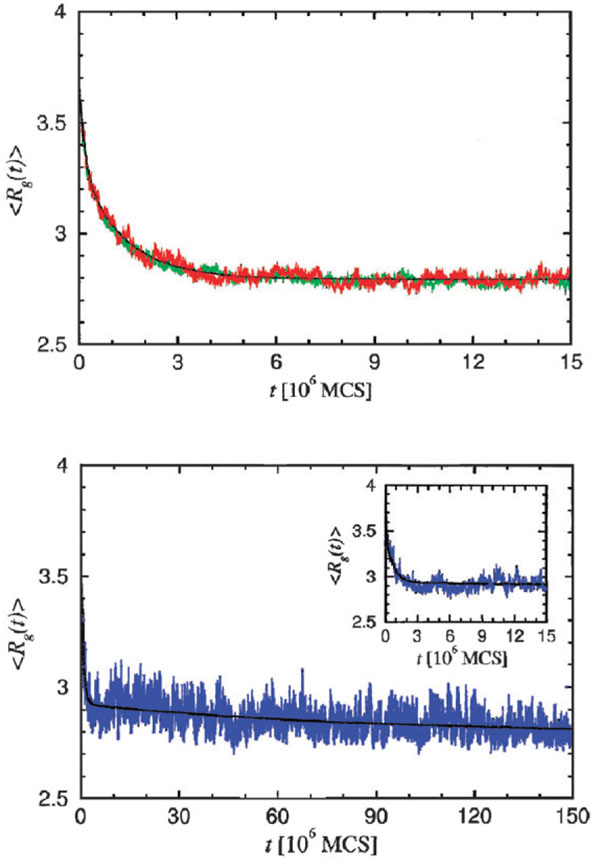
where r_ij = |r_i − r_j| is the distance between two residues i and j, ε_ij is the residue specific interaction energy and δ _x,a is the Kronecker delta function. The values of the residue-dependent interaction energies ε_ij were taken from the Miyazawa–Jernigan statistical potentials.⁶⁴ Using the energy function in eqn (8) we performed a Monte Carlo simulation for two sequences, each with identical maximally compact structure for the native state, but having different values for σ (small for sequence A and large for sequence B). The kinetics of collapse for fast track molecules (all sequence A and some of sequence B molecules) exhibits two distinct stages (Fig. 4A). In the earliest stage, following a temperature quench, considerable compaction occurs with the formation of structures with substantial non-native contacts. On the collapse time scale τ_c most of these are annealed after which folding occurs rapidly. For the fast track molecules, the folding time τ_f ~ (3–5) τ_c.

Fig. 4.

Lattice simulation of the collapse kinetics for two sequences with two different values of σ = (T_θ − T_f)/T_θ, that of sequence A being smaller than that of sequence B. Folding is initiated by quenching the temperature from T_θ to T_Q<T_f. The values of T_Q are adjusted so that the native states of A and B have the same stability. (A) Dependence of the radius of gyration, R_g(t), as a function of time for sequence A (green line) that undergoes specific collapse prior to reaching the native state. Time is measured in terms of Monte Carlo Steps (MCS). Red line shows R_g(t) for fast track molecules for sequence B, and the black line is a multi-exponential fit. The structures sampled by the denatured-state ensemble prior to reaching the native state for sequences A and B are similar. (B) R_g(t) as a function of t for the slow track molecules that pause in an ensemble of compact metastable structures. This curve is for sequence B. The transition to the metastable minima from the unfolded state occurs rapidly (inset). Note that the timescales in (A) and (B) are different.

Some sequence B molecules fold by the slow track (Fig. 4B), and for these R_g also decreases in multiple stages. The major initial compaction occurs in the first stage (Fig. 4B inset). However, subsequent compaction takes considerably longer. As a result the folding time for the slow track molecules is nearly two orders of magnitude larger than for those which fold by the fast track.

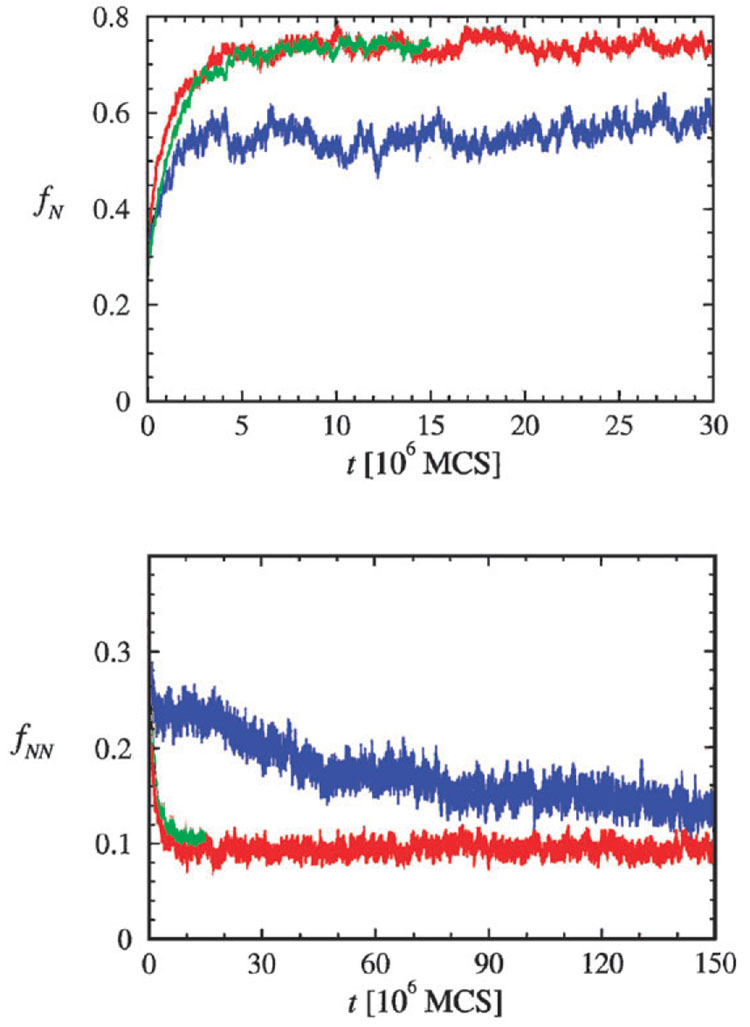
The dramatically different time scales on which collapse occurs for slow- and fast-track molecules are also observed in the kinetics of acquisition of native contacts and loss of nonnative contacts (Fig. 5A and B, respectively). For the fast track molecules the fraction of native contacts f_N reaches 〈f_N〉, its the equilibrium value, on a time scale τ_c. In contrast, for slow track molecules f_N(t ~ 7τ_c) ≠ 〈f_N〉 which implies that there are considerable non-native contacts that take a long time to anneal. These conformations are also evident in the time dependent decrease in the fraction of non-native contacts f_NN(t) (Fig. 5B). For the fast track molecules f_NN(t) reaches its equilibrium value on the time scale τ_c. In contrast, f_NN(_t) has not fully decayed to its small equilibrium value even when t ~ 50 τ_c for the slow track molecules. These results show that if a sequence is well-designed (small σ) or a molecule folds along the fast track, collapse is specific in the sense that on time scale τ_c compact structures with very few non-native structures are populated. For molecules that fold along the slow track collapse is non-specific and reaches structures with substantial number of non-native contacts. The predicted diversity in the nature of collapsed structures can be probed by using smFRET on proteins such as adenylate kinase whose energy landscape is sufficiently rugged so that its folding can be described by the kinetic partitioning mechanism.

Fig. 5.

Time-dependent acquisition of the native state. (A) The fraction of native contacts, f_N(t), for sequences A and B. Just as for R_g(t) the changes in f_N(t) for sequence A (green) and the fast track molecules in sequence B (red) are identical. The blue line shows f_N(t) for the slow track molecules of sequence B. (B) Fraction of non-native contacts f_NN(t) for sequence A (green), fast track molecules of sequence B (red), and slow track molecules of sequence B (blue). On a rapid time scale (~5 × 10⁶ MCS) f_NN(t) in the red and green curves reach the equilibrium values while f_NN(t) in blue curve has not decayed to the equilibrium value. Note that time scales in (A) and (B) are different.

b. Experimental observation of time-resolved collapse

Since it is expected that the collapse transition will precede folding,¹⁰ there have been many experimental attempts to measure the collapse time in proteins by rapidly changing the solution conditions from high value of [C] to concentrations that favor the native state. Many of these experiments detect the changes of a local probe, such as tryptophan fluorescence, which only indirectly reports on the overall change in the size of the protein (see e.g. ref. ⁶⁵). Thus, while such experiments may provide an estimate for the time-scale of collapse, they cannot provide information about the magnitude of the structural change involved. Therefore, experiments that reflect the changes in R_g as a function of time are needed to monitor the collapse of proteins. A number of time-resolved SAXS experiments have appeared in the last decade, providing some interesting glimpses of proteins as they collapse from an extended conformation to a compact, pre-folding conformation. ^{38,41,66–72} In such experiments, the protein is initially prepared in a high-concentration denaturant solution and quickly mixed into a low-concentration denaturant solution. Earlier experiments relied on standard stopped-flow apparatuses to obtain a time resolution of a few milliseconds. Later measurements used various continuous-flow instruments with a time-resolution down to a few microseconds. The results of many of these experiments are summarized in Table 2. Perhaps not surprisingly, the collapse seems to occur within the dead-time of even the fastest of these experiments, so that only an upper limit for the τ_c is obtained.

Table 2 .

Observation of collapse in time-resolved SAXS experiments

Protein	Estimate of collapse time	Rg valuesa	Reference
Protein L	No collapse prior to folding	—	38
Cytochrome c	<100–500 µs	30 Å (D), 18.1 Å (C), 13.9 Å (F)	66
Cytochrome c	<160 µs	24.3 Å (D), 21 Å (C), 15.6 A Å (F)	67
Bovine β-lactoglobulin	~2 µs	—	68
Myoglobin	<300 µs	29.7 Å (D), 23.7 Å (C), 18.2 Å (F)	69
Ubiquitin, common-type acylphosphatase	No collapse prior to folding	—	70
Monellin	<300 µs	25.5 Å (D), 18.2 Å (C), 15.8 Å (F)	71
Ribonuclease	<22 µs	25.6 Å (D), 20 Å (C), 15.6 Å (F)	72
Dihydrofolate reductase	<300 µs	30.7 Å (D), 23.2 Å (C), 16.6 Å (F)	41

^aValues given are for the denatured state (D), collapsed state (C), and folded state (F).

An upper limit for τ_c was also obtained in time-resolved FRET experiments, in which the change in the FRET efficiency of a protein labeled with a donor and an acceptor at particular sites was monitored as a function of time after a fast mixing step.^73–78 For example, Hamadani and Weiss⁷⁸ reported a time-resolved single-molecule FRET experiment, using a hydrodynamic focusing mixer. They found that for the small Chymotrypsin Inhibitor 2 (CI2) protein the collapse occurs within the 19 ms dead-time of their mixing device.

Two recent FRET experiments attempted to measure the time-scale of the collapse transition with a significantly better time-resolution. Munoz and coworkers performed a temperature jump experiment on a small acid-denatured protein, BBL.⁷⁹ They measured the change in FRET efficiency following a temperature jump of up to 12 °C, and found that the initial relaxation occurs with a time constant of 60 ns, which they attributed to hydrophobic collapse. The overall change in FRET efficiency, though, was just a few percent, so the observed relaxation time can only be taken as a lower limit to the time of the coil-globule phase transition, which involves a much larger change in size. Schuler and coworkers recently measured equilibrium fluctuations of FRET efficiency in the denatured cold shock protein.⁸⁰ The time scale of these fluctuations, which can be extracted by correlation analysis of the data, is related to the reconfiguration time of the protein chain. This time, a few tens of nanoseconds (depending on the concentration of denaturant in the experiment) also provides only a lower limit to τ_c, since the latter is a large out-of-equilibrium change in protein dimensions.

To conclude, both SAXS and FRET experiments indicate that a structural collapse does occur in many proteins, preceding the folding transition. In fact, this conclusion is also supported by experiments which do not directly probe global structural changes (see e.g. ref. ⁶⁵). However, the actual collapse time still remains elusive; current experiments give either an upper limit (of a few tens to a few hundred microseconds) or a lower limit (of a few tens of nanoseconds) to this time.

6. Collapse and secondary structure formation

Experiments and simulations show that the collapse transition leads to an ensemble of compact structures whose average size is only slightly larger than the native state. The question then arises as to whether this state already contains elements of secondary structure, or is devoid of any structure. This issue certainly has relevance to the folding transition, which follows the collapse, since the formation of secondary structure in the collapsed state may simplify the search for the folded state. Both off-lattice and lattice simulations show that considerable secondary and tertiary structures form during collapse (as already alluded to in the previous section). An interesting view on this problem was provided by Doniach et al.,⁸¹ who developed a homopolymer lattice model that includes a curvature energy which represents chain stiffness, thus mimicking the formation of secondary structure. As the temperature is lowered, the chain in this model collapses first into a liquid globule which possesses a substantial amount of secondary structure, then freezes into the folded state. Interestingly, the collapse transition temperature in the model does not depend on the curvature energy, suggesting that the CG transition is not driven by secondary structure formation.

However, the freezing (or folding) temperature increases with curvature energy, so that above a certain point freezing may occur directly from the swollen coil.

Experimentally, the concomitance of collapse and secondary structure formation can be kinetically explored using fast mixing devices. For example, Takahashi and coworkers⁶⁹ showed that apomyoglobin collapses within the 300 µs dead-time of their mixing device following a pH jump, with its R_g decreasing from 29.7 Å in the denatured state to 23.7 Å. At that time, 30% of the helical content of the protein already exists, as judged by a CD measurement. A similar contraction within the dead-time of the experiment was also seen in monellin,⁷¹ although in this β-sheet protein no secondary structure was observed in the collapsed state. Hoffmann et al. used synchrotron radiation CD measurements and a rapid mixer to probe the fast kinetics of collapse of CspTm, and showed that ~20% of the β-sheet secondary structure of this protein was formed in the collapsed state.⁵³

7. Conclusion and future prospects

We have described the collapse transition as it occurs in the denatured state of proteins. We showed that it is similar to the CG transition of homopolymers, and can be described with tools adapted from polymer theory. The concept of the collapse transition was shown to be relevant both to equilibrium experiments and time-resolved experiments, and the connection between the two was delineated. The collapse transition remains to be shown in larger proteins, where the folding process might be more complicated and can involve thermodynamically-stable intermediate states and kinetic partitioning.

Another interesting issue, which remains to be studied, is the effect of temperature on the collapse transition. Experimentally, thermal denaturation experiments are far more challenging the chemical denaturation, mainly due to aggregation of heat-denatured proteins. It is important to compare the denatured state characteristics at equal footing, i.e. at the same free-energy difference between folded and unfolded states. There is some preliminary indication in the literature, based on lattice-model simulations, that the thermally-denatured state is more compact than the chemically-denatured state.⁸² However, accurate experiments that can separate the contribution of the denatured state from that of the folded state and measure its size as a function of temperature remain to be conducted. The CG transition theory discussed in this perspective can readily treat temperature effects. It is likely that ε, the mean-field interaction energy of a monomer, will change in a non-monotonic fashion, due to the complex temperature dependence of the hydrophobic effect.

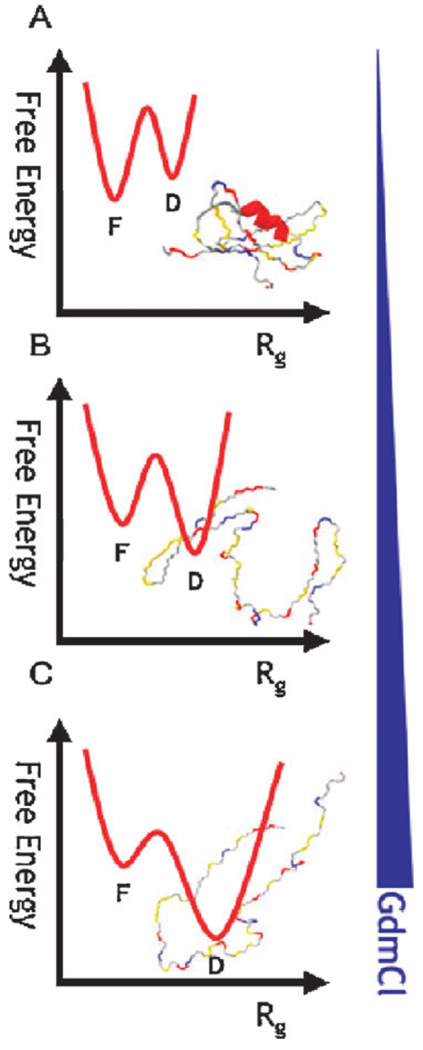
It is important to relate the collapse in the denatured state to the standard ‘two-state’ picture of folding in small proteins. Isn’t the gradual change in the properties of the denatured state with denaturant concentration in contrast to the twostate picture? Fig. 6 suggests how the two pictures might be reconciled. At each set of solution conditions a protein populates only two states, folded or denatured. However, the denatured state ensemble depends on the concentration of denaturant. As this concentration is lowered, denatured molecules collapse, but under the new conditions still only two states exist.

Fig. 6.

A unified view of two-state folding with denatured-state collapse/expansion. (A) under native conditions, the denatured state is fully collapsed (and potentially contains some residual secondary structure) and its free energy is higher than that of the folded state. (B) As denaturant concentration is increased, the denatured state expands and its Rg becomes larger, while its free energy becomes lower relative to the folded state. (C) In high [C], the denatured state has a much larger R_g than the folded state. Under each set of conditions, though, only two states co-exist, folded (labeled F) and unfolded (labeled D).

Finally, we touched here upon the interesting question of whether there is some structural or energetic relation between the collapse and folding transitions. It is possible that the CG transition is driven completely by non-specific structural properties of the protein, particularly the hydrophobic interaction between protein side chains. However, it is also possible that specific interactions, which are important for folding, contribute to the CG transition of proteins as well, making it intimately connected to the folding reaction. Theory and simulations discussed here point to the possible importance of a specific collapse, and some time-resolved experiments provide initial support for this idea. We hope that future research might be able to answer this conundrum more fully, as well as others raised in this Perspective, thus broadening our knowledge on this exciting frontier of the protein folding field.

Biographies

Gilad Haran

Gilad Haran is currently an associate professor in the Department of Chemical Physics of the Weizmann Institute of Science. He did his PhD at the Weizmann Institute with Profs. Ephraim Katchalsky-Katzir and Elisha Haas. He was then a post-doctoral fellow with Prof. Robin Hochstrasser at the University of Pennsylvania. Gilad Haran’s lab is using single-molecule spectroscopy to study molecular dynamics, from protein folding and association to charge transfer dynamics on metal surfaces.

Guy Ziv

Guy Ziv is currently a PhD student in the Department of Chemical Physics of the Weizmann Institute of Science. His thesis, supervised by Prof. Gilad Haran, focuses on single-molecule studies of protein folding, and the effects of conformational entropy on protein kinetics and thermodynamics.

D. Thirumalai

D. Thirumalai is a professor at the Institute of Physical Science and Technology of the University of Maryland. He did his PhD with Prof. Donald Truhlar at the University of Minnesota, and his postdoctoral studies with Prof. Bruce Berne at Columbia University. He is interested in theoretical chemistry, soft matter science, and biophysics. His current interests range from protein and RNA folding to functions of molecular machines.