From “Simple” DNA-Protein Interactions to the Macromolecular Machines of Gene Expression

Abstract

The physicochemical concepts that underlie our present ideas on the structure and assembly of the “macromolecular machines of gene expression” are developed, starting with the structure and folding of the individual protein and DNA components, the thermodynamics and kinetics of their conformational rearrangements during complex assembly, and the molecular basis of the sequence specificity and recognition interactions of the final assemblies that include the DNA genome. The role of diffusion in reduced dimensions in the kinetics of the assembly of macromolecular machines from their components is also considered, and diffusion-driven reactions are compared with those fueled by ATP binding and hydrolysis, as well as by the specific covalent chemical modifications involved in rearranging chromatin and modifying signal transduction networks in higher organisms.

BACKGROUND

The use of sophisticated biochemical and biophysical methods to understand the mechanisms of self-assembling macromolecular machines (2, 52) is now well advanced, and the combination of these approaches with significant advances in structure determination via X-ray crystallography and macromolecular NMR is currently yielding a flood of new information about how these machines are put together and how they operate in many biological contexts. Progress in understanding the macromolecular machines of gene expression, defined as complexes of proteins and nucleic acids that are involved in the copying (DNA → DNA) and translation (DNA → RNA → protein) of the genome, has been particularly rapid and builds on the sequential application of cycles of biophysical, biochemical and structural study, with each cycle focusing and refining the results obtained before. All these machines are integrated and controlled by labile intra- and inter-cellular signaling complexes that regulate the cell cycle and coordinate the functions of the synthesis machinery with cellular regulation, metabolism, repair, and apoptosis. All this is now, in principle, explicable by applying with subtlety and insight the principles of thermodynamics and kinetics to these often delicately balanced and kinetically competing biochemical pathways and reactions as new results emerge. ¹

STRUCTURES AND PROPERTIES OF PROTEINS AND NUCLEIC ACIDS

This progress began with detailed biochemical and biophysical studies of isolated DNA and protein (and eventually RNA) molecules, which provided initial insights into the structure and stability of these entities and told us how these properties respond to defined changes in base pair or amino acid residue sequences, as well as to changes in the solvent environment. Such studies made it possible to establish that the linear sequence of amino acid residues in the polypeptide chains of proteins, ordered by the conserved (colinear) coding sequences of the DNA strands of the genome via templated transcription and (through the genetic code) templated translation of the mRNA, suffices, in combination with the aqueous milieu, to determine the equilibrium conformations of these molecules. This postulate was initially established by the demonstration that some small proteins can fold spontaneously into stable free-energy minimum conformations in dilute solution (4). Subsequent developments—while validating the thermodynamic principle that proteins (and nucleic acids) fold into free-energy minimum states dictated by residue sequence and solvent—also showed that the larger and more complex of these molecules can easily be trapped in metastable folded or aggregated states from which they must (if they are to escape on a biologically useful timescale) be rescued by ATP-driven annealing machines (10), which can also bind to nascent proteins and thus prevent in vivo aggregation from occurring in the first place. These chaperone complexes do not direct the refolding of proteins into their thermodynamically correct forms; that is, they do not impose conformational specificity. Rather they simply catalyze correct folding by facilitating the unfolding of incorrectly folded proteins (or protein domains), thus providing another opportunity for these molecules to attain their relevant free-energy minima under the guidance of sequence and solvent. Thus chaperones help to control the kinetics of macromolecular folding and assembly, but not the underlying thermodynamics.

THERMODYNAMIC PRINCIPLES AND MACROMOLECULAR STRUCTURE

Crystallographic studies in the 1950s and early 1960s definitively established that proteins and nucleic acids do form specific and homogeneous three-dimensional structures, and by the late 1960s the principles governing the folding of these entities into their equilibrium forms were basically understood (74). Hydrophobic bonding, defined as the thermodynamic tendency to bury nonpolar residues in the interior of a protein (away from the aqueous solvent), was shown to be central to stable protein folding (36), and the related drive to decrease the surface exposure of the planar surfaces of the nucleic acid bases by base stacking was established as the dominant interaction stabilizing duplex DNA. This burial of nonpolar groups and surfaces results in the preferential exposure of polar and charged residues on the outside of the resulting conformations. The primary thermodynamic drive opposing folding is the decrease in the configurational entropy of the linear polypeptide or polynucleotide chain in going from a largely random coil form to a stable and defined structure.

The structural specificity of protein folding—meaning that each amino acid residue ends up in a specific position within the folded macromolecule—results from the requirement that the connectivity of the amino acid residues (held together by the largely polar polypeptide backbone) must be maintained. This in turn means that portions of this backbone (as well as some polar side chains) end up buried in the protein interior, resulting in structures with defined insides and outsides. The polar components that are buried carry hydrogen-bonding donors and acceptors, and the breaking of hydrogen bonds, without permitting the separated donors and acceptors to pair with acceptors and donors provided by water, is thermodynamically unfavorable (55).

The net conformational stability of a typical stably folded small protein is generally in the −5 to −10 kcal mol⁻¹ range, and since the breaking of a single interior peptide hydrogen bond without compensation by formation of substitute hydrogen bonds with water has a thermodynamic cost of ~+3 to +5 kcal mol⁻¹, the solution to the requirement that some peptide (and side chain) hydrogen bonds must be internalized in the protein is obviously that hydrogen bond donors and acceptors buried away from the aqueous solvent in the interior of the protein must be paired and aligned with properly paired acceptors and donors. It is largely this structural requirement (which becomes more severe when the simultaneous positioning of two or more sets of hydrogen bond donors and acceptors is involved) that accounts for the specific three-dimensional folding of protein molecules. Achieving optimal internal hydrogen-bonding alignments must work in concert with other interactions, including dipole-dipole interactions and van der Waals packing, within the protein interior and on its surface. Without these steric and volume-filling requirements, which follow from the mixed (polar and nonpolar) character of the polypeptide chain, proteins could organize their hydrophobic side chains to form micelle-like structures with a fluid nonpolar interior and a polar exterior (20). Such structures would be devoid of the ordered and defined interior conformations that make them amenable to analysis by X-ray crystallography.

These ideas also extend to the next level of assembly, in which stably folded proteins associate further (with one another and with nucleic acid components) to form specific and stable multisubunit complexes. The approaches taken above to justify the specific sequence- and solvent-dependent folding of individual polypeptide chains also apply to the assembly of protein and nucleic acid components into macromolecular machines, with each level of assembly involving the stable burial of component surfaces to form specific intermolecular interfaces. These interfaces are stabilized by hydrophobic bonding, as well as by favorable electrostatic interactions and (in some cases) by specific ligand and ion binding. Again, the overall complex that results in the physiological environment must have both a stable inside and a stable outside. Assembly reactions include concentration-dependent thermodynamic terms, meaning that the equilibrium stability of the resulting complex depends also on the free concentrations of its constituents. This follows because the free energy of each separate subunit carries mixing and orientational entropy components that are lost on assembly. The component concentrations at which stable assembly is achieved also depend on the properties and composition of the solvent environment.

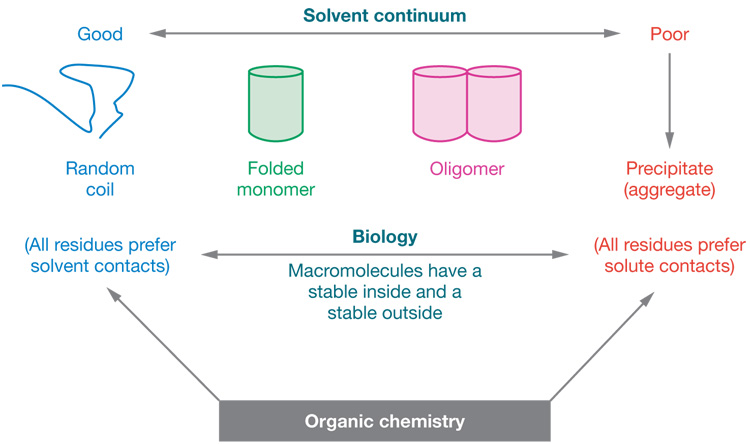
These ideas are schematized as a “solvent continuum” in Figure 1, with intramolecular folding and intermolecular assembly (both involving surface burial) preferred in poor solvents in which residue-residue interactions are favored over residue-solvent interactions, and less likely in good solvents in which residue-solvent interactions are favored over residue-residue interactions. Poor solvents can be formed by adding organic solvents, such as ethanol, to the aqueous solution, but the solvent environment can also be moved across the solvent continuum by adding various salts, usually at multimolar concentrations. The constituent ions of these salts can be arranged into Hofmeister series, which comprise ranked lists of the effectiveness of these ions in increasing or decreasing the goodness of the solvent (86). Chaotropic ions, such as iodides, thiocyanates, and perchlorates, destabilize structures and complexes by favoring residue exposure on surfaces, whereas stabilizingions, such as sulfates and phosphates, favor the burial of residues and thus promote oligomerization and aggregation (82). It is this latter property that makes concentrated ammonium sulfate solutions effective in protein fractionation. To a first approximation the effects of such solvent perturbants, including the classical denaturants urea and guanidinium chloride, are additive. For example, the denaturing effect of the guanidinium cation in guanidinium sulfate is overcome by the stabilizing effect of the sulfate anion, making this salt a net antidenaturant (87).

Figure 1.

Changing macromolecular interactions by changing the solvent environment. The “solvent continuum.” Biological macromolecules can form miniphases that have stable insides and outsides. Small molecules can only form mixed solutions or separate phases (see text).

Macromolecular crowding also favors the formation of stable and compact assemblies, since unfolded or dissociated components are excluded from large fractions of the solution by the presence of noninteracting polymer chains or macromolecules that effectively occupy connected elements of the solution into which the complex could otherwise unfold or dissociate (26). Because real cells contain large concentrations of macromolecules and macromolecular assemblies, macromolecular complexes are often more stable in vivo than in the dilute solutions studied by biochemists and enzymologists (50). Macromolecular assemblies can often be stabilized in vitro by adding significant concentrations of noninteracting polymers (polyethylene glycol or dextrans) of moderate molecular weight. This can increase the effective equilibrium association constants of multisubunit complexes in vitro by several orders of magnitude (28), thus stabilizing such assemblies for biophysical study at solution concentrations at which they would otherwise be largely dissociated.

SIMPLE PROTEIN–NUCLEIC ACID INTERACTIONS

By the late 1960s and early 1970s these general ideas were ripe for incorporation into biophysical approaches to simple protein–nucleic acid complex formation. An overview that Jim McGhee and I (84) wrote for the Annual Reviews of Biochemistry in 1972 represented one of the first efforts to define and systematize this developing field. In that sense it comprises (for me) a personal bookend to the present review, which deals with some points of the intervening history that (in my view) represent milestones in our progress to the present day.

DNA Structure, dsDNA Breathing, and dsDNA-ssDNA Melting Equilibria

In defining the underlying ideas of DNA-protein interactions, one can, in principle, choose to use the structure of either the DNA or the protein as a starting point, and then develop the properties of the other interaction partner(s) in complementary terms. It seemed logical in 1972, and continues to be largely appropriate today, to treat the structure and stability of the double-stranded (ds)DNA molecule, as first defined by Watson and Crick and subsequently refined by many others (e.g., 91), as an initial given, and then to develop the properties of the protein complexes that recognize it, bind to it, and transform it from such a DNA-centric perspective. As a consequence, dsDNA of appropriate sequence can to a first approximation be viewed as a preformed target for the various proteins and protein complexes that operate on and transform it in facilitating gene expression. However, it was early recognized that dsDNA must be a flexible target because, in addition to minor sequence-based variations, the DNA itself is often significantly perturbed in interacting with its protein partners, resulting in supercoiling, base-tilting, local unwinding, and base pair breathing. Nevertheless, we begin here by defining the dsDNA molecule in general terms and then ask what reactions need to be considered thermodynamically and kinetically to determine how it might interact with physiologically relevant proteins.

Where Is the Coding Information Located in the DNA and How Can Cellular Code-Reading Mechanisms Gain Access to It?

The Watson-Crick structure and the prior demonstration that A equals T and Gequals C (Chargaff’s rules) established that the strands of the DNA duplex are linked by complementary hydrogen bonding between dA · dT and dG· dC base pairs, providing a mechanism for base pair sequences to be preserved and ultimately (via the genetic code) to be expressed as defined sequences of amino acid residues of co-linear (with the DNA template) polypeptide chains. The Meselson-Stahl (49) experiment showed unambiguously that replication is semiconservative, and the biochemical isolation and characterization of a DNA polymerase that could effectively align free deoxyribonucleotide triphosphates (dNTPs) along a single-stranded (ss)DNA template and catalyze their sequential conversion into a phosphodiester-bond-linked ssDNA chain to form a new duplex with its preformed template strand provided a biochemical mechanism for DNA replication (37) and by extension for the elongation phase of RNA transcription. This then raised the question of how the two strands of dsDNA might be separated to expose ssDNA template sequences, ultimately in toto to permit overall DNA replication, but also locally and transiently to permit specific mRNA transcription at the level of individual genes.

Melting studies of dsDNA showed that the overall stability of a duplex DNA molecule, as defined by its melting temperature (T_m), is a linear function of base composition, with GC-rich regions significantly more stable than AT-rich regions (44). These thermodynamic results led to kinetic questions and efforts to establish the rates at which dsDNA molecules breathe (open and close) locally. The hydrogen-tritium exchange method, initially developed by Englander (15) to study the opening and closing of protein domains, was used to examine the rates of dsDNA breathing of sequences of varying composition at temperatures below T_m (45, 58). These experiments showed that base pairs do open and close spontaneously within dsDNA, presumably also transiently exposing potential ssDNA templating sequences to be trapped by polymerases or related helper proteins in the initiation of DNA replication and transcription. In more modern parlance these helper proteins are now called helicases and helicase-loading proteins. Functionally, they are tightly coupled to the central polymerases of the corresponding macromolecular machines (13, 81).

SSBPs and dsDNA Breathing

Having established that thermal fluctuations open dsDNA spontaneously and frequently at temperatures well below T_m, it was then asked whether the cell contains proteins that bind preferentially to such transiently exposed ssDNA sequences and perhaps stabilize them against reclosure. Alberts & Frey (3) soon demonstrated that single-stranded DNA binding proteins (SSBPs) do exist and form a central part of the phage T4 DNA replication complex. However, these proteins appeared to be kinetically blocked from initiating the opening of dsDNA themselves. Eventually various dsDNA helicases and helicase-loading proteins were discovered and shown to be required for the initial opening of dsDNA sequences in replication, while the role of the ssDNA binding proteins was to stabilize the ssDNA sequences exposed by these helicases so that they could function as templates for the DNA polymerases at the replication fork. It has been shown that the levels of SSBPs in cells are sufficiently high to permit stable binding at physiological temperatures, and the kinetic block that prevents them from acting as helicases on their own reflects the fact that spontaneous (thermally driven) opening of dsDNA sequences of sufficient length (7 bp for gene 32 protein, the SSBP of phage T4) is too infrequent to permit these proteins to gain stable access to the interior of dsDNA on their own. This contrasts with small-molecule SSBP models, such as formaldehyde, which require only the opening and unstacking of single base pairs for binding. Because dsDNA opening occurs primarily at the single base pair level, formaldehyde can (and does) bind and thus melts dsDNA to equilibrium at temperatures well below T_m (81).

SSBPs Bind ssDNA Lattices Nonspecifically, often Cooperatively, and with Overlapping Binding Sites

SSBPs generally bind to ssDNA lattices with little, if any, base sequence specificity. The main component of the free energy of this binding is electrostatic, involving the interaction of positively charged protein side chains located in the binding site of the protein with the negative phosphate groups of the ssDNA backbone. ssDNA is a highly charged polyelectrolyte and therefore subject to ion condensation; the condensed monovalent cations are then released (displaced) by the binding of multivalent cationic proteins. The treatment of ion condensation is developed in connection with the nonspecific (electrostatic) binding of proteins to dsDNA (see below), but for SSBPs also the mixing entropy of the displaced condensed cations dominates the interaction free energy of these moieties with their ssDNA binding targets, and the binding affinity decreases in a straight-line fashion in log-log plots of monovalent cation concentration as a function of the apparent equilibrium association constant (K_a).

Because they do bind nonspecifically and tend to interact with and span several nucleotide residues per bound SSBP monomer, these proteins show overlap binding to ssDNA lattices, meaning that the number of binding sites available on the lattice for the next bound protein ligand decreases more rapidly than linearly with increasing ligand binding density. This property is manifested in curved (convex upward) Scatchard binding plots and means physically that it is difficult to drive binding to saturation by increasing the SSBP concentration. This follows because the number of open binding sites large enough to accommodate another protein ligand becomes vanishingly small as the binding density increases, and considerable unfavorable mixing free energy is involved in reorganizing the last few uncovered lattice positions into gaps large enough to accommodate another bound ligand (47).

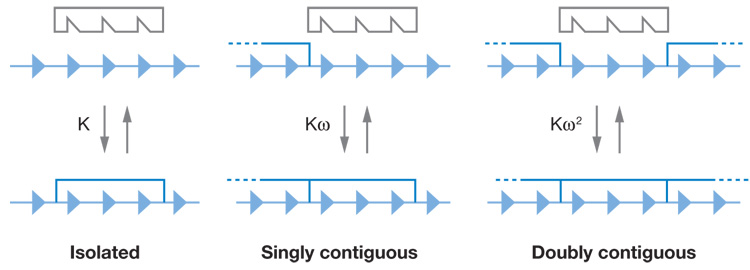
Nature has evolved a strategy to overcome this effect, because most SSBPs bind to the ssDNA lattice with significant positive binding cooperativity. This means that there is a good deal of additional favorable binding free energy associated with positioning an incoming SSBP next to an already occupied lattice binding site. Three parameters characterize the interaction of a ssDNA lattice with a nonspecific binding protein (Figure 2). These are n, the site size of the protein ligand (in units of nucleotide residues); K, the equilibrium binding (association) constant (moles/liter); and ω, the (unitless) equilibrium constant for shifting a bound protein from an isolated to a contiguous binding site (47). n ranges from 5 to 15 nucleotide residues for most SSBPs. K can vary widely and is generally salt concentration dependent. ω also varies widely, generally displays little or no salt concentration dependence, and is often large, with values in the 10³ range not unusual. At these levels of ω, the unfavorable effect of overlap binding on lattice saturation is overcome by the large positive binding cooperativity, Scatchard plots become humped (concave) upward, and lattice saturation becomes approachable. Titration methods to monitor SSBP binding to ssDNA and to evaluate best-fit binding parameters have been described (38). We note that Schellman (67a) early solved the problem of cooperative multisite binding of ligands to long lattices using a powerful sequence-generating function approach (40a) that is also applicable to many related problems.

Figure 2.

Three parameters characterizing the interaction of a ssDNA lattice with a nonspecific binding protein. The arrowheads represent a nucleic acid lattice position (nucleotide or base pair), and the protein shown covers three such positions (n = 3). The binding constant to an isolated lattice site is K, that to a singly contiguous site is Kω, and that to a doubly contiguous site is Kω² (see text). Taken from Reference 47.

The ultimate purpose of making such biophysical measurements and model interpretations of nonspecific binding is to permit quantitative and mechanistic interpretations of biological regulatory systems. An early example was posed by Gold and coworkers (40), who showed that the synthesis of the phage T4 gene 32 protein, which plays a central role in DNA replication in this organism, is autoregulated by the binding of the protein to a long and unstructured sequence of its own mRNA. This finding was subsequently explained and fully predictively modeled using measured binding parameters for the interaction of gene 32 protein with defined DNA and RNA molecules (48, 83).

Kinetics of Nonspecific Ligand Binding to DNA Lattices

Equilibrium binding experiments reveal the final distribution of proteins that display overlap and cooperative or noncooperative nonspecific binding to DNA and RNA lattices, but they do not tell us how the binding got this way or whether binding equilibrium has actually been attained. This is the domain of kinetics and is also important because rate information is required to determine whether such binding systems can indeed equilibrate before other reactions intervene, including those associated with other macromolecular machines of gene expression working with the same nucleic acid components. It was clear early on (42, 57) that the distribution of protein ligands bound nonspecifically along nucleic acid lattices involves initial direct binding from solution. However, subsequent rearrangement of these initial distributions must involve not only dissociation and rebinding, but also sliding, hopping, and intersegment transfer of ligands along the lattice (see below).

In terms of the equilibrium parameters previously defined, a kinetic treatment requires breaking down K and ω into on-rates and off-rates (k_on and k_off) and also partitioning the overall cooperativity of the binding reaction into association and dissociation components (ω_on and ω_off). The underlying mechanistic issues involved in such kinetic problems have been described (51), and theoretical solutions involving limiting assumptions have been put forward (6, 16, 17, 41). Currently we are attempting to assemble and test other approximate models for the analysis of the kinetics of the nonspecific binding of ligand to lattice, as well as to develop numerical methods to describe the kinetics of noncooperative and cooperative ligand binding to finite lattices that involves consideration of the rates of all the relevant redistribution reactions. This work, including full references to earlier approaches, will be presented elsewhere ( J.P. Goodarzi & P.H. von Hippel, manuscripts in preparation).

Nonspecific Binding of Proteins to dsDNA Is Primarily Electrostatic and Involves Ion Condensation and the Polyelectrolyte Effect

Manning (43), Oosawa (53), and others early appreciated that dsDNA, in particular, carries such a high-charge density that it cannot be treated as a normal polyanion subject to Debye-Huckel charge screening in salt solutions. Rather these workers proposed that electrostatic interactions between DNA and bound ligands must be considered in polyelectrolyte terms and must involve a condensed counterion atmosphere around the dsDNA cylinder that largely neutralizes the backbone phosphates of the DNA. These condensed cations would then be locally displaced by the binding of polyvalent cationic ligands.

These initial ideas were developed and experimentally tested by Record and coworkers (59, 62), who showed that the dependence of the apparent association constant (K_a) for the binding of cationic ligands (and, by extension, proteins with positively charged DNA binding sites) to dsDNA (and ssDNA) in Na (or K) Cl can be represented as a function of monovalent cation concentration:

$$\mathrm{\delta }\text{log}{\mathrm{K}}_{\mathrm{a}}/\mathrm{\delta }\text{log}[{\mathrm{M}}^{+}]=-m\prime \mathrm{\psi },$$ (1)

where K_a is the observed association equilibrium binding constant, [M⁺] is the monovalent cation concentration, ψ is the ion condensation parameter for the polyelectrolyte at issue (that is, the fraction of a counterion thermodynamically bound per DNA phosphate; 0.88 for B-form dsDNA) and m′ is the number of charge-charge interactions involved in the binding of the polyvalent ligand.

This surprisingly simple relationship provided an excellent representation of the apparent binding of oligolysines of varying length to long dsDNA molecules as a function of monovalent (and divalent) cation concentration, as well as of the nonspecific binding of positively charged DNA binding proteins (12, 61, 62). These workers also showed, using ion condensation parameters (ψ) calculated for various ssDNA and dsDNA conformations, that the resulting log-log plots of δ(log K_a) versus δ(log[M⁺]) could be interpreted directly in terms of the number of charge-charge interactions involved in the interaction between the ss- or dsDNA binding site and the oppositely charged binding site of the protein. This approach to estimating the number of charge-charge interactions involved in both the specific and nonspecific binding of proteins to DNA has recently been dramatically affirmed by the excellent agreement of the results of applying Equation 1 to specifically and nonspecifically bound lac repressor with the number of charge-charge interactions that can be directly counted in crystal structure representations of both of these bound forms (32, 78). A more complete treatment of the interactions involved in the specific and nonspecific binding of proteins to DNA, couched in terms of the burial of the interacting binding surfaces, has been developed by Spolar & Record (72) (also see Reference 77). An excellent general treatment of the whole problem of salt effects in protein–nucleic acid interactions, developed in terms of linked thermodynamic functions, is presented in (62a).

Given the sharp salt concentration dependence of the nonspecific binding of highly charged regulatory proteins to (especially) dsDNA, it is important to have a reasonable estimate of the effective salt concentration that controls binding of proteins to DNA inside the cell in order to determine the extent to which some of these in vitro binding interactions can actually be used to estimate competitive regulatory interactions in vivo (24, 85) (see below). To this end the concentrations of bound and free lac repressor (R) within the Escherichia coli cell (and therefore the in vivo binding constant of R to nonspecific genomic DNA, K_a,nonspec) were determined by measuring the fraction of the intracellular R bound to the dsDNA genome and that free in the cytoplasm (35). The latter fraction was determined using a minicell mutant of E. coli, which sheds bits of membrane-enclosed cytoplasm devoid of DNA, thus permitting measurement of free R separately from the total R present in the normal (DNA-containing) E. coli cells. A log-log plot of the in vitro binding of R to nonspecific DNA as a function of salt concentration as a calibration curve reveals that the estimated intracellular value of K_a,nonspec obtained from the minicell data corresponds to a salt concentration of ~0.160 MK⁺ and 5–10 mM Mg²⁺, permitting such salt solutions to be considered effectively equivalent to the cellular ionic environment.

This estimate should be treated as equivalent to rather than as the actual salt environment of the cytoplasm, because the cell contains many other positively charged components (for example polyamines) and high concentrations of other proteins that increase binding interactions by creating a macro-molecularly crowded in vivo environment. However, this value is useful for establishing dilute solution conditions that correspond roughly (in terms of the stability of DNA-protein interactions) to the cell interior. It is necessary to estimate the fraction of the cellular DNA of E. coli that can be considered naked (i.e., unencumbered by other proteins that interfere with the nonspecific binding of lac repressor) in terms of this interaction. Direct titration of isolated E. coli DNA genomes (nucleoid bodies) with lac repressor permitted us to estimate that the intracellular fraction of naked DNA in E. coli is ~15% (D. Noble, M. Schmid, D. Forbes&P.H. von Hippel, unpublished experiments). Recently others (60, 92) have undertaken a detailed biochemical and biophysical analysis of the E. coli cytoplasm. Thus better in vitro representations of the cell interior should be forthcoming.

DNA REGULATORY PROTEINS BIND THE dsDNA GENOME AT SITES OF DEFINED BASE PAIR SEQUENCE

As summarized above, many proteins bind to ss- and dsDNA electrostatically, with little or no dependence on base or base pair composition or sequence. Such nonspecific binding by SSBPs to ssDNA regions of the genome serves to coat and stabilize transiently formed ssDNA sequences and to protect them from attack by nucleases at the replication fork and during the phases of DNA recombination and repair that transiently open duplex sequences. SSBPs bind primarily to the sugar-phosphate backbones of the ssDNA exposed in these reactions, as expected for processes that must occur in a sequence-independent manner throughout the genome. A comparable situation exists for the dsDNA of the eukaryotic genome, which, at most stages of the cell cycle, is largely coated with histone complexes that wind the local dsDNA into nucleosomes and also bind to duplex DNA in a relatively non-base-pair-specific and largely electrostatic fashion (46). This generalized coating of the dsDNA with nucleosomes, in conjunction with the activities of other regulatory proteins, serves to control gene expression at many levels and represents the first level of genome compaction into chromatin. SSBPs and histones actually do show some sequence preference in their binding, and this minor specificity may have regulatory importance. SSBP binding generally involves putting the ssDNA backbone into a specific (often extended) conformation, and therefore sequences that contain significantly stacked bases or other secondary structure may require more than average deformation from their free solution conformations. Therefore these sequences bind SSBPs more weakly, effectively favoring binding elsewhere. In the same way, nucleosomes form preferentially at dsDNA sequences that are more bendable than average (71), again introducing some sequence preference (and regulatory possibilities) into the dynamics of nucleosome function.

A more glamorous form of protein interaction with dsDNA that has received much attention from molecular biologists is the binding of regulatory proteins to specific target sites on the genome, such as the binding of the paradigmatic lac repressor to the operator sites that occur at many E. coli promoters for genes involved in sugar metabolism. Such site-specific dsDNA binding proteins recognize defined base pair sequences within the DNA genome and serve to control gene expression at many levels, although the most studied and best understood of these regulatory proteins are involved in transcription control. How these DNA targets are located, bound, and then manipulated by their cognate regulatory proteins (assisted in eukaryotes by chromatin-modifying systems) to achieve regulatory function remains to be elucidated in detail for most systems.

Recognition of Specific Regulatory Target Sites by Proteins that Bind dsDNA with Sequence Specificity

Base-pair-sequence-specific binding proteins recognize their target sites primarily via specific hydrogen-bonding determinants located in the grooves of the dsDNA duplex. These sets of hydrogen bond donor and acceptor determinants can, in principle, distinguish the four (because of backbone polarity) canonical base pairs (A · T, T · A, G· C, and C· G) of dsDNA by recognizing the patterns of hydrogen bond donors and acceptors that are exposed through the major and minor groups of the DNA duplex. These patterns, as described in detail elsewhere (70, 76, 90), are recognized by complementary matrices of hydrogen-bonding acceptors and donors on the protein binding surface and, by displacing the water molecules that otherwise interact at these surfaces, form interfaces of complementary hydrogen-bonding patterns that can be buried out of contact with the aqueous surround with little or no thermodynamic penalty, but also with relatively little thermodynamic gain.

Holding together these recognition surfaces requires other sources of binding free energy. Hydrophobic interactions primarily serve this purpose for protein assemblies; for protein-DNA complexes electrostatic (charge-charge and dipole-dipole) interactions between the largely hydrophilic and negatively charged DNA backbones and the positively charged and dipolar amino acid side chains of the protein binding sites provide most of the requisite interaction free energy. Like hydrophobic interactions that depend primarily on the close packing (to exclude solvent) of relatively flexible and directionally undemanding nonpolar groups, these electrostatic interactions are also relatively undemanding in a positional sense. This follows because charge-charge interactions are also not directional and their distance dependence is not steep (the potential energy of charge-charge interactions changes with distance as 1/r; Coulomb’s law). In contrast, hydrogen-bonding free energies are significantly altered by minor changes in relative orientation and distance between acceptor and donor atoms.

Specific protein recognition and binding has three elements. The first is structure-based, as defined above. The second is informational (or coding) in nature and involves determining the number of base pairs that must be arranged in a specific sequence along the dsDNA to define a unique recognition site for a regulatory protein within the genome. The third is thermodynamic and requires the conversion of the first two components into the interaction free energies that achieve the specific and stable binding of the protein to its dsDNA target sites at defined (and generally regulated) concentrations of free protein.

This binding cannot be so tight as to make the dissociation rate of the protein unreasonably slow compared with the turnover time of the regulatory processes involved or the duration of the cell cycle. Thus the specific binding interactions must be strong enough to permit the regulatory protein to stick to its target site in the presence of competing nonspecific binding, but not strong enough to impede subsequent functional events. lac repressor, for example, achieves both tight binding and an appropriate rate of release by binding allolactose, a small-molecule inducer (I) that is an intermediate in the lactose pathway and, by binding to R, increases the dissociation rate of the repressor-operator (RO) complex. Another mechanism that makes binding weaker while retaining specificity involves the use of a regulatory protein that is unfolded in its free form, with folding occurring concomitantly with target binding. This mechanism permits some of the binding free energy, but not the binding specificity, to be offset by the unfavorable free energy of folding of the regulatory protein on binding to its target (14, 69).

Information Content of Specific Site Binding

At this level the arrangement of base pairs into a defined sequence is a coding rather than a structural problem. The base pairs required for regulatory function are usually defined by investigating the effects of mutations at known positions in the dsDNA binding site, although this genetic analysis tells us little about the relative shapes or positions of the complementary DNA and protein binding surfaces, nor about the magnitude of the free-energy contribution made by each conserved base pair to the final interaction. Because DNA (and protein) coding is linear (based on defined sequences of residues along linear polymer chains), such information content discussions are usefully couched in terms of linear sequences of defined DNA base pairs.

At a molecular level the binding specificity of a regulatory protein to its DNA target can be viewed in the same way as the binding of a complex ligand (for example, a hormone) to its protein receptor, with recognition and affinity depending on the fitting together of complementary surfaces (a lock and key model). For specific DNA sequences that serve as protein binding sites, the situation is vastly complicated by the fact that the target site, containing n defined base pairs, exists on a duplex DNA molecule that contains N overlapping sequences of the same size, where N is the length of the genome within which the specific site occurs. The first question one must then ask is how long (in base pairs) must a specific site be in order to avoid reoccurrence at random within a genome of length N?

This length is defined as a function of genome size by

$$n={\mathrm{P}}_n(2N),$$ (2)

where P_n is the probability of occurrence at random of a defined sequence of n bp located within a genome of size N that contains equal numbers of A · T, T · A, G· C, and C·G bp. Equation 2 is slightly more complicated for genomes of different overall base composition (76). It contains the factor 2 because any given sequence can be read in either direction along the duplex DNA genome (for palindromic sequences the factor 2 is omitted). End effects (very small for a large genome) are also omitted from Equation 2, or a circular genome is assumed. A central assumption of Equation 2 is that the base pair sequence of the genome can be treated as approximately chemically random, although it is obviously not genetically random. Early calculations with limited experimental data on the number of restriction enzyme cutting sites that occur in various genomes suggested that this chemical randomness assumption is approximately correct for sequences greater than 2 bp in length (76); the availability of many genome sequences now permits this assumption to be tested more rigorously.

With these assumptions a plot of n against log[P_n(2N)] will be linear. Equation 2 shows that n = 12 defined bp for a genome of the size of E. coli (N ≈ 10⁷ bp) with an overall fractional base composition of A = T = G = C = 0.25. This calculation is unrestrictive in terms of the actual details of how the n bp of defined sequence are distributed along the genome, as long as the linear order of these base pairs is maintained. This makes it easier to arrange the complementary protein surfaces that must read the sequence. Thus the defined n bp can be spaced out by inserting blank positions (containing undefined base pairs) anywhere within the sequence. The binding site can comprise two identical subsequences (arranged either head to tail or head to head) to facilitate reading by dimeric regulatory proteins. The site can be overspecified by making n larger, thus making the calculated value of P_n(2N) significantly smaller than unity to avoid complications from the competitive binding of the regulatory proteins to sites on the genome that differ from the canonical recognition site by one or two incorrect base pairs (see below). The top base of a defined base pair position can also be specified simply as a purine (Pu) or a pyrimidine (Py), thus decreasing its statistical weight by a factor of 2 relative to a fully defined base pair. n is smaller if the defined sequence contains mostly A ·TandT·A base pairs within a GC-rich genome, whereas n is larger for an AT-rich sequence within an AT-rich genome (76).

We next ask what happens to P_n as we replace one or more correct base pairs at defined positions within a sequence of n bp with any of the other three incorrect base pairs. In general, for a genome containing equal numbers of all four bases in which the probability of occurrence of a particular base pair at any random position is P_A = P_T = P_C = P_G = 0.25 (the subscript defines the top base of the base pair), we may write

$${\mathrm{P}}_{n,j}={(0.25)}^{n-j}{(0.75)}^j\{n!/j!(n-j)!\},$$ (3)

where P_n,j is the probability that a defined sequence of n bp contains j incorrect bp and (n−j ) correct bp at defined positions. P_n,j becomes much larger as j increases, because the multiplier for the incorrect base pairs is (0.75) ^j instead of (0.25)^n−j for the correct base pairs. In Figure 3 log(P_n,j) is plotted versus (n−j ) for three different sequences of overall defined length n and shows that P_n,j increases rapidly as (n−j ) decreases, peaking at ~0.3 at (n−j ) = 3 for all the sites in the genome that contain n defined bp. What does this mean in terms of the binding free energies of potential binding sites containing varying numbers of incorrect base pairs at defined positions?

Figure 3.

Probability of occurrence of base pair sequences containing defined numbers of correct and incorrect base pairs. Plot (as a function of n−j) of the logarithm of the probability of random occurrence of n defined bp (for n = 10, 12, and 14 bp), when n contains j incorrect bp and n−j correct bp for a genome with P_A = P_T = P_G = P_C = 0.25. Taken from Reference 76.

Thermodynamics of Nonspecific Binding from a Coding Perspective

Establishing the coding or information content of a specific DNA sequence as a recognition site for the binding of a particular biological regulatory protein to the DNA genome is a significant step forward, but it doesn’t tell us what we need to know to interpret such calculations in molecular terms. This follows because the real issue is to understand these sequences in the context of binding free energies, ideally at the level of stating what each specific evolutionarily conserved base pair contributes to the total binding free energy of the regulatory protein to its genomic target site, and then what this means in terms of function (79).

This is not straightforward. The simplest binding model is an additive one, with each correct base pair contributing 1/n of the total binding free energy of the regulatory protein to its genomic site. This model can be written as

$$\mathrm{\Delta }{\mathrm{G}}_{\text{int},\text{total}}=n(\mathrm{\Delta }{\mathrm{G}}_{\text{int},\text{bp}}),$$ (4)

where ΔG_int,total represents the total free energy of the specific binding interaction and (Δ_Gint,bp) is the specific binding free energy per defined base pair.We know that this simplest model does not work, in part because we have already established that most of the binding affinity that holds the protein to its target site depends not on the hydrogen-bond-based recognition interactions between the protein and the individual DNA base pairs as read from the grooves of the DNA duplex, but rather on the non-sequence-specific charge-charge (electrostatic) and nonelectrostatic interactions between the protein and the sugar-phosphate backbones of the duplex DNA.

A more realistic equation for the total interaction free energy for specific binding can be written as

$$\begin{array}{l}\mathrm{\Delta }{\mathrm{G}}_{\text{int},\text{total}}=n(\mathrm{\Delta }{\mathrm{G}}_{\text{int},\text{bp}})+m\prime (\mathrm{\Delta }{\mathrm{G}}_{\text{int},\text{ch}-\text{ch}})\\ \hfill +(\mathrm{\Delta }{\mathrm{G}}_{\text{int},\text{nonelec}}),\hfill \end{array}$$ (5)

where the n(ΔG_int,bp) term represents the part of the interaction free energy that is specific and can be partitioned between the individual specified base pairs, m' is the number of charge-charge interactions involved in the specific binding, ΔG_int,ch−ch is the binding free energy per charge-charge interaction, and Δ G_int,nonelec represents the total binding free energy for all the other non-base-pair-specific and nonelectrostatic interactions that hold the protein to the specific DNA target site. In general we have no a priori way to evaluate the parameters of Equation 5.

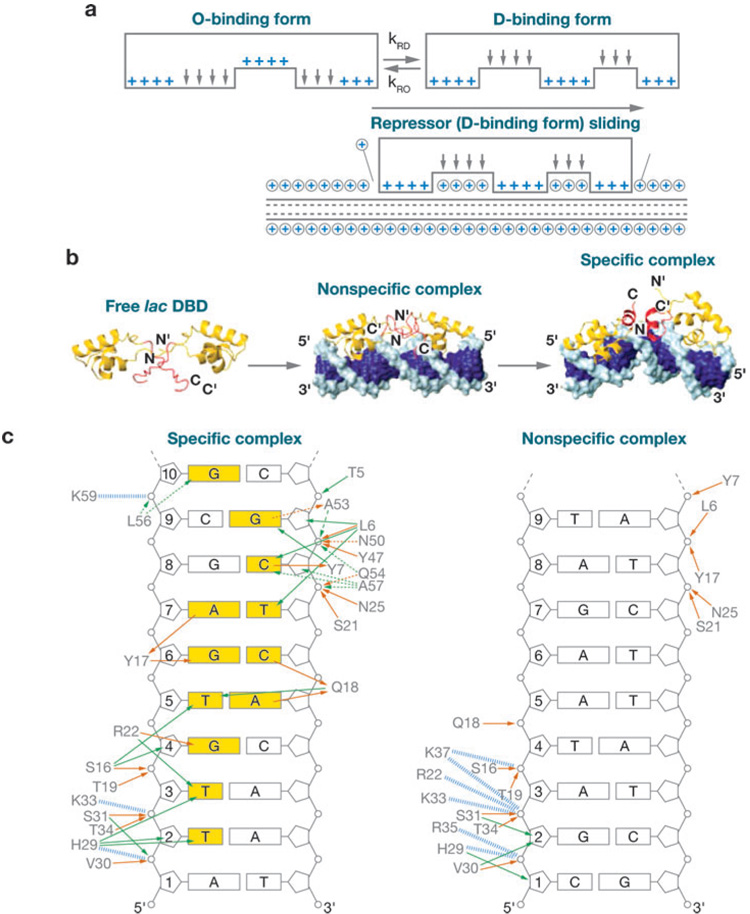
A different approach can be taken from a coding perspective if we ask what happens as the number of incorrect base pairs at defined positions in the specific correct sequence is increased. According to the simplest model (Equation 4), each incorrect base pair substituted at a defined position should decrease the favorable binding free energy to the specific site by a fixed amount and thus lead to a large distribution of nonspecific binding constants. However, this is not what is found. Rather, for defined sequences containing more than two or three incorrect base pairs, we find a single value (or small spread of values) of the nonspecific binding constant. This is congruent with the notion that increasing the number of incorrect base pairs in a given target beyond a certain point results in making the specific binding conformation of the regulatory protein unstable relative to that of a general nonspecifically binding form. In this latter conformation the hydrogen-bonding acceptors and donors responsible for recognizing the remaining correct specific base pairs are withdrawn from the protein binding surface, and the protein presents instead a nonspecific binding surface containing no base-pair-specific recognition contacts and a maximal number of basic residues that interact with the charged phosphate groups of the dsDNA backbone conformation (12, 61, 63, 78) (Figure 4).

Figure 4.

lac repressor-DNA complexes in operator-bound and nonspecifically bound forms. (a) The number of charge-charge interactions between lac repressor (R) and DNA changes from the 6–7 interactions present in the operator binding conformation (O-binding form, top left) to the ~11 interactions that are present in the nonspecifically bound conformation (D-binding form, top right). The remaining base pairs are moved away from close contact with the protein binding site to expose the specific binding surface of both the protein and the DNA to solvent and permit these hydrogen-bonding donors and acceptors to again be satisfied by interactions with water. The lower schematic shows the D-binding form sliding with displacement of condensed monovalent cations. Modified from Reference 80. (b) The actual structures of the free, nonspecifically bound and specifically bound forms of the head-groups of two subunits of R [free dimeric lac DBD (DNA-binding domain)]. Taken from Reference 32. (c) The interactions of amino acid residues of the active site of R with the nucleotide residues of the DNA in the specific target complex (left) and the nonspecific target complex (right). Taken from Reference 32. Entire figure is from Reference 78.

Comparison with Mutational Studies

To a first approximation this subtractive approach to looking at the effects on binding affinity (and function) works reasonably well for regulatory proteins binding to dsDNA target sites that contain only one or two incorrect base pairs. This approach is based on the notion developed above that it is not the right interactions at each base pair that stabilize the specific binding interaction; rather the introduction of wrong interactions destabilize it because of buried hydrogen bond mismatches. A single incorrect base pair might be expected to reduce the favorable free energy of specific binding by 2–3 kcal mol⁻¹, and this is approximately what is found.

On this basis one can start by defining the binding to the wild-type sequence—which may not be the one with the highest possible affinity (67)—of the specific DNA binding site as the baseline affinity for the interaction, and then asking how much the introduction of single incorrect base pairs changes the apparent binding affinity. Berg & von Hippel (8) used this approach to analyze the single and double mutant collection tabulated by Hawley and McClure for E. coli promoters (27), and showed that each mispairing identified by loss of function reduced the apparent affinity (as expressed through promoter function) by about the same amount. An interesting outcome of this study was that the effects of more than one mutation seemed (with the exception of one promoter position) to be approximately additive, suggesting that each mutational change in the promoter sequence affects function approximately independently, in accord (at least for the first few incorrect base pairs) with the crude subtractive model outlined above.

The difficulty with this approach is that the effects of promoter mutations were defined in phenotype (loss-of-function) terms, rather than directly in binding free energies. Assuming that increased binding must have been involved in the evolutionary selection of functional DNA regulatory sites, Berg & von Hippel (8) devised a statistical mechanical approach to deal with the problem of transforming the base pair sequences of the conserved binding sites into binding affinities. The theoretical results were reasonably satisfactory, but actual sets of experimental data generated subsequently for other specific binding complexes by Stormo and colleagues (19, 73), who used chemical selection (SELEX) methods to generate progressively stronger DNA binding target sites, permitted direct measurement of the reduction in protein binding affinity that accompanies defined increases in the numbers and positions of incorrect base pairs in the DNA binding site. Studies of this sort continue, but the overall picture sketched above, involving approximately linear decreases in binding affinity for the first few incorrect base pairs, followed by a discontinuous switch to a general nonspecific binding form of the regulatory protein, seems to apply and provides general support for the view of protein-DNA interactions described here.

The use of base pair sequence statistics to attempt to understand biological function has developed in many directions with the increased availability of genomic databases and the sophisticated development of statistical methods to explore these data. Schneider and coworkers (68) have cast the simple sequence probability ideas summarized above into the framework of Shannon’s information theory and subsequently developed a useful pictorial representation to depict the degree of sequence conservation at each DNA position within specific protein binding sites. It is likely, however, that a general predictive theory that can link conserved base pair sequences of DNA regulatory sites to protein binding and then function in a quantitative way is not achievable, largely because of the plasticity of protein structure and thus of protein–nucleic acid interactions discussed above.

We expect (and obtain) different results for the binding of proteins to DNA targets at which recognition and affinity are dictated primarily by unusual conformations (such as flipped-out bases, looped-out sequences, Holliday junctions, etc.) within the dsDNA, not by base pair sequence. The proteins that bind to such conformations are generally classified as structure specific rather than sequence-specific, and the modulation of their interactions with their DNA targets involves higher levels of nucleic acid structure together with more subtle effects of base pair sequence. Although the effects of changes in sequence are more indirect at these levels, the general interaction principles developed in this overview will continue to apply, albeit in more sophisticated and complex combinations.

Thermodynamics of Specific Site Binding

Site-specific proteins generally bind tightly to their regulatory target sites on the genome at physiological salt concentrations and under in vivo conditions (macromolecular crowding, etc.). This is important to permit these proteins to occupy their regulatory target sites and avoid being dissipated across the huge excess of nonspecific binding sites that also compete for them. Considering the parameters for lac repressor in E. coli, with ~10⁷ nonspecific sites in principle competing with one operator site and a ratio of specific to nonspecific binding constants (K_a,specific/K_{a,nonspecific}) of ~10⁸ (79), it is suggested that specific and nonspecific sites must be rather delicately carefully balanced so that nonspecific sites can effectively compete the binding protein away from any specific sites that have been significantly compromised by mutations that decrease the specific binding constant by as little as a factor of 10 to 100. This effect is counteracted partially by coverage of many potential nonspecific sites by other proteins and (in eukaryotes) by nucleosomes, but the fraction of effectively naked DNA that remains provides ample numbers of competing sites (see above).

This competition can be physiologically significant. For example, it has been shown for lac repressor (R), where free R and repressor-inducer (RI) complexes bind nonspecifically with equal affinity, that the free energy of inducer binding alone is not sufficient to shift the binding equilibrium toward RI dissociation into free solution. In fact it is the coupled equilibrium involving the binding of RI to the many nonspecific binding sites present on the genome that shifts the binding equilibrium sufficiently to remove R from the specific operator site so that RNA polymerase can bind (39, 85). A similar analysis of the regulation of sigma factors in the metabolic and developmental control of E. coli shows that function in this system also depends on a similar coupled equilibrium involving the nonspecific binding of the core- and various holo-forms of RNA polymerase to nonspecific DNA sites on the E. coli genome (24).

Kinetics of Specific Site Binding

The binding of genome target-specific regulatory proteins to nonspecific DNA sites has kinetic as well as thermodynamic components. The location of a particular target site within a whole genome by the three-dimensional diffusion of regulatory proteins that are present in limited number and low concentration might be expected to be slow, and competitive nonspecific binding of these proteins to other DNA sites would be expected to further slow target location. Yet initial measurements of the kinetics of binding of lac repressor to its target operator site (65) showed this binding to be significantly faster than diffusion controlled. This immediately indicated that the location of the operator target on the DNA does not occur by direct binding of R to O from solution. Instead this finding suggested that there must be intermediate states involved in the RO binding reaction that, in some way, significantly accelerate target location.

The most likely state(s) that could intervene in the formation of the RO complex must be the binding of R to the many nonspecific binding sites present in the dsDNA molecule, suggesting that the overall binding reaction should be written as

$$\begin{array}{l}\mathrm{R}+m\mathrm{D}+\mathrm{O}\iff {\text{RD}}_1+\mathrm{O}\iff \mathrm{........}\\ \hfill \iff {\text{RD}}_i+\mathrm{O}\iff \text{RO}+m\mathrm{D},\hfill \end{array}$$ (6)

where m is the number of nonspecific binding sites present in the genomic DNA and RD_1→i represents the series of intermediate RD complexes formed during the search process, and that this nonspecific binding must lead to facilitated target location by reducing the dimensionality of the target location process from a three- to a two- or a one-dimensional problem (1, 64, 80). This initial observation and interpretation has intrigued biophysicists for years and has led to an explosion of theoretical and experimental investigations of this phenomenon with many experimental systems (21, 25).

It was early suggested that diffusion in reduced dimensions should include processes such as one-dimensional sliding along the DNA, as well as short-range hopping (local dissociation and rebinding) and direct interstrand transfer of the regulatory protein between segments of the dsDNA polymer (Figure 5). All these mechanisms must be driven by diffusion, and clearly none of these reactions can be faster than the free solution diffusion of repressor in one dimension. The reason for the apparent increase in the observed rate of operator site location by the repressor must lie in preventing or limiting excursions of the protein into the three-dimensional diffusion mode, thus reducing the volume through which the target search must be conducted.

Figure 5.

Schematic views of lac repressor (R) interacting with large operator-containing DNA molecules in dilute solution. The DNA molecules are shown well separated into domains. The (upper right) expanded view shows R bound to a segment of nonspecific DNA, on which it can slide or hop in one-dimensional processes or engage in three-dimensional association-dissociation reactions in seeking its specific (operator) target site. The (lower right) expanded view shows a repressor molecule doubly bound to two DNA segments, corresponding to an intermediate in the intersegment transfer process. Modified from Reference 80.

The initial experimental studies of such systems were conducted in dilute solution with naked dsDNA, at low concentrations of regulatory proteins, and generally at low salt concentrations to increase nonspecific binding (7, 89). These studies showed that, although hopping and intersegment transfer within the dsDNA random coil were involved, sliding mechanisms dominated the observed kinetics of target location under these conditions. These early studies were performed as a function of salt concentration by standard filter-binding methods (the binding of R to O was essentially irreversible on the timescale of the experiment) to measure the apparent kinetics of operator location, with extensive theoretical modeling performed to interpret the kinetics in mechanistic terms (9). The outcome was quantitatively reasonable and showed that lac repressor slides along ds-DNA with a one-dimensional diffusion coefficient that is approximately one-tenth that of the one-dimensional diffusion constant of the protein in free solution. These experiments also showed that the search process shifts from mostly sliding at low salt toward more intersegment transfer and local dissociation of repressor with increasing salt concentration (22, 66, 80). The interpretations of Record and coworkers (61, 62) of the nonspecific binding of proteins to DNA in terms of polyelectrolyte theory and ion condensation provided a reasonable mechanistic model for how a positively charged protein (or one with a positively charged binding site) in a nonspecifically bound conformation might engage in essentially isoenergetic one-dimensional sliding over dsDNA, with rapid conformational fluctuations into a specific binding form permitting recognition of the hydrogen-bonding matrix of the target site when encountered during the sliding process (89) (Figure 5).

More recently these initial studies have been extended by single-molecule techniques of various types, permitting direct visualization of the facilitated transfer processes and showing, in particular, that one-dimensional sliding of the nonspecifically bound conformation of the protein along the charged sugar-phosphate backbones of the DNA duplex actually occurs along a helical path (31). Such helical sliding along the dsDNA backbones should optimally position the protein for effective scanning of the hydrogen-bonding patterns of the dsDNA from the grooves, with recognition involving a rapid conformational shift of the protein into a specific target recognition conformation (80, 89) (Figure 4). These approaches have also been semiquantitatively extended to more complex situations involving target location by regulatory proteins on genomes partially covered with other proteins or even folded into chromatin at physiological salt concentrations (33, 34). Under these conditions movement of the protein on the DNA by hopping and intersegment transfer probably dominates, with sliding pathways significantly shortened and serving primarily to facilitate the final docking of the protein on the DNA target site.

CHEMICAL FREE ENERGY AND THE REGULATION OF MACROMOLECULAR MACHINES

Both the conformational changes involved in the function of these complexes and the transport of these complexes and their components from one position to another are driven by diffusion, either in three dimensions or in reduced dimensions as described above. The existence of multiple conformational states and such facilitated diffusion, coupled with the potential multiplicity of subunit interactions, provides great potential mechanistic diversity and makes many biological reactions accessible. Nevertheless, reliance on diffusion has its limits, because the states available to a macromolecule or macromolecular system are effectively confined to those with conformations that differ in free energy by only two to three times kT, or that are separated by transition state barriers that are only a few kcal per mol in height and thus surmountable at reasonable rates under physiological conditions. This effectively means that a given molecule or complex can reach only a limited set of energy levels of a potential Boltzmann distribution of conformations, and that higher levels cannot be sufficiently populated to permit the associated interactions to proceed at reasonable rates or to reasonable extents on a biological timescale (23, 88). In addition, the rate of transport of macromolecules by diffusion is slow, both because proteins and DNA molecules are large and asymmetric and characterized by significant frictional coefficients, and because the distance over which a particle can be moved by diffusion is proportional to the square root of time $\left(\sqrt{t}\right)$.

Biology has found a way around this problem, because chemical free energy can also be utilized to drive both transport and conformational changes in cells. Generally ATP is the fuel of choice for driving biological transport and interactions, and the helicases that unwind double-stranded nucleic acids, as well as the molecular motors that carry cargo along cytoplasmic filaments, hydrolyze ATP in performing their functions. As a result, at saturating ATP concentrations tightly coupled (low slip) motors driven by ATP hydrolysis move over defined distances with a velocity that is directly proportional to time (5, 75), rather than with the much slower $\sqrt{t}$ dependence characteristic of diffusion. ATP binding and hydrolysis are also used to drive conformational change within the macromolecular machines of gene expression, and this permits fluctuations into conformational states and over barriers that are significantly higher than those that can be effectively surmounted by simple diffusion-driven reactions.

How does ATP bring this about? Most macromolecular machines of gene expression contain ATPases, and it was long thought that chemical free energy was released to drive these machines by the hydrolysis of one or both of the high-energy phosphate bonds (α-β or β-γ) of this ubiquitous biological substrate. More recently, however, it has become clear that it is usually ATP binding, rather than hydrolysis, that provides the free energy required to drive the necessary conformational changes, and that the purpose of the subsequent ATP hydrolysis is primarily to reset the system by forming the less tightly bound products (ADP and P_i or AMP and PP_i) of the hydrolysis reaction that are then subject to facile release from the ATP binding site. Systems that use such repeated cycles of ATP binding, hydrolysis, and release to move processively along their biological tracks include the various cytoplasmic motors and DNA replication helicases of the cell; the generality of such repeated ATP cycle reactions as the major motive force of biological transport is discussed in Reference 81. Cycles of ATP binding, hydrolysis, and release are also involved in many of the essential non-transport processes of the machines of gene expression. For example, this mechanism is used by the clamp-loading machinery of DNA replication to load the sliding clamps that hold the replication polymerases onto their respective leading- and lagging-strand templates, with ATP binding driving the process of loading the clamp onto the replication fork and ATP hydrolysis serving primarily to reset the system by releasing the clamp-loading assembly from the template DNA and from the clamp (29, 54).

A common theme in these systems is that conformational fluctuations of the components of macromolecular machines, either produced directly by thermal motion or initiated by such processes and then stabilized by the binding of ligands such as ATP, make reactive states accessible for trapping by appropriate subunit domains or interfaces. Thus helicases presumably trap and accumulate single-base-pair unwinding events that form at significant rates at replication forks and at the downstream edges of transcription bubbles (81). We are currently using near-UV spectroscopic probes, such as pairs of 2-aminopurine residues (11, 30) inserted site specifically into dsDNA oligomer models of replication forks and primer-template junctions, to monitor local breathing events at such loci and to examine how they are trapped and accumulated by helicases (D. Jose, N.P. Johnson, K. Datta & P.H. von Hippel, unpublished results). Others are using related ideas to approach allostery as a dynamic process (56).

FROM ATP BINDING AND HYDROLYSIS TO SIGNAL TRANSDUCTION AND CHROMATIN REMODELING

The ATP binding, hydrolysis, and release cycles that drive many conformational changes in prokaryotes are more analogous than they seem to the signal transduction and chromatin remodeling pathways that direct and control the machinery of gene expression in eukaryotes. Thus ATP binding (with its attendant changes in local charge distributions and interacting groups) makes new reactive conformations available or stabilizes potentially reactive states that cannot be significantly populated by thermal fluctuations alone. We can think of site-specific phosphorylation, acetylation, and methylation by histone-modification and chromatin-remodeling complexes (which are often driven by ATP binding and hydrolysis) as similarly providing surfaces or domains of modified interaction potential (18), with the associated phosphatases, deacetylases, and so forth serving to reset these systems in the same way as ATP hydrolysis does in lower organisms. However, the use of large numbers of exogenous enzymes and enzyme complexes to covalently attach and remove a variety of surface-modifying groups makes the eukaryotic palette of available chemical reactions and transconformation rates much richer.

ASSEMBLING AND CONTROLLING THE MACROMOLECULAR MACHINES OF GENE EXPRESSION

The above catalog of mechanisms, processes, and interactions, used in various combinations, serves to assemble, regulate, and control the functions and interactions of the protein–nucleic acid complexes involved in gene expression. As these assemblies become larger and more complex it becomes increasingly more important to regulate stringently their thermodynamics and kinetics. As described elsewhere (23), many of these machines have the potential to catalyze a variety of kinetically competing reactions, and how they function and interact depends on which reaction is favored under various cellular conditions. For example, the complexes that drive DNA replication, transcription, recombination, and repair all contain one or more central template-directed DNA or RNA polymerases, which in the absence of regulatory components and subunits are generally slow, nonprocessive, and ineffective. Polymerases only become biologically useful in coordinating the competing reaction pathways of the cell cycle, cellular metabolism, and development in the presence of a host of additional macromolecular components, all of which must be balanced and programmed to interact specifically by combinations of the simple protein-protein and protein–nucleic acid reaction mechanisms described here. We are still a long way from fully understanding any complete biological process or disease at this level, but if we hope ultimately to control or modify these processes in a less haphazard way, we must continue to strive to understand them at the level of physical chemistry.

SUMMARY POINTS

1. Protein and nucleic acid folding and assembly into specific structures and complexes are driven by the interactions of defined linear sequences of amino acid (and nucleotide) residues with the aqueous solvent environment.

2. DNA is a polyelectrolyte, and the nonspecific binding of proteins to DNA is largely electrostatic and is driven by the displacement of condensed counterions.

3. Base-pair-sequence-specific binding of proteins to DNA has structural, coding, and thermodynamic components. Most regulatory binding proteins have a specific and a nonspecific binding conformation.

4. The kinetics of target site location on the DNA genome by regulatory proteins depends on diffusion in reduced dimensions of these proteins in their nonspecific binding form.

5. Conformational rearrangements and translocation of proteins on DNA are driven by diffusion via thermal fluctuations or by chemical free energy derived from cycles of ATP binding and hydrolysis.

6. Conformational rearrangements driven by covalent modification at the chromatin level in eukaryotes are analogous to the reactions driven by ATP binding and hydrolysis in prokaryotic systems.

7. The same physicochemical principles are involved in the assembly of “simple” protein-DNA complexes and in the complex signal transduction networks that control gene expression in higher organisms.

Glossary

Macromolecular machines of gene expression

complexes that interact, directly or indirectly, with the DNA genome in driving and controlling DNA replication (including recombination and repair), transcription, and protein synthesis

dsDNA breathing

the transient and local unpairing of the duplex DNA genome driven by thermal fluctuations

Helicases

ATP-driven molecular motors that unwind duplex DNA (or RNA) replication and transcription

lac repressor

the paradigmatic transcriptional regulatory protein used to develop many of our ideas of specific and nonspecific binding mechanisms

Nucleosomes

the basic structures of chromatin, formed by wrapping DNA around a core of histone oligomers

Chromatin

the structure imposed on the DNA genome by the formation of nucleosomes and their higher-order folding

Information content

the number of base pairs in a linear sequence that must be specified to define a unique genomic DNA binding site