Enumeration of condition-dependent dense modules in protein interaction networks

Abstract

Motivation: Modern systems biology aims at understanding how the different molecular components of a biological cell interact. Often, cellular functions are performed by complexes consisting of many different proteins. The composition of these complexes may change according to the cellular environment, and one protein may be involved in several different processes. The automatic discovery of functional complexes from protein interaction data is challenging. While previous approaches use approximations to extract dense modules, our approach exactly solves the problem of dense module enumeration. Furthermore, constraints from additional information sources such as gene expression and phenotype data can be integrated, so we can systematically mine for dense modules with interesting profiles.

Results: Given a weighted protein interaction network, our method discovers all protein sets that satisfy a user-defined minimum density threshold. We employ a reverse search strategy, which allows us to exploit the density criterion in an efficient way. Our experiments show that the novel approach is feasible and produces biologically meaningful results. In comparative validation studies using yeast data, the method achieved the best overall prediction performance with respect to confirmed complexes. Moreover, by enhancing the yeast network with phenotypic and phylogenetic profiles and the human network with tissue-specific expression data, we identified condition-dependent complex variants.

Availability: A C++ implementation of the algorithm is available at http://www.kyb.tuebingen.mpg.de/~georgii/dme.html.

Contact: koji.tsuda@tuebingen.mpg.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Today, a large number of databases provide access to experimentally observed protein–protein interactions (PPIs). The analysis of the corresponding protein interaction networks can be useful for functional annotation of previously uncharacterized genes as well as for revealing additional functionality of known genes. Often, function prediction involves an intermediate step where clusters of densely interacting proteins, called modules, are extracted from the network; the dense subgraphs are likely to represent functional protein complexes (Sharan et al., 2007). However, the experimental methods are not always reliable, which means that the interaction network may contain false positive edges. Therefore, confidence weights of interactions should be taken into account.

A natural criterion that combines these two aspects is the average pairwise interaction weight within a module [assuming a weight of zero for unobserved interactions (Ulitsky and Shamir, 2007)]. We call this the module density, in analogy to unweighted networks (Bader and Hogue, 2003). We present a method to enumerate all modules that exceed a given density threshold. It solves the problem efficiently via a simple and elegant reverse search algorithm, extending the unweighted network approach by Uno (2007). Remarkably, the required computation time between two consecutive solutions is polynomial in the input size. The contribution of our article consists in (i) the development of a dense module enumeration (DME) algorithm for weighted networks, including a ranking scheme and an efficient strategy to identify locally maximal modules, (ii) its application to the protein interaction networks of yeast and human and (iii) the effective integration of constraints from additional data sources.

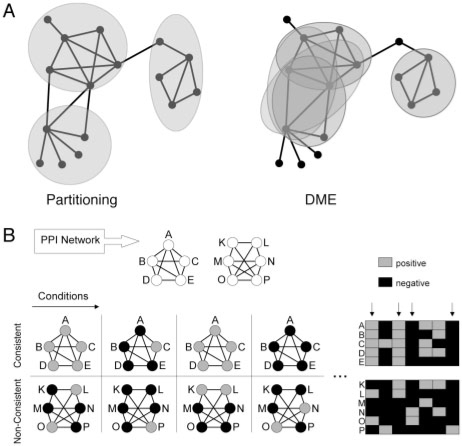
There is a large variety of related work on module discovery in networks. The most common group are graph partitioning methods (Chen and Yuan, 2006; Newman, 2006; van Dongen, 2000). They divide the network into a set of modules, so their approach is substantially different from DME, which provides an explicit density criterion for modules (Fig. 1A). Another group of methods define explicit module criteria, but employ heuristic search techniques to find the modules (Bader and Hogue, 2003; Everett et al., 2006). This contrasts with complete enumeration algorithms, which form the third line of research: they give explicit criteria and return all modules that satisfy them. For example, clique search has been frequently applied (Palla et al., 2005; Spirin and Mirny, 2003). The enumeration of cliques can be considered as a special case of our approach, restricting it to unweighted graphs and a density threshold of one. Further enumerative approaches use different module criteria assuming unweighted graphs (Haraguchi and Okubo, 2006; Zeng et al., 2006).

Fig. 1.

DME approach. (A). DME versus partitioning. While partitioning methods return one clustering of the network, DME discovers all modules that satisfy a minimum density threshold. (B). Combination with profile data. Integration of PPI and external profile data allows to focus on modules with consistent behavior of all member proteins in a subset of conditions.

Biological complexes are dynamic objects of changing composition. In particular, many proteins are not steadily present in the cell, but specifically expressed depending on organism, cell type, environmental conditions and developmental stage (Gavin et al., 2002). Module enumeration offers a meaningful way to detect such variations of complexes. Our DME algorithm can easily incorporate constraints from additional information like gene expression, evolutionary conservation, subcellular localization or phenotypic profiles. Thus, the search can be guided directly towards the modules of interest, for example, modules that show coherent behavior in a subset of conditions. The external data sources can provide further evidence for functional relationships of proteins and yield insights about possible functional roles of complexes and subcomplexes in different cellular contexts.

In recent years, many module finding approaches which integrate PPI networks with other gene-related data have been published. One strategy, often used in the context of partitioning methods, is to build a new network whose edge weights are determined by multiple data sources (Hanisch et al., 2002). Tanay et al., 2004 also create one single network to analyze multiple genomic data at once; however, they use a bipartite network where each edge corresponds to one data type only. In both cases, the different datasets have to be normalized appropriately before they can be integrated. In contrast to that, other approaches keep the data sources separate and define individual constraints for each of them. Consequently, arbitrarily many datasets can be jointly analyzed without the need to take care of appropriate scaling or normalization. Within this class of approaches, there exist two main strategies to deal with profile data like gene expression measurements. In the first case, the profile information is transformed into a gene similarity network, where the strength of a link between two genes represents the global similarity of their profiles (Pei et al., 2005; Segal et al., 2003; Ulitsky and Shamir, 2007). In the second case, the condition-specific information is kept to perform a context-dependent module analysis (Huang et al., 2007; Ideker et al., 2002; Yan et al., 2007). Our approach follows along this line, searching for modules in the PPI network that have consistent profiles with respect to a subset of conditions. In contrast to the previous methods, our algorithm systematically identifies all modules satisfying a density criterion and optional consistency constraints.

In this study, we evaluate our approach on the yeast interaction network in comparison with four other methods. Also, we report yeast modules restricted by evolutionary conservation and phenotypic profiles. Furthermore, we discuss our results obtained from human protein interactions in the context of gene expression data.

2 MODULE MINING APPROACH

We address the problem of extracting functional modules from PPI data using an enumerative density-based mining approach. Today, there exist various experimental techniques to determine PPIs. To analyze these data, it is common practice to integrate all interactions into one network where each node represents a protein, and an edge between two nodes indicates an interaction (Sharan et al., 2007). Then node sets with higher density in the interaction network are more likely to represent functional protein complexes. We propose a method to exhaustively enumerate all modules which satisfy a minimum density threshold. To avoid spurious modules, confidence weights of interactions are taken into account. In this section, we first describe the basic algorithm and then show how to integrate additional constraints in this framework. Finally, we explain our module ranking criterion.

2.1 Dense module enumeration

Formally, let us consider the interaction network as undirected weighted graph with node set V. Let W=(w_ij)_i,j∈V be the corresponding matrix representation, containing positive weight entries for the given interactions and zero entries otherwise (for missing edges). In the following, we assume w_ij≤1. Although we use weight matrices with non-negative entries in this work, the approach is suitable for mixed-sign data as well. A module is defined as a set of nodes U⊂V and its induced subgraph. The density of U refers to the average pairwise weight, given by

(1)

The largest possible density value is 1 [we define ρ_W(U)≔1 for |U|=1]. Now we define the problem of DME as follows.

Definition 1. Given a graph with node set V and weight matrix W, and a density threshold θ>0, find all modules U⊂V with ρ_W(U)≥θ.

The key point of any enumeration algorithm is the definition of an appropriate structure of the search space which allows for efficient traversal and pruning. To enumerate sets of entities, a canonical approach is to start with the empty set and then iteratively form larger sets by adding one element at a time; if it is evident that no further solutions can be derived from a certain set, the process of extension is stopped, i.e. unnecessary parts of the search space are pruned. It turns out that conventional pruning strategies as used in itemset mining (Han and Kamber, 2006), for example, are not suitable for DME. The reason is that supersets of a module can in general have arbitrarily higher or lower density than the module itself (see Supplementary Material). However, it is possible to traverse the search space in a way that allows for straightforward pruning. In fact, we define a tree-based parent–child relationship between modules such that along each path from the root to a leaf, the module size is increasing, whereas the module density is monotonically decreasing. Technically, our algorithm adopts the reverse search paradigm (Avis and Fukuda, 1996): in each iteration, we generate all direct supersets of the current module and select those which are indeed its children. Due to the monotonicity guarantee in our search tree, only children that fulfill the density criterion have to be further processed. To describe our approach in more detail, we need the definition of weighted degree.

Definition 2. Let W be the given weight matrix. For u∈U⊂V, the weighted degree of u with respect to U is defined as

The following lemma yields the key for defining the search tree.

Lemma 1. Let v∈U be a node with minimum weighted degree in U, i.e. ∀u∈U:deg_W(u, U)≥deg_W(v, U). Then, ρ_W(U ∖ {v})≥ρ_W(U).

The proof is given in the Supplementary Material. Further, we introduce a function ord, which defines a strict total ordering on the nodes, i.e. for each node pair u, v with u≠v either ord(u)<ord(v) or ord(u)>ord(v) holds. With this, we define the parent–child relationship for modules.

Definition 3. Let U be a module and v∈V ∖ U. U*≔U∪{v} is a child of U if and only if ∀u∈U one of the following conditions holds:

1. deg_W(v, U*)<deg_W(u, U*)

2. deg_W(v, U*)=deg_W(u, U*)∧ord(v)<ord(u)

In other words, we obtain the unique parent of a module by removing the smallest among the nodes with minimum weighted degree. From the lemma we know that each module has a smaller or equal density than its parent. Based on this, the DME algorithm starts with the empty set and recursively generates children as long as the density threshold is not violated (Algorithm 1), yielding thereby the complete set of dense modules. By the definition of the parent–child relationship, we cannot directly derive the children of a module U. Instead, we have to check for all possible extended modules with one additional node whether U is their parent or not (reverse search principle). In terms of complexity, DME belongs to the class of polynomial-delay algorithms, which means that, independently of the size of the results, the computation time between two consecutive solutions is polynomial in the input size (see Supplementary Material). By changing the density threshold, the user can regulate the size of the output. Also note that the computation can easily be parallelized. Finally, dense modules that are subsets of other solutions are not so informative; we call them non-maximal. While these redundant results could be eliminated by checking for each new module all previous solutions, it is possible to identify locally maximal modules without requiring additional computation or storage, as shown in Algorithm 1. A module U is locally maximal if and only if for all v∈V∖U, U∪{v} does not satisfy the minimum density threshold. Although a module with this property could still be non-maximal, it happens rarely in practice.

2.2 Integration of additional constraints

The DME framework makes it easy to incorporate and systematically exploit constraints from additional data sources. For illustration, consider the case where we have an additional dataset which provides profiles of proteins or genes across different conditions (Fig. 1B). For simplicity, let us assume binary profiles, being 1 if the protein is positively associated with the corresponding condition, and 0 otherwise. Then, dense modules where all member proteins share the same profile across a certain number of conditions are of particular interest; we call these modules consistent. The problem of DME with consistency constraints is formalized as follows.

Definition 4. Given a graph with node set V and weight matrix W, a density threshold θ>0, a profile matrix (m_ij)_i∈V,j∈C and non-negative integers n₀ and n₁, find all modules U⊂V with ρ_W(U)≥θ s.t. there exist at least n₀ conditions c∈C with m_uc=0 ∀u∈U and there exist at least n₁ c∈C with m_uc=1 ∀u∈U.

Given such a consistency constraint, we can stop the module extension during the dense module mining as soon as the constraint is violated. This is due to the fact that the number of consistent profile conditions cannot increase while extending the module; more generally, this property is called anti-monotonicity (see Supplementary Material). So we simply add to line 4 of the algorithm a further condition which checks for the consistency requirements. These are then automatically taken into account in the check for local maximality. The use of additional constraints can restrict the search space considerably, so it accelerates the computation and helps to focus on biologically interesting solutions. The described framework can incorporate any kind of anti-monotonic constraints. Furthermore, one can use arbitrarily many of those constraints at the same time. Sometimes, one might be interested in incorporating non-anti-monotonic constraints. While they cannot be directly exploited for pruning, they can be used to filter the obtained modules. As an example, our software allows to specify a minimum weighted degree threshold t such that deg_W(u, U)>t for all nodes u of all modules U. We set t=0 throughout the article.

2.3 Module ranking

The exhaustiveness of our DME approach enables us to exactly determine the uncommonness of the discovered substructures with respect to the network at hand. Let W=(w_ij)_i,j∈V be the matrix representation of the given network; the total number of nodes is denoted by |V|. Let U be a module with |U| nodes and density ρ_W(U). Then, the probability that a random selection of |U| nodes in the network produces a module with at least the same density as U is given by

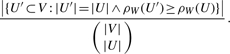(2)

The exact value of the numerator can be obtained as a side product of the DME algorithm. In the case of additional constraints, it includes only modules that satisfy them. The modules in the DME output are sorted by their probability values (in ascending order). This ranking scheme captures the intuition that the rank of a module should increase with its size and density, but from a theoretical point of view it is more principled than the ranking criterion used by Bader and Hogue (2003), which is the product of size and density. Furthermore, our probability calculation refers specifically to the network at hand, in contrast to measures derived from network models (Koyuturk et al., 2007).

3 EXPERIMENTAL RESULTS

3.1 PPI data

For our experiments with yeast (Saccharomyces cerevisiae), we combined protein interactions in PSI-MI format from DIP (Xenarios et al., 2000) and MPact (Guldener et al., 2006), which includes data from IntAct (Hermjakob et al., 2004), MINT (Chatr-aryamontri et al., 2007) and BIND (Bader et al., 2003), and interactions from the core datasets of the TAP mass spectrometry experiments by Gavin et al. (2006) and Krogan et al. (2006). For the human analysis, interactions were extracted from the IntAct, MINT, BIND, DIP and HPRD (Peri et al., 2004) databases.¹ One main challenge in the analysis of protein interaction networks are false positive edges. To deal with this, we determined edge weights that indicate the reliability of the corresponding experimental techniques, following the method by Jansen et al. (2003) (see Supplementary Material for details). The resulting interaction network for yeast consisted of 3559 nodes with 14 212 non-zero interactions having an average weight of 0.67. The human network contained 9371 nodes and 32 048 non-zero interactions having an average weight of 0.47.

3.2 Comparative analysis

First, we validated the performance of DME on the yeast interaction network in comparison with four other methods: clique detection (Clique, implementation from http://www.cfinder.org.), the clique percolation method (CPM, implementation from http://www.cfinder.org.) (Palla et al., 2005), a procedure for joining cliques of a certain size to larger clusters, CPMw (implementation from http://www.cfinder.org.) (Farkas et al., 2007), an extension of CPM which includes an additional clique filtering step, and Markov clustering (MCL, implementation from http://micans.org/mcl.) (van Dongen, 2000), a popular graph clustering method simulating random walks. As a reference set of confirmed complexes, we used the manually curated protein complexes provided by MIPS (Guldener et al., 2005). To properly assess methods which can produce overlapping modules, we chose performance measures that are based on protein pairs rather than modules; in that way, we avoid taking the same subset of nodes several times into account even if it occurs in more than one module. Defining the intersection of pairs from predicted modules and pairs from known complexes as correctly predicted pairs, we calculated precision and recall as follows.

(3)

(4)

To obtain precision–recall curves, we iteratively calculated the precision and recall values, each time extending the set of considered modules by the next highest-ranking module. As the other methods do not provide a module ranking and our criterion is only applicable to enumerative approaches, we used the scoring scheme by Bader and Hogue (2003) mentioned in Section 2.3. In fact, it produced for our DME results almost the same ranking as our criterion; the corresponding precision–recall curves are virtually equivalent. For each method, we tested a wide range of parameters (see Supplementary Material) and selected the configuration with the largest area under the precision–recall curve for Figure 2. Clique and CPM cannot handle edge weights directly, but they preselect edges according to a minimum weight threshold.

Fig. 2.

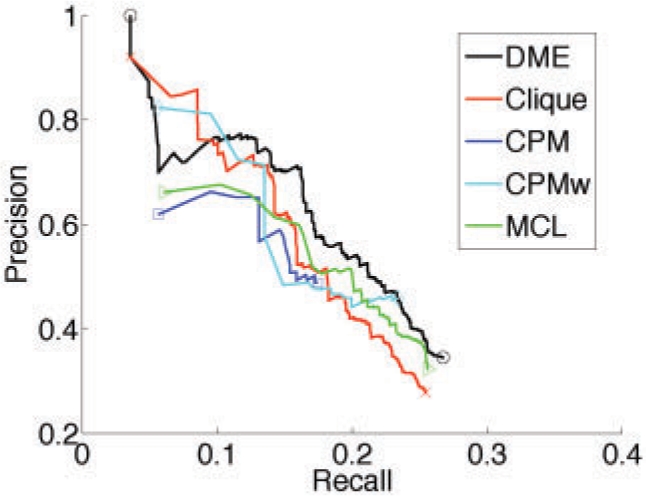
Comparative precision–recall analysis. To account for module overlap, the measures are based on protein pairs, see text.

Overall, DME shows the best prediction performance. It has high precision with respect to the highest-ranking modules and then shows a sudden drop, which is due to a big module not annotated as a known complex. Clique detects the same module, but there are some other higher ranked modules, so the drop happens later. MCL and CPM stay always below DME. Clique works quite well, however the precision drops quickly for higher recall values because edge weights are not taken into account. It seems that DME has a clear advantage compared to CPM: by explicitly using the edge weights and tuning the density parameter, it allows for more flexibility than the two-stage procedure of CPM, first selecting edges and subsequently joining together cliques that satisfy an overlap criterion. While CPMw allows to refine the module search, it still differs significantly from our approach. As it joins preselected cliques, it does not control directly the density of the produced modules and might also miss some dense modules. In our analysis, CPMw improved the result obtained by CPM, but is mostly inferior to Clique or DME.

Table 1 summarizes further statistics for the predicted modules. As DME and Clique produced a large number of very similar modules, we computed for better comparability the number of distinct modules. For that purpose, we grouped matching modules into clusters; each cluster was represented by its top-ranking module. To decide whether two modules match each other, we here computed the overlap score proposed by Bader and Hogue (2003), using a stringent cutoff of 0.5. It is defined as the fraction of overlapping proteins with respect to the size of the first module multiplied by the fraction of overlapping proteins with respect to the size of the second module. The same criterion was used to determine matches between predicted modules and known complexes. While DME and Clique discovered a comparable number of distinct modules, the DME modules match many more known complexes. Among these, we also find small-sized complexes, so the overall average size of retrieved complexes is lower than that for Clique. In addition, we report the number of complexes from which at least one protein pair was recovered as well as the area under the precision–recall curve from the pairwise analysis (Fig. 2). In both cases, DME is leading. Furthermore, we investigated the enrichment of the distinct modules with respect to Gene Ontology (GO) terms. For that purpose, we applied the TANGO tool (Shamir et al., 2005) using the default setting with P-value threshold 0.05 after correction for multiple testing. Beside the total number of enriched modules, we also counted the number of enriched modules among the top 50 distinct modules, showing that for each method that produced more than 50 modules, most of the high-ranking modules satisfy the enrichment threshold. For small modules the enrichment test fails even if they are totally pure.

Table 1.

Module statistics of the comparative analysis (see text for details).

	DME	Clique	CPM	CPMw	MCL
No. of distinct modules	1083	916	19	32	648
Average size of distinct modules	3	4	16	14	3
No. of raw modules	24 803	1971	19	33	648
Average size of raw modules	10	6	16	14	3
No. of matched complexes	84	54	9	20	59
Average complex size	5	7	19	14	7
No. of partially recovered complexes	133	107	20	33	117
No. of predicted interactions	5970	7066	2756	3935	6108
Area under prec.-rec. curve (AUC)	0.183	0.166	0.107	0.153	0.148
No. of enriched distinct modules	112	131	18	32	69
No. of enriched among top-50	47	44	–	–	45
No. of overlapping proteins	1010	1113	12	38	1
No. of overlapping interactions	3664	4340	24	114	0
AUC for overlapping interactions	0.152	0.082	0.000	0.001	–
No. of recovered complex overlaps	18	16	0	4	0
Running time (s)	2667	6	5	457	4

The average size of the raw modules can be larger than that of the distinct modules because larger modules allow for more variants. The time measurements were performed on a 2.2 GHz processor.

Finally, we assessed the impact of detecting overlapping modules. Concerning the number of proteins or protein pairs that appear in more than one module, there is large variation among the different methods. DME and Clique produced the largest numbers of overlapping proteins and overlapping pairs. Remarkably, the accuracy of overlapping DME interactions clearly increases with the number of modules in which they occur, whereas this is not true for Clique, as reflected by the difference of their AUC values (see also Fig. 4 in the Supplementary Material). The overall precision of overlapping pairs is 45% for DME and 35% for Clique. We also analyzed how many overlaps between known complexes were rediscovered by predicted modules. Formally, we counted the cases of overlapping known complexes C₁ and C₂ where there existed overlapping modules M₁ and M₂ such that the following conditions were satisfied: (i) M₁∩M₂ contains at least one element of C₁∩C₂, (ii) M₁∖M₂ contains at least one element of C₁∖C₂ and (iii) M₂∖M₁ contains at least one element of C₂∖C₁. Here, the number of recovered overlaps was only slightly higher for DME.

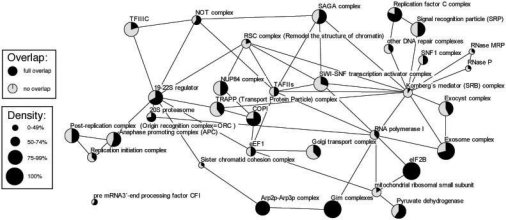
Fig. 4.

Yeast complexes matched by DME modules and their overlap with conserved DME modules. Only complexes with size ≥5 are shown. The node size corresponds to the density of the confirmed complex, and the pie chart indicates to which degree the complex is covered by a conserved module. Nodes are connected if there exist interactions between the corresponding sets of matching modules.

3.3 Phenotype-associated yeast modules

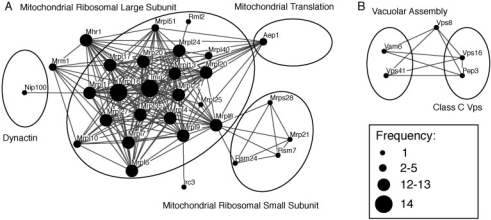
An additional feature of DME is the possibility to directly integrate constraints from external data sources. In this section, we investigated our yeast interaction network in the context of knockout phenotypes in order to identify essential parts of protein complexes. We took the growth phenotype profiles for knockout mutants in yeast under 21 experimental conditions (Dudley et al., 2005), considering three different phenotypic states: enhanced growth, normal growth, and growth defect. We applied DME requiring for each module at least one condition consistently associated with growth defect for all members. In order to get a set of modules covering a large number of proteins, but being at the same time as reliable as possible, we tested density thresholds between 0.95 and 0.80 using decrements of 0.01 and selected the one with the largest area under the precision–recall curve.

The results are summarized in Table 2. Each of the 13 highest-ranking modules covers a considerable part of the mitochondrial ribosomal large subunit as annotated by MIPS. In addition, our output list contained one further module that overlaps with the complex. Figure 3A shows the superposition of these 14 modules. Mrpl16 and Img2 appear in all, many other proteins in almost all of those modules, so they can be considered as the core of the complex. Knockout of any of the shown proteins caused growth defects with glycerol as carbon source. Some module members belong to other MIPS complexes, as depicted by the ellipses. In particular, there is a strong connection to the small subunit of the mitochondrial ribosome and to the mitochondrial translation complex. Furthermore, our results suggest that the mitochondrial ribosome is associated with Mhr1, a protein involved in homologous recombination of the mitochondrial genome (Ling et al., 2000). Some modules that are not related to MIPS complexes nevertheless represent known complexes. For instance, we exactly recovered the nucleoplasmic THO complex (Hpr1, Mft1, Rlr1, Thp2), which is known to affect transcription elongation and hyper-recombination (Chavez et al., 2000). Interestingly, all mutants exhibit growth defects under the stress condition of adding ethanol to the medium. Finally, in Figure 3B we show the highest-ranking module which covers at least 50% of two different MIPS complexes. The corresponding proteins are associated with growth defects under addition of the aminoglycoside hygromycin B. The module links the vacuolar assembly complex with the class C Vps complex. The latter is a specific subgroup of proteins involved in vacuolar protein sorting. Indeed, it has been shown that this complex associates with Vam6 and Vps41 to trigger nucleotide exchange of a rab GTPase regulating the fusion of vesicles to the vacuole (Wurmser et al., 2000).

Table 2.

Results of DME experiments with constraints

	Phenotype	Conservation	Expression
	(yeast)	(yeast)	(human)
No. of distinct modules	137	1067	460
Average size of distinct modules	3	3	2
No. of raw modules	160	1816	736
Average size of raw modules	4	5	3
No. of matched complexes	14	49	52
Average complex size	4	4	4
No. of partially recovered complexes	30	103	217
Running time (s)	19	5	8

Fig. 3.

Phenotype-associated yeast modules. (A). Superposition of all 14 modules overlapping with the large subunit of the mitochondrial ribosome (node size depends on the number of modules in which the protein occurs). (B). Module linking two complexes. The ellipses mark protein sets belonging to known complexes. For module visualization we used the Osprey tool (Breitkreutz et al., 2003).

3.4 Evolutionary conserved yeast modules

Next, we used the evolutionary conservation of proteins as side constraint for DME. For that purpose, we extracted for all yeast genes orthologs from the InParanoid database (O'Brien et al., 2005) with respect to 10 other representative eukaryotic species from Schizosaccharomyces pombe to Arabidopsis thaliana. More precisely, we created a profile indicating for each S.cerevisiae gene and each other model species whether there exist orthologs with a full inParanoid score in the other model species. We searched for modules in the yeast interaction network such that all member proteins have orthologs in at least three other species; the density threshold was determined using the same procedure as before (for a summary of the results, see Table 2).

Figure 4 shows an overview of the larger MIPS complexes which were retrieved in our DME results, with or without the conservation constraint. To define matches between complexes and predicted modules, we used the same criterion as in Section 3.2. Apparently, we could identify some low-density complexes by discovering their dense core parts, for example the translation elongation factor complex eEF1 and the pre-mRNA 3^′-end processing factor CFI. In black, we indicate the percentage of the known complex that is covered by a conserved dense module. From the total set of 33 recovered complexes shown in the figure, 19 overlap by at least 50% with such a module. Among them, we find the 20S proteasome and its cap and the translation initiation factor eIF2B complex. The remaining complexes have rather small overlaps with conserved modules, even though they are quite accurately matched by their unconstrained counterparts. Our conserved module predictions reveal putative core parts of complexes that are conserved across several species. As an example, we analyze the SNF1 complex, an essential element of the glucose response pathway consisting of six proteins. Indeed, while the components Snf1, Snf4 and Sip2 are strongly conserved in all eukaryotes and are covered by a conserved module, Sip1 and the transcription factor Sip4 have no orthologs in other species, and the Gal83 component has orthologs in two species only (Vincent and Carlson, 1999). Our approach predicted one additional conserved component of the complex, Sak1. This is biologically meaningful, as it functions as an activating kinase of the SNF1 complex (Elbing et al., 2006). The unconstrained module contained Sak1 and all SNF1 components except Sip4.

3.5 Tissue-specific modules in the human interaction network

Finally, we were interested in tissue-specific modules of the human interaction network. As side information, we downloaded the gene expression profiles by Su et al. (2004), containing measurements in 79 different human tissues and present/absent/marginal calls. For our purposes, we considered a gene to be expressed in a given tissue only if it was classified as present in both of the duplicated measurements. In order to find complexes which are present in several, but not all tissues, we applied DME to enumerate all modules that are consistently expressed in at least three tissues and consistently not expressed in at least 10 tissues. We used again the same procedure for selecting the density parameter and ended up with 460 distinct modules (Table 2).

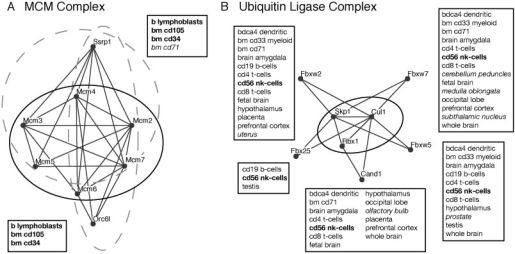
The two top-ranking modules cover the MCM complex (Fig. 5A). As a reference, we used a manually curated set of human complexes collected by MIPS (Ruepp et al., 2008). MCM is a hexameric protein complex required for the initiation and regulation of eukaryotic DNA replication. The DME modules contain two additional proteins, Ssrp1 and Orc6l. Orc6l is a member of the origin recognition complex (ORC), which plays a central role in replication initiation; in fact, the MCM and ORC complexes form the key components of the pre-replication complex (Lei and Tye, 2001). This is nicely reflected by the high interaction density as well as the common expression profiles of the proteins: the module is fully expressed in three different types of bone marrow cells and fully non-expressed in 42 tissues like brain, liver and kidney, where cells are differentiated and divide less. Ssrp1 is a member of the FACT complex, which is involved in chromatin reorganization (Orphanides et al., 1999).

Fig. 5.

Tissue-specific modules in human. (A). The two top-ranking modules, covering the MCM complex. Known complexes are indicated as solid ellipses, modules as dashed ellipses. (B). Top-five modules around the SCF ubiquitin ligase complex, revealing its tissue-specific organization. Boxes show the tissues of consistent positive expression for the respective module. Tissues associated with all modules are marked in bold, uniquely appearing tissues in italics.

Moreover, our analysis yields some insights about the tissue-specific reorganization of the SCF E3 ubiquitin ligase complex, which marks proteins for degradation. Figure 5B depicts the five top-ranking modules that cover the complex (beyond those, there were three other modules covering only a single protein of the complex). One of them contains as an additional component Cand1, a regulatory protein that inhibits the interaction of Cul1 with Skp1 (Zheng et al., 2002). The four other peripheral proteins are F-box proteins, which serve as substrate recognition particles for the SCF complex. Interestingly, the corresponding modules show different tissue specificities, indicating that the target proteins of SCF are selected in a tissue-dependent manner. This finding is in accordance with experimental studies (Cenciarelli et al., 1999; Kipreos and Pagano, 2000; Koepp et al., 2001). On the one hand, it has been shown that in human cells multiple variants of the SCF complex exist, each one containing a different F-box protein for substrate recognition. On the other hand, brain and blood cells have been identified as tissues of major expression for some F-box components, and expression variation of F-box components has been observed in several tissues like testis, prostate and placenta. In our results, all detected module variants are present in natural killer (nk) cells, which play an important role in immune response (Janeway et al., 2005), whereas only a few are present in B-cells and testis; in certain brain regions, for instance medulla oblongata, only the module variant with Fbxw7 is predicted to be active. As illustrated by this example, DME integrated with gene expression data can be a powerful tool to reveal functional and condition-specific variants of protein complexes.

4 CONCLUSION

Our algorithm, DME, extracts all densely connected modules from a given weighted interaction network. In addition to its completeness guarantee, a strength of the method lies in the possibility of transparent data integration, which is of crucial importance in biological applications. Due to its generality, we believe that DME is a useful tool in many different systems biology approaches. Our framework can also solve more general problems arising in the analysis of structured data, like dense subgraph detection in multi-partite graphs (cf. Everett et al., 2006; Tanay et al., 2004) or in hypergraphs (cf. Zhao and Zaki, 2005). Moreover, module finding can assist in network comparison and classification tasks (Chuang et al., 2007).