Multi-level modelling, the ecologic fallacy, and hybrid study designs

The ecologic fallacy

In this issue, Robinson's highly influential paper is reprinted,¹ along with a paper advocating the use of multi-level thinking by Subramanian et al.², and commentaries by Oakes³ and Firebaugh.⁴

On re-reading Robinson's paper, I was again struck by the clarity of the basic take-home message: ecological data can estimate individual associations in only very rare situations. Robinson illustrated the ecologic fallacy using correlation coefficients applied at different levels of aggregation, whereas more recent work has focused on loglinear models.^5,6 For common (in a statistical sense) outcomes, such as the illiteracy-race example considered in Robinson's paper, a logistic form is more appropriate (and is used by Subramanian et al.) but this form is less amenable to analytic study.⁷ There has been an abundance of work on the myriad causes of ecologic bias on estimates of individual-level associations, which include within-area variability in exposure, and within-area confounding.^8–13 One might think that the estimation of contextual associations can be carried out with ecologic data alone, but Greenland¹⁴ shows this is not the case. A key point is that contrary to what is claimed by some authors,¹⁵ ecologic data alone do not allow one to determine whether ecological bias is likely to be present in a particular dataset. The only solution to the ecologic fallacy is to supplement the ecologic data with individual-level data^8,13, a subject that we now briefly review.

Hybrid designs

Prentice and Sheppard¹⁶ describe a very powerful method for overcoming ecologic bias using within-area covariate samples. When the outcome is not rare, combining data is straightforward.¹³ When the model is linear, one may analytically evaluate which areas should be sampled in order to maximize information.¹⁷ Work on developing methods for combining ecologic and case–control data has also been carried out.^18–20 The ecologic data provide power, while the case–control data provide identifiability, and hence overcome ecologic bias, and only very small case–control samples are required. A closely related approach is to use two-phase methods^21–25 in an ecologic context.²⁶ A number of alternative models have also been proposed.^27,28

Multi-level models

Subramanian et al.² argue for the use of multi-level models and provide a range of interesting analyses of the Robinson data. Multi-level models are increasing in popularity but I would like to stress the importance of model checking (as does Oakes) and prior choice. Multi-level models are very flexible and allow the specification of complex nested and crossed structures, but as model complexity increases, in tandem increase the number of assumptions that need verification.

The random effects in multi-level models allow dependencies in data to be acknowledged but their use requires care. Outside of a linear-mixed effects model, little theory exists to support the reliability of estimation when violations of assumptions occur. Typically, random effects are assumed to be normally distributed and are required to be independent of any covariates in the model. An important decision is whether the random effect variances depend on covariates, since misspecification can lead to serious bias.²⁹ Numerical investigations of deviations from normality of random effects have been carried out^30,31 and indicate that for estimation of fixed effects misspecification may not be fatal. Serious bias can arise when the random effects are correlated with covariates, however.³² McCulloch et al.³³ provide a recent summary of what is currently known on the effect of misspecification of the random effect distribution. To summarize, it is crucial to assess the many layers of assumptions upon which reliable inference rests. With respect to prior choice, the specification for the variance components can be very important, as we illustrate shortly.

Exploratory data analysis

If possible, it is preferable to use the raw data to assess the assumptions required for the multi-level models that we are contemplating, before modelling has begun. After a model has been fitted, estimates of random effects reflect both the data and the assumed random effects distribution and so can be difficult to interpret.

To illustrate we calculate the empirical log odds for the data analysed by Subramanian et al., which consist of state-level counts of the number illiterate (cannot read and over 10 years of age), along with denominators, for each of the 49 states and three races (native-born white, foreign-born white, black). These data provide a relatively easy case study for model assessment since the counts are large, and the models envisaged are relatively simple. For each of the states, we also have a binary indicator that denotes whether Jim Crow laws were present in that state. These laws enforced racial segregation in all public places.

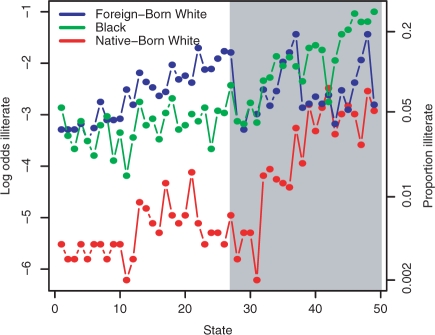
In Figure 1, we plot the log odds of illiteracy by race with points to the left corresponding to the 27 states without Jim Crow laws and those to the right those 22 states with Jim Crow laws. Within each collection of states the points are ordered by increasing overall illiteracy rate. We clearly see the effect of Jim Crow laws on native-born whites and blacks, and large between-state variability in illiteracy is also evident. We calculate summaries of these log odds by race and by Jim Crow status; the row labelled ‘Analysis 1’ in Table 1 gives the results. In both states with and without Jim Crow laws, the odds of illiteracy for foreign-born whites are roughly 15 times those of native-born whites in states without Jim Crow laws. Blacks in non-Jim Crow law states have odds that are eight times those of native-born whites, whereas relative to this category the odd ratio for blacks in Jim Crow states is 27. In Table 2, we present the standard deviations for the log odds for each of the 2 × 3 combinations of absence/presence of Jim Crow laws and race with ‘Analysis 1’ giving the empirical standard deviations. We see that for foreign-born whites the spread is roughly the same in both types of states, while for the other two races the spread is greater in Jim Crow states.

Figure 1.

Log odds of illiteracy by state and race, ordered by increasing proportion illiterate within states without Jim Crow laws (background white), and within states with Jim Crow laws (background grey)

Table 1.

Odds ratio summaries from three analyses, by Jim Crow status and race

		Race
		NBW	FBW	B
Non-Jim Crow	Analysis 1	Ref	15.3	8.1
	Analysis 2	Ref	14.5	7.9
	Analysis 3	Ref	15.0	8.2
Jim Crow	Analysis 1	4.5	15.8	27.4
	Analysis 2	4.3	14.5	25.8
	Analysis 3	4.8	16.7	30.0

NBW = native-born white; FBW = foreign-born whites; B = black. Analysis 1 is based on the empirical log odds. Analysis 2 is based on a multi-level model that assumes that the random effect distributions are identical for non-Jim Crow and Jim Crow states. Analysis 3 is based on a multi-level model with distinct random effect distributions for each of non-Jim Crow and Jim Crow states.

Table 2.

Standard deviation of log odds from three analyses, by Jim Crow status and race

		Race
		NBW	FBW	B
Non-Jim Crow	Analysis 1	0.48	0.55	0.40
	Analysis 2	0.81	0.54	0.54
	Analysis 3	0.48	0.56	0.37
Jim Crow	Analysis 1	1.08	0.53	0.68
	Analysis 2	0.81	0.54	0.54
	Analysis 3	1.09	0.53	0.69

NBW = native-born white; FBW = foreign-born whites; B = black. Analysis 1 is based on the empirical log odds. Analysis 2 is based on a multi-level model that assumes that the random effect distributions are identical for non-Jim Crow and Jim Crow states. Analysis 3 is based on a multi-level model with distinct random effect distributions for each of non-Jim Crow and Jim Crow states.

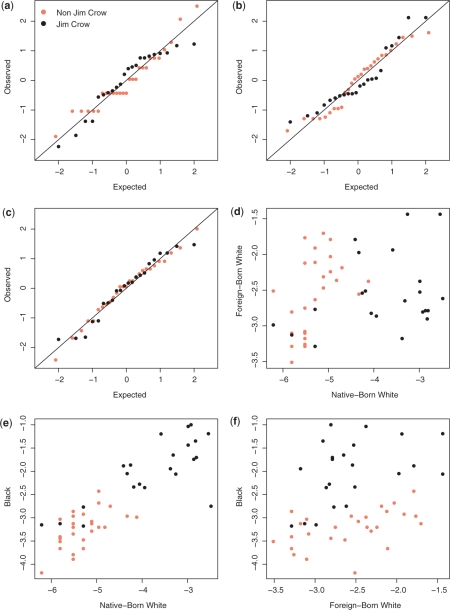
In Figure 2, we provide normal QQ plots of the log odds and scatterplots of the pairs of log odds by state. In the usual implementation of multi-level models, these log odds are modelled as random effects and assumed to be normally distributed. Panels (a)–(c) give normal QQ plots for each race (after standardization). Points close to the line indicate normality, and nothing appears terribly amiss here. As an aside, we note the collections of horizontal dots that are apparent, particularly in panel (a) for states without Jim Crow laws. On closer examination of the data, we see that many of the population totals for native-born whites end with ‘000’, ‘333’ or ‘667’, which suggests that some form of rounding has been carried out in their calculation. Panels (d)–(f) show the bivariate relationships. Panel (e) shows that the log odds are correlated within states for native-born whites and blacks, suggesting there are unmeasured state-level variables that influence illiteracy rates for these two races.

Figure 2.

Log odds of illiteracy by Jim Crow status and race. Panels (a)–(c) give normal QQ plots, for native-born whites, foreign-born whites and blacks, respectively (the log odds are standardized). Bivariate scatterplots for: (d) foreign-born white versus native-born white, (e) black versus native-born whites, (f) black versus native-born white. Orange/black points correspond to states without/with Jim Crow laws in place

Prior choice

We first describe issues pertinent to prior choice using a multi-level model, which is identical to model 4 of Subramanian et al.

Stage 1: observed data model

Let Y_i1, Y_i2, Y_i3 denote the number of native-born white, foreign-born white and black individuals who are illiterate in state i, N_i1, N_i2, N_i3 the respective denominators, and x_i=0/1 a state-level indicator for the absence/presence of Jim Crow laws. We define p_ij to be the proportion of illiterate individuals in the population of race j in state i, i=1,…,49, j=1,2,3.

Then Y_ij | p_ij ∼ _ind Binomial (N_ij,p_ij) with

Stage 2: random effects model

We assume

We write this latter distribution as b_i|σ ∼_iid N(0, Σ) so that an implicit assumption is that the random effects distribution does not depend upon whether Jim Crow laws are present in state i (which does not look reasonable from the results of Table 2). This model therefore allows the race-specific random effects to be correlated across areas. In a Bayesian analysis, we need to specify a prior distribution for the variance–covariance matrix of the random effects which is a tricky exercise since a variance–covariance matrix needs to be positive definite.

Stage 3: hyperpriors

We assume independent priors:

with β_j and γ_j, j=1,…,3, assigned flat (improper) priors. One choice of prior over positive definite matrices is the Wishart distribution, which is a multivariate generalization of the gamma distribution. Specifically, we assume that Σ⁻¹ ∼ Wishart (r, S), where r is a degrees of freedom and S is a scale matrix (we parameterize the matrix so that E[Σ⁻¹] = rS). The specification of these two parameters requires great care.

Subramanian et al. report the use of ‘diffuse’ priors in MLwiN. In addition to the above model, they fit a model with independent random effects, i.e. b_ij|σ² ∼_ind N(0,σ²_j) with σ⁻²_aj ∼ Gamma(a,b) and a=b=0.001. The latter is often used but can be influential for some datasets and should be avoided. As pointed out elsewhere,³⁴ under this prior, 99% of the prior mass for σ_j (the standard deviation of the random effects—these are the values that appear in Table 2) lies to the right of 6.4, which is clearly a ridiculous prior. We follow a previously suggested procedure,³⁵ the details of which are in Appendix 1, and give a range for exp(b_ij), the residual odds ratio for race j in state i, i.e. the odds of being illiterate compared with the median of the distribution of odds across states for race j. For example, for a range of residual odds of [exp (0.1), exp(10)] we obtain a=0.5,b=0.0164. This gives 2.5, 50 and 97.5% quantiles for σ_j of (0.08, 0.26 and 5.76), which are far more prudent. For the more general dependent case with 3 × 3 variance–covariance matrix Σ, Subramanian et al. choose the default in MLwiN which, according to the manual, is a data-dependent prior in which the matrix S is chosen based on the data, which though often not fatal, is not strictly legal since it is using the data twice. Appendix 1 contains details of how r and S may be chosen in this more general case. We again take the range of residual odds to be [exp(0.1), log(10)] with correlations of 0 (an alternative would be to pick a correlation > 0 to reflect the belief of shared unmeasured predictors of illiteracy across all races), along with an integer value of r which, in one sense, gives the most conservative prior (the variance of the prior decreases with increasing r, so a lower value of r gives larger variance). These choices give r = 3 and S a diagonal matrix with diagonal entries S_jj=30.45, j=1,2,3.

Hence, we see that prior specification is not straightforward, but is important since it may influence the results, particularly when the number of units (here, states) is small. As a minimum, priors should be clearly specified, along with the estimation method used. Ideally data and code should be made available on an author's; web site, or as Supplementary Material.

Interpretation

The interpretation of parameters in multi-level models requires great care. To illustrate, consider the model for native-born whites only:

with b_i1 ∼ _iid N(0, σ²₁). This model implies that the odds of exposure are log-normally distributed:

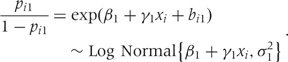For this model:

• exp(β₁+b_i1) is the odds of illiteracy for native-born whites in state i;

• exp(β₁) is the median illiteracy for native-born whites for states without Jim Crow laws. An alternative definition is the odds of illiteracy for native-born whites in a ‘typical’ state without Jim Crow laws; ‘typical’ here means b_i1=0;

• exp(β₁+γ₁) is the median odds of illiteracy for native-born whites in states with Jim Crow laws;

• exp(β₁+σ²₁/2)=E[exp(β₁+b₁)] is the average odds of illiteracy for native-born whites across states without Jim Crow laws, and

• exp(β₁± 1.96 × σ₁) is a 95% interval for the odds of illiteracy for native-born whites across states without Jim Crow laws. Hence, this function gives an indication of the variability in the odds of illiteracy across states without Jim Crow laws.

In Table 1, Analyses 2 and 3, we report the median odds ratios. For native-born whites in states without Jim Crow laws the median odds of illiteracy is estimated as 0.005. A 95% interval for these odds across states without Jim Crow laws is estimated as (0.002, 0.0123), so that the odds of illiteracy range between 1 in 500 and 1 in 80.

In Table 1, we report analyses with a common random effects distribution across all states (‘Analysis 2’ and model 4 of Subramanian et al.) and a model with distinct random effects for each category of states (absence/presence of Jim Crow laws); this model (‘Analysis 3’) is equivalent to separate fits to each category of states. We see that this final analysis is more appropriate, and essentially recovers the point estimates from the analysis with the empirical log odds, since here the denominators are large. Since the random effects are so well estimated, and the number of states is not small, the particular Wishart specification assumed here is not influential.

We might ask what multi-level Analysis 3 has added here, when compared the analysis based on the raw empirical log odds, since the point estimates are virtually identical. However, correct standard errors for odds ratios require an explicit model for the dependence between the counts within each state, and this is provided by the multi-level approach, but not by the empirical log odds calculations.

R and WinBUGS code for the analyses reported here are available from http://faculty.washington.edu/jonno.cv.html

Markov chain Monte Carlo

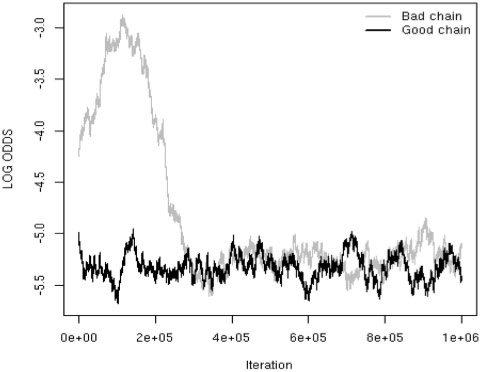
For these data, the Markov chain was very poorly behaved, as shown in Figure 3, which displays the time course of two chains for the log odds of illiteracy for native-born whites in states without Jim Crow laws. The chains were started from ‘good’ and ‘poor’ starting points. The good chain had initial values for the fixed effects set at the maximum likelihood estimates (MLEs), while the bad chain had fixed effects set to zero. The bad chain does not ‘mix’ with the good chain until around 300K iterations have elapsed. Recently,³⁶ a new approximation strategy for Bayesian inference has been described, and is ideally suited to data such as that considered here. The approach is considerably faster than Markov chain Monte Carlo (MCMC), and R code is available.

Figure 3.

Time course of two Markov chains for the log odds of illiteracy for blacks

Diagnosis of convergence in an MCMC context can be very difficult and is a black art, but various checks are available. For these data, we fit the model (with the same first two stages as the Bayesian model described above) using maximum likelihood, and then compare the results with the Bayesian analysis. For such abundant data, one would not expect too many differences, and this is confirmed in Table 3 for the model in which a common random effects distribution across all states is assumed.

Table 3.

Comparison of likelihood and Bayesian estimation techniques

	Likelihood	Bayes
Parameter	Estimate (SE)	Estimate (SD)
β1	−5.32 (0.15)	−5.25 (0.16)
β2	−2.58 (0.10)	−2.57 (0.10)
β3	−3.21 (0.10)	−3.19 (0.10)
γ1	1.52 (0.23)	1.43 (0.25)
γ2	0.03 (0.15)	0.02 (0.16)
γ3	1.22 (0.15)	1.18 (0.17)
σ1	0.79 (−)	0.81 (0.09)
σ2	0.53 (−)	0.54 (0.06)
σ3	0.52 (−)	0.54 (0.06)

For the likelihood summaries, we report the MLEs and the asymptotic standard errors, whereas for the Bayesian analysis we report the mean and standard deviation of the posterior distribution.

We end with the usual caveats concerning the analysis of observational data; clearly, we are far from being able to make causal statements for these data since the list of potential confounders is vast. Multi-level models are a useful way of structuring analyses, but their use requires care, and they cannot control for confounding.

Supplementary Data

Supplementary data are available at IJE online.

Funding

National Institute of Health (grant RO1 CAO95994).

Appendix 1

Prior choice

We begin with the independent random effects model with

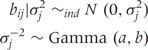for j=1,2,3. We can average over σ²_j to obtain the marginal distribution of exp(b_ij), the residual odds, which is a more interpretable quantity and describes the odds for race j in state i, relative to the median odds across states. The marginal distribution for exp(b_ij) is a log Student's; t-distribution with d = 2a degrees of freedom, location zero and scale Σ = b/a. We choose a = 0.5 so that the marginal distribution is a Cauchy distribution, and then choose b so that 95% of the residual odds lie within a range that we specify. In particular, for the range (1/R,R) we use the relationship 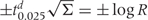, where t^d_r is the 100× r-th quantile of a Student's t random variable with d degrees of freedom, to give a=d/2, b=(log R)²d/2(t^d_1-(1-q)/2)². For example, for a range of [exp(0.1), exp(10)], we obtain b = 0.0164.

For the case of p dependent random effects, b_i=(b_i1,…,b_ip), we have

which, on marginalization over Σ, gives b_i as multivariate Student's; t with location 0, scale matrix [(r−p+1)S]⁻¹ and degrees of freedom d=r−p+1. The margins of a multivariate Student's; t are t also, which allows r and S to be chosen as in the univariate case. Specifically, the j-th element, b_ij follows a univariate student t distribution with location 0, scale S^jj/(r−p+1), and degrees of freedom d=r−p+1 where S^jj is element (j, j) of the inverse of S.

For other approaches to prior choice in hierarchical models see Gelman³⁷ and Gustafson et al.³⁸