A simple method for calibrating force plates and force treadmills using an instrumented pole

1 Introduction

Accurate measurements of ground reaction forces from force plates are important in many areas of biomechanics research. For example, inverse dynamics analysis is highly sensitive to errors in force magnitude and center of pressure (COP) location [1,2]. Force plates are also used to assess foot placement and its variability during human walking (e. g., [3]), again with a high sensitivity to error. Some errors may be due to misalignment of the force plates with respect to the motion capture coordinate system. Others may be caused by distortions in load-sensing elements due to imperfect mounting conditions [4]; a typical specification requires the mounting surface to be flat within 0.05 mm to ensure low distortions (AMTI, Watertown, MA). Instrumented treadmills, in which treadmills are mounted atop force sensing elements, are becoming increasingly prevalent in biomechanical analysis [5,6,7,8,9]. These tend to exacerbate accuracy concerns, not only because the mounting of the treadmill introduces additional distortions, but also because the compliance and dynamics of the mechanical structures reduce the fidelity of load measurements. These factors can lead to substantially large errors compared to original manufacturer specifications. The errors can potentially be reduced, however, through proper calibration performed after mounting the force plate and any optional structures, such as a treadmill.

Errors may be quantified by comparing force plate measurements such as center of pressure (COP) against external reference values such as those obtained from a motion capture system [10,11]. The reference COP location may easily be obtained from motion capture markers fixed to a rigid rod or pole, whose tip may be pressed against the force plate from arbitrary orientations and in arbitrary locations. Force magnitude errors may be assessed with a pole that is instrumented with a load cell [12].

Calibration methods adjust inaccurate force plate measurements based on their mismatch with reference values. Correction equations, whether linear or nonlinear in form, are characterized by unknown parameters or coefficients whose values are derived from observed errors, typically through optimization techniques. A particularly simple method is to apply purely vertical loads to the force plate in known locations. Verkerke et. al. [13] demonstrated that COP errors could thus be reduced substantially with a set of 10 coefficients in a polynomial correction formula. Rabuffetti et al. [14] showed that the loads need not be applied solely in the vertical direction, so long as the motion of the pole about the point of contact is recorded. It is further possible to correct not only COP, but also the other force and moment data sensed by the force plate [15]. This requires that loads be applied along other axes. Black et. al. [15] developed a custom-built test fixture for that purpose, capable of applying static loads along precise, externally-referenced axes. They optimized 36 nonlinear correction coefficients to reduce COP errors.

The various merits of these procedures might be combined into a single procedure. The application of loads to the pole in arbitrary directions [14] could be extended to provide reference data for not only COP location but also the applied forces, using an instrumented pole [12]. Doing so would allow for calibration of force and moment measurements about all axes as with [15], but without requiring a specialized fixture. Interesingly, the combination of the advantages from [14,12,15,13] would not require an increase in complexity. A procedure for calibrating all force plate axes could use fairly arbitrary loads applied in a number of locations, followed by a simple least-squares optimization of the appropriate correction coefficients.

We propose a simplified procedure that utilizes an instrumented pole and a least-squares optimization of a linear model to quickly calibrate force plates along all axes and over the full range of expected loading conditions. The corrections can reduce the effects of misalignment and distortion, and improve the accuracy of force, moment, and COP measurements. We term the proposed procedure the “Post-Installation Least-Squares” (PILS) Procedure, as it is intended to correct for errors introduced during installation of force plates. We demonstrate the PILS Procedure in two common applications: calibration of standard ground-embedded force plates, and calibration of a custom-built, split-belt, instrumented treadmill.

2 Methods

The proposed PILS procedure comprises four steps. These are (1) application of arbitrary forces to the force plate with an instrumented pole, (2) transformation of measured pole forces into total reference forces applied to the force plate, (3) compilation of reference forces and (presumably imperfect) force plate signals into two matrices containing all reference and force plate measurements, and (4) least-squares solution of a linear calibration matrix that corrects inaccurate force plate signals. This section describes these procedural steps, followed by a description of our implementation of the procedure on standard force plates and an instrumented treadmill. We then demonstrate the procedure and evaluate the error reductions using independent sets of force plate data.

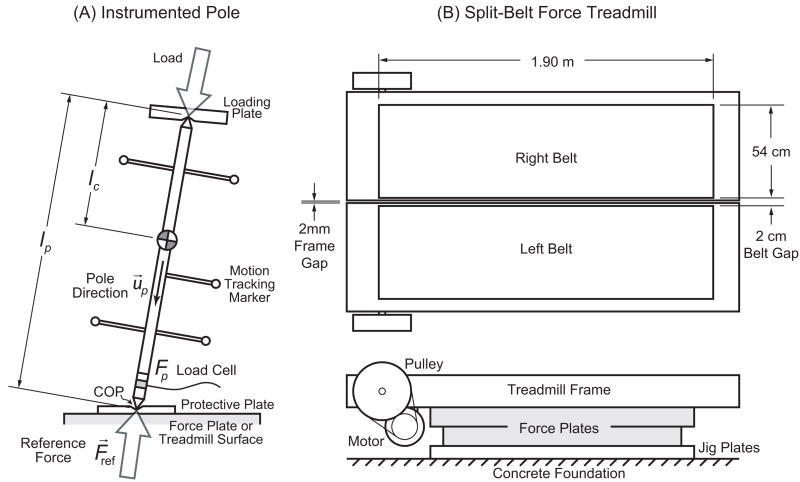
The instrumented pole allows for measurement of both the direction and magnitude of forces applied arbitrarily to the force plate (see Figure 1A). The pole is fitted with optical markers arranged to yield its three-dimensional configuration. It is also designed so that only axial loads may be applied: it has conical ends, with one fitting into an indented protective plate resting on the force plate or treadmill surface, and the other fitting into a similar plate to which the experimenter applies loads. The pole’s direction, described by unit vector u⃗_p, is determined from the optical marker locations, as measured by a motion capture system. The magnitude of axial pole force F_p is indicated by a load cell located near the tip of the pole. These quantities may then be transformed into reference force and moment vectors applied to the force plate, accounting for other factors such as the weight of the pole, which is generally not oriented vertically (as described below with implementation details). These vectors are measured over time in a series of location trials, in which the tip of the pole is placed in a variety of locations on the force plate or treadmill surface, with varying forces and directions applied for each location. The forces should ideally cover a range of directions that will produce non-zero and non-uniform reaction forces and moments in all force sensing elements, with magnitudes that are similar to those expected during normal operation of the force plate.

Figure 1.

Equipment used to demonstrate Post-Installation Least Squares (PILS) calibration procedure. (A) Instrumented pole used for force plate calibration. The pole allows arbitrary directions and magnitudes of force to be manually applied to the force plate in arbitrary locations, using a motion capture system to record kinematics. The pole (Motion Lab Systems MTD-2) is modified to include an axial load cell, similar to [12]. Its ends are tapered so that only axial forces can be applied. A loading plate with a shallow chamfered hole is used to apply loads to the top; a similar, protective plate transmits those loads to the force plate below. The pole’s direction u⃗_p is determined from locations of motion tracking markers, and the axial force F_p is measured by the load cell. These quantities contribute to the reference ground reaction force F⃗_ref that is used for calibration. (B) Custom-built, split-belt, instrumented force treadmill (not to scale). Independent treadmills are mounted atop separate force plates, with a gap of 2 cm between the treadmill belts. The mounting of a force plate to the ground, or of a treadmill to the force plate, can introduce distorting loads that adversely affect the accuracy of the force plate. The PILS procedure is also demonstrated on a standard set of force plates mounted flush with ground (not shown).

Reference forces and moments from all points in time and all trials are then stacked into a single reference matrix R. Each column of R represents a single data sample of the six force and moment components along the three axes of the laboratory coordinate system. The number of columns n therefore equals the total number of samples collected over all trials, typically a number in the thousands. Accompanying the reference matrix is a force plate signal matrix S of the same 6 × n dimension, containing data samples from the force plates. These will typically contain imperfect data that ideally would be identical to R (or any invertible linear transformation of R).

The general nonlinear relationship between reference and signal matrices is then linearized. We assume a one-to-one, nonlinear correspondence between each possible row of R and S, with

$$R=f(S).$$ (1)

The linearized relationship is

$$R=C·S$$ (2)

where C is an unknown 6×6 calibration matrix, representing the linear transformation that corrects for small, systematic errors in S. Equation 2 is obtained from the Taylor series expansion of Equation 1 about the unloaded condition, assuming that offsets are removed from both R and S so that both are zero when the force plate is unloaded. The matrix C may therefore also be regarded as the unknown Jacobian of the function f (S). It is also in the same form as, and can directly replace, the calibration matrix that is typically supplied by the force plate manufacturer.

The calibration is then determined by a matrix pseudo-inverse, which minimizes the mean-square error between the reference and the corrected signal matrix. The solution may be written as

$$C=R·S^T{(S{S}^T)}^{-1}$$ (3)

where the term to the right of R is the right pseudo-inverse of S. Given redundant force plate signals that span the space of those possible, C is the unique matrix that performs the best linear transformation of S into R. In subsequent application, measured force plate signals are again to be compiled into a matrix S, and the corrected signals C · S are used in inverse dynamics or other analyses.

We implemented this procedure on two sets of force plates. The first was a standard set of ground-embedded force plates mounted flush with the floor, as is typically used for overground walking trials. The second set was part of a custom split-belt instrumented force treadmill. We first gathered calibration data to determine C for each set of equipment. We also gathered another, similar set of independent data to test the precision of the procedure. We then calculated residual errors between measured and reference forces, moments and centers of pressure following PILS calibration in a set of static and dynamic trials. The details of the implementation are presented below.

The force plates on which we performed the PILS calibration were in two different configurations. The flush-mounted force plates (AMTI Inc., Watertown, MA) measured approximately 0.5 m on each side. Each force plate was bolted on four corners to aluminum rails which were in affixed with epoxy to the concrete building foundation. The treadmill force plates (Bertec, Columbus, OH) measured 1.2 m × 0.6 m, and were mounted to precision-machined jig plates epoxied to the concrete foundation. An independent treadmill (see Figure 1B) was mounted atop each force plate. The treadmills were loosely based on a previously-described design [16], modified to increase belt width and drive train power. Each independent side of the treadmill weighed 140 kg. A 0.002 m gap was maintained between the left and right treadmill assemblies, such that full individual leg forces and COPs could be independently measured. Each belt allowed for a walkable surface of 1.9 m by 0.54 m, with a 0.02 m gap between belts. Each belt was driven by a 2.5 kW speed-controlled motor (Allen Bradley, Milwaukee, WI).

We performed simple mechanical tests to measure the nominal mechanical performance of the treadmill. The lowest natural frequency was 41 Hz in mediolateral force, obtained by recording forces and moments following rubber mallet strikes. We next ran each treadmill at a typical walking speed of 1.25 m·s⁻¹ and measured the vibrational noise due to moving parts. The largest noise amplitudes were 42 N in anterior-posterior force and 11 N·m in vertical moment, with the first peak in power spectral density at 40 Hz and the highest peak at 100 Hz. When filtered at 25 Hz, the maximum noise amplitudes were below 1.5 N and 1.3 N·m for all signals. Finally, we measured belt speed using a single motion-tracked marker rigidly attached to an aluminum plate riding along the belt while both sides ran at 1.25 m·s⁻¹ and a 90 kg subject walked on the surface. The maximum deviation in belt speed was 0.023 m·s⁻¹ (1.8%) and the maximum deviation in belt position was 0.002 m during the course of a single stride. The two sides of the treadmill behaved nearly identically in these nominal mechanical tests. This mechanical performance is similar to other reported values (Table 1).

Table 1.

Comparison of force treadmill specifications and mechanical performance

Property	(units)	Kram [5]	Belli [6]	Dierick [8]	Paolini [17]	Collins et al.
belt		single	split	single	tri	split
belt length	(m)	1.5	2.0	1.5	2.8	1.9
belt width	(m)	0.35	0.50	0.50	0.66	1.1
sprung mass	(Kg)	90	250	190	-	140
natural freq.	(Hz)	87	58	30	210	41
motor power	(kW)	1.5	1.5	2.2	-	2.5
speed dev.	(m·s−1)	0.02	0.03	0.09	0.15	0.02
noise freq.	(Hz)	46	17	30	24	40
noise mag.	(N)	80	5	5	10	50

freq. is frequency, dev. is deviation, and mag. is magnitude

We used a pole instrumented with optical tracking markers and an axial load cell to apply reference loads for use in our calibration. The pole was a modified MTD-2 (Motion Lab Systems, Baton Rouge, LA, Fig 1). The pole weighed 1.4 kg and measured 1.079 m in length with markers at the ends of five rods mounted perpendicular to the pole. The pole ends were pointed to minimize transmission of non-axial loads. The pole was modified to include a single-axis load cell (LC202-3K, OMEGA Engineering, Inc., Stamford, CT) along the pole axis near the contact point. Engineering drawings of the interface components are available as supplementary materials. The mounted load cell was recalibrated using known masses ranging from 0 kg to 73 kg.

We used this instrumented pole to load each force plate while collecting force plate signals and measuring pole load and location, which were used to determine reference loads R. Each treadmill surface was loaded in 40 locations and each flush-mounted force plate was loaded in 20 locations in separate 5 s trials. Force plate and load cell signals were collected at 1200 Hz, while markers were tracked at 120 Hz (Motion Analysis Corporation, Santa Rosa, CA). Loading was applied to the instrumented pole through an interface plate that approximated a point contact and purely axial forces. Loading was provided by the body weight of either one or two individuals pushing on the pole with varying forces while it was slowly tilted through a range of angles about its contact point. Using this method, loads ranging from 100–1000 N were applied in the vertical direction, with simultaneous horizontal loads of 0–250 N resulting from pole angles of to 0–20° from vertical.

We then determined the applied reference forces using the pole load cell signal and marker positions, accounting for contributions from the masses of the pole and protective plate. These contributions were included, despite never exceeding 1% of the force magnitude. The weight of the protective plate was denoted m_plg⃗, and the non-axial component of the weight of the pole (not captured by the axial load cell) was equal to the vector weight of the pole m_pg⃗ minus the axial component of the vector weight, m_p(g⃗ · u⃗_p)u⃗_p. We then computed the portion of the non-axial weight which was borne by the force plate (as opposed to the loading bar) by multiplying by the ratio of the distance from the top point of the pole to the pole center of mass, l_c, to pole length, l_p (i.e. we performed a moment balance on the pole). We did not include forces from dynamic pole motions or from the weight of the lower point of the instrumented pole, which always contributed less than 1 N. Combining the applied forces,

$${\overrightarrow{F}}_{\text{ref}}=F_p{\overrightarrow{u}}_p+m_{pl}\overrightarrow{g}+\frac{l_c}{l_p}{m}_p(\overrightarrow{g}-({\overrightarrow{u}}_p·\overrightarrow{g}){\overrightarrow{u}}_p)$$ (4)

where F⃗_ref is the total calculated force applied to the force plate. We then transformed this force into a reference ground reaction force. For our laboratory, this was accomplished by reversing the sign of the first and third terms of each force vector.

Using the calculated reference forces and the measured pole marker positions, we derived the moments applied to the force plate about its geometric center. The reference moment vector M⃗_ref was calculated as the cross product of the position of the load application point ρ⃗_ref (relative to the force plate center) with the applied force F⃗_ref. The load application point was determined from the absolute (laboratory-referenced) positions of the tip of instrumented pole r⃗_COP and the force plate center r⃗_FPC. The tip position r⃗_COP was itself calculated from motion capture data of the pole’s optical markers, and was slightly above the surface of the force plate or treadmill by the thickness of the center of the protective plate. (We assumed the weight of the protective plate to be a downward point load vertically aligned with r⃗_COP.) We used manufacturer’s specifications to locate the force plate’s geometric center in the laboratory reference frame r⃗_FPC, which remained constant. Thus, the applied moments were calculated as:

$${\overrightarrow{M}}_{\text{ref}}={\overrightarrow{\rho }}_{\text{COP}}\times {\overrightarrow{F}}_{\text{ref}}=({\overrightarrow{r}}_{\text{COP}}-{\overrightarrow{r}}_{\text{FPC}})\times {\overrightarrow{F}}_{\text{ref}}$$ (5)

where M⃗_ref is the total calculated reference moment resulting from forces applied to the force plate.

We evaluated the calibration matrix using standard numerical linear algebra tools. Our particular implementation used the MATLAB (MathWorks, Natick, MA) “mrdivide” command, which took less than 1 second to evaluate. Sample code for the entire calculation is available as supplementary material.

We evaluated PILS-corrected force and COP measurements in an independent series of static and dynamic tests. We first set up the force plates and motion capture system according to standard manufacturer guidelines and calibration procedures (Standard Calibration), using EVaRT software (Motion Analysis Corp., Santa Rosa, CA). We then collected a set of applied force data to determine a PILS calibration matrix C. This was followed by a reset and recalibration of both the motion capture system and the instrumented pole, and the collection of another, independent set of static validation data, loading each treadmill surface in 20 new random locations and each flush-mounted force plate in 10 new random locations in separate 5 s trials. These independent data were used to evaluate the root-mean-square (rms) errors in force and COP for the Standard Calibration and PILS Calibration. In this evaluation, error was calculated as the difference between force plate measurements and reference values measured using the laboratory motion capture camera system and the intstrumented pole. Both of these reference measurements may have included small inaccuracies, which we discuss below. We also dynamically tested the force treadmill in an effort to crudely test whether static results could transfer to experimental conditions. We applied loads with the instrumented pole to each side of the treadmill while the belt ran at 1.25 m·s⁻¹. However, because we found it difficult to apply large moving loads, tests were only performed on the front medial quadrant of each treadmill.

3 Results

The proposed calibration procedure was found to reduce force and COP errors for both flush-mounted force plates and the custom instrumented force treadmill. In both cases, the calibration matrix C was very close to the manufacturer-specified matrix, with the greatest differences in off-diagonal terms. The small corrections nevertheless resulted in substantial decreases in error. Applied to the flush-mounted force plates, the procedure reduced force rms error from 1.9% (Standard Calibration) to 1.4% (PILS) and moment errors from 3.0% to 1.6%. The greatest initial force plate force and moment rms error components were 4.6% in medial-lateral force and 5.5% in vertical moment, and the greatest error components remaining following PILS Calibration were 3.1% in anterior-posterior force and 3.2% in vertical moment. Reductions were greater for the treadmill force plates. The PILS procedure reduced force rms errors from 1.7% to 1.4% and moment errors from 4.8% to 1.2%. The greatest initial force and moment component rms errors were 5.4% in anterior-posterior force and 4.8% in medial-lateral moment, and the greatest component errors remaining following PILS Calibration were 3.6% in medial-lateral force and 4.0% in vertical moment. All reported moment errors are in the force plate reference frame. These results are compared to the literature in Table 2.

Table 2.

Comparison of force and center of pressure errors. Errors are shown in terms of root-mean-square (rms) magnitude, the worst axis of the force plate, and the rms error in the direction of the worst axis. The worst axis is either anterior-posterior (AP), medial-lateral (ML), or vertical (V), with the long axis of each force plate aligned with the AP direction. Results are shown for standard flush-mounted force plates (FP) and for force treadmills (FTM).

	Lewis [12]	PILS	Kram [5]	Dierick [8]	Black [15]	PILS
Parameter	FP	FP	FTM	FTM	FTM	FTM
Force error
rms mag.	4.3%	1.4%	-	2.4%	1.7%	1.4%
worst axis	V	AP	-	AP	-	ML
rms worst axis	2.7%	3.1%	-	2.1%	-	3.6%
Static COP
rms mag.	0.009 m	0.003 m	0.008 m	0.042 m	0.003 m	0.005 m
worst axis	AP	ML	ML	AP	-	AP
rms worst axis	0.008 m	0.002 m	0.006 m	0.042 m	-	0.004 m
Dynamic COP
rms mag.	-	-	0.010 m	-	0.006 m	0.008 m

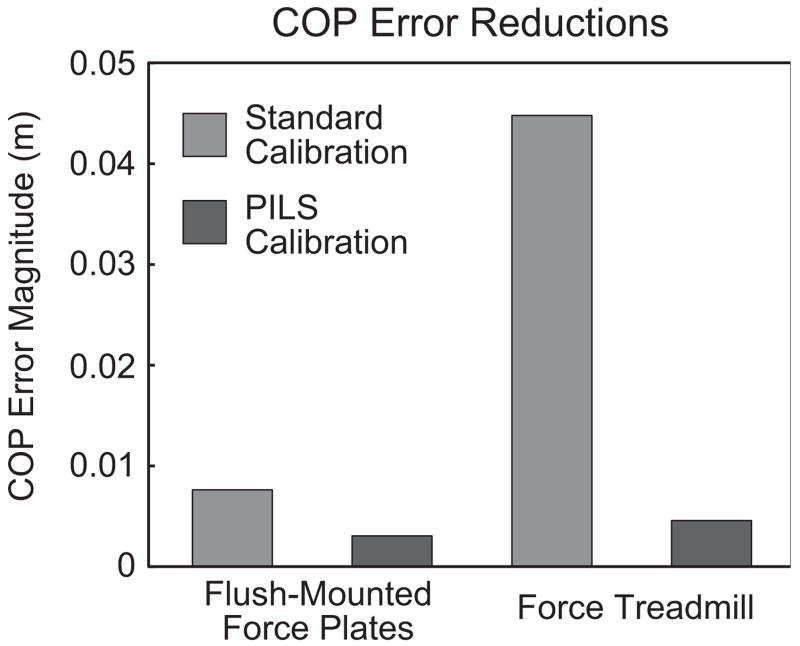
Center of pressure (COP) errors were also reduced by the PILS procedure (Figure 2). The procedure reduced COP rms errors in the flush-mounted force plates by 63%, from 0.008 m to 0.003 m (Figure 3). The greatest initial COP rms error component was 0.006 m in the medial-lateral direction, which was reduced to 0.002 m following PILS Calibration. COP rms error magnitudes in the instrumented treadmill were reduced by 91%, from 0.045 m to 0.005 m. The greatest initial COP rms error component was 0.037 m in the anterior-posterior direction, which was reduced to 0.004 m following PILS Calibration.

Figure 2.

Mean center of pressure (COP) locations for validation tests with (left) standard flush-mounted force plates and (right) the split-belt force treadmill. Plus symbols (+) mark reference locations determined through motion capture, squares (□) mark locations determined from the Standard Calibration using manufacturer-specified values, and circles (○) mark the corrected locations following PILS calibration.

Figure 3.

Effect of PILS calibration on COP error (plotted as root-mean-square error) for both sets of force plates. Errors were reduced by 63% for the flush-mounted force plates, and 91% for the instrumented force treadmill, comparing PILS to the Standard Calibration.

Center of pressure errors were greatest for data that were collected with reference forces of low magnitude. We found COP error magnitudes, e, to be negatively correlated with the magnitudes of applied loads, F, in a linear correlation of the form e = m · F + b. Values of m were similar pre- and post-calibration for each force plate, ranging from −4 · 10⁻⁶ to −9 · 10⁻⁵ m·N⁻¹, while values of b were greatly reduced by the PILS calibration and ranged from 0.070 to 0.005 m (r² = 0.21 ± 0.08, p = 1 · 10⁻¹⁶). To test the effect of greater COP errors at low reference forces on the PILS Calibration, we recalculated C using two length-matched subsets of the full calibration data, one which included only data collected with reference force magnitudes lower than 400 N, and the other which indluded only magnitudes greater than 600 N. We then evaluated the resulting PILS Calibrations against the independent validation data. We found that using lower reference forces resulted in greater residual COP rms errors (0.005 m for the force plates and 0.008 m for the instrumented treadmill), while limiting the calibration to only high reference forces resulted in no change. This suggests that the best calibration was achieved by applying reference loads comparable to those observed in experimental conditions.

Dynamic testing of the instrumented treadmill with the belt running also revealed reductions in COP errors following PILS calibration. COP rms error magnitudes were reduced from 0.017 m to 0.008 m. The initial error was lower in these dynamic trials due to the limited range of COP locations used in dynamic trials, all located within the front-medial quadrant of the treadmill, where the Standard Calibration was most accurate.

4 Discussion

We sought to test a new procedure for calibrating force plate measurements. We found the PILS method to reduce errors in forces, moments, and COP in independent validation tests. The reductions were greatest for the instrumented force treadmill, as would be expected given the mounting of a large structure atop a force plate. Following the PILS procedure, residual errors for the force treadmill were comparable to those for standard force plates. The procedure also reduced errors in the flush-mounted force plates, although these were accurate to begin with. Below we compare PILS to other procedures and consider its underlying assumptions.

There are three distinguishing features of the PILS procedure. First, it simultaneously calibrates forces and moments about all axes, rather than COP alone as with several other methods. PILS indirectly calibrates COP (Figure 3), while also correcting for the other force plate measures. Second, it does not require the application of loads along precise vertical or other axes, the latter typically requiring a carefully-aligned calibration fixture. Precise load application is unnecessary if arbitrary loads can be precisely measured. Third, it is formulated to yield a linear calibration matrix C, which is convenient to incorporate directly into data acquisition software. For example, EVaRT software readily accepts a new calibration matrix, but does not easily incorporate nonlinear corrections. The linear calibration is also computationally simple to implement, requiring only one line of MATLAB code (see supplementary materials).

A linear calibration procedure is justified for typical force plate systems. PILS directly calibrates forces and moments, which are linearly related to the outputs of a force plate’s load-sensing elements such as strain gauges. Force plates are generally designed for, and indeed predicated on, a linear operating range for their load-sensing elements. Many causes of misalignment between force plate and laboratory coordinates are also expected to be linear. For example, scaling, translation, and rotation of the force plate axes are all linear transformations. In contrast, the COP measurement is based on the ratio of moments to forces and is therefore nonlinear, requiring a more complex correction. The correction of COP alone also has the potential of introducing incompatibilities between the force and moment measurements. There may nevertheless be situations that could benefit from some nonlinear corrections. We experimented with additional second-order nonlinear terms (e.g. F_z · M_x or $M_x^2$) in our calibration, and did not find them to significantly reduce errors for either of the two force plate systems.

Any calibration procedure can potentially introduce over-fitting errors, wherein the calibration works well for the data used in its derivation but does not generalize well to other data sets. One way we guarded against over-fitting was by performing validation tests on a set of data independent from those used in the fitting. We also evaluated residual errors in terms of COP (Figure 3), an outcome variable not directly employed in the procedure itself. In addition, the 6 × 6 matrix C is the invertible transformation of least dimension that corrects for all forces and moments. It is of the same form and performs the same function as the manufacturer-specified calibration matrix, except that it takes into account errors introduced by imperfect mounting. It is therefore unlikely that the PILS procedure overfits to calibration data.

We found the instrumented pole to be convenient for calibration. The optical markers provide accurate force locations [11], and the single-axis load cell provides force magnitude measurements [12] that are easy to calibrate. We tried to apply loads comparable in magnitude and direction to those expected under normal operation (i. e., human walking), generally employing two people to apply the loads. A single person could apply smaller loads that are still comparable to those applied in most other calibration procedures, though our comparison of high- and low-force reference data indicates that this would likely result in an increase in residual COP errors. This is presumably due to the reduced signal to noise ratio at low loads. By contrast, we have found that errors could be reduced to a comparable degree using as few as 20 locations per treadmill or 10 locations per standard force plate to determine C. It is nonetheless preferable to record from as many locations as is practical, with loads close to those expected in operation, but substantial error reduction could be expected from an abbreviated procedure performed by one person.

We used motion capture to measure reference positions and the instrumented pole to measure reference forces, even though these measurements likely include small inaccuracies. Although we carefully calibrated both systems before each data collection, any tool used to make reference measurements will be imperfect. In the case of reference forces, it is important to use the most accurate measurement tool available, since any inaccuracy will be reflected in post-calibration force measurements. In the case of reference positions, it is usually most important to maintain a high degree of consistency between spatial measurements made by force plates and motion capture, for instance to avoid inconsistencies between COP and joint location measurements, which can lead to significant errors in estimated joint torques [1]. The COP errors we report therefore represent the expected mismatch error in inverse dynamics analyses performed using the PILS-calibrated system. In cases where no motion capture system is available, procedures using only vertical loads or external fixtures are then most appropriate [13,15]. Because we performed recalibration of the reference systems before validation, reported errors include error associated with the reference calibrations, and are therefore a robust estimate of expected mismatch error.

Dynamic testing of the PILS Calibration on the instrumented treadmill revealed similar reductions in COP errors as in static tests. We found it difficult to apply dynamic loads in a range and number of locations comparable to the static loads, making dynamic tests limited to a spot check. The results nevertheless suggest that the PILS Calibration can improve force measurements made under experimental conditions.

We found the PILS procedure to be no more difficult, and often more convenient, than the methods previously reported in the literature. It requires modest equipment, and the calibration procedure can be performed relatively quickly. The linear calibration matrix yields results comparable to nonlinear calibration methods, yet is easier to incorporate into commercial data acquisition software. It appears to combine most of the advantages of the alternative calibration methods. We also found that the (necessarily imperfect) mounting of a treadmill atop a force plate introduced substantial errors in force and center of pressure measurements. The application of the PILS procedure reduced these errors to levels comparable to those of standard laboratory force plates.