Manipulating the edge of instability

Abstract

We investigate the integration of visual and tactile sensory input for dynamic manipulation. Our experimental data and computational modeling reveal that time-delays are as critical to task-optimal multisensory integration as sensorimotor noise. Our focus is a dynamic manipulation task “at the edge of instability.” Mathematical bifurcation theory predicts that this system will exhibit well-classified low-dimensional dynamics in this regime. The task was using the thumbpad to compress a slender spring prone to buckling as far as possible, just shy of slipping. As expected from bifurcation theory, principal components analysis gives a projection of the data onto a low dimensional subspace that captures 91-97% of its variance. In this subspace, we formulate a low-order model for the brain+hand+spring dynamics based on known mechanical and neurophysiological properties of the system. By systematically occluding vision and anesthetically blocking thumbpad sensation in 12 consenting subjects, we found that vision contributed to dynamic manipulation only when thumbpad sensation was absent. The reduced ability of the model system to compress the spring with absent sensory channels closely resembled the experimental results. Moreover, we found that the model reproduced the contextual usefulness of vision only if we took account of time-delays. Our results shed light on critical features of dynamic manipulation distinct from those of static pinch, as well as the mechanism likely responsible for loss of manual dexterity and increased reliance on vision when age or neuromuscular disease increase noisiness and/or time-delays during sensorimotor integration.

Introduction

Dynamic sensorimotor behaviors are quintessentially complex, nonlinear and high-dimensional, making it challenging to gain insight into their underlying neural control (Valero-Cuevas, 2005). For example, we handle objects easily without looking at them, but rely on vision when our fingers are numb. Revealing the mechanism behind this contextual use of vision is also of clinical value, since it can provide critical insight into why we drop objects more frequently as we grow old. Using a novel mechanics-based approach to experimentally and mathematically characterize dynamic manipulation we give an explanation for the contextual use of vision (Cole and Abbs, 1988; Johansson et al., 1992; Häger-Ross and Johansson, 1996; Cole et al., 1998; Augurelle et al., 2003) in the framework of task-optimal multisensory integration (Ernst and Bulthoff, 2004).

Most nonlinear dynamical systems exhibit low-dimensional dynamics at the edge of instability according to mathematical results from bifurcation theory (Guckenheimer and Holmes, 1983). The center manifold theorem states that the dynamics of high-dimensional systems at the edge of instability reduces to a low dimensional normal form on a center manifold (Guckenheimer and Holmes, 1983). Based on this insight, we designed an experiment where compressing a slender spring using the thumbpad (Fig. 1) brought the fused thumb+spring+nervous system to the edge of instability (Valero-Cuevas et al., 2003; Venkadesan et al., 2005). Motivated by spring buckling mechanics (Timoshenko, 1961; El Naschie, 1990), we hypothesized that the dominant dynamics of the fused thumb+spring+nervous system at the edge of instability will resemble a subcritical pitchfork bifurcation.

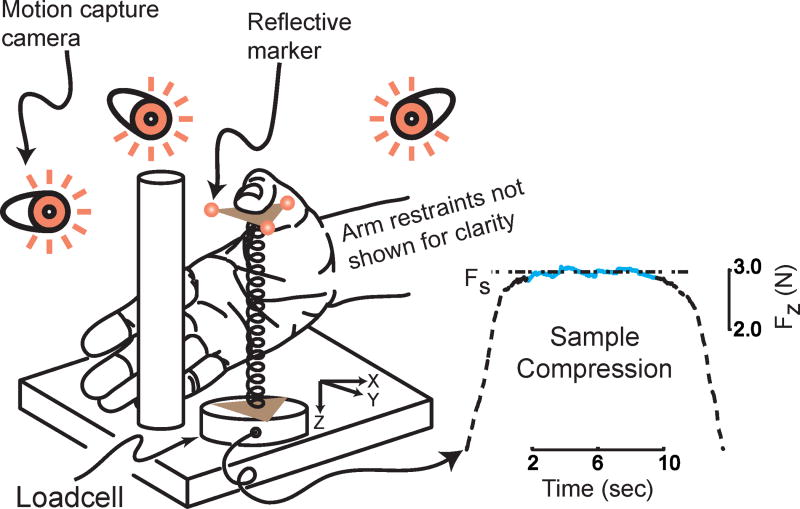
Figure 1.

Schematic of the experimental setup. A representative sample compression is shown on the right, where a subject slowly compressed the spring to minimize the volume of the audio feedback provided (not shown), without letting the spring slip and maintained that compression for 7 seconds before slowly releasing the spring. For the sake of clarity, we have not shown the hand and arm restrains.

We use our data to test the additional hypothesis that task-optimal multisensory integration in the presence of both noise and time-delays explains the contextual use of vision depending on the availability/quality of digital sensors. The time-delays of interest in the context of multisensory integration are only those arising from sensory transduction, nerve conduction and neural processing. Previous studies on multisensory integration (Wolpert et al., 1995; van Beers et al., 2002; Ernst and Bulthoff, 2004; Körding and Wolpert, 2004; Kuo, 2005; Sober and Sabes, 2005) revealed that the relative utility of redundant sensory channels depends on their respective noisiness. For example, (Wolpert et al., 1995) applied Bayesian inference to study the effect of sensory noise but ignored effects of time-delays. However, both noise and time-delays are pervasive in the nervous system and affect sensorimotor control (Collins and Deluca, 1994; Cabrera and Milton, 2002). This suggests that the nervous system uses a task-optimal multisensory integration strategy that combines effects of noise and time-delays in each of vision, thumbpad sensation and non-digital sensors (e.g., muscle spindles, Golgi tendon organ, and non-digital cutaneous afferents).

Methods

After giving written informed consent, nine males and three females (19-40 years of age, mean=23 years) participated in our study that was approved by the Cornell University Committee on Human Subjects. All subjects were right-handed, healthy young adults with no known impairments or recent injuries to their hand and had normal visual acuity or normal with correction. They had no prior experience with this experimental task.

Experimental setup

Subjects were asked to compress a slender helical spring prone to buckling using just their thumbpad (Venkadesan et al., 2005) (Fig. 1). The design specifications for the spring are – free length=76.2mm, mean diameter=8.7mm, wire diameter=0.79mm, total coils=24, material: music wire (#12201, Century Spring Corp., Los Angeles, CA), which we mounted in polymer (ABS P400) endcaps. The top endcap was flat (friction coefficient∼0.5) with a small (0.1 mm) conical projection, precisely coincident with the cylindrical axis of the spring, providing a tactile cue for its geometric center. We mounted the spring on a uniaxial load cell (SML-25, Interface Inc., Scottsdale, AZ), and logged vertical compressive force at 1000Hz using a 16-bit analog-to-digital data acquisition system. We also recorded 3D location and orientation of the spring's endcap at 200Hz using a 4-camera motion capture system (Vicon Peak, Lake Forest, CA; Fig. 1) that tracked the 3 reflective markers attached to the top endcap. We did not use any digital filters on either the force or the motion data for our analyses.

The thumb rested on the endcap with the distal phalanx horizontally oriented, fingers curled around a vertical post and the forearm fixed using a vacuum pillow (Versa Form, Sammons Preston Roylan, Bolingbrook, IL) with the wrist placed in neutral flexion-extension / ad-abduction (Fig. 1) and the elbow at 90° flexion. We did not fix the base of the thumb or the wrist since non-digital mechanoreceptors could contribute to object manipulation (Häger-Ross and Johansson, 1996). Subjects could view the entire spring-thumb assembly from a self-selected angle and their palm never touched the spring.

We provided audio feedback using a clearly audible 500 Hz tone that linearly decreased in volume as the vertical compressive spring force increased. We calibrated this inverse relationship so that no subject made the tone faint enough to be inaudible since the volume vanished only when the compressive force exceeded 4N, which was not attained by any subject.

Experimental protocol

We instructed subjects to, “Slowly compress the spring using only your thumbpad to make the tone volume as faint as possible (i.e., maximize vertical compressive spring force) without letting the spring slip. Once you have reached the point where you cannot decrease the tone volume without letting the spring slip, hold the compressive load so that the tone volume, although now faint, remains constant and slowly release the spring after 10 seconds. It does not matter if the spring bends or oscillates, it only matters that the volume stays constant once you reach the minimum attainable volume and that the spring does not slip.” Only trials with loading/unloading rate less than 5N/s were considered “successful”.

Metric of performance: F_s

The mean compressive spring force during the sustained hold phase was the metric of performance (F_s). The hold phase was “sustained” if the coefficient of variation (COV) of the compressive spring force was less than 5% for 7 seconds. We used three largest F_s values of ten attempts per treatment condition per subject as repeated measures for our statistical analyses. We provided over 1 minute rest after every five compressions.

Experiments to test for effects of training, loss of vision and thumbpad sensation

The experiment was performed over two days. On day one, subjects performed 100 compressions of training and we measured their performance before and after training with normal visual and thumbpad sensibility. On day two, we first measured performance with normal thumbpad sensibility, both with and without vision. An experienced hand surgeon then administered 5cc of 1% Lidocaine solution on the ulnar and radial sides of the base of the thumb (just below the metacarpophalangeal (MCP) joint of the thumb, but away from the thenar eminence) to obtain a digital nerve-block without affecting any musculature (and associated sensors). Cutaneous sensation proximal to the thumb MCP joint was unaffected (tested using the same procedure used below). The nerve-block was considered effective when vision-occluded subjects could not detect a 10g load randomly moved across or applied on their thumbpad using a pointed tip. The point-load was applied using a pair of forceps (weighing 10g) that was lightly held at its base by the experimenter while the pointed end rested on the subject's skin surface to be tested for sensitivity. Note that subjects could detect the small pointed projection at the center of the spring's endcap by pressing their thumbpad forcefully. We then measured task performance after the loss of digital cutaneous sensation, both with and without vision.

We measured maximum isometric force that subjects could produce in two postures, namely key and opposition pinch postures (Valero-Cuevas et al., 2003) using a pinch meter before the nerve block on both days. The largest reading of three attempts was recorded as pinch strength. We gave over 2 minutes rest at the end of strength measurement and extra rest if asked for.

Safety-margin of F_s

To see if subjects reached a compressive force consistently shy of the force at spring slip (safety-margin), we tested whether F_s or F_max (maximum compressive load) changed for successful vs. slipped trials. We redefined F_s when the spring slipped by requiring only a 3s hold for being a “successful” trial, since slippage often occurred before 7s elapsed.

Analysis of endcap rotation

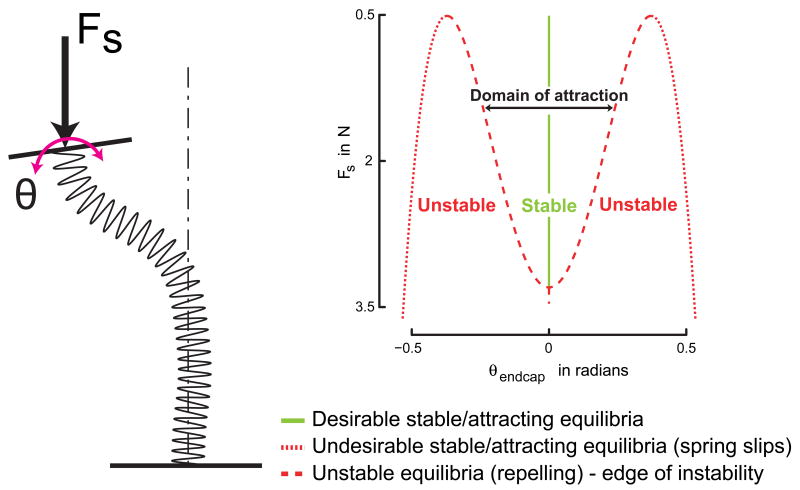
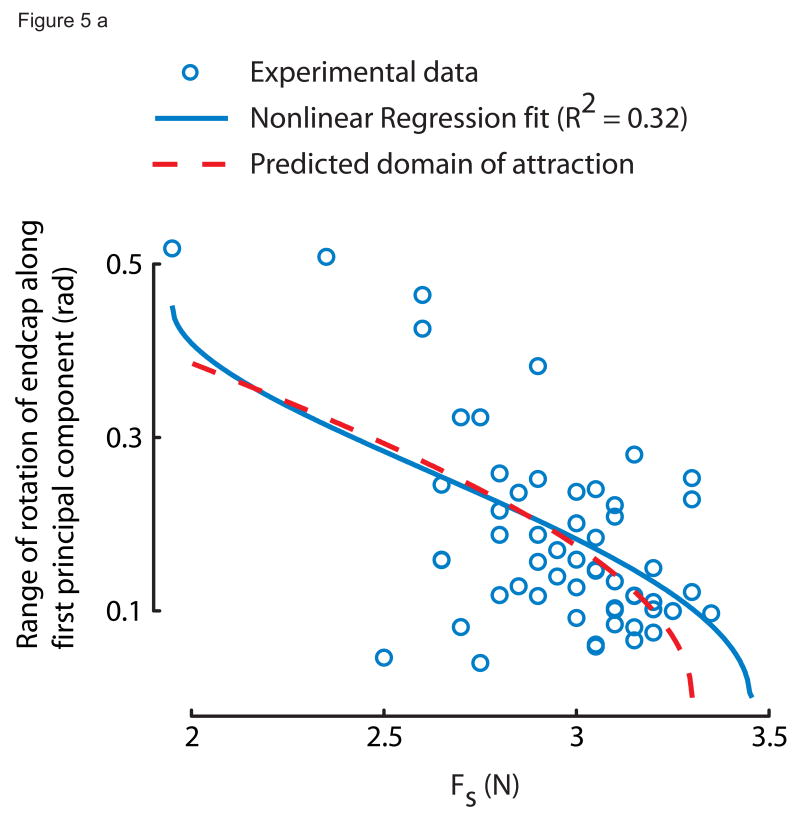
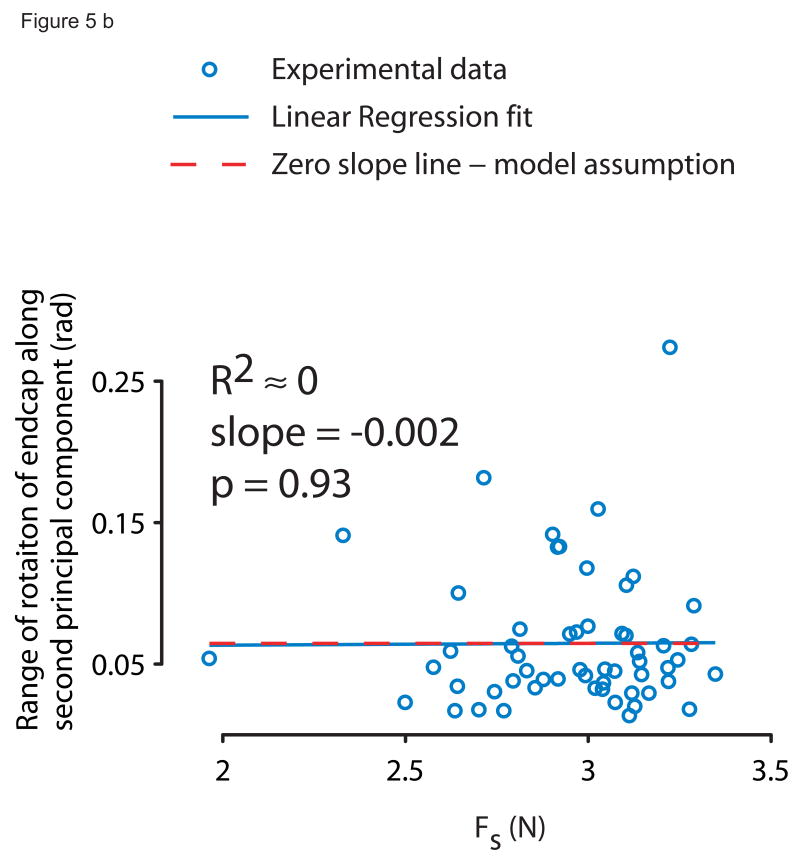
To analyze 3D endcap rotation we calculated the unit normal vector to the plane of the endcap and determined whether one principal component could explain most of the endcap rotation. We then tested whether the rotation projected onto its first principal component (θ_range) varied with F_s as predicted by the subcritical pitchfork bifurcation normal form (equation 1) using a nonlinear least square regression. The central region around the solid line at θ = 0 bounded by the dashed curves in Fig. 2 is the domain of attraction, which narrows with increasing F_s, i.e., it is the predicted θ_range as the spring is compressed when the spring doesn't slip. We also performed a linear regression of endcap rotation projected onto the second principal component vs. F_s.

Figure 2.

Subcritical pitchfork bifurcation diagram. This bifurcation diagram on the right shows the loci of both stable (solid line) and unstable/undesirable (dashed/dotted curves) equilibria for the thumb+spring+nervous system's closed loop dynamics without noise or time-delays as the spring is compressed, which is a succinct description of the underlying deterministic (no time-delays / noise) dynamics of our model. The region bounded by the dashed curves around θ = 0 (the endcap orientation we want to stabilize), in which the endcap is attracted towards θ = 0 is the domain of attraction at any particular value of F_s. If the endcap strays too far outside this region, then it will be rapidly attracted towards the points far out (dotted curves, close to 0.5rad), which is representative of a spring slip. The schematic of a buckled spring on the left clarifies the physical meaning of the variables F_s and θ.

We chose endcap angle as the kinematic variable for our analyses because of the typical spring profile observed during experiments (Fig. 2, left). The spring was typically laterally displaced from the centerline (allowed by task instructions – “It does not matter if the spring bends…”), but the endcap remained nearly horizontal for successful trials and rapidly rotated away from horizontal for slipped trials. This suggested that endcap angle best captured the relevant dynamics of active control.

Statistical analyses

The independent treatments were training and available sensory modalities. The dependent variable for all our statistical analyses was F_s, except for the “safety-margin” analyses, where F_max was an additional dependent variable. We had six treatments: (i) Day 1, pre-training, (ii) Day 1, post-training, and (iii)-(vi) Day 2, four combinations of presence/absence of vision/thumbpad sensation. We set α=0.025 as the threshold for significance, since we performed two repeated-measures ANOVAs: (i) effect of the above six treatments with planned comparisons as post-hoc tests, and (ii) effect of slip vs. no-slip for all six treatments. Subjects were random factors for all ANOVAs.

We also performed a multiple regression analysis of F_s vs. key and opposition pinch strength using an ANCOVA. Subjects were random factors and the six treatments were fixed factors. Since a mixed factor ANCOVA does not provide a model R², we used a regular ANCOVA to determine approximate model R².

We verified necessary assumptions for the validity of each ANOVA/ANCOVA, namely, normality and identical distribution of the residuals. We used SAS (SAS, Cary, NC) for all statistical analyses.

Mathematical modeling of multisensory integration

We modeled the overall 1D dynamics of the closed-loop system as a subcritical pitchfork bifurcation of the endcap angle (θ) projected onto its first principal component, given by (Fig. 2):

$$\dot{\theta }=\alpha \left(F_S-K\right)\theta +\beta {\theta }^3-\gamma {\theta }^5$$ (1)

where, α, β and γ are scaling parameters, F_S represents compressive spring force and K represents the maximum attainable compressive spring force or equivalently, effective feedback gain.

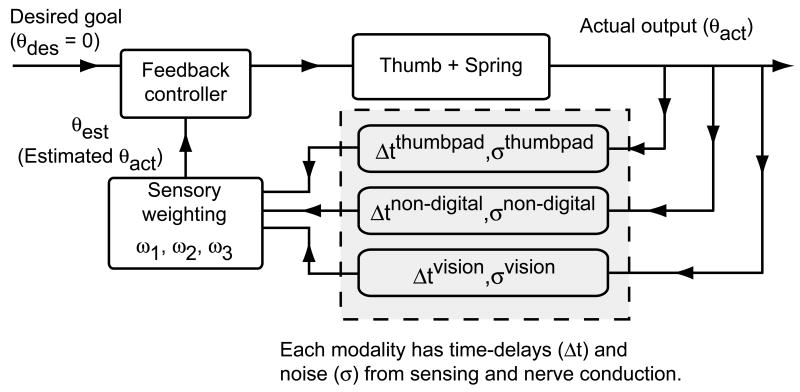
We incorporated multisensory feedback using a simple proportional controller with input a weighted sum of three sensory signals (Fig. 3, equation 2): thumbpad sensation, non-digital mechanoreceptors, and vision. We added zero-mean Gaussian noise $(N_i(0,{\sigma }_i^2);i=1,2,3)$ and a constant time-delay (τ₁,τ₂,τ₃) to each sensory signal and assumed that all sensors were unbiased $(\text{mean}({\theta }_i^{\text{sen}})=\theta )$.

Figure 3.

A block diagram showing feedback control using three sensory modalities, namely, (1) thumbpad sensation, (2) non-digital mechanoreceptors and, (3) vision. The mathematical model is a specific implementation of this block diagram that uses simple proportional feedback control and the entire closed-loop dynamics of this system is modeled as a subcritical pitchfork bifurcation. Time-delays (Δt) and noise (σ) are explicitly labeled only for the sensory branches since for the purpose of this study, only the sensory time-delays and noise affect the relative usefulness of various modalities.

Human visual acuity is known to be at least 1 minute arc at a viewing distance of 250 mm (Liang and Westheimer, 1993; Saunders and Knill, 2004). Subjects' heads were typically 100-170 mm from the spring in our experiment. Because the endcap radius was 40 mm, the estimated standard deviation for visual sensation was σ₃ = 0.0009 rad. Estimated standard deviation of thumbpad sensation based on reported tactile discrimination ability (Wheat et al., 1995) was σ₁ = 0.0007 rad. To account for the reported unreliability of non-digital mechanoreceptors (Häger-Ross and Johansson, 1996; Macefield and Johansson, 1996), we used σ₂ = 0.003 rad (10× the variance of vision). Since the greatest F_s load that subjects could stabilize was ≈3N, we chose the proportional feedback constant K=3.3 (90% of 3.3≈3). The spring slips only when the angle of the endcap with respect to the horizontal exceeds the friction angle (∼0.5 radians). We could directly solve α/γ and β/γ so that the mean friction angle (dotted curve in Fig. 2) was 0.5 and was never less than 0.4 (80% of the average) since there are two unknowns (α/γ,β/γ) and two equations (mean and minimum of friction angle). We tuned γ (time-scale, the only parameter we could not determine from frictional or neurophysiological properties) so that for physiologically realistic time-delays and noise, the simulation (with time-delays and noise) yielded F_s values within experimental range when both thumbpad sensation and vision were occluded. The resulting model is given by the following equations (Fig. 3):

$$\begin{array}{l}\frac{d\theta }{dt}=\stackrel{\begin{array}{l}\text{Subcritical pitchfork bifurcation}\\ \text{normal form equation}\end{array}}{\overbrace{\alpha F_s\theta (t)+\beta \theta {(t)}^3-\gamma \theta {(t)}^5}}-\stackrel{\begin{array}{l}\text{Proportional feedback using estimated}\\ \text{task}-\text{relevant parameter}\end{array}}{\overbrace{\alpha K\widehat{\theta }(t,t-{\tau }_1,t-{\tau }_2,t-{\tau }_3)}}\\ \widehat{\theta }=\sum _{i=1}^3{\omega }_i(\theta (t-{\tau }_i)+{\tau }_i{\upsilon }_i);\text{task}-\text{relevant parameter estimate}\\ {\upsilon }_i\sim N_i(0,1);i=1,2,3;\text{independent Gaussian white noise processes}\end{array}$$ (2)

where, α = 2.639, β = 106.512, γ = 385, K = 3.3 and the time-delays are, τ₁ = 65 ms (Cole and Abbs, 1988; Johansson et al., 1992; Eliasson et al., 1995; Kandel et al., 2000; Johansson and Birznieks, 2004), τ₂ = 65 ms to 120 ms in 5 ms increments to model the large variability in reported time-delay for non-digital sensors (Cole and Abbs, 1988; Johansson et al., 1992; Eliasson et al., 1995; Kandel et al., 2000; Johansson and Birznieks, 2004), τ₃ = 120 ms (Prablanc and Martin, 1992; Paillard, 1996; van Beers et al., 2002).

Numerical optimization

The objective function, namely, performance, was F_s, numerically defined so that the endcap is stable (θ < 0.5 rad) for 80% (±5%) of the trials (“success-rate”) during the 7s hold (“survival-time”). Using success-rates and survival-times to define the metric of performance is necessary for stochastic differential equations such as equation 2 (Cabrera and Milton, 2004). We performed an exhaustive search of all possible sensory weights (2D optimization problem; Supplementary Notes) to find task-optimal sensory weights. Additionally, we compared task-optimal sensory weights against weights that minimize the effect of noise alone (as hypothesized by Bayesian inference for static tasks) (Ernst and Bulthoff, 2004) using the formula ${\omega }_i=(1/{\sigma }_i^2)/\sum _j(1/{\sigma }_j^2)$, where ω are sensory weights and σ² are the variances of each sensory modality. All simulations used the MATLAB^® environment.

Results

Principal components analysis revealed that the experimentally measured endcap rotation collapsed to 1D at the edge of instability, and the stable domain of attraction shrunk with increasing compressive spring force in close resemblance to the subcritical pitchfork bifurcation normal form equation (Fig. 4a, 4b). The first principal component explained 94.5% of the variance in 3D motion of the unit normal vector (99.9% confidence interval = (91.2%, 96.6%)), i.e., rotation about one fixed axis described almost 95% of endcap rotational dynamics. The experimentally obtained relationship between range of endcap rotation along the first principal axis vs. F_s (Fig. 5a: solid curve, α̂_estimate = 0.0017, β̂_estimate = 0.11, K_estimate = 3.45, R²=0.32) agreed well with the mechanics-based (namely, frictional constraints) model prediction (equation 1, Fig. 5a: dashed curve, α̂_model = 0.0069, β̂_model = 0.28, K_model = 3.3). Further, the range of endcap rotation along the second principal component showed no dependence on F_s (Fig. 5b; slope=0, p=0.96, R²≈0).

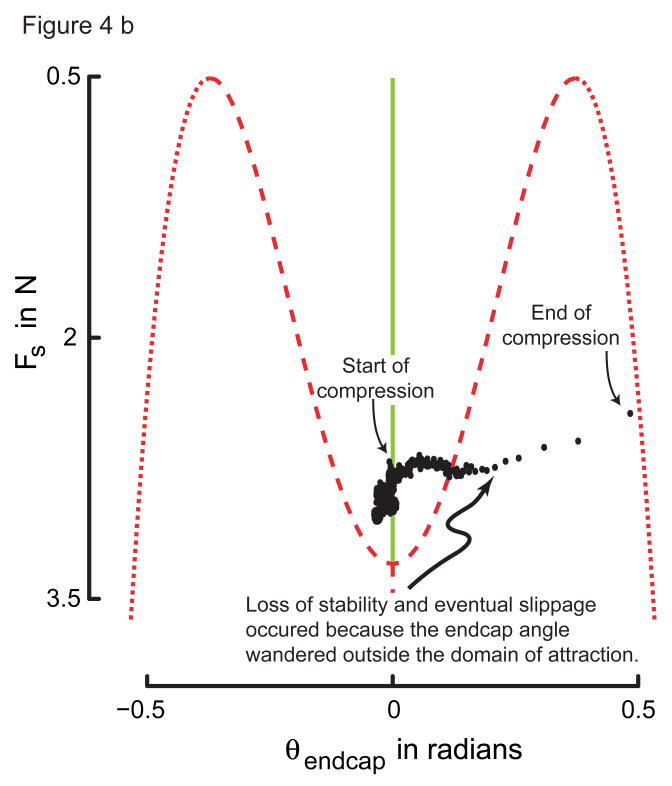
Figure 4.

Figure 4a: Representative trial showing endcap rotation time-history for a successful trial. This trial was with all sensations intact. Note how the endcap rotation is better regulated as the compressive spring force increases. Importantly, the endcap rotation angle stays well within the domain of attraction predicted by the subcritical pitchfork bifurcation normal form.

Figure 4b: Representative trial showing endcap rotation time-history when the spring slipped. This trial was with all sensations intact. Note that the spring slipped when the endcap rotation angle exceeded the domain of attraction. Importantly, the load at slip was lower than when the spring did not slip (cf. Fig. 4a).

Figure 5.

Figure 5a: The first principal component captures all relevant endcap rotational dynamics. The spatiotemporal dynamics of the normal form model were indistinguishable from experimental measurements projected onto the first principal component. The best nonlinear least squares fit for the relationship between range of endcap rotation vs. F_s along the first principal components is nearly identical to model prediction for a subcritical pitchfork bifurcation (Fig. 3). The low R² means that the system is very noisy.

Figure 5b: The independence of the dynamics (range of endcap rotation) from F_s (slope indistinguishable from 0) along the second principal component further supports our model rationale since it indicates that all relevant endcap rotational dynamics were captured by the first principal component and the second component provides no additional information.

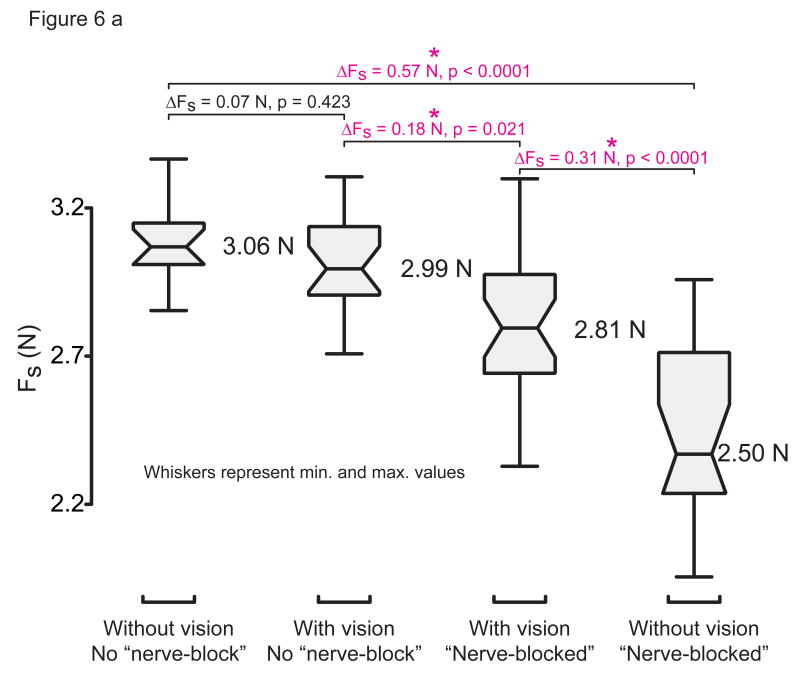
Experimentally, the occlusion of vision had a measurable impact on performance only when thumbpad sensation was also occluded (Fig. 6a). When thumbpad sensation was lost, F_s always decreased ( $\Delta F_s^{\text{effect of nerve}-\text{block with vision}}=F_s^{\text{normal}}-F_s^{\text{numb}}=0.18\text{N}$, p=0.021; $\Delta F_s^{\text{effect of nerve}-\text{block with vision}}=F_s^{\text{normal}}-F_s^{\text{numb}}=0.57\text{N}$, p<0 0001; Fig. 6a) After visual occlusion however, F_s remained unchanged when the thumbpad was intact ( $\Delta F_s^{\text{effect of vision}1}=F_s^{\text{vision}}-F_s^{\text{blind}}=-0.07\text{N}$, p=0 423), but decreased by a large amount when the thumbpad was numb ( $\Delta F_s^{\text{effect of vision}2}=F_s^{\text{vision}}-F_s^{\text{blind}}=0.31\text{N}$, p<0.0001).

Figure 6.

Figure 6a: Box plots of experimental results of sensory occlusion. The horizontal bars inside the box plots is the median, the notches are the robust 95% confidence interval of the median, the boxes are bounded by the 75^th percentile and 25^th percentile, the numeric values next to each box is the sample mean, and the whiskers represent the entire range of the data. The expected contextual use of vision is found by comparing columns 1 vs. 2 and columns 3 vs. 4. The differences in F_s marked with a ‘*’ symbol are the only significant ones at the preset significance level of 0.025.

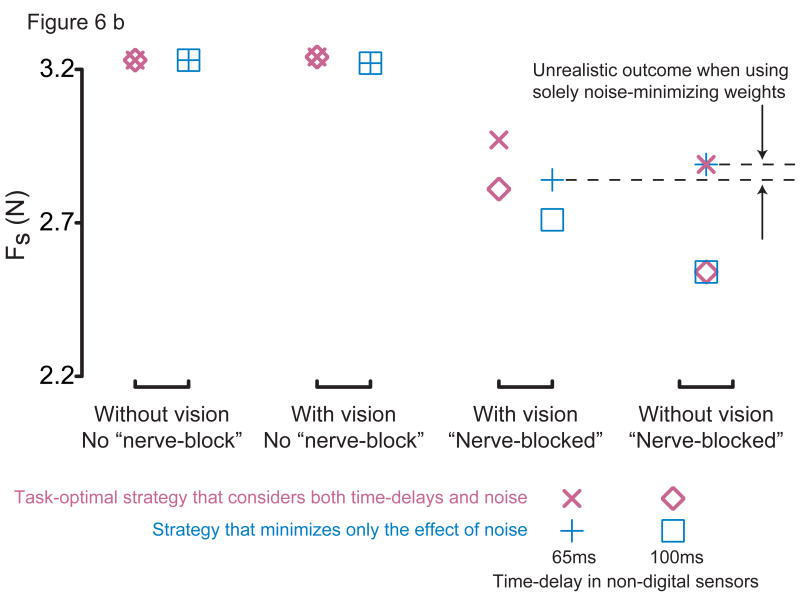
Figure 6b: Results of simulations using two alternate sensory weighting strategies. Only simulations with 65ms time-delay for non-digital sensors (‘×’, ‘+’) and with 100ms time-delay for non-digital sensors that best replicated experimental data (‘◊’, ‘□’) are shown above. The task-optimal strategy (‘×’, ‘◊’) yields better performance (larger F_s) than the noise-minimizing strategy (‘+’, ‘□’) demonstrating the effect of time-delays on multisensory integration. The 100ms-simulation (‘◊’, ‘□’) using a task-optimal strategy (‘×’, ‘◊’) best agreed with experimental data (cf. 3^rd vs. 4^th columns). Noise-minimizing sensory weights (‘+’, ‘□’), however, yield unrealistic and non-robust results such as an increase in performance after visual occlusion over and above loss of thumbpad sensation (again, cf. 3^rd vs. 4^th columns). Note that when both thumbpad sensation and vision are absent there is no multisensory integration required since only the non-digital mechanoreceptors remain intact. The sensory weights used in the simulations are listed in Table 1.

Computationally (equation 2, Fig. 3), by using numerical optimization, we found that this contextual use of vision emerged for sensory weights (for thumbpad sensors, non-digital sensors and vision) that maximized performance (F_s), i.e., by accounting for both sensory noise and time-delays (Fig. 6b, Table 1) despite large uncertainty in time-delay for non-digital sensors (closest match to experimental data when τ_{non–digital} = 100ms). In contrast, purely noise-minimizing sensory weights (disregarding time-delays) led to unrealistic results such as an improvement in performance after loss of vision and thumbpad sensation (Fig. 6b column 3 vs. 4. when τ_{non–digital} = 65ms).

Table 1.

Task-optimal and noise-minimizing sensory weights for all simulations. The columns of sensory weights in this table correspond to the columns in Fig. 6b.

Simulations with τnon–digital = 65 ms
Sensory conditions	No vision No “nerve-block”		With vision No “nerve-block”		With vision “Nerve-blocked”		No Vision “Nerve-blocked”
Strategy§	TO	NM	TO	NM	TO	NM	TO = NM
Digital (ω1)	0.96	0.95	0.96	0.65	-	-	-
Non-digital (ω2)	0.04	0.05	0.04	0.03	0.35	0.09	1
Visual (ω3)	-	-	0	0.32	0.65	0.91	-
Simulations with τnon–digital = 100 ms
Digital (ω1)	0.99	0.95	0.95	0.65	-	-	-
Non-digital (ω2)	0.01	0.05	0	0.03	0.27	0.09	1
Visual (ω3)	-	-	0.05	0.32	0.73	0.91	-

^§TO: Task-optimal; NM: Noise-minimizing

Training had no effect on F_s on day 1 ( $\Delta F_s^{\mathrm{Day}1}=F_s^{\mathrm{post}–\mathrm{train}}-F_s^{\mathrm{pre}–\mathrm{train}}=0.08\text{N}$, p=0.248). Performance on day 2 was also not statistically different from that on day 1 (numerically greater by 0.05N and lower by 0.03N than the start and end of day 1, respectively).

Subjects did not maintain any consistent “safety-margin”, indicating that they were truly at their sensorimotor limit when sustaining maximal compression of the spring. There was no difference in F_s or F_max between successful trials vs. when the spring slipped for all four sensory occlusion conditions (p>0.530, p>0.197, respectively; Table 2).

Table 2.

Statistical post-hoc planned comparisons of F_s (sustained load) and F_max (maximal load) for trials when the spring slipped vs. when the spring did not slip. The above values are all for Day 2. These results indicate that subjects did not maintain a “safety margin” during the successful (i.e., no-slip) performance of this dynamic manipulation task. The ANOVA across conditions, was significant with p<0.0001.

Subject Condition	$\Delta F_s=F_s^{\mathrm{slip}}-F_s^{\mathrm{no}–\mathrm{slip}}$ in N	p-value	$\Delta F_{max}=F_{max}^{\mathrm{slip}}-F_{max}^{\mathrm{no}–\mathrm{slip}}$ in N	p-value
Normal	0.01	0.912	0.03	0.708
No vision	0.15	0.530	-0.07	0.688
Nerve-blocked	0.05	0.667	0.12	0.197
No vision, Nerve-blocked	-0.01	0.900	0.03	0.700

The COV of pinch strength (mean=99.41 N, COV = 13.8%) was almost three times that of F_s with normal sensibility on day 2 (mean = 2.99 N, COV = 5.2%, < 5% of pinch strength). Moreover, a multiple regression of F_s for all sensory conditions on day 2 vs. static pinch strength (key and opposition; p = 0.969, and p = 0.338 respectively, overall R² = 0.66,) was statistically non-significant. The high R² indicates that one can reliably conclude that F_s was independent from strength.

Discussion

A mechanics-based low-order normal form equation from bifurcation theory produced dynamics indistinguishable from experimental measurements at the edge of instability in a dynamic manipulation task. Using this normal form equation, we successfully developed a model of multisensory integration which replicated the contextual use of vision found in our sensory occlusion experiments. The contextual use of vision was robust to neurophysiologically tenable uncertainty in the time-delay for non-digital sensors only for a task-optimal multisensory weighting strategy that accounted for both time-delays and noise. However, a static Bayesian inference strategy that accounted solely for noise did not possess this robustness. Thus, we revealed the effect of time-delays over and above the known effects of noise on multisensory integration. It is worth noting the ability of our nonlinear low-order model to capture both the effects of sensory occlusion and the spatiotemporal dynamics of the task. Importantly, our model had only one free parameter (time-scale for overall dynamics) and all other parameters were obtained from basic frictional constraints and previously reported neurophysiological data for sensory time-delays and noise variances.

Our study critically extends our understanding of the neural control of manipulation by indicating important differences between static and dynamic grasp. First, subjects did not maintain a detectable safety-margin when compressing the spring, unlike static grasp (Cole and Abbs, 1988; Johansson et al., 1992; Eliasson et al., 1995; Cole et al., 1998; Augurelle et al., 2003). Second, we found no relationship between dynamical performance (F_s) and pinch strength. The fact that our experimental paradigm focuses on very low forces (F_s < 5% of pinch strength) allows us to conclude that we are investigating the limit of hand sensorimotor integration, independently of muscle strength.

There are some limitations of this study that, while not affecting the validity of our results, do open new directions for future research. We argue that feedback control is used for preventing slippage at the edge of instability in contrast to a predictive forward/inverse dynamic model (Wolpert et al., 1995; van der Kooij et al., 1999; Kuo, 2005) or a preset thumbtip impedance (Burdet et al., 2001). When the spring+thumb+nervous system is close to the edge of instability, sensitivity to noise and other uncertainties increases dramatically (Stein, 2003), thus rendering unlikely, the use of time-delay compensation or predictive control. Also, sensory occlusion severely affected performance indicating that a preset (feedforward) thumbtip impedance was not the dominant form of control. This claim is further supported by preliminary evidence from a separate study (Valero-Cuevas et al., 2006). Moreover, a high-impedance strategy would be dependent on thumb strength (Hogan, 1984), and would be destabilizing due to signal-dependent noise in muscles (Harris and Wolpert, 1998). As with any modeling work, we cannot conclusively prove that the nervous system indeed uses a task-optimal strategy. Nevertheless, our results agree with and add valuable insight to the existing body of evidence for optimality principles in sensorimotor control (Harris and Wolpert, 1998; Todorov, 2004).

Our results are compatible with other studies of multisensory integration (Wolpert et al., 1995; Ernst and Bulthoff, 2004; Körding and Wolpert, 2004) and precision pinch (Cole and Abbs, 1988; Johansson et al., 1992; Augurelle et al., 2003), but go beyond them to investigate for the first time, multisensory integration during a complex, nonlinear and dynamic manipulation task. Our novel task – by virtue of being dynamic, unstable and nonlinear, and exploiting the dimensional collapse at the edge of instability – was able to reveal how both time-delays and noise affect multisensory integration, unlike past studies that used static task goals.

In summary, using mathematically predicted properties of nonlinear dynamical systems we find that dynamic manipulation at the edge of instability becomes mathematically tractable without compromising the complexity of the task or oversimplifying the analysis. We found that time-delays affect multisensory integration in addition to the previously known effects of noise and the contextual use of vision arises naturally from task-optimal multisensory integration. This work sheds light on the loss of dexterity with aging – by providing a paradigm within which to assess the different consequences of degradation of tactile sensors vs. increased cortical processing (i.e., “computational”) time-delays (Cole et al., 1998) to the efficacy of multisensory integration for dynamic manipulation. Additionally, we found that the neural control of dynamic manipulation detects and regulates incipient instabilities such as an imminent slip. In conclusion, since the dimensional collapse at the edge of instability is ubiquitous in almost all nonlinear dynamical systems, we can extend this paradigm to other sensorimotor systems. Together with our simple, low-order mathematical model based on bifurcation theory, our novel and simple paradigm of pushing the combined body+world+nervous system to an edge of instability is a powerful tool that opens up research directions to reveal the nature of sensorimotor control in development, ageing, disease and treatment.