The universal distribution of evolutionary rates of genes and distinct characteristics of eukaryotic genes of different apparent ages

Abstract

The evolutionary rates of protein-coding genes in an organism span, approximately, 3 orders of magnitude and show a universal, approximately log-normal distribution in a broad variety of species from prokaryotes to mammals. This universal distribution implies a steady-state process, with identical distributions of evolutionary rates among genes that are gained and genes that are lost. A mathematical model of such process is developed under the single assumption of the constancy of the distributions of the propensities for gene loss (PGL). This model predicts that genes of different ages, that is, genes with homologs detectable at different phylogenetic depths, substantially differ in those variables that correlate with PGL. We computationally partition protein-coding genes from humans, flies, and Aspergillus fungus into age classes, and show that genes of different ages retain the universal log-normal distribution of evolutionary rates, with a shift toward higher rates in “younger” classes but also with a substantial overlap. The only exception involves human primate-specific genes that show a heavy tail of rapidly evolving genes, probably owing to gene annotation artifacts. As predicted, the gene age classes differ in characteristics correlated with PGL. Compared with “young” genes (e.g., mammal-specific human ones), “old” genes (e.g., eukaryote-specific), on average, are longer, are expressed at a higher level, possess a higher intron density, evolve slower on the short time scale, and are subject to stronger purifying selection. Thus, genome evolution fits a simple model with approximately uniform rates of gene gain and loss, without major bursts of genomic innovation.

All genomes are collections of genes that widely differ with respect to their histories and characteristic rates of evolution. In prokaryotes, a major phenomenon that shapes evolutionary histories of genes is horizontal gene transfer owing to which each bacterial or archaeal genome contains genes from many different sources (1–3). Eukaryotes are chimeric organisms to begin with, owing to the ancient mitochondrial endosymbiosis (4–6), and different eukaryotic lineages have experienced massive influx of bacterial genes as a result of secondary endosymbiosis, plants being the premier case in point (7). Apart from endosymbiosis, horizontal gene transfer in eukaryotes seems to be uncommon but both loss of genes and emergence of new genes, apparently, have been extensive throughout eukaryotic evolution (8, 9).

The mechanisms that lead to the birth of new genes are not fully understood. The most common route of innovation is thought to be gene duplication followed by a major acceleration of evolution so that the similarity to the ancestral genes becomes undetectable (10–12). Of course, more exotic modes of innovation, such as the actual origin of protein-coding genes from noncoding sequences (13), also might contribute to genome evolution but their contributions are unlikely to be comparable to that of gene duplication. Furthermore, loss of genes, which is an intrinsic aspect of the evolutionary process and was extensive in some lineages (9, 14, 15), also can produce the appearance of emergence of new genes when a gene present in a particular lineage seems novel because its homologs in other lineages have been lost in the course of evolution. The processes of gene gain and loss are inextricably linked in that both, typically, involve a period of evolutionary “free fall” when a gene is free from the constraints of purifying selection.

Systems biology enriched our outlook of biological evolution by revealing complex and, often, unexpected connections between functional and evolutionary attributes of genes (16–20). Traditionally, it is assumed, explicitly or more often implicitly, that the characteristic rate of evolution of a protein-coding gene depends, primarily, on the structural-functional constraints that are intrinsic to the encoded protein (21). In a prescient early discussion, Wilson et al. (22) proposed that the sequence evolution rate of a protein-coding gene would depend on, first, the intrinsic structural-functional constraints and, second, the biological role of the protein in the organism: R_i = f(P_i)f(Q_i) where R_i is the sequence evolution rate, f(P_i) is the functional-constraint factor, and f(Q_j) is the dispensability (biological role) factor. Because the functions and structures of proteins are, indeed, widely different and so are the rates of sequence evolution, it was generally (and more or less tacitly) assumed that the first term in Wilson's equation was the decisive one.

With the advent of functional genomics and systems biology, it became possible to measure the correlations between many “genomic” and “phenomic” variables (16–20). Surprisingly, little if any correlation was found to exist between the fitness effect of a gene knockout and the rate of its sequence evolution: at best, nonessential genes evolve slightly faster than essential genes (14, 23–26). By contrast, but also unexpectedly, a highly significant, although moderate in magnitude, negative correlation has been shown to exist between gene expression level and the sequence evolution rate: highly expressed genes evolve significantly slower than lowly expressed ones (14, 27–29). So far, among the analyzed phenomic variables, expression level is definitely the best correlate of the sequence evolution rate (14, 28, 30, 31). The analysis of the connections between other genomic and phenomic variables, including but not limited to the numbers of physical and genetic interactions, positions in different types of networks, and codon usage, and the evolution rate yielded a complex pattern of correlations (16–19, 29, 32). However, all these correlations are weaker than that seen for the expression level, so that the independence and hence the ultimate relevance of these correlations remain in question. In a separate line of analysis, it has been shown that the length of the protein encoded by a gene is significantly and negatively correlated with the evolution rate, that is, longer proteins, on average, are more highly conserved in evolution than short ones (33).

Taken together, these findings might throw new light on the nature of the fundamental factors that affect gene evolution. It has been suggested that specific functional constraints might not be nearly as crucial as generally thought. Instead, the real driving force of protein evolution could be the selection for protein robustness to misfolding caused by amino acid misincorporation, primarily, during translation (28). The fitness cost of misfolding is an intrinsic feature of protein domains but is thought to be amplified by the rate of translation, hence the observed negative correlation between the expression level and sequences evolution rate (31).

Gene evolution can be characterized not only by the sequence evolution rate, but also by the propensity of a gene to be lost (or, conversely, retained) during evolution. A gene's rate of loss/retention during evolution appears to be more naturally linked to the broadly conceived biological importance than the sequence evolution rate considering that, almost by definition, a gene will not be lost in any lineage if and only if it is essential (and there is no substitute). Propensity for gene loss (PGL) is linked to the expression level by a negative correlation that is as strong as, if not stronger than, the correlation between expression and the sequence evolution rate (14). Moreover, unlike the sequence evolution rate, the PGL showed a highly significant correlation with a gene's dispensability: in yeast, genes with a low loss rate were much more likely to be essential than genes with a high loss rate (14, 15).

Here, we demonstrate the universality of the distribution of evolutionary rates of protein-coding genes in diverse lineages of eukaryotes and prokaryotes and describe a simple model of genome evolution that is compatible with this universal distribution and predicts substantial differences between the properties of genes that belong to different “age classes,” that is, possess detectable homologs at distinct phylogenetic depths. We delineate age classes of genes in humans, flies and Aspergillus fungus, and reveal systematic differences between the age classes in terms of expression, protein size, intron density, short-term evolutionary rates, and selection pressure.

Results

Universal Distribution of Evolutionary Rates of Genes.

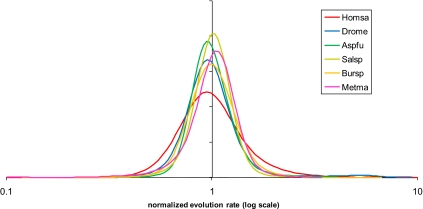
Previous work has shown that the distributions of evolution rates of genes were very similar even in genomes separated by a wide range of evolutionary distances (34). We verified this observation, using new genomic data from eukaryotes, bacteria, and archaea, and found that all rate distributions across orthologous gene sets from closely related pairs of species representing the 3 domains of cellular life are virtually indistinguishable (Fig. 1). In an extension of this observation, normalized distributions of evolution rates between orthologs from one species and its relatives at different evolutionary distances are virtually identical after normalization as illustrated by the comparison of human against other vertebrates and of Aspergillus against other fungi (see SI Appendix). This (approximately) log-normal distribution emerges as a universal of genome evolution that applies not only to complete, genome-wide sets of genes but also to various subsets of genes as described below. Put another way, these findings suggest that the distribution of evolutionary rates of genes across genomes remained (almost) the same throughout the 3 billion years or so that cellular life exists on earth.

Fig. 1.

Distributions of nucleotide sequence evolution rates for pairs of closely related eukaryotic, archaeal, and bacterial genomes. The evolutionary distances were calculated using the Jukes–Cantor correction and normalized so that the mean of each distribution was equal to 1. Metma, Methanococcus maripaludis C5 vs. M. maripaludis C7 (Euryarchaeota); Bursp, Burkholderia cenocepacia MC0–3 vs. B. vietnamiensis G4 (Proteobacteria); Salsp, Salinispora arenicola CNS-205 vs. S. tropica CNB-440 (Actinobacteria). The probability density curves were obtained by Gaussian-kernel smoothing of the individual data points (64).

Steady State Model of Gene Gain and Loss During Genome Evolution.

Evolution of genomes involves extensive loss and gain of genes, and the PGL values of individual genes differ widely (14, 15). Nevertheless, the distribution of evolutionary rates across genes remains (nearly) constant over enormous time spans (Fig. 1), with the rather unexpected implication that genes that are lost have the same rate distribution as gained genes. To examine this prediction, we developed a simple mathematical model of genome evolution by gene gain and loss.

Consider a genome of a constant size under a steady state process of gene gain and loss. It can be easily shown (see SI Appendix) that, if the intrinsic loss rate x (equivalent of the PGL) is distributed with the probability density function g(x) in newly acquired genes, the genome arrives at an equilibrium with the joint distribution of gene loss rates x and gene ages a l(a, x) ∼ e^−axg(x). Several corollaries follow from this relation: (i) The overall distribution of the gene loss rates in the genome is f(x) ∼ $\frac{1}{x}$g(x). (ii) The genes that are lost at any given time have the same distribution of their loss rates as the genes that are gained (g(x)). (iii) The overall distribution of the gene ages in the genome is p(a) ∼ ∫e^−axg(x)dx. (iv) For any given interval of gene ages A = [a₁,a₂] (gene age class), there exists a distribution of gene loss rates x that is specific to the given age class q(x, A)∼∫_a1^a₂ e^−axg(x)da. (v) Considering that other characteristics of genes, such as expression level, sequence evolution rate, and others, are significantly (even if not necessarily strongly) correlated with the PGL (14, 35), it follows that these variables also will be distributed (nearly) identically among genes that are lost and genes that are gained. Thus, the model validates the qualitative implication of the constant distribution of evolutionary rates. (vi) The correlation between PGL and other variables further implies that all these variables will also have distinct, age-class-specific distributions. In particular, it can be shown that, for “old” genes, the distributions of the PGL and variables that are positively correlated with the PGL, such as the sequence evolution rate, will be shifted toward lower values (slow evolution, low loss rate) compared with “young” genes (see SI Appendix). Conversely, the distributions of variables that are negatively correlated with the PGL are predicted to be shifted toward higher values in older age classes, e.g., “old” genes are expected to be highly expressed, on average.

Age Classes of Eukaryotic Genes and Their Distinct Features.

We sought to test the prediction of the steady-state model of genome evolution that genes of different age classes (genes gained at different time during the evolution of a lineage) substantially differ in the characteristics that are correlated with the PGL. There is no single, optimal method to define the age of a gene. Considering that new genes typically emerge as a result of gene duplication, one of the more sophisticated approaches includes evolutionary reconstructions that map each duplication to a specific branch in the corresponding species tree and consider that branch the “birth date” of the gene in question (36, 37). However, this approach is both labor-consuming and error-prone, so we used a more straightforward (and cruder) procedure for partitioning genes into age classes. A gene was considered to belong to a certain class, for instance, mammal-specific genes in human, if the amino acid sequence of the encoded protein failed to show significant sequence similarity (exceeding the specified expectation value threshold; see Methods for details) to protein sequences outside the given taxon (in this case, mammals). The procedure was fine-tuned to eliminate potential artifacts, such as contaminations, and appropriate major taxonomic levels were chosen for the 3 analyzed genomes, human, the fly Drosophila melanogaster, and the ascomycete fungus Aspergillus fumigatus (see Methods for details).

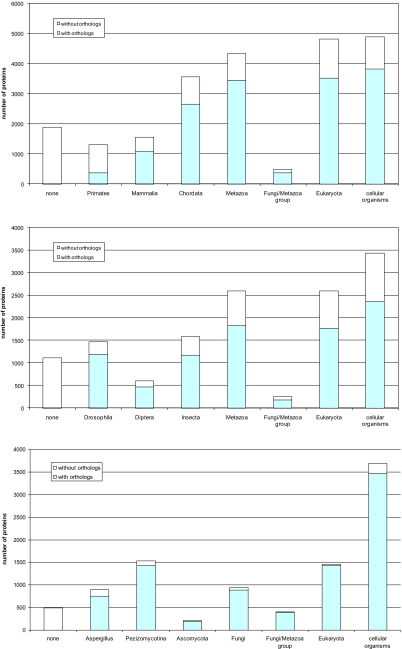
On the basis of the taxonomic breakdown of the nonredundant protein sequence database search results, the gene sets from the 3 organisms were each partitioned into 8 age classes (Fig. 2); qualitatively, the same results were obtained with a series of cut-off values used for the assignment of genes to classes (see SI Appendix). The 2 “ancient” classes (Eukaryota and Cellular Organisms) were the same for all 3 analyzed organisms whereas the “younger” classes differed in accordance with the taxonomy (compare Fig. 2 A–C). In all 3 genomes, the most “ancient” class“ (Cellular Organisms) was also most populous although only in Aspergillus the excess of genes in this class over others was dramatic (Fig. 2C), perhaps owing in part to fungal-specific acquisition of bacterial genes via HGT. Most of the classes, with the exception of the ”Fungi-Metazoa“ class, included sufficiently large numbers of genes for statistically valid comparisons of various features as described below.

Fig. 2.

Partitioning of eukaryotic gene sets into age classes. The filled portion of each bar shows those genes for which likely orthologs were identified in the corresponding closely related species, and the empty portion shows the remainder of the genes for which orthologs were not detected. (Top) Homo sapiens (orthologs in Macaca mulatta). (Middle) Drosophila melanogaster (orthologs in D. simulans). (Bottom) Aspergillus fumigatus (orthologs in Neosartorya fischeri).

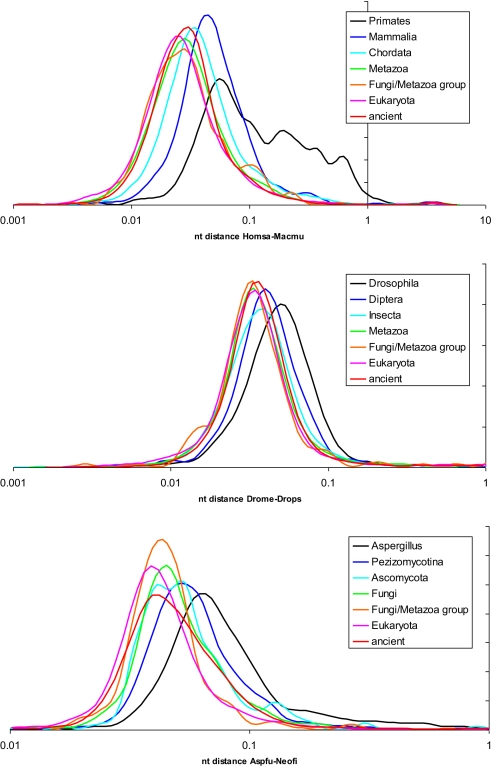
We then compared the short term evolution rates of the genes from different age classes. To this end, probable orthologs were identified in the corresponding closely related organisms (such orthologs were detected for the majority but not all genes, presumably in large part owing to gene annotation errors, but possibly, also because of lineage-specific gene duplications and gene losses; Fig. 2), and evolutionary distances were calculated. The distributions of these distances all have the same shape that closely resembles the universal, approximately log-normal distribution (Fig. 1) but the distributions for the younger classes are shifted toward greater evolutionary distances (rates) compared with the distributions for older classes (Fig. 3). For example, among human genes, the mammal-specific genes on average evolve substantially (and highly significantly) faster than chordate-specific genes or genes that belong to the more “ancient” classes (Fig. 3A), and very similar results were seen for the other two organisms (Fig. 3BC).

Fig. 3.

Distributions of nucleotide sequence evolution rates for different age classes of eukaryotic genes. The evolutionary distances were calculated as in Fig. 1 but not normalized. (Top) H. sapiens (vs. M. mulatta). (Middle) D. melanogaster (vs. D. simulans). (Bottom) A. fumigatus (vs. N. fischeri). The probability density curves were obtained by Gaussian-kernel smoothing of the individual data points (64).

The significant differences in the rate distributions between the age classes notwithstanding, all of the distributions strongly overlap (Fig. 3). In other words, there is, for instance, a considerable number of mammal-specific genes that evolved very slowly since the divergence of human and macaque from their last common ancestor, and conversely, ancient human genes with homologs in prokaryotes that have been evolving very fast over the last ≈23 million years [after the divergence of humans and macaques form their last common ancestor (38)]. Moreover, there is almost no difference in the distributions of the evolutionary rates between the 5 “oldest” gene classes in each of the 3 organisms (Fig. 3). Thus, the short term evolutionary rates seem to preserve the “memory” of the origin of the respective genes over several hundred million years but the memory of the deepest evolutionary past is lost.

The only rate distribution that was noticeably different from the others was the one for the human primate-specific genes. This distribution contains an extremely heavy tail of rapidly evolving genes (Fig. 3A), an observation suggesting that this class of human genes could include a large admixture of incorrect gene predictions that are carried over to the annotation of the macaque genome. A recent analysis of “primate-specific genes” led to the conclusion that most of these were false predictions because there was not demonstrable difference between the properties of these “genes” and noncoding sequences (39). The present results, however, indicate that the distribution of the evolutionary rates of primate-specific genes contains a substantial approximately log-normal portion, suggesting that over half of the members of this class are bona fide genes (Fig. 3A).

We compared the age classes of eukaryotic genes in terms of the pressure of purifying selection that affects protein coding sequences by using the measure commonly used for this purpose, the ratio of the rates of nonsynonymous to synonymous substitutions, dN/dS (40, 41). The results were congruent with the observations on evolutionary rates in that the younger classes were characterized by a relatively weak median selection pressure whereas the older classes appeared to be subject to a substantially stronger purifying selection. As with the evolutionary rates, the effect disappeared in comparisons between the oldest classes, e.g., metazoan-specific human genes evolved under approximately the same selective pressure as the eukaryote-specific genes (Fig. S1).

The proteins encoded by genes in the new age classes were significantly shorter than those encoded by genes from the older classes. The difference in protein lengths was dramatic between the youngest and the old classes, e.g., eukaryote-specific proteins in humans are, on average, twice as long as the mammal-specific proteins, but similarly to the case of evolutionary rates and selective pressure, the difference petered off in the old classes (e.g., from the metazoan-specific proteins up in humans and flies) (Fig. S2).

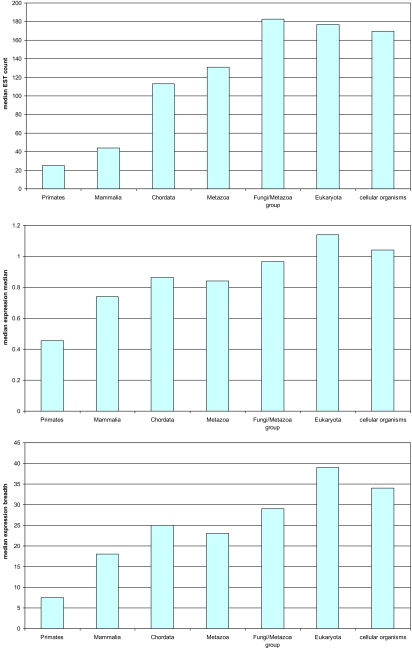
The most impressive difference between the age classes of genes was seen when we compared their characteristic expression levels. The mammal-specific genes in humans showed an approximately 4-fold lower median EST count than the eukaryotic proteins; notably, in this comparison, significant differences were seen even between the older classes, e.g., eukaryote-specific genes had significantly more ESTs than animal-specific genes (Fig. 4A). The results obtained when expression level was determined from microarray data (Fig. 4B) and a comparison of gene expression breadth across human tissues (Fig. 4C) revealed a similar, although somewhat weaker trend. We further investigated the tissue distribution of expression of human genes depending on their apparent age and detected considerable tissue-specific differences in the ratio of mean expression levels of ancient (animal-specific and older) and younger genes (see SI Appendix). There was a highly consistent trend for higher expression of ancient genes in hematopoetic tissues whereas the preferential expression of younger genes was seen, primarily, in nonbrain nerve tissues. Conceivably, these differences have to do with the extent of differentiation and characteristic cell proliferation rate of the tissues, with ancient genes preferentially expressed in the least differentiated, actively proliferating tissues.

Fig. 4.

Expression of human genes from different age classes. (Top) The median EST counts. (Middle) The median expression level in microarray experiments. (Bottom) The median expression breadth (number of tissues where the gene is expressed) in microarray experiments.

We also observed a significant difference in intron density between the age classes of genes, with a greater density in the ancient classes (Fig. S3). This observation might seem puzzling but appears to be compatible with the other distinctions between the age classes considering that introns are known to contribute to eukaryotic gene expression (42) and that highly conserved genes appear to gain introns at a greater rate than poorly conserved genes (43).

Functional Distribution of the Genes in Different Age Classes of Eukaryotic Proteins.

The functional characteristics of human genes in different age classes were determined by analyzing the Gene Ontology (GO) terms (44) that were significantly enriched in each class. The distinctions between the classes were immediately obvious (see SI Appendix). The youngest classes, the primate-specific and mammal-specific genes, were dominated by genes implicated in various forms of defense (in particular, diverse aspects of immune response among the mammal-specific genes) and sensory perception. Some of the detected distinctions between the classes clearly illustrate functional specialization in the direction from the older to the younger classes: for instance, among the mammal-specific genes, the GO term that shows the greatest enrichment is “sensory perception of taste” whereas “sensory perception of smell” and “sensory perception of chemical stimulus” are among the most-enriched terms among the chordate-specific genes. The animal-specific class is enriched, mostly, in genes implicated in development and various forms of signal transduction, and regulatory processes, in particular, regulation of transcription. The genes characterized by the respective terms were enriched also in the chordate-specific class but the list is augmented by genes involved in developmental and signal transduction processes. The fungi-metazoa class is also enriched in genes that contribute to certain highly conserved regulatory pathways, in particular, those centered around the Ras superfamily GTPases. By contrast, the 2 oldest classes, the eukaryote-specific genes and genes common to cellular life, are associated, mostly, with biosynthetic (including translation, transcription and replication) and metabolic processes. The preponderance of the metabolism-related genes in the, formally, most ancient class, the genes with homologs in prokaryotes, in part, is probably explained by the acquisition of these genes from the mitochondrial endosymbiont.

Overall, not unexpectedly, the genes in the young classes are involved, mostly, in lineage-specific processes whereas the old classes consist, primarily, of genes encoding functions that are common to a broad range if not all cells. This distribution of functions among the age classes of genes is compatible with the hypothesis that these classes reflect distinct origins of the respective genes that, at least, approximately coincide with the emergence of new, specialized functions.

The difference in expression between age classes of eukaryotic genes is in part independent of the difference in length and sequence evolution rate. As shown above, the age classes of eukaryotic genes have significantly different distributions of sequence evolution rates and protein lengths. A previous analysis of age classes of genes (45) has been countered with the hypothesis that the appearance of the age classes and all of the differences between them are explained solely by the homolog detection bias, i.e., that the “new” classes emerge solely because the respective genes encode short and/or fast-evolving proteins so that their homologs in distant taxa are hard to detect (46). This interpretation was supported by the results of a simulation of evolution of genes of the same age (46). However, the present results indicate that detection bias cannot be the only cause of the existence distinct age classes of genes. On the contrary, the overlap of the rate distributions between all classes and the lack of significant difference in either the (short-term) evolutionary rate or the lengths of the encoded proteins between the ancient classes (e.g., metazoan and older in animals; Fig. 3 and SI Appendix, Fig. A2) suggest that, at least, these classes actually include genes of distinct origins.

We performed a more direct test of the relevance of the age classes of genes as correlates of the gene expression level by using rank-based linear regression. We found that 0.083 of the original variance in EST count ranks between the age classes could be explained through a linear combination of the evolutionary rate (in this case, the maximum likelihood estimate of the amino acid distance between human and mouse orthologs) and protein length, with an effective correlation coefficient of 0.29. However, the rank residuals showed a highly significant difference between the combined new (primate-specific to metazoa-specific) and old (older than metazoa-specific) age classes (P = 1.5 × 10⁻²¹ using Student's t test). Thus, the differences in the expression levels between the age classes of eukaryotic genes are, at least, in part, independent of the differences in evolutionary rates and protein lengths, and appear to comprise an intrinsic characteristic of the age classes. In addition, we compared the magnitudes of the correlation between the sequence evolution rate and the expression level for the new and old genes, and found significant negative correlations in both case, but with typically higher correlation coefficients for the old classes (see SI Appendix). Together, these findings support the conclusion that the new age classes are not a mere artifact of our failure to detect homologs of small, fast-evolving genes.

Discussion

We found that the distribution of sequence evolution rates is universal across the entire diversity of life, in agreement with previous, less extensive observations (34). This universal distribution is compatible with a simple, steady state model of genome evolution by gene gain and loss where the distributions of loss rates (PGL) are the same for the sets of genes gained and lost over any long time interval. The model implies the existence of age classes of genes that substantially differ in terms of various evolutionary and phenomic variables. The empirical analysis of 3 widely diverged eukaryotic genomes indeed revealed similar distributions of genes by the apparent ages. In part, the age classes of genes are artificial groups in that the “new” classes undoubtedly include many genes that encode short and fast-evolving proteins for which homologs in distant taxa exist but are not readily detectable. The age class and the rate of sequence evolution are inherently dependent variables but this dependence is nontrivial because we measure relatively short-term rates of sequence evolution whereas the majority of the age classes are defined so as to reflect ancient events of gene gain and loss. Conceivably, the genes in the youngest classes evolve faster than those in the ancient classes because, on the relatively small scale where the evolutionary rate is measured (for instance, the ≈23 million years separating humans and macaque), these genes still experience the acceleration associated with their “birth,” e.g., around the time of the origin of chordates (≈600 Myr). By contrast, the lack of difference in the rates between the older classes suggests that the ancient innovations are already “forgotten,” i.e., their accelerating effect has tapered off. The extensive overlap of the evolutionary rate distributions (Fig. 3) indicates that “young” genes cannot be equated with fast-evolving ones, and conversely, “old” genes do not necessarily evolve slowly.

The observations on the age classes of genes and their distinct evolutionary rate distributions are, at least, qualitatively, compatible with the previous findings that genes in new age classes evolve, on average, faster than genes in old classes (45). It was argued that the age classes are sheer artifacts of sequence similarity detection so that the only conclusion possible from this type of analysis was that “slowly evolving genes evolve slowly” (46). Our findings are hardly compatible with this viewpoint. First, as emphasized above, the rate distributions of age classes in our empirical analysis strongly overlap, in a sharp contrast to the virtually nonoverlapping distributions yielded by the simulations of Elhaik et al. (46). Second, we found that the interclass differences in expression levels did not disappear after correction for evolutionary rate and protein length. Third, in agreement with previous observations (45), we observed sharp functional contrasts between genes of different age that seem to reflect the process of functional specialization during the evolution of a lineage. Indeed, most of the genes in the oldest classes, not unexpectedly, encode proteins involved in central information processing functions (translation, transcription and replication) and metabolism whereas the new classes are enriched for taxon-specific (e.g., animal-specific) functions such as various forms of defense, perception, and signal transduction.

The distinctions between the age classes fit the concept of a gene's “status” (18, 19, 32): The old classes are enriched for high-status genes and the new classes consist mostly of low-status genes. A high status of a gene entails large protein size, evolutionary conservation including both the low propensity of the gene to be lost and slow sequence evolution, strong selection pressure, high expression level, high intron density, and numerous physical and genetic interactions (not included here); the low-status genes possess the opposite characteristics. These results are compatible with the demonstration that nematode genes of different apparent ages substantially differ in terms of the biological effects of inactivation, with the ancient genes on average being associated with a higher penetrance than younger ones (47).

The finding that the age classes of genes differ both in the expression level and in evolution rates is compatible with the mistranslation-induced misfolding hypothesis according to which highly expressed genes are subject to stronger purifying selection than lowly expressed ones because the cost of protein misfolding is proportional to expression level (28, 30, 31). However, additional factors could both constrain the evolutionary rate and favor higher expression of ancient genes, for instance, their higher level of pleiotropy.

The sharp functional distinctions between age classes of genes suggest the possibility that these classes originate from bursts of functional innovation associated with the advent of new forms of life, e.g., eukaryotes or, subsequently, animals. A contribution of such transitional events cannot be ruled out but our present analysis suggests that a simpler, steady-state model of genome evolution by gene gain and loss is sufficient to explain the appearance of age classes, considering the previously demonstrated wide range of the characteristic loss rates among genes (14, 32). Emergence of numerous new genes during short time intervals associated with rapid cladogenesis (48) contrasted to the (near)stasis in between these bursts of innovation does not seem to be the quantitatively dominant pattern of the eukaryotic genomic evolution. These conclusions are at odds with the view that (almost) no new genes appeared in the ≈100 million years since the divergence of the mammalian orders (39) and with the implication of the model of Elhaik et al. (46) according to which gene birth is, essentially, an artifact caused by gradual deterioration of sequence similarity between duplicated genes beyond recognition (hence no distinct age classes of genes). The present model differs in that, although duplication is still seen as the principal route of gene evolution, gene birth appears as a real event whereby rapid divergence shortly after duplication ushers a gene into a new age class.

The simple model of gene gain and loss used here to account for the constant distribution of gene evolution rates in evolving genomes is conceptually analogous to the results of the analysis of the distribution of the sizes of paralogous gene families in a broad range of organisms. This universal power-law distribution is accurately reproduced by simple birth-and-death models (49, 50) despite substantial functional differences between the families that undergo lineage-specific expansion in different taxa (51, 52). The congruence of these findings suggests that genome evolution and the observed properties of genomes can be modeled with considerable accuracy without directly implicating functional adaptation and relying instead on general evolutionary properties of genes.

A fundamental question that remains unanswered is why the evolutionary rate distribution among orthologous genes and the distributions of the PGL values among gained and lost genes that sustain the rate distribution under our model apparently remained the same for billions of years, unaffected by major changes in genomic and phenotypic properties of organisms. The constancy of the distributions despite major differences in gene functions across the range of analyzed organisms and the log-normal shape of the universal rate distribution seem to imply that they are determined, primarily, by a combination of stochastic rather than selective factors. Development of an explicit theory to explain these observations remains a fundamental challenge for the future.

Methods

Genomic Data.

Genome sequences of Homo sapiens (Homsa), Macaca mulatta (Macmu), Mus musculus (Musmu), Aspergillus fumigatus Af293 (Aspfu) and Neosartorya fischeri NRRL 181 (Neofi), were obtained from the National Center for Biotechnology Information RefSeq database (53). Genome sequences of Drosophila melanogaster (Drome) and D. simulans (Drosi) were obtained from the FlyBase database. For the 3 “master” genomes (Homsa, Drome and Aspfu) the datasets were reduced to one (the longest) transcript per locus.

Age Classes of Genes.

Proteins from the 3 master genomes (Homsa, Drome, and Aspfu) were used as queries in a BLASTP search (54) against the National Center for Biotechnology Information RefSeq database with an E value threshold of 0.1 and the composition-based score adjustment (55); taxonomic affiliations of all hits were recorded. For each of the master genomes, 7 broad taxonomic levels were defined: Primates, Mammalia, Chordata, Metazoa, Fungi/Metazoa group, Eukaryota, and cellular organisms for Homsa; Drosophila, Diptera, Insecta, Metazoa, Fungi/Metazoa group, Eukaryota, and cellular organisms for Drome; Aspergillus, Pezizomycotina, Ascomycota, Fungi, Fungi/Metazoa group, Eukaryota, and cellular organisms for Aspfu. For each query protein, the number of taxonomically distinct hits was counted at each level; the deepest level at which the number of hits exceeded the predefined threshold (for the results presented in the main text, the cut-off E < 10⁻⁶ was used; for the result obtained with other cut-off values, see SI Appendix) was assigned to the query protein as its point of evolutionary origin (age class). Proteins that did not have the sufficient number of hits in any of these classes were assigned to an additional, nominally, the youngest, age class (species-specific).

Orthologs and Evolutionary Distances.

For the 3 “master” genomes, reciprocal BLASTP searches (E value threshold 1 × 10⁻⁶, effective database size 2 × 10⁷, no low-complexity filtering or composition-based statistics) were performed against the genomic datasets of their respective close relatives (Homsa-Macmu, Drome-Drosi and Aspfu-Neofi). Putative orthologs were identified as bidirectional best hits (56). Protein sequences of orthologs were aligned using the MUSCLE program (57); the corresponding CDS sequences were aligned codon by codon, using the protein sequence alignment as the template. Nucleotide P distances were estimated by dividing the raw number of nucleotide differences in the alignment by the alignment length (excluding sites with gaps); nucleotide difference of 0.5 was artificially assigned when the sequences of orthologs were identical. P distances were converted to linearized nucleotide distances, using the Jukes–Cantor correction (58). For the nucleotide sequence alignments concatenated within the age class the maximum likelihood dN/dS ratio was estimated using the PAML program (59) with equilibrium codon frequencies, basic codon substitution model and a uniform dN/dS ratio for all codons.

Additionally, Homsa-Musmu orthologs were identified using the same scheme. Maximum likelihood estimates of the amino acid distances between the aligned sequences of orthologs were calculated using the PROTDIST program of the PHYLIP package (60) with the JTT evolutionary model (61) and gamma-distributed site rates with shape parameter 1.0.

The distributions of the evolutionary rates among orthologous genes were normalized by computing the geometric mean of all rates and dividing the original rates by this mean value, thus bringing the geometric mean of the normalized distribution to 1. The variance of the evolutionary rate was not normalized.

Gene Expression Data.

Human microarray expression profiles were downloaded from the UCSC Genome Browser (62), using the table hgFixed.gnfHumanAtlas2All. Probes without a unique assignment to a gene were discarded; profiles for the multiple probes associated with the same gene were averaged. Tissue-specific scores were averaged between the two repeats. All scores were normalized by their respective tissue-specific medians. Median normalized value across all tissues was used to represent the characteristic expression level of a gene. Number of tissues (ranging from 0 to 79) where the normalized expression value exceeded a threshold (adjusted to produce an approximately equal proportion of wide- and narrow-expressed genes) was used to represent the expression breadth of a gene. Human EST counts were downloaded from the National Center for Biotechnology Information Unigene database (53).

Using Gene Ontology for Functional Classification of Genes.

The GO terms (44) associated with the human genes in each age class were identified and analyzed using the GoMiner program and the UniProtKB protein dataset, false discovery rate (FDR) cut-off of 0.05 and 100 GoMiner runs to estimate FDR (63).