A neural network model for constructing endophenotypes of common complex diseases: an application to male young-onset hypertension microarray data

Abstract

Motivation: Identification of disease-related genes using high-throughput microarray data is more difficult for complex diseases as compared with monogenic ones. We hypothesized that an endophenotype derived from transcriptional data is associated with a set of genes corresponding to a pathway cluster. We assumed that a complex disease is associated with multiple endophenotypes and can be induced by their up/downregulated gene expression patterns. Thus, a neural network model was adopted to simulate the gene–endophenotype–disease relationship in which endophenotypes were represented by hidden nodes.

Results: We successfully constructed a three-endophenotype model for Taiwanese hypertensive males with high identification accuracy. Of the three endophenotypes, one is strongly protective, another is weakly protective and the third is highly correlated with developing young-onset male hypertension. Sixteen of the involved 101 genes were highly and consistently influential to the endophenotypes. Identification of SLC4A5, SLC5A10 and LDOC1 indicated that sodium/bicarbonate transport, sodium/glucose transport and cell-proliferation regulation may play important upstream roles and identification of BNIP1, APOBEC3F and LDOC1 suggested that apoptosis, innate immune response and cell-proliferation regulation may play important downstream roles in hypertension. The involved genes not only provide insights into the mechanism of hypertension but should also be considered in future gene mapping endeavors.

Availability: Microarray data and test program are available at http://ms.iis.sinica.edu.tw/microarray/index.htm

Contact: pan@ibms.sinica.edu.tw or hsu@iis.sinica.edu.tw

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

To effectively map disease genes of complex diseases is one of the ultimate goals of genomic research. However, etiology of complex diseases involves multiple pathways and their dynamic interactions with environmental factors (Sing et al., 2003; Zerba et al., 1996). Gottesman and Gould (2003) advocated reducing genetic heterogeneity and introduced the concept of endophenotypes with characteristics that are closer to disease genes than the disease itself. Pan et al. (2006) suggested taking advantage of the vast amount of transcriptomic and proteomic data from patients and, via data mining, generating endophenotypes that conceptually resemble ‘pathway clusters’ which can then be utilized as binary phenotypes or quantitative trait loci (QTLs) for gene mapping. It has been demonstrated repeatedly that microarray data from gene expression can be reduced to the gene signature of specific cancer types and used for diagnosis/prognosis (Macgregor, 2003; Perez-Diez et al., 2007; Quackenbush, 2006). Little effort has been made to apply genome-wide expression data to reveal a complex disease's etiology or to facilitate gene mapping.

Data-mining technology has been widely used in the analysis of microarray data (Quackenbush, 2002; Valafar, 2002; Verducci et al., 2006). To date, most studies have concentrated on identifying differentially expressed genes between case and control subjects, clustering the identified genes using certain correlation measures and then linking the gene clusters to known functional pathways. However, this scheme, which relies heavily on correlation measures between genes, is more suitable for mapping rare diseases than common complex diseases, which often involve multiple common variants (Collins et al., 1997) and complex mechanisms (Gu et al., 2002). In this article, we assume that multiple endophenotypes (pathway clusters) for a complex disease exist and that such a disease can be induced by various up/downregulated patterns of these endophenotypes. To simulate the gene–endophenotype–disease relationship that fulfills the above assumptions, we propose using a one-hidden-layer, feed-forward neural network model with endophenotypes represented by hidden nodes.

We describe below the procedure to construct the neural network model used to obtain the gene–endophenotype–disease relationship. We used microarray data obtained from a case–control study in Taiwan to construct a gene-endophenotype-disease model for male young-onset hypertension and tested the effectiveness and consistency of the constructed model and endophenotypes.

2 METHODS

2.1 A neural network-based gene-endophenotype-disease model

Based on current research, we made the following two assumptions regarding the etiology of young-onset hypertension.

1. There exist multiple endophenotypes, each of which represents a pathway or a cluster of pathways (Pan et al., 2006), comprised of a set of genes. In addition, each endophenotype can be in either an up- or a downregulated mode predicted from the expression profiles of the associated genes.

2. The development of hypertension requires specific up/downregulated patterns of endophenotypes, and there exist distinct up/downregulated patterns of endophenotypes for hypertensive cases and normotensive controls.

We constructed a hypothetical gene-endophenotype-disease model that involves n genes and m endophenotypes. The model can be represented by a one-hidden-layer neural network with n input nodes and m hidden nodes as follows: (i) the n input nodes correspond to n potential genes for hypertension; (ii) the m hidden nodes correspond to m endophenotypes; (iii) the connection weight, w_i,j¹, between input node i and hidden node j represents the influence of gene i on endophenotype j (1 ≤i≤n, 1 ≤j≤m, a zero weight denotes that the gene is not connected to, or has virtually no effect on, the endophenotype); (iv) the connection weight, w_j², between hidden node j and the output node indicates the influence of endophenotype j on the disease; (v) all of the hidden nodes and the output node use sigmoid functions to determine the status (active/inactive) of the nodes where θ^1L_j is a threshold value for hidden node j and θ₂ is a threshold value for the output node. Next, we developed a training algorithm to determine the network parameters, including the number of hidden nodes and all the connection weights.

2.2 Determination of model's parameters

Conventional network training algorithms, which focus on minimizing the training error, require a data size that is usually much larger than modern microarray studies can provide. However, training with insufficient data can lead to poor generalization of the resultant network (Marinov and Weeks, 2001). To generalize solutions for our gene-endophenotype-disease model, we imposed the following five objectives for the network training: (i) maximize the classification accuracy (E); (ii) maximize the proportion (P_uniq) of unique genes (genes that are not involved in multiple endophenotypes) in the endophenotypes; (iii) maximize the absolute correlations (R_int) among gene expression levels in an endophenotype; (iv) maximize the correlation (R_BP) between average model outputs and average blood pressure measurements of patient subgroups determined by the patterns of binarized hidden node output; and (v) maximize the proportion of the unused genes (P_unused). For the first objective, the proportion of data that are correctly classified as hypertensive or as normotensive is used to represent the classification accuracy. The second objective is designed to involve a gene in as few endophenotypes as possible by setting some of the connection weights, w_i,j^1L, to zero (<10⁻³ in our model). The third objective aims to construct endophenotypes by assembling genes with similar (both highly correlated and highly anti-correlated) expression profiles across patients. The fourth objective tends to link the model outputs with blood pressure measurements, and the fifth objective is employed to remove redundant or irrelevant genes.

Let the network parameters (a combination of w_i,j^1L, θ_j^1L, w_j^2L and θ₂) be denoted by a vector w, and m represents the number of hidden nodes in the network (and the number of endophenotypes in the proposed model). We propose to solve the following multiple objective (MO) problems to construct our neural network model:

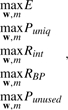(1)

subject to

This is a mixed-integer, non-linear, MO problem. The task of simultaneously determining the optimal values of w and m is NP-hard. We propose to solve this MO problem with the following procedure:

• Step 1:

  Set m=m_init;

• Step 2:

  Repeat steps 2.1–2.2 until m=m_final;

  • Step 2.1:

    Solve the unconstrained MO problem (1);

  • Step 2.2:

    Record the computed objective values and the corresponding w, and then set m=m+1.

• Step 3:

  Set the minimal network complexity m_opt to m′, where the average of the sum of the recorded objective values reaches the maximum.

• Step 4:

  Among those w's that satisfy (1) as m=m_opt, choose the one that meets the prespecified requirement for model construction.

We note that, in an MO problem, a point that simultaneously reaches the global optimal solutions of all the objective functions is usually non-exist. Instead, there are infinite so-called ‘global non-inferior solutions’ that are of interest in an MO problem (Coello, 1999; Fonseca and Fleming, 1995). We employed the Strength Pareto Evolutionary Algorithm (SPEA) (Zitzler and Thiele, 1999) in our study because of its effectiveness in finding multiple near global non-inferior solutions (see Appendix A in Supplementary Material for details). The SPEA statistical search method is less efficient in convergence speed compared with gradient-based search methods. To overcome such a drawback, we initially employed SPEA to reach near-global non-inferior solutions, chose the suitable ones with high E, R_int and R_BP, and then used a greedy search method to obtain global non-inferior solutions. In this study, the greedy search was performed by solving a series of constrained, single-objective, optimization problems. That is, the five objectives were solved one at a time, leaving the other four constrained by their most updated values.

We also adopted a 5-fold cross-validation technique to improve the generalization of computed network parameters and to test the consistency of the constructed endophenotypes. In each of the five validation iterations, we first trained the network by solving (1) using SPEA for 300 generations to obtain near-global non-inferior solutions. Then, the solution with the highest sum of E, R_int and R_BP was used as the starting point and a greedy search was employed to obtain a global non-inferior solution. During the training process, early stopping was used to avoid overtraining (Amari et al., 1996). The final network parameters were selected from the resultant five solutions that had the best average performance on the five datasets.

2.3 Identification of significant hypertension genes and mechanisms

To probe the finer structure and to identify key elements in each of the computed endophenotypes, we constructed a tree of gene clusters for each endophenotype based on correlations between gene profiles. First, the correlations between all pairs of genes in an endophenotype were computed. And then the average linkage method, Unweighted Pair Group Method with Arithmetic mean (UPGMA), was adopted for the tree construction. In each endophenotype, the hierarchical structure of gene clusters determined successively in their mergence order may reveal certain sequential relationships, e.g. from upstream to downstream. To relate a gene cluster to its corresponding endophenotype, we first computed the weighted sum of genes in a cluster for connection weights, and then correlated it with the endophenotype output. Clusters with a high correlation coefficient were considered influential to their corresponding endophenotype.

Significance of a gene in an endophenotype was evaluated by two indices: (i) the connection weight between a gene and its corresponding endophenotype and (ii) the sum of the correlations between a gene and all other genes in the endophenotype. The first index characterizes the influence of a gene on its corresponding endophenotype and thus genes with a high connection weight may be somewhat downstream in the disease pathogenesis. On the other hand, the second index indicates the degree of association with other genes in the endophenotype, therefore, genes with a high correlation sum may play a significant role upstream in the pathway of disease pathogenesis. In selecting potential hypertension genes in each endophenotype, we targeted those genes that both had the top 15 index values for either one of the two indices and also were within influential gene clusters.

2.4 Data collection and preprocessing

The study was approved by the Institution Review Board of Academia Sinica and all participants provided written informed consent. Subjects were recruited from the clients of MJ Life Enterprise Co. Ltd. (Taiwan), a healthcare facility, from September 8 to December 31, 2004. The inclusion criteria were: (i) 20–50 years of age; (ii) BMI < 35; (iii) fasting for at least 8 h; (iv) fasting blood sugar < 126 mg/dl; (v) not taking hypertension medication; (vi) no history of cancer or other major illnesses of the liver, kidneys, heart or lungs; and (vii) no acute hypertension-related symptoms in the previous 2 weeks. Blood pressure was measured three times for each participant according to the established protocol (Pan et al., 2001) and the average of the last two was used for hypertension diagnosis. A participant was classified as a hypertension case if the systolic pressure was >140 mmHg, or the diastolic pressure was >90 mmHg; otherwise, the participant was classified as a normotensive control. Secondary hypertension patients were excluded. A total of 77 newly diagnosed non-medicated young-onset male hypertensive cases (age 37.6 ± 7.2) and 82 male normotensive controls (age 36.9 ± 6.6) were included in this study.

Unlike in the field of cancer genetics, it is difficult to acquire affected tissue from hypertensive patients. Fortunately, using blood instead of affected tissue to obtain gene expression profiles has been proposed as a possible alternative in several proof-of-concept studies (Bull et al., 2004; Chon et al., 2004; Matsunaga et al., 2002). In this study, fasting blood (10 ml) was obtained from each participant, then stabilized and frozen immediately at –7^○C. Then, total RNA was extracted from the whole blood. Finally, four replicates of microarray data were generated for each participant, using Human OneArray (Phalanx Biotech Group, Taiwan), a one-channel array. Each microarray chip contained 39 200 polynucleotide data, of which 22 184 were mapped to the latest draft of the human genome.

Micoarray arrays data were subjected to quality control using parameters: percentage of present calls, coefficient of variations (CV) and Pearson correlation (R), and array quality filter (see Appendix B in Supplementary Material for details). For each subject, the qualified (392 out of 636) replicates were merged using a weighted (1/SD) average. A logarithm and Z-score global normalization were then applied to all the averaged values. A total of 103 out of 22 184 genes that were differentially expressed (P < 0.01) between hypertensive and normotensive groups were used in the model construction. We divided our dataset into a training set and a test set: the former containing 61 hypertensive cases (age 38.0 ± 7.3) and 61 age-matched normotensive controls (age 37.1 ± 6.9), whereas the latter comprised of the remaining 16 hypertensive cases (age 36.4 ± 6.8) and 21 normotensive controls (age 36.4 ± 5.9). The training set was further divided into five subsets (of sizes 12, 12, 12, 12 and 13) for model construction and selection via 5-fold cross-validation. According to the sample size table suggested by Tsai et al.(2005), our training dataset (sample size 61 and gene number 22184) was more than capable of achieving an accuracy of 0.99 or a sensitivity of 0.95 at the family-wise power of 90%, at the expected number of false positive of 1, and at mean difference (standardized effect size) of 2. In addition, our technical replications are likely to further improve the above figures.

3 RESULTS

3.1 Model's architecture and performance

Following the construction process described in Section 2.2, we first set m_init=2, and set m_final=8 to ensure that the computed endophenotypes contained a sufficient number of genes. During each iteration, the MO problem solver, SPEA (3000, 500, 0.9, 0.9, 0.9, 300) (see Appendix A in Supplementary Material for details), was employed to solve the associated MO problem. After computation of nearly all the near-global non-inferior solutions, we observed that the maximal mean value of the objective sums occurred at m=3. In addition, the standard deviation of the objective sum was also small when m=3 suggesting that the model was rather stable at this value. Therefore, we adopted a three-endophenotype model for the remainder of the model construction process.

We then evaluated the performances of the five neural network models constructed via the 5-fold validation datasets. Table 1 provides simple performance statistics of the five models. We selected the third model (constructed via the third dataset) because it had the best average performance (E=0.967, P_uniq=0.772, R_int=0.499, R_BP=0.734 and P_unused=0.019, with training and validation datasets combined) and minimum performance variations in most of the objectives. Accordingly, the constructed model was capable of achieving an accuracy of 96.72% (i.e. 118 out of 122 subjects) in distinguishing hypertensive cases from normotensive controls in the dataset. The three constructed endophenotypes contained 62, 33 and 38 genes. Among these genes, 78 (41, 14 and 28 accordingly in the three endophenotypes) were unique (contained in only one endophenotype) and 23 were shared (contained in more than one endophenotypes) resulting in 101 genes that were actually used in the model. As a result, the proportion of unique genes, P_uniq, was 0.772 (78/101) and the proportion of unused genes, P_unused, was 0.019 (2/103). Furthermore, the minimal averaged gene correlation, R_int, of the three endophenotypes was 0.499, while the correlation between the average network outputs and the average blood pressure measurements in each subgroup, R_BP, was 0.734. The three endophenotypes are illustrated in Figure 1 and detailed information about the selected genes is listed in Appendix C in Supplementary Material.

Table 1.

Performances of the five neural network models constructed via the 5-fold cross-validation

	E	Puniq	Rint	RBP	Punused
Model 1
Training sets	0.959 ± 0.012	0.612	0.461 ± 0.005	0.626 ± 0.158	0
Validation sets	0.960 ± 0.047	0.612	0.708 ± 0.013	0.289 ± 0.139	0
Test set	0.865	0.612	0.654	0.775	0
Model 2
Training sets	0.959 ± 0.010	0.709	0.417 ± 0.021	0.564 ± 0.084	0
Validation sets	0.960 ± 0.040	0.709	0.664 ± 0.021	0.207 ± 0.250	0
Test set	0.811	0.709	0.609	0.711	0
Model 3a
Training sets	0.967 ± 0.009	0.772	0.452 ± 0.006	0.815 ± 0.073	0.019
Validation sets	0.967 ± 0.035	0.772	0.689 ± 0.028	0.412 ± 0.292	0.019
Test set	0.946	0.772	0.648	0.895	0.019
Model 4
Training sets	0.951 ± 0.014	0.738	0.451 ± 0.011	0.741 ± 0.058	0
Validation sets	0.950 ± 0.054	0.738	0.709 ± 0.012	0.466 ± 0.490	0
Test set	0.811	0.738	0.668	0.725	0
Model 5
Training sets	0.976 ± 0.009	0.738	0.432 ± 0.007	0.825 ± 0.109	0
Validation sets	0.976 ± 0.035	0.738	0.696 ± 0.014	0.479 ± 0.292	0
Test set	0.865	0.738	0.654	0.781	0

^aModel 3 is adopted as the final model which is specified by values in bold face.

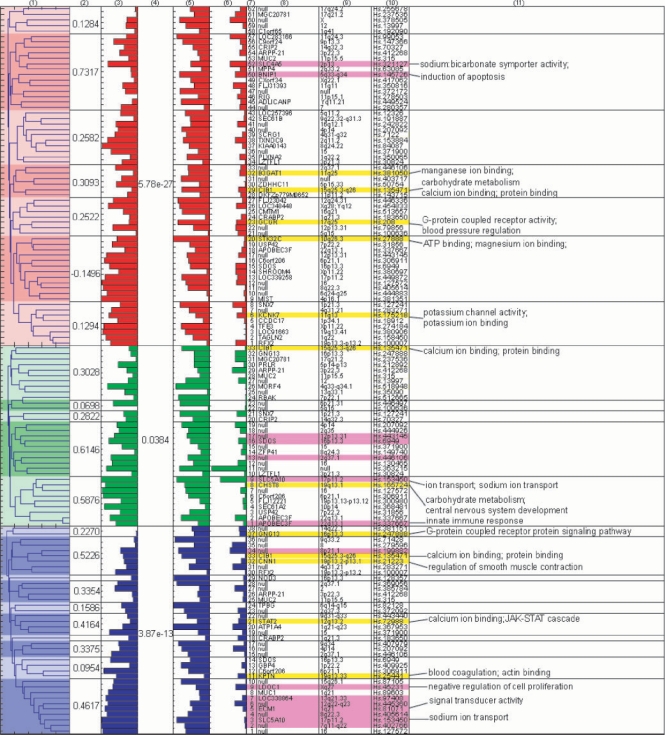
Fig. 1.

The three constructed endophenotypes indicated in red, green and blue. From left to right the figure shows: (1) cluster tree of genes in each endophenotype (the dark and light shades are used to distinguish subclusters), (2) correlation coefficient between the gene cluster and its corresponding endophenotype, (3) normalized correlation (0–1) of the gene with others in the endophenotype, (4) P-value of the endophenotype to hypertension, (5) P-value (0–0.01) of a gene to hypertension, (6) absolute weight (0–0.7) of a gene to its corresponding endophenotype, (7) sequence number of the gene in the endophenotype, (8) gene symbol (highly consistent and influential genes are highlighted in purple, while genes with hypertension-related functions are highlighted in yellow), (9) cytogenetic information, (10) Unigene ID from Unigene build #163 and (11) major functions of selected genes.

Similar performances were achieved on the test data (E=0.946, P_uniq=0.772, R_int= 0.648, R_BP=0.895 and P_unused=0.019). The test accuracy of 94.59% (35 out of 37) may seem high for a machine learning algorithm. However, the test accuracies of the other four models were 86.49% (32 out of 37), 81.08% (30 out of 37), 81.08% and 86.49%, respectively, making the average test accuracy of all five models at 85.95%. The high accuracy of 94.59%, although there are only five cases differing from the lowest accuracy of 81.08%, may be due to high correlation between the test dataset and the third training dataset.

3.2 Characteristics and effectiveness of the constructed endophenotypes

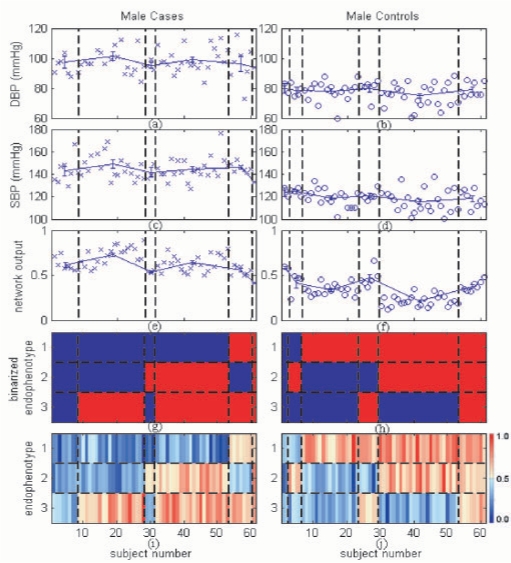
To visualize different endophenotypic patterns in the hypertensive cases and in the normotensive controls, using a threshold of 0.5, we binarized the values of the endophenotypes to either 1 (Fig. 2g and h; red color indicates upregulation) or 0 (Fig. 2g and h; blue color indicates downregulation). For example, the pattern {Blue, Blue, Blue} of the first patient group (first column, Fig. 2g) was interpreted as genes having little rather than no effect for the three endophenotypes on hypertension. For comparison purposes, the original endophenotype values were also shown in Figure 2i and j. Similar patterns were observed on the test dataset (Figure in Appendix D in Supplementary Material). We observed four phenomena from the two figures.

Fig. 2.

Average blood pressure values [diastolic blood pressure (DBP), systolic blood pressure (SBP)] and average network outputs across various endophenotypic patterns using training data: a blue circle or cross indicates a data point for an individual; error bars indicate the means and standard errors (SEs) of subject subgroups. (a and b) Individual DBP, their mean values and SEs. (c and d) Individual SBP, their mean values and SEs. (e and f) The network outputs, their mean values and SEs. (g and h) Binarized endophenotype values (using a threshold of 0.5) showing endophenotypic patterns. (i and j) Original endophenotype values represented in a gradation of red and blue colors (refer to the color bar at the right-hand side for actual magnitude); the vertical blocks between the black dashed lines denote subject subgroups defined by different endophenotype patterns (refer to g and h); horizontal blocks denote endophenotypes.

Observation 1—unique hypertensive patterns: two major and unique (not seen in normotensive controls) patterns {Blue, Blue, Red} (second column, Fig. 2g) and {Blue, Red, Red} (fourth column, Fig. 2g) were observed in the male hypertensive patients. In combining the training and test results, 28 cases were associated with the former pattern and 29 cases with the latter, which comprised a total of 74.03% (57/77) of the hypertensive population.

Observation 2—unique normotensive patterns: two major and unique (not seen in hypertensive cases) patterns {Red, Blue, Blue} (second column, Fig. 2h) and {Red, Red, Blue} (fourth column, Fig. 2h) were observed in the male normotensive subjects. With the training and test results combined, 21 controls were associated with the former pattern and 30 controls with the latter, which included a total of 62.20% (51/82) of the normotensive population.

Observation 3—overlapping patterns: five patterns {Blue, Blue, Blue}, {Blue, Red, Blue}, {Red, Blue, Red}, {Red, Red, Red} and {Blue, Red, Red} were observed in both the case and control groups. Subjects associated with these patterns seemed to have borderline blood pressure measurements (systolic/diastolic blood pressure=140/90 mmHg) than those with the unique patterns.

Observation 4—protective/risk endophenotypes for hypertension: endophenotype 3 was upregulated in most of the hypertensive cases (65/77) and downregulated in most of the normotensive controls (61/82) (Fig. 2g and h). This finding suggests that endophenotype 3 has a strong effect on raising blood pressure. In contrast, a reverse pattern in endophenotype 1 suggests its strong effect on reducing blood pressure. The effect of endophenotype 2 is rather ambiguous. It was upregulated in more than half of the controls (47/82) and in less than half of the hypertensive cases (34/77), suggesting that endophenotype 2 is weakly associated with reducing blood pressure. Similar conclusions can be drawn using the magnitude and sign of the connection weights (2.1797, −1.5534 and −2.0513 for endophenotypes 1, 2 and 3, respectively) between the endophenotypes and the decision nodes of the model. In comparison with individual genes, the constructed endophenotypes also improved the efficacy of distinguishing hypertensive cases from normotensive controls. For a single gene, MIST was the most differentially expressed gene between cases and controls in our dataset (unadjusted P=2.11 × 10⁻⁵). However, the three endophenotypes were differentially expressed [P=(5.78 × 10⁻²⁷, 0.0384 and 3.87 × 10⁻¹³), respectively] between cases and controls.

3.3 Gene cluster structure and major genes

Gene clusters that were determined successively in their mergence order are presented by colored blocks in the first column of Figure 1. Clusters with a high correlation coefficient between cluster outputs and the outputs of their corresponding endophenotypes were considered influential to their corresponding endophenotype (Fig. 1, second column, clusters containing genes highlighted in purple).

We evaluated the significance of each gene in an endophenotype using the two indices described in Section 2.3 (Fig. 2, bar height in the sixth column represents index 1 and that in the third column shows index 2). Among the 15 genes with the highest index 1 values in each endophenotype, many were present within the influential gene clusters, including: the 48th (FLJ31393), 50th (BNIP1), 52nd (SLC4A5) and 57th (LOC283116) genes in endophenotype 1, the 1st (APOBEC3F), 5th (FLJ12221), 9th (SLC5A10), 11th, 12th, 18th and 19th genes in endophenotype 2, and the 6th, 9th (LDOC1), 20th (ATP1A4), 21st (STAT2), 22nd, 31st, 34th and 35th genes in endophenotype 3. Among these genes, SLC4A5 and STAT2 were previously identified as candidate genes for hypertension (Hunt et al., 2006; Pan et al., 1997); ATP1A4 was correlated with hypertension in an animal study (Tian et al., 2001). Furthermore, according to the Gene Ontology Annotation (GOA) database (Camon et al., 2004), SLC5A10, BNIP1 and LDOC1 are related to sodium ion transport, induction of apoptosis and negative regulation of cell-proliferation, respectively.

With regards to the second index, the top 15 genes in each endophenotype included within the most influential clusters were the 52nd (SLC4A5) in endophenotype 1, the 1st, 2nd (APOBEC3F), 4th (SEC61A2), 6th (C6orf206), 7th, 8th (CHST8), 9th (SLC5A10), 11–13th, 16th (SDOS), 17th and 19th genes in endophenotype 2, and the 1st, 2nd, 3rd (SLC5A10), 4th, 5th (ECM1), 6th, 7th (LOC338864), 8th (MUC1), 9th (LDOC1), 10th, 15th and 19th genes in endophenotype 3. Among these genes, SEC61A2 is known to interact with ApoB, the main apolipoprotein of chylomicrons and low-density lipoprotein (LDL) (Chen et al., 1998) and according to GOA, CHST8 is associated with central nervous system development.

4 DISCUSSION

4.1 Generalization of the constructed model

An artificial neural network is a powerful classification tool capable of generating complex boundaries between different classes of data. However, with limited and noisy data, some training algorithms may construct a network that picks up noise in the data and thus loses its generalization capability. The 85.95% (average) accuracy evaluated on the test dataset suggested that our procedure is capable of constructing a generalized neural network model to simulate the gene–endophenotype–hypertension relationship. The overall 26 misclassifications by the five models in the test dataset were due to 11 normotensive controls and 2 hypertensive cases. Most of the misclassified subjects had borderline blood pressure (SBP/DBP=120/80 mmHg). Of the 11 misclassified controls, 10 were prehypertension (SBP > 120 or DBP > 80) and 1 was hypotension (SBP/DBP=101/56.5). Of the 10 prehypertensive subjects, 7 were high-normal (SBP > 130 or DBP > 85 based on JNC VI). On the other hand, both misclassified hypertensive cases (SBP/DBP=137.5/93 and 143.5/77.5) were in stage-1 hypertension (SBP=140–159 or DBP=90–99 based on JNC VI) with relatively lower blood pressure values.

Recall that our model and endophenotypes were computed via the third dataset prepared for 5-fold validation. We evaluated the consistency of the endophenotypes and that of the identified significant genes by comparing them with those computed via the other four datasets. For the consistency of the endophenotypes, we found that 48 (out of 62), 23 (out of 33) and 29 (out of 38) genes in the three endophenotypes were also appeared in the corresponding endophenotype computed via at least two other datasets (reproducibility=75.19%). For the consistency of the significant genes identified by index 1, we found that 4, 4 and 4 of the top 15 genes in the three endophenotypes were also among the top 15 genes of the corresponding endophenotype computed via at least two other datasets. On the other hand, when using index 2, there were 13, 4 and 10 of the top 15 genes in the three endophenotypes that also appeared in the top 15 genes of the corresponding endophenotype computed via at least two other datasets. The significant genes selected by index 1 were less consistent than those by index 2, most likely because index 1 was computed using a single connection weight, which is very sensitive to the quality of data.

Four of the 12 consistent significant genes identified by index 1 were among the aforementioned influential gene clusters, including BNIP1 in endophenotype 1, APOBEC3F in endophenotype 2, the 34th gene and LDOC1 in endophenotype 3. On the other hand, 12 of the 27 consistent significant genes identified by index 2 were among the influential gene clusters, including SLC4A5 in endophenotype 1; SLC5A10, SDOS, the 13th and 17th genes in endophenotype 2; and SLC5A10, ECM1, LOC338864, LDOC1, the 2nd, 4th and 6th genes in endophenotype 3.

4.2 Potential mechanisms in the endophenotypes

We proposed that genes with high correlations to other genes in an endophenotype may be closer to the genetic origin of hypertension. In our model, SLC4A5, SLC5A10 and LDOC1 belong to such a type suggesting that sodium/bicarbonate transport, sodium/glucose transport and cell-proliferation regulation may play important upstream roles in pathogenesis of hypertension. On the other hand, genes with large connection weights to an endophenotype may be closer to the development of hypertension. BNIP1, APOBEC3F and LDOC1 are such genes consistently identified in our models, suggesting that induction of apoptosis, innate immune response and cell-proliferation regulation may play important downstream roles in development of hypertension.

Although not as consistent as the aforementioned genes, ATP1A4 and STAT2 with high index 1 values suggesting that magnesium/potassium ion transport and calcium ion binding may lead to the development of hypertension. In addition, CHST8 and SEC61A2 with high index 2 values suggesting that central nervous system and LDL may also contribute to the hypertension onset. The roles of several genes with either high index 1 or 2 remain unknown and require further investigation.

4.3 Identification of causal pies and patient groups

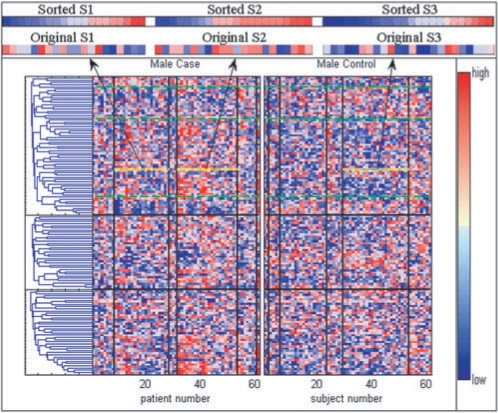
Rothman's (1976) concept of sufficient causes provides a theoretical framework of how multiple causal pies or phenocopies of a disease dilute the effect of target genes, resulting from either genetic or environmental causes. The following example demonstrates how the significance of a gene can vary in different types of patients. We compared the expression levels of GCGR, a candidate gene for hypertension, obtained from two major case subgroups (denoted as S1 and S2 in Fig. 3) with those obtained from a major control subgroup (denoted as S3 inFig. 3). The GCGR was not significantly differentiable (P = 0.16) between S1 and S3, however, it was significantly differentiable (P = 0.03) between S2 and S3. Therefore, conventional approaches for modeling a particular disease may fail to identify potential genes when only examining gene expression profiles.

Fig. 3.

Gene expression plot of the three endophenotypes: each vertical strip represents a subject; each horizontal strip represents a gene; the colors used to indicate expression level is illustrated at the color bar in the right-hand side. The vertical blocks between black lines denote subject subgroups defined by different endophenotypic patterns (refer to Fig. 2g and h); horizontal blocks denote endophenotypes. The ‘S1’, ‘S2’ and ‘S3’ are magnified views of GCGR expression level of the three major subject groups (indicated in the three yellow boxes).

Although the gene expression profile in Figure 3 is not as clear as those of many gene mapping studies in the field of cancer genomics, it still exhibits certain patterns that differentiate hypertensive cases from controls. For example, in the top gene cluster (endophenotype 1 in our model), the predominantly {Red, Blue, Red, Blue} pattern (the dominant color in the block between the green dashed lines) is evident in the majority of male hypertensive cases. In contrast, the predominantly {Blue, Red, Blue, Red} pattern is evident in the majority of male controls. Patterns containing multiple color blocks were also observed in other gene clusters of cases and controls. Such patterns show how multiple mechanisms may work together to trigger disease onset.

4.4 Potential improvement

To ensure that the constructed endophenotypes are biomedically significant, we linked the model's outputs to blood pressure measurements. Participants' blood pressures were obtained at different time points throughout the day; thus, these values may not truly reflect the condition of the participants. We linked the average model outputs to the average blood pressure measurements in each subgroup to reduce fluctuation between individuals. A model with more meaningful outputs could be constructed if multiple blood pressure readings (e.g. over a 24 h period) were available.

The model performance could also be improved if more genes are used for model construction. Due to multiple causal pathways and genetic heterogeneity, certain disease genes may not express differentially between diseased and normal groups on the surface. In the absence of a priori knowledge regarding disease pathogenesis, this problem can be resolved by introducing more genes into the model. Because our training procedure adopts a SPEA approach instead of a gradient-based approach, the memory and computation time requirement remain manageable for large datasets. Regarding cardiovascular disease, Sing et al. (2003) pointed out that a biological model of genome–phenotype relationships should incorporates interactions between possible genetic and environmental factors. Although gene–gene interactions (these are partly included in our endophenotypes) and environmental factors were not considered in this study, they can be input into the model if properly encoded. However, the sample size must also be increased with the number of variables to ensure that the computed results are statistically meaningful.

5 CONCLUSIONS

We have proposed a neural network-based model that simulates the gene–endophenotype–disease relationships for complex diseases where genetic heterogeneity is involved. In a real application, we successfully constructed a three-endophenotype model for Taiwanese hypertensive males. The model achieved high identification accuracy and was generalized to an independent set of data. The three computed endophenotypes, one strong protective, another weakly protective and the third highly risk, can be applied to predict young-onset male hypertension and to determine patient subgroups. Moreover, the three endophenotypes were consistent among datasets.

Among the 101 genes involved in our model, we identified SLC4A5, SLC5A10 and LDOC1 as key upstream genes in each of the three endophenotypes, whereas BNIP1, APOBEC3F and LDOC1 were identified as key downstream genes in hypertension pathogenesis. In addition, four genes (ATP1A4, GCGR, SLC4A5, STAT2) were hypertension candidate genes and eight genes were associated with hypertension-related functions. These findings may help researchers to better understand the causes of hypertension. Several novel genes residing in multiple chromosomes were also found to be highly influential to the three endophenotypes. However, future studies are needed to examine whether and how these genes are involved in the pathogenesis of hypertension.

We have also developed a procedure for constructing the proposed model. The procedure is capable of computing multiple models in a single iteration so that researchers can choose the most suitable one for their research needs. The developed procedure is applicable to other microarray platforms as well as to other genetic markers, such as single nucleotide polymorphisms (SNPs) and short tandem repeat polymorphic (STRP) markers.