Balanced amplification: a new mechanism of selective amplification of neural activity patterns

Abstract

In cerebral cortex, ongoing activity absent a stimulus can resemble stimulus-driven activity in size and structure. In particular, spontaneous activity in cat primary visual cortex (V1) has structure significantly correlated with evoked responses to oriented stimuli. This suggests that, from unstructured input, cortical circuits selectively amplify specific activity patterns. Current understanding of selective amplification involves elongation of a neural assembly’s lifetime by mutual excitation among its neurons. We introduce a new mechanism for selective amplification without elongation of lifetime: “balanced amplification”. Strong balanced amplification arises when feedback inhibition stabilizes strong recurrent excitation, a pattern likely to be typical of cortex. Thus, balanced amplification should ubiquitously contribute to cortical activity. Balanced amplification depends on the fact that individual neurons project only excitatory or only inhibitory synapses. This leads to a hidden feedforward connectivity between activity patterns. We show in a detailed biophysical model that this can explain the cat V1 observations.

1 Introduction

Neurons in cerebral cortex are part of a highly recurrent network. Even in early sensory areas receiving substantial feedforward input from sub-cortical areas, intracortical connections make up a large fraction of the input to cortical neurons [e.g., Binzegger et al. 2004, Stepanyants et al. 2008, Thomson and Lamy 2007]. One function of this recurrent circuitry may be to selectively amplify certain patterns in the feedforward input, enhancing the signal-to-noise ratio of the selected patterns [e.g., Douglas et al. 1995, Ganguli et al. 2008].

A side effect of such selective amplification is that the selected patterns should also be amplified in the spontaneous activity of the circuit in the absence of a stimulus [Ganguli et al. 2008]. We imagine that spontaneous activity is driven by feedforward input that is unstructured except for some spatial and temporal filtering. Thus, all patterns with similar spatial and temporal frequency content should have similar amplitudes in the feedforward input. In the circuit response, those patterns that are selectively amplified should then have larger average amplitude than other, unamplified patterns of similar spatial and temporal frequency content. This may underlie observations that cerebral cortex shows ongoing activity in the absence of a stimulus that is comparable in size to stimulus-driven activity [Anderson et al. 2000b, Arieli et al. 1996, Fiser et al. 2004, Fontanini and Katz 2008, Kenet et al. 2003], and that in some cases the activity shows structure related to that seen during functional responses [Fontanini and Katz 2008, Kenet et al. 2003].

Existing models of selective amplification are “Hebbian-assembly” models, in which the neurons with similar activity (above baseline or below baseline) in an amplified pattern tend to excite one another while those with opposite activity may tend to inhibit one another, so that the pattern reproduces itself by passage through the recurrent circuitry [e.g. Douglas et al. 1995, Goldberg et al. 2004, Seung 2003]. In these models, selective amplification of an activity pattern is achieved by slowing its rate of decay. In the absence of intracortical connections, each pattern would decay with a time constant determined by cellular and synaptic time constants. Because the pattern adds to itself with each passage through the recurrent circuitry, the decay rate of the pattern is slowed. Given ongoing input that equally drives many patterns, patterns that decay most slowly will accumulate to the highest amplitude and so will dominate network activity. (Note that, if a pattern reproduces itself faster than the intrinsic decay rate, it will grow rather than decay. This along with circuit nonlinearities provides the basis for “attractors”, patterns that can persist indefinitely in the absence of specific driving input, but our focus here is on amplification rather than attractors.)

In V1 and other regions of cerebral cortex, recurrent excitation appears to be strong but balanced by similarly strong feedback inhibition [Chagnac-Amitai and Connors 1989, Haider et al. 2006, Higley and Contreras 2006, Ozeki et al. 2009, Shu et al. 2003], an arrangement often considered by theorists [e.g. Brunel 2000, Latham and Nirenberg 2004, Lerchner et al. 2006, Tsodyks et al. 1997, van Vreeswijk and Sompolinsky 1998]. Here we demonstrate that this leads to a new form of selective amplification, which we call balanced amplification, that should be a major contributor to the activity of such networks, and that involves little slowing of the dynamics. The basic idea is the following. The steady-state response to a given input involves some balance of excitatory and inhibitory firing rates. If there is a fluctuation in which the balance is variously tipped toward excitatory cell firing or inhibitory cell firing in some spatial pattern, then, because excitation and inhibition are both strong, both excitatory and inhibitory firing will be driven strongly up in regions receiving excess excitation, and be driven strongly down in regions receiving excess inhibition. That is, small patterned fluctuations in the difference between excitation and inhibition will drive large patterned fluctuations in the sum of excitation and inhibition. The same mechanism will also amplify the steady-state response to inputs that differentially drive excitation and inhibition. The amplification from difference to sum will be largest for patterns that match certain overall characteristics of the connectivity, thus allowing selective amplification of those patterns. This represents a large, effectively feedforward connection from one pattern of activity to another, i.e. from a difference pattern to a sum pattern. Although the circuitry is fully recurrent between neurons, there is a hidden feedforward connectivity between activity patterns. Because the sum pattern does not act back on the difference pattern and neither pattern can significantly reproduce itself through the circuitry, neither pattern shows a slowing of its dynamics. This form of amplification should make major contributions to activity in any network with strong excitation balanced by strong inhibition, and so should be a ubiquitous contributor to cortical activity.

We show in particular that this mechanism can explain a well-studied example of selective amplification in primary visual cortex (V1) of anesthetized cat. V1 neurons respond selectively to oriented visual stimuli. In cats, nearby neurons prefer similar orientations and there is a smooth map of preferred orientations across the cortical surface. Kenet et al. [2003] compared the spatial patterns of spontaneous activity, in the absence of a visual stimulus, across V1 upper layers with either the pattern evoked by an oriented visual stimulus (“evoked orientation map”) or a similarly structured control activity pattern. An evoked orientation map is a pattern in which neurons with preferred orientation near the stimulus orientation are coactive and other neurons are inactive. While on average the correlation coefficient between snapshots of spontaneous activity and the evoked map or control was 0, the distribution of correlation coefficients was significantly wider for the evoked map than for the control pattern. That is, excursions of the spontaneous activity were significantly larger in the direction of an evoked orientation map than in the direction of other similarly structured patterns. This seems likely to result from the preferential cortical amplification, from unstructured feedforward input, of activity patterns in which neurons of similar preferred orientation are co-active. The likely substrate for such amplification is orientation-specific connectivity. Neurons in middle and upper layers of V1 receive both excitatory and inhibitory input predominantly from other neurons with similar preferred orientations [Anderson et al. 2000a, Marino et al. 2005, Martinez et al. 2002], and orientation-specific excitatory axonal projections can extend over long distances [Gilbert and Wiesel 1989].

A “Hebbian-assembly” model of this amplification has been proposed [Goldberg et al. 2004]. However, a significant problem for such a model is that that it relies on slowing of the dynamics, and the data of [Kenet et al. 2003] show limited slowing (see Discussion). The amplified patterns of spontaneous activity observed in V1 fluctuate with a time scale of about 80 ms (Kenet et al. 2003, and M. Tsodyks, private communication), comparable to the time scales over which inputs are correlated [DeAngelis et al. 1993, Wolfe and Palmer 1998]. We show that balanced amplification provides a robust explanation for the amplification observed in V1 by Kenet et al. [2003] and its time scale. We cannot rule out that Hebbian mechanisms are also acting, but even if they contribute, balanced amplification will be a significant and heretofore unknown contributor to the total amplification.

2 Results

We will initially study balanced amplification using a linear firing rate model. When neural circuits operate in a regime in which synchronization of spiking of different neurons is weak, many aspects of their behavior can be understood from simple models of neuronal firing rates [e.g. Brunel 2000, Ermentrout 1998, Pinto et al. 1996, Vogels et al. 2005]. In these models, each neuron’s firing rate approaches, with time constant Τ, the steady-state firing rate that it would have if its instantaneous input were maintained. This steady-state rate is given by a nonlinear function of the input, representing something like the curve of input current to firing rate (F-I curve) of the neuron. When the circuit operates over a range of rates for which the slopes of the neurons’ F-I curves do not greatly change, its behavior can be described by a linear rate model:

$${\rm T}\frac{d\mathbf{r}}{\mathit{dt}}=-\mathbf{r}+\mathbf{Wr}+\mathbf{I}=-(\mathbf{1}-\mathbf{W})\mathbf{r}+\mathbf{I}$$ (1)

Here, r is an N-dimensional vector representing the firing rates of a population of N neurons (the i^th element r_i is the firing rate of the i^th neuron). These rates refer to the difference in rates from some baseline rates, e.g. the rates in the center of the operating region, and so can be either positive or negative. W is an N × N synaptic connectivity matrix (W_ij is the strength of connection from neuron j to neuron i). Wr represents input from other neurons within the network. I represents input to the network from neurons outside the network, e.g. feedforward input.

The essential mechanisms of selective amplification can be understood from this model. Equation 1 is most readily analyzed in terms of patterns of activity across the network, rather than the individual firing rates of the neurons. The overall network activity r(t) can be represented as a weighted sum of a set of N basis patterns, denoted p^μ, μ = 1, …, N, with weights (“amplitudes”) r_μ(t): r(t) = Σ_μr_μ (t)p^μ. Similarly, the input can be decomposed I(t) = Σ_μ I_μ (t)p^μ. Each basis pattern or “mode” represents a set of relative rates of firing of all neurons in the network, e.g. neuron 2 fires at 3 times the rate of neuron 1 while neuron 3 fires at 1/2 the rate of neuron 1, etc. The i^th element of the μ^th pattern, $p_i^{\mu }$, represents the relative rate of firing of neuron i in that pattern. Examples of basis patterns can be seen in Fig. 3B, where each row shows two basis patterns, labeled p⁻ and p⁺, each representing a pattern of activity across the excitatory (E) and inhibitory (I) neurons in a model network; this figure will be explained in more detail later.

Figure 3. Difference modes (p⁻) and sum modes (p⁺) in a spatially extended network.

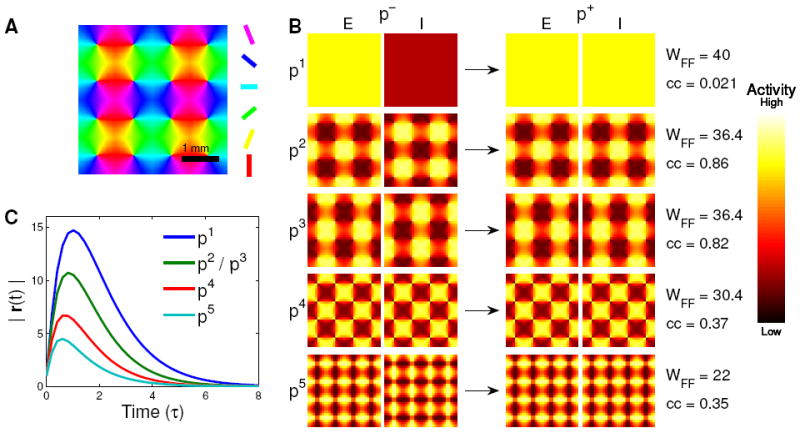
A) Orientation map for both linear and spiking models. Color indicates preferred orientation in degrees. B) The five pairs of difference modes (p⁻, left) and sum modes (p⁺, right) of the connectivity matrix with the largest feedforward weights w_FF (listed at right), by which the difference activity pattern drives the sum pattern (as indicated by arrows). Each pair of squares represents the 32 × 32 sets of excitatory firing rates (E, left square of each pair) and inhibitory firing rates (I, right square) in the given mode. In the difference modes (left), inhibitory rates are opposite to excitatory, while in the sum modes (right), inhibitory and excitatory rates are identical. Also listed on the right are the correlation coefficient (cc) of each sum mode with the evoked orientation map with which it is most correlated. Pairs of difference and sum modes are labeled p¹ to p⁵. The second and third patterns are strongly correlated with orientation maps. C) Plots of the time course of the magnitude of the activity vector, |r(t)|, in response to an initial perturbation of unit length consisting of one of the difference modes from B (indicated by line color).

The basis patterns are typically chosen as the eigenvectors of W; this is the only basis set whose amplitudes evolve independently of one another. p^μ is an eigenvector if it satisfies Wp^μ= w_μ p^μ where w_μ, a (possibly complex) number, is the eigenvalue associated with p^μ. That is, p^μ reproduces itself, scaled by the number w_μ, upon passage through the recurrent circuitry. Thus, eigenvalues with positive real part, which correspond to patterns that add to themselves by passage through the circuitry, are the basis of Hebbian amplification. To understand the response to ongoing input, it suffices to know the response to input to each single basis pattern at a single time, because responses to inputs to different patterns at different times superpose. When the eigenvectors are the basis patterns, inputs to or initial conditions of the pattern p^μ affect only the amplitude of that pattern, r_μ, with no crosstalk to other patterns. In the absence of input, r_μ decays exponentially with time constant Τ_μ = Τ/(1 − R(w_μ)), where R(w_μ) is the real part of w_μ. These are the mathematical statements that the amplitude of each pattern evolves independently of all others, and that, if w_μ has positive real part (but real part < 1 to ensure stability), then the decay of r_μ will be slowed, yielding Hebbian amplification

However, for biological connection matrices, this solution hides key aspects of the dynamics. Because individual neurons project only excitatory or only inhibitory synapses, synaptic connection matrices have a characteristic structure, as follows [e.g. Ermentrout 1998, Wilson and Cowan 1972, 1973]. Let $\mathbf{r}=\left(\begin{array}{c}{\mathbf{r}}_E\\ {\mathbf{r}}_I\end{array}\right)$, where r_E is the sub-vector of firing rates of excitatory neurons and r_I of inhibitory neurons. Let W_XY be a matrix with elements ≥ 0 describing the strength of connections from the cells of type Y (E or I) to those of type X. Then the full connectivity matrix is $\mathbf{W}=\left(\begin{array}{cc}{\mathbf{W}}_{\mathit{EE}}& -{\mathbf{W}}_{\mathit{EI}}\\ {\mathbf{W}}_{\mathit{IE}}& -{\mathbf{W}}_{\mathit{II}}\end{array}\right)$. The left columns are non-negative and the right columns are non-positive. Such matrices are non-normal, meaning that their eigenvectors are not mutually orthogonal (see Supplemental Materials, S3). If non-orthogonal eigenvectors are used as a basis set, the apparently independent evolutions of their amplitudes can be deceiving, so that even if all of their amplitudes are decaying, the activity in the network may strongly but transiently grow [Trefethen and Embree 2005, Trefethen et al. 1993]. This also yields steady-state amplification of steady input that is not predicted by the eigenvalues. We will illustrate this below. We will show that, given biological connection matrices with strong excitation balanced by strong inhibition, this robustly yields strong balanced amplification, which will occur even if all eigenvalues of W have negative real part so that there is no dynamical slowing; and that these dynamics are well described using a certain mutually orthogonal basis set (a “Schur basis”) rather than the eigenvectors.

The simplest example of balanced amplification is a network with two populations of neurons, one excitatory (E cells) and one inhibitory (I cells), each making projections that are independent of postsynaptic target (Fig. 1A). In terms of Eq. 1, $\mathbf{r}=\left(\begin{array}{c}{r}_E\\ r_I\end{array}\right)$ and $\mathbf{W}=\left(\begin{array}{cc}w& -k_{I}w\\ w& -k_{I}w\end{array}\right)$ (the case in which all four weights have distinct values gives similar results, Supplementary Materials S3.3). Here, r_E and r_I are the average firing rates of the E and I populations, respectively, and w and k_Iw are the respective strengths of their projections. We assume inhibition balances or dominates excitation, that is, k_I ≥ 1. The eigenvalues of W are 0 and w − k_Iw = −w₊ where w₊ = w(k_I − 1), so W has no positive eigenvalues and there is no Hebbian amplification. Because inhibition balances or dominates excitation, when r_E and r_I are equal, the synaptic connections contribute net inhibition. That is, letting, ${\mathbf{p}}^{+}=\left(\begin{array}{c}1\\ 1\end{array}\right)$, which is the pattern with equal excitatory and inhibitory firing, then Wp⁺ = −w₊p⁺. However, when there is an imbalance of excitatory and inhibitory rates, then the rates are amplified by the synaptic connections. That is, letting ${\mathbf{p}}^{-}=\left(\begin{array}{c}1\\ -1\end{array}\right)$, representing equal and opposite changes in excitatory and inhibitory rates from baseline, then Wp⁻ = w_FFp⁺ where w_FF ≡ w + k_Iw = w (k_I + 1). This means that small changes in the difference between E and I firing rates drive large changes in the sum of their rates (note that, if recurrent excitation and inhibition are both strong, then w_FF is large). We refer to p⁺ as a sum mode and p⁻ as a difference mode. Note that p⁺ and p⁻ are orthogonal, and that p⁻ is not an eigenvector.

Figure 1. Balanced amplification in the two population case.

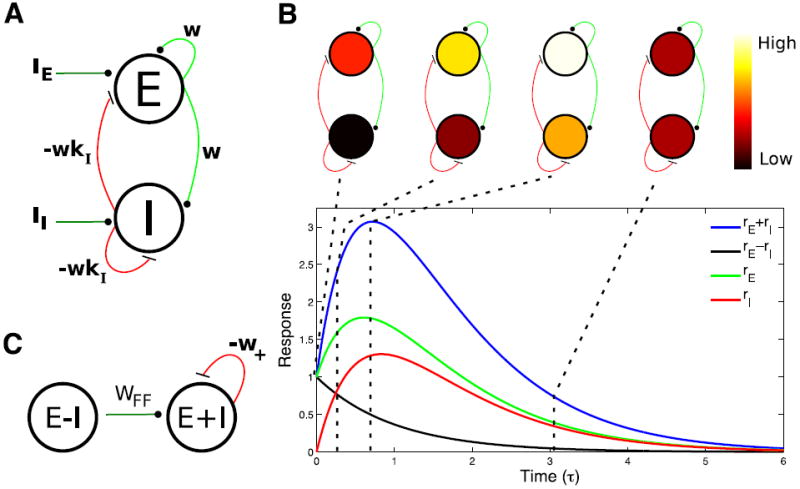
A) Diagram of a balanced circuit with an excitatory and an inhibitory population. Excitatory connections are green and inhibitory connections are red. B) Plot of the sum (blue line) and difference (black line) between activity in the excitatory (r_E, green line) and inhibitory (r_I, red line) populations in response to a pulse of input to the excitatory population at time 0 that sets r_E (0) = 1 (r_I (0) = 0). Diagrams above the plot represent the color-coded levels of activity in the excitatory and inhibitory populations at the time points indicated by the dashed lines. C) The circuit depicted in A can be thought of as equivalent to a feedforward network, connecting difference activity pattern to sum activity pattern with strength w_FF = w(1+k_I). In addition, the sum pattern inhibits itself with strength w₊ = w(k_I − 1). Parameters: k_I = 1.1; $w=4\frac{2}{7}$ (for reasons explained in Fig. 2 legend).

We decompose r(t) as a sum of these two basis patterns, r(t) = r₊(t)p⁺ + r₋ (t)p⁻, with r₊(t) and r₋ (t) respectively representing the sum and difference of excitatory and inhibitory activities: $r_{+}(t)=\frac{1}{2}(r_E(t)+r_I(t)),r_{-}(t)=\frac{1}{2}(r_E(t)-r_I(t))$. Then the dynamics in the absence of external input can be written

$${\rm T}\frac{{\mathit{dr}}_{+}}{\mathit{dt}}=-(1+w_{+})r_{+}+w_{\mathit{FF}}{r}_{-}$$ (2)

$${\rm T}\frac{{\mathit{dr}}_{-}}{\mathit{dt}}=-r_{-}$$ (3)

The network, despite recurrent connectivity in which all neurons are connected to all others (Fig. 1A), is acting as a two-layer feedforward network between activity patterns (Fig. 1C). The difference mode activates the sum mode with feedforward (FF) connection strength w_FF, representing an amplification of small firing rate differences into large summed firing rate responses, and the sum mode inhibits itself with the negative weight −w₊, but there is no feedback from the sum mode onto the difference mode. As expected for a feedforward network, the amplification scales linearly with the feedforward synaptic strength, w_FF, and can be large without affecting the stability or time scales of the network.

The resulting dynamics, starting from an initial condition in which excitation but not inhibition is active above baseline, is illustrated in Fig. 1B. The excess of excitation drives up the firing rates of both excitation and inhibition, until inhibition becomes strong enough to force both firing rates to decay. In terms of the sum and the difference of the rates, the difference decays passively with time constant Τ. The difference serves as a source driving the sum, which increases until its intrinsic decay exceeds its drive from the decaying difference. The sum ultimately decays with a somewhat faster time constant ${{\rm T}}_{+}=\frac{{\rm T}}{1+w_{+}}<{\rm T}$. This is the basic mechanism of balanced amplification in circuits with strong, balancing excitation and inhibition: differences in excitatory and inhibitory activity drive sum modes with similar excitatory and inhibitory firing patterns, while the difference itself decays. In the absence of a source, the sum mode then decays.

The description of these same dynamics in terms of the eigenvectors of W is deceptive, because the eigenvectors are far from orthogonal. If orthonormal basis patterns (meaning mutually orthogonal and normalized to length 1) are used, then the amplitudes of the basis patterns will accurately reflect the amplitudes r_e and r_i of the actual neural activity, in the sense that the sum of the squares of the amplitudes of the basis patterns is equal to the sum of the squares of the neuronal firing rates. Transformation to a non-orthogonal basis, such as that of the eigenvectors of a non-normal matrix, distorts these amplitudes. In the case of a network like that in Fig. 1, this distortion is severe: what is actually transient growth of the firing rates becomes monotonic decay of each amplitude in the eigenvector basis (for reasons explained in Trefethan and Embree, 2005 and in Supplemental Materials, S3.2).

To understand balanced amplification in more intuitive terms, we consider the response of the excitatory population to an external input I_E to the excitatory population (Fig. 2). We contrast the balanced network just studied (Fig. 2, right) with a Hebbian counterpart: a single excitatory population of neurons recurrently exciting itself with strength w (Fig 2, left). We set w for the Hebbian network to produce the same integrated excitatory cell response to a delta-pulse of input (a pulse confined to a single instant of time), and thus the same overall amplification in response to a sustained input, as the balanced network. The responses are plotted with (red lines) and without (blue lines) recurrent connections.

Figure 2. Amplification of response to a pulse input and a sustained input.

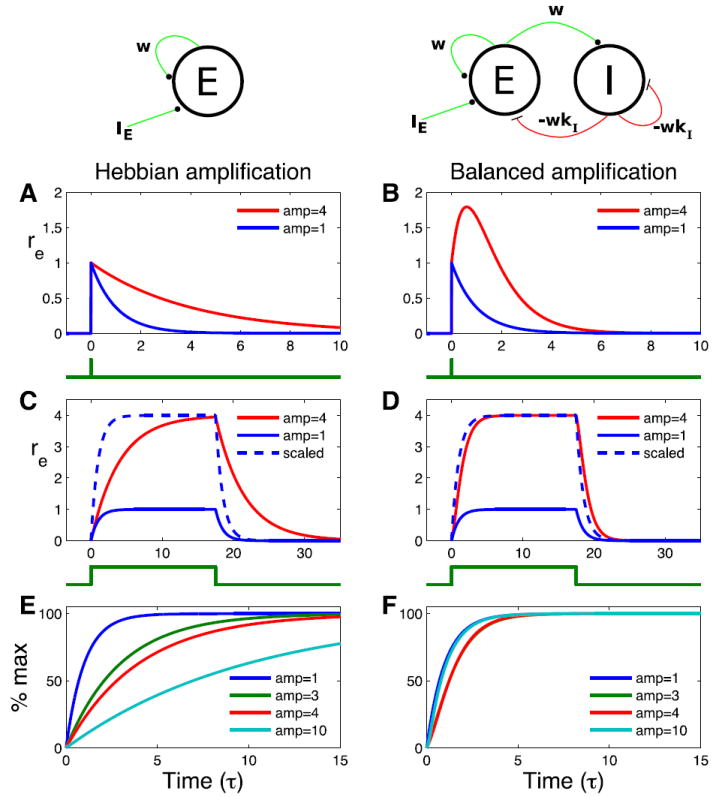
The firing rate response r_E of the excitatory population to an external input I_E to the excitatory population, in two models. Left column: The excitatory population makes a recurrent connection of strength w to itself, leading to Hebbian amplification. Right column: Balanced network as in Fig. 1, k_I = 1.1. In all panels, blue lines show case without recurrent connections (w = 0). A, B) response to a pulse of input at time 0 that sets r_E (0) = 1. Time course of input is shown below plots. Red curve shows response with weights set so that integral of response curve is 4 times greater than integral of blue curve (A, w = 0.75; B, $w=4\frac{2}{7}$). C, D) Response to a sustained input I_E = 1 (time course of input shown7). below plots). Blue dashed line shows w = 0 case scaled up to have same amplitude as the recurrently connected case. E, F) Time course of response to a sustained input, I_E = 1, in recurrent networks with weights set to ultimately reach a maximum or steady-state amplitude of 1 (blue), 3 (green), 4 (red), or 10 (cyan). All curves are normalized so that 100% is the steady-state amplitude. Blue curves have w = 0. Other weights are: E, w = 2/3 (green), w = 3/4 (red), w = 0:9 (cyan); F, w = 2.5 (green), $w=4\frac{2}{7}$ (red), w = 90 (cyan).

We first consider the response to a delta-pulse of input sufficient to set the initial excitatory state to r_E (0) = 1 (Figs. 2A-B); for the balanced network, r_I (0) = 0. In the Hebbian network, the effect of the recurrent circuitry is to extend the decay time from Τ to $\frac{{\rm T}}{1-w}$. In contrast, as we saw above, in the balanced network, the recurrent circuitry produces a positive pulse of response without substantially extending the response time course. This extra pulse of response represents the characteristic response of r₊ to a delta-pulse input to r₋ (Supplementary Materials S1.1, S3.4), which is added to an exponential decay with the membrane time constant. For the sum to produce an initially increasing response in the E population, as shown, the circuit must have w > 1. This means that the excitatory network by itself is unstable, but the circuit is stabilized by the feedback inhibition, a regime likely to characterize circuits of cerebral cortex [Chagnac-Amitai and Connors 1989, Latham et al. 2000, Ozeki et al. 2009]. Given the unbalanced initial condition, the activity of the unstable excitatory network starts to grow, but it also drives up the activity of the inhibitory population, which ultimately stabilizes the network.

We next consider the response to a sustained input I_E = 1 (Figs. 2C-D). Because the system is linear, the sustained input can be regarded as identical delta-pulses of input at each instant of time, and the response as the sum of the transient responses to each delta-pulse of input. The time-course of the rise to the steady-state level is thus given by the integral of the transient response – that is, the rise occurs with the time course of the accumulation of area under the transient curve. Thus, the stimulus onset response is greatly slowed for the Hebbian network, but only slightly slowed for the balanced network, relative to the time course in the absence of recurrent circuitry. This can be seen by comparing the scaled versions of the responses without recurrent circuitry (blue dashed lines) to the responses with recurrent circuitry (red lines).

As we increase the size of the recurrent weights by increasing w to obtain more and more amplification, the delta-pulse response of the Hebbian network decays more and more slowly, so the approach to the steady state becomes slower and slower (Fig. 2E). For the balanced network, increased amplification leads to a higher and higher pulse of response without a slowing of the decay of this response. In fact, higher levels of amplification yield increasing speed of response, due to the increasingly negative eigenvalue w⁺, so that for large w the response speed becomes identical to the speed without recurrence (Fig. 2F, and see Supplementary Materials S1.1.2). In sum, in the Hebbian mechanism, increasing amplification is associated with increasingly slow responses. This leads to an inherent tradeoff between the speed of a Hebbian network’s response and the amount by which it can amplify its inputs. For the balanced mechanism, responses show little or no slowing no matter how large the amplification.

In spatially extended networks with many neurons, balanced amplification can selectively amplify specific spatial patterns of activity. We first consider a case with two simplifications. We take the number of excitatory and inhibitory neurons to be equal; using realistic (smaller) numbers of inhibitory neurons, with their output weights scaled so that each cell receives the same overall inhibition, does not change the dynamics. We also assume that excitatory and inhibitory neurons, though making different patterns of projections, make projections that are independent of postsynaptic cell type. Then, if W_E describes the spatial pattern of excitatory projections and W_I of inhibitory projections, the full weight matrix is $\mathbf{W}=\left(\begin{array}{cc}{\mathbf{W}}_E& -{\mathbf{W}}_I\\ {\mathbf{W}}_E& -{\mathbf{W}}_I\end{array}\right)$. A full analysis of this connectivity is in Supplemental Materials (S1.2); here we report key results. If W_E and W_I are N × N, then W has N eigenvalues equal to zero and another N equal to the eigenvalues of the matrix W_E − W_I. We take inhibition to balance or dominate excitation, by which we mean the eigenvalues of W_E − W_I have real part ≤ 0. Thus, W has no eigenvalues with positive real part and there is no Hebbian amplification. But there is strong balanced amplification.

We can define a set of N pairs of spatially patterned difference and sum modes, p^μ− and p^μ+, μ = 1, …, N, that each behave very much like the difference and sum modes, p⁻, p⁺ in the simpler, two-neuron model we studied previously. The E and I cells in the μ^th pair each have an identical spatial pattern of activation, given by the μ^th eigenvector of W_E + W_I, up to a sign; this pattern has opposite signs for E and I cells in p^μ− but identical signs for E and I cells in p^μ+. The feedforward connection strength from p^μ− to p^μ+ is given by the μ^th eigenvalue of W_E + W_I. That is, the strongest amplification is of spatial patterns that are best matched to the circuitry, in the sense of best reproducing themselves on passage through W_E + W_I. W_E + W_I has entries that are non-negative and large, assuming excitation and inhibition are both strong, so at least some of these feedforward weights will be large. The difference modes p^μ− decay with time constant Τ, while the sum modes p^μ+ decay at equal or faster rates that depend on the eigenvalues of W_E−W_I. Thus, there is differential amplification of activity patterns without significant dynamical slowing. This mechanism of transient spatial pattern formation (or sustained amplification of patterned input) should be contrasted with existing mechanisms of sustained pattern formation, which involve dynamical slowing [Ermentrout 1998].

The five pairs of difference modes p^μ− and sum modes p^μ+ with the five largest feed-forward weights w_FF are illustrated in Fig. 3B, for a simple model of synaptic connectivity based on known properties of V1. In this model, the strength of a synaptic connection between two neurons is determined by the product of Gaussian functions of distance and of difference in preferred orientation (see Methods). The orientation map is a simple 4×4 grid of pinwheels (Fig. 3A). The only difference between the patterns of excitatory and inhibitory synapses is that excitatory synapses extend over a much larger range of distances, as is true in layer II/III of V1 [Gilbert and Wiesel 1989]. The orientation tunings of excitatory and inhibitory synapses are identical, as is suggested by the fact that intracellularly measured excitation and inhibition have similar orientation tuning in upper layers of V1 [Anderson et al. 2000a, Marino et al. 2005, Martinez et al. 2002]. Inhibition is set strong enough that all the eigenvalues of W have real part ≤ 0. Next to each pair of modes in Fig. 3B is the weight w_FF between them, and the maximal correlation coefficient (cc) between the sum modes and any stimulus-evoked orientation map (evoked maps are computed as the response of a rectified version of Eq. 1 to an orientation-tuned feedforward input).

The mode corresponding to the largest w_FF is spatially uniform. Kenet et al. [2003] filtered out this mode in their experiments because it can result from artifactual causes, but it shows much variance (M. Tsodyks, private communication). The next two modes closely resemble evoked orientation maps. To characterize the time course of this amplification, we examine the time course of the overall size of the activity vector, |r(t)|, in response to an initial perturbation consisting of one of the difference modes (Fig. 3C). The first mode follows the time course $w_{\mathit{FF}}\frac{t}{{\rm T}}{e}^{-t/{\rm T}}$ once $\frac{t}{{\rm T}}\gg 1/w_{\mathit{FF}}$, corresponding to a zero eigenvalue of W_E−W_I. Subsequent modes peak progressively earlier, interpolating between timecourses proportional to $\frac{t}{{\rm T}}{e}^{-t/{\rm T}}$ and e^t/Τ, representing the influence of increasingly negative eigenvalues (see Supplemental Materials S1.1.2). Thus, patterns that resemble evoked orientation maps can be specifically amplified by balanced amplification without significant dynamical slowing, given a circuit with balanced, orientation-specific excitatory and inhibitory circuitry. We will show shortly that this can account well for the observations of Kenet et al. [2003] in the context of a nonlinear spiking network.

In the more general case, when W_EE, W_EI, W_IE, and W_II all have distinct structure, one cannot write a general solution, but one can infer that similar results should apply if strong inhibition balances or dominates strong excitation (see Supplementary Materials, S3.3, S3.5). Any such matrix has strong hidden feedforward connectivity, as shown by the Schur decomposition (Supplementary Materials, S3.2). We have seen that use of an orthonormal basis set provides strong advantages for understanding the dynamics. The Schur decomposition finds a (non-unique) orthonormal basis in which the matrix, which means the effective connectivity between basis patterns, is as simple as possible given orthonormality: the effective connectivity includes only self-connections and feedforward connections, but no loops. The dynamics can be analytically solved in this basis (Supplementary Materials, S3.4). In Fig. 1, the orthogonal sum and difference vectors (if properly normalized) are a Schur basis. For a normal matrix, the Schur basis is the eigenvector basis. In the eigenvector basis, a matrix is simply the diagonal matrix of eigenvalues, that is, there are only self-connections (Fig. 4A). However, these basis patterns are not mutually orthogonal for non-normal matrices, such as biological connection matrices. A non-normal matrix in the Schur basis also has the eigenvalues as diagonal entries or self-connections, and zeros below the diagonal, but there are non-zero entries above the diagonal. These entries represent feedforward connectivity between patterns: there can only be a connection from pattern i to pattern j if i > j (Fig. 4B). Given strong excitation and inhibition, the strongest feedforward weights should be be from difference-like patterns (meaning patterns in which excitatory and inhibitory activities tend to have opposite signs) to sum-like patterns (in which they tend to have the same signs) (Supplemental Materials, S3.5), as shown. If the eigenvalues are small due to inhibition balancing excitation, but the original matrix entries are large, then there will be large entries off the diagonal in the Schur decomposition, because the sum of the absolute squares of the matrix entries is the same in any orthonormal basis. That is, strong but appropriately balanced excitation and inhibition leads to large feedforward weights and small eigenvalues, so that the effective connectivity becomes almost purely feedforward (Fig. 4C) and involves strong balanced amplification.

Figure 4. Alternative pictures of the activity dynamics in neural circuits.

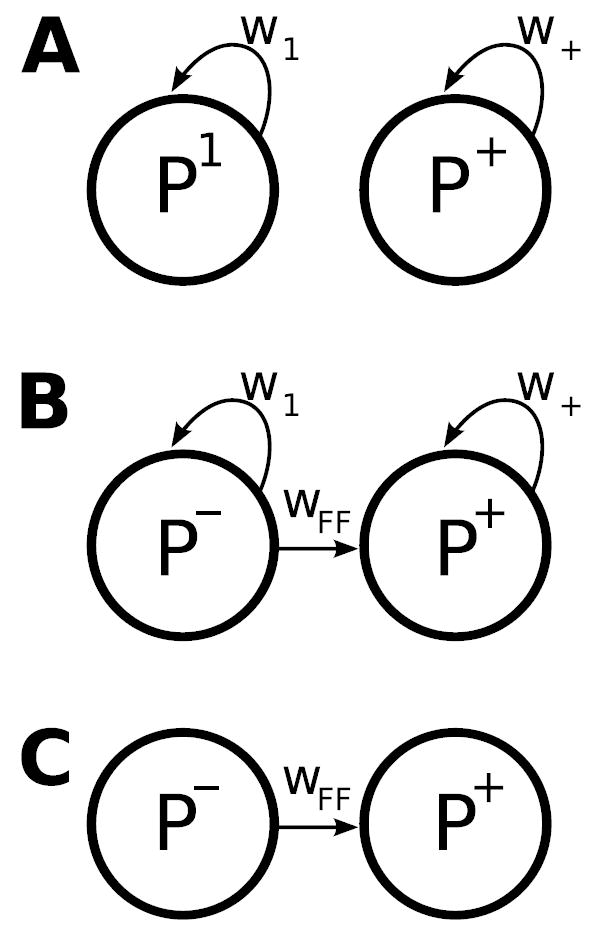
A The eigenvector picture: when the eigenvectors of the connectivity matrix are used as basis patterns, each basis pattern evolves independently, exciting or inhibiting itself with a weight equal to its eigenvalue. The eigenvectors of neural connection matrices are not orthogonal, and as a result this basis obscures key elements of the dynamics. B The orthogonal Schur basis. Each activity pattern excites or inhibits itself with weight equal to one of the eigenvalues. In addition, there is a strictly feedforward pattern of connectivity between the patterns, which underlies balanced amplification. There can be an arbitrary feedforward tree of connections between the patterns, but in networks with strong excitation and inhibition, the strongest feedforward links should be from difference patterns to sum patterns, as shown. There may be convergence and divergence in the connections from difference to sum modes (not shown, e.g., see Supplemental Materials, S1.2). At least one of the patterns will also be an eigenvector, as shown. C If strong inhibition appropriately balances strong excitation, so that patterns cannot strongly excite or inhibit themselves (weak self-connections), the Schur basis picture becomes essentially a set of activity patterns with a strictly feedforward set of connections between them.

The eigenvector picture illuminates a simple biological fact hidden in the biological connectivity matrix: some activity patterns may excite themselves or inhibit themselves, and if so their integration and decay times are slowed or sped up, respectively. This fact, which underlies Hebbian amplification, is embodied in the eigenvalues, and is retained in the Schur picture: the eigenvalues continue to control the integration and decay times of the Schur basis patterns, exactly as for the eigenvector basis patterns. However, there is another biological fact hidden in the biological connectivity matrix that remains hidden in the eigenvector picture: small amplitudes of some patterns (difference patterns) can drive large responses in other patterns (sum patterns). This fact underlies balanced amplification. In the eigenvector picture, this fact is hidden in the non-orthogonal geometry of the eigenvectors (Supplemental Materials S3.2). In the Schur picture, this biological fact is made explicit in the feedforward connection from one pattern to another.

The linear rate model demonstrates the basic principles of balanced amplification. To demonstrate that these principles apply to biological networks, in which neurons are nonlinear, spiking, and sparsely connected, we study a more detailed biophysical model capturing basic features of V1 connectivity. The model is highly simplified and is not meant to serve as a complete and accurate model of V1. It consists of 40,000 excitatory and 10,000 inhibitory integrate-and-fire neurons connected by fast conductance-based synapses. The excitatory and inhibitory neurons are each arranged on square grids spanning the orientation map used previously (Fig. 3A). The neurons are connected randomly and sparsely, with probabilities of connection proportional to the weight matrix studied in the linear model, that is, dependent on distance and difference in preferred orientation. Each neuron receives feedforward input spike trains, modeled as Poisson processes with time-varying rates, to generate sustained spontaneous activity. The input rates vary randomly with spatial and temporal correlations, determined by filtering spatiotemporally white noise with a spatial and a temporal kernel, that reflect basic features of inputs to upper layers. During visually evoked activity each neuron receives a second input spike train, modeled as a Poisson process whose rate depends on the difference between the neuron’s preferred orientation and the stimulus orientation. The network exhibits irregular spiking activity as in other models of sparsely connected spiking networks with balanced excitation and inhibition [Brunel 2000, Lerchner et al. 2006, van Vreeswijk and Sompolinsky 1998] (see Supplementary Materials, S4.1 and Figure S1).

By averaging the response of the network to a stimulus of a given orientation, we produce an evoked orientation map. Frames of spontaneous activity frequently resemble these evoked maps (Figs. 5A,B). As in Kenet et al. [2003], we quantify the similarity between two patterns by the correlation coefficient between them. We chose our parameters so that frames of spontaneous activity show a distribution of correlation coefficients with a given evoked map that is 2 times as wide as that for a control map (Fig. 5C), the same as the amplification observed by Kenet et al. [2003] (Supplemental Materials, S2.2). We examine the dynamics of the amplified pattern by examining the autocorrelation of its time series of correlation coefficients. This results from two factors. The inputs to cortex, created by filtering white noise with a temporal kernel, have a correlation time of about 70 ms. This input is amplified by balanced amplification, which filters with a pulse response whose time course varies between te^−t/Τ and e^−t/Τ (Fig. 3C, Supplemental Material S1.1.2). Here Τ is Τ_m, the neuronal membrane time constant, which has an average value of 20ms during spontaneous activity (the synaptic time constants could also play a role, but are very fast in our model, ≈ 3ms). The time series autocorrelation is well described by the autocorrelation of this doubly-filtered white noise, with the larger input correlation time dominating the total timescale (Figs. 5D,E). If all recurrent weights are scaled up by a common factor, amplification increases but the time scale of the amplified pattern only decreases, due to the decreased membrane time constant caused by the increased conductance (Fig. 6). That is, the recurrent connectivity amplifies input activity patterns resembling evoked maps while causing no appreciable slowing of their dynamics, as predicted by balanced amplification. We show that this conclusion holds across a variety of network parameters, and contrast this with Hebbian amplification, in Supplemental Materials S4.3 and Figure S2.

Figure 5. Spontaneous patterns of activity in a spiking model.

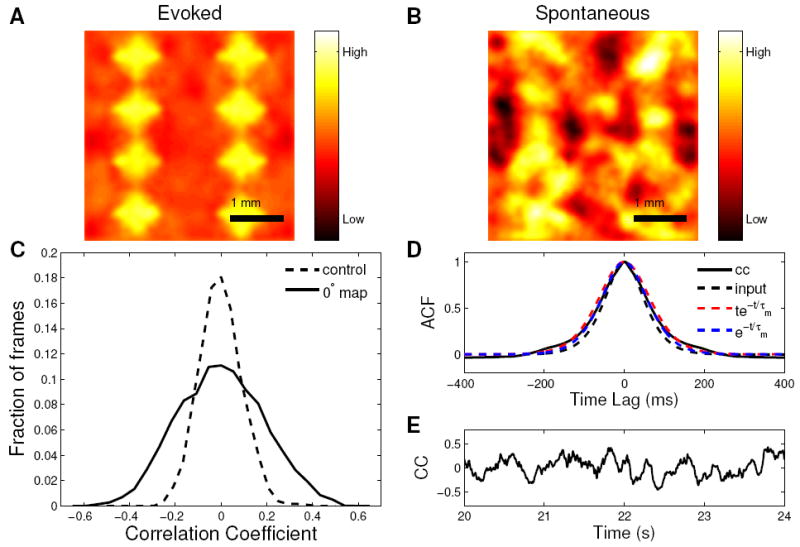
A) The 0° evoked map. B) Example of a spontaneous frame that is highly correlated with the 0° evoked map (correlation coefficient = 0.53). C) Distribution of correlation coefficient for the 0° evoked orientation map (solid line) and the control map (dashed line). The standard deviations of the two distributions are 0.19 and 0.09 respectively. The figure represents 40000 spontaneous frames corresponding to 40 seconds of activity. D) The solid black line is the autocorrelation function (ACF) of the time series of the correlation coefficient (CC) for the 0° evoked map and the spontaneous activity. It decays to 1/e of its maximum value in 85ms. The dashed black line is the autocorrelation function of the input temporal kernel. It decays to 1/e of its maximum value in 73ms. The widening of the ACF of the response relative to the ACF of the 3uctuating input is controlled by the same time scales that control the rise time for a steady-state input (Supplemental Materials S1.1.2) and, for a balanced network, is expected to be between the ACF of the convolution of the input temporal kernel with te^−t/Τ_m (dashed red lines) and with e^−t/Τ_m (dashed blue lines). E) A four-second-long example section of the full timeseries of correlation coefficient used to compute the autocorrelation function in panel D. All results are similar using an evoked map of any orientation.

Figure 6. Increasing Strength of Balanced Amplification Does Not Slow Dynamics in the Spiking Model.

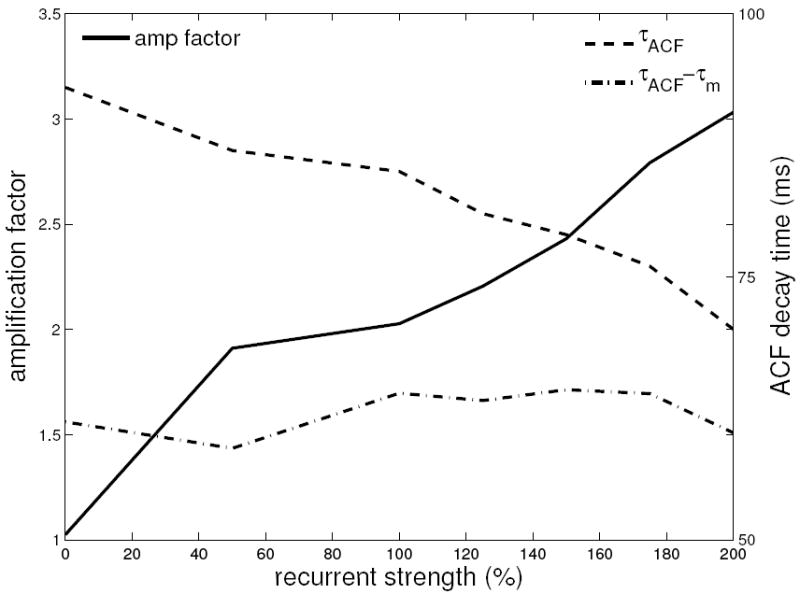
All recurrent synaptic strengths (conductances) in the spiking model are scaled as shown, where 100% is the model of Figs. 5 and 7. The amplification factor increases with recurrent strength (this is the ratio of the standard deviation of the distribution of correlation coefficient of the 0° evoked orientation map to that of the control map; these are shown separately in Supplemental Materials Fig. S2B). The correlation time of the evoked map’s activity Τ_ACF monotonically decreases with recurrent strength (dashed line) (Τ_ACF is the time for the autocorrelation function (ACF) of the time series of evoked map correlation coefficient to fall to 1/e of its maximum). This is because the membrane time constant Τ_m is decreasing due to the increased conductance. The difference Τ_ACF − Τ_m does not change with recurrent strength (dashed-dot line), while amplification increases 3-fold.

To further demonstrate that balanced amplification underlies selective amplification in the spiking model, we examine additional predictions. The difference patterns in Fig. 3B should each produce a time course of the corresponding sum pattern like that shown in Fig. 3C. In the spiking model, we cannot use a pure difference pattern as an initial condition because it leads to synchronized spiking responses. Instead, we probe the noisy spontaneous activity for the same effect. If difference modes are being amplified and converted into sum modes, patterns of activity resembling sum modes will tend to be strongest shortly after patterns of activity resembling their corresponding difference mode. We find that this is the case, with very similar behavior in the spiking model and in a rectified linear model that closely resembles the linear cases we analyzed. We project the network activity onto the sum and difference patterns of Fig 3B in one millisecond intervals and calculate the cross-covariance between each pair of projection timeseries. For both the spiking model (Fig. 7A) and the rectified linear model (Fig. 7B): (1) the peak of the cross-covariance is shifted to the right of zero, reflecting conversion of difference modes to sum modes; (2) the peak covariances are larger for patterns with larger amplification; and (3) the effect is specific: little cross-covariance is seen between mismatched sum and difference patterns (“control”), which have no feedforward connection.

Figure 7. Cross-covariance of difference and sum modes in spiking and linear rectified models.

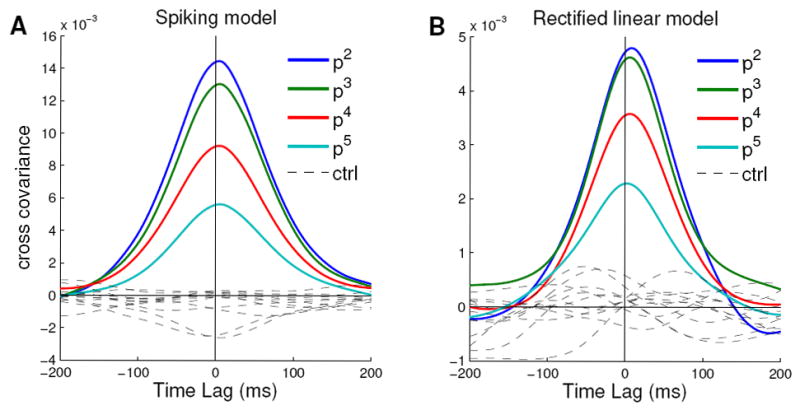
Cross-covariance functions between sum modes and difference modes in spiking (A) and linear rectified B) versions of model in Fig. 3 (spiking model as in Fig. 5). The four colored curves plotted in each figure labeled r2 through r5 correspond to the 2nd through fifth pairs of modes illustrated in Fig. 3. The time series of projections of the spontaneous activity pattern onto each sum mode and each difference mode were determined, and then the cross-covariance was taken between the time series of a given difference mode and that of the corresponding sum mode. Positive time lags correspond to the difference mode amplitude preceding the sum mode’s. The dashed lines labeled control show all combinations of difference modes from one pair and sum modes from a different pair.

The balanced amplification model also predicts that the difference modes should not be differentially amplified and so should have roughly equal amplitudes in the spontaneous activity (all the leading modes, sum and difference, have roughly equal power in the input). The sum modes, being differentially amplified, should have larger amplitudes that decrease with mode number (i.e. with decreasing feedforward weight). Examining the standard deviation of the amplitudes of patterns 2-8 (the first pattern is filtered out in the model, as in the experiments), this prediction is well obeyed. In the spiking model, the difference modes show little variation (mean 0.076 with root mean square (rms) difference from the mean 0.010) and no tendency to grow larger or smaller with mode number (r = 0.28, p = 0.54). The sum modes monotonically decrease with mode number (though modes 2 and 3 are very similar), from 0.2 for mode 2 to 0.075 for mode 8. The linear rectified model behaves similarly.

3 Discussion

In cortical networks, strong recurrent excitation coexists with strong feedback inhibition [Chagnac-Amitai and Connors 1989, Haider et al. 2006, Higley and Contreras 2006, Ozeki et al. 2009, Shu et al. 2003]. This robustly produces an effective feedforward connectivity between patterns of activity, in which small, spatially patterned imbalances between excitatory and inhibitory firing rates (“difference patterns”) drive, and thus amplify, large, spatially patterned balanced responses of excitation and inhibition (“sum patterns”). This balanced amplification should be a ubiquitous feature of cortical networks, or of any network in which strong recurrent excitation and strong feedback inhibition coexist, contributing both to spontaneous activity and to functional responses and their fluctuations. If inhibition balances or dominates excitation, then balanced amplification can occur without slowing of dynamics. If some patterns excite themselves and thus show Hebbian slowing, then Hebbian amplification and balanced amplification will coexist (see Fig. 4 and Supplemental Materials, S3.4).

Given stochastic input, we have found that balanced amplification in a network in which excitatory and inhibitory projections have similar orientation tuning produces orientation-map-like patterns in spontaneous activity, as observed in cat V1 upper layers [Kenet et al. 2003]. This is consistent with results from intracellular recordings that cells in cat V1 upper layers receive excitatory and inhibitory input with similar tuning [Anderson et al. 2000a, Marino et al. 2005, Martinez et al. 2002]. Previous work [Goldberg et al. 2004] found that these patterns could be explained by Hebbian slowing, but this relied on “Mexican hat” connectivity in which inhibition is more broadly tuned for orientation than excitation to create positive eigenvalues for orientation-map-like patterns.

The ≈ 80ms timescale of experimentally observed evoked-map patterns in spontaneous activity (Kenet et al. 2003, and M. Tsodyks, private communication) and their amplification of about 2X relative to control patterns (Supplemental Materials, S2.2) place significant constraints on the degree of Hebbian slowing. As we discuss in detail in Supplemental Materials, S4.4, given the correlations of the inputs [DeAngelis et al. 1993, Wolfe and Palmer 1998], a purely Hebbian-assembly model of this requires an intrinsic (cellular/synaptic) decay time, in the absence of recurrent connections, of no more than about 20 ms. This is plausible, but so too is a considerably longer intrinsic time scale. The intrinsic decay time reflects both the decay of synaptic conductances and the membrane time constant [Ermentrout 1998, Shriki et al. 2003]. Conductances in excitatory cortical synapses include a significant component driven by N-methyl-D-aspartate (NMDA) receptors [Feldmeyer et al. 1999, 2002, Fleidervish et al. 1998], which at physiological temperatures have decay time constant > 100 ms [Monyer et al. 1994]. If these contribute significantly to the intrinsic decay time of cortical activity, the Hebbian-assembly scenario would produce too long a time scale.

With present data, we cannot rule out a contribution of Hebbian slowing to the observations of Kenet et al. [2003]. However, we have shown that balanced amplification will play a major role in the dynamics of circuits with strong but balanced excitation and inhibition, as is believed to be the case for cerebral cortex [Chagnac-Amitai and Connors 1989, Haider et al. 2006, Higley and Contreras 2006, Ozeki et al. 2009, Shu et al. 2003]. Thus, we can say that balanced amplification is almost surely a significant contributor, and may be the sole contributor, to the observations of Kenet et al. [2003]. Comparison of the dynamics of control patterns and amplified patterns in the spontaneous data would reveal the extent, if any, to which amplification is accompanied by slowing.

In sum, balanced amplification represents a mechanism by which arbitrarily strong recurrent connectivity can shape activity in a network with balanced, similarly tuned excitation and inhibition, while maintaining the fast dynamics normally associated with feed-forward networks.

Implications for Experiments

The experiments of Kenet et al. [2003] were conducted in anesthetized animals. The connection between spontaneous activity and columnar structures such as evoked orientation maps is less clear in awake animals (D. B. Omer, L. Rom, U. Ultchin, A. Grinvald. Program No. 769.9, 2008 Neuroscience Meeting Planner. Washington, DC: Society for Neuroscience, 2008. Online.). Awake cortex may also show a significant difference in the time scale of network activity relative to anesthetized cortex: in awake V1 (Fiser et al. 2004 and J. Zhao, G. Szirtes, M. Eisele, J. Fiser, C. Chiu, M. Weliky, and K.D. Miller, unpublished observations) and in awake monkey LIP [Ganguli et al. 2008], one mode involving common activity among neurons across some distance has a decay time of hundreds of milliseconds, while all other modes have considerably faster decay times. These differences suggest differences in the effective connectivity of awake and anesthetized states. For example, a decrease in the overall level of inhibition in the awake state could cause one common-activity mode to show Hebbian slowing. More subtle changes in effective connectivity might disrupt the amplification of evoked-map-like activity or its spatial or temporal coherence.

From the patterns with largest variance in spontaneous activity in a given state, predictions of connectivity that would amplify those patterns and of further tests for such connectivity can be made. Comparing this predicted connectivity across states may suggest key loci for state-dependent modulations of circuitry [Fontanini and Katz 2008]. Similarly, experiments could characterize the fluctuations of activity around visually evoked responses in both states. Individual neurons in upper layers have variable responses to a drifting grating [reviewed in Kara et al. 2000], which might be part of larger patterns like the patterned fluctuations in spontaneous activity [Fontanini and Katz 2008]. If there is similar effective connectivity in spontaneous and evoked activity, one would expect in anesthetized animals to see patterns resembling evoked maps of all orientations in the fluctuations about the response to a particular orientation (although nonlinearities, e.g. synaptic depression/facilitation, might suppress or enhance the evoked map relative to others).

It should soon be possible to directly test for the presence of balanced amplification in cortical networks by optically exciting or inhibiting identified excitatory or inhibitory neurons over an extended region of the upper layers of cortex [e.g. Zhang et al. 2007]. Suppose the excitatory network by itself is unstable and is stabilized by feedback inhibition, as appears to be the case for V1 during visual stimulation [Ozeki et al. 2009]. Then balanced amplification causes a brief stimulation of excitatory cells to yield a positive pulse of transient response among both excitatory and inhibitory neurons, as in Fig. 2B. Hebbian amplification causes a slowed decay of the response, as in Fig. 2A. Coexistence of both mechanisms would yield both a positive pulse and a slowed decay. A circuit transient might occur over a time difficult to separate from the time course of closure of the light-activated channels. One could instead examine the response to sustained activation of inhibitory cells, which paradoxically leads to a steady-state decrease of inhibitory cell firing if the excitatory subnetwork is unstable [Ozeki et al. 2009, Tsodyks et al. 1997]. This effect reflects the same dynamics that underly balanced amplification (Supplemental Text S1.1.3).

The intrinsic decay time of cortical responses in the absence of recurrent connections might be measurable, allowing determination of the slowing induced by the recurrent circuitry. In V1 upper layers, this might be accomplished by intracellularly measuring voltage rise and decay times to the onset and offset of visual stimuli under normal conditions and after optically-induced inhibition of excitatory cells in those layers. This would leave feedforward excitation and inhibition intact so that, after compensating for conductance-induced changes in membrane time constant, the differences in response times would reflect the infiuence of the local recurrent network.

Other Models

Previous models have examined dynamical effects of the division of excitation and inhibition into distinct neuronal classes [Ermentrout 1998, Kriener et al. 2008, Li and Dayan 1999, Pinto et al. 2003, Wilson and Cowan 1972, 1973]. Wilson and Cowan [1973] observed “active transients”, in which a sufficiently large initial condition was amplified before it decayed, in some parameter regimes in simulations of a nonlinear rate model, and argued that this may be the regime of sensory cortex. Pinto et al. [2003] modeled somatosensory (S1) cortex as a similar “excitable system”, in which a threshold level of rapidly increased input engages excitatory recurrence that raises excitatory firing rates before slower inhibition catches up and stabilizes the system. There are likely to be interesting ties between these results and the dynamics exposed here. Kriener et al. [2008] recently showed that random connnectivity matrices with separate excitatory and inhibitory neurons produce much more variance than random matrices without such separation. This effect can be understood from non-normal dynamics: the separation yields large effective feedforward weights that greatly increase the variance of the response to ongoing noisy input, as in the amplification of evoked-map-like patterns.

Li and Dayan [1999] suggested a different mechanism of selective amplification that also depends on the division into E and I cells. They studied a rate model with a threshold nonlinearity. When a fixed point is unstable, which can be induced by a slow inhibitory time constant, the network can oscillate about the fixed point. This oscillation may have large amplitude, so that at its peak a pattern like the fixed point is strongly amplified. This differs from the present work both in mechanism and in biological implications. Their mechanism would yield a periodic rather than a steady response to a steady input, and for spontaneous activity would predict a periodic alternation in the autocorrelation function of the time series of correlation coefficients that is not seen in the data.

The role of excitatory and inhibitory neurons in generating balanced amplification is specific to neural systems, but similar dynamical effects can arise through combinations of excitatory and inhibitory feedback loops [Brandman and Meyer 2008]. More generally, the ideas of feedforward connectivity between patterns arising from non-normal connection matrices may be applicable to any biological networks of interacting elements, such as signaling pathways or genetic regulatory networks. Non-normal dynamics have been previously applied to biology only in studies of transient responses in ecological networks [Chen and Cohen 2001, Neubert and Caswell 1997, Neubert et al. 2004, Townley et al. 2007].

In conclusion, the well-known division of neurons into separate excitatory and inhibitory cell classes renders biological connection matrices non-normal and opens new dynamical possibilities. When excitation and inhibition are both strong but balanced, as is thought to be the case in cerebral cortex, balanced amplification arises: small patterned fluctuations of the difference between excitation and inhibition drive large patterned fluctuations of the sum. The degree of drive between a particular difference and sum pair depends on overall characteristics of the excitatory and inhibitory connectivity, allowing selective amplification of specific activity patterns, both in responses to driven input and in spontaneous activity, without slowing of responses. This previously unappreciated mechanism should play a major and ubiquitous role in determining activity patterns in the cerebral cortex, and related dynamical mechanisms are likely to play a role at all levels of biological structure.

4 Experimental Procedures

4.1 Linear Model

The linear model consists of overlapping 32×32 grids of excitatory and inhibitory neurons, each assigned an orientation according to a superposed orientation map consisting of a 4×4 grid of pinwheels and taken to be 4mm × 4mm. Each pinwheel is a square and each grid point inside a given pinwheel is assigned an orientation according to the angle of that point relative to the center of the square, so that orientations vary over 180° as angle varies over 360°. Individual pinwheels are then arranged in a 4×4 grid such that the orientations along their borders are contiguous. This is accomplished by making neighboring pinwheel squares mirror images, flipped across the border between them.

The strength of a synaptic connection from neuron j of type X (E or I) to neuron i is determined by the product of Gaussian functions of the distance (r_ij) and the difference in preferred orientation (θ_ij) between them: $W_{\mathit{ij}}^X(r_{\mathit{ij}},{\theta }_{\mathit{ij}})\propto e^{-r_{\mathit{ij}}^2/{(w_r^X)}^2}{e}^{-\theta {\mathit{ij}}^2/{(w_{\theta }^X)}^2}$, with parameters $w_r^E=4\mathrm{mm}$, $w_r^I=0.4\mathrm{mm}$, and $w_{\theta }^E=w_{\theta }^I=20°$. The input synaptic strengths to each neuron are normalized (scaled) to make the sum of excitatory and of inhibitory inputs each equal 20.

To generate evoked orientation maps we simulate response of a rectified version of the linear equation to an orientation-tuned feed-forward input. The rectified equation is Eq. 1 with Wr replaced by W[r]₊ (this is the appropriate equation if r is regarded as a voltage rather than a firing rate), where [v]₊ is the vector v with all negative elements set to zero. The feedforward input to each neuron, excitatory or inhibitory, is a Gaussian function of the difference θ between the preferred orientation of the neuron and the orientation of the stimulus: R_evoked = 4e^{−θ2/(20°)2}. The evoked orientation map is the resulting steady-state pattern of activity.

4.2 Spiking Model

The network consists of forty thousand excitatory and ten thousand inhibitory integrate-and-fire neurons. The voltage of each neuron is described by the equation:

$$C\frac{\mathit{dV}}{\mathit{dt}}=g_{\mathrm{leak}}(E_{\mathrm{leak}}-V)+g_e(E_e-V)+g_i(E_i-V)$$ (4)

Here C is the capacitance, and g_leak, g_e and g_i are the leak, excitatory, and inhibitory conductances with corresponding reversal potentials E_leak, E_e and E_i. When the voltage reaches spike threshold, V_thresh, it is reset to V_reset and held there for t_refract. Parameters, except for C, are from Murphy and Miller [2003] and are the same for excitatory and inhibitory neurons: g_leak = 10nS, C = 400pF, E_leak = −70mV, E_e = 0mV, E_i = −70mV, V_thresh = −54mV, V_reset = −60mV and t_refract = 1:75ms. The capacitance is set such that, taking into account mean synaptic conductances associated with ongoing spontaneous activity, the membrane time constant is about 20 ms. At rest, with no network activity, the membrane time constant is 40 ms.

Conductances

The time course of synaptic conductances is modeled as a difference of exponentials:

$$g(t)=\sum _{\mathrm{\Delta }{t}_j}\overline{g}(e^{-\mathrm{\Delta }{t}_j/{{\rm T}}_{\mathrm{fall}}}-e^{-\mathrm{\Delta }{t}_j/{{\rm T}}_{\mathrm{rise}}})$$ (5)

Here Δt_j is defined as (t − t_j), where t_j is the time of the jth pre-synaptic action potential that has t_j < t. For simplicity we include only fast synaptic conductances, AMPA and GABA_A, with identical timecourses for excitation and inhibition: Τ_rise = 1ms, Τ_fall = 3ms. The equality and speed of timecourses are not necessary for our results (see Supplemental Materials, S4.5). What is necessary is that the inhibition not be so fast or strong that it quenches the response to the feedforward connection before it can begin to rise, nor so slow or weak that it fails to stabilize the network if the excitatory subnetwork alone is unstable. The network operates in the asynchronous irregular regime in which neurons fire irregularly and without global oscillations in overall rate (see Supplemental Materials, S4.1 and Figure S1). To operate in this regime, time constants must be chosen appropriately [Brunel 2000, Shriki et al. 2003, Wang 1999], but this is not a tight constraint.

The sizes of the synaptic conductances evoked by a pre-synaptic action potential, ḡ, are defined in terms of the integrated conductance ḡΤ_int where ${{\rm T}}_{\mathrm{int}}={\mathit{\int }}_0^{\infty }\mathit{dt}(e^{-t/{{\rm T}}_{\mathrm{fall}}}-e^{-t/{{\rm T}}_{\mathrm{rise}}})=2\mathrm{ms}$. Values used are ḡ_iΤ_int = 0.02875nS ·ms and ḡ_eΤ_int = 0.001625nS · ms. These are chosen to produce a certain strength of orientation-map like patterns in the spontaneous activity, while maintaining average conductance during ongoing spontaneous activity of roughly 2 times the resting leak conductance [Destexhe and Paré 1999]. Increasing the overall size of the conductances or the ratio of excitation to inhibition increases the strength of the patterns.

Synaptic connectivity

Neurons are in an evenly spaced grid, 200×200 for excitatory neurons and 100×100 for inhibitory neurons (inhibitory cell spacing is twice excitatory cell spacing). As in the linear model, each neuron is assigned an orientation from a superposed orientation map consisting of a 4×4 grid of pinwheels.

The synaptic connectivity is sparse and random, with the probability $P_{\mathit{ij}}^X$ of a connection from neuron j of type X (E or I) to neuron i equal to $k_i^X{W}_{\mathit{ij}}^X$, where $W_{\mathit{ij}}^X$ is the function used in the linear model. $k_i^X$ is chosen to separately normalize excitatory and inhibitory connections to each neuron so that the expected number (average over random instantiations) of connections received by each neuron is N_e = 100 excitatory and N_i = 25 inhibitory connections.

Because the connections are random, some neurons will receive more or fewer connections. To obtain similar firing rates for all neurons in the network we scale up or down the excitatory and inhibitory synaptic conductances received by each neuron so that its ratio of excitatory to inhibitory conductances is $R=\frac{N_e{\overline{g}}_e}{N_i{\overline{g}}_i}$. To achieve this, all the excitatory conductances onto a given neuron by scaled by f_e, and inhibitory conductances f_i, with $f_e=\frac{2.0}{1+1/x}$, $f_i=\frac{2.0}{1+x}$ and x = N_en_i/(N_in_e). Here n_e and n_i are the actual number of excitatory and inhibitory synapses received by the given neuron. This sets $\frac{n_e{f}_e{\overline{g}}_e}{n_i{f}_i{\overline{g}}_i}=R$ for the cell, while also setting (1.0 − f_e) = (f_i − 1.0). The latter condition imitates a homeostatic synaptic plasticity rule in which excitation and inhibition are increased or decreased proportionally to maintain a certain average firing rate.

Spontaneous and Evoked Input

During spontaneous activity each neuron receives background feed-forward input consisting of an excitatory Poisson spike train, with rate randomly determined by convolving white noise with a spatial and temporal filter. The spatial filter is proportional to e^{−x2/(200μm)2}, the temporal filter to t²e^−γt with γ = 40Hz. This kernel is slower than the average temporal kernel of LGN cells [Wolfe and Palmer 1998], but is closer in speed to the temporal kernels of simple cells in layer 4 [DeAngelis et al. 1993] that provide the main input to layers 2/3. For simplicity, we do not replicate the biphasic nature of real LGN or simple-cell temporal kernels, but simply try to capture the overall time scale.

We set the standard deviation of the unfiltered, zero-mean input noise to 1250 Hz and normalize the integrals of the squares of the spatial and temporal filters to 1 to produce filtered noise with the same standard deviation. This rate noise is added to a mean background rate of 10250 Hz. Each input event evokes synaptic conductance 0.00025 nS · ms. Steady input at the mean background rate is sufficient to just barely make the neurons fire (less than 1Hz), while steady input at the mean plus three standard deviations yields a firing rate of about 24Hz.

Visually evoked orientation maps are generated by averaging frames of network activity (see Comparison to Experiment below) for three seconds in response to a visually evoked input added to the background input. The evoked input to a neuron is a Poisson spike train with a rate R_evoked = 10000_e^{−(Δθ)2/(20°)2} where Δθ is the difference between the neuron’s preferred orientation and the stimulus orientation. Synaptic conductance is again 0.00025 nS · ms.

Comparison to Experiment

To compare spontaneous and visually evoked activity we compute the correlation coefficient between frames of spontaneous activity and the visually evoked orientation map every millisecond. A frame is constructed by taking the shadow voltages of all the excitatory neurons, subtracting the mean across these neurons, and spatially filtering with a Gaussian filter with p a standard deviation of $80/\sqrt{2}=56\mu m$. The shadow voltage is the membrane potential of the neuron integrated continuously in time without spike threshold, i.e. it is not reset when it reaches spike threshold. This is meant to approximate the voltage in the portions of the cell membrane not generating action potentials, which appear to dominate the voltage-sensitive-dye signal [Berger et al. 2007]. The filter is used because we are comparing to experimental data that does not resolve individual neurons. The filter width is chosen to conservatively underestimate the point spread function of the experimental images [Polimeni et al. 2005]. We also compute the correlation coefficient between frames of spontaneous activity and a control pattern. This control pattern is constructed by starting with Fourier amplitudes corresponding to the average power spectrum of the evoked orientation maps, assigning random phases, and transforming back to real space. We then subtract off any components in the space spanned by the evoked maps so that the correlation with each evoked map is zero. The width of the distribution of correlation coefficient depends strongly on the width of the Gaussian filter used, and cannot be directly compared to experiment because both the filtering and the noise in the experimental system are unknown. The ratio of the widths of the real and control distributions shows a gentler dependence on the filter width(Fig. S3) and is likely to be a better number to compare to experiment (further discussed in Supplement S2.2).