Protein Dynamics Explain the Allosteric Behaviors of Hemoglobin

Summary

Bohr, Hasselbalch, and Krogh discovered homotropic and heterotropic allosteric behaviors of hemoglobin (Hb) in 1903/1904. A chronological description since then of selected principal models of the allosteric mechanism of Hb, such as the Adair scheme, the MWC two-state concerted model, the KNF induced-fit sequential model, the Perutz stereochemical model, the tertiary two-state model, and the global allostery model (an expanded MWC models), is concisely presented, followed by analysis and discussion of their limitations and deficiencies. The determination of X-ray crystallographic structures of deoxy- and ligated-Hb and the structure-based stereochemical model by Perutz are an epoch-making event in this history. However, his assignment of low-affinity deoxy- and high-affinity oxy-quaternary structures of Hb to the T- and R-states, respectively, though apparently reasonable, and as well as his hypothesis that the T-/R-quaternary structural transition regulates the oxygen-affinity, have created confusions and side-tracked studies of Hb on the structure-function relationship. The differences in static molecular structures of Hb between T(deoxy)- and R(oxy)-quaternary states reported in detail by Perutz and others are ligation-linked structural changes, but not related to the control/regulation of the oxygen-affinity. The oxygen-affinity (K_T and K_R) of Hb has been shown to be regulated by the heterotropic effector-liked tertiary structural changes without involving the T/R quaternary changes. However, a recent high-resolution crystallographic analysis of Hb with different oxygen-affinities shows that static molecular structures of Hb determined by crystallography can neither identify the nature of the T(low-affinity) functional state nor decipher the mechanism by which Hb stores free energy in the T(low-affinity) functional state. Molecular dynamics simulations show that fluctuations of helices of oxy-Hb are increased upon de-oxygenation and/or binding 2,3-biphosphoglycerate. These are known to lower the oxygen-affinity of Hb. It is proposed that the coordination mode of the heme Fe with proximal and distal His is modulated by these helical fluctuations, resulted in the modulation of the oxygen-affinity of Hb. Therefore, it is proposed that the oxygen-affinity of Hb is regulated by pentanary (the 5^th-order time-dependent or dynamic) tertiary structural changes rather than the T-/R-quaternary structural transitions in Hb. Homotropic and heterotropic allosteric effects of Hb are oxygen- and effector-linked, conformational entropy-driven entropy-enthalpy compensation phenomena and not much to do with static structural changes. The dynamic allostery model, which integrates these observations, provides the structural basis for the global allostery model (an expanded MWC model).

1. Introduction

This review presents a brief description of the progression of hypotheses concerning the structure-function relationship of human hemoglobin A (Hb), followed by a critical review of the major models seeking to account for the allosteric mechanism of Hb and their limitations. It also explains how molecular dynamics simulations offer a solution to the two currently unresolved problems on the Hb allostery [the physical/chemical nature of the T(low-affinity)-functional states of Hb and the mechanism of storage of the cooperative free energy in the T(low-affinity)-functional states].

Hemoglobin A, the oxygen-binding tertrameric protein found in the blood, is one of the best-recognized proteins of the human body due to its uniquely bright red color and its color changes in relation to health and diseases such as anemia, hypoxia, cyanide- and carbon monoxide-poisoning. Thus, Hb has not only drawn the attentions of the general public, but also that of physicians and physiologists since ancient times. Modern quantitative analysis of the structure and function of Hb started in the late 1800s and early 1900s.

2. Homotropic Allostery

The first important observation of the Hb allostery is attributed to C. Bohr who reported in 1903 that its oxygen-binding process was sigmoidal or cooperative [1]. Then Bohr, Hasselbalch, and Krogh reported in 1904 that the position of oxygen-binding curve of the blood was sensitive to changes in P_CO2 (and H⁺ or pH), i.e., the Bohr effect [2]. These observations marked the first quantitative description of the allosteric behaviors of Hb and, in contemporary terms, they are referred to as the homotropic and heterotropic allostery of Hb, respectively [3,4] (Fig. 1).

Fig. 1.

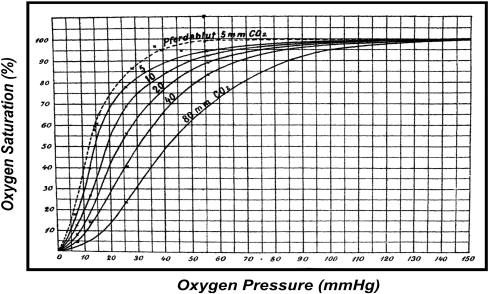
Original oxygen-binding curves of Hb as a function of P_CO2 (mmHg) by Bohr, Hasselbalch, and Krogh (1904). The sigmoidicity (or cooperativity) and P_CO2-dependence (or the Bohr effect) represent the first quantitative observations of homotropic and heterotropic allostery of Hb, respectively.

After Adair demonstrated that Hb contains four oxygen-binding hemes per molecule [5], it was well understood that the binding of oxygen to the first heme must increase the oxygen-affinity of the second heme and of successive hemes, during the four-step oxygen-binding process in Hb either via direct electronic contacts among the neighboring four heme groups or through conformational changes of the carrier protein (globin). Adair formulated this as the model-independent Adair equation (Equation 1) in 1925 (Fig. 2A) [6]:

Fig. 2.

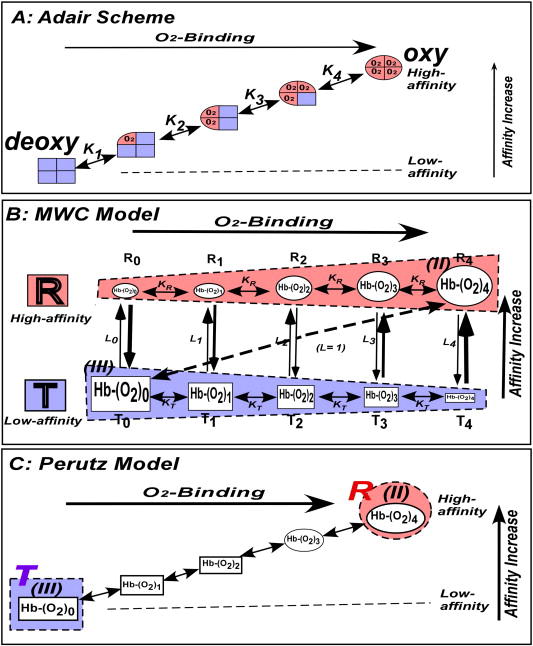
Models of the oxygen-binding equilibria of Hb. (A) Adair scheme in 1925, (B) MWC model in 1965, and (C) Perutz model in 1970. It should be noted that the full set of ligation states [Hb(O₂)_{n (n = 0→4)}] are assigned to either the T(low-affinity)- and R(high-affnity)-functional states (the blue and red shaded regions, respectively) in the MWC model (B). On the other hands, (III) Hb(O₂)₀ and (II) Hb(O₂)₄, the two end-products of the oxygen-binding equilibrium, which are equivalent to “E” and “ES” of an enzyme system, are assigned to T(deoxy)- and R (oxy)-quaternary states (the blue and red shaded circles), respectively, in the Perutz model (C).

$$\mathrm{Y}=\frac{{\mathrm{K}}_1\mathrm{p}+3{\mathrm{K}}_1{\mathrm{K}}_2{\mathrm{p}}^2+3{\mathrm{K}}_1{\mathrm{K}}_2{\mathrm{K}}_3{\mathrm{p}}^3+{\mathrm{K}}_1{\mathrm{K}}_2{\mathrm{K}}_3{\mathrm{K}}_4{\mathrm{p}}^4}{1+4{\mathrm{K}}_1\mathrm{p}+6{\mathrm{K}}_1{\mathrm{K}}_2{\mathrm{p}}^2+4{\mathrm{K}}_1{\mathrm{K}}_2{\mathrm{K}}_3{\mathrm{p}}^3+{\mathrm{K}}_1{\mathrm{K}}_2{\mathrm{K}}_3{\mathrm{K}}_4{\mathrm{p}}^4},$$ 1

where Y and p are the degree of oxygen-saturation and the partial pressure of oxygen, respectively, and K₁, K₂, K₃, and K₄ are the intrinsic oxygen-association equilibrium constants at oxygenation steps 1, 2, 3, and 4, respectively. In 1966 Koshland, Nemethy, and Filmer (KNF) elaborated this idea to present the induced-fit sequential model of cooperative protein systems [7]. The KNF model implies that binding of a ligand/substrate to a polymeric protein induces a conformational change solely in this subunit, which will in turn alter the conformation/reactivity of the neighboring subunits. Each subunit of a polymeric protein is assumed to have two conformations, reactive and inactive (or less reactive) tertiary states. In a sense, the KNF model [7] adds the structural implication to the model-independent Adair scheme [6], namely the induced-fit tertiary structural changes in the subunits of a polymeric protein.

Monod, Wyman, and Changeux proposed the two-state concerted model for allostery in 1965 (Fig. 2B) [4]. They postulated that the cooperative reactions of polymeric enzymes result from an allosteric equilibrium between conformational states: R (the most reactive)- and T (the least reactive)-conformational states, which are regulated by substrates as well as heterotropic allosteric effectors. They presented a mathematical formulation involving K_R, K_T, and L₀ (Equation 2):

$$\mathrm{Y}=\frac{{\mathrm{L}}_0{\mathrm{K}}_{\mathrm{T}}\mathrm{p}{(1+{\mathrm{K}}_{\mathrm{T}}\mathrm{p})}^3+{\mathrm{K}}_{\mathrm{R}}\mathrm{p}{(1+{\mathrm{K}}_{\mathrm{R}}\mathrm{p})}^3}{{\mathrm{L}}_0{(1+{\mathrm{K}}_{\mathrm{T}}\mathrm{p})}^4+{(1+{\mathrm{K}}_{\mathrm{R}}\mathrm{p})}^4,},$$ 2

where Y is the degree of saturation with oxygen, p is the partial pressure of oxygen, K_T and K_R are oxygen-association equilibrium constants^* of T (low-affinity) and R (high-affinity)-functional states^**, respectively, and L₀ = [T₀]/[R₀] is the allosteric equilibrium constant, where [T₀] and [R₀] stand for the equilibrium molar concentrations of the T(low-affinity)- and R(high-affinity)-conformers in the deoxy state, respectively. They further stated statistically that allosteric interactions frequently appear to be correlated with alterations of the quaternary structure of the proteins. This model was applied to Hb to propose that the T(low-affinity)- and R(high-affinity)-functional states to the low- and high-affinity conformational states, which include all the ligation-intermediates of Hb (blue and red rectangles, respectively, in Fig. 2B).

The MWC two-state concerted model is mathematically more elegant, as the sigmoidal oxygen-binding of Hb can be expressed with only two affinity states and three parameters (K_T, K_R, and L₀), rather than four affinity states and four parameters (K₁, K₂, K₃, and K₄) of Adair model and more complex parameters of the KNF sequential model. This simplicity has made it the most favored model for experimentalists and theoreticians, as analyses and interpretations of experimental data become significantly simpler. The 1963 discovery of the two-quaternary states in Hb by Muirhead and Perutz [8] may have further reinforced the position of the MWC model as the most plausible functional model. The four hemes of the Hb tetramer were separated from one another by more than 20Å. This fact had conclusively eliminated the involvement of direct electronic heme-heme interactions in the cooperative mechanism.

Perutz presented the stereochemical model of Hb in 1970 (Fig. 2C) [9], to integrate structure and function of Hb. This represents a landmark event, now considered as the starting point of the “structural biology” which assumes that molecular structure determines the behaviors/functions of proteins and other biological macromolecules. Perutz assigned the low-affinity deoxy- and high-affinity oxy-Hbs to the T(deoxy)- and R(oxy)-quaternary states, respectively. Perutz [9] observed that a set of inter-subunit salt-bridges and the out-of-plane position of the heme Fe were present in the T(deoxy)-quaternary state, but absent in the R(oxy)-quaternary state. Thus, he proposed that the shift in the heme Fe position from “out-of-plane” to “in-plane” upon oxygen-binding triggers displacement of the proximal F-helix, followed by a series of helical rearrangements [9]. These in turn lead to successive breakage of the inter-subunit salt bridges, eventually resulted in the quaternary structural changes from the T(deoxy)- to R(oxy)-conformations. Since this hypothesis involved a series of structural changes in subunits, prior to the final two-state quaternary structural transition, Perutz [10] stated his model as an amalgamation of the KNF and MWC models.

3. Heterotropic Allostery

The oxygen-affinities of T(low-affinity)- and R(high-affinity)-functional states (K_T and K_R) were originally considered constant [4], which we observed at K_T = 0.3 torr^-1 and K_R = 10 torr^-1, respectively, and thus the cooperativity (K_R/K_T) of 30 in the absence of heterotropic allosteric effectors (in stripped Hb under Condition A of Fig. 3)[11]. Small heterotropic effects exhibited by then-known physiological effectors such as H⁺, Cl^-, and CO₂ were interpreted to shift the allosteric equilibrium toward T(low-affinity)-functional states or to increase the L₀ value without changing K_T and K_R values [4,9]. The simultaneous discovery of allosteric effects of 2,3-biphorphoglycerate (BPG), a glycolysis intermediate found in the erythrocytes, on Hb function by Chanutin and Curnish [12] and Benesch and Benesch [13] in 1967 opened a new chapter. Arnone [14] showed that BPG cross-links two β-subunits of deoxy-Hb by electrostatically interacting with positively charged residues located in the central cavity between the β₁- and β₂- subunits. Perutz [9,10] then incorporated these observations in his stereochemical model to interpret the effects of BPG and other physiological effectors such as H⁺, Cl^-, and CO₂. He proposed that they shift the allosteric equilibrium toward the T(low-affinity)-state and thus to lower the oxygen-affinity of Hb.

Fig. 3.

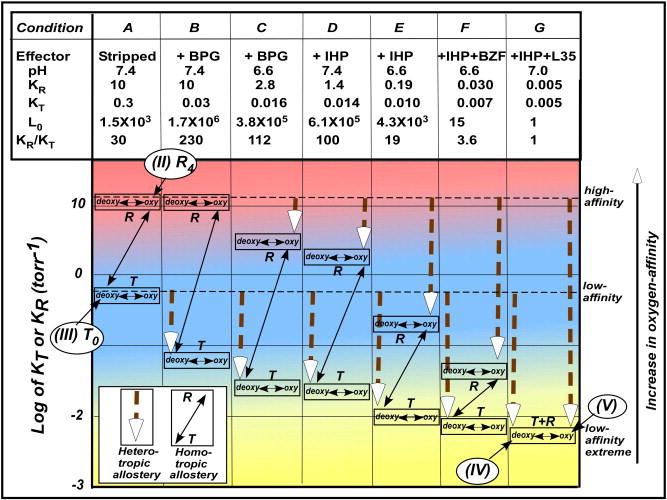
Global allostery model of allostery of Hb, describing the relationship among the oxygen-affinity, homotropic and heterotropic allostery. The oxygen-affinities (K_T and K_R) of T(low-affinity)- and R(high-affinity)-functional states are regulated by effector-linked tertiary structural changes, but not by the T/R-quaternary structural changes. The K_T and K_R values reach the lowest value of 0.005 torr^-1 under the maximal allosteric potency (the low-affinity-extreme state), which is considered as the (lowest-afinity)-functional-state of Hb (Condition G) in the global allostery model, an expanded MWC model. The original T(low-affinity)-functional state with K_T = 0.3 torr^-1(Condition A) is that in the absence of the heterotropic effect (stripped Hb). Under each of these well-defined conditions, the oxygen-binding equilibrium strictly follows the MWC model, determining K_T, K_R and L₀ under such a defined condition. Thus, K_T and K_R values are floating as a function of allosteric potencies ([effector]* ^TK_effector and [effector]* ^RK_effector) according to Equations 3 and 4, respectively.

Imai’s careful oxygen-binding study [15] showed that BPG lowers K_T, but not K_R. This led Minton and Imai [16] to propose a new S-state having a lower “K_T” value, since the T(low-affinity)-functional state of the MWC model is supposed to have the lowest oxygen-affinity. Subsequently, inositol-hexaphosphate (IHP) [17] and other synthetic hydrophobic compounds like bezafibrate [18] and L35 [19], and even BPG [20] were found to lower not only K_T but also K_R. These observations showed that effectors could bind not only to T(deoxy)-Hb preferentially but also to R(oxy)-Hb. It then became crucial to ask, “How low can the K_T and K_R values of Hb go?” and “Where is the ultimate T(low-affinity)-functional state with the lowest K_T value?”

To answer these questions, a comprehensive oxygen-equilibrium analysis based on the MWC model was performed by Yonetani et al. in 2002 [11]. They demonstrated that K_T and K_R values were reduced by as much as 60- and 2,000-folds, respectively, in the presence of the most potent allosteric effectors (Fig. 3). There, the T(low-affinity)-and R(high-affinity)-functional states of Hb converge into the same oxygen-affinity level or the oxygen-equilibrium becomes non-cooperative and of extreme low-affinity, K_T ≈ K_R ≈ 0.005 torr^-1 and L₀ ≈ L₄ ≈ 1 (Condition G of Fig. 3). Thus, this state (Condition G) attains the lowest oxygen-affinity state for Hb with P₅₀ = 200 torr [11], compared with a stripped state with P₅₀ = 0.5 torr in the absence of allosteric effectors (Condition A). These observations indicate that heterotropic allosteric effectors can significantly broaden the range of the oxygen-affinity of Hb, in fact, to a degree previously never assumed (Fig. 3). Yonetani et al. proceeded to formulate their global allostery model [11]. This model effectively demonstrates that the oxygen-affinities (K_T and K_R) of the T(low-affinity)-and R(high-affinity)-functional states of Hb were changed by the hetrotropic effector-linked tertiary structural changes without changing the respective T(deoxy)- and R(oxy)-quaternary states, as probed by proton NMR [11]. Thus, the effector-linked tertiary structural changes were shown to regulate the oxygen-affinities (K_T and K_R) of both T(low-affinity)- and R(high-affinity)-functional states of Hb. This can be expressed by the following two empirical equations (Equations 3 and 4):

$${\mathrm{K}}_{\mathrm{T}}={\mathrm{K}}^{\mathrm{minimum}}+{\mathrm{K}}_{\mathrm{T}}^{\mathrm{maximum}}/(1+[\mathrm{effector}]\ast {}^{\mathrm{T}}\mathrm{K}_{\mathrm{effector}})$$ 3

and

$${\mathrm{K}}_{\mathrm{R}}={\mathrm{K}}^{\mathrm{minimum}}+{\mathrm{K}}_{\mathrm{R}}^{\mathrm{maximum}}/(1+[\mathrm{effector}]\ast {}^{\mathrm{R}}\mathrm{K}_{\mathrm{effector}}),$$ 4

where K^minimum = 0.005 torr^-1, K_T^maximum = 0.3 torr^-1, and K_R^maximum = 10 torr^-1, whereas ^TK_effector and ^RK_effector are association equilibrium constants of effectors to the T(low-affinity)- and R(high-affinity)-functional states, respectively. It should be possible to compute ^TK_effector and ^RK_effector from Equations 3 and 4, respectively. Under each of defined medium conditions, the oxygen-binding equilibrium follows the MWC Model (Equation 2), where K_R > K_T is maintained, except for Condition G. The cooperativity (K_R/K_T) changes from 30 to 230 to ~1 depending on the differential allosteric potency ([effector]* ^TK_effector and [effector]* ^RK_effector). This idea is further strengthened by the observation that heterotropic effectors can reduce the oxygen-affinity of non-cooperative semi-Hb αβ-dimers [α(-)β(Fe) and α(Fe)β(-)] as much as 10²-folds, where no T/R-quaternary transition is involved [21]. The allosteric equilibrium between the T(low-affinity)- and R(high-affinity)-functional states changes as a function of the number of the ligands bound, as the MWC model states [4]. Therefore, the ligation controls the position of the T/R-allosteric transition point at L_n = 1. Thus, it gives an apparent impression that the T/R-quaternary structural transition determines the oxygen-affinity of the T(low-affinity)- and R(high-affinity)-functional states. However, the true determinant of the oxygen-affinity is the effector-linked tertiary structural changes in the global allostery model. The function-based MWC model (Fig. 2B) and global allostery model (Fig. 3) point to the following criteria for the structural features for the low-affinity states: they are (i) effector-linked tertiary structural changes, (ii) common among the ligation intermediates, [Hb(O₂)_{n (n = 0 → 4)}] or [T_{n (n = 0 → 4)}], within the T(low-affinity)-functional states [T₀ ↔ T₁ ↔ T₂ ↔ T₃ ↔ T₄], thus, (iii) independent of ligation states and ligation processes, and (iv) can occur in either T(low-affinity)- or R(high-affinity)-functional states depending on medium conditions or the potency of the heterotropic effects. None of the structural features previously proposed for the T(low-affinity)-functional states of Hb fulfils these criteria. This has casted a strong doubt about the validity of Perutz’s hypothesis of the quaternary structural control of the oxyen-affinity, one of the most widely held belief in the Hb community. For instance, Shulman et al. commented on the MWC model as follows in 1975 [22], “Certainly the model would be shown to be inadequate if controlled experiments showed a similar change in affinities of 2 orders of magnitude without accompanying quaternary changes.” The values of K_T and K_R reported by Yonetani et al. more than fulfill Shulman’s condition for non-validation of the MWC model (actually the Perutz structural model rather than the MWC functional model) [11]. Further, Shulman stated in 2001 [23], “All (i.e. allosteric effectors,αβ inequivalence, and cooperativity within a quaternary structure) have been shown to perturb the functional MWC model, but their effects upon affinity have been very small compared to the effect of quaternary structure.” It should be noted that this gratuitous statement was not substantiated [11]. In 1999, Eaton et al. stated that [24] “…at least the homotropic part of cooperative oxygen binding in hemoglobin is well understood and (we) might treat it as a closed subject.” In a more recent review article in 2007, Eaton et al. [25] argued, “Although understanding the regulation of oxygen affinity by heterotropic effectors is of more general applicability to other allosteric systems, to include analysis of the effects of protons, carbon monoxide, chloride and 2,3-diphosphoglycerate in any detail introduces too much complexity to consider in this brief account.”

Since under physiological conditions Hb is definitely under homotropic as well as heterotropic allosteric controls by oxygen as well as H⁺, CO₂, and BPG, one can not set aside the latter for the sake of expediency in explaining the “physiologically relevant” allosteric mechanism of Hb. Yonetani et al. have clearly demonstrated that heterotropic allostery, rather than homotropic allostery, is the major regulatory mechanism of Hb [11], just like most allosteric enzymes [4]. The ultimate, lowest-affinity-functional-state of Hb (Condition G) is achieved only in the presence of the most potent allosteric effect [11], so that one cannot separately deal with homotropic and heterotropic allostery to elucidate the physiologically relevant allosteric mechanism of Hb. Without knowing the answers to the fundamental questions [the structural base of the T(low-affinity)-functional state and the location of the cooperative free energy storage], how can one claim, “Mission accomplished! (at least for the homotropic part of cooperative oxygen-binding in hemoglobin)” [24]?

Eaton et al. proposed tertiary two-state model [24,25]. This model assumes that the subunits of Hb in both the T(deoxy)- and R(oxy)-quaternary states have two ligation-linked high- and low-affinity states, denoted as t- and r-states to explain the observed variations of K_T and K_R values of Hb. In a sense, this model is an adaptation of the KNF model [7] into the Perutz’s structural model [9]. However, it is no longer compatible with the MWC model [4], where the oxygen-affinity (K_T and K_R) of the T(low-affinity)- and R(high-affinity)-functional states are independent of the ligation process (Fig. 2B). This model suffers from the lack of physical evidences for the presence of such t- and r-structural/affinty states within each of the subunits of Hb and the introduction of more parameters needed for the mathematical formulation and thus a more complex analytical formula for data analyses.

4. MWC Two-State Concerted Model versus Adair Model

Can one determine which of the MWC two-state model or Adair model is correct by measuring oxygen-binding curves accurately? Imai showed that the oxygen-binding data of Hb in the presence and absence of BPG could be similarly simulated by the MWC parameters as well as by the Adair parameters [15]. Oxygen-binding data of Hb reported by Yonetani et al. in a much wider range of functional states were also well simulated by both MWC and Adair parameters, leading to the conclusion that the oxygen-binding data, no mater how accurately determined, were insufficient to distinguish the MWC model from the Adair sequential scheme [11]. However, even though K_T and K_R (in the MWC model) and K₁ and K₄ (in the Adair scheme) were differently defined, their numerical values determined from the oxygen-binding data were identical within experimental error (Table I)[11]. Therefore, K_T, K_R, K₁ and K₄ can be treated as model-independent parameters, which can be estimated either numerically from Equations 1 and 2 or graphically from the upper and lower asymptotes of Hill plots of oxygen equilibrium [15].

Table I.

Comparison of MWC and Adair parameters of hemoglobin in O₂-binding equilibria^*.

pH	KT	KR	L0	K1	K2	K3	K4	ΔH+average
9.0	5.5E-2	9.0E+0	5.2E+5	4.77E-2	4.97E-2	5.56E-1	9.44E+0	-0.3
8.6	3.3E-2	5.3E+0	2.6E+5	3.16E-2	5.15E-2	3.56E-1	5.37E+0	-0.6
8.2	1.8E-2	3.4E+0	7.9E+5	1.66E-2	3.39E-2	7.77E-2	3.71E+0	-0.9
7.8	1.2E-2	1.2E+0	3.8E+5	1.15E-2	1.85E-2	2.46E-2	9.52E-1	-1.1
7.4	1.0E-2	1.3E-1	1.6E+3	9.20E-3	1.30E-2	1.64E-2	8.71E-2	-0.7
7.0	7.0E-3	3.0E-2	3.3E+1	7.20E-3	1.05E-2	1.15E-2	2.33E-2	-0.3
6.6	6.0E-3	2.0E-2	1.5E+1	6.30E-3	9.10E-3	1.15E-2	1.79E-2	-0.1

^*Oxygen-binding equilibria were measured in 0.1M HEPES buffer, pH 6.6-9.0 in the presence of 0.1M Cl^-, 10mM BZF, and 2mM IHP at 15°C [11].

5. Implications of X-Ray Crystallographic Structures

Since the pioneering work of Muirhead and Perutz [8], a wealth of 3D structures have been reported for Hb, abnormal Hbs, recombinant Hbs, and chemically modified Hbs in different states of ligation and oxidation and in the presence and absence of heterotropic effectors. As of 2007, the RCSB data bank currently lists 379 Hb structures, with 20 more awaiting release. More structural differences between (III) low-affinity T(deoxy)- and (II) high-affinity R(oxy)-quaternary states of Hb have been examined since Perutz’s landmark work on the stereochemical model in 1970 [9]. Yet Perutz’s initial hypothesis that the T(deoxy)- and R(oxy)-quaternary structural transition and associated tertiary structural changes such as inter-subunit salt-bridges and the out of plane heme Fe position control and regulate the oxygen-affinity of Hb has been accepted by subsequent Hb researchers as “a hard fact,” in spite of its lack of rigorous experimental demonstration.

6. Limitations and Deficiencies of Current Hypotheses

At first glance, Perutz’s assignment of the (III) low-affinity deoxy- and the (II) high-affinity oxy-Hb to the T(deoxy)- and R(oxy)-quaternary structures seemed reasonable, as it was logical to correlate function [1,2,6] to known Hb structures [8,9]. However, this assignment has created serious problems in integrating the structure-based Perutz model with the function-based MWC model, because the definitions of “T” and “R” in these two models are not only completely different, but also incompatible with each other.

Let us explain. It takes two to tango! A set of two components, namely Hb and Hb-O₂, are required for the [Hb↔Hb-O₂] equilibrium to define an oxygen-affinity state, as in the MWC model. It is well known that association equilibrium constants such as K_T and K_R (the MWC model) as well as K_{n (n=1,2,3,&4)} (the Adair scheme) are kinetically defined by the ratios of the on- and off-rate constants (k_on in [Hb + O₂ → HbO₂] and k_off in [Hb-O₂ → Hb + O₂], respectively, so that both Hb and Hb-O₂ must be in the same affinity state. In other words, it should be understood here that the oxygen-affinity states are defined by the [Hb(O₂)_n ↔ Hb(O₂)_{n+1, n = 0,1,2,and 3}] equilibrium, so that all the ligation intermediates (i.e. Hb(O₂)_{n, n = 0→4}) are involved in each of the T(low-affinity)- and R(high-affinity)-functional states in the MWC two-state model (the blue and red rectangles in Fig. 2B).

In contrast, Perutz assigned the two end-states of the four-step Hb oxygen-equilibrium (equivalent to “E” and “ES” of an enzyme reaction), to the (III) T(deoxy)- and (II) R(oxy)-quaternary states (Fig. 2C). It follows that one cannot describe the T(low-affinity)- and R(high-affinity)-functional states of the MWC model in terms of the Perutz’s definition of the (III) T(deoxy)- and (II) R(oxy)-quaternary states of Hb.

This fact has not been generally recognized by the Hb community, with the result that MWC’s T/R-functional states and Perutz’s T/R-structural states were interchangeably used, with investigators cherry-picking certain structural features of the X-ray structural data, and applying them to the functional MWC model to propose “more refined” hypotheses and reformulations of the Hb structure-function relationship [22-28, for example]. This has created many contradictions and inconsistencies in understanding the allostery of Hb. The unfortunate consequence is that, once Perutz’s assignment of the deoxy- and oxy-Hb to the T(deoxy)- and R(oxy)-quaternary states, the two end-products of oxygen-binding equilibria, is accepted, all the functional Hb models fall under the umbrella of the Perutz’s “two-state” model, because two end-products identified as the (III) T(deoxy)- and (II) R(oxy)-quaternary states, are always involved in oxygen-binding equilibria of Hb. Perutz’s stereochemical model (Fig. 2C) may be actually a wolf (the fundamentally sequential model) in a sheep’s skin (Perutz’s “T/R two-state” definition). Thus, even the Adair scheme (Fig. 2A) and the KNF model as well as the statistic-mechanical model [26] and the tertiary two-state model [24,25], which are all basically forms of the sequential model, have to wear the sheep’s skin of the Perutz’s T/R definition.

To distinguish the T/R definitions between the MWC and Perutz models, we deliberately express MWC’s definition of “T-” and “R-” as T(low-affinity)- and R(high-affinity)-functional states, whereas Perutz’s definition of “T-” and “R-” as T(deoxy)- and R(oxy)-quaternary states (cf. footnote ^**) in this article with no conflict/contradiction whatsoever. This means that Perutz’s “T-” and “R-”states are synonymous with “deoxy-” and “oxy-”states, respectively. However, “T-” and “R-”, evoke functional connotations of the MWC model, though they have none, and thus create confusion/mis-interpretation. We, therefore, propose that Perutz’s terms should be abandoned and replaced simply by “deoxy-” and “oxy- or ligated-” quaternary structures or any other suitable terms except for “T” and “R”, respectively, to avoid confusion. A glaring example of this inconsistency can be seen in the oxygen-binding equilibrium of Hb in the presence of the most potent heterotropic effectors (Condition G in Fig. 3). Its oxygen-saturation curve is hyperbolic or non-cooperative, so that this equilibrium system, consisting of all the ligation intermediates, Hb(O₂)_{n (n= 0→4)}, is supposed to be in the non-coperative ultimate lowest=-affinity-state in the global allostery model, an expanded MWC model (Fig. 3). However, (IV) Hb(O₂)₀ and (V) Hb(O₂)₄ (in solution) within this equilibrium system were found to have Perutz’s T(deoxy)- and R(oxy)-quaternary structures, as determined by proton-NMR [11], though both of them have the lowest oxygen-affinity, K_T ≈ K_R ≈ 0.005 torr^-1, respectively [11]. This is one of the clearest demonstrations that Perutz’s T(deoxy)- and R(oxy)-quaternary structures do not correlate with the oxygen-affinity of Hb. This will be discussed in detail below.

A more serious problem is Perutz’s hypothesis that the T(deoxy)-/R(oxy)-quaternary structural transitions control/regulate the oxygen-affinity of Hb, which has been widely accepted by subsequent researchers. Has this tenet been really proven beyond reasonable doubt? The apparent parallelism between the quaternary structure and the oxygen-affinity is not a proof of their correlation. Let us examine how Perutz’s hypothesis became dogma. From 1904 [1,2,] to 1970 [9], (III) low-affinity deoxy-Hb, (II) high-affinity oxy-Hb, and their sigmoidal oxygen-binding behaviors [(III) ↔ (II)] were the only well-recognized observations underlying the Hb structure-function relationship (Fig. 2A). When Monod, Wyman, and Changeux proposed the two-state concerted model, they also observed statistically among then-known allosteric proteins that allosteric transitions frequently involve alterations in quaternary structures[4]. This observation may have given an impetus to Perutz [9] to assign two different quaternary structures, determined for low-affinity deoxy- and high-affinity oxy (ligated)-Hb, to the T(low-affinity)- and R(high-affinity)-states of the MWC model. Since then, Perutz’s hypothesis of the quaternary structural control of the oxygen-affinity in Hb has been widely accepted as “a hard fact” rather than “an interpretation,” in spite of its lack of firm proof. Thus, the structural differences between the crystallographically determined T(deoxy)- and R(oxy)-Hbs, e.g., in subunit-packing, inter-subunit salt-bridges, and the out-of-plane/in-plane heme Fe position [9,10], have been accepted de facto as the oxygen-affinity-linked structural features without proof! On the other hand, we never question the fact that the differences in the absorption spectra of T(deoxy)- and R(oxy)-Hbs is strictly ligation-linked, but not oxygen-affinity-linked. Thus, spectrophotometry has been used to determine the degree of ligand-saturation in, rather than the oxygen-affinity of, Hb in thermodynamic studies [11-13,15-20] as well as kinetic assays [22-25] of oxygen-binding.

Perutz’s structural comparison of (III) low-affinity T(deoxy)-Hb with (II) high-affinity R(oxy)-Hb is a case of comparing apples to oranges, because it involves both ligation-linked and oxygen-affinity-linked structural differences (Figs. 2C, 3 and 5C). Perutz was unable to distinguish between these two possibilities and assumed optimistically that the observed structural differences were exclusively assignable to the oxygen-affinity-linked structural features, because there was no means available to differentiate between these two possibilities at that time [9,10]. The availability of potent heterotropic effectors, however, recently provided the means (Condition G of Fig. 3 and Fig. 5C) [11]. We can compare the crystallographic structures of (III) low-affinity T(deoxy)-Hb, (II) high-affinity R(CO)-Hb, (IV) low-affinity-extreme T(deoxy)-Hb-effector, and (V) low-affinity-extreme R(CO)-Hb-effector (Conditions A and G of Fig. 3 and Fig. 5C), all recently determined at high-resolution [29]. The oxygen-binding equilibria between (IV) and (V) are non-cooperative (K_T ≈ K_R ≈ 0.005 torr^-1). Therefore, any crystallographic structural differences between (IV) and (V) are strictly ligation-linked features. We find that the structural differences between (IV) and (V) are identical to those between (III) and (II), reported by Perutz, in terms of the quaternary structure, the inter-subunit salt bridges, and the heme Fe position (Fig. 5A and B). This proves that the structural differences between (III) and (II) reported by Perutz [9] are not oxygen-affinity-linked, but merely ligation-linked. This clearly invalidates Perutz’s hypothesis that the T/R-quaternary structural transition controls/regulates the oxygen-affinity of Hb.

Fig. 5.

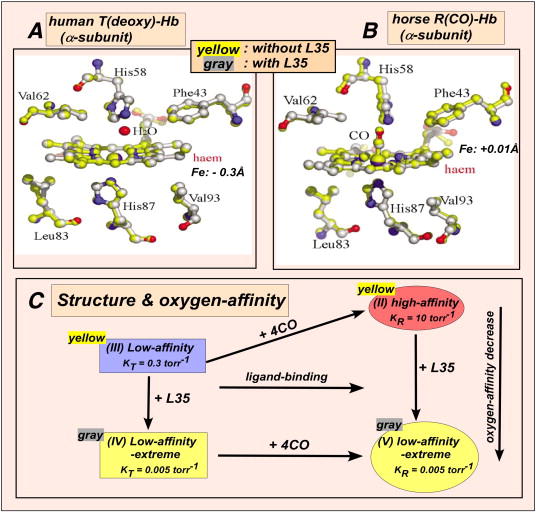
X-ray crystallographic comparison of the α₁-heme environments of (A) human (III) T(deoxy)-Hb and (B) horse (II) R(CO)-Hb in absence (yellow-shaded) and presence (grey-shaded) of L35, (IV) and (V), respectively. (C) The oxygen-affinities of (III) T(deoxy)-Hb and (II) R(oxy)-Hb are reduced as much as ~60- and 2,000-folds in the presence of L35, (IV) and (V), respectively. However, there is no detectable difference of the tertiary heme environments and the quaternary structures in the presence and absence of L35.

The consequences of this conclusion are far reaching, since almost all previous theoretical and experimental studies investigating the Hb structure-function relationship since 1970 have been based upon the validity of Perutz’s unsubstantiated assumption. However, we should not fault Perutz for proposing his refreshingly new bold hypothesis [9,10]. The fault should be placed squarely on subsequent researchers, including ourselves, who have accepted his hypothesis as dogma without critically evaluating it.

All subsequent model refinements and re-formulations, including the statistical-mechanical model [26], the kinetic two-state model [22,23], the tertiary two-state model [24,25], the cooperon model [27], and the molecular code model [28], were based on the assumed validity of Perutz’s hypothesis of the quaternary control of the oxygen-affinity in Hb. Likewise, well discussed Hb structural topics, such as the inter-subunit salt-bridge-linked constraints [9,10,30], the trigger mechanism [9,10,30], the hinge and switch regions [9,10,30], the allosteric core constraint [31], the α₁-β₂ (or α₂-β₁) interfaces [9,10,30], the R-, R₂-, and R₃-quaternary structures [32-35], emsembles of R(oxy)- and T(deoxy)-quaternary structures [36,37], the plasticity of the T(deoxy)-quaternary state [38], and the cooperativity within the T(deoxy)-quaternary state [28] are all based on the validity of Perutz’s hypothesis of the quaternary structural control of the oxygen-affinity of Hb. The ligation-linked T/R-quaternary structural transitions are not the determinant of the oxygen-affinity but merely control the allosteric transition between the T(low-affinity)- and R(high-affinity)-functional states (Figs. 2B and 3). They are, thus, linked to the T/R-transition step at L₀ =1 (Fig. 2B), which is a function of the number of ligands bounds in the MWC model [4].

7. Static Molecular Structures and Low Oxygen-Affinity States

Our recent detailed comparison of high-resolution X-ray crystallographic structures of (III) low-affinity T(deoxy)-Hb versus (IV) low-affinity-extreme T(deoxy)-Hb-L35 (Fig. 5A) and (II) high-affinity R(CO)-Hb versus (V) low-affinity-extreme R(CO)-Hb-L35 (Fig. 5B) under Conditions A and G in Fig. 3 and Fig. 5C, where the differences in the oxygen-affinity are maximal, showed no detectable structural difference attributable to changes in the oxygen-affinity [29]. Thus we have not been able to demonstrate the effector-linked tertiary structural changes which are considered as the structural basis for the low-affinity functional states, as proposed by the global allostery model (Fig. 3) [11]. This applies to all the molecular structures that can be determined by crystallography, especially in the oxygen-binding heme environment in both T(deoxy)-Hb (Fig. 5A) and R(CO)-Hb (Fig. 5B) in the presence (the grey structure) and absence (the yellow structure) of a potent allosteric effector, L35 [29], though their oxygen-affinities were reduced as much as 60- and 2,000-folds, respectively [21]. Thus, we have not been able to identify the structural basis of the low oxygen-affinity states within both T(deoxy)- and R(oxy)-quaternary structures of Hb even with the use of the latest high-resolution techniques. This suggests that changes in protein flexibility may play an important role in controlling the ligand-affinity of Hb [29]. Since 1963, the elucidation of the molecular structures of Hb has greatly advanced our knowledge of detailed structural features of Hb. However, it is evident that static ground-state molecular structures determined by crystallography can neither identify the nature of the low oxygen-affinity state nor decipher the mechanism by which Hb stores free energy in the low oxygen-affinity state, the two long-sought-after questions of fundamental importance in Hb allostery.

8. Molecular Dynamics Simulations

The absence of obvious structural basis of the low oxygen-affinity states in static crystallographic structures clearly implies a contribution from protein dynamics. This is confirmed by our recent molecular dynamics (MD) simulations, performed on (III) T(deoxy)- and (II) R(oxy)-Hb models in the absence and presence of the physiologically important effector, BPG, [(IV) and (V)], on a timescale effectively preventing the occurrence of the quaternary transition [39]. The results showed a significant effector-induced change in Hb dynamics, allowing reformulation of our previous global allostery model [11] as the dynamic allostery model. This revised model is compatible with the MWC mechanism for an allosteric enzyme and taking the role of protein dynamics into account. In this model, Hb can achieve low-affinity functional states via a dynamic mechanism which allow the protein stores free energy in the low-affinity state as conformational entropy, an insight that could not be provided by static structural studies. That the obvious contribution of protein dynamics to Hb function remained ignored for so long is due to the resilience of Perutz’s assumption over the past decades and to the lack of Hb simulations addressing this particular issue.

Figure 6 describes the main contributions to Hb collective motions extracted from simulations for all four models, describing only tertiary changes. For simplicity’s sake, we only show the E and F helices of the α₁-subunit. It is immediately obvious that the fluctuations of (II) R(oxy)-Hb are quite restricted when compared to that of the other models. Up to now, Perutz’s model and its extensions assumed that (II) R(oxy)-Hb was a “relaxed” state while (III) T(deoxy)-Hb was “tense” [9,30]. It was also generally assumed that BPG, which electrostatically cross-links two β-subunits in T(deoxy)-Hb [9,14], would make Hb more rigid or more constrained. However, our MD simulations have generated totally unexpected and counter-intuitive results, showing that (II) R(oxy)-Hb is dynamically relatively rigid and that Hb becomes more and more flexible upon either deoxygenation (III) and/or binding BPG [(IV) and (V)]. These are known to lower the oxygen-affinity of Hb. The estimated frequency and maximal amplitude of these helical fluctuations are of the order of one cycle/~2ns (or ~500MHz) and <3Å, respectively [39]. In both T(deoxy)- and R(oxy)-models, tertiary structural rearrangements upon binding of BPG occur throughout the entire Hb tetrameric molecule. They are particularly noticeable in the loop regions between helices. In addition, the simulations reveal that the amplitude of concerted helical fluctuations is strongly affected by BPG and oxygen, as shown for the E-F helical region, which clamp the heme (Fig. 6). By comparing the dynamic behavior with the oxygen-affinities of (II), (III), (IV), and (V) described in Fig. 6, one can readily recognize the apparent parallelism between the decreasing oxygen-affinity and the increasing amplitude of E- and F-helical fluctuations.

Fig. 6.

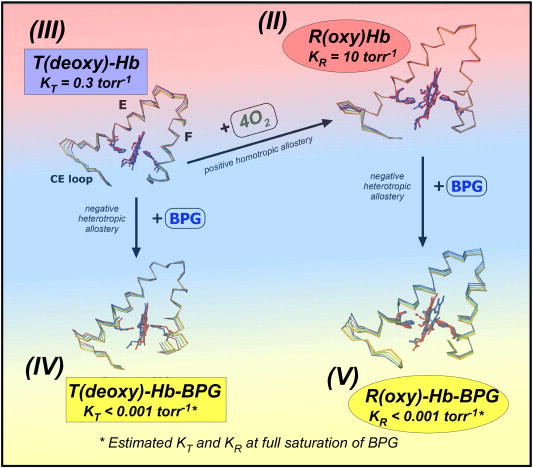
Effector-linked E- and F-helical fluctuations of (III) T(deoxy)-Hb, (II) R(oxy)-Hb, (IV) T(deoxy)-Hb-BPG, and (V) R(oxy)-Hb-BPG, determined by MD simulations. (II) R(oxy)-Hb is dynamically relatively rigid, whereas the amplitude of helical fluctuations increases upon de-oxygenation and/or binding BPG, which reduce the oxygen-affinity.

9. Dynamic Allostery Model

It is entirely conceivable that high-frequency (~500MHz), <3Å-amplitude helical fluctuations, particularly in the E- and F-helices and associated proximal and distal side-chain rotamer motions, could indeed modulate the heme coordination structure and its environment. In particular, they could distort the heme plane [40], change the electronic properties of the heme, and modulate the heme Fe-proximal His coordination [41]. Another effect would be formation/dissolution of the hydrogen-bond between oxygen and the distal His [42,43] as well as changes in the distal environment, including modification of the steric hindrance in the oxygen diffusion processes into and out of the protein matrix [44,45]. Some and/or all of these factors are probably involved in the modulation of the oxygen- affinity of Hb.

The nature of the distal residues such as the type, size, charge, and hydrophobicity in the heme pocket strongly affect the oxygen-affinity in myoglobin [46]. However, Hb can change its oxygen-affinity by as much as >10³-folds without changing its primary, secondary, static tertiary heme environment [29] (Fig.5A and B), or quaternary structures [11,29], so that Hb must employ an alternative mechanism to regulate its oxygen-affinity.

The oxygen-affinity of the heme Fe is strongly affected by the coordination of the heme group, particularly the nature and mode of the 5^th (axial) nitrogenous ligand (Fig. 7) [41]. In addition, the hydrogen bonding of the heme-bound oxygen to the distal His [42,43] increases the oxygen-affinity by a factor of at least 10 in myoglobin and Hb. The concerted fluctuations of the Hb E-F helical region [39] modulate the positions of the distal and proximal His residues, relative to the heme Fe. This was proposed as the mechanism of modulation of the oxygen-affinity of the Hb hemes or the effector-linked tertiary structural changes (the structural basis for the low-affinity state) in the dynamic allostery model (Fig. 8). It is important to note that this dynamic structural basis for the low-affinity functional state is consistent with structural criteria i, ii, iii, and iv for the T(low-affinity)-functional states, as mentioned previously in Chapter 3. Qualitatively speaking, oxygen-binding to (III) deoxy-Hb decreases backbone flexibility and increases the reactivity of the heme Fe (II). Thus, loss of conformational entropy is coupled with gain in enthalpy. The binding of BPG to both deoxy- and oxy-Hbs [(IV) and (V)] increase backbone flexibility (and also conformational entropy). This is coupled to a decrease in the oxygen affinity of the heme Fe (and thus decreasing enthalpy). Is this not another example of the enthalpy-entropy compensation? In other words, the free energy of binding of heterotropic effectors such as BPG may be conserved in part as conformational entropy in the fluctuations of the backbone and associated side-chain rotamer motions in both T(deoxy)-and R(oxy)-states. In essence, this is a dynamic version of Hopfield’s distributed strain model [47]. We speculate that the difference in conformational entropy (or in the amplitude of the helical fluctuations) between (III) T(deoxy)- and (II) R(oxy)-Hb may correspond to the free energy of cooperativity, which is utilized for high-affinity oxygen-binding by (II) R(high-affinity)-functional states of Hb. The free energy of cooperativity for Hb in the presence of BPG at pH 7.4 with a cooperativity of K_R/K_T = 230 (the maximal value of cooperativity thus far observed in Hb) has been calculated from experiment to be 3.1 kcal/mol [11]. When Hb is under maximal hetrotropic allosteric influence, the helical fluctuations of T(deoxy)- and R(oxy)-Hb become similarly maximal [(IV) and (V)], and Hb becomes a non-cooperative (or K_T ≈ K_R ≈=0.005 torr^-1) oxygen-carrier with extremely low oxygen-affinity, as shown under Condition G of Fig. 3, and Figs. 5C and 8. Thus, there is no difference in conformational entropy between (IV) T(deoxy)- and (V) R(oxy)- Hb (or the cooperative free energy is ~zero). We term this state of Hb, involving both deoxy- and oxy-forms, the Low-Affinity Extreme state, which corresponds to the T (lowest-affinity)-functional state of the MWC model [4] and the dynamic allostery model. We explained above why the traditional terms, T(ense)- and R(elaxed)-quaternary states, were not appropriate to describe the structures of deoxy- and oxy-Hb. Taking the dynamic behaviors of these states into consideration justifies even more our proposal (see Section 6) to redefine Perutz’s terms simply as deoxy- and oxy-quaternary states. Although Monod, Wyman, and Changeux observed statistically that allosteric transitions frequently involve alterations in quaternary structure, this is not an imperative requirement for the MWC model [4]. Rather, simple consideration of the role of protein dynamics shows that the oxygen-affinity changes of Hb correlate to changes in dynamics rather than in quaternary structures. Messana et al. [48] reported a calorimetric study showing that the binding of IHP to oxy-Hb is mostly entropy-driven at pH >7. The IHP-binding to oxy-Hb not only reduces the oxygen-affinity of oxy-Hb by ~50-folds (K_R = 10 → 0.02 torr^-1 [11]) without changing the R(oxy)-quaternary structure. It also presumably increases helical fluctuations of Hb, just like BPG. Thus, this finding is consistent with the energetics of the dynamic allostery model. The interactions of heterotropic effectors, including BPG and IHP, with oxy-Hb have been shown to broaden the ring-current-shifted proton NMR resonances of methyl groups of Val E11 without changing the R(oxy)-quaternary structure [11], indicating the changes in dynamics of the heme environment upon biding of the effectors. This observation is also consistent with the proposed changes in helical fluctuations upon binding BPG.

Fig. 7.

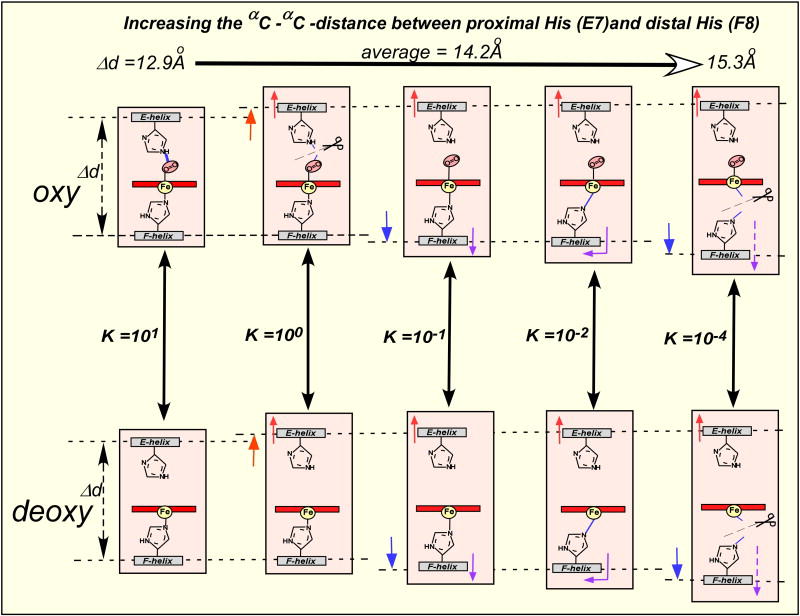
Possible modes of the heme Fe coordination of Hb during cycles of helical fluctuations. During the cycles of helical fluctuations these different modes are time-shared, modulating the oxygen-affinity of the heme Fe in a wide range of >10³-folds from 10 torr^-1 (P₅₀ = 0.1 torr) to 0.005 torr^-1 (P₅₀ = 200 torr) in both deoxy- and oxy-Hb.

Fig. 8.

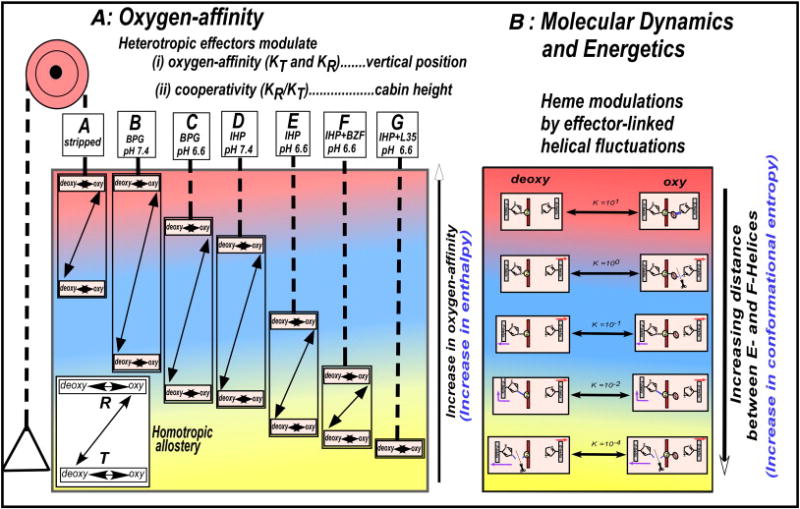
Elevator-expression of the dynamic allostery model, indicating the correlation between the effector-linked changes in the oxygen affinity and the effector-linked dynamic tertiary structural fluctuations. (A) The effector-linked tertiary structural changes (varying amplitudes of the helical fluctuations) not only regulate the floor level [the oxygen-affinities (K_T and K_R)] of the allosteric equilibrium system, but also control the cabin height (the cooperativity). The ligation process (the T- to R-quaternary structural transition) is responsible for the switch of the allosteric equilibrium from K_T-dominant to K_R-dominant states, resulted in an apparent increase in the oxygen-affinity (K_T →K_R) of the allosteric system. (B) The effector-linked helical fluctuations modulate the coordination structure of the heme Fe, resulting in the continuous modulations of the oxygen-affinity of the heme Fe.

Once the dynamic nature of the low oxygen-affinity state of Hb is understood, one can readily postulate the molecular mechanism for cooperativity, or for the positive homotropic allosteric effect of oxygen: when oxygen binds to a heme group, the bound oxygen forms a cross-link between the E- and F-helices in this subunit by forming a hydrogen bond with the distal His [42,43], thus suppressing the fluctuations of the low oxygen-affinity state and bringing Hb to more constrained, higher oxygen-affinity states. In the case of non-hydrogen-bonding ligands like CO, simple steric hindrance by the bound ligand may interfere with the helical fluctuation, albeit to a lesser degree. Whether such changes take place within one particular subunit (the sequential mechanism [6,7,24-26]) or throughout four subunits of Hb (the concerted mechanism [4,11]) could be addressed by MD simulations modeling successive additions of oxygen to deoxy Hb.

This dynamic low-affinity state of Hb also provides an answer to the long-standing puzzle as to why the breakage of the heme-Fe-proximal His bonds in the α-subunits causes Hb to assume the low-affinity-extreme state, as observed in α-nitrosyl Hb, HbM_Iwate (His^α87 → Tyr), HbM_Boston (His^α58→Tyr), in the recombinant Hb mutant (His^α87→Gly) [41], and α-porphyrin-β-heme hybrid Hb [49]. The breakage or absence of the heme-Fe-proximal His bonds, particularly in the α-subuints, would allow maximal helical fluctuations, leading to the Low-Affinity-Extreme state.

Some α-metal hybrid Hb such as α(Ni)₂β(Fe)₂, α(Zn)₂β(Fe)₂, and α(Mg)₂β(Fe)₂ sometimes exhibit very low oxygen-affinities of the β(Fe)-subunits [50-52]. The Ni-proximal His bonds in the α-subunits are relatively weak and readily broken at acidic pHs [52], leading to the low-affinity-extreme state [51]. The Zn- and Mg-proximal His bonds in the α-subunits are also weak, so that α(Zn)₂β(Fe)₂, and α(Mg)₂β(Fe)₂ may have such bonds broken during the dynamic helical fluctuations, leading to the low-affinity-extreme state [51,52], though static X-ray structures of these hybrids show no such bond-breakage [53].

Enzyme catalysis requires the precise geometric orientation of several critical residues at the catalytic and substrate-binding sites, so that the elucidation of the static crystallographic structure of an enzyme is of critical importance. However, oxygen-binding in Hb involves a simple, single axial bond-formation at the heme Fe, the oxygen-affinity of which is readily modulated by the bonding mode of the heme Fe. The weaker the heme Fe-proximal His bond is, the lower the oxygen-affinity becomes [41]. Various modes of coordination of the heme Fe, as schematically illustrated in Fig. 7, are always time-shared during cycles of helical fluctuations, resulting in variable degrees of reduction in the oxygen-affinity depending upon the amplitude of the helical fluctuations. It is as if Hb has an ultra-zoom focusing lens, so that its oxygen-affinity (K_T and K_R) can be continually reset at any points within a wide (>10³) range between 10 torr^-1 (P₅₀ = 0.1 torr: the highest oxygen-affinity) and 0.005 torr^-1 (P₅₀ = 200 torr: the lowest oxygen-affinity), as shown in Figs. 3 and 4. Thus, Hb utilizes a simple, yet elegant dynamic mechanism to modulate its oxygen-affinity in a continuum, in proportion to the allosteric potency of homotropic as well as heterotropic (Equations 3 and 4) effectors, by regulating the amplitude of the E- and F-helical fluctuations.

Fig. 4.

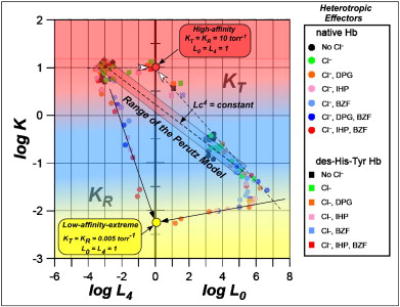
Allosteric plot describing the ranges of K_T, K_R, L₀, and L₄ as a function of heterotropic allosteric effects (at pH 6.6 to 9.0) in the global allostery model. The lowest-affinity-state (the yellow circle) has K_T ≈K_R ≈ 0.005 torr^-1 and L₀ ≈ L₄ ≈ 1, whereas the highest-affinity state (the red circle) has K_T ≈ K_R ≈ 10 torr^-1 and L₀ ≈ L₄ ≈1.

With the dynamic nature of the low oxygen-affinity state of Hb elucidated, our previous global allostery model [11], derived from functional studies, has now attained a firm, comprehensive dynamic and energetics basis in the dynamic allostery model (Fig. 8). The T(deoxy)- and R(oxy)-quaternary structures of Hb then become merely the structural signatures of deoxy- and oxy-Hbs, respectively, so that both sigmoidal and hyperbolic Hb deoxygenation/oxygenation processes (Conditions A and G, respectively) are indeed coupled to the T(deoxy)/R(oxy)-quaternary transition (Figs.3 and 8). Thus, these quaternary structural changes are not directly involved in the modulation of the oxygen-affinity, but simply control the allosteric transition point. As heterotropic effectors preferentially bind to (III) deoxy-Hb, the deoxy/oxy-quaternary states may have an indirect influence on the modulation of the oxygen-affinity by preferentially reducing the oxygen-affinity (K_T) of the T(low-affinity)-functional-state.

The ligation-linked T(deoxy)/R(oxy)-quaternary structural transition and the oxygen-affinity-linked helical fluctuations are operating simultaneously during the sigmoidal oxygen-binding process (Fig. 9), but at different structural dimensions, the one in the X-, Y-, and Z-dimensions and the other operating in a 4^th dimension (the time domain). The former is readily detectable by static crystallography and other spectroscopic methods but the latter requires taking dynamics into account. The oxygen- and effector-linked dynamic helical fluctuations of Hb provides the first rational basis for the regulation of the oxygen-affinity of Hb by oxygen (the positive homotropic allostery or the cooperativity) as well as by BPG (the negative heterotropic allostery) in both T(deoxy)- and R(oxy)-states of Hb.

Fig. 9.

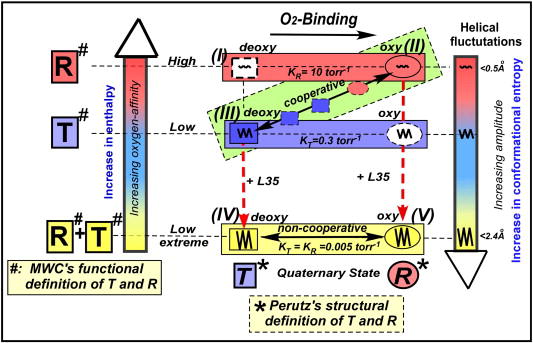
Dynamic allostery model: Integrated relationship of structure, function, homotropic and heterotropic allostery, dynamics, and energetics of Hb. The difference in the definition of “T” and “R” between the MWC and Perutz models is explicitly indicated.

If we accept that allosteric effects are transmitted to and exerted onto the hemes via a common intermediary vehicle of helical fluctuations without going through specific pathways in the protein matrix, we can readily understand why heterotropic effectors widely different in size, charge, hydrophobicity, and binding-sites, such as H⁺, Cl^-, CO₂, BPG, IHP, BZF, L35, and other hydrophilic and hydrophobic compounds can exert identical allosteric effects, i.e. lowering the oxygen-affinity of both T(deoxy)- and R(oxy)-Hb. We can also gain insight into the mechanism by which effector-signals can be transmitted long-distance from various effector-binding sites to four hemes in different subunits. The remaining question concerning the mechanism of allostery is to elucidate the mechanism by which these different effectors can regulate the helical fluctuations. Likewise, how the homotropic effect of the bound oxygen is transmitted to neighboring hemes via helical fluctuations (without passing through a specific pathway such as Perutz’s trigger mechanism [9]) remains to be investigated. The out-of-plane and in-plane positions of the heme Fe in 5- and 6-coordinate hemes, respectively, are normal geometries of the heme coordination in both protein-free and protein-bound states [41]. The structural/mechanistic significance of the oxygenation-linked shift of the Fe position may have been overly emphasized [9,10,30]. Since the heme environment has been shown to fluctuate with a <3Å-amplitude, it immediately follows that the famous ~0.3Å-shift of the heme Fe in the so-called trigger mechanism can not have the crucial mechanistic significance proposed by Perutz [9,10].

10. Epilogue

It is well-known that globular proteins like Hb are not rigid masses, but that they are “breathing” [54], dynamically fluctuating biological macromolecules [55,56]. It is also been established that proteins have evolved to use these inherent conformational fluctuations to carry out their functions [57-59] and that conformational entropy plays vital roles in modulating the free energy of protein-ligand and protein-protein interactions [60]. The dynamic allostery model is yet another example of the functional role of protein dynamics, demonstrating that Hb modulates its intrinsic dynamics to maximal advantage to perform its function efficiently, i.e., the allosteric regulation of oxygen-affinity and the free energy conservation in the low-affinity state.

We note that some previous reports are consistent with the dynamic allostery model. For example, Wyman [61], observing that the shape of the oxygen-binding curves was invariant with temperature, suggested that cooperative effects in Hb are essentially entropic in nature. Hopfield [47] considered that small strains throughout the protein stores free energy of cooperativity in the distributed strain model. Kotani [62], extended the MWC model by proposing that, instead of quantizing possible states into two discrete ones, a better description could be achieved by considering thermal fluctuations over a continuum of states. He further formulated the continuous distribution model statistic mechanically to account for the cooperative ligand-binding of Hb on the basis of the concerted transition concept of the MWC model.

The dynamic allostery model is a rational integration of the structure, function, homotropic and heterotropic allosteries, and energetics of Hb. This perspective represents a radical departure from widely-held current concepts of the allosteric mechanism of Hb, since it proposes that pentanary structural (or tertiary structural dynamics) variations, rather than traditional quaternary structural changes [9,10], play the central role in the regulation of the oxygen-affinity. This basic qualitative framework of the new allosteric mechanism of Hb is presented as a prelude to more quantitative descriptions expected to arise from more detailed analyses of simulations and associated energetics.

A number of MD simulations were performed on Hb [39,63-67], including a more recent work [68]. Most of them [63-68], however, were designed, carried out, and interpreted on the basis of Perutz’s hypothesis of the quaternary structural control of the oxygen-affinity and essentially confirmed Perutz’s stereochemical model [9,10]. With the invalidation of Perutz’s hypothesis, it is now clear that these simulations merely investigated the ligation-linked structural changes between the T(deoxy)- and R(oxy)-quaternary structures, without offering valid insight into the allosteric function of Hb.

Abbreviations

Hb

hemoglobin

MD

molecular dynamics

BPG

2,3-biphosphoglycerate

MWC

Monod, Wyman, and Changeux

KNF

Koshland, Nemethy, and Filmer