High-pressure polymeric phases of carbon dioxide

Abstract

Understanding the structural transformations of solid CO₂ from a molecular solid characterized by weak intermolecular bonding to a 3-dimensional network solid at high pressure has challenged researchers for the past decade. We employ the recently developed metadynamics method combined with ab initio calculations to provide fundamental insight into recent experimental reports on carbon dioxide in the 60–80 GPa pressure region. Pressure-induced polymeric phases and their transformation mechanisms are found. Metadynamics simulations starting from the CO₂-II (P4₂/mnm) at 60 GPa and 600 K proceed via an intermediate, partially polymerized phase, and finally yield a fully tetrahedral, layered structure (P-4m2). Based on the agreement between calculated and experimental Raman and X-ray patterns, the recently identified phase VI [Iota V, et al. (2007) Sixfold coordinated carbon dioxide VI. Nature Mat 6:34–38], assumed to be disordered stishovite-like, is instead interpreted as the result of an incomplete transformation of the molecular phase into a final layered structure. In addition, an α-cristobalite-like structure (P4₁2₁2), is predicted to be formed from CO₂-III (Cmca) via an intermediate Pbca structure at 80 GPa and low temperatures (<300 K). Defects in the crystals are frequently observed in the calculations at 300 K whereas at 500 to 700 K, CO₂-III transforms to an amorphous form, consistent with experiment [Santoro M, et al. (2006) Amorphous silica-like carbon dioxide. Nature 441:857–860], but the simulation yields additional structural details for this disordered solid.

The search for high-pressure structures of CO₂ has resulted in numerous experimental reports and theoretical predictions over the last several decades (1–14). There are many reasons for the large number of studies on this molecular system characterized by weak intermolecular bonding in the solid state at low pressures. There is the distinct possibility that CO₂ may convert to a 3-dimensional network solid that is extraordinarily hard and light, at high pressures. It has also been suggested that CO₂ may be present in the Earth's mantle with structures that are similar or identical to structures of SiO₂ having either 4- or 6-coordinated carbon atoms (12). There are many remaining unresolved issues relating to the detailed structure of solid CO₂ and changes in the chemical bonding that may occur at high pressures. These include questions about the transformation from a quadrupolar molecular solid to an extended network structure, the onset of the bending of the CO₂ linear molecule, and the structural relationship to other materials such as SiO₂.

At moderate temperatures up to ≈700 K, and pressures of 50–80 GPa, transformations from the molecular phases are reported yielding a stishovite-like P4₂/mnm structure (1) starting with molecular phase II of CO₂. However, the stishovite-like structure is energetically unfavorable and mechanically unstable according to first-principles calculations (15). There is also a recent report indicating that CO₂ transforms at moderately high temperatures from the Cmca phase III to a network-forming amorphous phase (2, 3) with mixed 3- and 4-coordinated carbon atoms (15). At high temperatures, the Cmca phase III was reported to transform to a “superhard” material (7, 8). Theoretical investigations have predicted and examined a variety of competing phases with structures ranging from those found in SiO₂ to a layered HgI₂-type structure (7, 9, 11, 12). Theoretical studies have generally used density-functional methods such as total-energy calculations and relaxations and constant-pressure molecular dynamics. Total-energy calculations provide accurate predictions of the lowest energies or enthalpies of candidate structures but may not include all possibilities. The recently developed method for simulation of structural transitions in crystals (16) based on the metadynamics algorithm (17) has been demonstrated to have distinct advantages over the constant-pressure molecular dynamics approaches that can have difficulty in crossing high barriers on potential surfaces. This technique permits the exploration of a much broader range of candidate structures at finite temperatures and can also provide details of transformation mechanisms. This ab initio metadynamics method has been successfully applied to several systems [e.g., SiO₂ (18), MgSiO₃ (19) and Si (20)], where the results were in very good agreement with experiments.

In this study, we applied the recent version of the metadynamics method (18) for study of structural transformations in solids. We explore the transformations and stability of CO₂ at 60–80 GPa and 0–700 K. We find that the structure of phase VI is not stishovite-like, but is layered and tetrahedral. We also predict a phase that may be obtained kinetically in low temperature experiments starting from molecular phase III.

Results

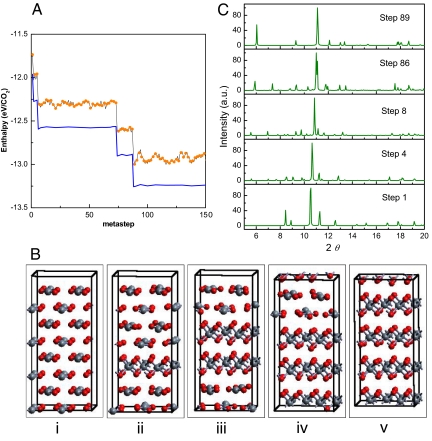
Transition from Phase II to Phase VI.

Metadynamics calculations starting from the Pa-3 (dry-ice) phase of CO₂ were carried out to test the method. A simulation at 25 GPa and 300 K yielded the expected Cmca phase III of CO₂. Metadynamics starting from CO₂-II (P4₂/mnm, Z = 2) was then performed at 60 GPa and 600 K with a 32 molecule cell to explore for the appearance of a disordered stishovite-like structure as recently identified in experiment (1). The evolution of the enthalpy starting from the P4₂/mnm molecular structure is plotted in Fig. 1A. There is a clear stepwise evolution of the enthalpy. An initial polymeric layer is first quickly formed (metasteps 2–5) followed by the addition of polymeric layers at succeeding downward steps in the enthalpy and yielding the final fully polymeric phase (P-4m2, Z = 1) (Fig. 1B). The optimized coordinates of P-4m2 phase at 60 GPa are a = b = 2.243 (4) Å, c = 3.450 (8) Å, carbon atom at 1c (0.5, 0.5, 0.5), and oxygen at 2g [0.0, 0.5, 0.7334 (0)]. The calculated X-ray diffraction patterns for structures at selected metasteps representing different concentrations of polymeric layers are shown in Fig. 1C. There is clear resemblance to the experimental diffraction patterns reported (1). The dominant peak in the diffraction pattern at 10.5° in phase II shifts upward and merges with a peak located at 11.3°. The 2 lower angle peaks at 8.4 and 8.9° decrease in intensity with structural evolution at 60 GPa and 600 K. In addition, a fairly strong peak at ≈6° is seen with the formation of the final polymeric phase. This peak corresponds to the (001) Miller indices of the planar P-4m2 phase and strengthens as the layers of this planar structure develop and their number increases. The 2 peaks at 10.5 and 11.3 degrees in the P4₂/mnm as indicated in the experimental data reported (1) merge and become the strongest diffraction peak (101) in the P-4m2 layered polymeric structure. The peak at ≈6° was not, however, reported in the experiment and, together with the incomplete merging of 2 prominent peaks near 11° in the experimental data, suggests that the final concentration of polymeric layers had not yet fully developed in the experiment (1).

Fig. 1.

Metadynamics simulations for a 32-molecule Phase II supercell at 60 GPa and 600 K. (A) Enthalpy evolution (orange solid circles) and enthalpies for the configurations quenched to 60 GPa and 0 K (blue solid line). (B) Structural evolution at step 1, 4, 8, 86, and 89. (C) Calculated X-ray diffraction pattern for the structures taken from selected metasteps (X-ray wavelength: 0.3682 Å).

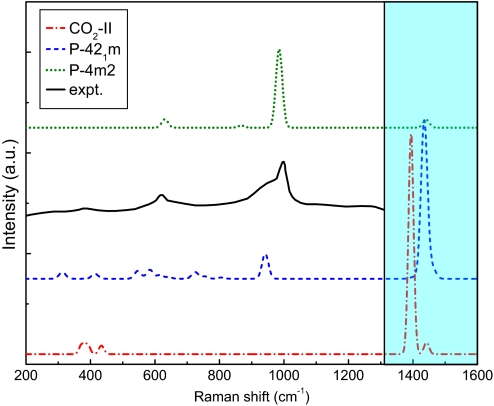
Raman spectra for phase II, for a representative intermediate state structure (P-42₁m) obtained from simulations with a 16-molecule cell at 60 GPa and 600 K (shown in Fig. S1), and for the final layered polymeric phase (P-4m2) are shown in Fig. 2, together with the experimental spectrum (1). The Raman modes at 1,400 cm⁻¹ in phase II merge in the intermediate structure but decrease greatly in intensity when the P-4m2 structure forms. This feature was not, however, accessible in the diamond anvil experiments (1). The intermediate strength peak at 940 cm⁻¹ reflects the appearance of polymeric layers and becomes the strongest peak in the P-4m2 structure. The weaker peaks calculated for the intermediate state in the 300–600-cm⁻¹ region are consistent with the weaker features in the experimental spectrum when one considers that the experimental spectrum is for a disordered material and that the concentration of polymeric layers may differ from the calculation. A Raman active peak is also calculated at 2,442 cm⁻¹, which is higher than the broad band observed in the experiment. Absorption or scattering in the 2,000-cm⁻¹ region is either due to overtone absorption as proposed (1) or to the disorder-allowed scattering from a partial transformed amorphous “carbonia” (15). Therefore, the overall agreement with measured Raman spectrum (1) is very good. Within the accuracy of our method, which is limited mainly by the well-known uncertainties of DFT-GGA and the relatively small system size, our results provide a strong argument for identification of experimentally found phase VI with a partially polymerized planar structure. A recent report (21) using density functional calculations for structural optimization combined with lattice dynamics at T = 0 also confirmed that phase II and the planar structures are closely related.

Fig. 2.

Calculated and experimental Raman spectra (red, CO₂ - II; blue, P-42₁m; green, P-4m2; black, experimental data from ref. 1. The blue shadowed region shows the inaccessible range in DAC experiments.

Compression Starting from Phase III.

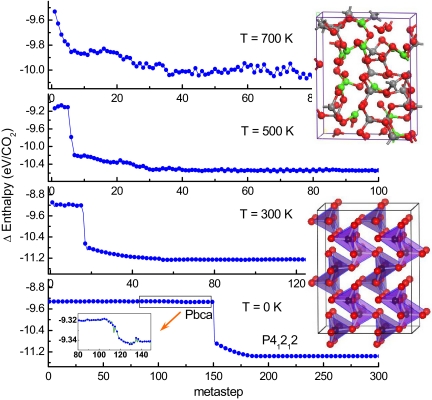
The results for the enthalpy evolution at 0, 300, 500, and 700 K starting from the CO₂-III (Cmca) structure at 80 GPa are shown in Fig. 3. The 100-K simulation details are shown in Fig. S2. Metadynamics simulations at 700 K and 500 K obtained amorphous structures in which carbon atoms are mixed with 3- and 4-coordination, in good agreement with recent reports (2, 3, 15). Simulations at 100 K and 300 K sometimes resulted in amorphous structure but also produced perfectly tetrahedral α-cristobalite-like structure. The frequency for appearance of defects decreases as the temperature is lowered from 300 K, which coincides with the recent room temperature experiment (3) that obtained an amorphous structure. When the temperature is <300 K, the chances for obtaining α-cristobalite-like phase substantially increases. At 0 K, the transformation requires more metasteps but yields the same final structure as at 300 K; as shown in Fig. 3, CO₂-III remains stable for more than 100 metasteps, followed by a small compression at approximately step 115, where CO₂ molecules rotate slightly out of the planar configuration and the enthalpy decreased by ≈0.02 eV/CO₂. The intermediate structure is identified as molecular with an orthorhombic Pbca spacegroup (Z = 4) after optimization at step 125. The optimized lattice constants at 80 GPa and 0 K are a = 4.142 (6) Å, b = 3.836 (5) Å, c = 5.013 (1) Å, with carbon atoms at 4a (0, 0, 0) and O atoms at 8c [0.5596 (4), 0.2543 (9), 0.1232 (0)] positions, respectively. In (9, 22), a structure obtained in this Pbca space group is also suggested to be present in the boundary region between the Pa3 phase I and the Cmca phase III.

Fig. 3.

Evolution of the enthalpy of CO₂ starting from Phase III (Cmca) at 80 GPa and at 0, 300, 500, and 700 K. All of these simulations were performed in a 32-molecule box with a Gaussian width and height of 5 (kbar·Å³)^1/2 and 25 kbar·Å³, respectively. (Inset, Lower Left) Shown is the enthalpy drop at 0 K that yields the intermediate molecular Pbca phase. (Insets, Upper and Lower Right) The final amorphous structure (the 3- and 4-coordinated carbon atoms are shown in green and gray, respectively) and the final alpha-cristobalite-like phase.

After the appearance of the Pbca structure, a final P4₁2₁2 structure evolves (Fig. 3, Lower Inset). This is a perfect tetragonal α-cristobalite-like structure (P4₁2₁2, Z = 4), at 80 GPa, with lattice parameters are a = b = 3.745 (2) Å, c = 4.870 (5) Å. The atomic positions are C(4a) [0.1624 (2), 0.1624 (2), 0.0) and O(8b) (0.2171 (2), 0.8051 (1), 0.0157 (9)]. This is one of the hypothetical structures discussed in ref. 23 but no structural details were given. The details of this structure, the conditions, and microscopic mechanism for its formation are revealed directly from dynamical simulations in this study. Our results directly suggest that a polymeric phase of CO₂ with an α-cristobalite-like structure could be obtained by pressurization of phase III at temperatures substantially lower than the room temperature.

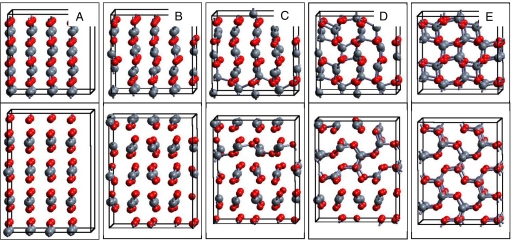
The configurations at selected steps obtained in the 300 K simulation are shown in Fig. 4. The structural evolution begins with tilting of molecules away from the ordered Cmca structure. At metastep 16, bonds between CO₂ molecules in adjacent layers begin to form resulting in one-dimensional chainlike structures. This is quickly followed by formation of bonds between chains that yield set of rings composed of 6 carbon and 6 oxygen atoms and evolution to the same final α-cristobalite-like structure as at 0 K and 100 K (Fig. S2). Simulations with a 16 molecule Phase III (Cmca) cell at 80 GPa and 0 K yielded the layered HgI₂-like structure as found in Parrinello–Rahman simulations at 130 GPa (12). The transformation found for the 32-molecules system is expected to be more realistic than the one in 16-molecules supercell.

Fig. 4.

Illustration of the intermediate structures (metastep 1, 14, 16, 17, 100) during the transformation of CO₂ from phase III (Cmca) to the α-cristobalite-like phase (P4₁2₁2) at 80 GPa and 300 K, where upper frames are top views and lower frames are side views. The density increases from 3.63 to 4.23 g/cm³ from metastep 1 to metastep 100.

Discussion

In a previous density functional theory study, the enthalpy for another structure, β-cristobalite was calculated to be lower up to 60 GPa (23). This structure was also confirmed as the ground state by a recent study applying evolutionary algorithms (33). β-cristobalite-type CO₂, however, has not been reported in experiments, and we do not recover it in this work with metadynamics simulations. A likely reason for this in both experiment and our simulation is that there is a much higher energy barrier preventing its appearance although the expected transition path from alpha- to beta- cristobalite is displacive.

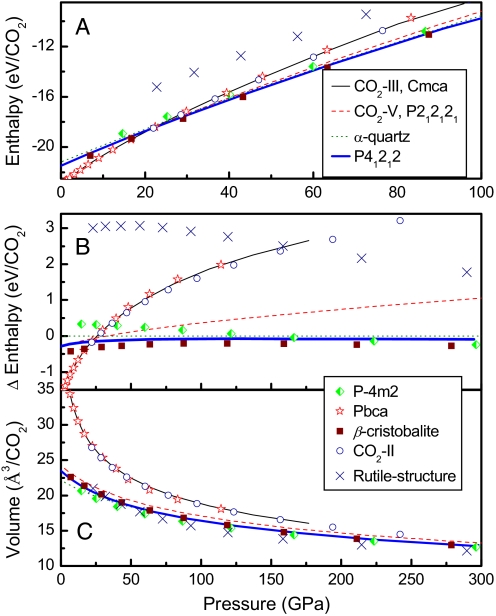
The calculated enthalpies for several CO₂ candidate structures are shown in Fig. 5. The molecular phases, CO₂ II, CO₂ III, and the Pbca structures all have similar enthalpies, higher than the polymeric phases as expected, at least over the pressure range of 60–80 GPa considered in the present study. The structure with space group P4₁2₁2 has a slightly higher enthalpy than the β-cristobalite structure. However, the P4₁2₁2 structure has a lower enthalpy than the CO₂ V P2₁2₁2₁ (Z = 8) structure (7) and the α-quartz-like phase (12). The rutile structure has higher enthalpy than both the phase II structure and the P4₁2₁2 structure over this pressure range. At much higher pressures, >≈300 GPa, the enthalpy of the layered phase is lower than that of 3-dimensional extended phases. The polymeric phases all have similar low compressibilities but the rutile structure is predicted to have a slightly higher compressibility.

Fig. 5.

Pressure dependence of enthalpies (A), enthalpies relative to that of α-quartz-like CO₂ (B), and equations of states (C) for the solid CO₂ structures.

Conclusions

In summary, a recently developed ab initio metadynamics algorithm is applied to predict structures of solid CO₂ that would be obtained in the 60–80 GPa pressure range. Phase II of CO₂ transforms to a fully tetrahedral layered structure (P-4m2) at 60 GPa and 600 K, with a variety of partially polymeric structures as intermediate metastable states. The calculated X-ray diffraction pattern and Raman frequencies of the intermediate states of the transformation are in very good agreement with experimental data (1) for phase VI, suggesting that the structure observed in ref. 1 could be the result of an incomplete transformation of the molecular phase II to a layered tetrahedral phase, rather than a disordered stishovite-like phase with carbon in sixfold coordination. At low temperature, phase III of CO₂ transforms to a predicted P4₁2₁2 polymeric structure resembling α-cristobalite that has an enthalpy lower than that of the CO₂-V extended phase reported in refs. 7 and 8 in this pressure range. When the temperature is >300 K a defective or amorphous structure with mixed 3- and 4-coordinated carbon atoms is obtained as observed in experiment (2, 3). Formation of the P4₁2₁2 structure is found in the metadynamics simulations to proceed via an intermediate structure with space group Pbca below room temperature. A temperature dependence is therefore predicted in the high pressure structural transition of phase III CO₂ at 80 GPa, resulting in amorphous and crystalline structures above and below room temperature, respectively. These results obtained from fully dynamical simulations reveal hitherto unknown microscopic transformation mechanisms, and illustrate the transformation from a molecular solid characterized by intramolecular π-bonding to polymerized structure. The absence of intermediate structures with bent molecules in this study indicates that the transformation from molecular to nonmolecular phases could be structurally more abrupt than speculated (6, 29). The transformation takes place at pressures within the range of those found in the Earth's mantle, where significant amounts of oxidized carbon are thought to be present, either in the form of carbonates or as a fluid (32, 33). The large and abrupt changes in the bonding properties of CO₂ reported here hint to possible discontinuities in the carbon chemistry of the mantle, although whether such changes extend to carbonate or fluid phases remains to be determined. Future experiments and simulations at both low and moderately high temperatures, and in the fluid, will provide tests of the present predictions.

Materials and Methods

The metadynamics method was adapted in this study to simulations by using the projector-augmented plane-wave (PAW) method with the Vienna ab initio simulation (VASP) code (24–26). A PAW potential with a 300-eV energy cutoff was used with a Perdew–Burke–Ernzerhof exchange-correlation functional (27) for molecular dynamics and 500 eV for structure optimizations. The metadynamics simulations were carried out at 0, 100, 300, 500, and 700 K with simulation cells consisting of 16, 24, and 32 CO₂ molecules by using Γ-point sampling. The system was first equilibrated at given temperature and pressure. The Hessian matrix required for metadynamics (18) was then constructed by geometry optimization at 0 K by using finite differences of the stress tensor followed by diagonalization. Raman calculations were carried out by using density functional perturbation theory as implemented in the Quantum-ESPRESSO code (28), and Troullier–Martins norm-conserving pseudopotentials were used with plane-wave cutoff energies of 80 Ryd.

In the metadynamics simulation, each metastep consisted of 200 MD steps for a total simulation time of 0.4 ps. At 0 K, direct relaxation and optimization of the internal atomic coordinates was performed. The initial structures used were the molecular phase II (spacegroup P4₂/mnm) (29) and phase III (spacegroup Cmca) (30) of solid CO₂. Structures obtained in selected steps in the simulations (metasteps) were quenched to 0 K for identification of their crystal structures by using the Materials Toolkit (31).