Statistical methods for characterizing similarities and differences between semantic structures

Abstract

This paper describes a variety of statistical methods for obtaining precise quantitative estimates of the similarities and differences in the structures of semantic domains in different languages. The methods include comparing mean correlations within and between groups, principal components analysis of interspeaker correlations, and analysis of variance of speaker by question data. Methods for graphical displays of the results are also presented. The methods give convergent results that are mutually supportive and equivalent under suitable interpretation. The methods are illustrated on the semantic domain of emotion terms in a comparison of the semantic structures of native English and native Japanese speaking subjects. We suggest that, in comparative studies concerning the extent to which semantic structures are universally shared or culture-specific, both similarities and differences should be measured and compared rather than placing total emphasis on one or the other polar position.

We begin with the premise that people in all cultures hold concepts in their minds from a variety of semantic domains, such as animals, colors, kin terms, and emotions. Further, within any given semantic domain, the concepts vary in the extent to which they are similar to each other in meaning; that is, they constitute what we define as a semantic structure. The primary aim of this paper is to present a variety of methods for characterizing how similar the “picture” of a semantic structure in the mind of one person (or group of persons) corresponds to the picture held in the mind of another person (or group of persons). Even though the example we use throughout this paper is the comparison of the semantic structure of emotion terms between native English and Japanese speaking subjects, the methods are generalizable to other semantic domains in other languages and to the comparison of profile data in general.

The first section of the paper provides a brief summary of methods for characterizing the structure of semantic domains (1–4), that is, obtaining a picture of the interrelationship among the emotion terms. The items of the semantic domain are represented in Euclidean space in which items that are judged more similar are closer to each other than items that are judged less similar. The second section focusses on individuals and examines ways of characterizing the extent to which individuals in a single culture, such as English or Japanese, share knowledge of the semantic structure. The focus is on similarities among subjects rather than on similarities among items. The third section examines methods for the comparison of cultural differences, for example, between native English and Japanese speakers. The final sections present graphical methods for visual representation of the data and consider statistical significance tests for the methods. Implications are discussed at the end of the paper.

The paper illustrates how a variety of statistical methods such as comparing mean correlations within and between subgroups, principal components analysis (PCA), analysis of variance (ANOVA), and simple visualization techniques can be appropriately applied to partitioning shared cultural knowledge into the following segments: (i) a universal portion shared by all subjects regardless of language; (ii) an additional culture-specific portion shared only by subjects speaking the same language; and (iii) a residual portion for each subject due to sampling variability, measurement error, and true differences among subjects. All of the methods produce results consistent with each other, although each contributes some unique insight and perspective of the data. A comparison of the various methods illustrates the general principle that statistical procedures, insofar as they are warranted and appropriately carried out, point to the same conclusions, whatever the process of statistical reduction.

Describing Semantic Domains.

One important part of culture consists of the structure of semantic domains such as animals, kin terms, emotions, or colors. Each individual has an internal cognitive representation of the semantic structure in which the meaning of a term is defined by its location relative to all the other terms. In a series of previous articles, the theory (5) and the methods (1–4) have been developed in which the picture inside the mind of a single individual may be thought of as a cognitive representation of the structure of the corresponding semantic domain. A “composite picture” of the culturally shared semantic domain may be obtained by aggregating the individual cognitive representations into a single picture.

A semantic domain may be defined as an organized set of words, all on the same level of contrast, that refer to a single conceptual category, such as kinship terms, animal names, color terms, or emotion terms. The items in any particular domain for a culture may be obtained by asking a sample of members to free list as many words as possible that belong to the domain (6). The structure of the semantic domain is defined as the arrangement of the terms relative to each other as represented in some metric system such as Euclidean space and described in terms of a set of interpoint distances obtained by scaling judged similarity data. The meaning of each term is defined by its location relative to all the other terms.

To illustrate the various methods, we use a subset of data from a previous study (2) comparing native English and Japanese speakers' semantic structure of 15 emotion terms using single word professional level translations. The sample of subjects used for illustration consists of 33 monolingual English speakers interviewed in the United States and 32 monolingual Japanese speakers interviewed in Japan. The task that all subjects completed was a paired-comparison rating of all 105 possible pairs of emotion words. The task was to rate each word pair in terms of how similar the words are in meaning on a scale of 1 (most dissimilar) to 5 (most similar). Further details may be found in the earlier study (2).

The initial step is to characterize the semantic structure of the emotion terms for both English and Japanese subjects. The first step in the quantification is to use correspondence analysis to obtain individual representations, one for each of the 65 subjects in the total sample. The correspondence analysis is applied to a 975 × 15 matrix obtained by stacking the 15 × 15 matrices of judged similarity data of all 65 subjects into a single matrix. The analysis results in 65 individual representations that have the same orientation and size in a common Euclidean space. This makes it possible to aggregate representations from any combination of individuals by taking the mean location of each term. Details of the methods are described in earlier publications (1–4).

Fig. 1 summarizes the representations of the semantic structures separately aggregated over the 33 English subjects and the 32 Japanese subjects. The location of each term is denoted by a symbol (a star for English and a circle for Japanese) and represents an aggregate position computed by taking the mean of the placements of that term for the English and Japanese subjects, respectively. In this spatial representation, emotion terms that are judged as more similar are closer to each other than terms that are judged less similar. For example, in both groups, anger and hate are very similar (close) to each other and quite dissimilar (distant) from happy.

Figure 1.

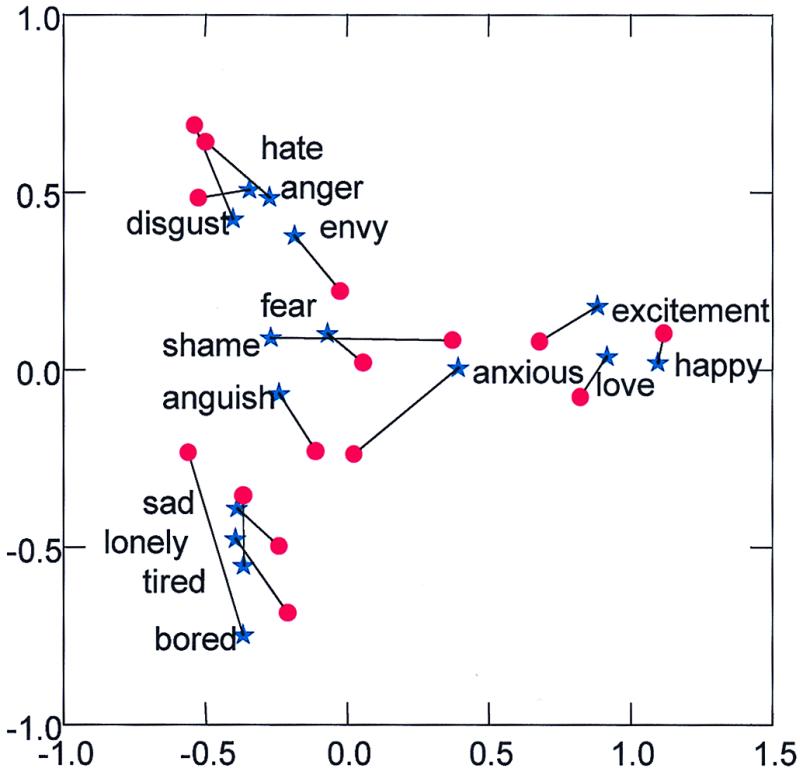
A comparison of the semantic structure of English speaking subjects (blue) and Japanese speaking subjects (red) for 15 emotion terms.

Vectors connect equivalent words in the two languages and are included to facilitate comparison between the configurations and will be discussed later. For the emotion terms, Dimension 1 appears to correspond to what Osgood (ref. 7 and ref. 8, p. 173) called the Evaluative Factor, “represented by scales such as good-bad, pleasant-unpleasant, and positive-negative,” whereas Dimension 2 appears related to his Activity Factor, “represented by scales such as fast-slow, active-passive, and excitable-calm.” The first dimension goes from unpleasant on the left to pleasant on the right, whereas the second dimension goes from passive at the bottom to active at the top.

We emphasize that the meaning of each term is defined by its location relative to all the other terms. Clearly, this model does not capture all of the aspects of semantics in linguistic theory. However, it does provide an important aspect of semantic meaning captured by judged similarity data. About 50% of the variance in the raw data can be accounted for by the two dimensions displayed in Fig. 1. Four dimensions account for over two-thirds of the variance. Most importantly, the model provides a fully quantified structure for measurement of every term relative to every other term for every subject. This quantification is essential for the investigation into the extent to which the two representations are similar and different.

Describing Subject–Subject Similarities Within Cultures.

This section focuses on the similarities within groups of native speakers. Subjects of each group are compared in terms of the overall configuration of their individual Euclidean representations of the semantic structures that are summarized in Fig. 1. The following notation is used. Let d_nm denote the interpoint distance between the mth term pair for the nth subject, where n = 1, 2, … , N and m = 1, 2, … , M. In our example, the combined sample of subjects yields N = 65, and the 15 terms yield M = 105 pairs. Then, the resulting matrix of subject vectors is given by D_n = (d_nm)_N×M.

There are a variety of ways in which similarities among pairs of subjects might be measured. The use of interpoint distances is motivated by Rao and Suryawanshi's (9) suggestion that information on the shape of a configuration is encoded in terms of the k (k − 1)/2 Euclidean distances between all possible pairs of critical points, where the k points are selected to reflect important aspects of the shape. In our study, the points are defined by the locations of the 15 emotion terms in the spatial configuration obtained above. The Euclidean distances for each subject are computed from their row score coordinates from the correspondence analysis by using four dimensions (see refs. 1–4) where the remaining dimensions are treated as noise.

Next, the subject vectors for each group are placed separately into two rectangular matrices with 33 rows for the English subjects and 32 rows for the Japanese subjects. In both matrices, the rows represent subjects, and the 105 columns represent the pairs of the 15 emotion terms. The rows of these matrices are each standardized to have a mean of zero and a variance of one by subtracting the row mean and dividing by the row standard deviation. We refer to these row standardized rectangular matrices as standardized shape matrices and denote them by Z₁ and Z₂, for native English and Japanese speakers, respectively.

In this section, the analyses are based on the shape matrices as well as subject-by-subject correlation matrices obtained from them: namely, R_i = Z_iZ_i^T/M, for i = 1, 2. The methods that we illustrate on these matrices will be considered in the following order: comparing mean correlations, principal components analysis of the correlation matrices, and analysis of variance of the rectangular shape matrices. For now, we are using these statistics in a descriptive manner: that is, to characterize the similarity and differences within and between groups; however, we will mention some inferential approaches later.

The degree of similarity as measured by the mean correlations within a cultural group reflects the degree of knowledge of the group members. The mean correlations are easily obtained from the R_i by taking the mean of all the entries. The main diagonal of the R_i are ones that denote the correlation of each subject with themselves, and it is useful to denote by r̄_d the mean with the diagonal included and r̄ the case where the diagonal is excluded. In previous work, we (2, 4) demonstrated that an approximate estimate of the degree of shared knowledge characterizing the various portions of semantic structure may be obtained by making a few assumptions that are widely used in psychometrics (10) and that trace back to Spearman's work early in the century (11). The first assumption is that the magnitude of the mean correlation among a set of subjects indicates the extent to which a common shared pattern exists. The second assumption is that the correlation between two subjects, i and j, is the product of the correlation of each subject with the relevant shared cultural pattern (11), or the “truth”: that is, using “t” for the shared pattern, r_ij = r_itr_jt. The magnitude of the r_it for each subject may be interpreted as measuring his or her cultural knowledge. Of course, our confidence in these assumptions will rise as the mean magnitude of the correlations goes up and the variance among them goes down.

Given these assumptions, it follows that the square root of the average correlation within any given category of subjects (e.g., English) is an approximation of the average knowledge of the relevant cultural pattern among subjects within that group. This general approach is related to culture consensus theory (12–17); however, the present data are not appropriate for a formal process model of the cultural consensus theory (because we are using data derived from scaling and not the original response data, and there is a lack of independence among the 105 interpoint distances). Nevertheless, the results reported in this paper may be considered as approximate empirical estimates of cultural knowledge as defined in the more formally derived process models of cultural consensus (12–17).

We performed the calculations on the present data and obtained the following results. The square root of the mean correlation, r̄_d, among English subjects is 0.776 and among Japanese subjects is 0.779. As stated above, these figures may be interpreted as an estimate of the amount of knowledge the average subject shares with other subjects speaking the same language.

We now turn to principal components analysis (PCA) of the correlation matrices (18). We implement the PCA by performing a singular value decomposition of each correlation matrix. The result can be represented in a matrix product given by R = PDP^T, where P is an N × N matrix whose jth column contains the normalized characteristic vector associated with the eigenvalue, λ_j, and D is a diagonal matrix whose jth main diagonal entry is λ_j. We weight the eigenvectors by the square root of the eigenvalues to obtain the loading, 1_nj = p_nj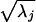. Under these conditions, the mean of the values of the first loading vector is comparable to the square root of the mean correlation reported in the paragraph above. One advantage of PCA over the other methods is that the loading value of the first principal component for each subject can be viewed as an estimate of the r_it corresponding to competence in the cultural consensus model (14, 15).

In the special case in which all correlations are equal and positive, PCA has a known relation to the mean correlation. In particular, the first eigenvalue is related to the mean correlation, r̄, by the following formula: λ₁ = 1 + (n − 1)r̄ (ref. 18, pp. 244–245). In cases in which the correlations are not equal but all positive, the relation is often a close approximation. Because our data matrices contain a small number of negative correlations, the formula does not hold exactly, but very good estimates are obtained: namely, 20.256 estimated vs. 20.121 actual eigenvalue for English and 19.813 estimated vs. 19.848 actual for Japanese.

Another approach to estimating the average knowledge of the subjects within a single culture involves an ANOVA design. Haggard (ref. 19, p. 152) proved in 1958 that, under specified conditions, the mean correlation among the rows of a matrix, such as one of our shape matrices, exactly equals the proportion of variance accounted for (R² or Eta²) in an ANOVA in which the columns constitute the levels of a single factor. The specified conditions are that the rows have been standardized to a mean of zero and a variance of one as they have been in our shape matrices.

To be specific, we can analyze each shape matrix, Z_i, by decomposing the total sum of squares given by S_T = Σ_n=1^N Σ_m=1^M (z_nm − z̄)² into the between sum of squares, S_B = N Σ_m=1^M (z̄_m − z̄)², and the within sum of squares, S_W = Σ_n=1^N Σ_m=1^M (z_nm − z̄_m)², where z̄ is the grand mean of all entries and z̄_m = 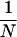Σ_n=1^N z_nm, the mean for item m. It is well known that, for any rectangular matrix of real numbers, such as our shape matrices, it is the case that S_T = S_W + S_B. In this framework, the variance representing knowledge on the part of the subjects is simply the proportion “explained” by differences in the column means: that is, Eta² = S_B/S_T. What Haggard (19) proved was that S_B/S_T = r̄_d. This can be seen by first noting that z̄ = 0, and M = Σ_m=1^M z_nm², for n = 1, … , N, from the row standardization of the shape matrices. Then, it is easy to compute

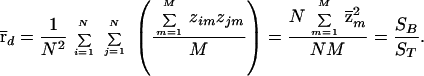Thus, the estimates from mean correlations, the mean of the first loading in PCA, and ANOVA are all numerically equivalent.

Table 1 presents empirical examples of how these equivalences work out for the English and Japanese subjects taken as separate cultures. The three methods give the same empirical results within rounding error, illustrating their equivalence. The substantive interpretation of the results indicates that the average English subject knows about 77.6% and the average Japanese subject knows about 77.9% of the semantic structure, defined as the four-dimensional representation of the emotion terms of which the first two-dimensions are illustrated in Fig. 1.

Table 1.

Estimates of mean knowledge of English (n = 33) and Japanese (n = 32) samples using three separate methods of analysis: ANOVA, PCA, and mean correlation

	English	Japanese
ANOVA
SW	2,085.018	2,039.057
SB	1,379.982	1,320.943
ST	3,465	3,360
R2 or Eta2	0.6017	0.6069
R or Eta	0.7757	0.7790
PCA
Mean of first eigenvector	0.7755	0.7787
Correlations
Mean of all correlations	0.6017	0.6069
Square root of mean	0.7757	0.7790

Comparing Similarities and Differences Between Cultures.

In the last section, we established the equivalence between mean correlations, the mean of the first loading in PCA, and ANOVA for estimating the average knowledge among subjects of a single culture. In this section, we illustrate the measurement of the similarities and differences between the English and Japanese subjects using mean correlations. Identical results may be obtained with PCA and ANOVA by using similar logic but will not be detailed here.

We begin by computing a 65 × 65 correlation matrix, R, representing the 33 English and 32 Japanese subjects. This matrix consists of four quadrants; the upper-left and lower-right quadrants consist of correlations among English subjects and Japanese subjects, respectively, and are identical to the R₁ (with a mean = r̄_d1) and R₂ (with a mean = r̄_d2) matrices of the last section. The upper-right quadrant and its transpose in the lower-left quadrant contain correlations between English and Japanese subjects: i.e., cross-language only. The mean correlation of these quadrants may be denoted by r̄_c. By following the same logic due to Spearman (11) as was done for the separate analyses of R₁ and R₂, we can postulate a common truth, t_c, and postulate that subject-by-subject cross language correlations, r_ij, are decomposed as r_ij = r_itcr_jtc. Then, the square root of this figure is the estimated knowledge common to both English and Japanese, the universal aspect. In the current study, the result is 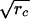= 0.631.

To estimate the culture-specific contribution, that is, the incremental knowledge shared by same-language speakers, we simply subtract this universal estimate from the mean of the two within-language knowledge estimates reported in the last section, where the means are weighted by sample size. This effectively partitions the knowledge into three portions: a between portion common to both English and Japanese (0.631), a culture-specific portion within a common language (0.146), and a portion representing sampling variability, any true individual variability, and error (0.223).

The fact that we have three methods that give equivalent answers to the problem of measuring similarities and differences among cultures increases our confidence that the measures are valid and reliable. In terms of the substantive issue of the semantic structure of emotion terms in our example, it is useful to summarize the results in terms of a pie chart as in Fig. 2. The use of such a graphic makes clear the relative amount of similarity and difference between subjects' knowledge.

Figure 2.

Relative contributions to knowledge of semantic structure from universally shared, culture specific, and sampling and error variance components.

Interpreting Similarities and Differences Between Cultures.

Of course, as the pie chart shows, the amount of shared knowledge between the Japanese and English subjects in this study is a function both of random error and the individual subjects' cultural knowledge. Further, it is bounded by how much the two cultures themselves share. To get an additional insight into the latter component that is relatively free of random error, it is useful to return to Fig. 1, which reports the mean placements in each group. Note that, on this measure, most terms are in close agreement between languages, although a few terms appear to be more widely separated, especially anxious, bored, and shame. The term anxious has a more unfavorable meaning in Japanese than it does in English, whereas the term bored is more active in meaning in Japanese than in English. The term shame is more unfavorable in English than in Japanese. An overall comparison of the similarities between the two cultures is possible by interpreting the analyses reported earlier by PCA that provided estimates of the r_it indicating each subject's knowledge of their own culture. Because averaging substantially reduces the error variance in the individual subjects' distances, we could interpret the “t” to be approximated by the distances between pairs of mean placements in Fig. 1, obtained by taking the means of the columns in the shape matrices separately for the English and Japanese groups. In this interpretation, an estimate of the relationship between the two cultures would be the correlation over pairs of the distances for the English and Japanese terms in the figure. That correlation is 0.658, which is comparable to the 0.631 figure obtained earlier by taking the square root of r̄_c. Of course, if we accept the mean placements of the terms in Fig. 1 as a proxy for the cultural truth, it is possible to estimate the r_it directly by correlating each subject's distance against the distances based on the mean placements. In the current study, this approach very closely matched the r_it estimated from PCA.

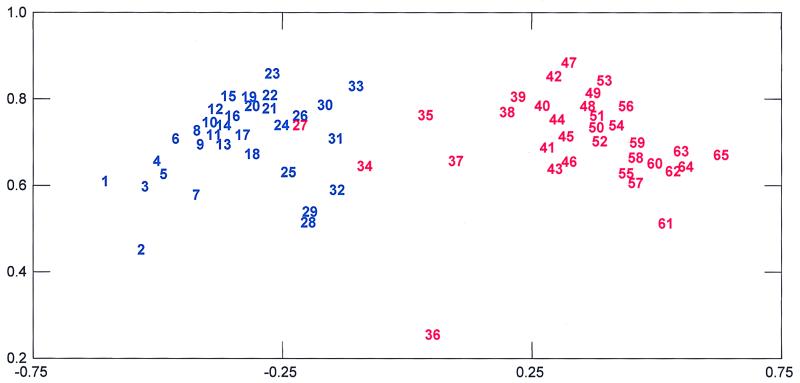
Although the two structures in Fig. 1 appear fairly similar, different observers may vary in the extent to which they would emphasize the differences or similarities between the pictures. For this reason, it is useful to gain additional perspective on the differences between the two cultures. This is facilitated by examining more closely the results of the principal components analysis. In the previous discussion, we utilized only the information in the first principal component. By analogy with concepts in cultural consensus analysis (12–17), this first component was interpreted as the amount of knowledge shared by each subject with the presumed cultural norm. In general, additional information on individual differences can be obtained by looking at the variation among individuals on the succeeding principal components. These dimensions may contain information on differences among subjects from different cultures, where the cultures have distinct configurations. In the present case, the second component contains the English–Japanese difference. Fig. 3 presents a plot of the first and second components of all 65 subjects. In Fig. 3, the vertical dimension represents the first principal component, and we interpret it as the amount of knowledge each individual has of the overall shared configuration. The horizontal dimension reflects the difference between English and Japanese subjects. The subjects have been ordered on the basis of the second principal component. The order can be read from Fig. 3, beginning with the smallest value (subject 1) on the left and ending with the largest value (subject 65) on the right. The order of the subjects is, in effect, from the “most English-like” to the “most Japanese-like.”

Figure 3.

First two principal components plot with the vertical axis representing each subjects' knowledge and the horizontal axis representing the difference between English-speaking subjects (blue) and Japanese-speaking subjects (red).

Examination of Fig. 3 reveals an obvious difference among the English and Japanese subjects. Subjects from each culture tend to cluster most closely together around distinct locations, the English on the left and the Japanese on the right. There is only one subject that seems misplaced; number 27 is a Japanese subject who is more similar to the English pattern than to the Japanese. The most extreme subject on the English end of the scale is number 1 whereas the most extreme subject on the Japanese end is number 65. This dimension captures the differences in the semantic structure of emotion terms as displayed in Fig. 1. The main differences are due to the placements of the three terms that were judged differently by the two cultures: namely, anxious, bored, and shame.

On the vertical dimension that represents knowledge, most of the subjects are above 0.6. The most apparent exception is subject 36, a Japanese subject with very low knowledge. Subject 61 is another Japanese with fairly low knowledge. Subject 2 is the lowest English subject with respect to knowledge. Subjects 28 and 29 are other English subjects with low knowledge. Overall, subjects tend to have fairly low variability on the knowledge dimension, a reflection that cultural knowledge of the semantic structure aspect of language is highly shared.

Our final suggestion for obtaining an overall visual representation of the similarities and differences among English and Japanese subjects' shared knowledge of the semantic structure of emotion terms is to represent the subject-by-subject correlation matrix coded with colors varying from light to dark. In Fig. 4, the subjects are again ordered on the basis of the second principal component proceeding from subject 1 in the upper-left corner to subject 65 in the lower-right corner of the figure. Because we are representing a square correlation matrix, the figure is symmetrical about the diagonal of ones (because each subject correlates perfectly with self), and each row is identical with its corresponding column. In the figure, the darker colors represent higher correlations and the lighter colors lower correlations (the few negative correlations were set to zero).

Figure 4.

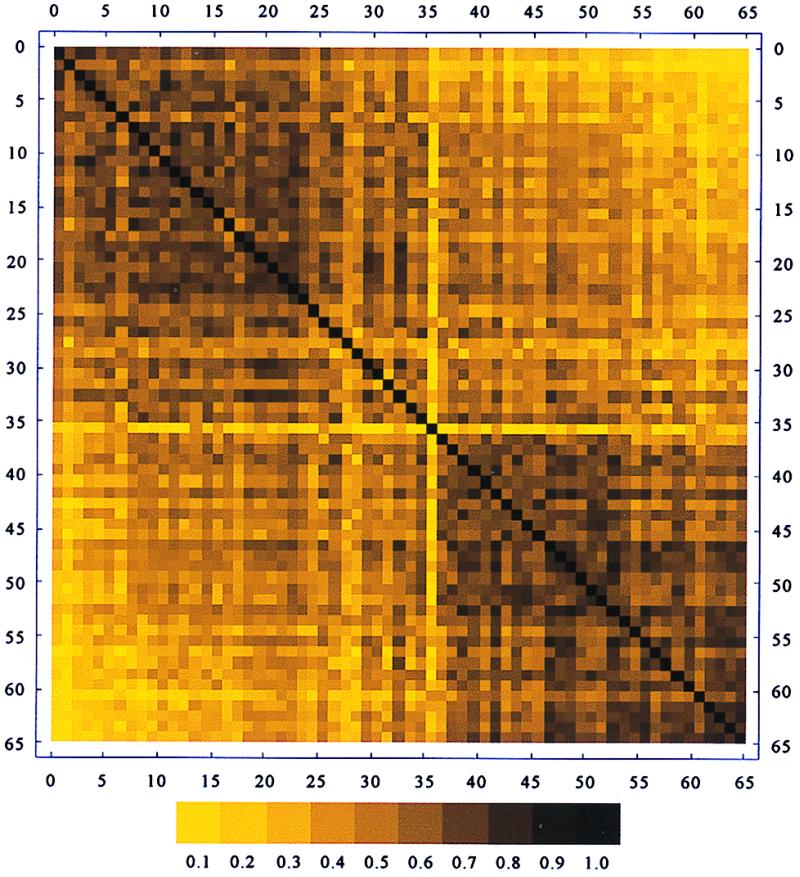
Color-coded correlation matrix for 65 subjects (ordered as in Fig. 3, beginning with subject 1 in upper-left corner), with darker colors representing higher correlations.

The first overall impression of Fig. 4 is the clear-cut visual separation of the English subjects in the upper-left from the Japanese subjects in the lower-right. Because the information in the rows and the columns is identical due to the symmetry of the correlation matrix, it is easiest to focus on the rows of the figure. There are various patterns visible that might not have emerged in the previous representations. Most obvious is the low knowledge of Japanese subject 36 (noted in Fig. 3), reflected in uniformly low correlations indicated by lighter colors across the whole row compared to other subjects. Another detail that emerges is that a subject may have fairly low knowledge and still be extreme on the English–Japanese dimension. Subject 2 has the lowest knowledge of any English subject but is next most extreme toward the English pattern. The Japanese subjects seem to form a more homogeneous grouping with smaller internal variance (with the obvious exceptions of subjects 36 and 27) than the English subjects, as reflected by the generally lighter cast of subjects in the middle of the figure.

Tests of Significance.

In the previous sections, we confined ourselves to the descriptive use of statistics. Inferential use of statistics were not needed to detect the difference between English and Japanese semantic structures because the separation was so complete. In other situations, the results may be ambiguous and a test would be appropriate. Some standard tests, such as the analysis of variance, are not legitimate for inferential use because the rows in the standardized shape matrix (65 × 105) were derived from interpoint distances that are not independent of each other. Rao and Suryawanshi (9) discuss tests of significance and suggest various approaches, including picking a subset of the k (k − 1)/2 interpoint distances. They point out that only 2k − 3 distances are necessary to recover all k (k − 1)/2 distances (ref. 9, p. 12134). They present methods for testing whether populations differ in shape or in size (where their first dimension, “size” corresponds to our knowledge).

Alternative methods exist, and we mention and illustrate examples using our present data. Quadratic assignment (20–21) provides an appropriate nonparametric test for whether within-culture correlations are different than between-culture correlations. Resampling methods (22–23) may be used for the same purpose. In the present case, we ran 10,000 trials testing for within- and between-language correlation differences and found no case that gave as large a value for Hubert's Gamma (20) as did the observed data, indicating a significant difference between English and Japanese subjects.

The PCA provides quantifications that may be treated as interval level data for tests of significance using standard parametric methods. For example, the first component corresponds to a shared knowledge dimension. A t test on the first principal component for English and Japanese shows that the observed difference is not significant, with t = 0.03 and P = 0.98. In contrast, a test on the second principal component, representing the distinction between English and Japanese structures, as can be inferred from Fig. 3, is highly significant, with t = 16.88 and P < 0.0001.

Discussion and Implications.

The methods and substantive results presented in this paper relate to a controversy in anthropology, linguistics, and psychology over semantic universals. There is general agreement on the idea that all languages classify various domains of natural kinds, such as animals, plants, colors, emotions, etc., in characteristic ways. The conflict is over whether each language is semantically arbitrary relative to every other language or whether there are universal constraints that result in fundamental similarities in the semantic structure of all languages. These constraints would include such things as shared cognitive and sensory apparatus characteristic of humans, inherent features of the items being classified, and the interaction between the two.

Extreme relativity accurately characterizes the majority position among linguists and anthropologists concerning the semantic structure of the domain of emotion terms. This viewpoint maintains that languages have complete freedom in the way they structure the emotions and that this leads to incommensurability among languages (24–25). This view is maintained despite several empirical studies that demonstrate widespread similarity among languages that are unrelated to each other (2, 4, 26, 27).

In our view, the extent of the polarization has prevented an objective approach to investigating the similarities and differences among semantic structures in different cultures. As in most polarized arguments, the solution resides somewhere between the extremes. Clearly, not all languages are identical in the way they classify the various domains. Consider, for example, the t value of 16.88 reported above between English and Japanese subjects on the second principal component. This result might support the argument that cultures are different and suppress any search for similarities. However, as large as this difference may appear, it does not logically imply that there are no similarities. The magnitude of the similarities is an empirical question. Similarities in the two structures are reflected in the average shared knowledge between an English and Japanese subject of 0.63. When both similarities and differences are properly characterized and quantified, the two structures are more similar than different.

In this paper, we have demonstrated that a variety of statistical methods may be integrated in an approach that allows a reasonable characterization of the structure within each language as well as precise quantitative estimates of the similarities and differences in the semantic structures of different languages. This paper should make clear that taking one of the polar positions in the universality vs. cultural relativism debate is unwarranted. The real question now should concentrate on measuring how similar and how different.

It should also be noted that the various methods (i.e., mean correlations, PCA, ANOVA, and graphics) are applicable to a wide range of problems beyond those treated in this paper. For example, Weller (28, 29) has applied some of these methods to the comparison of a variety of medical beliefs among four widely separated Spanish-speaking communities. Any cross-cultural or comparative study in which subjects are characterized by a vector of information would lend itself to the use of these methods.

Abbreviation

PCA

principal components analysis