Abstract
Membrane-associated proteins are likely to contribute to the regulation of the phase behavior of mixed lipid membranes. To gain insight into the underlying mechanism, we study a thermodynamic model for the stability of a protein-decorated binary lipid layer. Here, proteins interact preferentially with one lipid species and thus locally sequester that species. We aim to specify conditions that lead to an additional macroscopic phase separation of the protein-decorated lipid membrane. Our model is based on a standard mean-field lattice-gas description for both the lipid mixture and the adsorbed protein layer. Besides accounting for the lipid-protein binding strength, we also include attractive lipid-lipid and protein-protein interactions. Our analysis characterizes the decrease in the membrane’s critical interaction parameter as a function of the lipid-protein binding strength. For small and large binding strengths we provide analytical expressions; numerical results cover the intermediate range. Our results reiterate the crucial importance of the line tension associated with protein-induced compositional gradients and the presence of attractive lipid-lipid interactions within the membrane. Direct protein-protein attraction effectively increases the line tension and thus tends to further destabilize the membrane.
INTRODUCTION
Peripheral adsorption of proteins (as well as for peptides) onto mixed lipid membranes is an ubiquitous phenomenon in cellular biology. Typically, proteins bind preferentially to one (or more) lipid species, while there is no preferential interaction with other lipids. Among a plethora of examples for the dependence of protein binding on membrane composition are phospholipase A2,1, 2 lysozyme,3 α-synuclein,4 cytochrome c,5 various cytoskeletal proteins,6 and antimicrobial peptides.7 A direct consequence of preferential binding is the sequestration of the favored lipid species by the proteins. That is, in the vicinity of each individual protein the membrane composition is shifted from the average value towards that preferred by the protein. The degree of sequestration depends on the differences in affinity of the protein for the various lipid species. In some cases the sequestration may be small so that it is difficult to detect;8 yet, in other cases it has been observed experimentally8, 9, 10, 11 and in molecular simulations.12
Even in the absence of associated proteins, lipid membranes are able to form lateral domains or to macroscopically phase separate. Most of the current interest to study domain formation in model membranes is motivated by the discovery of lipid rafts in biological membranes and their various functional roles.13, 14 It is well documented that many binary lipid membranes exhibit nonideal mixing properties.15, 16, 17 In the presence of cholesterol, appropriate ternary lipid mixtures undergo lateral phase separation.18, 19 For a number of mixtures lipid-lipid interaction parameters have been extracted based on fluorescence resonance energy transfer, by means of cross-linking of individual lipids, and heat capacity measurements (reviewed in Ref. 20).
An unresolved question is how proteins modulate the phase propensity of a mixed bilayer. As discussed recently, proteins may participate in the process of domain formation actively through attractive protein-protein interactions or passively by interacting preferentially with one lipid species or with the domain interface.20, 21 Clustering of proteins within lipid domains (or at domain boundaries) has been suggested based on experimental results for a large number of systems, including lipid monolayers,22, 23 model membranes,3, 4, 24, 25, 26, 27, 28, 29 and lipid mixtures from the plasma membrane,30 the latter at sufficiently low temperature. There is also experimental evidence that proteins are able to induce phase separation in both model31, 32 and biological33 membranes. Yet, the mechanisms how membrane-associated proteins influence domain formation and phase behavior of the lipid bilayer remain elusive. Current theoretical approaches suggest a role of immobile proteins in the restriction of domain sizes,34 domain formation through wetting of proteins by lipids,35, 36 and a dynamic membrane remodeling through nonequilibrium lipid transport and interactions with membrane proteins.37 Other models are based on inclusion-induced elastic membrane deformations.38, 39, 40 Here, proteins are described as rigid inclusions that induce elastic deformations in the host membrane. If that deformation is coupled energetically with one lipid species, an inclusion-induced macroscopic phase transition can result. Still another mechanism, based on the experimentally observed repartitioning of streptavidin protein coats from the liquid-disordered to the liquid-ordered phase upon forming an ordered structure, was suggested by Manley et al.28 Here, protein ordering is associated with an entropic penalty that is smaller in the liquid-ordered phase and thus may drive the repartitioning. This mechanism could contribute, quite generally, to the tendency of proteins to repartition into more ordered phases upon their oligomerization.41 Finally, Monte Carlo simulations9, 35, 42, 43 have played a pivotal role in studying the ability of proteins (and also flexible polypeptides44, 45) to induce lipid sequestration and domain formation. We note that Monte Carlo simulations typically employ a lattice model for the mixed membrane. For example, Almeida et al.20 recently reviewed the quantitative determination of lipid-lipid interaction parameters by modeling fluorescence measurements of protein-induced membrane reorganization through Monte Carlo simulations. As we shall see below, our present work is based on a similar lattice model, analyzed through mean-field level calculations of phase boundaries.
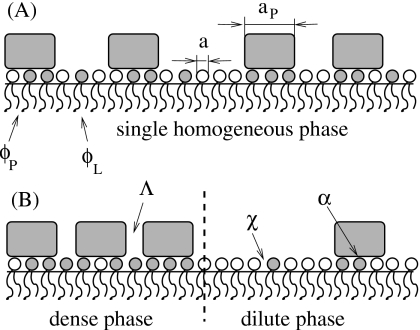
Proteins that locally sequester lipids of one species do not necessarily induce phase separation of the host membrane. The sequestration is a local process that must be distinguished from macroscopic global phase separation. Figure 1 displays schematically two protein-decorated lipid layers; both sequester lipids underneath the proteins but only layer (B) exhibits macroscopic phase separation whereas layer (A) does not. A theoretical study46 has addressed the question of what interactions are needed to render a mere sequestration into macroscopic phase separation. It was shown that the presence of attractive interactions among lipids of the same species in the host membrane can be sufficient. In this case, phase separation is driven solely by the line tension between the two regions of different compositions (that at the protein adsorption sites and that of the bare membrane). The line tension between coexisting fluidlike macroscopic phases in a lipid membrane is on the order of ≈1 pN.47 It has been suggested to result (at least partially) from the thickness mismatch between the coexisting phases.48, 49 More generally, the line tension in a nonideally mixed binary fluid simply results from compositional gradients.50 Thus, if the host membrane exhibits attractive lipid-lipid interactions, then a line tension appears as a consequence of lipid sequestration at the boundary between a protein adsorption site and bare membrane. Reduction in the line tension contribution is the driving force for protein clustering and phase separation. In a related study51 detailed electrostatic calculations were presented for a number of generic model proteins adsorbed onto a mixed membrane, corroborating the importance of the line tension for the ability of proteins to induce membrane phase separation.
Figure 1.
Schematic illustration of (A) local lipid segregation vs (B) global phase separation. In the former case, proteins (shaded rectangles) bind to a preferred lipid species (lipids with shaded headgroups) without causing the formation of large domains. Even though the membrane compositions ϕP and ϕL,within the protein-covered regions and bare membrane, respectively, may differ from each other, the membrane remains homogeneous on a macroscopic scale. In the latter case, there is macroscopic phase separation into a protein-dense and protein-dilute phase. The ability of proteins to induce phase separation depends on the lipid-protein binding strength (α), lipid-lipid interaction (χ), and protein-protein interaction (Λ). The only structural parameter that enters our model is the protein’s number of binding sites or, equivalently, protein-to-lipid size ratio σ=aP∕a, where aP and a denote the cross-sectional areas per protein and lipid, respectively.
We note that the above-mentioned previous modeling studies46, 51 have focused on indirect membrane-mediated interactions between adsorbed proteins. That is, the presence of attractive interactions between membrane lipids (and the corresponding line tension) can be sufficient to induce phase separation. The influence of direct attraction between the adsorbed proteins on the stability of the membrane was not considered. The objective of the present work is thus to include direct protein-protein interactions into the model of Ref. 46. Specifically, we shall employ a two-state model (see also Ref. 52) where lipids can reside either at the protein adsorption region or within the bare (protein-free) membrane. The model is investigated on the mean-field level, thereby allowing for (i) a preferential binding of one lipid species with adsorbed proteins, (ii) lipid-lipid attraction within the host membrane, and (iii) direct protein-protein attraction. Below, we shall characterize these interactions by the three parameters, α (lipid-protein), χ (lipid-lipid), and Λ (protein-protein). In the limits of both small and large lipid-protein binding strength α, we shall derive simple analytical expressions that show how attractive interactions among lipids and among proteins can act together to destabilize the composite membrane.
It should be noted that the model employed in the present study is a minimal model; it is simple enough to reveal a number of analytical results and a clear understanding of the underlying physics. At the same time it employs various approximations such as its lattice character, mean-field treatment, and the neglect of membrane-mediated elastic forces. The latter ones act also between proteins adsorbed on a single-component lipid membrane and have been studied extensively in that context.53
THEORY
We consider a large planar lipid layer of lateral area A=Na that contains N lipids, each of cross-sectional area a. The lipid layer is composed of two different lipid species with molar compositions ϕ and 1−ϕ. Let a number M of proteins be peripherally adsorbed on the lipid layer. The extent of protein coverage on the lipid layer can be characterized by the fraction θ=M∕Mmax, where Mmax is the maximal number of adsorbed proteins. Note that usually the cross-sectional area per adsorbed protein aP will be considerably larger than a, implying the size ratio σ=aP∕a⪢1. In the following we analyze a simple two-state model that is based on a lattice-gas description of an incompressible fluid. Here, both the lipid layer and the adsorbed proteins are described as two energetically coupled lattice gases. For simplicity, we treat the number of protein adsorption sites to be dictated by area conservation, aPMmax=aN, implying Mmax=N∕σ. In the two-state approximation lipids can reside in only two energetically distinct states, within either the bare lipid layer or protein-covered regions. We denote the molar compositions corresponding to these two states by ϕL and ϕP, respectively. On the mean-field (Bragg–Williams) level, we write for the total free energy f=F∕N of the protein-decorated lipid layer, measured per lipid,
| (1) |
where here and in the following all energies are expressed in units of the thermal energy kBT. In Eq. 1, the functions fP(ϕP) and fL(ϕL) denote the free energies per lipid in protein-covered and protein-free regions of the lipid layer, respectively. The function fpr(θ), appearing in the third term of Eq. 1, accounts for the free energy contribution of the adsorbed protein layer, measured per protein. The additional factor 1∕σ converts to measuring f in units of “per lipid.” Finally, the last term in Eq. 1 describes the additional line tension between the bare lipid layer and its protein-covered regions. The presence of this term is a consequence of the compositional changes in the lipid layer;50 within the present two-state model these changes are expressed in terms of the compositional difference Δϕ=ϕP−ϕL between the protein-covered and protein-free regions. Moreover, the line tension contribution is proportional to the total length of the boundary between the two regions and thus, on the mean-field level, contains the prefactor θ(1−θ). Note that λ is a material constant that is independent of ϕ and θ.
The free energy f=f(ϕ,θ) [see Eq. 1] is a function of the two independent compositional variables ϕ and θ. Note that Δϕ=Δϕ(ϕ,θ) is not an independent variable but must be determined from the equilibrium condition ∂f∕∂Δϕ=0. Hence, the equation describing breakdown of local thermodynamic stability (the spinodal equation)
| (2) |
depends on the second derivatives of f with respect to the two degrees of freedom ϕ and θ. Even without specifying the structure of the functions fP(ϕP), fL(ϕL), and fpr(θ) one may transform Eq. 2 into the equivalent expression
| (3) |
The derivation of Eq. 3 is sketched in the Appendix0. Note that this form of the spinodal equation is expressed entirely in terms of the second derivatives of the unspecified functions fP(ϕP), fL(ϕL), and fpr(θ), and as a function of Δϕ. That is, no derivative of Δϕ is involved, which will prove valuable for a numerical determination of the spinodal (see below). We also remark that in the limit of vanishing line tension, λ→0, Eq. 3 is fulfilled if or . Here, the stability of the lipid and adsorbed protein layers is independent of each other. In the opposite limit, that of large line tension (λ→∞), all compositional changes are suppressed, implying Δϕ=0 in Eq. 3. Hence, in this case the lipid layer remains laterally homogeneous on a microscopic scale.
We note that the free energy in Eq. 1 has been considered in a previous study46 subject to the condition of fixed chemical potential μP=∂f∕∂θ of the membrane-adsorbed proteins. Clearly, by appropriately choosing μP we may adjust the protein coverage θ=θ(ϕ,μP) to any desired value. The relevant thermodynamic potential is then . The corresponding spinodal can be written in the form
| (4) |
as previously presented in Ref. 46. The Appendix0 of the present work outlines the derivation of Eq. 4.
Let us specify the functions fP(ϕP), fL(ϕL), and fpr(θ). In order to include, on the mean-field level, interactions within the lipid layer, between the proteins, and between lipids and proteins, we chose
| (5) |
where fmix(x)=x ln x+(1−x)ln(1−x) is the free energy (per site of a lattice gas) of ideal mixing. The free energy of the bare protein-free lipid layer fL(ϕL) is given by the familiar Bragg–Williams expression for an incompressible binary lattice gas with nearest-neighbor interactions where the effective interaction strength is characterized by the parameter χ. Note that χ depends on the mutual molecular interactions ω11, ω22, and ω12, among and between the two lipid species, through χ=z[ω12−(ω11+ω22)∕2], where z is the coordination number of the lattice. The spinodal of a bare lipid layer is χ=1∕[2ϕ(1−ϕ)], implying the critical interaction parameter χc=2 and the corresponding critical composition ϕc=1∕2. That is, for χ>χc, there is a compositional range where the membrane is unstable with respect to macroscopic phase separation.
The second equation, that for fP(ϕP), is identical to the one for fL(ϕP) apart from an additional favorable interaction of the protein with one lipid species. Assuming that each bound high-affinity lipid contributes the same amount to the protein binding energy renders the interaction term in this equation proportional to ϕP, the composition at the protein adsorption site. The prefactor α>0 (the binding strength per high-affinity lipid, measured in units of kBT) thus provides the driving force for the adsorption. We note that our model treats the protein-to-lipid size ratio σ to be equal to the number of lipid-protein binding sites, thus rendering B=ασ the maximal protein adsorption strength (which becomes equal to the actual protein adsorption strength in the limit of complete lipid sequestration, ϕP→1).
Finally, the free energy fpr(θ) of the adsorbed proteins is again given by the Bragg–Williams expression for a binary lattice gas. (Alternative expressions based on the van der Waals gas or scaled particle theory yield more involved expressions for the mixing entropy of membrane-adsorbed proteins5, 54—using them would not alter the physical mechanism of protein-induced phase separation studied in the present work.) The interaction strength Λ that appears in fpr(θ) accounts for direct interactions between the adsorbed proteins. We shall assume that these interactions alone are insufficient to induce phase separation of the adsorbed protein layer, implying Λ<2. This assumption focuses our attention on the influence of the lipid layer in inducing lateral phase separation. We note that the present study extends previous work46 by including the protein-protein interaction constant Λ. We also note that our assumption of a constant Λ will not be fulfilled if protein conformation changes as function of coverage θ. Yet, even with constant Λ the total interaction between proteins includes not only a direct but also an indirect membrane-mediated contribution, which depends on membrane composition and protein coverage as shown below in Eq. 11.
To sum up, we have introduced in Eq. 5 mean-field expressions for the functions fL(ϕL), fP(ϕP), and fpr(θ). They involve the three material constants χ, α, and Λ, describing the strengths of lipid-lipid, lipid-protein, and protein-protein interactions, respectively.
The line tension term in Eq. 1 represents the excess free energy penalty due to the presence of compositional changes within the lipid layer. Our two-state model involves compositional changes (of magnitude ∣Δϕ∣) only at the boundaries between the bare lipid layer and the protein-covered regions. The total length of all boundaries is on the mean-field level (where is the spatial extension of a single protein). On the other hand, the lipid’s excess free energy per unit length of the boundary—the line tension—can be written as , where b is a numerical prefactor and a is the spatial extension of a single lattice site (which represents a lipid). Note that the line tension depends on the compositions of the two phases through Δϕ; it vanishes for Δϕ→0 as would be the case when approaching a critical point. The line tension contribution to the total free energy per lipid is thus . Comparing this expression with the last term in Eq. 1 yields
| (6) |
We note that the numerical prefactor is generally b≈1; its exact magnitude depends on the geometry of the protein species or, equivalently, on the curvature of the domain boundary. More specifically, it is b=1 for a perfectly straight boundary. That value would somewhat increase for a curved boundary (as will be the case for finite-sized proteins) and would decrease if the constraint of a sharp, steplike, compositional change between bare lipid layer and protein-covered region was relaxed. In the present work it is convenient and sufficient to simply use b=1.
Let us finally verify consistency of the expression for the line tension, , with experiment. For example, Tian et al.47 obtained Ft∕L≤3.3 pN, inside the fluid-fluid coexistence region of a ternary lipid mixture containing cholesterol. That value was observed to decrease toward 0 when approaching the critical point. Using reasonable values such as a=0.65 nm2, χ=1, b=1, our present model predicts Ft∕L=4(Δϕ)2 pN, in agreement with both the magnitude and pronounced composition dependence measured by Tian et al.47
RESULTS AND DISCUSSION
Equation 1 together with Eqs. 5, 6 define the free energy f=f(ϕ,θ;χ,α,Λ) as functions of the two degrees of freedom ϕ and θ, and in terms of the molecular interaction constants χ, α, and Λ. The region of spinodal stability within the ϕ, θ-phase diagram is determined by Eq. 2 [or, equivalently, by Eq. 3 or Eq. 4]. A spinodal curve will only exist for χ<χc. Any choice χ>χc corresponds to a membrane that is stable with respect to lateral phase separation. For the specific choice χ=χc the spinodal degenerates to a point ϕc, θc in the ϕ, θ-phase diagram. The corresponding critical interaction parameter χc=χc(α,Λ) can thus be expressed in terms of α and Λ. Recall, that for a bare (protein-free) membrane χc=2. An interesting question is thus to what extent protein adsorption (α>0) is able to reduce χc below the value of 2. For Λ=0 this question has been addressed in previous work.46 The main objective of the present study is to study the influence of direct protein-protein interactions as expressed through Λ. The full relation χc=χc(α,Λ) can only be calculated numerically (see below). However, in the limits of small and large lipid-protein binding strengths α, analytical solutions are available.
In the limit of small binding strength (α⪡1) the solution of the equilibrium condition ∂f∕∂Δϕ=0 for the compositional difference Δϕ=Δϕ(ϕ,θ) can be calculated, yielding
| (7) |
Using this expression in the spinodal equation, we obtain for the critical interaction parameter
| (8) |
The corresponding critical compositions are ϕc=θc=1∕2. Equation 8 shows that adsorbed proteins are able to reduce the critical interaction parameter χc of the lipid layer even in the limit of small α, if direct protein-protein attraction (Λ>0) is present.
The other limit, that of large interaction strength α⪢1, is most conveniently analyzed for fixed chemical potential μP of the membrane-adsorbed proteins, see Eq. 4. In this case, the coverage θ adjusts until all lipids that interact favorably with the proteins are localized within the protein-covered regions. This implies ϕL=0 and θϕP=ϕ. Hence, dθ∕dϕ=1∕ϕP and Δϕ=ϕP. Equation 4 now is equivalent to
| (9) |
and adopts its minimum for ϕP=1 and θ=1∕2. Thus, for α→∞ the critical point is specified by ϕc=θc=1∕2 and
| (10) |
In the special case of vanishing protein-protein interactions Λ=0, this coincides with the previously derived result .46 The presence of direct protein-protein attraction further destabilizes the membrane.
For intermediate α the critical interaction parameter χc must be determined numerically. This is most conveniently accomplished using Eq. 3 because no derivatives of Δϕ(ϕ,θ) appear in that equation. Specifically, we first determine Δϕ from solving the equilibrium condition ∂f∕∂Δϕ=0. With that, we minimize the spinodal χ=χ(ϕ,θ) in Eq. 3 with respect to ϕ and θ. The minimum specifies the critical interaction parameter χc and the corresponding critical compositions θc and ϕc, for any given α and Λ.
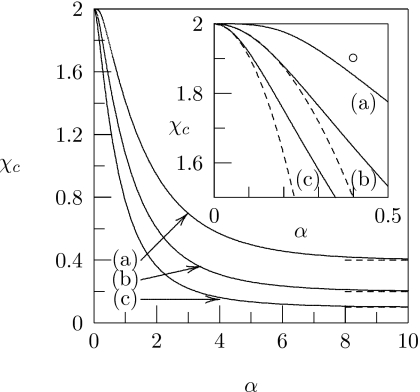
Figure 2 shows numerical results for χc as a function of α; the three different curves correspond to different choices of Λ. All curves are calculated for σ=25. The prediction for large α according to Eq. 10 is indicated by the corresponding horizontal dashed lines. The inset of Fig. 2 redisplays the small-α region and shows [dashed lines for curves (b) and (c)] χc(α) according to the analytical result for small α, see Eq. 8. The numerical results confirm the trend predicted by the analytical expressions in the limits of small and large α. Direct protein-protein attraction further destabilizes the membrane.
Figure 2.
The critical interaction parameter χc plotted as a function of α. The different curves correspond to (a)Λ=0, (b) Λ=1.0, and (c) Λ=1.5. In all cases σ=25. Dashed lines indicate the approximation for large α in Eq. 10. The inset shows the same graphs for small α. Here the dashed lines correspond to the limiting behavior for small α according to Eq. 8. The open circle corresponds to the parameters used to calculate the phase diagrams in Fig. 4.
Let us discuss Fig. 2. As reported previously,46 protein-induced phase separation of the lipid bilayer does not require the presence of direct protein-protein interaction. Indeed, even for Λ=0 the critical membrane interaction parameter χc is reduced below its bare-membrane value χc=2; see curve (a) in Fig. 2. The reason that phase separation can occur even in the absence of direct protein-protein interactions is the line tension contribution to the membrane’s free energy—the last term in Eq. 1. That is, adsorbed proteins induce a compositional difference Δϕ between the protein-covered and protein-free regions. The corresponding energy penalty can be diminished by protein clustering (thus reducing the total length of the boundary between protein-covered and protein-free regions). Hence, phase separation of the protein-decorated lipid layer is—for Λ=0—mediated entirely by the lipid’s line tension. We note that the role of the line tension contribution can also be illustrated by setting λ=0 in Eq. 1. The result for the critical membrane interaction parameter is then χc=2, irrespective of Λ and α. Thus, in the absence of line tension (λ=0), protein adsorption does not affect the stability of the underlying lipid layer. The presence of direct protein-protein attraction, 0<Λ<2, adds another energy penalty in addition to the line tension contribution of the membrane, which leads to a further reduction in χc. Indeed, both the lipid’s line tension contribution in Eq. 1 and the protein’s nonideal mixing contribution in fpr(θ) [see Eq. 5] provide terms ∼θ(1−θ). The excess free energy per unit length L of the boundary between the bare lipid layer and the protein-covered region is thus
| (11) |
which explicitly shows the two contributions. In particular, because of Δϕ=Δϕ(ϕ,θ) the line tension depends on lipid compositions and protein coverage.
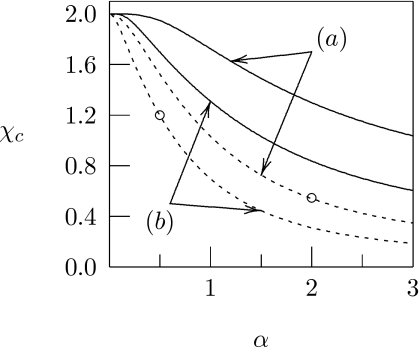
Increasing the number of binding sites σ on the protein reduces the stability of the membrane. This can be seen from our analytical expressions, Eqs. 8, 10, in the limits of small and large α, respectively. Figure 3, which shows χc=χc(α) for different combinations of σ and Λ, corroborates this behavior for intermediate α. Increasing the number of binding sites σ on the protein, while conserving the maximal adsorption strength B=ασ, does not usually (unless α⪢1) reduce χc, but it yields a larger slope . For example, compare the behavior of χc at the points indicated by the two open circles in Fig. 3. Both cases correspond to the same maximal adsorption strength B=18. The larger protein species (σ=36 and α=0.5) implies a more stable membrane but increased sensitivity of χc with respect to changes in α. This larger sensitivity may be one advantage of having many weak (instead of a single or a few strong) binding sites of a protein with membrane lipids. Many weak binding sites increase the impact of small variations in lipid binding strength on lateral membrane organization.
Figure 3.
The critical interaction parameter χc plotted as a function of α. Curves marked (a) and (b) correspond to σ=9 and σ=36, respectively. Solid curves are calculated for Λ=0, dashed curves for Λ=1.5. The two open circles mark the critical interaction parameters for Λ=1.5 at fixed maximal adsorption strength B=18, calculated for α=0.5 and α=2, see discussion in the text.
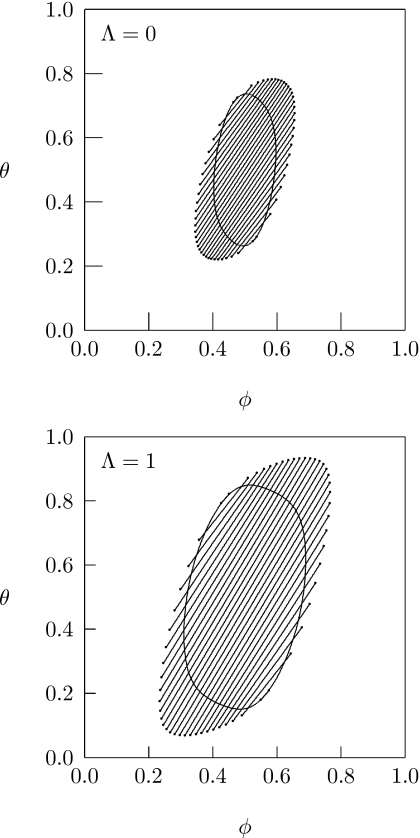
So far, our analysis has only addressed the behavior of the critical interaction parameter χc. For any χ>χc the protein-decorated lipid layer is unstable in a certain region within the ϕ, θ-diagram. Stronger direct protein-protein attraction increases the size of that region. As an illustration, Fig. 4 presents two phase diagrams, both calculated for χ=1.9, α=0.4, and σ=25. At this particular point (marked by a circle in the inset of Fig. 2) it is χ>χc for any choice of Λ (with Λ>0). The two phase diagrams in Fig. 4 correspond to the specific values Λ=0 and Λ=1. Displayed are the spinodal lines, which represent solutions of Eq. 2, and a number of tie lines. The tie lines correspond to solutions of the four familiar coexistence equations
| (12) |
for the two points ϕA, θA and ϕB, θB [with fA=f(ϕA,θA) and fB=f(ϕB,θB) and given ϕ and θ for any given tie line]. Comparison of the two phase diagrams in Fig. 4 corroborates our notion of reduced stability of the protein-decorated lipid layer in the presence of direct protein-protein attraction.
Figure 4.
Phase diagrams for Λ=0 (top) and Λ=1 (bottom). In both cases χ=1.9, α=0.4, and σ=25. (The points χ=1.9 and α=0.4 are marked in the inset of Fig. 2 by an open circle.) The closed loops correspond to the spinodal lines. The endpoints of the tie lines form the binodal region.
Let us discuss the context of our present model and its possible implications for the interpretation of experimental results. As mentioned in Sec. 1, protein-induced elastic membrane deformations provide an alternative theoretical concept to explain lateral remodeling of lipid membranes. These models account for proteins that impose elastic deformations onto the mixed host membrane. Examples include transmembrane proteins that have a conelike shape,55 a mismatch in hydrophobic thickness with respect to their host bilayer,56 or are incorporated into a membrane that is subject to substantial bending deformations.57 Similar models have also been applied to mixed membranes.36, 38, 39, 40 Note that nonelastic interactions are usually ignored in order to extract elasticity-based physical mechanisms. Our present model adopts a complementary approach. It ignores elastic deformations but accounts for specific interactions (lipid-lipid, lipid-protein, and protein-protein). As we demonstrate in the present work, membrane-mediated protein-protein interactions may be strong enough to induce macroscopic phase separation, even in the absence of elastic membrane deformations. Of course, the presence of elastic membrane deformations may further enhance the tendency to phase separate.
Our model is likely to be relevant in a number of situations. First, membrane-matching transmembrane proteins and peripherally adsorbed proteins are unlikely to evoke significant elastic deformations. For example, membrane reorganization induced by the C2 protein motif in various peripheral proteins has been modeled using Monte Carlo simulations that employ the same lattice description as we use in the present study.9, 10 Second, supported membranes and lipid monolayers have reduced capacity to undergo bending deformations. Hence, our model could be relevant for the observed ability of the peripheral protein α-synuclein to induce macroscopic phase separation on supported phosphatidylcholine∕phosphatidylglycerol membranes.32 Similarly, it may be used to describe annexin A2-induced formation of large domains in supported bilayers composed of phosphatidylcholine∕phosphatidylserine.29 Finally, recent experiments demonstrated that cross-linking of the minor membrane component ganglioside GM1 by cholera toxin subunit B (CTB) can induce macroscopic phase separation in model31 and biological33 membranes. Here, the membrane is primed to undergo phase separation, which is initiated by the CTB-induced cross-linking. In terms of our present model the membrane resides close to the phase boundary prior to the cross-linking. Addition of CTB effectively induces sequestration of GM1. The fact that sequestration may give rise to macroscopic phase separation is exactly the subject of our present model.
CONCLUSIONS
We have studied the stability of a protein-decorated mixed lipid layer with respect to lateral phase separation. The proteins are assumed to preferentially interact with only one species of a binary membrane. Starting with the assumption that both the isolated lipid layer and the adsorbed protein layer each on their own are stable (χ<2 and Λ<2), we have addressed the question of whether the coupled system is able to undergo phase splitting. The energetics of the protein-decorated lipid layer depends generally on three effective interaction strengths, lipid-protein (α), lipid-lipid (χ), and protein-protein (Λ). Our present model is complete in the sense that it accounts for all these interactions; it extends a previous study46 in which only the interaction constants α and χ were taken into account. As in that study, we find that protein adsorption onto a stable binary membrane can induce lateral phase separation, as expressed by the reduction in the critical interaction parameter χc even for Λ=0. The driving force for the phase transition is the membrane line tension contribution to the free energy. Beyond that we quantify the role of direct protein-protein attraction (Λ>0). These generally enhance the destabilization of the lipid layer. That is, both χc is further reduced and the region of instability in the ϕ, θ-phase diagram widens as a function of growing Λ.
ACKNOWLEDGMENTS
This work was supported by NIH Grant No. GM077184. The authors would like to thank Dr. Alexander Wagner for illuminating discussions.
APPENDIX A: DERIVATION OF EQUATIONS 3 AND 4
Equation 2, the spinodal equation, defines the boundary between local thermodynamic stability and instability in the ϕ, θ-diagram. (For a numerical calculation of the spinodal see the phase diagrams in Fig. 4.) To calculate the spinodal based solely on Eq. 1, we point out that the two compositions ϕP and ϕL in, respectively, the protein-covered and protein-free regions of the lipid layer are connected through the lever rule ϕ=θϕP+(1−θ)ϕL. Together with the definition of Δϕ=ϕP−ϕL this implies,
| (A1) |
In thermal equilibrium, the compositional difference Δϕ adjusts so as to minimize f, implying that the equilibrium condition ∂f∕∂Δϕ=0 must be fulfilled. Using Eq. 1 this is equivalent to
| (A2) |
which defines the relation Δϕ=Δϕ(ϕ,θ). Hence, the free energy f=f(ϕ,θ) in Eq. 1 depends only on the two compositional degrees of freedom ϕ and θ. Furthermore, partially differentiating the equilibrium condition Eq. A2 with respect to θ and ϕ leads to two equations that can be combined to yield the relation
| (A3) |
Together with Eq. A1 this becomes
| (A4) |
Using Eqs. A1, A2, A3, A4 allows us to calculate the first derivatives
| (A5) |
and from that the second derivatives
| (A6) |
Inserting these relations into the spinodal Eq. 2 gives rise to
| (A7) |
The derivative ∂ϕL∕∂ϕ can be obtained by differentiating the equilibrium condition for Δϕ, Eq. A2, with respect to ϕ. The result is
| (A8) |
Together with Eq. A8, the spinodal in Eq. A7 yields the final result in Eq. 3.
Let us also outline the derivation of Eq. 4. The (fixed) chemical potential μP=∂f∕∂θ of the membrane-adsorbed proteins is given in Eq. A5. Taking the full derivative of μP with respect to θ results in
| (A9) |
Using Eq. A9 we eliminate from Eq. A7. The spinodal, Eq. A7, then becomes
| (A10) |
However, (dϕL∕dθ)∕(∂ϕL∕∂ϕ)=−Δϕ+(dϕ∕dθ), and we thus obtain Eq. 4. We note again that the calculations in this Appendix0 are valid irrespective of the structure of the functions fP(ϕP), fL(ϕL), and fpr(θ).
References
- Winget J. M., Pan Y. H., and Bahnson B. J., Biochim. Biophys. Acta 1761, 1260 (2006). [DOI] [PubMed] [Google Scholar]
- Leidy C., Linderoth L., Andresen T. L., Mouritsen O. G., Jorgensen K., and Peters G. H., Biophys. J. 10.1529/biophysj.105.070987 90, 3165 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorbenko G. P., Ioffe V. M., and Kinnunen P. K. J., Biophys. J. 10.1529/biophysj.106.102749 93, 140 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stockl M., Fischer P., Wanker E., and Herrmann A., J. Mol. Biol. 10.1016/j.jmb.2007.11.051 375, 1394 (2008). [DOI] [PubMed] [Google Scholar]
- Heimburg T., Angerstein B., and Marsh D., Biophys. J. 10.1016/S0006-3495(99)77410-2 76, 2575 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niggli V., in Advances in Molecular and Cell Biology, Vol. 37, edited by Kurana S. (Elsevier, San Diego, CA, 2006), pp. 221–250. [Google Scholar]
- Neville F., Cahuzac M., Konovalov O., Ishitsuka Y., Lee K. Y. C., Kuzmenko I., Kale G. M., and Gidalevitz D., Biophys. J. 90, 1275 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golebiewska U., Gambhir A., Hangyas-Mihalyne G., Zaitseva I., Rädler L., and McLaughlin S., Biophys. J. 10.1529/biophysj.106.081562 91, 588 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinderliter A., Almeida P. F. F., Creutz C. E., and Biltonen R. L., Biochemistry 10.1021/bi0024299 40, 4181 (2001). [DOI] [PubMed] [Google Scholar]
- Hinderliter A., Biltonen R. L., and Almeida P. F. F., Biochemistry 10.1021/bi036334t 43, 7102 (2004). [DOI] [PubMed] [Google Scholar]
- Wang J. Y., Gambhir A., McLaughlin S., and Murray D., Biophys. J. 10.1016/S0006-3495(04)74260-5 86, 1969 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz C. D., Faraudo J., and Travesset A., Langmuir 10.1021/la703550t 24, 1654 (2008). [DOI] [PubMed] [Google Scholar]
- Simons K. and Vaz W. L. C., Annu. Rev. Biophys. Biomol. Struct. 10.1146/annurev.biophys.32.110601.141803 33, 269 (2004). [DOI] [PubMed] [Google Scholar]
- McMullen T. P. W., Lewis R. N. A. H., and McElhaney R. N., Curr. Opin. Colloid Interface Sci. 10.1016/j.cocis.2004.01.007 8, 459 (2004). [DOI] [Google Scholar]
- Lehtonen J. Y. A., Holopainen J. M., and Kinnunen P. K. J., Biophys. J. 10.1016/S0006-3495(96)79738-2 70, 1753 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garidel P., Johann C., and Blume A., Biophys. J. 10.1016/S0006-3495(97)78863-5 72, 2196 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redfern D. A. and Gericke A., J. Lipid Res. 46, 504 (2005). [DOI] [PubMed] [Google Scholar]
- Veatch S. L. and Keller S. L., Biochim. Biophys. Acta 10.1016/j.bbamcr.2005.06.010 1746, 172 (2005). [DOI] [PubMed] [Google Scholar]
- Kahya N. and Schwille P., Mol. Membr Biol. 10.1080/09687860500489099 23, 29 (2006). [DOI] [PubMed] [Google Scholar]
- Almeida P. F. F., Pokorny A., and Hinderliter A., Biochim. Biophys. Acta 10.1016/j.bbamem.2005.12.004 1720, 1 (2005). [DOI] [PubMed] [Google Scholar]
- Epand R. M., Biochim. Biophys. Acta 1778, 1576 (2008). [DOI] [PubMed] [Google Scholar]
- Yim H., Kent M. S., Sasaki D. Y., Polizzotti B. D., Kiick K. L., Majewski J., and Satija S., Phys. Rev. Lett. 10.1103/PhysRevLett.96.198101 96, 198101 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosetti C. M., Maggio B., and Oliveira R. G., Biochim. Biophys. Acta 1778, 1665 (2008). [DOI] [PubMed] [Google Scholar]
- Horton M. R., Radler J., and Gast A. P., J. Colloid Interface Sci. 10.1016/j.jcis.2006.08.057 304, 67 (2006). [DOI] [PubMed] [Google Scholar]
- Herrig A., Janke M., Austermann J., Gerke V., Janshoff A., and Steinem C., Biochemistry 10.1021/bi061064a 45, 13025 (2006). [DOI] [PubMed] [Google Scholar]
- Pokorny A., Yandek L. E., Elegbede A. I., Hinderliter A., and Almeida P. F. F., Biophys. J. 10.1529/biophysj.106.085027 91, 2184 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicolini C., Baranski J., Schlummer S., Palomo J., Lumbierres-Burgues M., Kahms M., Kuhlmann J., Sanchez S., Gratton E., Waldmann H., and Winter R., J. Am. Chem. Soc. 10.1021/ja055779x 128, 192 (2006). [DOI] [PubMed] [Google Scholar]
- Manley S., Horton M. R., Lecszynski S., and Gast A. P., Biophys. J. 10.1529/biophysj.107.124024 95, 2301 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menke M., Gerke V., and Steinem C., Biochemistry 10.1021/bi051585i 44, 15296 (2005). [DOI] [PubMed] [Google Scholar]
- Baumgart T., Hammond A. T., Sengupta P., Hess S. T., Holowka D. A., Baird B. A., and Webb W. W., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0611357104 104, 3165 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammond A. T., Heberle F. A., Baumgart T., Holowka D., Baird B., and Feigenson G. W., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0405654102 102, 6320 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandey A., Rochet J. C., and Hovis J. S., Biophys. J. Suppl. S, 224A (2007) [Google Scholar]
- Lingwood D., Ries J., Schwille P., and Simons K., Proc. Natl. Acad. Sci. U.S.A. 105, 10005 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yethiraj A. and Weisshaar J. C., Biophys. J. 10.1529/biophysj.106.101931 93, 3113 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gil T., Sabra M. C., Ipsen J. H., and Mouritsen O. G., Biophys. J. 10.1016/S0006-3495(97)78204-3 73, 1728 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akimov S. A., Frolov V. A. J., Kuzmin P. I., Zimmerberg J., Chizmadzhev Y. A., and Cohen F. S., Phys. Rev. E 10.1103/PhysRevE.77.051901 77, 051901 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J., Sammalkorpi M., and Haataja M., Phys. Rev. Lett. 10.1103/PhysRevLett.100.178102 100, 178102 (2008). [DOI] [PubMed] [Google Scholar]
- Sens P. and Safran S. A., Eur. Phys. J. E 10.1007/s101890050026 1, 237 (2000). [DOI] [Google Scholar]
- Schiller P., Mogel H. J., Wahab M., and Reimer U., J. Phys. Chem. B 106, 12323 (2002). [Google Scholar]
- Schiller P., Wahab M., and Mogel H. J., J. Non-Newtonian Fluid Mech. 119, 145 (2004). [Google Scholar]
- Sengupta P., Hammond A., Holowka D., and Baird B., Biochim. Biophys. Acta 1778, 20 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sperotto M. M., Eur. Biophys. J 26, 405 (1997). [Google Scholar]
- Heimburg T., Curr. Opin. Colloid Interface Sci. 10.1016/S1359-0294(00)00059-5 5, 224 (2000). [DOI] [Google Scholar]
- Tzlil S. and Ben-Shaul A., Biophys. J. 10.1529/biophysj.105.068387 89, 2972 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzlil S., Murray D., and Ben-Shaul A., Biophys. J. 10.1529/biophysj.108.132522 95, 1745 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- May S., Harries D., and Ben-Shaul A., Phys. Rev. Lett. 10.1103/PhysRevLett.89.268102 89, 268102 (2002). [DOI] [PubMed] [Google Scholar]
- Tian A. W., Johnson C., Wang W., and Baumgart T., Phys. Rev. Lett. 10.1103/PhysRevLett.98.208102 98, 208102 (2007). [DOI] [PubMed] [Google Scholar]
- Kuzmin P. I., Akimov S. A., Chizmadzhev Y. A., Zimmerberg J., and Cohen F. S., Biophys. J. 88, 1120 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Towles K. B. and Dan N., Biochim. Biophys. Acta 1778, 1190 (2008). [DOI] [PubMed] [Google Scholar]
- Safran S. A., Statistical Thermodynamics of Surfaces, Interfaces, and Membranes, 2nd ed. (Westview, Boulder, CO, 2003). [Google Scholar]
- Mbamala E. C., Ben-Shaul A., and May S., Biophys. J. 10.1529/biophysj.104.048132 88, 1702 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haleva E., Ben-Tal N., and Diamant H., Biophys. J. 10.1529/biophysj.104.053165 86, 2165 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goulian M., Curr. Opin. Colloid Interface Sci. 1, 358 (1996). [Google Scholar]
- Chatelier R. C. and Minton A. P., Biophys. J. 10.1016/S0006-3495(96)79430-4 71, 2367 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou T., Kim K. S., and Oster G., Biophys. J. 10.1016/S0006-3495(01)76086-9 80, 1075 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Planque M. R. R. and Killian J. A., Mol. Membr. Biol. 20, 271 (2003). [DOI] [PubMed] [Google Scholar]
- Sens P., Johannes L., and Bassereau P., Curr. Opin. Cell Biol. 20, 476 (2008). [DOI] [PubMed] [Google Scholar]