Identifying critical residues in protein folding: Insights from ϕ-value and P_fold analysis

Abstract

We apply a simulational proxy of the ϕ-value analysis and perform extensive mutagenesis experiments to identify the nucleating residues in the folding “reactions” of two small lattice Gō polymers with different native geometries. Our findings show that for the more complex native fold (i.e., the one that is rich in nonlocal, long-range bonds), mutation of the residues that form the folding nucleus leads to a considerably larger increase in the folding time than the corresponding mutations in the geometry that is predominantly local. These results are compared to data obtained from an accurate analysis based on the reaction coordinate folding probability P_fold and on structural clustering methods. Our study reveals a complex picture of the transition state ensemble. For both protein models, the transition state ensemble is rather heterogeneous and splits up into structurally different populations. For the more complex geometry the identified subpopulations are actually structurally disjoint. For the less complex native geometry we found a broad transition state with microscopic heterogeneity. These findings suggest that the existence of multiple transition state structures may be linked to the geometric complexity of the native fold. For both geometries, the identification of the folding nucleus via the P_fold analysis agrees with the identification of the folding nucleus carried out with the ϕ-value analysis. For the most complex geometry, however, the applied methodologies give more consistent results than for the more local geometry. The study of the transition state structure reveals that the nucleus residues are not necessarily fully native in the transition state. Indeed, it is only for the more complex geometry that two of the five critical residues show a considerably high probability of having all its native bonds formed in the transition state. Therefore, one concludes that, in general, the ϕ-value correlates with the acceleration∕deceleration of folding induced by mutation, rather than with the degree of nativeness of the transition state, and that the “traditional” interpretation of ϕ-values may provide a more realistic picture of the structure of the transition state only for more complex native geometries.

INTRODUCTION

The folding kinetics of the vast majority of small, single domain proteins is remarkably well modeled by a two-state process, where the unfolded state (U) and the native fold (N) are separated by a high free energy barrier, on the top of which lays the transition state (TS).¹ Due to its transient nature, the structural characterization of the folding TS represents a particularly challenging task in protein biophysics. Indeed, experimental studies to date have typically relied on the application of a particular class of protein engineering methods, the so-called ϕ-value analysis, pioneered by Fersht and co-workers² in the 1980s. In the ϕ-value analysis a mutation is made at some position in the protein sequence; the ϕ-value is obtained by measuring the mutation’s effect on the folding rate and stability, namely, ϕ=−RT ln(k_mut∕k_WT)∕ΔΔG^N−U, where k_mut and k_WT are the folding rates of the mutant and wild-type (WT) sequences, respectively, and ΔΔG^N−U is the free energy of folding. For a nondisruptive mutation (i.e., a mutation that does not change the structure of the native state and does not alter the folding pathway either), −RT ln(k_mut∕k_WT) can be approximated by the change in the activation energy of folding upon mutation, ΔΔG^TS−U, and therefore ϕ=ΔΔG^TS−U∕ΔΔG^N−U.

A ϕ-value of unity means that the energy of the TS is perturbed on mutation by the same amount the native state is perturbed, which has traditionally been taken as evidence that the protein structure is folded at the site of mutation in the TS as much as it is in the native state. Conversely, residues which are unfolded in the TS, as much as they are in the unfolded state, should exhibit ϕ-values of zero. The interpretation of a fractional ϕ-value is, however, not straightforward as it might indicate the existence of multiple folding pathways,^{3, 4} or it may underlie a unique TS with genuinely weakened interactions.³ An alternative interpretation of mutational data has been recently proposed by Weikl and co-workers that instead considering the effect of each individual mutation collectively considers all mutations within a fold’s substructure (e.g., a helix). Such an interpretation is able to capture the so-called nonclassical ϕ-values (ϕ<0 or ϕ>1) and explains how different mutations at a given site can lead to different ϕ-values.^{5, 6}

In the case of the 64-residue protein chymotrypsin-inhibitor 2 (CI2), the extensive use of ϕ-value analysis revealed only one residue (Ala 16) with a distinctively high ϕ∼1, whereas the vast majority of CI2’s residues show typically low fractional ϕ-values.⁷ These findings were taken as evidence that CI2 folds via the so-called nucleation-condensation mechanism, with the folding nucleus (FN) consisting primarily of the set of bonds [mostly local but also a few long range (LR)] established by the residue with the highest ϕ-value,^{3, 8} which is identified as a nucleation site. Interestingly, the very first microscopic evidence for the existence of a nucleation mechanism in protein folding was obtained in the scope of Monte Carlo (MC) simulations of a simple lattice model, where Abkevich et al.⁹ observed that once the FN, consisting of a specific set of native bonds, is established the native fold is achieved very rapidly. Additional studies in vitro^{10, 11, 12, 13} and in silico,^{14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24} using more sophisticated protein models and other simulational methodologies, have provided further evidence for the existence of nucleation sites in CI2 as well as in other target proteins. For this reason the nucleation mechanism is typically considered the most common folding mechanism among small two-state proteins.²⁵

A few years ago, Sánchez and Kiefhaber reported a set of experimental data indicative that ϕ-values are considerably inaccurate unless the difference in the folding free energy upon mutation is larger than 7 kJ∕mol.²⁶ A refute by Fersht followed based on the premise that the 7 kJ∕mol cutoff was based on mutations that are unsuitable for ϕ-value analysis because they are disruptive.²⁷ More recently, a collaborative effort between three laboratories in North America investigated the relationship between ϕ-value reliability and the change in the free energy of folding, ΔΔG^N−D, using the generally employed experimental practices and conditions. A conclusion came out from this study stating that the precision of experimentally determined ϕ-values is poor unless ΔΔG^N−D>5 kcal∕mol.²⁸ In a related study, Raleigh and Plaxco pointed out that only 3 out of the 125 more accurately determined ϕ-values reported in the literature lie above 0.8, and that about 85% of the mutations characterized for single domain proteins show ϕ-values below 0.6.²⁹ Overall, these findings have prompted a discussion regarding the existence of specific nucleation sites, and therefore some controversy has been generated regarding the nucleation mechanism of protein folding.

The goal of the present study is to contribute to clarify this controversy by applying two different procedures that identify the nucleating residues in the folding of small lattice proteins. One of these procedures, a simulational proxy of the ϕ-value analysis, leads to a supposedly “inaccurate” identification of the FN’s residues that is made irrespective of the free energy changes caused by mutation. The other procedure, which is based on the use of the reaction coordinate P_fold,³⁰ allows for an accurate∕rigorous identification of the TS and of the native contacts which make up the FN. By comparing the results obtained from both approaches insight is gained on the suitability of the ϕ-value analysis as a tool to identify kinetically determinant residues in protein folding and on the nucleation mechanism of folding.

Since native geometry is known to play a major role in the folding kinetics of small two-state proteins,^{31, 32, 33, 34, 35, 36} we study two model proteins with considerably different native geometries.

This article is organized as follows. In the next section we describe the protein models and computational methodologies used in the simulations. Afterwards, we present and discuss the results. In the last section we draw some concluding remarks.

MODELS AND METHODS

The Gō model and simulation details

We consider a simple three-dimensional lattice model of a protein molecule with chain length N=48. In such a minimalist model amino acids, represented by beads of uniform size, occupy the lattice vertices and the peptide bond, which covalently connects amino acids along the polypeptide chain, is represented by sticks with uniform (unit) length corresponding to the lattice spacing.

To mimic protein energetics we use the Gō model.³⁷ In the Gō model the energy of a conformation, defined by the set of bead coordinates $\left\{{\stackrel{⃑}{r}}_i\right\}$, is given by the contact Hamiltonian

$$H\left(\left\{{\stackrel{⃑}{r}}_i\right\}\right)=\sum _{i>j}^Nϵ\Delta \left({\stackrel{⃑}{r}}_i-{\stackrel{⃑}{r}}_j\right),$$ (1)

where the contact function $\Delta \left({\stackrel{⃑}{r}}_i-{\stackrel{⃑}{r}}_j\right)$ is unity only if beads i and j form a noncovalent native contact (i.e., a contact between a pair of beads that is present in the native structure) and is zero otherwise. The Gō potential is based on the principle that the native fold is very well optimized energetically. Accordingly, it ascribes equal stabilizing energies (e.g., ϵ=−1.0) to all the native contacts and neutral energies (ϵ=0) to all non-native contacts.

The motivation to use the Gō potential in the present study is as follows. In their original nucleation paper Abkevich et al.⁹ noted that several nonhomologous sequences, which were designed to fold into the same conformation, featured the same FN suggesting the importance of native geometry versus energetic details in determining the TS ensemble. This observation was subsequently confirmed experimentally by Geierhaas et al.³⁸ who found similar folding nuclei in Ig fold proteins with vastly different sequences. These findings suggest that the character of the TS ensemble may be robust with respect to particular energetic scheme used for simulations, and native-centric Gō model represents an efficient way to simulate folding in a statistically significant manner.

In order to mimic the protein’s relaxation toward the native state we use a Metropolis MC algorithm^{39, 40, 41} together with the kink-jump move set.⁴² A MC simulation starts from a randomly generated unfolded conformation and the folding dynamics is monitored by following the evolution of the fraction of native contacts, Q=q∕L, where L is number of contacts in the native fold and q is the number of native contacts formed at each MC step. The number of MC steps required to fold to the native state (i.e., to achieve Q=1.0) is the first passage time (FPT) and the folding time t is computed as the mean FPT of 100 simulations. Except otherwise stated folding is studied at the so-called optimal folding temperature, the temperature that minimizes the folding time.^{43, 44, 45, 46} The folding transition temperature T_f is defined as the temperature at which denatured states and the native state are equally populated at equilibrium. In the context of a lattice model it can be defined as the temperature at which the average value ⟨Q⟩ of the fraction of native contacts is equal to 0.5.⁴⁷ In order to determine T_f we averaged Q, after collapse to the native state, over MC simulations lasting ∼10⁹ MCS.

The Metropolis algorithm was originally developed to compute equilibrium properties of physical systems by integrating quantities in the configurational space. In this sense, its use to simulate dynamical processes, such as the search of the native state in protein folding, is not strictly correct. However, by comparing dynamic MC and Brownian dynamics results of the folding of alpha-helical hairpin proteins, Rey and Sklonick⁴⁸ were able to confirm the essential physical character of the dynamic MC simulations. Since the 1990s the MC method has been extensively used to perform dynamic simulations in the context of lattice and off-lattice models of protein folding.⁴⁹

Target geometries

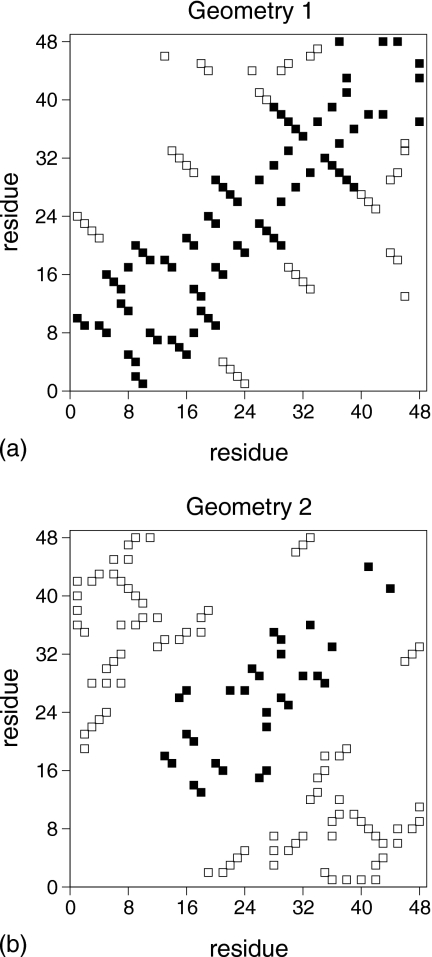
Two native folds, which are among the “simplest” (geometry 1) and the most “complex” (geometry 2) cuboid geometries found through lattice simulations of homopolymer relaxation, were considered in this study. A contact map representation, which emphasizes their distinct geometrical traits, is shown in Fig. 1. Table 1 provides a summary of kinetic and thermodynamic features of both protein models.

Figure 1.

Geometries 1 and 2 represented through their contact maps. Each square represents a native contact. For structures that like ours are maximally compact cuboids with N=48 residues there are 57 native contacts. A nonlocal contact between two residues i and j is defined as LR if their sequence separation is at least 12 units, i.e., ∣i−j∣≥12 (Ref. ³²). Accordingly, the number of LR (white squares) contacts in geometry 1 is 19 and in geometry 2 is 42. The predominance of LR contacts in geometry 2 leads to considerably higher values of the LR order (Ref. ³²) (0.88 vs 0.40 for geometry 1) and (absolute) contact order (Ref. ³¹) parameters (21.4 vs 9.9 for geometry 1).

Table 1.

Summary kinetic and thermodynamic properties of the protein models considered in this study. E is the native state’s energy, T is the optimal folding temperature, and log₁₀(t) is the logarithmic folding time computed at T. Also shown is the folding transition temperature T_f.

Geometry	E	T	log10(t)	Tf
1	−57.00	0.66	5.64±0.04	0.762
2	−57.00	0.67	6.29±0.05	0.795

Folding probability

The folding probability P_fold(Γ) of a conformation Γ is defined as the fraction of MC runs which, starting from Γ, fold before they unfold.³⁰ It was shown in the context of lattice models that P_fold features the appropriate characteristics for a reaction coordinate. Accordingly, conformations that are members of the TS have P_fold=1∕2, while pre- and post-TS conformations have smaller and larger folding probabilities, respectively.

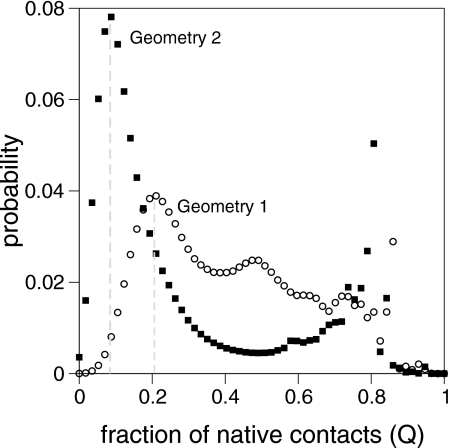
Because a P_fold calculation amounts to a Bernoulli trial, the relative error resulting from using M runs scales as M^−1∕2.⁵⁰ Thus, in order to accurately compute P_fold we consider 500 MC runs divided equally into five sets of 100 folding simulations. The average value of P_fold is computed for each set, and the mean of all five sets, together with its standard deviation, is evaluated. Each MC run stops when either the native fold (Q=1.0) or some unfolded conformation is reached. A conformation is deemed unfolded when its fraction of native contacts Q is smaller than some cutoff, Q_U. In order to estimate Q_U we compute the probability of finding some fraction of native contacts Q as a function of Q in 200 MC folding runs (Fig. 2). A high-probability peak, centered around the fraction of native contacts Q=0.2, is readily apparent in the graph reported for geometry 1. In the case of geometry 2 the highest probability peak appears around Q=0.1. These fractions of native contacts are considerably low and therefore identify states with minimal residual structure. In this work we use these fractions of native bonds to establish the cutoff value Q_U for each model protein.

Figure 2.

Probability distribution for the fraction of native contacts, Q, for geometries 1 and 2. A conformation is considered unfolded when Q<Q_U (Q_U is indicated by the dotted line)

A total of 8000 conformations was collected from 8000 independent MC folding runs, each conformation being sampled from the run’s last 5×10⁶ MCS. The folding probability of each conformation was measured as outlined above and conformations were partitioned into seven ensembles with P_fold=0.2,0.3,…,0.8, each ensemble containing approximately 400 conformations.

Structural clustering analysis

Here we summarize a graph-theoretical method, similar to that described in Refs. ^{51, 52} which is used to cluster conformations within each P_fold ensemble based on their structural similarity. The measure of structural similarity r between two conformations is the number of native bonds they have in common normalized to the maximum number of native bonds in the pair. Every possible pair of conformations is considered in each P_fold ensemble. Two conformations are structurally similar (i.e., linked) if r is larger than a cutoff R, which is fixed so that the largest cluster, the so-called giant component, contains approximately half of the conformations in the starting ensemble. Two conformations belong to the same cluster if they are linked by a path of connected conformations.

IDENTIFYING CRITICAL RESIDUES WITH A SIMULATIONAL PROXY OF THE ϕ-VALUE ANALYSIS

ϕ-value dynamics

The mechanistic equivalent of the ϕ-value of residue i at time t, ${\varphi }_i^{\mathrm{mec}}\left(t\right)$, is defined as the ratio between the number of native bonds $q_i^{\Gamma }\left(t\right)$ residue i establishes in some conformation Γ at time t, and the number of bonds $q_i^{\text{fold}}$ it establishes in the native fold, ${\varphi }_i^{\mathrm{mec}}\left(t\right)=q_i^{\Gamma }\left(t\right)∕q_i^{\text{fold}}$.^{16, 50, 53}

Since the formation of the FN is the rate-limiting step in two-state folding, the residues that belong to the FN will remain in their native environment during a small fraction of the overall folding time. In other words, for a FN’s residue i, ${\varphi }_i^{\mathrm{mec}}\left(t\right)$ is likely to attain the value of 1 only very close to folding into the native state, and for most values of t${\varphi }_i^{\mathrm{mec}}\left(t\right)$ will be smaller than 1. Moreover, as a result of structural correlations driven by chain connectivity, residues that are covalently bonded to FN’s residues in the polypeptide chain should behave in a similar way. A similar behavior is also expected for the two terminal residues and their respective neighbors in the chain.

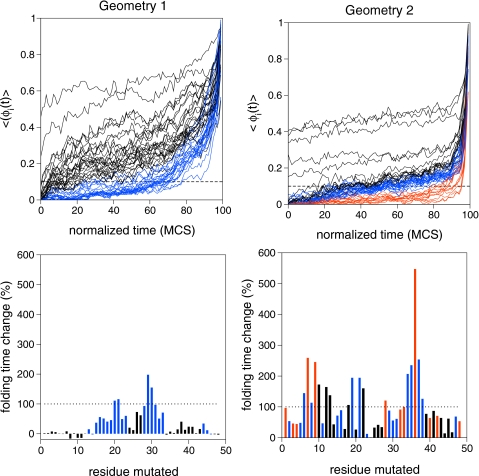
In order to investigate how ${\varphi }_i^{\mathrm{mec}}\left(t\right)$ evolves during folding we proceed as follows. An ensemble of 100 folding runs is considered, and each folding run is divided in 100 bins of length Δt=FPT∕100 MCS. The 100 time bins correspond to a normalized integer time coordinate k that goes from 0 to 100 in all the MC runs. For each individual residue and each run, the time average ${\varphi }_{\mathrm{ik}}^{\mathrm{mec}}$ of ${\varphi }_i^{\mathrm{mec}}\left(t\right)$ when t is in the kth bin is computed. Then, the averages ${\varphi }_{\mathrm{ik}}^{\mathrm{mec}}$ for each residue are averaged over the 100 MC runs. Results obtained for both geometries are reported in Fig. 3 (top), where the blue curves refer to the residues for which the average value of ${\varphi }_i^{\mathrm{mec}}$ is smaller than 0.1, at least during 50% of the time, and increases to unity only very late in folding. The red curves in the graph of geometry 2 report residues for which the average value of ${\varphi }_i^{\mathrm{mec}}$ is smaller than 0.1, at least during 90% of the time, and increases very sharply only late in folding.

Figure 3.

Time evolution of the mechanistic equivalent of the ϕ-value, ${\varphi }_i^{\mathrm{mec}}\left(t\right)$ (top), and change in folding time, relative to the WT sequence, upon performing a single-point mutation for geometry 1 (left) and geometry 2 (right).

A qualitatively global analysis of the two sets of 48 curves shows interesting differences. For example, the average value of ${\varphi }_i^{\mathrm{mec}}\left(t\right)$ is considerably much lower for geometry 2 than for geometry 1. Also, for geometry 2, the curves within each identified subset are closely matched together, which may be taken as an indication that the corresponding residues make and break bonds in a rather independent manner (i.e., bonds form and break more cooperatively in geometry 2 than in geometry 1).

Site-directed mutagenesis

If the formation of the FN is the rate-limiting step in folding, site-directed mutations on the nuclear core residues are supposed to have a significant effect on the folding rate (or alternatively in the folding time).⁵⁴ Therefore a comparison of different mutations is important to identify which particular residues are involved in the TS.⁵⁵ In the Gō model interactions between residues can either be neutral or stabilizing. Likewise, a single-site mutation within the context of the Gō model is equivalent to replacing the set of native bonds established by one residue with neutral bonds (i.e., bonds to which zero energy is ascribed). Because the amino acid sequence is not changed, as in a mutagenesis experiment with real proteins, in principle, one can study the influence of the native contacts without changing the native structure and without significantly changing the folding pathway.

Site-directed mutations were performed for every individual residue and the folding time of the mutant evaluated. The percent change in folding time (relative to the WT sequence) is reported in Fig. 3 (bottom), where different colors have been used to establish a link with the residue’s ϕ-curves. There is a striking difference between both geometries considered here, which regards the considerably larger folding times observed for geometry 2. Of note, there are several (neutral) mutations (e.g., on residues 1, 2, 6, and 12) that do not change the folding time of the WT sequence in geometry 1. Moreover, for geometry 1, there are also a few “abnormal” mutations (e.g., on residues 8, 10, and 11) that actually lead to a decrease in WT protein’s folding time. In general, for both geometries, the mutations that lead to a larger increase in the folding time are on the residues that spend a very little amount of time in their native environment during folding.

To proceed with the identification of the FN we combine data from both experiments described above and investigate only the dynamics of the subset of residues that (i) spend (on average) less than 10% of time in their native environment during in folding (blue and red bars in Fig. 3, bottom) and (ii) whose mutation leads to an increase of at least 100% in the folding time. A residue satisfying conditions 1 and 2 is deemed potential nucleation site (PNS).

Geometry 1

We have performed double-point mutations by combining all the pairs of residues which were identified as PNSs and selected only those mutants whose folding time is larger than that observed for the most deleterious (i.e., severe) single-point mutation. Several double mutants have folding times that are more than one order of magnitude larger than that of the WT sequence. A particularly large increase (of 1.6 orders of magnitude) in the folding time is observed when residues 30 and 20 were simultaneously mutated (Table 2). To proceed with the identification of the FN we have considered triple-point mutations and, perhaps not surprisingly, we have found that residues 20 and 30 participate in three of the most deleterious mutations of this kind, which also involve residues 21 and 29 (Table 2). Thus, according to the ϕ-value analysis, the nucleating residues for geometry 1 are residues 20, 21, 29, and 30, and the set of bonds they establish is the FN for this geometry.

Table 2.

Mutations and resulting folding times observed for geometry 1. The folding time for the wild type sequence is log₁₀(t)=5.64±0.04. Also shown is the number of contacts disrupted (i.e., the number of interactions to each zero energy is ascribed) by each mutation.

Mutation on bead(s)	No. of contacts disrupted	log10(t)
33	3	5.87±0.04
20	4	5.96±0.03
21	3	5.97±0.04
30	4	6.04±0.04
29	4	6.11±0.04
29, 30	8	6.64±0.04
20, 33	7	6.65±0.04
29, 20	7	6.87±0.04
30, 21	7	6.92±0.04
29, 21	7	6.97±0.04
30, 20	8	7.27±0.05
30, 20, 33	10	7.71±0.05
30, 20, 29	11	7.77±0.05
30, 21, 29	11	7.85±0.04
30, 20, 21	11	8.05±0.05

Geometry 2

A procedure identical to that used for geometry 1 was applied to geometry 2 that revealed the kinetic relevance of residues 7, 34, 35, 36, and 37. Indeed, the folding times registered upon (double-point) mutating the pairs of residues 35 and 36, 37 and 7, 7 and 34, as well as residues 36 and 7 all lead to folding times that are at least 1.4 orders of magnitude larger than that displayed by the WT protein (Table 3). Furthermore, several triple-point mutations combining these residues lead to extraordinary high folding times, which are up 2.3 orders of magnitude larger (for residues 7, 34, and 37) than that of the WT sequence, or even folding failure (for residues 7, 35, and 36 and residues 7, 35, and 37) (Table 3). These findings are suggestive that for this model protein, the nucleating residues are residues 7, 34, 35, 36, and 37.

Table 3.

Mutations and resulting folding times observed for geometry 2. The folding time for the wild type sequence is log₁₀(t)=6.29±0.05. Also shown is the number of contacts disrupted (i.e., the number of interactions to which zero energy is ascribed) by each mutation. The folding time of the triple-point mutations marked with an * is estimated. Indeed, for the triple mutants 7:35:36 and 7:35:37 only 71% and 56% of the MC runs, respectively, reached the native state in the allowed number of MC steps.

Mutation on bead(s)	No. of contacts disrupted	log10(t)
8	3	6.62±0.04
28	4	6.63±0.04
6	3	6.68±0.06
10	2	6.72±0.05
19	4	6.76±0.05
21	2	6.76±0.05
34	3	6.78±0.05
9	3	6.83±0.05
34	1	6.78±0.05
35	2	6.82±0.04
7	4	6.84±0.05
37	3	6.84±0.05
36	4	7.10±0.05
37, 34	6	7.24±0.05
7, 35	7	7.60±0.04
36, 9	7	7.31±0.04
9, 37	6	7.33±0.04
9, 34	6	7.42±0.05
35, 37	7	7.46±0.04
36, 34	7	7.51±0.05
36, 37	7	7.52±0.04
36, 7	7	7.56±0.05
7, 34	7	7.73±0.05
7, 37	7	7.76±0.04
35, 36	7	7.80±0.04
36, 37, 34	10	8.00±0.04
7, 34, 36	10	8.45±0.04
7, 37, 34	10	8.58±0.04
7,35,36*	11	9.46±0.06
7,35,37*	10	9.61±0.05

IDENTIFYING CRITICAL RESIDUES WITH P_fold-ANALYSIS

Folding pathways

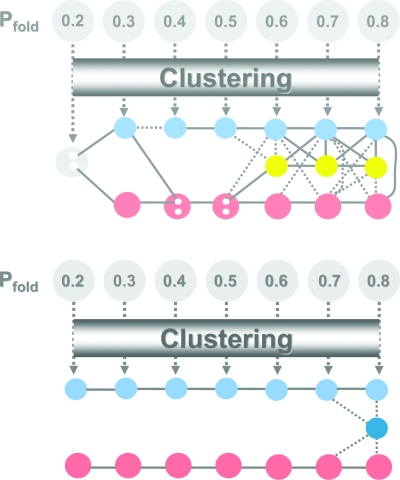
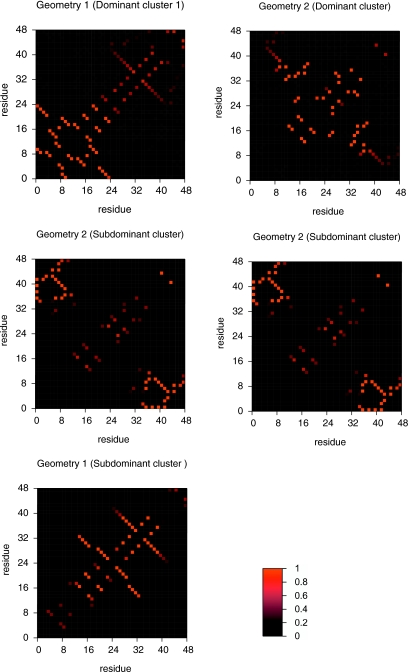
A folding pathway is a sequence of conformational changes leading to the native structure starting from some unfolded conformation. In order to identify potentially relevant conformational states in the folding “reactions” of geometries 1 and 2 we have applied the structural clustering method previously outlined to several ensembles of conformations with P_fold ranging from 0.2 (early folding) to 0.8 (late folding), which were collected from 8000 independent folding trajectories. Two clusters of relevant size, named hereafter the dominant cluster (or giant component) and subdominant cluster (this is the largest cluster after the giant component), emerge at successive values of P_fold for both geometries (Fig. 4). For geometry 1, a third cluster of size similar to that of the subdominant cluster emerges from P_fold=0.6 onward (Table 4). Also, for certain P_folds and after the subdominant cluster segregates from the starting ensemble, it is possible to discriminate between two considerably different conformational states within the dominant cluster by applying further clustering to conformations therein. We name these distinct conformational states, dominant cluster 1 and dominant cluster 2. Such a “refining” of the clustering process helps to reveal the more complicated intertwining folding pathways to geometry 1.

Figure 4.

Structural classes found along the reaction coordinate P_fold for geometry 1 (top) and geometry 2 (bottom). In both graphs the dominant cluster (i.e., the giant component) is shown on the bottom row, while the subdominant cluster is represented on the top row. For geometry 2, a trapped state appears at P_fold=0.8, while for geometry 1 a third cluster, of size similar to that of the subdominant cluster, develops from P_fold=0.6 onward. Two clusters are connected through a dotted line if (on average) their conformations share between 0.45 and 0.55 native bonds. A full line is drawn between clusters if their average similarity parameter $\overline{r}$ is larger than 0.55. Alternatively, no line is drawn between clusters if $\overline{r}<0.45$.

Table 4.

Structural clusters identified for geometry 1 along the reaction coordinate P_fold. ⟨Q⟩ is the average fraction of native contacts formed in the starting ensemble, D stands for dominant cluster, SD for subdominant cluster, and T represents the third cluster that emerges from P_fold=0.6 onward. The (averaged mean) time to fold starting from the conformations in each cluster is shown as a fraction of the folding time starting from a random coil conformer.

Pfold	No. of conformations	⟨Q⟩	Cluster (No. of conformations)	Time to fold (%MFPT)
0.2	598	0.45	D1:108; D2:28	(41%, 35%)
0.3	498	0.48	D:240; SD:65	(33%, 28%)
0.4	450	0.49	D1:133; D2:48; SD:21	(32%, 28%, 17%)
0.5	452	0.50	D1:127; D2:39; SD:31	(33%, 25%, 17%)
0.6	427	0.51	D:111; T:57; SD:41	(21%, 41%, 17%)
0.7	541	0.54	D:215; T:67; SD:73	(28%, 22%, 17%)
0.8	1170	0.59	D:674; T:170; SD:71	(17%, 30%, 16%)

A set of conformations is detected late (at P_fold=0.8) in the folding to geometry 2 that corresponds to a trapped state. Indeed, folding simulations starting from these conformations last for approximately the same time as folding simulations starting from random-coil-type conformers, and are one order of magnitude slower than simulations starting from other conformations having the same P_fold (Table 5). This is possibly a direct consequence of the fact that non-native contacts form with a high probability (>70%) in these high-P_fold conformers. For this geometry, we have also found that folding simulations starting from conformations in the subdominant cluster are, for all considered values of P_fold, systematically faster than folding simulations starting in conformations pertaining to the dominant cluster (Table 5). The difference in folding speed attained is particularly striking in the cases of TS and pre-TS conformations with P_fold=0.4 (Table 5). This is, however, not surprising because conformations that belong to those subdominant clusters have the vast majority of their LR native bonds formed with very high probability, which means they have already surmounted most of the entropic cost of establishing LR bonds. On the other hand, conformations in the dominant clusters, while having about the same fraction of native bonds (Q≈0.40) formed as conformations in the subdominat clusters, still lack the vast majority of their LR contacts whose formation slows down folding.

Table 5.

Structural clusters identified for geometry 2 along the reaction coordinate P_fold. ⟨Q⟩ is the average fraction of native contacts formed in the starting ensemble, D stands for dominant cluster, SD for subdominant cluster, and Trp represents a trapped state.

Pfold	No. of conformations	⟨Q⟩	Cluster (No. of conformations)	Time to fold (%MFPT)
0.2	482	0.33	D:215; SD:27	(22%, 16%)
0.3	443	0.35	D:207; SD:38	(50%, 14%)
0.4	406	0.39	D:219; SD:46	(58%, 8.8%)
0.5	401	0.41	D:228; SD:55	(31%, 7.7%)
0.6	337	0.40	D:148; SD:24	(19%, 7.7%)
0.7	338	0.42	D:119; SD:29	(16%, 7.4%)
0.8	449	0.46	D:117; SD:76; Trp:27	(11%, 6.2%, 49%)

We have determined the mean value of the similarity parameter, $\overline{r}$, between two clusters by averaging the structural similarity parameter r between every pair of conformations (one from each cluster). In Fig. 4, two clusters are connected by a full line if $\overline{r}\ge 0.55$, while those for which $0.45\le \overline{r}<0.55$ are linked with a dotted line. No line is drawn between clusters if $\overline{r}<0.45$. Along the successive values of P_fold the resemblance between clusters of the same type (e.g., between subdominant clusters) is typically larger than the resemblance between clusters of different types. This is particularly evident in the case of geometry 2. For geometry 1, however, once the TS is crossed, a considerable amount of structural similarity develops between clusters of different types.

To accurately establish the existence of folding pathways it is necessary to determine if the successive P_fold clusters are dynamically linked. A folding pathway exists if a conformation within a cluster can be reached from (at least) one conformation pertaining to a cluster of lower P_fold. In this case, since the successive dominant (and subdominant) clusters are, on average, very similar to each other (as shown by the high values of $\overline{r}$), it is perhaps straightforward for a conformation in the dominant (subdominant) cluster at P_fold=0.2 to develop into a conformation in the dominant (subdominant) cluster at P_fold=0.3, and so on. Therefore, we assume the existence of a set of microscopic folding pathways (to simplify let us name it folding route 1) linking the dominant clusters and of another set of microscopic folding pathways (folding route 2) linking the subdominant clusters. Folding routes 1 and 2 are parallel if no conformation within a certain P_fold cluster in one route can lead to a conformation within any cluster (of larger P_fold) in the other route. For geometry 2, we have found that starting folding from TS conformations, folding routes 1 and 2 are indeed parallel tracks to the native state. Indeed, 100% of folding runs starting from conformations in the subdominant cluster at P_fold=0.5 lead to conformations in the equivalent cluster at P_fold=0.8 prior to unfolding (i.e., without having to pass through an unfolded conformation). Similarly, 90% of the simulations that start from conformations in the dominant cluster at P_fold=0.5 end up in conformations within the dominant cluster at P_fold=0.8, the remaining 10% developing into conformers representative of the trapped state (Table 6). A completely different scenario holds for geometry 1 where, once the TS is crossed, conformations within folding route 1 evolve into conformers of folding route 2. For example, although 75% of the conformations in the TS’s subdominant cluster develop into conformations in the subdominant cluster at P_fold=0.8, 11% of the folding runs end up leading to conformers in the third cluster, and 14% of the runs end up in the dominant cluster. A similar crossing between pathways is observed for folding runs starting from conformations belonging to the dominant cluster (Table 7). Therefore, in the case of geometry 1, the folding routes linking dominant and subdominant clusters are not parallel routes to the native state.

Table 6.

Number of conformations in the different clusters (dominant, subdominant, and trapped state) at P_fold=0.8 as a function of the starting conformations for geometry 2.

Startingconformations	D atPfold=0.8	SD atPfold=0.8	Trp atPfold=0.8
Unfolded state	117∕220=53%	76∕220=35%	27∕220=12%
D at Pfold=0.5	44∕51=90%	0%	5∕51=10%
SD at Pfold=0.5	0%	100∕100=100%	0%

Table 7.

Number of conformations in the different clusters (dominant, subdominant, and third cluster) at P_fold=0.8 as a function of the starting conformations for geometry 1.

Starting conformations	D atPfold=0.80	T atPfold=0.95	SD atPfold=0.80
Unfolded state	674∕915=74%	170∕915=19%	71∕915=7.8%
D1 at Pfold=0.5	239∕255=93%	16∕255=6.6%	0%
D2 at Pfold=0.5	13∕78=17%	65∕78=83%	0%
SD at Pfold=0.5	100∕133=75%	14∕133=11%	19∕133=19%

The structural and geometric characterization of the TS

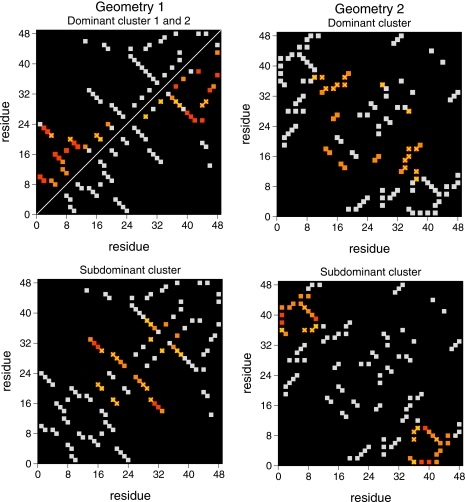
The structural characterization of the TS comprises not only the identification of the multiplicity of the pathways leading to it but also the degree of structural diversity in the ensemble itself. A meaningful discussion of whether the TS is considered to be heterogeneous with alternative forms depends on the resolution at which two such structures differ within the ensemble. Sosnick et al.⁵⁶ proposed the following three classes of TS heterogeneity: (1) a single essential TS nucleus with some partially formed interactions, (2) a structurally heterogeneous ensemble where some residues are critical for the FN but different groups of structures exist at the TS (i.e., conserved FN with microscopic heterogeneity), and (3) the nuclei can be structurally disjoint, each with a diverse set of necessary structures comprising distinct nuclei. To proceed with the structural characterization of the TS ensemble of the two model proteins considered in the present study, we have evaluated the probability that a native contact is formed in both the dominant and subdominant clusters at P_fold=0.5. For the TS ensemble of geometry 2 (Fig. 5, right) two structural classes can be clearly distinguished. The conformations pertaining to the subdominant cluster are characterized for having a well-defined group of ≈20 nonlocal LR bonds that form with a considerably high probability (>0.7); in these conformers the probability of forming any of the remaining native bonds is, on the contrary, vanishingly small. Such a “nonlocal” structural class has an average absolute contact order of ACO=22.7, which is about 106% of the native structure’s ACO. This particular subset of LR bonds has a small probability of forming in the dominant cluster’s conformations, which are, for this very reason “local” conformations. Such a larger number of local bonds naturally translates into a smaller average ACO of 15.5, which is about 72% of the native fold’s ACO. Thus, the two TS structures identified for geometry 2, more than structurally disjoint, are actually structurally complementary. For geometry 1, there is not such a striking structural difference between dominant and subdominant clusters (Fig. 5, left). Indeed, not only they have a balanced amount of local and nonlocal bonds (which naturally reflects in their average ACOs of 8.3, 8.3, and 7.3, for the dominant clusters 1 and 2 and subdominant cluster, respectively), but the subdominant cluster actually shares with the two identified structures of the dominant cluster about 25% of its highly probable native bonds. This picture is suggestive of the presence of one broad structural class, representative of a single FN, which is structurally heterogeneous.

Figure 5.

TS contact maps for geometry 1 (left) and geometry 2 (right) showing the probability of forming a native bond in the identified structural classes.

The FN

The bonds that exhibit the most dramatic changes between pre- and true TS conformations are of key interest. Such bonds are comprised of the FN residues whose contacts both define and guarantee that the TS is reached.²⁰ In order to determine which residues nucleate each identified TS structure we have determined the differential probability increase in each native bond between pre-TS conformations (P_fold=0.05) and the identified TS structures. Results reported in the differential probability maps (Fig. 6) refer to the native bonds whose probability increase is higher than 50%. Bonds that show a probability increase larger than 70% (i.e., between 70% and 95% for geometry 1 and between 70% and 85% for geometry 2) are colored red. A cross is used to mark the native bonds that are established by the residues identified as nucleating residues through ϕ-value analysis. Interestingly, these are associated with the five native bonds that show the largest probability increases (>80% for geometry 1 and >70% for geometry 2) between pre- and TS structures. This finding strongly suggests that ϕ-value analysis is able to pinpoint kinetically relevant residues independently of the change in the free energy of folding caused by mutation. For geometry 2, however, the P_fold and ϕ-value analyses give more consistent results than for geometry 1. Indeed, for geometry 2, there is a considerably larger overlap (75%) than for geometry 1 (42%) between the set of bonds identified as “key” bonds via P_fold analysis (these are the bonds colored red in the differential probability maps) and the set of bonds established by the residues indentified as critical residues via the ϕ-value analysis.

Figure 6.

Differential probability contact maps between pre-(P_fold=0.05) and TS (P_fold=0.5) conformations for geometry 1 (left) and geometry 2 (right). In the case of geometry 1, the two structural classes identified within the dominant cluster, namely, dominant clusters 1 and 2, are represented above and below the main diagonal of the corresponding contact map, respectively. Native contacts that show a significant increase (>50%) in contact probability are colored orange, while those colored red show the highest increase [between 70% and 95% (85%) for geometry 1 (2)] in contact probability. Native contacts in common with those identified as critical through ϕ-value analysis are marked with a cross.

A word of caution about these observations is, however, pertinent at this point. It is known that lattice Gō models tend to overstabilize local interactions in the denatured state (Ref. ⁵⁷ and references therein), which facilitates the formation of residual structure in the unfolded ensemble. Since geometry 1 is rich in local contacts one can imagine that the scenario of a structured denatured state might hold for this geometry. In that case, by mutating the residues that are involved in the formation of the denatured state’ structure the whole energy landscape is shifted up. This translates into a decrease in the change of the activation energy of folding, ΔΔG^TS−U, and also into a decrease in the change of the free energy of folding upon mutation, ΔΔG^N−U, giving rise to large errors in theestimation of the ϕ-values. This behavior can be at the origin of the less consistent results obtained via the two considered methodologies for geometry 1.

Geometry 1

In geometry 1 all the kinetically relevant residues 20 (via bond 20:29), 21 (via bonds 16:21 and 21:28), 29 (via bond 20:29), and 30 (via bond 17:30) nucleate the subdominant cluster. Residue 30 participates in the bond that shows the largest probability increase (93%). Dominant cluster 1 is nucleated by residues 20 (via bond 9:20) and 21 (via bonds 4:21 and 16:21) and, in this case, it is residue 21 the one that participates in the bond with the highest probability increase (90%). Dominant cluster 2 is nucleated by residues 29 (via bond 29:44) and 30 (via bond 30:45). The very fact that the same residue can mediate the folding reaction through different pathways is suggestive of a unique TS with microscopic heterogeneity.

Geometry 2

In geometry 2 the structural class that is rich in LR bonds (i.e., the subdominant cluster) is exclusively nucleated by residues 7 (via bonds 7:36 and 7:42) and 36 (via bonds 9:36 and 7:36). Residue 36 is associated with the two bonds whose probability increases the most (>74%) between pre- and the TS conformations. On the other hand, residues 34 (via its bonds 13:34 and 15:34), 35 (via its bonds 18:35 and 16:35), and 37 (via its bonds 18:37 and 12:37) exclusively nucleate the dominant cluster. This suggests the existence of two structurally disjoint TSs.

CRITICAL RESIDUES AND THE STRUCTURE OF THE TS

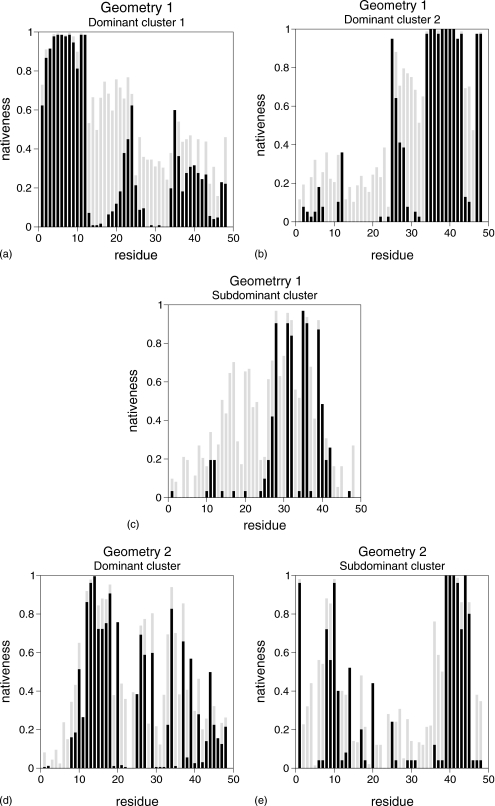
Here we investigate how the residues that are the determinant in the kinetics of folding are structured in the TS ensemble. In order to do so we measure the degree of nativeness of every residue in each model protein by means of two different quantities. One such quantity is the probability that a residue is fully native (i.e., has all its native bonds formed) in the TS, the other being the average fraction of native bonds formed by each residue in TS conformations. These two quantities are represented through the black and gray bars, respectively, in Fig. 7.

Figure 7.

Probability that a residue is fully native (black) and mean fraction of native bonds established by each residue (gray) in the TS’s dominant and subdominant clusters for geometry 1 (top and middle row) and geometry 2 (bottom row).

For geometry 1, all the four residues identified as being kinetically relevant have a vanishingly small probability of being fully native in all the identified TS structures. On average, however, residues 20 and 21 have 70% of its native bonds formed in the dominant cluster 1, while residues 29 and 30 have about the same percent of bonds established in conformations pertaining to dominant cluster 2. In general, the dominant cluster is considerably more structured than the subdominant one. Indeed, residues 2–12, below the chain midpoint, have a probability larger than 81% of being fully native in the dominant cluster 1, and residues 34–43, above the chain midpoint, have a very high probability >97% of being fully native in the dominant cluster 2. The subdominant cluster is more polarized: only residues 31, 32, 35, and 36 have all its native bonds established with a high probability (>84%).

The TS of geometry 2 is considerably more polarized than that of geometry 1. Indeed, in this case only residues 12, 13, 14, and 18 have a high probability >80% of being fully native in the dominant cluster, and in the subdominant cluster it is residues 10, 39, 40, 41, and 44 that are fully native with a similarly high probability. Possibly due to topological constraints, one observes that residues 12–18, as well as residues 30–42, have on average more than 80% of its native bonds formed. Except for residues 34 and 37, which have probabilities 75% and 62% of being fully native in the dominant cluster, the other kinetically relevant residues (namely, residues 7, 35, and 36) have either a small or a vanishingly probability of having its all its native bonds formed in the TS.

CONCLUSIONS

The ϕ-value analysis and other related methods⁵⁶ are used as major tools to probe the structure of TS and to identify the presence in this ensemble of the FN, i.e., the set ofcritical residues and associated native bonds that are the determinants of the folding kinetics.

Here we have employed a simulational proxy of the ϕ-value analysis to identify the critical (i.e., nucleating) residues in two model proteins differing in native geometry. Results from extensive “mutagenesis” experiments, within the context of the lattice Gō model, revealed a set of residues whose mutation leads to a considerably large increase in the folding time. We found out that for the more complex protein geometry, which has predominantly nonlocal, LR contacts, mutation of the critical residues has a much stronger impact on the folding time than for the geometry that is predominantly local.

An advantage of computer simulations over in vitro experiments with real proteins is the possibility to isolate and directly investigate the structure of TS conformations. The results of a thorough analysis, based on the reaction coordinate P_fold and on the use of structural clustering, revealed a complex picture of the TS ensemble. Indeed, for both protein models the TS ensemble is heterogeneous, splitting up into subpopulations of structurally similar conformations. For the more complex geometry of the native structure the two identified populations are actually structurally disjoint, being associated with the existence of parallel folding pathways.

For both geometries, the identification of the critical residues via the accurate P_fold analysis agrees with the identification of the critical residues carried out with the ϕ-value analysis, which suggests that the latter can identify kinetically relevant residues in protein folding, independently of the change in free energy of folding induced by mutation. For the most complex geometry, however, the P_fold and ϕ-value analyses give more consistent results than for the more local geometry. This can be inferred from the overlap between the set of bonds identified as core critical bonds via the two considered methodologies, which is 30% larger for the more complex geometry.

The study of the TS structure reveals that the residues identified as critical through the ϕ-value analysis are not necessarily fully native in neither of the identified TS ensemble subpopulations. Indeed, it is only for the more complex geometry that two of the five critical residues show a considerably high probability (up to 75%) of having all its native bonds formed in the TS. Therefore, one concludes that, in general, the ϕ-value correlates with the acceleration∕deceleration of folding induced by mutation, rather than with the degree of nativeness of the TS,⁴ and that the “traditional” interpretation of ϕ-values may provide a more accurate picture of the TS structure only for more complex native geometries.

Overall, our results suggest that native folds having predominantly nonlocal bonds are more suitable targets for ϕ-value analysis than other protein geometries.