Toward accurate reconstruction of functional protein networks

Abstract

Genome-scale screening studies are gradually accumulating a wealth of data on the putative involvement of hundreds of genes/proteins in various cellular responses or functions. A fundamental challenge is to chart out the protein pathways that underlie these systems. Previous approaches to the problem have either employed a local optimization criterion, aiming to infer each pathway independently, or a global criterion, searching for the overall most parsimonious subnetwork. Here, we study the trade-off between the two approaches and present a new intermediary scheme that provides explicit control over it. We demonstrate its utility in the analysis of the apoptosis network in humans, and the telomere length maintenance (TLM) system in yeast. Our results show that in the majority of real-life cases, the intermediary approach provides the most plausible solutions. We use a new set of perturbation experiments measuring the role of essential genes in telomere length regulation to further study the TLM network. Surprisingly, we find that the proteasome plays an important role in telomere length regulation through its associations with transcription and DNA repair circuits.

Introduction

In recent years, several studies have addressed the problem of inferring a specific subnetwork within a global protein–protein interaction (PPI) network that is associated with some disease or phenotype. These studies can be roughly classified into two categories: those that use a known core of proteins involved in the disease as a basis for subnetwork expansion (Goehler et al, 2004; Lim et al, 2006; Pujana et al, 2007) and those that overlay phenotypic or expression information on the protein network to identify subnetworks that are enriched with responsive proteins (Said et al, 2004; Calvano et al, 2005; Scott et al, 2005; Chuang et al, 2007).

Our study falls under the second category. Given a genome-wide experiment identifying a subset of genes as phenotype-related, we seek a PPI subnetwork linking the identified genes. We focus on phenotypes for which there is a strong evidence for an end target, or anchor point, to which signaling-regulatory pathways should lead from the phenotype-related genes identified. For example, maintaining telomere length in yeast (Shachar et al, 2008) depends on a large number of proteins (Askree et al, 2004; Gatbonton et al, 2006). However, their phenotypic effect is primarily mediated by a small group of telomerase-related enzymes and nucleases (Shachar et al, 2008), which can serve as the single anchor point of the system. Another prevalent example comes from large-scale measurements of expression changes in response to perturbation of a certain transcription factor (Workman et al, 2006). In this case, one is interested in the pathways connecting the two differentially expressed genes and the perturbed transcription factor, where the latter serves as the anchor point.

One can think of two basic conceptual approaches to reveal the underlying functional protein subnetwork given this kind of experimental setup. The first is to search for the most probable pathways that go from the phenotype-related genes to the anchor point. The corresponding optimization criterion is local, as the subnetwork model is constructed independently (and in parallel) for each gene. Such an approach was recently taken by Shachar et al (2008) for the set of telomere-length maintenance genes in yeast. Although this approach maximizes the likelihood of the connecting pathways, it tends to include in the inferred subnetwork many ‘surplus' genes that are not known to be phenotype-related. This motivates a second alternative that aims at minimizing the number of such ‘surplus' genes. This is a global optimization criterion that considers all the phenotype-related genes concomitantly and is known as the Steiner tree problem (Winter, 1987; Scott et al, 2005). Although maximizing network compactness and parsimony, the global approach may miss many phenotype-related genes that for some reason did not come up on the biological screens. Naturally, this motivates an intermediary approach, which aims at satisfying both optimization goals (local and global) as best as possible. The need for such an approach is further reinforced by our theoretical analysis, showing that a solution that maximizes only one goal can lead to quite poor results in terms of the other goal, and vice versa. Here, we present a novel algorithm for network reconstruction, indexed by a single parameter that provides explicit control over the relative importance of the local and global criteria, thus allowing the exploration of different intermediary regimens.

We test the different approaches for network reconstruction using two case studies: the controlled cell death system of apoptosis in humans and the telomere-length maintenance system in yeast. Both systems involve complex processes and encompass multiple proteins and pathways. However, as a case study they are fundamentally different. The core machinery of the apoptotic pathways and the identity of the proteins involved are quite well established. Conversely, the coverage of genes responsible for telomere length maintenance (TLM), and the pathways through which they act is very partial (Verdun and Karlseder, 2007; Shachar et al, 2008).

Our contribution in this paper is two-fold. From a computational standpoint, we study how the amount of data available on a system should modulate the choice of algorithmic approach. We show that when the relevant genes are mostly known, a global approach should be preferred. Conversely, when the information is partial, we show that the intermediary approach prevails. From a biological standpoint, this paper presents novel reconstructions of two basic cellular networks: TLM and apoptosis. We further investigate the TLM system both computationally and experimentally obtaining new insights on its regulation mechanisms. In particular, we provide novel evidence for the crucial role of the proteasome in telomere length regulation.

Results

Problem definition and the local/global trade-off

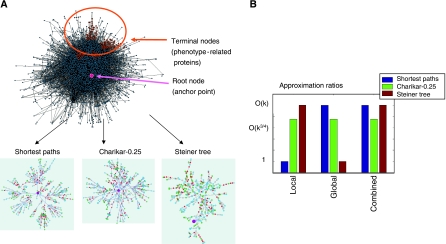
Given a network of PPIs, weighted by their reliabilities, a single root node (representing the anchor point) and a set of terminal nodes (representing the phenotype-related genes), we seek a connected subnetwork H that links the root to the terminals (Figure 1A). In the global variant of the problem, we wish to maximize the likelihood of the subnetwork H, which translates to minimizing the sum of weights (denoted F_G) of the edges in H. This is precisely the Steiner tree problem, which is known to be NP hard, but admits efficient constant approximation algorithms (Gropl et al, 2001). In the local variant of the problem, we seek the most probable (minimum weight) path from the root to each terminal separately. Thus, we wish to optimize the sum of weights of edges along these paths, which we denote by F_L. Clearly, an optimal value of F_L can be obtained efficiently by taking the union of all the shortest (lowest weight) paths from the terminals to the root (see Materials and methods for a detailed description of the problem and the two optimization criteria).

Figure 1.

Method overview. (A) Illustration of the network construction problem. We are given a network of interacting proteins, a subset of phenotype-related proteins (terminal nodes), and an anchor point (root node). The goal is to construct a subnetwork composed of signaling-regulatory pathways that lead from the phenotype-related set to the anchor point. We use three approaches for reconstructing these subnetworks––local optimization using the shortest path algorithm, global optimization using the Steiner tree algorithm and the intermediate approach using the Charikar-α algorithm. (B) Theoretical approximation bounds are displayed for the global, local and combined objectives. k is the number of terminal nodes. In this figure, we use an α value of 0.25. In the general case (0⩽α⩽0.5), Charikar-α provide bounds of O(k^1–α), O(k^½+α), and O(k^{max{1–α,½+α}}) for the global, local and combined objectives respectively (Supplementary information).

As both optimization criteria are desirable, it is paramount to evaluate each algorithmic approach on both optimization criteria. A theoretical asymptotic worst-case evaluation of the approaches is summarized in Figure 1B, and the pertaining ‘adversary' examples appear in Supplementary Figure 5. Evidently, obtaining an optimal overall compactness for the entire subnetwork (minimizing F_G) does not ensure obtaining highly probable specific terminal-root paths (minimizing F_L). Conversely, obtaining such highly probable terminal-root paths does not guarantee an overall probable model. Aiming at optimizing both criteria simultaneously, we suggest a new combined objective—their normalized sum (Materials and methods). We design a novel algorithm that provides approximation guarantees with respect to this new function and, consequently, with respect to each criterion by itself.

The reconstruction algorithm

Our intermediary approach for network reconstruction borrows ideas from both the Steiner tree (global) and shortest path (local) approaches. This is done by an extension of a previous algorithm by Charikar et al (1999) for the Steiner tree problem in directed graphs. The extended algorithm, which we call Charikar-α, has a single parameter, 0⩽α⩽0.5, that provides explicit control over the trade-off between the global (preferring large values of α) and local (preferring small values of α) approaches. The algorithm is based on an iterative search of edge-reliable subtrees that connect the root to subsets of the terminals, until the entire set of terminals is covered. The approximation guarantees of the algorithm are summarized in Figure 1B. Owing to space limitation, we defer the detailed description of the algorithm and the proofs of its approximation guarantees to the Supplementary information.

In the following analyses, we experimented with the two extreme approaches (Steiner tree and shortest paths) as well as the Charikar-α algorithm with three different α values (0, 0.25 and 0.5), spanning the entire spectrum for that parameter (see Supplementary information for implementation details). As expected from the theoretical bounds (Figure 1B), in both our case studies (apoptosis and TLM) the Charikar-0.25 algorithm performed best in terms of the combined objective (Supplementary Tables I and II). Henceforth, we focus our attention on the biological significance of the obtained subnetworks.

Analyzing the apoptosis data set

Apoptosis is a controlled cell death process that plays a major role in morphogenesis and tissue sculpting, tissue homeostasis and elimination of infectious pathogens (Taylor et al, 2008). The core apoptotic machinery comprises of death receptors which, through cascades of molecular events, lead to activation of caspase proteins. Subsequent cleavage of the various caspase substrates causes a number of events (such as chromatin condensation, DNA fragmentation, etc.) that eventually lead to the collapse of the cell.

We manually assembled a group of 77 proteins (denoted as the APT proteins) known to act as the core machinery of the apoptotic pathways in humans. This is a comprehensive list, based on a large amount of biochemical, genetic and cell-based experiments conducted over more than two decades of intensive work (see Supplementary information for a list of relevant references). We added a new node downstream to the caspase substrates, and used it as the root. We then applied the different network reconstruction methods to reveal how the APT proteins (serving as the terminal set) act through one or more of the caspase substrates. Details of the construction and analysis of the apoptosis system, including specific biological case studies, are provided in the Supplementary information.

Large-scale performance comparison

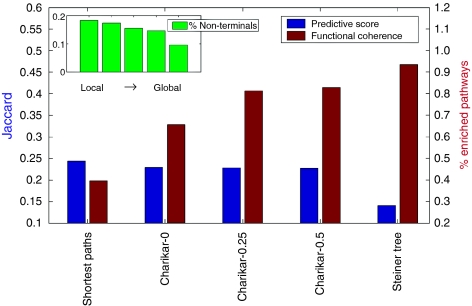
For each protein in the APT set, we computed the union of all paths connecting it to the root node, and call this path collection a pathway. We then defined the functional coherence of a subnetwork model as the percentage of pathways that is significantly coherent in terms of the gene ontology annotations (Harris et al, 2004). The results in Figure 2 show a clear increase in performance as we go from the local to the global extreme. Similar trends were observed with an alternative functional coherence measure that is based on manual curation of the APT set (Supplementary information).

Figure 2.

Performance of the different approaches on the apoptosis data. Presented measures include functional coherence (fraction of functionally coherent pathways) and predictive score (the ability to recover unannotated APT proteins, measured using the Jaccard index). The percentage of non-terminal nodes (i.e. proteins not on the APT set) in the models is presented in the inset, with methods ordered similarly to the main figure.

As a second quality measure, we tested the ability of the models to recover unannotated APT proteins. This was done in a cross-validation setting, using the predictive score (Supplementary information). The results in Figure 2 show that the local and Charikar-α algorithms perform well, and quite similar to each other, whereas the global approach is substantially outperformed by the rest.

The apoptosis case study reflects well the trade-off between the global and local approaches. We see that when the entire set of APT proteins is considered, then the global approach produces the most accurate model. Indeed, as the optimization goal of this approach is to maximize the overall network parsimony, it is the reasonable choice when the list of proteins involved is comprehensive (Figure 2, inset). On the other hand, as suggested by its poor predictive score, this optimization approach tends to miss many relevant proteins when not all the data are available. Unlike the two extreme approaches, the intermediate one manages to perform reasonably well on both scenarios.

After comparing the different approaches in this well-established system, we now proceed to explore the TLM in yeast—a more common case study that involves a substantially larger amount of proteins, many of which are still unknown.

Analyzing the TLM data set

Telomeres are specialized DNA–protein structures at the ends of eukaryotic chromosomes, which protect them from being recognized as double-strand breaks (de Lange, 2005). Telomeric DNA is synthesized by the enzyme telomerase, which is expressed at the early stages of development, but not in most somatic cells. Telomeres shorten with replicative age, leading eventually to cellular senescence.

In yeast, the length of the telomere is constantly maintained by a complex and delicate balance between positive and negative signals through mostly unknown pathways (Verdun and Karlseder, 2007). Two genome-wide surveys were recently performed to study this system by measuring the telomere length of deletion mutants of non-essential genes (Askree et al, 2004; Gatbonton et al, 2006). The relatively small overlap between the gene lists uncovered by the two studies implies a high rate of false negatives, even among non-essential genes, estimated at almost 50% by Shachar et al (2008).

The TLM data set consists of 250 non-essential genes identified in the two genome-wide surveys, and 23 genes reported in the literature to be related to telomeres but not identified in either screen (Shachar et al, 2008). Each of the 250 non-essential genes is also assigned with a phenotypic label (short or long), in accordance with the effect that its knockout had on the telomere length in the pertaining TLM screening experiment. We considered a group of 10 telomere-binding proteins, including subunits of the telomerase and telomerase-interacting proteins, as the ‘telomerase machinery' (Shachar et al, 2008), serving as an anchor point to which the TLM genes should be connected. This was achieved, as before, by adding a root node to the network (labeled TELOMERE), and connecting it to the telomerase machinery proteins. In the following, we examine the biological relevance and applicability of the different methods by using large-scale measures as before, and by inspecting specific test cases. In addition, we examine the obtained subnetworks against new experimental data.

Large-scale performance comparison

We use similar measures as in the apoptosis system to assess the functional coherence and predictive ability of the different methods. Two additional measures specifically designed for the TLM knockout screens are: monochromaticity—the overall consistency of the pathways to the TELOMERE node in terms of knockout effect (short or long); and phenotype vs location—the correlation between the magnitude of the knockout effect of the TLM proteins and their location in the network (see Supplementary information for a detailed description of these performance measures).

A comparison of the different models (Table I) reveals that in most cases the intermediary approach outperforms the extreme ones. The very long paths from the TLM proteins to the TELOMERE node that characterize the Steiner tree (global) model (Supplementary Figure 6; Supplementary Table I) are much less coherent in terms of phenotypic effect (assessed by the monochromaticity measure) than the remaining models. On the other hand, these pathways are more coherent in terms of functional annotation than the other models. In terms of generalization power (the predictive score), the global approach performs significantly worse than the rest. The remaining methods show significantly higher coverage of the left out sets, with the best coverage obtained by the Charikar-0 variant. Finally, we see a substantially higher correlation between the topology of the model and the magnitude of the phenotype (the phenotype vs. location measure), with the Charikar-α variants (especially with α=0.25, 0.5) than with either the local or the global models.

Table 1.

Performance of the different approaches on the TLM data

Method	M-C	F-C	P-S	PvL	N-T	Suc	PPA
Shachar et al	0.73	0.55	—	0.03, NS	0.44	0.15	0.72 [16/22]
Shortest paths	0.81	0.35	0.041	0.035, NS	0.46	0.28	0.81 [13/16]
Charikar-0	0.81	0.31	0.043	0.026, NS	0.45	0.28	0.81 [13/16]
Charikar-0.25	0.79	0.38	0.041	0.008, 0.12 (P=0.057)	0.45	0.33	0.86 [13/15]
Charikar-0.5	0.81	0.42	0.042	0.001, 0.157 (P=0.013)	0.44	0.38	0.73 [11/15]
Steiner tree	0.64	0.91	NS	NS, NS	0.41	0.22	0.55 [11/20]

Displayed measures include: monochromaticity (mean coherence in telomere length phenotype, M-C); functional coherence (fraction of functionally coherent pathways, F-C); predictive score (the ability to recover unannotated TLM proteins, P-S) and the phenotype vs. location (PvL) measure (including the hypergeometric score, the partial correlation index that factors out the distance to the telomere, and the corresponding P-value, see Supporting Information). N-T is the ratio of non-terminal nodes (i.e. proteins not on the TLM set) included in the model. The last two columns present the success rate (Suc) and phenotype prediction accuracy (PPA) on the new experimental data. The numerator and denominator of the PPA are given in parentheses. We use a cutoff of 0.05 on the P-values. Non-significant results are marked as NS. The best result in each column appears in bold.

Experimental testing of predicted TLM proteins

In a set of recently conducted experiments (Ungar et al, submitted), we investigated the role of essential genes in telomere length regulation by screening the decreased abundance by mRNA perturbation (DAmP) (Schuldiner et al, 2005) yeast library. This procedure yielded 67 essential genes that had a TLM phenotype (Materials and methods). We use this new experimental data in conjunction with a new data set published by Shachar et al (2008) as an important source to validate and further study the different models. Overall, we collected 99 genes for which we had new experimental data and were not used in the reconstruction process. This set included 20 non-essential genes and 79 essential genes; in total, 89 of these genes exhibited defects in telomere length (53 were short and 36 exhibited elongated telomeres).

We assess the performance of the different models with respect to these new experiments in two manners. First, we measure a success rate, reflecting the extent to which the models include new proteins that exhibited defects in telomere length and exclude proteins with no phenotypic effect. Second, we measure for each method its accuracy in predicting the observed phenotypes (short or long). The performance measures and the phenotype prediction method are described in the Supplementary information. As summarized in Table I, the local and intermediate approaches have a roughly similar performance, whereas the global approach performs substantially worse than the rest. The best overall performance is achieved by Charikar-0.25, with a success rate of 33% and prediction accuracy of 86%.

Biological case analysis: the proteasome

A comparative analysis of the TLM subnetworks generated by the different methods is provided in the Supplementary information. This analysis has revealed time and again the superiority of the Charikar-α approach and in particular the Charikar-0.25 algorithm, as demonstrated in several examples concerning the Est, Rad53 and Tel1 proteins. In the following, we use the Charikar-0.25 model to draw new biological insights on the workings of the TLM system and its relation to the proteasome (see Supplementary information for an additional interesting case involving the Rsc8 chromatin remodeling subunit).

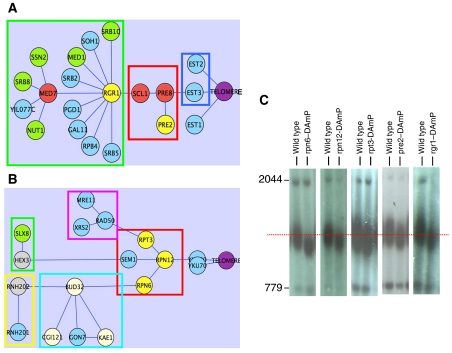
Figure 3A depicts one of the submodels obtained by the Charikar-0.25 algorithm, suggesting a connection between the RNA polymerase II mediator complex and Est3p, a component of the telomerase holoenzyme (Hughes et al, 2000), through Scl1p and Pre8p, members of the proteasome (Groll et al, 1997). The Saccharomyces cerevisiae mediator complex is essential for RNA polymerase II-mediated transcription (Kim et al, 1994). Est2p, the reverse transcriptase subunit of the telomerase holoenzyme, is bound to the telomere constitutively, whereas Est1p and Esp3p are important telomerase-binding proteins absent during G1 phase (Taggart et al, 2002). Recent studies have suggested that this phenomenon is due to proteasome-dependent degradation of Est1p (Osterhage et al, 2006). In addition, new studies have revealed strong connections between RNA polymerase II transcription and the ubiquitin/proteasome pathway (Gillette et al, 2004). Our results thus suggest that the association between transcription-related mechanisms and proteasome-dependent degradation plays a role in telomere maintenance. In addition, our model predicts that both Rgr1 (mediator) and Pre2 (proteasome), two essential genes not tested in the original TLM screens, have a short telomere length phenotype. This was validated by inspecting the corresponding DAmP mutants that exhibited short telomeres (Figure 3C).

Figure 3.

The proteasome's role in telomere length regulation. Green nodes: TLM proteins, the mutants of which have elongated telomeres; blue nodes: TLM proteins, the mutants of which have short telomeres; yellow nodes: essential proteins that showed a short TLM phenotype in our new experimental data set. Beige nodes, TLM protein from the literature, the effect (short or long) of which on telomere length is not readily available; red nodes: protein products of essential genes (not on the TLM list); gray nodes: protein products of non-essential genes and not on the TLM list; purple node: the TELOMERE anchor node. (A) The mediator complex and the proteasome. Green frame: mediator complex components; red frame: proteasome subunits; blue frame: Est1/3 components of the telomerase. (B) DNA repair components and the proteasome. Green frame: Slx5(Hex3)–Slx8 complex; red frame: proteasome subunits; light blue frame: KEOPS complex; pink frame: MRX complex; yellow frame: ribonuclease H2 subunits. (C) Telomere Southern blot of the essential genes RGR1, PRE2, RPN6, RPN12 and RPT3 from the DAmP Yeast Library. DNA was digested with XhoI and probed with telomeric sequences and with unique genomic sequences used as markers (Askree et al, 2004). A red line marks the telomere size of the wild-type strain.

The submodel in Figure 3B suggests a major pathway of telomere length regulation based on DNA repair mechanisms, with the proteasome as the central core. This core includes the Rpn6, Sem1, Rpt3 and Rpn12 subunits that act as mediators, connecting other complexes involved in DNA transactions. Indeed, in the last few years, proteasome activity has been linked to DNA repair and DNA damage response. For example, the human ortholog of Sem1 (part of the proteasome's lid subcomplex) has been shown to associate with the tumor suppressor protein Brca2 (Marston et al, 1999), involved in the repair of DNA double-strand breaks. A similar role has been shown for the yeast ortholog (Krogan et al, 2004).

Connected to the proteasome, the Charikar-0.25 model correctly assembles the Mre11–Rad50–Xrs2 (MRX), and the KEOPS complexes as well as the Ku heterodimer (consisting of Yku70 and Yku80), which have well-characterized roles in TLM. Specifically, the MRX complex is required for DNA repair; it is involved in double-strand break repair, meiotic recombination, telomere maintenance and checkpoint signaling (Bressan et al, 1999). The KEOPS complex has been implicated in transcription regulation and telomere maintenance (Downey et al, 2006; Bianchi and Shore, 2007). Furthermore, Rnh201 and Rnh202, two ribonuclease H2 subunits, were found to be linked to the proteasome through Bud32. The ribonuclease H2 complex removes RNA primers during Okazaki fragment synthesis, cooperating with Rad27/FEN1 nuclease during DNA replication and repair. The proteasome units were also connected by the model to the Slx8/Hex5 heterodimer, which links ubiquitination and SUMOylation to genome stability activities (Burgess et al, 2007; Xie et al, 2007). This suggests a possible involvement of SUMO as a regulator of proteasome activity at telomeres.

Out of the four proteasome subunits that act as mediators, three (Rpn6, Rpt3 and Rpn12) are essential for viability, and thus were not included in the two genome-wide screens that tested TLM (Askree et al, 2004; Gatbonton et al, 2006). The fourth subunit (Sem1) is non-essential and was found by Gatbonton et al (2006) to have a short phenotype. Our model predicts that mutations in the essential proteasome subunits should lead to short telomeres. Reassuringly, all three were validated on our new experiments to have a short TLM phenotype (Figure 3C). Overall, these results suggest a major pathway of telomere length regulation based on DNA repair mechanisms, with the proteasome serving as its central core.

Discussion

We have presented a novel algorithm for subnetwork reconstruction and have applied it to reconstruct two basic cellular networks: apoptosis and TLM. The well-established apoptosis core machinery was very useful as a first case study as it allowed us to explore different levels of data coverage. We discovered that when we make the majority of the relevant proteins available, the global approach performs best in terms of constructing the relevant subnetwork. Using cross-validation, we then saw that when the available data are partial, then the global approach performs poorly in predicting unannotated relevant protein. In both cases, the intermediary approach yielded reasonable solutions. In the TLM system, which represents the more common case where a substantial amount of the relevant proteins is unknown, the intermediary approach gave the most plausible models. Specifically, it outperformed the local and global approaches in all functional measures we have used (except for functional coherence). Inspecting the biological validity of the global approach and Charikar-α revealed that the latter (and in particular the Charikar-0.25 variant) are more plausible. Finally, using new experimental data, we see that the Charikar-0.25 variant achieves the highest accuracy in terms of predicting new TLM proteins. Most importantly, detailed inspection of the Charikar-0.25 model in conjunction with our new experimental data has provided a number of novel biological insights on the TLM system and the role of the proteasome in its regulation.

As we have demonstrated, the α-parameter allows combating different rates of false negatives (at least in the case studies used in this paper). Controlling for false positives is more challenging and could be approached for example by employing prize collecting variants of the different objectives presented here. In these variants, the requirement that all terminals should be connected to the anchor is relaxed and, instead, a prize is awarded for each terminal that is connected to the anchor.

In a recent publication, Mozdy et al (2008) carried out an analysis of the TLM mutants, looking for those that exhibit defects in the level of TLC1, the RNA moiety of yeast telomerase. One of their findings was that the Paf1 complex, an RNA polymerase II-associated factor, is important for TLC1 synthesis. In the Charikar-0.25 model, the proteins of this complex cluster together, and, interestingly, seem to interact with the telomeric ssDNA-binding protein Cdc13 through their connections to SPT16, a subunit of the FACT complex, which is another RNA polymerase II-interacting complex. In addition, Mozdy et al found that tpd3 cells show decreased, and ppe1 cells show increased levels of telomerase RNA. These results make sense if one considers that Tpd3 and Ppe1 are two regulators of protein phosphatase 2A (PP2A) activity with opposing effects. Our model shows that indeed protein phosphatase activity plays a central role in determining telomere length by controlling TLC1 expression: Rrd1, Pph21, Pph22 and Cdc55, additional regulators of PP2A, all map to the same branch in our model (Supplementary Figure 4). Moreover, all these proteins are connected to the telomere node through Zds2, a protein that plays a role in telomeric silencing, suggesting that it may be the target of regulation by phosphorylation–dephosphorylation cycles.

It is pertinent to view our results for the TLM system in the context of Shachar et al (2008) who recently reconstructed it: (i) The basic notion of their method was local, i.e. connecting each TLM protein to the telomerase machinery independently from the rest. Our approach is conceptually different as it takes into account the importance of interdependencies between the proteins and probes the spectrum between local and global reconstructions. (ii) The intermediary approach has outperformed the model of Shachar et al in most of our large-scale performance measures (Table I). (iii) We use new experimental data of essential TLM genes and show that the intermediary approach performs substantially better in recovering the newly identified TLM proteins (and excluding the non-TLM proteins), and in predicting their phenotypic effect. (iv) Albeit local, the actual algorithmic methodology of Shachar et al is different from the shortest path approach presented here and could not be solved efficiently. Consequently, their model could only cover 71% of the TLM proteins, whereas the models presented here cover all of them. Importantly, many of the new proteins involved in the biological cases discussed above (including the Rgr1 protein, Rsc8 protein and most of the proteasome subunits) were not included in the model of Shachar et al.

Methods for reconstructing functional protein networks play a pivotal role in understanding and modeling cellular systems. A subnetwork model of the type discussed in this paper encapsulates many hypotheses about the underlying architecture of the investigated system. Among others, it can shed light on the actual signaling-regulatory pathways underlying the system and on central proteins that are essential for its functioning. Another useful property is that it provides specific predictions of proteins involved in the system that were not previously detected. Indeed, as our results show, the reconstructed network models have the ability to recover relevant and previously unknown proteins, accurately predict their phenotypic effect and supply a working hypothesis as to how these proteins are ‘wired' to each other and to the anchor point.

Materials and methods

PPI network construction

We assembled PPI data from public databases and recent publications to construct a comprehensive PPI network of yeast (Xenarios et al, 2002; Christie et al, 2004; Gavin et al, 2006; Krogan et al, 2006; Reguly et al, 2006), and humans (Peri et al, 2003; Rual et al, 2005; Stelzl et al, 2005; Ewing et al, 2007). In the latter case, we embedded the network with a small set of manually curated interactions between APT proteins that were missing from the public data sets (Supplementary information). The PPIs were assigned confidence scores based on the experimental evidence available for each interaction using a logistic regression model adapted from Sharan et al (2005).

Denote by P(e) the reliability assigned with an edge e. Assuming independence of edges, the probability that all the edges within a subgraph H exist is simply 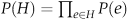. To avoid bias toward specific highly probable sets, we follow the approach of Shachar et al (2008) and add a size-penalizing factor, by redefining the probability of a given subgraph H as: 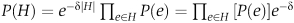. Thus, the reliability of an edge e is set to P(e)·e^–δ. In our implementation, we set the free parameter δ such that the per-edge penalty, e^–δ, equals the weight of an edge at the 25th percentile. We also experimented with other edge penalty values and obtained similar results (Supplementary Figure 7).

Problem definition

Let G=(V, E, ω) be an undirected weighted graph on n vertices, where the weight of an edge is the −log transform of its reliability. Given a root (anchor point) r∈V and a set X⊆V of terminals, our goal is to construct a connected subgraph H=(V_H, E_H) of G that connects the root to the terminals (in particular X ⋃ {r}⊆V_H).

In the global variant of the reconstruction problem, we seek a connected subgraph H with maximum overall likelihood. Assuming that edge reliabilities are independent, this likelihood is simply the product of edge reliabilities or, equivalently, the −log likelihood is the sum of edge weights in H. Formally, our optimization goal is to minimize the sum:

In the local variant of the problem, we seek a most probable path from the root to each terminal separately. Thus, we look for a subgraph H in which the sum of −log likelihoods of the paths connecting a terminal node to the root is minimum: 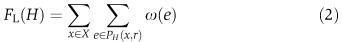where P_H(x; r) is the shortest path from a terminal x∈X to the root node r in H.

The combined objective of the two optimization functions is defined as their normalized sum c·F_G+F_L. To balance the two terms, we set the normalizing factor c to OPT_L/OPT_G, where OPT_G and OPT_L are the optimal values of F_G and F_L, respectively. Note that c depends on the input instance. Also note that unless the Steiner tree and shortest path solutions identify, no subgraph can attain an optimum value under both F_G and F_L.

In the Supplementary information, we show that the local variant has an approximation bound of O(k) (where k=∣X∣) for F_G and for the combined objective. Similarly, the global variant has an approximation bound of O(k) for F_L and the combined objective. The new Charikar-α algorithm, however, has bounds of O(k^1−α), O(k^½+α) and O(k^{max{1−α,½+α}}) for F_G, F_L and the combined objective, respectively.

Screening for essential genes involved in TLM

Strains from the DAmP Yeast Library (Schuldiner et al, 2005) were grown in YPD medium at 30°C. After 2 days, the yeast DNA was extracted and Southern blots were carried out as described in Askree et al (2004). Each strain and the isogenic wild-type controls were run in triplicate. Marker PCR fragments containing a genomic region that hybridizes to two bands (2044- and 779-bp long) were included in the labeled probes. Telomere length in all strains was extremely reproducible, with a standard variation of <10%. After an initial screen, all strains suspected as having a significant telomere length phenotype were re-tested, starting from fresh duplicate cultures. Tetrad analysis was used to confirm co-segregation between telomere length and resistance to G418 (conferred by the KanMX allele at the DAmP allele). The list of essential genes that exhibit short or long telomere phenotype is provided on the Supplementary information website http://www.cs.tau.ac.il/~niryosef/CHAR/summary/.

Supplementary Material

Supplementary Materials 1

Supporting information and figures

Supplementary Materials 2

The apoptosis data set