Abstract
Biochemical and regulatory interactions central to biological networks are expected to cause extensive genetic interactions or epistasis affecting the heritability of complex traits and the distribution of genotypes in populations. However, the inference of epistasis from the observed phenotype–genotype correlation is impeded by statistical difficulties, while the theoretical understanding of the effects of epistasis remains limited, in turn limiting our ability to interpret data. Of particular interest is the biologically relevant situation of numerous interacting genetic loci with small individual contributions to fitness. Here, we present a computational model of selection dynamics involving many epistatic loci in a recombining population. We demonstrate that a large number of polymorphic interacting loci can, despite frequent recombination, exhibit cooperative behavior that locks alleles into favorable genotypes leading to a population consisting of a set of competing clones. When the recombination rate exceeds a certain critical value that depends on the strength of epistasis, this “genotype selection” regime disappears in an abrupt transition, giving way to “allele selection”—the regime where different loci are only weakly correlated as expected in sexually reproducing populations. We show that large populations attain highest fitness at a recombination rate just below critical. Clustering of interacting sets of genes on a chromosome leads to the emergence of an intermediate regime, where blocks of cooperating alleles lock into genetic modules. These haplotype blocks disappear in a second transition to pure allele selection. Our results demonstrate that the collective effect of many weak epistatic interactions can have dramatic effects on the population structure.
Keywords: gene interactions, population genetics
Selection acting on genetic polymorphisms in populations is a major force of evolution (1–4) and it is possible to identify specific loci under positive selection, e.g., the Adh locus in Drosophila (4). However, the attribution of fitness differentials to specific allelic variants and combinations remains a great challenge (5). Efforts to correlate quantitative phenotypes with genetic polymorphisms typically identify a small number of loci with a significant contribution to the observed phenotypic variance, but leave much of the variance unaccounted for (6). This unaccounted variance is believed to arise from a large number of loci with small individual contributions, or be due to epistasis and quite likely involves both effects. New studies accumulate evidence that epistasis is widespread and accounts for a significant fraction of phenotypic variation, e.g., in yeast (7–9). Additional evidence for epistasis comes from crosses of mildly diverged strains, where the recombinant progeny often has reduced average fitness, i.e., displays outbreeding depression. The reduction in fitness is attributed to the breakdown of favorable combinations of alleles in the ancestral strains (10). Outbreeding depression is often observed in partly selfing organisms such as Caenorhabditis elegans (11) or plants (12), species with strong geographic isolation such copepod (13) or facultatively mating organisms such as yeast (14). Although most recombinant genotypes are less fit, novel genotypes that perform better than either parental strain can be generated as well (15). Such outcrossing events could play an important role in evolution.
Competition between epistatic selection and recombination, explicit in the outbreeding depression phenomenon, is the focus of the present study. In the presence of epistasis, selection, by increasing the frequency of favorable genotypes, establishes correlations between alleles at different loci. Recombination however reshuffles alleles and randomizes genotypes breaking up coadapted loci. Because the recombination rate between any 2 loci is largely determined by their physical distance on the chromosome, the effect of genetic interactions depends on gene location. It is known that functionally related genes tend to cluster (16, 17), suggesting selection on gene order. Furthermore, chromosomes have regions of infrequent recombination, interspersed with recombination hotspots (18). Does selection have a hand in defining low recombination regions? To understand how evolution shaped genomes as we observe them today, we have to tackle the problem of how selection acts on many interacting polymorphisms for a large range of recombination rates (19).
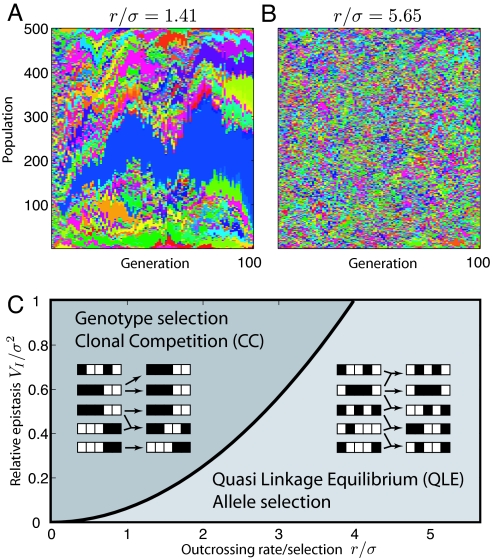
Standing variation harbored in natural population provides important raw material for selection to act upon, in particular after a sudden change in environments or hybridization events (20). In such a situation, selection will reduce genetic variation until a new mutation-selection equilibrium is reached. Here, we show that the selection dynamics on standing variation at a large number of loci can be strongly affected by epistasis, even if the individual contribution of each locus is small. The competition between selection on epistasis and recombination gives rise to 2 distinct regimes at high and low recombination rates separated by a sharp transition. The population dynamics in the two regimes is illustrated in Fig. 1 A and B: (i) the “clonal competition” (CC) regime, which occurs for recombination rates r < rc and (ii) the quasi linkage equilibrium (QLE) regime for r > rc. The different nature of the two regimes is best understood by considering the limiting cases of no and frequent recombination. In the case of purely asexual reproduction, selection operates on entire genotypes and results in clonal expansion of the fitter ones. The genetic variation present in the initial population is lost on a timescale inversely proportional to the average magnitude of fitness differentials between genotypes present in the population. Successful genotypes persist in time, which is apparent as continuous broad stripes of one color in Fig. 1A. The amplification of a small number of fit genotypes induces strong correlations or linkage disequilibrium among loci. In presence of epistasis, a little recombination does not change this picture qualitatively, because most recombinant genotypes are less fit than the prevailing clones and novel successful clones are rare. Nevertheless recombination is very important because it continuously introduces new genotypes leading to an increase in fitness attained by the population at long times. In the limit of high recombination genotypes are short-lived and essentially unique, resulting in a “pointillist” color pattern in Fig. 1B. Each allelic variant is therefore selected on the basis of its effect on fitness, averaged over many possible genetic backgrounds. The time scale on which allele frequencies change is given by the inverse of these marginal fitness effects. The term “linkage equilibrium” in QLE refers to the negligible correlations between loci, which are constantly reshuffled by recombination.
Fig. 1.
The two regimes of sexual reproduction. (A and B) The simulated time course of the genotype distribution in a population of 500 individuals with epistatic fitness variance VI = σ2 = 0.005 and outcrossing rate r = 0.1 (A) and r = 0.4 (B; RE model defined below). Like genotypes are assigned the same color and stacked on top of each other. (C Insets) Sketches illustrating the population dynamics in the 2 cases. At low outcrossing rates, fit genotypes can proliferate. The genotype distribution rapidly coarsens and clones form (horizontal stripes in A). With frequent outcrossing, genes are rapidly reshuffled and genotypes do not persist over many generations, resulting in the pointillist pattern in B. Fixation happens at later time and is not shown. (C) The two regimes are separated by a sharp boundary set by the strength of epistasis. For r < rc, the population dynamics is described by clonal competition (CC); for r > rc by quasi linkage equilibrium (QLE).
As we show below, the transition between the two regimes sharpens as the number of segregating loci L increases. The sharpening of the transition is related to the different scaling of the time scale of selection in the two regimes. For large L, the marginal fitness effects of individual loci become small compared with fitness differentials among individuals (assuming they are all of similar size, this ratio decreases as ∼1/). Hence, the dynamics in the QLE regime slows down compared with the CC regime as L increases. The CC and QLE regimes correspond to different regions of the parameters space spanned by the relative strength of epistasis and the ratio of outcrossing or recombination rate to the strength of selection, as sketched in Fig. 1C. The QLE dynamics was first described by Kimura (21) in the limit of weak selection/fast recombination for a pair of biallelic loci and subsequently generalized to multiloci systems (22, 23). The possibility of a collective behavior involving linkage disequilibrium among many loci and selection effectively acting on the whole chromosome as a unit has been pointed out before in the context of overdominance by Franklin and Lewontin (24) in the strong selection limit. However, these studies of the two different limits do not reveal the breakdown of QLE and the transition to CC as the generic behavior of multilocus epistatic systems.
To underscore the general nature of the results, have studied 2 different models of epistasis. The first model follows the common treatment of epistasis in quantitative traits, which assumes that the epistatic contribution to fitness is disrupted when the parental genes are mixed in sexual reproduction (25, 26). This assumption becomes exact when the epistatic component of fitness of a specific genotype is a random number (which depends on the genotype, but is fixed in time) and we call this model the random epistasis (RE) model. Within the RE model, any change in the genotype randomizes the epistatic component of fitness so that the latter is not heritable when nonidentical parents mate. It is, however, faithfully passed on to the offspring in asexual reproduction. For the RE model, genomes are propagated asexually with probability 1 − r and with probability r are a product of mating where all genes are reassorted, as would be exactly correct if all genes were on different chromosomes. This model of facultative mating approximates reproductive strategies common in fungi (e.g., yeast) or nematodes and plants. As a more realistic alternative, we also study a model with only pairwise interactions between loci (27). This pairwise epistasis (PE) model allows epistatic contribution to be partly heritable, because interacting pairs have a chance to be inherited together (28). For the PE model, we assume that all genes are arranged on a single chromosome with a uniform cross-over rate ρ, which allows us to explore haplotype block formation and implications for recombination rate evolution.
The strength of selection is determined by the variance σ2 of the distribution of fitness in the population. Within our models, the fitness F(g) of a genotype g is the sum of an additive component A(g) representing independent contributions of alleles and an epistatic part E(g). For the RE model, the latter is a random number drawn from Gaussian distribution, whereas for the PE model it is a sum of pairwise interactions with random coefficients fij. The variances VA and VI of the distributions of A(g) and E(g) add up to σ2 and their relative magnitude determines the importance of additive effects compared with epistasis. The two different models and their parameters are given explicitly in Methods. For the sake of simplicity, we assume haploid genomes. Random and pairwise epistasis represent 2 opposite extremes in the complexity of epistasis. Although the pairwise model is more realistic, the generic behavior is most clearly demonstrated using the RE model with random gene reassortment and facultative mating.
Results
Two Regimes of Selection Dynamics.
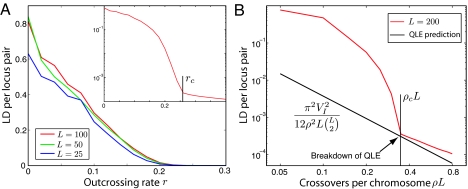
We performed extensive computer simulation of our two models for different relative strength of epistasis, L = 25–200 loci and populations sizes between N = 500 and 106. We initialize simulations in a genetically diverse state as would result from multiple crossings of 2 diverged strains and examine the evolution under selection and recombination. The two regimes differ strongly in the amount of linkage disequilibrium (LD) (see Methods) build up by selection. Fig. 2A shows the average LD per locus pair for the RE model as a function of the outcrossing rate r. For r < rc, the LD per locus pair is of order 1 and independent of L or N, indicating genome-wide LD. LD builds up despite a large number of different genotypes in the population interbreeding constantly. For r > rc, the LD is much smaller, with the observed value determined by the sampling noise due to the finite population size (see Fig. 2A Inset and Fig. S1). Similar behavior occurs in the PE model, as shown in Fig. 2B. Above a critical recombination rate ρc, the observed linkage disequilibrium is time independent and well described by the QLE approximation (21, 22) (straight line) (see SI Appendix). The QLE approximation (in the high ρ/σ limit) predicts LD to be proportional to the strength of pairwise epistasis. Below ρc, the observed LD is dramatically larger than the QLE expectation. Here, recombination is sufficiently infrequent such that genotypes with a synergistic alleles are amplified faster than they are taken apart by recombination, see below. As a result, the few fittest genotypes grow exponentially in number, leading to the strong correlation in the occurrence of cooperating alleles, independent of physical linkage (i.e., proximity on the chromosome). This extensive LD leads to a complete failure when extrapolating results valid in the high recombination regime across the transition. The relevant quantity that determines whether fit genotypes can be maintained is the probability that no cross-over occurs, which is given by e−ρL. Hence, ρc is inversely proportional to L.
Fig. 2.
The clonal competition regime is characterized by extensive linkage disequilibrium. (A) Random epistasis model: For small r, the LD per locus pair is of order 1 and fairly independent of L. (Inset) Data for L = 100 on a logarithmic scale and a mark at the value of rc. The LD for r > rc is due to sampling noise, see Fig. S1. (B) Pairwise epistasis model. For pairwise epistasis, the QLE approximation gives explicit predictions for LD, which describes the observed LD very accurately for ρ > ρc, black line. For ρ < ρc, LD is a much larger than the QLE prediction. For A and B, LD is measured when allelic entropy has decayed 30% from the initial value (σ2 = 0.005, VA = 0.1σ2 and VI = 0.9σ2). In A, N = 105, and the data shown are averaged over 100 realizations. To avoid boundary and finite size effects, we used N = 106, assumed a circular chromosome for B, and averaged over 10 realizations.
Self-Consistency Condition for QLE.
The fitness of a genotype can be decomposed as F = A + E, where A is the heritable additive part and E is the nonheritable epistatic part. As a coarse-grained descriptor of the population, we consider the joint distribution P(A, E; t) of the fitness components. In the QLE state, P(A, E; t) evolves approximately as
The first term accounts for the exponential growth of genotypes with fitness advantage F − F̄ and the loss due to recombination at rate r. The second term accounts for the production of genotypes through recombination. To a good approximation, the distribution of A among recombinant offspring is identical to that among the parents ϑ(A) = ∫ dE P(A, E), which in turn is approximately Gaussian (29). The distribution of E among recombinant offspring is independent of the parents and a random sample from the distribution of epistatic fitness ρ(E), which in our models is a zero-centered Gaussian. The latter is exactly true for the RE model and holds approximately for the PE model, where the correlation of E between ancestor and offspring halves every generation (28).
Eq. 1 admits the factorized solution P(A, E; t) = ϑ(A; t)ω(E) with ∂t ϑ(A; t) = (A−Ā)ϑ(A; t) and a time-independent distribution of E
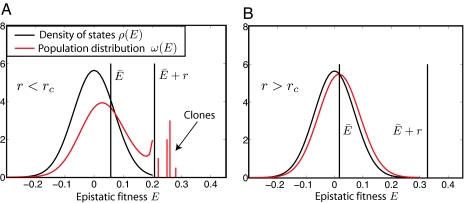
where Ē is determined by the condition that ω(E) has to be normalized. This solution exists only if E < r + Ē for all genotypes; otherwise, fit genotypes escape recombination and grow as clones. These two scenarios are illustrated in Fig. 3.
Fig. 3.
The break-down of QLE. (A) When the recombination rate decreases below rc, some individuals have epistatic fitness E larger than Ē + r, and the QLE solution for the distribution of epistatic fitness in the population breaks down. Individuals to the right of Ē + r form clones that grow exponentially and the population condenses into a small number of genotypes. (B) For r > rc, even the largest epistatic fitness contributions do not result in a growth advantage that exceeds the recombination rate.
The normalization condition can be fulfilled only if r is larger than some rc. Note that ρ(E) has to go to 0 faster than linear for rc to exist. The value of rc is proportional to the maximal E and hence proportional to the strength of epistasis . However, it is not the absolute maximum of E among all possible 2L genotypes that determines rc, but the maximal E that is encountered by the population before fixation. Hence, rc depends on the population size and the functional form of this dependence is determined by the upper tail of the distribution ρ(E). For the Gaussian distribution used here, rc ≈ , where τ is the time scale of QLE dynamics discussed below. The product rNτ then is the number of genotypes generated through recombination before fixation. A more detailed discussion is given in the SI Appendix.
The breakdown of the QLE state has some similarity to the error-threshold transition of a quasi-species model (30) in a rugged fitness landscape (31): Recombination of epistatic loci acts as deleterious mutations and prevents the emergence of quasi-species or clones (32, 33) for r > rc.
Maintenance of Genetic Diversity.
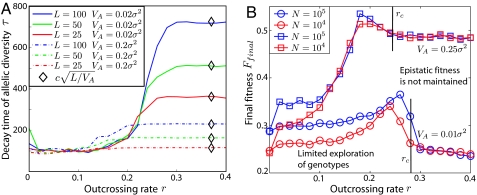
The transition between the two regimes leaves its imprint in virtually every quantity of interest in population genetics. For instance, the characteristic time for the decay of genetic diversity, τ (which we quantify via allele entropy, see Methods) scales differently with L in the two regimes, as shown in Fig. 4A. At low outcrossing rates, τ depends only on the total variance in fitness and neither on the number of loci nor the relative strength of additive contributions. This is consistent with the notion that in the CC regime genotypes are the units on which selection acts. With more frequent outcrossing, τ tends to be larger for weak additive contributions and large L. Beyond a certain outcrossing rate rc, τ becomes independent of r attaining a value inversely proportional to the additive contribution of the individual loci independent of VI (black diamonds in Fig. 3A). This observation confirms our assertion that for r > rc, outcrossing decouples the loci and that the allele frequencies evolve independently under the action of the additive component of fitness. Given an additive variance VA, the typical single locus fitness differential is f ∼ such that τ grows as for r > rc. To uncover the universal behavior in the vicinity of the transition in the limit of large genomes, we show that the data for different VI, VA, and L collapses onto a single master curve after appropriate rescaling of the axis, see Fig. S2. This scaling collapse demonstrates the existence of a sharp transition in the limit L → ∞, the scaling of τ with and shows that rc is proportional to , as expected from the self-consistency argument outlined above and sketched in Fig. 1C. The suppression of allele dynamics by 1/ in the QLE regime is at the basis of Fisher's infinitesimal model put forward to explain sustained response to selection (6). In one generation, the allele frequencies change by approximately f, which can be sustained over ∼f−1 generations. The mean fitness increases by VA per generation, consistent with Fisher's theorem (23, 26). Our results show, that epistasis causes the breakdown of the infinitesimal model for r < rc. The pairwise epistasis model is more complex than the random epistasis model, because the partition of the fitness variance in additive and epistatic contribution depends on the allele frequencies and epistasis is “converted” into additive fitness as the population approaches fixation (34).
Fig. 4.
Decay of genetic diversity and success of selection for RE model. (A) The time τ it takes to reduce the allelic entropy by 30% as a function of r for different parameters. For small r, τ is independent of L but increases with r. For r > rc, τ settles at c (black diamonds) in accord with the theoretical prediction for single locus dynamics (with c a fitting parameter). Additional data for VA = 0, VA = 0.5σ2 and a collapse confirming the scaling of τ is shown in Fig. S2. (B) The fitness of the fixated genotype Ffinal as a function of r for 2 different strength of epistasis. At r = 0, the final fitness only depends on the population size N and is independent of the strength of epistasis. Ffinal increases with r, followed by a pronounced drop right below rc. Above rc, Ffinal is almost constant and is independent of N. In both A and B, σ2 = 0.005. Data are averaged over 25 realizations in A and over 100 realizations in B. L = 100 in B.
The properties of the genotype that will eventually fixate in the population depend on the regime in which it was obtained. We find, that the fitness of this fixated genotype depends nonmonotonically on the outcrossing rate and peaks just below the transition, see Fig. 4B. This can be understood as follows. Without recombination, the final state can be no fitter than the fittest genotype initially present. With some recombination, the population explores a greater number genotypes, potentially finding ones with higher fitness so that the fitness of final state increases with r in the CC regime. A similar benefit of infrequent recombination due to exploration of genotype space has been studied in the context of virus evolution for additive fitness functions (35). As genotype selection gives way to allele selection, different loci decouple and the epistatic contribution to fitness is missed, leading to possible fixation of less fit genotypes and a sharp drop of the final fitness as r approaches rc. The dependence of the final fitness on the population size N highlight the distinct properties the dynamics in the two regimes: In the QLE regime, the final fitness is virtually identical for different N. This is a consequence of the fact that the relevant dynamical variables are allele frequencies, which are well sampled by  (N) individuals. Fluctuations of the allele frequencies are therefore negligible and the dynamics is essentially deterministic. This is different in the CC regime, where the dynamics is driven by the generation of rare, exceptionally fit genotypes. The rate, at which genotypes are generated is proportional to the N, resulting in a pronounced dependence on the population size. QLE ceases to be deterministic once the marginal fitness effects become comparable to inverse population size and random genetic drifts overwhelms selection (see Fig. S3).
(N) individuals. Fluctuations of the allele frequencies are therefore negligible and the dynamics is essentially deterministic. This is different in the CC regime, where the dynamics is driven by the generation of rare, exceptionally fit genotypes. The rate, at which genotypes are generated is proportional to the N, resulting in a pronounced dependence on the population size. QLE ceases to be deterministic once the marginal fitness effects become comparable to inverse population size and random genetic drifts overwhelms selection (see Fig. S3).
Selection on Genetic Modules.
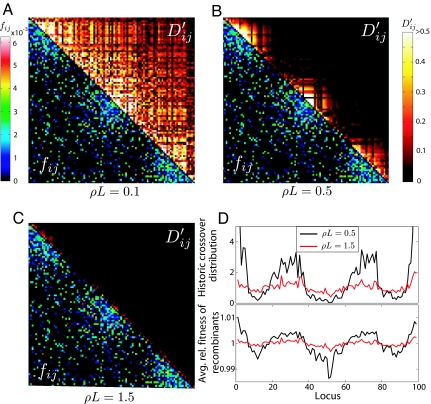
So far, we assumed that each pair of loci is equally likely to interact epistatically, regardless of their physical distance on the chromosome. However, there is evidence that the order of genes along the chromosome is far from random and that related genes tend to cluster (16, 17). To emulate such a situation we use the PE model and construct an interaction matrix fij where arbitrary pairs interact with a small probability while clusters of neighboring genes interact with a high probability (see Methods). For such a hierarchical epistatic structure, we observe, as a function of increasing cross-over rate ρ, a sequence of 2 transitions that define, sandwiched between CC and QLE, an intermediate Modular Selection (MS) regime, where the genome-wide LD characteristic of the CC regime has broken down to a set of modular blocks that are in quasi linkage equilibrium with each other. The resulting linkage disequilibrium patterns are shown in Fig. 5. The observed block structure of LD in the MS regime resembles haplotype blocks (18, 19), which are normally associated with regions of little recombination flanked by recombination hotspots. Indeed, the cumulative recombination history of the chromosomes in the population show a very heterogenous recombination distribution, as shown in Fig. 5D. However, here the origin of these blocks is not intrinsically low recombination (i.e., physical linkage) but the collective effect of epistatic selection: The surviving individuals have recombined more often in regions of low epistasis than in regions of high epistasis, even though the attempted cross-overs are uniformly distributed along the chromosome. Clusters of epistatic interaction can therefore exert selective pressure to lower recombination within the cluster. This lack of recombinant survival has been observed in experiments with mice (36), where inbreeding results in strong selective pressure on localized clusters of genes generating blocks with high LD and reduced effective recombination.
Fig. 5.
Clonal competition, modular selection and quasi linkage equilibrium. (A–C) LD, measured as D′ij between 2 loci i and j, is shown above the diagonal for a linear chromosome of length L = 100 at 3 different cross-over rates ρ. The interaction matrix fij is shown below the diagonal. At low ρ (A), the sparse long range interactions suffice to produce genome wide LD. At intermediate ρ (B), distant parts of the genome are decoupled, but the more strongly interacting clusters still show high LD, which vanishes at even higher recombination rates (C). (D) (Upper) The distribution of historic cross-overs. (Lower) The relative fitness of recombinants as a function of the cross-over location. LD was measured when allelic entropy was at 90% of the initial value, σ2 = VI = 0.005 and N = 106.
Conclusion
We have shown that the competition of epistatic selection and recombination can give rise to distinct regimes of population dynamics, separated by a transition that becomes sharp for large number of interacting loci. The QLE and CC regimes are realizations of the opposing views on evolution of R. A. Fisher and S. Wright. For r > rc alleles are selected for the their additive contributions while selection acts on whole genotypes for r < rc. The fundamental differences between these two regimes show up most clearly in the different scaling properties of the total LD and the decay time of genetic diversity. In the low recombination regime, LD is produced independent of physical linkage by the collective effect of many interactions. In the high recombination regime, LD can be attributed to specific interactions between pairs of loci and its value, determined by the ratio of the interaction strength and the rate of recombination between the loci, is small. Our results not only apply to the transition between genotype and allele selection, but also to localized clusters of interacting genes on the chromosome. Whenever the epistatic fitness difference between different allelic compositions of a cluster exceeds the recombination rate of the cluster, the fittest will amplify exponentially. Because such clusters are often small (36) (one to a few Mb) their recombination rates are low (in the centimorgan range)—hence fitness differentials around 1% can suffice to establish CC dynamics. Selective pressure to reduce recombination load, i.e., the fitness loss through recombination, will therefore favor the evolution of clusters of interacting genes and might be an important driving force for the evolution of recombination rate (37, 38). The effects described above may provide an explanation for the functional clustering associated with low and high LD regions reported in HapMap (18).
Methods
Random Epistasis Model.
A genotype g is described by L binary variables si = ± 1, i = 1, …, L. To each genotype we assign a fitness
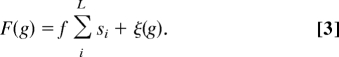 |
The first term is the sum of the additive fitness contributions of the individual loci, each of which has equal magnitude f = . The second term is the nonheritable epistatic fitness, where ξ(g) is drawn from a normal distribution with 0 mean and variance VI. For a uniform distribution of genotypes, the additive fitness variance is VA, the epistatic variance is VI, and the total variance is σ2 = VA + VI.
Pairwise Epistasis Model.
Here, we consider epistasis due to pairwise interactions between the different loci. Such pairwise interactions correspond to sisj terms in the fitness function. The fitness of a particular genotype g is determined by the independent effects of the individual loci and the sum of the interactions between all pairs.
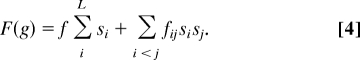 |
When assuming uniform epistasis between all possible pairs, we draw the interaction strength fij from a Gaussian distribution with 0 mean and variance
Clustered Epistasis.
To mimic localized clusters of strongly interacting genes on a weakly interacting background, we constructed the matrix of fij's as follows. The sparse background epistasis was modeled by assigning each fij a Gaussian random number with probability P = 0.1 and 0 otherwise. Then we built 3 epistatic clusters with centers ck = 10, 50, 90 by adding a Gaussian random number to each fij with probability
with r = 10 for k = 1, 2, 3. All fij were rescaled such that Σi < jf ij2 = VI.
Selection.
Our model assumes nonoverlapping generations. In each generation a pool of gametes is produced, to which each individual contributes a number of copies of its genome, which is drawn from a Poisson distribution with parameter exp(F(g) − F̄).
Gene Reassortment.
To model gene reassortment in a facultatively mating population, 2 gametes are chosen with probability r and a new genotype is formed by assigning each locus the allele of one or the other parent at random. Otherwise, the new genotype is an exact copy of 1 gamete.
Cross-Overs.
Given a cross-over rate ρ per locus, the number of cross-overs is drawn from a Poisson distribution with parameter (L − 1)ρ and the cross-over locations are chosen at random. When the number of cross-overs is 0, the offspring inherits the entire genome from 1 parent. To model circular chromosomes, the number of cross-overs is multiplied by 2 enforcing an even number of cross-overs.
Measuring Genetic Diversity.
The allele entropy is a convenient descriptor of genetic diversity that is readily calculated from the evolving population. It is defined as SA = −Σi [νiln νi+(1 − νi)ln (1 − νi)], where νi is the allele frequency at locus i.
Measuring Linkage Disequilibrium.
LD is the deviation of the frequency of a pair of alleles from the random expectation on the basis of the individual allele frequencies, i.e., Dij = 〈sisj〉 − 〈si〉〈sj〉. Kimura (21) showed that in QLE
is time independent despite changing allele frequencies νi and νj (ν̄i = 1 − νi). To measure genome wide LD, we calculate the sum of all squared LD terms Σi < jψij2. Pairs with νi or νj <0.01 or >0.99 were omitted. A different normalization is used in Fig. 5, where
is shown (see ref. 19 for a recent review).
Supplementary Material
Acknowledgments.
We thank Michael Elowitz and Marie-Anne Felix for comments on the manuscript and acknowledge financial support from National Science Foundation Grant PHY05–51164.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0812560106/DCSupplemental.
References
- 1.Begun DJ, et al. Population genomics: Whole-genome analysis of polymorphism and divergence in Drosophila simulans. PLoS Biol. 2007;5:2534–2559. doi: 10.1371/journal.pbio.0050310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Desai MM, Fisher DS. Beneficial mutation selection balance and the effect of linkage on positive selection. Genetics. 2007;176:1759–1798. doi: 10.1534/genetics.106.067678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gerrish PJ, Lenski RE. The fate of competing beneficial mutations in an asexual population. Genetica. 1998;102–103:127–144. [PubMed] [Google Scholar]
- 4.McDonald JH, Kreitman M. Adaptive protein evolution at the Adh locus in Drosophila. Nature. 1991;351:652–654. doi: 10.1038/351652a0. [DOI] [PubMed] [Google Scholar]
- 5.Mackay TF. Quantitative trait loci in Drosophila. Nat Rev Genet. 2001;2:11–20. doi: 10.1038/35047544. [DOI] [PubMed] [Google Scholar]
- 6.Barton NH, Keightley PD. Understanding quantitative genetic variation. Nat Rev Genet. 2002;3:11–21. doi: 10.1038/nrg700. [DOI] [PubMed] [Google Scholar]
- 7.Brem RB, Storey JD, Whittle J, Kruglyak L. Genetic interactions between polymorphisms that affect gene expression in yeast. Nature. 2005;436:701–703. doi: 10.1038/nature03865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schuldiner M, et al. Exploration of the function and organization of the yeast early secretory pathway through an epistatic miniarray profile. Cell. 2005;123:507–519. doi: 10.1016/j.cell.2005.08.031. [DOI] [PubMed] [Google Scholar]
- 9.Segrè D, Deluna A, Church GM, Kishony R. Modular epistasis in yeast metabolism. Nat Genet. 2005;37:77–83. doi: 10.1038/ng1489. [DOI] [PubMed] [Google Scholar]
- 10.Dobzhansky T. Genetics of natural populations. XIX. Origin of heterosis through natural selection in populations of Drosophila pseudoobscura. Genetics. 1950;35:288–302. doi: 10.1093/genetics/35.3.288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dolgin ES, Charlesworth B, Baird SE, Cutter AD. Inbreeding and outbreeding depression in Caenorhabditis nematodes. Evolution. 2007;61:1339–1352. doi: 10.1111/j.1558-5646.2007.00118.x. [DOI] [PubMed] [Google Scholar]
- 12.Parker M. Outbreeding depression in a selfing annual. Evolution. 1992;46:837–841. doi: 10.1111/j.1558-5646.1992.tb02090.x. [DOI] [PubMed] [Google Scholar]
- 13.Edmands S. Recombination in interpopulation hybrids of the copepod Tigriopus californicus: Release of beneficial variation despite hybrid breakdown. J Hered. 2008;99:316–318. doi: 10.1093/jhered/esn008. [DOI] [PubMed] [Google Scholar]
- 14.Kuehne HA, Murphy HA, Francis CA, Sniegowski PD. Allopatric divergence, secondary contact, genetic isolation in wild yeast populations. Curr Biol. 2007;17:407–411. doi: 10.1016/j.cub.2006.12.047. [DOI] [PubMed] [Google Scholar]
- 15.Wright S. Evolution in Mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hurst LD, Pál C, Lercher MJ. The evolutionary dynamics of eukaryotic gene order. Nat Rev Genet. 2004;5:299–310. doi: 10.1038/nrg1319. [DOI] [PubMed] [Google Scholar]
- 17.Roy PJ, Stuart JM, Lund J, Kim SK. Chromosomal clustering of muscle-expressed genes in Caenorhabditis elegans. Nature. 2002;418:975–979. doi: 10.1038/nature01012. [DOI] [PubMed] [Google Scholar]
- 18.International HapMap Consortium. A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449:851–861. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Slatkin M. Linkage disequilibrium—understanding the evolutionary past and mapping the medical future. Nat Rev Genet. 2008;9:477–485. doi: 10.1038/nrg2361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Teotónio H, Chelo IM, Bradić M, Rose MR, Long AD. Experimental evolution reveals natural selection on standing genetic variation. Nat Genet. 2009;41:251–257. doi: 10.1038/ng.289. [DOI] [PubMed] [Google Scholar]
- 21.Kimura M. Attainment of quasi linkage equilibrium when gene frequencies are changing by natural selection. Genetics. 1965;52:875–890. doi: 10.1093/genetics/52.5.875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Barton NH, Turelli M. Natural and sexual selection on many loci. Genetics. 1991;127:229–255. doi: 10.1093/genetics/127.1.229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nagylaki T. The evolution of multilocus systems under weak selection. Genetics. 1993;134:627–647. doi: 10.1093/genetics/134.2.627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Franklin I, Lewontin RC. Is the gene the unit of selection? Genetics. 1970;65:707–734. doi: 10.1093/genetics/65.4.707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Falconer DS, Mackay TFC. Introduction to Quantitative Genetics. Harlow, UK: Longman; 1996. [Google Scholar]
- 26.Lynch M, Walsh B. Genetics and Analysis of Quantitative Traits. Sunderland, MA: Sinauer; 1998. [Google Scholar]
- 27.Hansen TF, Wagner GP. Modeling genetic architecture: A multilinear theory of gene interaction. Theor Population Biol. 2001;59:61–86. doi: 10.1006/tpbi.2000.1508. [DOI] [PubMed] [Google Scholar]
- 28.Bulmer MG. The Mathematical Theory of Quantitative Genetics. Oxford: Oxford Univ Press; 1980. [Google Scholar]
- 29.Turelli M, Barton NH. Genetic and statistical analyses of strong selection on polygenic traits: What, me normal? Genetics. 1994;138:913–941. doi: 10.1093/genetics/138.3.913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Eigen M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften. 1971;58:465–523. doi: 10.1007/BF00623322. [DOI] [PubMed] [Google Scholar]
- 31.Franz S, Peliti L. Error threshold in simple landscapes. J Phys A Math Gen. 1997;30:4481–4487. [Google Scholar]
- 32.Boerlijst M, Bonhoeffer S, Nowak M. Viral quasi-species and recombination. Proc R Soc London Ser B. 1996;263:1577–1584. [Google Scholar]
- 33.Park J.-M, Deem MW. Phase diagrams of quasispecies theory with recombination and horizontal gene transfer. Phys Rev Lett. 2007;98 doi: 10.1103/PhysRevLett.98.058101. 058101. [DOI] [PubMed] [Google Scholar]
- 34.Turelli M, Barton NH. Will population bottlenecks and multilocus epistasis increase additive genetic variance? Evolution. 2006;60:1763–1776. [PubMed] [Google Scholar]
- 35.Rouzine IM, Coffin JM. Evolution of human immunodeficiency virus under selection and weak recombination. Genetics. 2005;170:7–18. doi: 10.1534/genetics.104.029926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Petkov PM, et al. Evidence of a large-scale functional organization of mammalian chromosomes. PLoS Genet. 2005;1:313–322. doi: 10.1371/journal.pgen.0010033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Barton NH, Otto SP. Evolution of recombination due to random drift. Genetics. 2005;169:2353–2370. doi: 10.1534/genetics.104.032821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nei M. Modification of linkage intensity by natural selection. Genetics. 1967;57:625–641. doi: 10.1093/genetics/57.3.625. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.