Abstract
The ability to represent time is an essential component of cognition but its neural basis is unknown. Although extensively studied both behaviorally and electrophysiologically, a general theoretical framework describing the elementary neural mechanisms used by the brain to learn temporal representations is lacking. It is commonly believed that the underlying cellular mechanisms reside in high order cortical regions but recent studies show sustained neural activity in primary sensory cortices that can represent the timing of expected reward. Here, we show that local cortical networks can learn temporal representations through a simple framework predicated on reward dependent expression of synaptic plasticity. We assert that temporal representations are stored in the lateral synaptic connections between neurons and demonstrate that reward-modulated plasticity is sufficient to learn these representations. We implement our model numerically to explain reward-time learning in the primary visual cortex (V1), demonstrate experimental support, and suggest additional experimentally verifiable predictions.
Keywords: reinforcment learning, visual cortex
Our brains process time with such instinctual ease that the difficulty of defining what time is, in a neural sense, seems paradoxical. There is a rich literature in experimental neuroscience describing the temporal dynamics of both cellular and system-level neuronal processes and many insightful psychophysical studies have revealed perceptual correlates of time. Despite this, and the clear importance of accurate temporal processing at all levels of behavior, we still know little about how time is represented or used by the brain (1). Temporal processing is classically understood as a higher order function, and although there is some disagreement (2, 3), it is often argued that dedicated structures or regions in the brain are responsible for representing time (4). Because different mechanisms are likely responsible for computing timing at different time scales (1, 5, 6), and because there is evidence for modality specific temporal mechanisms (7), an alternative possibility is that timing processes develop locally within different brain regions.
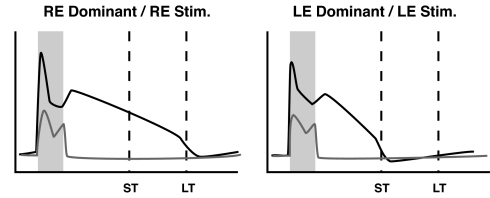
Recent evidence indicates that temporal representations are expressed in primary sensory cortices (8–10) and that reward-based reinforcement can affect the form of stimulus driven activity in the primary somatosensory cortex (11–13). In particular, Shuler and Bear (9) showed that neurons in rat primary visual cortex can develop persistent activity, evoked by brief visual stimuli, that robustly represents the temporal interval between a visual stimulus and paired reward (Fig. 1). A mechanistic framework capable of describing how a neural substrate can learn the observed temporal representations does not exist.
Fig. 1.
Schematic illustration summarizing key features from experimental results. Plots show the firing frequency response of a right-eye (RE) dominant neuron to RE stimulation and a left-eye (LE) dominant neuron to LE stimulation. In the naı̄ve animal, both LE and RE neurons respond (gray lines) only during the period of stimulation (shaded box). During training, LE and RE stimulations are paired with rewards delivered after a short (ST) or long (LT) delay period (dashed lines). After training, neuronal responses (black lines) persist until the reward times paired with each stimulus. See Fig. S1 for examples of real neural activity.
Here, we explain how these temporal signals can be encoded in recurrent excitatory synaptic connections and how a local network can learn specific temporal instantiations through reward modulated plasticity. Although our model is potentially applicable to different brain regions, we present it in terms of V1. Our goal is not to fully reproduce the experimental results, but rather to describe a theoretical mechanism that captures the key temporal features of the experimental data. We first present a description of our model that explains how a recurrent excitatory network can represent time. We then demonstrate that reward modulated synaptic plasticity allows local networks to learn specific temporal representations. We describe functional consequences of this form of learning that can be verified experimentally and present experimental results that are consistent with predictions specific to our model.
Representing Time in a Recurrent Cortical Network
Our aim is to construct and describe a model, with a minimal number of assumptions, that describes how a network can learn to represent time as a function of reward. Here, we describe the model and its key features; for mathematical and implementation details, see SI Appendix.
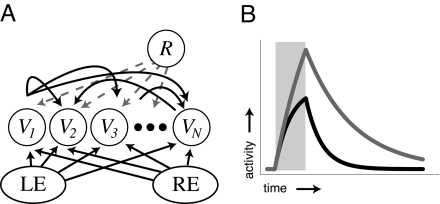
We start with a simplified network structure (Fig. 2A) that is generally appropriate for neurons in V1, which have largenumbers of synapses with local origin and where extrastriate feedback accounts for a small percentage of total excitatory current (14, 15). To gain insight into the functional role network structure plays in determining the temporal activity profile of individual neurons, we first analyze network dynamics following external stimulation as a function of the excitatory synaptic weights between linear passive integrator neurons.
Fig. 2.
Representing time. (A) Network structure. Neurons in the recurrent layer are shown with a subset of the recurrent excitatory synaptic connections (curved black arrows) and labeled with their associated activity levels (Vi). Actual network connectivity is all-to-all. Each neuron also receives external input from the left or right eye. The reward signal (R) projects to all neurons in the recurrent layer. (B) Example neural activity profiles from a single rate-based neuron after stimulation (shaded box) when isolated (black line, no recurrent stimulation, decay rate set by τm) and when embedded in a network with small lateral synaptic weights (gray line, decay rate τdμ). In our model, encoded time is represented by the decay rate of neural activity in the recurrently connected layer.
In our network of N neurons, the firing rate of each single neuron is approximated by an abstract activity variable, V, with dynamics described by a first order ODE:
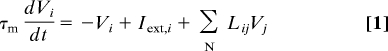 |
where Iext,i is the external feed-forward input to neuron i and Li,j is the weight connecting presynaptic cell j to postsynaptic cell i. For the sake of analytical tractability, this model makes the simplifying assumption that neural activity increases linearly with input (16). Absent recurrent connections, the activity of each neuron decays with an intrinsic neuronal time constant (τm) after brief feed-forward stimulation (Fig. 2B, black line). If, however, the neurons are connected laterally via small excitatory synapses (Eq. 2) reverberatory propagation of activity in the network will decrease each neuron's effective activity decay rate (Fig. 2B, gray line). This phenomenon, through which the network structure modifies the response duration of individual neurons, explains how excitatory synapses can serve as a physical substrate of temporal representations.
We define encoded time as the effective decay rate of individual neurons responsive to a given stimulus engendered by network structure. Given 2 orthogonal input vectors, Iμ, corresponding to inputs from the left (μ = 1) and right (μ = 2) eyes, it is possible to encode a desired decay rate, τdμ, by constructing a recurrent weight matrix L such that the connection between each neuron i and j has the form:
 |
where
In the Shuler and Bear study (9), animals were trained to lick a “lick-tube” for a water reward while the activities of single neurons were recorded extracellularly in V1. Each trial was initiated with delivery of a brief (400-ms) full-field visual stimulus to either the left or right eye and reward was delivered with a temporal offset, specified by number of licks, depending on which eye was stimulated (n licks for left eye, 2n licks for right). Following this paradigm, our goal is to encode the offset between stimulation and reward. We next propose a learning rule that explains how the network can learn appropriate weights as a function of reward timing.
Encoding Time Through Reward-Dependent Expression of Synaptic Plasticity (RDE)
Eqs. 2 and 3 specify that synapses between neurons coactive during stimulation should be potentiated to a level dependent on the timing of the paired reward. Because reward in the naı̄ve animal comes long after evoked activity returns to baseline levels (see Fig. 1), it is unclear how neural activity at the time of reward can be used to set the correct weights (an example of the temporal credit assignment problem). To correlate a visual stimulus with its associated time of reward, the brain has to bridge the gap in time-scales between τm (tens of milliseconds) and the reward time T (a few seconds). Accomplishing this necessarily requires some process operating with sufficiently slow dynamics to maintain an evoked activity trace until the time of reward. We therefore propose a learning rule that postulates that reward signals can regulate the expression of a slow molecular process, which we refer to as a “proto-weight,” that leads to long-term synaptic potentiation.
Our proposed plasticity rule, which depends on the reward dependent expression of these proto-weights, has 4 tenets (see SI Appendix for details):
There are 2 activity dependent processes: the permanent (expressed) weight matrix L and a temporary (unexpressed) proto-weight matrix LP.
Proto-weights increase in an activity dependent Hebbian manner and decay with time constant τp., We assume that τp is sufficiently long so that the proto-weights do not decay to baseline before the time of reward (i.e., τp > T).
Reward signals express proto-weights into permanent synaptic weights only at the time of reward, T, and the change in the permanent weights is proportional to the concurrent value of the proto-weights.
Ongoing cortical activity inhibits the ability of the reward signal to express proto-weights into permanent weights. This ensures that the weights will not continue to increase beyond the correct values with continued training.
To gain insight into how the plasticity rule affects network activity it is useful to consider the conditions necessary for synaptic change at the time of reward. The values of the synaptic proto-weights are determined by the network dynamics and the Hebbian plasticity function, H. Assuming an appropriate selection of H, Li,jp will be greater than zero between all neurons i and j responsive to a given stimulus at the time of reward. If network activity decays quickly (as it will in the naı̄ve case) the reward signal will be uninhibited by cortical activity and synapses between neurons in the responsive population will potentiate. This potentiation will decrease the network decay rate in subsequent trials. As training progresses, the activity level at the time of reward will increase, resulting in an inhibition of reward and a decrease in the magnitude of expressed synaptic change. Eventually, activity will be sufficiently high to completely inhibit reward and plasticity will cease. If the cortical activity at the time of reward is too large, RDE will cause a decrease in the synaptic weights. A critical insight is that proto-weights act as markers, transiently storing information about coincident activation of presynaptic and postsynaptic neurons, and play no role in driving network activity; changes in their values are antecedent to changes in actual synaptic efficacies.
Training the Network to Represent Reward Time Intervals Using RDE
Training was based on the experimental protocol outlined above. Our simulated networks were trained by randomly presenting either a “left” or “right” eye stimulus pattern and delivering rewards at associated offset times. We first implemented the deterministic linear neuron model in a network of 40 neurons. The 40 × 40 weight matrix was initialized to small random values and the proto-weight matrix was initialized to zero. During each trial, 1 of 2 orthogonal (monocular) binary input patterns was randomly chosen and presented for 400 ms as feed-forward input to the network. Reward was given at either t = 1,000 or t = 1,600 depending on which input was selected and plasticity was based on RDE.
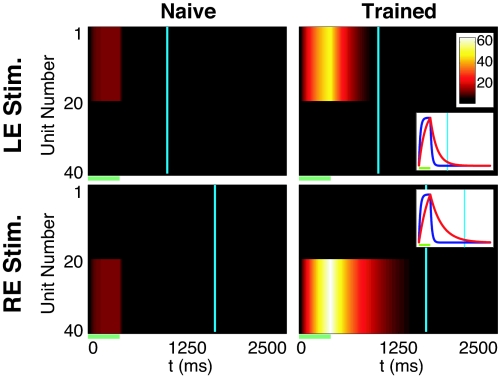
Fig. 3 shows results of simulations with the linear model trained with RDE. Initially the neural responses decayed with the intrinsic neuronal time constant. The duration of cortical activity increased monotonically during training and stabilized when the cortical activity at the time of reward reached the desired level (see Fig. S2). The SI Appendix also demonstrates that our framework can train binocularly responsive neurons (Figs. S3 and S4) and works when reward activity is inhibited by either the average network activity (global form) or the activity of individual neurons (local form).
Fig. 3.
RDE in a network of passive integrator neurons. In the naı̄ve network (left column), monocular stimulation of either the left (LE, stimulation of units 1–20) or right eye (RE, stimulation of units 21–40) elicits a brief period of activity (V, with values indicated by colorbar) that decays rapidly after the end of stimulation (green bar). There is no activity at the time of reward (cyan lines) for either input pattern. In the trained network (right column), stimulus-evoked activity decays with a time constant associated with the appropriate reward time. Plotting V (normalized, Insets) for example neurons (unit number 5 for LE, 25 for RE) in naı̄ve (blue) and trained networks (red) shows that training increases the effective decay time constant.
The linear neuron model, although mathematically tractable, captures neither the nonlinear spiking of cortical neurons nor the complex interactions between ionic species responsible for driving the subthreshold membrane voltage. To verify that our approach works in a more realistic neural environment, we also implemented RDE in a network of conductance based integrate and fire neurons with biologically plausible parameters (17), where current is a function of membrane voltage and various ionic conductances (see SI Appendix for details). These nonlinear neurons receive stochastic feed-forward inputs and constant background noise that generates spontaneous activity. In this stochastic implementation, firing times and rates are not precise.
The network architecture and training used with the integrate and fire model were similar to those used to train the continuous neuron model. The network contained 100 neurons, and noise was introduced by stimulating each neuron in the recurrent layer with independent inhibitory and excitatory Poisson spike trains, approximately balanced to produce spontaneous firing rates of 2–3 Hz in the naı̄ve network. Injected noise was independent from neuron to neuron and recurrent weights were entrained using RDE.
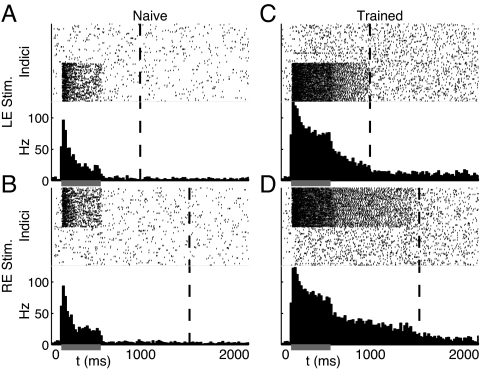
Fig. 4 shows the response of this network to monocular inputs in both naı̄ve and trained networks. As before, the naı̄ve network responds transiently only during stimulus presentation; after training, network driven activity persists until the associated reward times. Because of increased lateral weights, both the baseline spontaneous and stimulus evoked spike frequencies in the trained network are higher than in the naı̄ve network. Unlike the rate-based neuron model, dynamics in the spiking network are not exponential. After stimulation, firing rates decay slowly before dropping abruptly back to baseline levels at the approximate time of reward. Despite an inherent sensitivity to the precise setting of synaptic weights, RDE training is sufficient to learn temporal representations even with a noisy, stochastic implementation.
Fig. 4.
RDE with stochastic spiking neurons. Each subplot shows a raster plot for all neurons in the network over the course of a single stimulus evoked response (Upper) and the resultant spike histogram (Lower) indicating the average firing frequency in Hz for the whole network. (A and B) The 2 monocular stimulus patterns elicit brief periods of activity during stimulation (gray bar) in responsive subpopulations of the naı̄ve network that decay before the times of reward (dashed lines) for each input. (C and D) After training with RDE, evoked activity persists until the appropriate reward times.
Evaluating Activity Changes with Training
An implication of our model is that training will increase the firing rate of neurons participating in temporal representations as increasing recurrent excitation amplifies network activity through excitatory feedback. This effect can clearly be seen by comparing both evoked responses and spontaneous firing rates in naı̄ve and trained model networks; as expected, higher levels of activity exist in the trained network than in the naı̄ve.
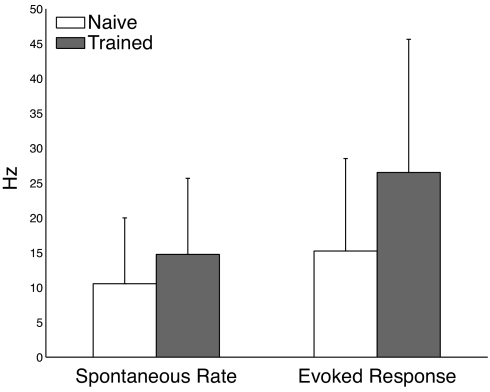
To determine whether biological neurons show the increased activity predicted by our model, we calculate and compare the average firing rate of neurons recorded by Shuler and Bear (9) in naı̄ve and trained animals in a 100-ms window immediately before stimulation (spontaneous rate) and in the 100-ms window immediately after the onset of stimulation (evoked response). Means and standard deviations were calculated for dominant eye responses in the group of neurons recorded before training and for all neurons classified as showing a sustained increase after training. The t test was used to determine whether changes in these measures over training are statistically significant.
As shown in Fig. 5, there is a statistically significant increase in both spontaneous (40% increase) and evoked responses (74% increase) in the experimental data (recorded from 65 neurons before training and 65 neurons classified as belonging to the sustained response class after training). These results, in agreement with the predictions of our model, suggest that a recurrent mechanism may be responsible for the timing responses seen in V1.
Fig. 5.
Experimental results demonstrating that training increases spontaneous firing rates and evoked responses as predicted by the model. Training evokes a 40% increase in the spontaneous firing rate and a 74% increase in evoked response. Error bars show standard deviation. Differences between naı̄ve and trained responses are statistically significant for both metrics (spontaneous P = 0.01, evoked P = 1.5 × 10−4).
Discussion
We contend that the duration of evoked activity, as seen in V1 after brief periods of visual stimulation, could be used by the brain to represent time and that lateral excitatory connections between neurons in local cortical networks can create reverberations that underlie these temporal representations. In this paradigm, time is encoded using mechanisms similar to those thought to underlie working memory (2, 3, 10). We propose that the brain can learn specific temporal intervals through reward dependent plasticity and have demonstrated that our RDE framework is sufficient to create de novo neural representations of the interval between seemingly disparate external events.
The proposed network structure is minimal, requiring only recurrent excitation and a globally available reward signal. Importantly, our framework does not require specialized network structures, such as stimulus-locked tagged delay lines or phase-locked oscillators, used in many previous models (6, 18). Our RDE model combines elements of reinforcement learning (19, 20), reward modulated plasticity (21–24) and models of recurrent network dynamics (25–28). The framework is able to qualitatively account for the most prevalent class of reward-timing sensitive neurons recorded by Shuler and Bear (9) and can serve, in principle, as a general model of how reward timing can be learned locally in different brain regions.
Previous studies in multiple brain regions have described timing processes manifested by climbing neural activity after stimulation (25, 29), and various models have been developed to account for these results (30, 31). The V1 neurons we are modeling do not exhibit this ramping behavior; instead they show evoked activity that decays slowly until the time of reward. Because different mechanisms are thought to be responsible for representing time at different scales (1, 5, 6), and within different sensory modalities (7), it is plausible to assume that these different types of responses could result from different neural machinery. It is also possible that persistent activity generated by RDE in primary sensory regions could serve as the input to higher order timing processes, analogous to the way orientation selective receptive fields in V1 project to higher order receptive fields in other visual areas.
In addition to the sustained neuronal responses that we have modeled, Shuler and Bear also reported smaller numbers of neurons that were inhibited until reward or whose firing rates peaked at the time of reward. The temporal representation generated in our model can conceptually form the basis for these other forms of representation. For example, the efferent target of inhibitory neurons driven by our recurrent layer will naturally show a decrease from their baseline spontaneous firing rates that will persist until the time of reward (Fig. S5). Our model as proposed however, does not include a substantive role for inhibition in the creation of temporal representations. Nonetheless, as Fig. S6 demonstrates, our network can continue to report reward time in the presence of inhibitory interneurons, and our learning rule can in principle create weight matrices that compensate for inhibition. Previous models of working memory (28, 32, 33) have shown that persistent activity driven by excitatory feedback can exist in recurrent networks including biologically plausible ratios between excitation and inhibition.
One distinctive property of the theory proposed here is that a network can learn temporal representations without requiring any specialized timing mechanisms. Other models of temporal processing that do not require these specialized mechanisms have been proposed (34–36) based on the idea that changes in network state, dictated by intrinsic neuronal and synaptic dynamics, can be decoded to infer the elapsed time since an input was presented. The capacity and robustness of these models is currently under investigation. They are similar to our model in that they use network dynamics to encode time, but differ in that they do not use plasticity to modify the network structure to encode specific temporal instantiations.
Our results might seem to contradict previous work demonstrating that background activity decreases the effective membrane time constant (37). The previous analysis, however, was based only on feed-forward background stimulation. By including feed-back excitation, our model allows the closed-loop network to increase evoked activity duration with both the linear rate-based and conductance-based spiking neuron models. Spontaneous background activity will still result in a reduction of the effective time constant, but RDE is able to learn the correct weights to obtain desired temporal dynamics despite the shorter effective time constant.
A unique implication of our model is that activity levels will increase as the network learns temporal representations. An increase in activity is evident in our simulated data (Figs. 3 and 4) and present in the reported experimental data (Fig. 5 and Fig. S1). The agreement between model prediction and experimental observation suggests that the brain may be using a mechanism based on recurrent stimulation to produce the responses reported in V1.
The theory proposed here has other specific testable consequences. Our assumption that the representation of timing is stored in lateral connections implies increased noise correlations between neurons selective to the same stimulus in a trained network (38). Because the change in synaptic weights constituting the neural substrate of temporal encoding in our model is spread over the entire recurrent weight matrix, increases in cross-correlation between individual neurons in the network are very small. As explained in SI Appendix, we are able to demonstrate significant noise correlations in our trained network only by grouping responses across populations of neurons known to participate in a particular temporal representation (Fig. S7). Because of limitations of current recording methods, the original study did not record sufficient spontaneous out-of-task spiking activity to confirm this prediction of the model.
The particular form of reward-modulated plasticity described by RDE implies that changing the probability of reward will not change the firing pattern of V1 neurons in trained animals although it might alter the rate at which neurons learn these representations. Our theory also predicts that blocking the putative reward signal locally in V1 will eliminate the learning of cue-reward intervals. Conversely, experimental delivery of a biochemical reward signal directly to V1 after visual stimulation could be used to mimic the effects observed after pairing of visual cues with behaviorally achieved reward. This method could distinguish between local and global loci of reward inhibition (see SI Appendix for discussion); if global, mimicry should bypass the inhibition of reward nuclei and prevent convergence to the appropriate timing. Alternatively, if the mechanisms of inhibition are local, the network should converge to the timing of the mimicked signal.
To provide a complete account of this model, concrete physiological and biochemical processes must replace our abstract notions of “reward signal,” “inhibition of reward,” and proto-weights. Because it is well established that neuromodulators are essential for experience dependent plasticity in cortex (39, 40), and that they regulate synaptic plasticity in cortical slices (41, 42), they are natural candidates for our reward signals. It is often assumed that dopamine is responsible for implementing rewards (43), and it is known to modulate the perception of time (2) in both human (5, 44) and non-human (45) subjects. Dopamine projections into V1, however, are relatively sparse (46). Another possibility is that cholinergic nuclei, which are known to be involved in the satiation of thirst (47, 48) and which project into V1 (49, 50) could signal reward to the visual cortex. Effects similar to the reported voltage sensitivity of G protein coupled ACh receptors (51) could provide a biochemical mechanism of reward inhibition.
Our model predicts the presence of biological proto-weights. Although we do not propose specific molecular processes as proto-weight candidates, neural modulators are known to effect synaptic plasticity by regulating critical kinases (42) and we can speculate that they are implemented by a posttranslational modification of some kinase or receptor type (52). An implication of this work is that the activity dependent modifications of postsynaptic proteins may play an important computational role in solving credit assignment problems.
Because the duration of response is set by network structure, it is robust to the specific dynamics of the processes associated with learning. The form of learning does, however, set loose bounds on functionally acceptable dynamical ranges. The duration of the reward signal in our model should be significantly shorter than the interval between stimulus and reward, consistent with the brief response duration (≈200 ms) of dopamine neurons after delivery of liquid reward (43, 53). Likewise, our model requires that the time course of proto-weight activation be less than the intertrial interval and greater than the reward interval, a range consistent with the time course of phosphorylation de-phosphorylation cycles in some proteins (54, 55). The molecular substrates of the RDE theory can be explored using biochemical analysis of tissue extracted from trained and untrained animals or explored directly in analogous slice experiments.
Sustained activity and reward dependent processing are not classically assigned to the low level sensory regions. Demonstrations of reward dependent sustained activity in somatosensory cortex (11) and sustained responses in auditory cortex (8) might indicate that temporal and reward processing occur in lower order areas of the brain than previously thought. Additionally, because local neural populations throughout the cortex meet our model's minimal requirements, the fundamental concept of using an external signal to modulate plasticity (23, 24) could be the basis of elementary mechanisms used throughout the brain to process time. Our RDE framework conceptualizes and formalizes how such networks can reliably learn temporal representations and leads to predictions that can be tested experimentally. Experimental demonstration that temporal representations emerge endogenously within local neuronal populations would indicate that the brain processes time in a more distributed manner than currently believed.
Supplementary Material
Acknowledgments.
This work was supported by a Collaborative Research in Computational Neuroscience grant, National Science Foundation Grant 0515285, the Howard Hughes Medical Institute (M.G.H.S. and M.F.B.), and Israel Science Foundation Grant 868/08 (to Y.L.).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0901835106/DCSupplemental.
References
- 1.Mauk MD, Buonomano DV. The neural basis of temporal processing. Annu Rev Neurosci. 2004;27:307–340. doi: 10.1146/annurev.neuro.27.070203.144247. [DOI] [PubMed] [Google Scholar]
- 2.Lewis PA, Miall RC. Remembering the time: A continuous clock. Trends Cogn Sci. 2006;10:401–406. doi: 10.1016/j.tics.2006.07.006. [DOI] [PubMed] [Google Scholar]
- 3.Staddon JE. Interval timing: Memory, not a clock. Trends Cogn Sci. 2005;9:312–314. doi: 10.1016/j.tics.2005.05.013. [DOI] [PubMed] [Google Scholar]
- 4.Meck WH. Neuropsychology of timing and time perception. Brain Cogn. 2005;58:1–8. doi: 10.1016/j.bandc.2004.09.004. [DOI] [PubMed] [Google Scholar]
- 5.Rammsayer TH. Neuropharmacological evidence for different timing mechanisms in humans. Q J Exp Psychol B. 1999;52:273–286. doi: 10.1080/713932708. [DOI] [PubMed] [Google Scholar]
- 6.Buonomano DV, Karmarkar UR. How do we tell time? Neuroscientist. 2002;8:42–51. doi: 10.1177/107385840200800109. [DOI] [PubMed] [Google Scholar]
- 7.Merchant H, Zarco W, Prado L. Do we have a common mechanism for measuring time in the hundreds of millisecond range? Evidence from multiple-interval timing tasks. J Neurophysiol. 2008;99:939–949. doi: 10.1152/jn.01225.2007. [DOI] [PubMed] [Google Scholar]
- 8.Moshitch D, Las L, Ulanovsky N, Bar-Yosef O, Nelken I. Responses of neurons in primary auditory cortex (A1) to pure tones in the halothane-anesthetized cat. J Neurophysiol. 2006;95:3756–3769. doi: 10.1152/jn.00822.2005. [DOI] [PubMed] [Google Scholar]
- 9.Shuler MG, Bear MF. Reward timing in the primary visual cortex. Science. 2006;311:1606–1609. doi: 10.1126/science.1123513. [DOI] [PubMed] [Google Scholar]
- 10.Super H, Spekreijse H, Lamme VA. A neural correlate of working memory in the monkey primary visual cortex. Science. 2001;293:120–124. doi: 10.1126/science.1060496. [DOI] [PubMed] [Google Scholar]
- 11.Pantoja J, et al. Neuronal activity in the primary somatosensory thalamocortical loop is modulated by reward contingency during tactile discrimination. J Neurosci. 2007;27:10608–10620. doi: 10.1523/JNEUROSCI.5279-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pleger B, Blankenburg F, Ruff CC, Driver J, Dolan RJ. Reward facilitates tactile judgments and modulates hemodynamic responses in human primary somatosensory cortex. J Neurosci. 2008;28:8161–8168. doi: 10.1523/JNEUROSCI.1093-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weinberger NM. Associative representational plasticity in the auditory cortex: A synthesis of two disciplines. Learn Mem. 2007;14:1–16. doi: 10.1101/lm.421807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Johnson RR, Burkhalter A. Microcircuitry of forward and feedback connections within rat visual cortex. J Comp Neurol. 1996;368:383–398. doi: 10.1002/(SICI)1096-9861(19960506)368:3<383::AID-CNE5>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- 15.Budd JM. Extrastriate feedback to primary visual cortex in primates: A quantitative analysis of connectivity. Proc Biol Sci. 1998;265:1037–1044. doi: 10.1098/rspb.1998.0396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dayan P, Abbott LF. Theoretical Neuroscience: Computational Modeling of Neural Systems. Cambridge, MA: MIT Press; 2001. [Google Scholar]
- 17.Machens CK, Romo R, Brody CD. Flexible control of mutual inhibition: A neural model of two-interval discrimination. Science. 2005;307:1121–1124. doi: 10.1126/science.1104171. [DOI] [PubMed] [Google Scholar]
- 18.Matell MS, King GR, Meck WH. Differential modulation of clock speed by the administration of intermittent versus continuous cocaine. Behav Neurosci. 2004;118:150–156. doi: 10.1037/0735-7044.118.1.150. [DOI] [PubMed] [Google Scholar]
- 19.Rescorla RA, Wagner AR. In: Classical Conditioning II: Current Research and Theory. Black AH, Prokasy WF, editors. New York: Appleton-Century-Crofts; 1972. pp. 64–69. [Google Scholar]
- 20.Sutton RS, Barto AG. Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- 21.Frey U, Morris RG. Synaptic tagging and long-term potentiation. Nature. 1997;385:533–536. doi: 10.1038/385533a0. [DOI] [PubMed] [Google Scholar]
- 22.Izhikevich EM. Solving the distal reward problem through linkage of STDP and dopamine signaling. Cereb Cortex. 2007;17:2443–2452. doi: 10.1093/cercor/bhl152. [DOI] [PubMed] [Google Scholar]
- 23.Loewenstein Y. Robustness of learning that is based on covariance-driven synaptic plasticity. PLoS Comput Biol. 2008;4:e1000007. doi: 10.1371/journal.pcbi.1000007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Loewenstein Y, Seung HS. Operant matching is a generic outcome of synaptic plasticity based on the covariance between reward and neural activity. Proc Natl Acad Sci USA. 2006;103:15224–15229. doi: 10.1073/pnas.0505220103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Brody CD, Romo R, Kepecs A. Basic mechanisms for graded persistent activity: Discrete attractors, continuous attractors, and dynamic representations. Curr Opin Neurobiol. 2003;13:204–211. doi: 10.1016/s0959-4388(03)00050-3. [DOI] [PubMed] [Google Scholar]
- 26.Seung HS. How the brain keeps the eyes still. Proc Natl Acad Sci USA. 1996;93:13339–13344. doi: 10.1073/pnas.93.23.13339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang XJ. Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci. 2001;24:455–463. doi: 10.1016/s0166-2236(00)01868-3. [DOI] [PubMed] [Google Scholar]
- 28.Amit DJ, Brunel N. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb Cortex. 1997;7:237–252. doi: 10.1093/cercor/7.3.237. [DOI] [PubMed] [Google Scholar]
- 29.Watanabe M. Reward expectancy in primate prefrontal neurons. Nature. 1996;382:629–632. doi: 10.1038/382629a0. [DOI] [PubMed] [Google Scholar]
- 30.Miller P, Brody CD, Romo R, Wang XJ. A recurrent network model of somatosensory parametric working memory in the prefrontal cortex. Cereb Cortex. 2003;13:1208–1218. doi: 10.1093/cercor/bhg101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Reutimann J, Yakovlev V, Fusi S, Senn W. Climbing neuronal activity as an event-based cortical representation of time. J Neurosci. 2004;24:3295–3303. doi: 10.1523/JNEUROSCI.4098-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Barbieri F, Brunel N. Irregular persistent activity induced by synaptic excitatory feedback. Front Comput Neurosci. 2007;1:5. doi: 10.3389/neuro.10.005.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang XJ. Synaptic basis of cortical persistent activity: The importance of NMDA receptors to working memory. J Neurosci. 1999;19:9587–9603. doi: 10.1523/JNEUROSCI.19-21-09587.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Karmarkar UR, Buonomano DV. Timing in the absence of clocks: Encoding time in neural network states. Neuron. 2007;53:427–438. doi: 10.1016/j.neuron.2007.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Maass W, Natschlager T, Markram H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002;14:2531–2560. doi: 10.1162/089976602760407955. [DOI] [PubMed] [Google Scholar]
- 36.White OL, Lee DD, Sompolinsky H. Short-term memory in orthogonal neural networks. Phys Rev Lett. 2004;92:148102. doi: 10.1103/PhysRevLett.92.148102. [DOI] [PubMed] [Google Scholar]
- 37.Bernander O, Douglas RJ, Martin KA, Koch C. Synaptic background activity influences spatiotemporal integration in single pyramidal cells. Proc Natl Acad Sci USA. 1991;88:11569–11573. doi: 10.1073/pnas.88.24.11569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tsodyks M, Kenet T, Grinvald A, Arieli A. Linking spontaneous activity of single cortical neurons and the underlying functional architecture. Science. 1999;286:1943–1946. doi: 10.1126/science.286.5446.1943. [DOI] [PubMed] [Google Scholar]
- 39.Bear MF, Singer W. Modulation of visual cortical plasticity by acetylcholine and noradrenaline. Nature. 1986;320:172–176. doi: 10.1038/320172a0. [DOI] [PubMed] [Google Scholar]
- 40.Kilgard MP, Merzenich MM. Cortical map reorganization enabled by nucleus basalis activity. Science. 1998;279:1714–1718. doi: 10.1126/science.279.5357.1714. [DOI] [PubMed] [Google Scholar]
- 41.Kirkwood A, Rozas C, Kirkwood J, Perez F, Bear MF. Modulation of long-term synaptic depression in visual cortex by acetylcholine and norepinephrine. J Neurosci. 1999;19:1599–1609. doi: 10.1523/JNEUROSCI.19-05-01599.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Seol GH, et al. Neuromodulators control the polarity of spike-timing-dependent synaptic plasticity. Neuron. 2007;55:919–929. doi: 10.1016/j.neuron.2007.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schultz W. Predictive reward signal of dopamine neurons. J Neurophysiol. 1998;80:1–27. doi: 10.1152/jn.1998.80.1.1. [DOI] [PubMed] [Google Scholar]
- 44.Gibbon J, Malapani C, Dale CL, Gallistel C. Toward a neurobiology of temporal cognition: Advances and challenges. Curr Opin Neurobiol. 1997;7:170–184. doi: 10.1016/s0959-4388(97)80005-0. [DOI] [PubMed] [Google Scholar]
- 45.Meck WH. Neuropharmacology of timing and time perception. Brain Res Cogn Brain Res. 1996;3:227–242. doi: 10.1016/0926-6410(96)00009-2. [DOI] [PubMed] [Google Scholar]
- 46.Papadopoulos GC, Parnavelas JG, Buijs RM. Light and electron microscopic immunocytochemical analysis of the dopamine innervation of the rat visual cortex. J Neurocytol. 1989;18:303–310. doi: 10.1007/BF01190833. [DOI] [PubMed] [Google Scholar]
- 47.Sullivan MJ, et al. Lesions of the diagonal band of broca enhance drinking in the rat. J Neuroendocrinol. 2003;15:907–915. doi: 10.1046/j.1365-2826.2003.01066.x. [DOI] [PubMed] [Google Scholar]
- 48.Whishaw IQ, O'Connor WT, Dunnett SB. Disruption of central cholinergic systems in the rat by basal forebrain lesions or atropine: Effects on feeding, sensorimotor behaviour, locomotor activity and spatial navigation. Behav Brain Res. 1985;17:103–115. doi: 10.1016/0166-4328(85)90023-3. [DOI] [PubMed] [Google Scholar]
- 49.Mechawar N, Cozzari C, Descarries L. Cholinergic innervation in adult rat cerebral cortex: A quantitative immunocytochemical description. J Comp Neurol. 2000;428:305–318. doi: 10.1002/1096-9861(20001211)428:2<305::aid-cne9>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- 50.Wenk H, Bigl V, Meyer U. Cholinergic projections from magnocellular nuclei of the basal forebrain to cortical areas in rats. Brain Res. 1980;2:295–316. doi: 10.1016/0165-0173(80)90011-9. [DOI] [PubMed] [Google Scholar]
- 51.Ben-Chaim Y, et al. Movement of “gating charge” is coupled to ligand binding in a G-protein-coupled receptor. Nature. 2006;444:106–109. doi: 10.1038/nature05259. [DOI] [PubMed] [Google Scholar]
- 52.Hu H, et al. Emotion enhances learning via norepinephrine regulation of AMPA-receptor trafficking. Cell. 2007;131:160–173. doi: 10.1016/j.cell.2007.09.017. [DOI] [PubMed] [Google Scholar]
- 53.Schultz W. The reward signal of midbrain dopamine neurons. News Physiol Sci. 1999;14:249–255. doi: 10.1152/physiologyonline.1999.14.6.249. [DOI] [PubMed] [Google Scholar]
- 54.Driska SP, Stein PG, Porter R. Myosin dephosphorylation during rapid relaxation of hog carotid artery smooth muscle. Am J Physiol. 1989;256:C315–321. doi: 10.1152/ajpcell.1989.256.2.C315. [DOI] [PubMed] [Google Scholar]
- 55.King MM, et al. Mammalian brain phosphoproteins as substrates for calcineurin. J Biol Chem. 1984;259:8080–8083. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.