Abstract
The microarray is an important and powerful tool for prescreening of genes for further research. However, alternative solutions are needed to increase power in small microarray experiments. Use of traditional parametric and even non-parametric tests for such small experiments lack power and have distributional problems. A mixture model is described that is performed directly on expression differences assuming that genes in alternative treatments are expressed or not in all combinations (i) not expressed in either condition, (ii) expressed only under the first condition, (iii) expressed only under the second condition, and (iv) expressed under both conditions, giving rise to 4 possible clusters with two treatments. The approach is termed a Mean-Difference-Mixture-Model (MD-MM) method. Accuracy and power of the MD-MM was compared to other commonly used methods, using both simulations, microarray data, and quantitative real time PCR (qRT-PCR). The MD-MM was found to be generally superior to other methods in most situations. The advantage was greatest in situations where there were few replicates, poor signal to noise ratios, or non-homogenous variances.
Keywords: Quantitative Genetics, Expression Arrays, Differential Expression, Mixture Models, Power
Introduction
Microarrays provide unique insight into gene regulation networks as impacted by any number of factors, including tissue, time, treatment, condition, or genetic background, see Walsh and Henderson (2004) for a review. The major statistical questions posed by such experiments were summarized by Allison et al.(2002), and included: 1) evidence of differential expression (DE), 2) number of genes with true DE, 3) confidence interval (CI) of mean expression difference, 4) threshold above which genes are interesting and should be followed up, and what proportion of genes in this list are likely to be false positives, and 5) what proportion of genes not declared interesting are likely to be false negatives. As Allison et al. (2002) concluded, if the power of the experiment was near perfect, then ordinary frequentist significance testing would be sufficient to answer these questions. However, due to costs of microarray chips, many experiments have few replicates per condition, while the number of genes to be analyzed per chip is large, resulting in the so-called small n large p problem (Martella, 2006). A solution to this problem is the use of mixture models (MM), first developed for other applications (Aitkin and Wilson, 1980; Edelbrock, 1979) and later proposed by a number of researchers for microarray analysis. Most MM were developed to cluster samples e.g. (Alexandridis et al., 2004; Asyali and Alci, 2005; Ghosh, 2004; Kauermann and Eilers, 2004; Kendziorski et al., 2003; Lai et al., 2007; Martella, 2006; McLachlan et al., 2002; McLachlan et al., 2006; Pan et al., 2006) but several cluster genes e.g. (Allison et al., 2002; Do et al., 2005; Efron et al., 2001; Lee et al., 2000;McLachlan et al., 2005; Newton et al., 2004; Pan, 2002; Pan, 2003; Reverter et al., 2006). Each of these methods employs a different sets of assumptions, yet no method has been commonly accepted as a standard. The majority of these MM are based on clustering of test statistics (such as t or F) e.g. (Efron et al., 2001; McLachlan et al., 2002; Pan, 2002; Reverter et al., 2006), p-values derived from test statistics e.g. (Allison et al., 2002), or z values derived from p-values e.g. (Lai et al., 2007; McLachlan et al., 2006).
Unfortunately, methods that cluster based on test statistics, or their derivatives, may be susceptible to a critical problem that occurs with small sample sizes. Allison et al. (2002) notes that with very small sample size parametric tests of the differences between levels of gene expression will be more sensitive to assumed distributional forms of the expression data, and resulting p-values may not be accurate. Allison et al. (2002) also states that although non-parametric tests, such as bootstrapping p-values, could potentially solve this problem, if n<5, then p-values will be affected by the discreteness of the bootstrapped distribution and there will be a limited number of possible distinct p-values. As such Allison et al. (2002) concludes that the resulting MM analysis with small sample sizes might be unreliable. Results presented by Jeffery et al. (2006) support this conclusion. The authors used cross validation analysis of data from several microarray experiments using 10 different feature selection methods. They found that with low replication, or high variance, gene ranking based on these statistics were poor, and simple fold and non-parametric methods were more powerful than parametric methods.
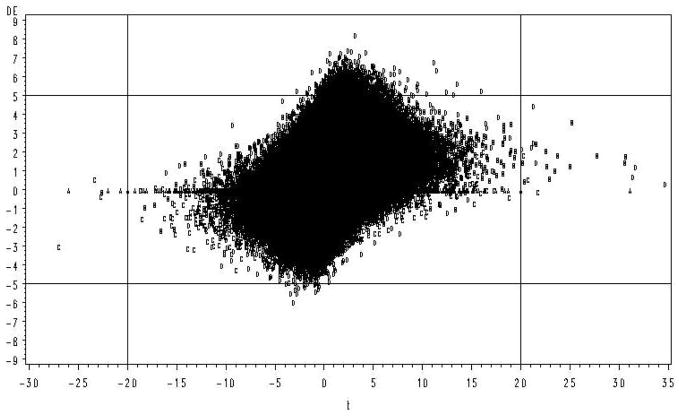
An example of this phenomenon supporting the concern of Allison et al. (2002) is illustrated in Figure 1. These data were sampled from a distribution with a common error variance across genes (Figure 1 is illustrated from Case 16 in Table 1, details are given in the Simulations section). Those genes with the largest values of t (those greater than an arbitrary critical value of ±20) are the first genes to be statistically significant at some Type I error rate, but represent some of the smallest true differences. In the left tail 50% of the largest values of t are false positives, i.e. from the null distribution (the distribution is skewed to the right because the mean of one of the clusters was increased by a treatment). In contrast, those genes with greatest true DE (those greater than an arbitrary DE of ±5 on the Figure) were all contained within zero ± 7 units of t and the coefficient of determination for regression of t on DE was very poor (R2 = .09). In this example the assumption of homogeneous error variances was true, thus one would expect the correlation between t and DE to be greater because the numerator of the t statistic is DE while the expected value of the denominator is constant. These results confirm that for small n, clustering based on parametric test statistics or their derivatives and p values is likely to identify genes that exhibit modest or even no difference in expression in response to a given treatment. The apparent discrepancy between the test statistic and true DE results from the fact that the t statistic is a ratios and by chance the denominator may be unusually small. As the number of replicates increases this problem becomes increasingly rare. However, due to the current high costs of microarrays, experiments with 2 treatments and 4 (or fewer) biological replicate chips per treatment (8 total) are not uncommon particularly for preliminary or exploratory type experiments (Pedra et al., 2004; Wayne and McIntyre, 2002).
Figure 1.
Simulation results for two treatments, each with 4 replicates. Treatment effects and random errors were sampled from a normal distribution. True DE plotted against the calculated value of t. Observations associated with each of the 4 distributions are identified by letter (A=D(0), B=D(1), C=D(1′), D=D(2))
Table 1.
Alternative parameters used for each of the simulated cases*.
| Case | Proportion in Each Distribution |
r |
Variances |
sn | Average Expression Levels Under Each Condition |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| π0 | π1 | π1′ | π2 | μYe | μYu | μZe | μZu | |||||||
| 1 | .9 | .025 | .025 | .05 | 4 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | ||
| 2 | .9 | .025 | .025 | .05 | 16 | 1 | 1 | 2 | 0 | 0 | 0 | 0 | ||
| 3 | .9 | .025 | .025 | .05 | 4 | 16 | 1 | 4 | 0 | 0 | 0 | 0 | ||
| 4 | .9 | .025 | .025 | .05 | 4 | 1 | 16 | .4 | 0 | 0 | 0 | 0 | ||
|
| ||||||||||||||
| 5 | .5 | .125 | .125 | .25 | 4 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | ||
| 6 | .5 | .125 | .125 | .25 | 16 | 1 | 1 | 2 | 0 | 0 | 0 | 0 | ||
| 7 | .5 | .125 | .125 | .25 | 4 | 16 | 1 | 4 | 0 | 0 | 0 | 0 | ||
| 8 | .5 | .125 | .125 | .25 | 4 | 1 | 16 | .4 | 0 | 0 | 0 | 0 | ||
|
| ||||||||||||||
| 9 | .5 | .125 | .125 | .25 | 4 | 1 | 1† | 1† | 0 | 0 | 0 | 0 | ||
| 10 | .5 | .125 | .125 | .25 | 16 | 1 | 1† | 2† | 0 | 0 | 0 | 0 | ||
| 11 | .5 | .125 | .125 | .25 | 4 | 16 | 1† | 4† | 0 | 0 | 0 | 0 | ||
| 12 | .5 | .125 | .125 | .25 | 4 | 1 | 16† | .4† | 0 | 0 | 0 | 0 | ||
|
| ||||||||||||||
| 13 | .5 | .125 | .125 | .25 | 4 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | ||
| 14 | .5 | .125 | .125 | .25 | 16 | 1 | 1 | 2 | 1 | 0 | 0 | 0 | ||
| 15 | .5 | .125 | .125 | .25 | 4 | 16 | 1 | 4 | 1 | 0 | 0 | 0 | ||
| 16 | .5 | .125 | .125 | .25 | 4 | 1 | 16 | .4 | 1 | 0 | 0 | 0 | ||
π0, π1, π1′, π2 = proportion of genes expressed in neither, the first, the second, or both conditions, respectively; r = replicates; , assumed common to all genes, but heterogeneous and unique to each gene where indicated with†; ; sn = signal to noise ratio ; μYe, μYu, μZe, μZu= mean of all genes expressed and not expressed in the first condition, and expressed and not expressed in the second condition, respectively.
The number of components (clusters) is the next major concern in MM analysis. Except for those MM proposed by Lee et al. (2000) and Reverter et al. (2006), the number of components proposed in a microarray MM is based on desired outcomes, not the underlying biology. The maximum number of components based on desired outcomes is usually 2 (Efron et al., 2001; Liao et al., 2004; Martella, 2006; McLachlan et al., 2002; Newton et al., 2004; Pan, 2002), (defined as differentially expressed and null or affected and not), but 3 (Lai et al., 2007) (defined as up, down, or null), and k (Allison et al., 2002) clusters have also been proposed. In contrast, Lee et al. (2000) and Reverter et al. (2006) based the number of components on biology. The concept of Reverter et al. (2006) was that connection of genes to pathways is dependent on condition (tissue, time, or treatment). When genes are connected they are expressed, but connection and level of expression can vary between treatments. This is an important concept to capture in a MM because expressed genes have variation in transcript number due to other cis or trans-acting elements They partition not only by DE, but also by pathway, and because there can be any number of biological pathways, the number of clusters is the same. Lee et al. (2000) on the other hand, based the number of components on expressed and not expressed genes, but for a single condition (treatment).
Our desire was to examine MM methods that would be applicable to experiments with small number of replicates and based on underlying modes of gene action. From the above considerations, we avoided MM method based on clustering test statistics, or their derivatives. The alternative approach was to simply use the raw (or normalized) data as proposed by Lee et al. (2000). But, we desired to model DE based on patterns of gene expression, i.e. connectivity by condition combined with direction. Given these goals, we considered the most viable approach was to generalize the methods of Lee et al. (2000) to the case of differential expression. We will show that estimates of the variance associated with each cluster have relevant interpretations in terms of biological process useful in answering questions posed by Allison et al.2002.
What we are proposing is a special case of the more general field of MM. General programs are readily available for MM based on any normally distributed variable, e.g. EMMIX (McLachlan et al., 2002). The purpose of our reseach is to examine how well a MM approach based on raw data, with components defined by connectivity and direction, works for detecting DE genes in experiments with small replication. The approach was to compare accuracy and power to other commonly used methods of microarray analysis. Because the procedure is based on clustering differences between means, we call the method MD-MM for Mean Difference-Mixture Model to differentiate it from other clustering methods.
Statistical Methods
MD-MM development
Consider first a single condition for which a replicated microarray experiment is completed. This is exactly the situation described by Lee et al. (2000). There will be two categories of genes: those that are expressed to some degree, and those that are not to any degree, i.e. the genes are either turned on (connected) or not. If turned on, they may have differing numbers of gene transcripts due to genetic (cis and trans-acting elements) and environmental factors. Next consider a second condition for which the same microarray is again used in a replicated manner. In this second condition, the same or different set of genes would have the same or different levels of expression. Our approach is to combine both results into one analysis for differential expression. In this development, we expect a maximum of four categories of genes, which are described as: (i) not expressed in either condition, (ii) expressed only under the first condition, (iii) expressed only under the second condition, and (iv) expressed under both conditions. We do not expect to be able to identify all genes in each of these categories, but rather we aim to find those genes that have greatest differential expression as found in the tails of the distributions. In addition, not all categories may be present in all experiments. For example, the same set of genes may be on or off on both conditions in a particular experiment, and in such case there would be only two categories (i and iv).
Modeling gene expression under different conditions
For what follows assume a microarray oligo chip, or a spotted cDNA membrane, with a single channel or dye, with N genes. The methods can be extended to 2-dye spotted chips after adjusting expression levels for block and dye effects using an appropriate mixed model for the design, such as those given by (Wolfinger et al., 2001). The usual assumption is made that errors are independent of treatment or that suitable transformation is applied to correct the problem if exists.
For each treatment condition, assume r biological replicates, from each of which RNA is isolated and either converted to cDNA or directly hybridized to independent chips or membranes, depending on the technology used. For the first condition, let these observations (after suitable transformation and normalization) be denoted Zij for expression of the jth replicate (j=1, 2,…, r) of the ith gene (i=1, 2,…, N). These observations are modeled differently depending on whether the gene is expressed or not. For expressed genes assume the following model:
| (Equation 1) |
where is the observed level of expression (signal intensity) for the jth replicate (j=1, 2,…, r) of the ith gene (i=1, 2,…, n1), μZe is the average gene expression under that condition, Gi is the effect of the ith gene, ε(i)j is biological sampling error and includes genetic variation among individuals, and ∂(ij) is technical error due to experimental procedures. The terms Gi, ε (i) j and ∂(ij) are assumed to be normally distributed, independently from each other, with means zero and variances and , respectively. The signal variance of the expressed genes is then . For those genes that are not expressed, any non null average refers to background as there is no transcript being produced for such genes. Thus we assume the following model:
| (Equation 2) |
where is the observed signal intensity for the jth replicate of the i′th gene i′ (i′=1, 2,…, n2), μZu is the average of the unexpressed genes (background noise) and ∂(i′ j) is the technical error. Because these genes are not expressed, it is not possible for the environment or other conditions to have an effect, thus all variation is due to technical variation. The signal variance of these non-expressed genes is , thus it follows that . Because genes can only be in one of these two categories N=n1+n2.
Assume that under another condition the same genes are measured with the same number of replicates and denoted as Yij (a balanced design is considered hereinafter without loss of generalization as the methods can be easily extended for cases with unequal number of replication). For these measurements, the same or different set of genes may be expressed at the same or different levels. The expressed genes are described by the following model:
| (Equation 3) |
and not expressed by:
| (Equation 4) |
with corresponding definitions as for the first condition.
Putative differential expression for each gene is estimated as the difference between means as: . Depending on whether a gene is expressed under neither, only one, or both conditions, the Di are modeled by different equations: (i) Not expressed under either condition (k=0): , with conditional expectation , because the mean of the unexpressed genes is expected to be the same regardless of condition; (ii) expressed only under the first condition (k=1): with conditional expectation: ; (iii) expressed only under the second condition (k=1′): with conditional expectation: and, (iv) expressed under both conditions (k=2): with conditional expectation: . The marginal expectations and variances are:
Mixture Models
Estimation
The conditional distributions, given the subset class k and respective parameters, , for k = 0, 1, 1′, or 2, are . The overall distribution is , where πk is the respective mixing proportion of each distribution and . The incomplete-data log likelihood function of the mixture model is , which can be maximized using the EM algorithm (Dempster et al., 1977). The associated complete-data log likelihood function is: , where is an indicator variable such that if the ith gene belongs to cluster k, and otherwise. The expectation of the complete-data log likelihood function is: , and the EM algorithm proceeds as follows. For a given initial set of parameter values, the E-step is: , and the M-step is: , and . The procedure is repeated until convergence is achieved. Because convergence to a local maximum may occur, rather than to the global maximum, a grid of starting points spanning the solution space should be examined. Note that there is a natural ordering of the variances: ; this result can be used to help discern genes that are associated with which class.
Although we have defined four components, it is possible that less than four may be needed for a given situation, i.e. all genes are truly null, or all genes are expressed, or some other combination. Also, categories 2 and 3 (k=1, 1′) may be difficult to separate as they both have the same variance structure and may have only slightly different expectations. For a 3 component model, and for those genes expressed only in one condition or the other, an average across both single expression distributions will result, i.e. D(*) = (D(1) + D(1′))/2. Thus, the number of components in the mixture models can be chosen using some model selection criteria such as Akaike’s information criterion (AIC, Akaike, 1974) and the Bayesian Information Criterion (BIC, Schwarz, 1978).
False Discovery Rate (pFDR)
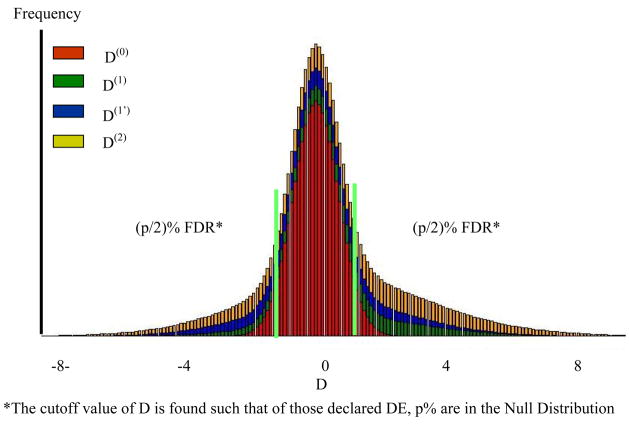
After the parameters are estimated, the data is sorted by Di for a one sided test for differential expression, or abs(Di) for a 2-tailed test, and for each gene , the probability the gene belongs to the null cluster, is calculated. Next for the mth ordered value we compute , which is the cumulative average proportion of genes expected under the null distribution and is conceptually equivalent to the q values of Storey (2003). For a (100α)% pFDR simply find m such that qm ≤ α (Allison et al., 2002) Conceptually these areas are given in Figure 2 for the data shown in Figure 1.
Figure 2. Distribution of D associated with each component of the MM and FDR.
*The cutoff value of D is found such that of those declared DE, p% are in the Null Distribution
The method used by Storey (2003) to find the pFDR is essentially based on a 2-component mixture model based on clustering t or p values, but is, as they state, always biased except for the case when all genes are null. The estimate of the mixing proportion for k = 0, the null distribution, could be combined with the pFDR method of Storey et al. (2004) to give a more accurate q-value estimates.
Methods for Validation and Comparison
Simulations
For the simulations, a wide variety of genetic parameters were used with the intention of capturing the range of possibilities that might be encountered in actual experiments, those cases are given in Table 1. The data were generated based on Equations 1–4 with differing proportions of observations under each condition. Cases 1–12 were a worse case scenarios where the overall mean expression level over all genes for each treatment was not different. In cases 13–16 means over treatments were different. For most cases gene effects, biological, and technical errors were sampled from independent normal distributions with expectations of zero and variance and , respectively. Although the assumption of a common variance for technical and environmental error seemed reasonable, the assumption that all genetic effects (Gi) are sampled from a common distribution is questionable, but unavoidable with our approach. The effect of this assumption was tested in Cases 9–12 of Table 1, whereby we simulated a different variance among biological samples associated with each gene, those variances being a base value as given in Table 1 plus a random value from a uniform distribution (uniform on 0 to 9), for each gene.
A chip with 50,000 genes was assumed; the mixing proportion for the expressed genes was set to either low (π0 = .9, Equations 1 and 3 were used for 2,500 genes; Equations 1 and 4 for 1,250 genes; Equations 2 and 3 for 1,250 genes, and Equations 2 and 4 for 45,000 genes) or high (π0 = .5, Equations 1 and 3 were used for 12,250 genes; Equations 1 and 4 for 6,250 genes; Equations 2 and 3 for 6,250 genes, and Equations 2 and 4 for 25,000 genes). The overall mean for all equations was set to 0, except for Cases 13–16 where the mean of the expressed genes was set to 1, i.e. μYe = 1. The signal to noise ratio, , was set to either high, medium, low, and very low by holding constant and changing either or r. These factors were not considered in all combinations, as too many results would be generated, rather 16 selected combinations were examined as given in Table 1. The data sets are given in the supplemental material along with the MD-MM programs.
For comparison, several popular methods of microarray analysis were examined, these included the simple t-tests with FDR (Benjamini and Hochberg, 1995) or pFDR (Storey, 2003; Storey et al., 2004) approaches for multiple testing, and the permutation-based attenuated t-test of SAM software (Tusher et al., 2001). Comparisons were based on total errors (Type I and Type II) and Power = (1-Type II).
Data halving and mutual validation
We analyzed a microarray experiment using the Arabidopsis Affymetrix® GeneChip® containing 22,819 genes. The design was a 2×2 factorial of genotypes (‘wild type’ vs. the pickle) and exposure treatments (uniconazole-P or no uniconazole-P) as described by Rider et al. (2003). There were 6 replicate chips for each treatment combination using different biological samples for each replicate for a total of 24 chips. For comparison purposes, data from only the pickle mutant, with and without uniconazole exposure, were used. This restriction, combined with data halving, resulted in a two-treatment experiment with few replicates (r = 3), the situation we are addressing. These data were split into two sets (A and B), with three replicates per treatment (uniconazole exposure or not) in each set.
Consistency was determined by the chi-square statistic and correlation. The data within each partition were divided into those genes which were classified as DE, and not, for each method. The results were then tested for non-independence using a chi-square 2 × 2 contingency table. The chi-square statistics ( ) determines the degree to which classification into each set is non-random. A second measure of consistency is the correlation of calls between data sets rAB. For data set A, a dummy variable XA is coded 0 if the null is accepted and 1 if rejected for each gene. Similarly for data set B, a dummy variable XB is coded 0 if the null is accepted and 1 if rejected; then is computed. It can be shown that .
The relative power = rPower is defined to be the number rejected by both data sets over N. We consider a reasonable basis for comparison of methods as that which gives the highest rPower along with the greatest consistency, as measured by either rAB or . Obviously this method of comparison has limitations and by itself may give false conclusions, especially if all hypotheses are accepted or rejected in both data sets, but if used in conjunction with other methods of comparison, adds to the strength of the final conclusion.
Correlation between microarray analysis and quantitative real time PCR
Quantitative real time PCR (qRT-PCR) is considered the most robust method for quantitative analysis of differential expression and is commonly used to confirm differential expression as identified by microarray analysis. We used an ABI Prism 7000 analysis performed using RNA from a single pooled sample across biological replicates in association with the Arabidopsis experiment (Rider et al., 2003). 18S rRNA was used as a standardization control for these expression studies. Because only a single pooled sample was analyzed, statistical significance could not be determined. Rather, the data were correlated with the decisions made using each method. First the qRT-PCR data was separated into 2 categories, those with a difference in cycle numbers between treatment of ΔCT >1 and ΔCT<1. This data was cross classified with those genes declared DE and not DE by each method in the microarray analysis. A 2×2 chi-square was then used to test if the association was different from random. Second, the correlation between decision category and qRT-PCR category was estimated.
Results
Comparison by simulations
For the examples used, a 4-component MD-MM resulted in the best fit, but not significantly better than the 3-component model. This result was expected whenever the absolute values of means of genes in components 2 and 3, and their variances, were similar, such as in scenarios 1–12. However, even for scenarios 13–16, where the absolute value of means of genes in components 2 and 3 were different, but variances the same, the 4-component model did not fit significantly better than a 3-component model. But, a 3-component model always fit significantly better than a 2-component model. Thus a 3-component model was fit to all cases; results are given in Table 2.
Table 2.
Total error rate (%) and power (%) for alternative methods of microarray analysis for cases given in Table 1.
| Case | Method |
|||||||
|---|---|---|---|---|---|---|---|---|
| FDR | pFDR | SAM | MD-MM | |||||
| Errors | Power | Errors | Power | Errors | Power | Errors | Power | |
| 1 | 10 | 0 | 10 | 0 | 9.6 | 3.6 | 9.0 | 9.8 |
| 2 | 8.1 | 19.6 | 8.1 | 20 | 7.5 | 25.5 | 6.5 | 35.4 |
| 3 | 6.8 | 33.2 | 6.7 | 34.4 | 3.9 | 61 | 3.8 | 63.9 |
| 4 | 10 | 0 | 10 | 0 | 10 | 0 | 5.8 | 43.8 |
|
| ||||||||
| 5 | 50 | 0 | 49.9 | 0.1 | 48.2 | 3.7 | 40.1 | 17.1 |
| 6 | 35.2 | 30.5 | 33.8 | 33.8 | 32.2 | 36.5 | 26.2 | 49.4 |
| 7 | 24.4 | 52.6 | 21.9 | 58.9 | 23.1 | 55.1 | 14.6 | 72.8 |
| 8 | 50 | 0 | 50 | 0 | 50 | 0 | 24.7 | 51.8 |
|
| ||||||||
| 9 | 50 | 0 | 50 | 0 | 49.9 | 0.1 | 22.1 | 56.9 |
| 10 | 49 | 2 | 48.9 | 2.2 | 48.8 | 2.5 | 18.6 | 64.1 |
| 11 | 45.9 | 8.3 | 45.3 | 9.7 | 42.5 | 15.4 | 12.2 | 77.8 |
| 12 | 50 | 0 | 50 | 0 | 50 | 0.1 | 15.0 | 71.8 |
|
| ||||||||
| 13 | 50 | 0 | 49.8 | 0.4 | 42.4 | 15.6 | 35.8 | 31.3 |
| 14 | 29 | 43.2 | 27.3 | 47.3 | 25.7 | 50.6 | 21.9 | 58.5 |
| 15 | 24.2 | 52.8 | 21.8 | 58.9 | 19.7 | 63.2 | 14.8 | 72.4 |
| 16 | 50 | 0 | 50 | 0 | 50 | 0 | 22.6 | 56.3 |
|
| ||||||||
| Ave | 33.9 | 15.6 | 33.3 | 17.4 | 32.1 | 20.4 | 18.2 | 52.5 |
Power=100[1−(# false negatives/# true DE)]
Errors=100(# false positives + # false negatives)/N.
For MD-MM, the null distribution was always defined as the distribution centered at 0 with smallest variance, genes in all other distributions were declared DE.
In all cases examined and methods compared, use of the MD-MM approach resulted in the greatest levels of power and lowest total errors. On average, over all cases, the MD-MM had three times the power and with 14% fewer total errors than the next best method (SAM). The MD-MM particularly excelled where the signal to noise to noise ratio was poor (Cases 4, 8, 12, and 16). In cases 4, 8, and 16, only the MD-MM was able to detect any differentially expressed genes, and in all those cases did so with power ranging between 43% and 72%. With heterogeneous variances (Cases 9–12), regardless of the signal to noise ratio (sn), the MD-MM resulted in almost an order of magnitude greater power than t-tests coupled with the FDR and pFDR approaches and three times that of SAM. For a differentially expressed distribution with a mean greater than zero, i.e. biased toward up regulation (Cases 13–16), the power and error rate of the MD-MM was improved as the distributions have less overlap.
These results show that even for the most difficult cases, where the centers of the distributions of the component distributions are the same, differentially expressed genes can be distinguished. As seen from these results, the key to distinguishing differentially expressed genes, from both the null distribution and from lowly differentially expressed genes within the same distribution, is through exploiting the information that expressed genes have greater variances. Of course, if the means of the distributions are also different, then the ability to distinguish differentially regulated genes may also improve, but only in one direction, because the center of the expressed distribution will have decreased overlap with the null distribution in one direction but increased in the other.
Estimation of proportion of transcriptome differentially expressed
Estimation of the proportion of genes in the null distribution is given in Table 3. By definition, all other genes not in the null cluster are either expressed in one environment or the other or both. The MD-MM accurately and precisely estimated the proportion in the null distribution, being on average within 0.3±0.9% of the true value. In contrast, the pFDR method was consistently biased upward, usually by a large degree, averaging 38.7±8.4% overestimation. Storey (2003) acknowledges that their estimator is always biased upward, except for the case where all genes are truly null. The null distribution was identified as that distribution with a mean of 0 and smallest variance, i.e. due only to technical variation.
Table 3.
True and estimated proportion of genes in null distribution with the MD-MM and pFDR methods*.
| Estimated Percent in Null Distribution | Percent Error | ||||
|---|---|---|---|---|---|
| Case | True Percent in the Null Distribution | MD-MM | pFDR | MD-MM | pFDR |
| 1 | 90 | 84.3 | 95.9 | −6.3 | 6.5 |
| 2 | 90 | 90.1 | 92.8 | 0.1 | 3.1 |
| 3 | 90 | 89.9 | 91.5 | −0.1 | 1.6 |
| 4 | 90 | 85.2 | 98.9 | −5.3 | 9.9 |
| 5 | 50 | 54.1 | 80.2 | 8.2 | 60.3 |
| 6 | 50 | 49.9 | 69.9 | −0.2 | 39.8 |
| 7 | 50 | 49.7 | 58.9 | −0.6 | 17.9 |
| 8 | 50 | 51.9 | 96.3 | 3.8 | 92.6 |
| 9 | 50 | 52.5 | 94.8 | 5.0 | 89.6 |
| 10 | 50 | 51.6 | 86.5 | 3.2 | 73.0 |
| 11 | 50 | 49.5 | 77.7 | −1.0 | 55.5 |
| 12 | 50 | 51 | 46.7 | 2.0 | −6.6 |
| 13 | 50 | 49.1 | 75.2 | −1.8 | 50.3 |
| 14 | 50 | 49.8 | 63.4 | −0.4 | 26.8 |
| 15 | 50 | 50.1 | 59.3 | 0.2 | 18.6 |
| 16 | 50 | 49.3 | 89.7 | −1.4 | 79.5 |
|
| |||||
| MEAN | 60.0 | 59.9 | 79.9 | 0.3±0.9 | 38.7±8.4 |
Comparison by data halving and mutual validation
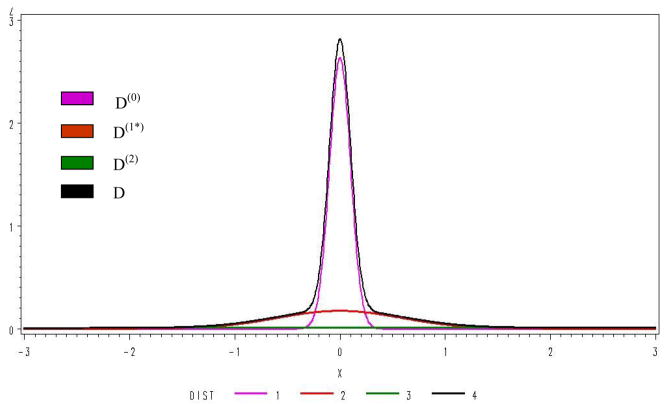
For the analysis of the first half of the data by the MD-MM method, we found that a 3 component MM fit significantly better (BIC=12776) than a 2 component (BIC=16,902), but a 4 component MM (BIC=12,782) was not better than a 3, results using the AIC criteria were the same. Distributions fit using the 3 components are shown in Figure 3. Genes expressed in neither treatment, in only one treatment (up or down), and expressed in both treatments (up or down) accounted for respectively 66%, 25%, and 9% of the total distribution. Analysis of the second half of the data gave similar results. It is interesting that the primary form of DE is expression under one condition, and not the other indicating that genes are turned on or off and infrequently modulated by treatments. Consistency and rPower are given in Table 4. The MD-MM had the greatest rPower, followed by SAM, pFDR and FDR. The rPower of MD-MM was twice that of SAM and almost 3 times that of pFDR. The consistency across data sets, as measured by chi-square, was similar for FDR, pFDR, and SAM, but approximately 2.5 times greater for the MD-MM.
Figure 3.
Distribution of the MM components.
Table 4.
Comparison of power and consistency among methods using data splitting*
| Method | Data Set A | Data Set B | Consistency | rP% | |||
|---|---|---|---|---|---|---|---|
| C | R | rAB | |||||
| FDR | C | 22,056 | 439 | 0.27 | 1,670 | .5 | |
| R | 196 | 119 | |||||
|
| |||||||
| pFDR | C | 21,100 | 365 | 0.33 | 2,525 | 1.6 | |
| R | 990 | 355 | |||||
|
| |||||||
| SAM | C | 13,324 | 7,530 | 0.26 | 1,576 | 7.0 | |
| R | 350 | 1,606 | |||||
|
| |||||||
| MD-MM | C | 16,635 | 953 | 0.74 | 12,413 | 17.9 | |
| R | 1135 | 4,087 | |||||
C = accept, R = reject, rP=rPower
Correlation between microarray analysis and quantitative real time PCR
Results for all methods are given in Table 5. The MD-MM correctly identified DE genes almost twice that of the other methods while total errors were less. Even more striking differences between methods were obtained using those same treatments but with the wild type genetic background (see Appendix Table A1).
Table 5.
Correlation of decision by method and classification by qRT-PCR for each data set and for which qRT-PCR results were available.
| Method | Data Set | qRT-PCR |
X2 | Correlation | |||
|---|---|---|---|---|---|---|---|
| ΔCT<1 Decision* | ΔCT>1 Decision* | ||||||
| Not DE | DE | Not DE | DE | ||||
| FDR | A | 139 | 5 | 138 | 33 | 28 | .28 |
| B | 180 | 16 | 114 | 57 | 38 | .31 | |
|
| |||||||
| pFDR | A | 181 | 15 | 113 | 58 | 40 | .33 |
| B | 162 | 34 | 88 | 83 | 40 | .33 | |
|
| |||||||
| SAM | A | 192 | 4 | 134 | 37 | 36 | .31 |
| B | 179 | 17 | 93 | 78 | 35 | .31 | |
|
| |||||||
| MD-MM | A | 139 | 59 | 52 | 119 | 59 | .40 |
| B | 131 | 67 | 46 | 125 | 53 | .38 | |
Decision based on 5% FDR (FDR, pFDR, SAM); or overlap with null distribution (MD-MM).
Appendix Table A1.
Correlation of decision for uwt vs. wt comparison by method and classification by qRT-PCR for each data set and for which qRT-PCR results were available
| Method | Data Set | qRT-PCR |
X2 | Correlation | |||
|---|---|---|---|---|---|---|---|
| ΔCT<1 Decision* | ΔCT>1 Decision* | ||||||
| Not DE | DE | Not DE | DE | ||||
| FDR | A | 220 | 0 | 142 | 5 | 8 | .14 |
| B | 219 | 1 | 141 | 6 | 6 | .13 | |
|
| |||||||
| pFDR | A | 219 | 1 | 138 | 8 | 9 | .16 |
| B | 218 | 2 | 137 | 10 | 10 | .16 | |
|
| |||||||
| SAM | A | 218 | 1 | 136 | 11 | 14 | .19 |
| B | 218 | 2 | 135 | 12 | 13 | .19 | |
|
| |||||||
| MD- MM | A | 167 | 53 | 49 | 89 | 63 | .41 |
| B | 171 | 49 | 47 | 100 | 76 | .46 | |
Decision based on 5% FDR (FDR, pFDR, SAM); or overlap with null distribution (MD-MM).
Discussion
We used three approaches for verification and comparison among methods, each has advantages and disadvantages. The first was simulated data. The advantage of simulation is the answers are known without error, but the major disadvantage is the data structures and distributions simulated may not accurately reflect real world microarray data. The second method used was actual microarray data, but combined with data splitting, where half of the data are used to verify the remainder. Here, the advantage is that the data structures and distributions are valid, but we can only infer the accuracy of the methods on agreement between different subset. The third method used was correlation of decisions with expression levels as determined by qRT-PCR. Here, the advantage is that qRT-PCR is a robust approach that is commonly used by biologists to confirm differential expression as identified by microarray analysis, but this analysis was limited by the additional time and expense and by the fact that qRT-PCR is itself subject to error. However, because all three methods were used, each contributed to the strength of the conclusions.
Simulation results over a wide variety of parameters and assumptions showed that the MD-MM had the greatest power and lowest total errors of the methods compared. Results using data halving and qRT-PCR on real data confirmed these findings for at least one experimental situation. All three methods of comparison support each other, not only as to robustness and power of alternative methods, but also under which conditions the orders are determined. Additionally, our results appear to be the first to incorporate qRT-PCR analysis as one of several approaches to extensively compare methods of microarray analysis for both Type I and II errors, as well as power.
The simulation results indicate that the advantage of the MD-MM approach increased when applied under any of the following conditions: increased variance among biological replicates, low replication, and non-homogenous variances. All of these factors result in a decrease in the overlap between the distributions of the null and differentially expressed genes, thus cumulatively or individually lending strength to the MD-MM approach. These same factors either have no impact or weaken the ability of the simple t-test to distinguish genes. The only factor that can increase power (for a given significance level) of the simple t-test, or similar methods, is to increase numbers of replicates. Although the data were generated based on our set of assumptions, these are the same set of assumptions needed for analysis of variance, i.e. normality and common variance. Thus comparisons were between parametric methods (SAM, FDR, pFDR) based on the same set of assumption, although SAM is less dependent on those assumptions and should be more robust.
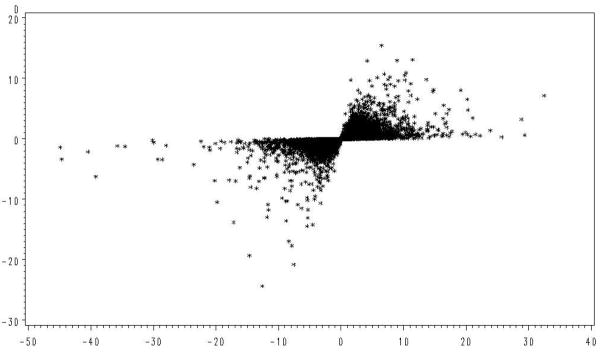
The microarray data also supports our concern regarding use of t-tests with small replication to find genes with large expression differences. As shown in Figure 1, those genes with the largest values of t were often due to underestimation of the error variance, rather than large differences in expression. This relationship was examined with the real data in Figure 4 where the calculated value of t and observed differences in treatment means for each gene is given. Here the greatest values of t are again associated with some of the smallest mean differences while the largest mean differences are associated with the smallest values of t.
Figure 4.
Observed relationship of the t statistic with normalized treatment differences (D).
Similarly, this concern can be demonstrated with qRT-PCR. We examined the top 25 ranked genes with the highest differential expression, as determined by qRT-PCR, in data sets A and B (Table 5) and found that the MD-MM found 36% and 28% respectively of these genes. In contrast, pFDR identified 4% and 4%, SAM identified 0% and 8%, and FDR identified 0 and 4% respectively of these genes. Thus ranking genes based on the simple t-test does not necessarily identify a high proportion of genes with detectable DE, whereas a MM based on raw, or transformed, differences does. In addition to having better success at identifying genes that exhibit DE, MD-MM has other technical advantages that are worth noting. Estimates of magnitudes for sources of variation can be used for quality control purposes and experimental design to determine samples sizes needed to achieve a desired power.
One critical feature of MD-MM that allows it to better describe the transcriptome is the recognition that genes can only fall into four expression categories, with three different variance structures. Genes in Category 4, i.e. expressed in both conditions, may include genes with minimal or negligible difference in expression in the two conditions, whereas all genes in Category 1 cannot have any real difference in expression, yet both situations can result in genes that are (virtually) not differentially expressed. However, microarray data that arise from expressed genes are influenced by biological background, sampling, and technical errors, whereas those related to null genes are only influenced by technical errors. Thus each category of gene is expected to have a different variance structure. Therefore fitting differential expression into two categories (differentially expressed and not) as commonly found in the literature is a vast oversimplification that either assumes 1) all expressed genes are expressed under both conditions, but at different levels, or 2) that genes are only expressed in one condition but not the other. There is no allowance for a combination of 1) and 2).
Use of our MD-MM to declare significant DE genes requires careful consideration of our definition of DE. All genes expressed in at least one environment or condition are by definition DE, even those that are expressed in both environments at approximately the same level. This is because there is a zero probability of two expressed genes having a true difference of zero. From a pragmatic perspective, genes which are expressed in both environments but near equally will overlap the null distribution, which by definition is centered at zero, and will be declared not-DE. In Figure 2, all those genes contained within the (p/2)%FDR interval are considered not DE because they overlap the null by (1-p)%, but for genes in any interval, we can give the probability of being associated with each of the distributions.
Although the MD-MM method uses raw (or transformed) differences as the metric of DE, the result should not be interpreted as a fold change test. A fold change test is based on a constant critical value for significance, usually 1 if log2 transformed. As a result, power can decrease as sample size increases (Allison, et. al, 2002), which is the opposite of what the MD-MM method achieves. With the MD-MM the critical value, determined by the overlap of expressed gene distributions with the null distribution, decreases directly with sample size, i.e. . However, we implicitly assume a common variance for genes within a cluster and common technical variation across clusters. This assumption is certainly false but appears adequate for our MD-MM approach based on both simulations with heterogeneous variances and actual data. Thus our mixture model also takes into account variance structure of gene expression levels, which is not accounted for with simple fold change. Another beneficial feature of using a MM approach is that it can be used to facilitate a meta-analysis across labs and platforms by standardizing the deviations within labs/platforms to a phenotypic variance estimated for that lab/platform before combining data. For a meta-analysis, the D statistic is standardized using the phenotypic standard deviation among expression levels across the transcriptome. Because of the large number of genes in an array, this variance can be measured with great precision.
In conclusion, the MD-MM as developed here allows for greater power in poorly replicated experiments and also with poor signal to noise ratios.
Acknowledgments
We greatly appreciate the critical review and comments of an earlier draft by Drs. Rebecca Doerge and Hans Cheng. WMM and GR were supported in part by a grant from the USDA Biotechnology Risk Assessment Program no 2004-33120-15204. BRP was supported by a National Institutes of Health Grant (NIH 1R01 AI51513-01). SX: NIH grant with No: R01-GM55321; JO was supported in part by grants from the National Institutes of Health (R01GM059770-01A1 and 5R01GM59770-02). SDR was supported by funds from BASF. This paper was developed as part of the NCC204 USDA/CSREES Regional Project
Abbreviations
- FDR
false discovery rate
- pFDR
positive FDR
- SAM
significance analysis of microarrays
- qRT-PCR
quantitative reverse transcriptase polymerase chain reaction
Footnotes
Data sets used for the simulations are available upon request
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Reference List
- Aitkin M, Wilson GT. Mixture-Models, outliers, and the EM algorithm. Technometrics. 1980;22:325–331. [Google Scholar]
- Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19(6):716–723. [Google Scholar]
- Alexandridis R, Lin SL, Irwin M. Class discovery and classification of tumor samples using mixture modeling of gene expression data - a unified approach. Bioinformatics. 2004;20:2545–2552. doi: 10.1093/bioinformatics/bth281. [DOI] [PubMed] [Google Scholar]
- Allison DB, Gadbury GL, Heo MS, Fernandez JR, Lee CK, Prolla TA, Weindruch R. A mixture model approach for the analysis of microarray gene expression data. Computational Statistics & Data Analysis. 2002;39:1–20. [Google Scholar]
- Asyali MH, Alci M. Reliability analysis of microarray data using fuzzy c-means and normal mixture modeling based classification methods. Bioinformatics. 2005;21:644–649. doi: 10.1093/bioinformatics/bti036. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate - a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B-Methodological. 1995;57:289–300. [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via EM Algorithm. Journal of the Royal Statistical Society Series B-Methodological. 1977;39:1–38. [Google Scholar]
- Do KA, Muller P, Tang F. A Bayesian mixture model for differential gene expression. Journal of the Royal Statistical Society Series C-Applied Statistics. 2005;54:627–644. [Google Scholar]
- Edelbrock C. Mixture model tests of hierarchical clustering algorithms - problem of classifying everybody. Multivariate Behavioral Research. 1979;14:367–384. doi: 10.1207/s15327906mbr1403_6. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani R, Storey JD, Tusher V. Empirical Bayes analysis of a microarray experiment. Journal of the American Statistical Association. 2001;96:1151–1160. [Google Scholar]
- Ghosh D. Mixture models for assessing differential expression in complex tissues using microarray data. Bioinformatics. 2004;20:1663–1669. doi: 10.1093/bioinformatics/bth139. [DOI] [PubMed] [Google Scholar]
- Jeffery IB, Higgins DG, Culhane AC. Comparison and evaluation of methods for generating differentially expressed gene lists from microarray data. BMC Bioinformatics. 2006;7:359. doi: 10.1186/1471-2105-7-359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kauermann G, Eilers P. Modeling microarray data using a threshold mixture model. Biometrics. 2004;60:376–387. doi: 10.1111/j.0006-341X.2004.00182.x. [DOI] [PubMed] [Google Scholar]
- Kendziorski CM, Newton MA, Lan H, Gould MN. On parametric empirical Bayes methods for comparing multiple groups using replicated gene expression profiles. Statistics In Medicine. 2003;22:3899–3914. doi: 10.1002/sim.1548. [DOI] [PubMed] [Google Scholar]
- Lai YL, Adam BL, Podolsky R, She JX. A mixture model approach to the tests of concordance and discordance between two large-scale experiments with two-sample groups. Bioinformatics. 2007;23:1243–1250. doi: 10.1093/bioinformatics/btm103. [DOI] [PubMed] [Google Scholar]
- Lee MLT, Kuo FC, Whitmore GA, Sklar J. Importance of replication in microarray gene expression studies: Statistical methods and evidence from repetitive cDNA hybridizations. PNAS. 2000;97:9834–9839. doi: 10.1073/pnas.97.18.9834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao JG, Lin Y, Selvanayagam ZE, Shih WCJ. A mixture model for estimating the local false discovery rate in DNA microarray analysis. Bioinformatics. 2004;20:2694–2701. doi: 10.1093/bioinformatics/bth310. [DOI] [PubMed] [Google Scholar]
- Martella F. Classification of microarray data with factor mixture models. Bioinformatics. 2006;22:202–208. doi: 10.1093/bioinformatics/bti779. [DOI] [PubMed] [Google Scholar]
- McLachlan GJ, Bean RW, Jones LBT. A simple implementation of a normal mixture approach to differential gene expression in multiclass microarrays. Bioinformatics. 2006;22:1608–1615. doi: 10.1093/bioinformatics/btl148. [DOI] [PubMed] [Google Scholar]
- McLachlan GJ, Bean RW, Peel D. A mixture model-based approach to the clustering of microarray expression data. Bioinformatics. 2002;18:413–422. doi: 10.1093/bioinformatics/18.3.413. [DOI] [PubMed] [Google Scholar]
- McLachlan GJ, Peel D, Bean RW. Modelling high-dimensional data by mixtures of factor analyzers. Computational Statistics & Data Analysis. 2003;41:379–388. [Google Scholar]
- Newton MA, Noueiry A, Sarkar D, Ahlquist P. Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics. 2004;5:155–176. doi: 10.1093/biostatistics/5.2.155. [DOI] [PubMed] [Google Scholar]
- Pan W. A comparative review of statistical methods for discovering differentially expressed genes in replicated microarray experiments. Bioinformatics. 2002;18:546–554. doi: 10.1093/bioinformatics/18.4.546. [DOI] [PubMed] [Google Scholar]
- Pan W. On the use of permutation in and the performance of a class of nonparametric methods to detect differential gene expression. Bioinformatics. 2003;19:1333–1340. doi: 10.1093/bioinformatics/btg167. [DOI] [PubMed] [Google Scholar]
- Pan W, Shen XT, Jiang AX, Hebbel RP. Semi-supervised learning via penalized mixture model with application to microarray sample classification. Bioinformatics. 2006;22:2388–2395. doi: 10.1093/bioinformatics/btl393. [DOI] [PubMed] [Google Scholar]
- Pedra JHF, McIntyre LM, Scharf ME, Pittendrigh BR. Genom-wide transcription profile of field- and laboratory-selected dichlorodiphenyltrichloroethane (DDT)-resistant Drosophila. PNAS. 2004;101:7034–7039. doi: 10.1073/pnas.0400580101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reverter A, Ingham A, Lehnert SA, Tan SH, Wang YH, Ratnakumar A, Dalrymple BP. Simultaneous identification of differential gene expression and connectivity in inflammation, adipogenesis and cancer. Bioinformatics. 2006;22:2396–2404. doi: 10.1093/bioinformatics/btl392. [DOI] [PubMed] [Google Scholar]
- Rider SD, Henderson JT, Jerome RE, Edenberg HJ, Romero-Severson J, Ogas J. Coordinate repression of regulators of embryonic identity by PICKLE during germination in Arabidopsis. Plant Journal. 2003;35:33–43. doi: 10.1046/j.1365-313x.2003.01783.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Annals of Statistics. 1978;6(2):461–464. [Google Scholar]
- Storey JD. The positive false discovery rate: A Bayesian interpretation and the q-value. Annals of Statistics. 2003;31:2013–2035. [Google Scholar]
- Storey JD, Taylor JE, Siegmund D. Strong control, conservative point estimation and simultaneous conservative consistency of false discovery rates: a unified approach. Journal of the Royal Statistical Society Series B-Statistical Methodology. 2004;66:187–205. [Google Scholar]
- Tusher VG, Tibshirani R, Chu G. Significance analysis of microarrays applied to the ionizing radiation response. PNAS. 2001;98:5116–5121. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh B, Henderson D. Microarrays and beyond: What potential do current and future genomics tools have for breeders. Journal of Animal Sciences. 2004;82(Suppl):E292–E299. doi: 10.2527/2004.8213_supplE292x. [DOI] [PubMed] [Google Scholar]
- Wayne ML, McIntyre LM. Combining mapping and arraying: An approach to candidate gene identification. PNAS. 2002;99:14903–14906. doi: 10.1073/pnas.222549199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfinger RD, Gibson G, Wolfinger ED, Bennett L, Hamadeh H, Bushel P, Afshari C, Paules RS. Assessing gene significance from cDNA microarray expression data via mixed models. Journal of Computational Biology. 2001;8:625–637. doi: 10.1089/106652701753307520. [DOI] [PubMed] [Google Scholar]