Skip to main content
PMC home page
Molecular Systems Biology logoLink to Molecular Systems Biology
. 2008 Nov 4;4:228. doi: 10.1038/msb.2008.60

Finding multiple target optimal intervention in disease-related molecular network

Kun Yang 1,2, Hongjun Bai 1,2, Qi Ouyang 2, Luhua Lai 1,2,a, Chao Tang 2,3
PMCID: PMC2673713  PMID: 18985027

Abstract

Drugs against multiple targets may overcome the many limitations of single targets and achieve a more effective and safer control of the disease. Numerous high-throughput experiments have been performed in this emerging field. However, systematic identification of multiple drug targets and their best intervention requires knowledge of the underlying disease network and calls for innovative computational methods that exploit the network structure and dynamics. Here, we develop a robust computational algorithm for finding multiple target optimal intervention (MTOI) solutions in a disease network. MTOI identifies potential drug targets and suggests optimal combinations of the target intervention that best restore the network to a normal state, which can be customer designed. We applied MTOI to an inflammation-related network. The well-known side effects of the traditional non-steriodal anti-inflammatory drugs and the recently recalled Vioxx were correctly accounted for in our network model. A number of promising MTOI solutions were found to be both effective and safer.

Keywords: anti-inflammatory, arachidonic acid metabolic network, drug efficacy prediction, multiple target drug design, network-based drug design

Introduction

The one-target one-drug paradigm has been the dominating drug discovery approach in the past decades (Lindsay, 2003). The paradigm focuses on identifying a single chemical entity that binds to a single target. This single-target-based method was believed to be more efficient than the traditional in vivo approach because of its greater screening capacity and the associated rational drug discovery programs. However, the number of successful drugs did not increase as expected (FDA, 2004; Sams-Dodd, 2005). Problems occur when the target itself is uncertain and when multiple targets have to be involved in disease control. It was long realized that the behavior of drug molecules in a disease network can be complex. Drugs with efficacy predicted only from their specific target-binding experiment may not have the same effect in clinical treatment due to interactions between pathways in the disease network (Csermely et al, 2005). Side effects often occur because of the unexpected effects of the drug. For example, in the case of inflammation, two pathways, the COX (cyclooxygenase) pathway and the 5-LOX (5-lipoxygenase) pathway, produce inflammatory mediators. Molecules important for normal physiology, such as vasoactive substance prostacyclin (PGI2) and thromboxane A2 (TXA2), are metabolized in the same system as well. Selective COX-2 inhibitors can effectively prohibit the production of certain inflammatory mediators, such as prostaglandins (PGs). But this leads to a concomitant increase of leukotrienes (LTs), another kind of inflammatory mediator (Rainsford, 1993; Brooks, 1998). Even worse, it causes a cardiovascular side effect due to the induced unbalance between PGI2 and TXA2 (Wang et al, 2005).

To overcome the limitations of the single-target-based drugs, growing attention has been paid to drug discoveries involving multiple targets and at the level of disease networks (Csermely et al, 2005; Frantz, 2005; Kitano, 2007; Zimmermann et al, 2007). Some clinical data support the benefits of multi-target drugs. Examples of such strategy can be found in the combinatorial therapy of AIDS, atherosclerosis, cancer, and depression (Korcsmaros et al, 2007). The discovery that some traditional remedies and empirically selected drugs act on multiple targets also suggests that multi-target drugs can be beneficial (Sharom et al, 2004). Several marketing successes of multicomponent therapies have already been reported: salmeterol/fluticasone (Advair; GlaxoSmithKline) (Nelson, 2001), nicotinic acid/lovastatin (Advicor; Kos Pharmaceuticals) (Gupta and Ito, 2002; Bays et al, 2003) and AZT–3TC (Combivir; GlaxoSmithKline) (Larder et al, 1995).

A diverse range of work has been carried out in the emerging field of multi-target drug design. Cell-based phenotypic assays were employed to construct better models of disease systems (Borisy et al, 2003; Zimmermann et al, 2007). Ligand promiscuity was studied to design inhibitors against multiple targets (Hopkins et al, 2006). Disease-related networks were reconstructed to gain insights at a global and systems level (Bouwmeester et al, 2004; Duarte et al, 2007). Various databases have been developed for systematic analysis (Peri et al, 2003; Ganter et al, 2005). Theoretical and computational studies in this and related areas are also picking up pace. It was proposed that system-oriented drug design should take into account the intrinsic properties of biological systems, for example, robustness (Kitano, 2007). Many mathematical models of disease-relevant pathways have been constructed with the potential to elucidate underlying mechanisms of diseases and to identify treatment strategies (Schoeberl et al, 2002; Rajasethupathy et al, 2005). Network properties were analyzed to find potential drug targets and to understand connectivity between them (Sung and Simon, 2004; Hwang et al, 2008). However, practical and systematic computational strategies and methods are in need for multi-target drug design based on disease network modeling.

In the present study, we develop a computational method for finding multiple target optimal intervention (MTOI) solutions in a disease network. For a given disease network, the method tries to identify effective points of intervention and the combination of interventions that can best restore the disease network to a desired normal state. Instead of focusing on a single drug target, the MTOI method analyzes the relevant network as a system to extract information about the inter-conversion of the disease and the normal state of the network. The method has two end products: (1) it generates a list of potential drug targets in a given disease network and their corresponding regulation (inhibition or activation) needed for treatment; (2) it suggests a list of optimal combinatorial multi-target intervention solutions for any user-defined therapeutic requirements. As a concrete example, we have applied MTOI to an inflammation-related network—the arachidonic acid (AA) metabolic network (AAnetwork). The long history of the anti-inflammatory struggle has not yet succeeded in safe and effective drugs, but has accumulated abundant experimental and clinical data. This allowed us to construct an AAnetwork model in human polymorphonuclear leukocyte (PMN), presented in our earlier study (Yang et al, 2007). Here, we further extended this model to other cell types to construct a more accurate model with improved toxicity prediction. With this new AAnetwork, we simulated the drug effects of popular anti-inflammatory medicines, such as aspirin, Vioxx and so on. The known bleeding or cardiovascular side effects of these drugs were correctly reproduced. We applied MTOI to the new AAnetwork and identified five drug targets in the network: phospholipase A2 (PLA2), PGE synthetase (PGES), COX-2, 5-LOX and LTA4 hydrolase (LTA4H). A number of optimal combinations of target intervention (MTOI solutions) were found that are both effective in controlling the inflammation mediators and are safe with minimal side effects.

Results

MTOI for disease network

Feedback loops, cross-talk and other network-intrinsic properties can make the effects of drug molecules much more complicated than what a linear one-drug one-target approach would predict (Araujo et al, 2007; Kitano, 2007; Lehar et al, 2007). It is therefore necessary to systematically analyze the disease network as a whole to find points of intervention that are the most effective and with the least side effects. We have developed a computational method for finding multiple target intervention solutions with user-defined therapeutic effects. This method contains two stages. The first stage is the identification of the potential drug targets. This stage can be skipped if the drug targets have been identified or are given. The second stage is the search and optimization of multiple target intervention solutions, which are the core functions of the method. Two network states are defined: the disease state and the normal (or desired) state. The disease state is a network state in which the production of disease-related molecules is abnormal. The normal (or desired) state is the network state one would like to achieve after taking medicine, which can be customer-defined. The main procedure of MTOI is to perturb the network and optimize it toward the desired state. The procedure can be carried out by various optimization algorithms; here, we used Monte Carlo simulated annealing (MCSA). By comparing the perturbed network that has achieved the desired state with the network that generated the disease state, we are able to find potential drug targets and the MTOI solutions that best restore the disease network state to the desired one.

Drug target identification

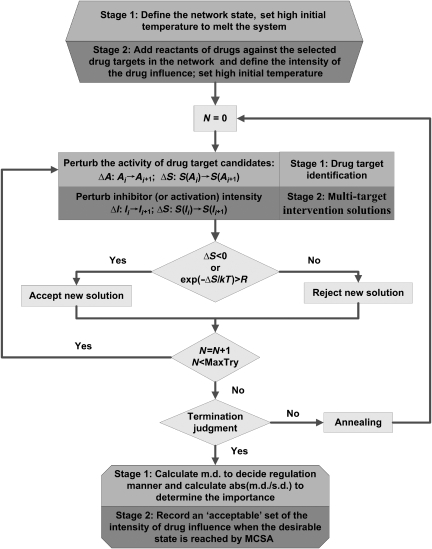
Before searching for the MTOI solutions, we need to identify the potential drug targets in the disease network. These targets are selected according to a criterion that measures their robust ‘influence' in restoring the network state when being perturbed. Specifically, we define an objective function to be the difference between the current network state and the user-defined desired state. The function is then minimized with an MCSA algorithm (Figure 1), by changing the activity of drug target candidates, until the network state is sufficiently close to the desired one. We record the activities of drug target candidates in the final state, and this is called an acceptable MCSA run. After many acceptable runs of MCSA, many sets of activities of drug target candidates that achieved the desired state are obtained. Two parameters are then calculated to analyze the robust influence of a drug target candidate on the network state (see details in Materials and methods). One is the standard deviation (s.d.) of the activities of the drug target candidate in all acceptable runs. This parameter describes the consistency of the activity of the candidate in restoring the desired state. The other is the median deviation (m.d.) of the activities of the drug target candidate in the desired state from that of the disease state. Median deviation describes how far on average, does the activity of drug target candidate in the desired state deviate from that in the disease state. Drug target candidates with larger m.d. are more responsive to perturbations that restore the network to the desired state. The absolute value of the ratio of m.d. to s.d. is used to rank drug target candidates. The larger the ∣m.d./s.d.∣ is, the more likely that perturbing the target will have a significant effect in steering the network toward the desired state. Median deviation also provides information about the manner of regulation that should be adopted in the treatment. When the m.d. value is negative, the corresponding drug target should be inhibited in the treatment; otherwise, the target should be activated. With all the information above, a set of drug targets is selected, which will be the subject of the multiple targets control solution search in stage 2 of MTOI described below.

Figure 1.

Figure 1

Open in a new tab

The flow chart of MTOI. MTOI functions in two stages: drug target search and optimal multi-target control solution identification. MCSA is employed as the optimization method. Differences in stages 1 and 2 are highlighted by light and dark gray, respectively.

Optimal multiple targets intervention solutions

With the potential drug targets in the disease network identified, we search for the best sets of combinatorial control on these targets that can restore the network to the desired state. Similar to stage 1, MCSA is utilized to search for solutions that can turn the network state into the desired one (Figure 1). The difference with stage 1 is that (1) the optimization is performed only on a pre-specified set of drug targets that are selected in stage 1 and (2) the perturbation on the targets is modeled in detail with corresponding equations of inhibition or activation (see details in Materials and methods). Therefore, at the end of an acceptable MCSA run, which resulted in a network state sufficiently close to the desired one, we obtain a set of inhibition and/or activation intensities on the drug targets. We call this set an optimal solution of the multi-target control for the specified targets. After many runs of MCSA, we can, in principle, find all possible optimal solutions for the combinatorial multi-target control with desired therapeutic effects for the disease network.

Application of MTOI to inflammation network

The AAnetwork model in human PMN, endothelial and platelet cells

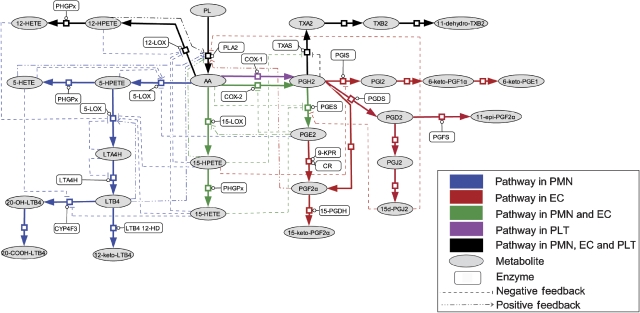
Inflammation is a basic way in which the body reacts to infection, irritation or other injuries. Standard drug targets such as COX-2 and 5-LOX are among the key enzymes involved in the network responsible for generating inflammation mediators. However, essentially all single-target drugs so far have side effects in anti-inflammatory treatment. To find safer multi-target intervention solutions, we employed MTOI in an inflammation-related network, the AA metabolic network (AAnetwork) with a multi-cellular ensemble of human PMN, endothelial (EC) and platelet (PLT) cells (Figure 2, the separate AAnetworks in PMN, EC and PLT can be found in Supplementary Figure S1). The model was developed partly based on our previous AAnetwork model for human PMN (Yang et al, 2007). However, the metabolism of AA in different cell types is different. LTs are the major inflammatory mediators produced in PMN (Simmons et al, 1983; Abbate et al, 1990). PGI2, PGF2α and PGE2 are the main eicosanoids detected in EC (Camacho et al, 1998). PGE2 is an important inflammatory mediator causing fever and pain (Ivanov and Romanovsky, 2004; Samuelsson et al, 2007), whereas PGI2 inhibits PLT aggregation and relaxes smooth muscle (Honn et al, 1981). PLT cells produce abundant TXA2, which is a potent inducer of PLT aggregation and vasoconstriction (Smith et al, 1980). The new AAnetwork model produced a better simulation of inflammation course in human blood vessel. In addition, the ratio of PGI2/TXA2 can be calculated to evaluate cardiovascular or bleeding side effects of the drugs (Kiviniemi et al, 1987; Kyrle et al, 1989; Martin et al, 1996; Kobayashi et al, 2004).

Figure 2.

Figure 2

Open in a new tab

The metabolic network of arachidonic acid in human PMN, EC and PLT. Two pathways are responsible for the production of inflammatory mediators: COX-2 pathway and 5-LOX pathway. LTB4 and PGE2 are major inflammatory mediators produced in the AAnetwork. PGI2 and TXA2 are vasoactive molecules, the abnormal production of which causes bleeding and cardiovascular disease. The separate AAnetworks in PMN, EC and PLT can be found in Supplementary Figure S1.

Ordinary differential equations (ODEs) were constructed to simulate the dynamic course of AA metabolism, where 24, 29 and 11 equations were used for PMN, EC and PLT, respectively (see details in Supplementary information). The concentrations of PMN, EC and PLT in the model were adopted according to their ratios in the human vessel (see details in Materials and methods). As signaling interactions among cells are complex in real circumstances and there is not enough experimental data, we did not include them in the current model. Among the 117 parameters in the ODE model, 46 were taken directly from experiments, whereas the others were determined by parameter fitting to experimental curves (see details in Supplementary information), including the production of LTB4 and ω-LTB4 in PMN (Shak and Goldstein, 1984), the production of PGF2α, PGE2 and 6-keto-PGF1α in EC (Camacho et al, 1998), and the production of TXA2 and TXB2 in PLT (Anderson et al, 1978). It is to be noted that in addition to these parameters, the concentrations of the enzymes and the initial concentrations of metabolites are also variables. Multiple parameter sets were obtained, which fit the curves equally well (Supplementary Table SI).

Drug targets search in the AAnetwork

We performed MTOI to identify drug targets in the AAnetwork. The disease state of the AAnetwork is defined as a state where the output of PGs and LTs is markedly above the normal level. As the experimental curves used in parameter fitting corresponded to the abnormal metabolism of PGs and LTs, we used the parameter sets derived there to describe the disease state (see details in ‘The AAnetwork model in human PMN, endothelial and platelet cells'). The desired state was defined as low output of inflammatory mediators, that is, the cumulative output of LTB4 and PGE2 should be smaller than 10% of that in the disease state, respectively. The threshold of 10% was selected here arbitrarily as it is impossible to give a definite cutoff to divide normal from disease in this case. The situation would depend on conditions such as the type of inflammation, the development level of disease and so on. We have tested the effect of cutoff on the results by changing the threshold to 20%. The same drug targets were selected by the new threshold (Supplementary Table SII). The entire 17 enzymes in the AAnetwork were selected as drug target candidates and their activities (Kcat [E]/Km, where [E] is the concentration of an enzyme) were perturbed during optimization. The absolute value of m.d./s.d. was calculated to determine the importance of the enzyme, and the corresponding manner of regulation was determined by the sign of m.d. (see details in Materials and methods). To get reliable results, many runs of MCSA were performed until the s.d. and m.d. for all candidates converged. As multiple parameter sets can fit the experimental data equally well, the drug targets identified can, in principle, depend on which parameter set we use. However, we note that the top drug targets (scored according to ∣m.d./s.d.∣) are always the same, independent of the parameter set used, although their rank order may vary. This implies that the results of MTOI are rather robust, which depend more on the network structure than on the value of the individual parameters. Table I shows the result of the search for drug targets of one particular parameter set derived from the parameter fitting. Results for other parameter sets are summarized in Supplementary Table SII. In the five parameter sets that we studied, the enzymes identified as top the five in at least four parameter sets were selected as drug target candidates. They are PLA2, LTA4H, COX-2, 5-LOX and PGES. Interestingly, all the five drug targets have negative m.d. values, indicating that the corresponding drugs should be inhibitors. Some other enzymes also have close ∣m.d./s.d.∣ values to the top five targets, such as PHGPx in Table I. However, they were not selected as drug targets for our further studies in stage 2, because their m.d. values are positive. Their corresponding drugs would be enzyme activators, which is normally difficult to realize in drug development.

Table 1.

Results from drug targets search by MTOI

Rank Enzyme abs(m.d./s.d.) m.d.
1 PLA2 0.9081 −1
2 LTA4H 0.8135 −0.84
3 5-LOX 0.774 −0.88
4 PGES 0.7199 −0.72
5 COX-2 0.6748 −0.72
6 PHGPx 0.538 0.6
7 TXAS 0.1756 0.2
8 CYP4F3 0.1063 0.12
9 PGDS 0.1041 0.12
10 12-LOX 0.1022 0.12
11 15-LOX 0.0699 0.08
12 CR 0.0349 0.04
13 15-PGDH 0 0
14 COX-1 0 0
15 9-KPR 0 0
16 PGFS 0 0
17 PGIS 0 0
Open in a new tab

The parameter set used is the same as in Figure 3. The top five enzymes were selected as drug targets and their corresponding regulations were all predicted to be inhibition.

MTOI solutions for the AAnetwork

We performed MTOI to search for optimal multi-target anti-inflammatory intervention solutions. The disease state at this stage is the same as in the previous section, modeled by the parameter sets derived from fitting experimental curves. The desired state, on the other hand, is slightly modified. In addition to reducing the inflammatory mediators, we have added requirements that minimize possible side effects. Specifically, we require that the desired state should satisfy the following conditions: (1) the cumulative production of LTB4 must be below 10% of that in the disease state; (2) the cumulative production of PGE2 must be below 10% of that in the disease state and (3) the change in the PGI2/TXA2 ratio between the desired and disease states must be smaller than a preset small value (here, we use 20%). This condition ensures that the drugs will not break the balance between PGI2 and TXA2 to cause cardiovascular or bleeding side effects. We took the top five drug targets identified in stage 1 (in the previous section) for further optimization of multi-target control in this stage. Other enzymes have not been selected for their low ∣m.d./s.d.∣ value and positive m.d. Considering that most COX-2 inhibitors will inhibit COX-1 at the same time to a certain extent due to the high homology of the two enzymes, we included COX-1 in the drug target list and but constrained because the inhibition on COX-2 and COX-1 should coexist. Thus, six drug targets were selected at stage 2, in which five of them (excluding COX-1) were predicted to be subjected to inhibition at stage 1. We assumed that the drugs against these enzymes were all competitive inhibitors and defined their inhibition intensity as the ratio of inhibitor concentration to inhibition constant ([I]/Ki). The values of [I]/Ki for the five drugs were perturbed in MCSA and the difference between the present network and the desired states was employed as the objective function for minimization (see details in Materials and methods).

To obtain reliable results, many runs of MCSA were performed. The set of [I]/Ki for inhibiting the six enzymes at the end of each acceptable run would correspond to an optimal multi-target intervention solution. These solutions from multiple runs were then clustered into distinct groups. We note that whereas at stage 1 all parameter sets studied gave the same top five drug targets, the results of stage 2 depended somewhat on parameter sets. We have used five different parameter sets in the study of stage 2. Although there is a large overlap in the solutions from different parameter sets, some solutions were found only in individual parameter sets (Table II). Perhaps this is not very surprising given the great uncertainty about the parameters. What is interesting is that there are common features in solutions among all the parameter sets. Thus, we can still make some concrete conclusions about the MTOI solutions even with partly uncertain parameters. First, none of the solutions in any parameter sets is single target, implying the necessity for multi-target control in this network. Second, the solutions involving the larger number of targets are more robust. The six-target solution and certain five- and four-target solutions appear in the solutions of all parameter sets. This result suggests a strategy when facing uncertainties in parameters: simultaneous intervention of many targets that are ‘influential' for the network state. If one views genetic and other variations in the system as a source of parameter uncertainty, this strategy may also be used to maximize the ‘bet' in the case of limited information. Ideally, the efficacy and safety of a robust multi-target intervention solution should not be sensitive to small changes in the inhibition intensities of the solution. We defined this sensitivity as the ratio of the percentage change of the objective function over that of the inhibition intensities (see details in Materials and methods). As can be seen from Table II, this sensitivity is extremely small for the MTOI solutions we found.

Table 2.

Multi-target control solutions found by MTOI

No. PLA2 COX-2 PGES 5-LOX LTA4H COX-1 Frequency 〈S〉
1 √ √ — — — √ 1 0.0011
2 √ √ √ — — √ 1 0.0011
3 — √ √ √ √ √ 5 0.002
4 — √ √ — √ √ 5 0.0021
5 — — √ √ √ — 2 0.0026
6 √ √ √ √ √ √ 5 0.0028
7 — √ √ √ — √ 5 0.0033
8 √ √ √ — √ √ 5 0.0034
9 — √ — √ √ √ 5 0.0036
10 √ √ — √ √ √ 5 0.0037
11 √ √ √ √ — √ 5 0.0041
12 √ √ — — √ √ 5 0.0042
13 — √ — — √ √ 5 0.0048
14 √ — √ √ √ — 1 0.0057
15 — — √ √ — — 2 0.0061
16 — — √ — √ — 3 0.0072
17 √ √ — √ — √ 5 0.0075
18 — √ — √ — √ 5 0.01
19 √ — √ — √ — 1 0.0123
20 √ — √ √ — — 1 0.0241
21 √ — — √ √ — 1 0.0431
22 √ — — — √ — 1 0.0569
23 √ — — √ — — 1 0.0624
Open in a new tab

The frequency of MTOI solutions appearing in five parameter sets was also shown. The sensitivity 〈S〉 is averaged over the parameter sets in which the solution appeared. ‘—' denotes no regulation and ‘√‘ denotes that the corresponding enzyme is inhibited.

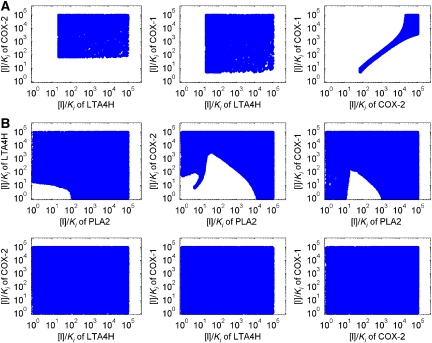
Furthermore, we analyzed the effective and safe range of the drug intensity ([I]/Ki) of the multi-target solutions (‘therapeutic window'). These distributions of [I]/Ki are obtained by sampling the intensity [I]/Ki of the inhibitors to the multi-targets specified by the solution, and recording the combination of [I]/Ki that can change the disease state into the desired state. As the intensity space [I]/Ki is highly dimensional (with the dimensionality being the number of targets), we project the distribution onto every pair of two dimensions. In Figure 3, we show the [I]/Ki distribution of the inhibitors for two different MTOI solutions, with three targets (Figure 3A) and four targets (Figure 3B), respectively. Results of other MTOI solutions are listed in the Supplementary information. In general, inhibitors against more drug targets have larger therapeutic windows. It is to be noted that when all six targets are inhibited, the [I]/Ki distributions not only have very wide ranges but are also essentially uncorrelated with each other. This makes the multi-target solutions much more practical, both in terms of the drug design and of the clinical use. The inhibition of PLA2 and/or COX-1/2 has strong effect on the ratio of PGI2/TXA2. When PLA2 is not inhibited, the ratio of COX-1 and COX-2 inhibition has to be fixed within a narrow range to maintain the ratio of PGI2/TXA2 (Figure 3A). Balanced inhibition of these two COX isoenzymes would be important to avoid side effects. Selective COX-1/2 inhibitors were known to conduct either gastrointestinal or cardiovascular damage (Suleyman et al, 2007). With balanced inhibition, the therapeutic window of COX inhibition can be very large. As COX-1 and COX-2 are isoenzymes, designing an inhibitor with a fixed ratio of affinities should not be difficult. This fixed ratio of COX-1/2 inhibition is no longer necessary when PLA2 is inhibited simultaneously (Figure 3B).

Figure 3.

Figure 3

Open in a new tab

The distribution of [I]/Ki of MTOI solutions. (A) Inhibition against LTA4H, COX-1 and COX-2. (B) Inhibition against PLA2, LTA4H, COX-1 and COX-2.

Verification of the AAnetwork model by simulating the effects of known non-steriodal anti-inflammatory drugs

If the constructed AAnetwork is reasonably reliable, we should be able to simulate the behavior of anti-inflammatory drugs to assess their efficacy and potential side effects within the network model. We have made so far a long list of anti-inflammatory drugs covering most currently used non-steriodal anti-inflammatory drugs (NSAIDs). They include non-selective NSAIDs, selective COX-2 inhibitors, and dual functional COX-2/5–LOX inhibitor. The relative IC50 values of these medicines were taken from the published experimental data (Patrono et al, 2001; Vidal et al, 2007). The ratio of PGI2/TXA2 was calculated as the indicator for side effects—a large increase in this ratio after taking the medicine would imply bleeding risks, whereas a significant decrease of the ratio would raise cardiovascular risks (Martin et al, 1996; Kobayashi et al, 2004). The simulation results are shown in Table III.

Table 3.

Efficacy simulation of currently used medicines in AAnetwork

Inhibitor Relative IC50 Inhibition of PGE2 (%) Inhibition of LTB4 (%) [PGI2]/[TXA2]
Control — — — 0.6817
Aspirin IC50(COX-1:COX-2)=0.01 90.0 — 5.1947
Ibuprofen IC50(COX-1:COX-2)=0.5 90.0 — 3.5599
Naproxen IC50(COX-1:COX-2)=0.7 90.0 — 2.2915
6-MNA IC50(COX-1:COX-2)=1.5 90.0 — 2.2334
Acetaminophen IC50(COX-1:COX-2)=1.6 90.0 — 2.1574
Indomethacin IC50(COX-1:COX-2)=1.9 90.0 — 1.9613
Meloxicam IC50(COX-1:COX-2)=18 90.0 — 0.5335
Nimesulide IC50(COX-1:COX-2)=19 90.0 — 0.5207
Diclofenac IC50(COX-1:COX-2)=29 90.0 — 0.4399
Celecoxib IC50(COX-1:COX-2)=30 90.0 — 0.4347
Rofecoxib (VIOXX) IC50(COX-1:COX-2)=267 90.0 — 0.2804
Licofelone IC50(5-LOX)=0.18 μM IC50(COX-2)=0.21 μM IC50(COX-1)=1 μM 96.5 90.0 0.6983
Open in a new tab

The same parameter set as in Table I and Figure 3 was used here. The ratio of PGI2/TXA2 the reflects possible side effects of the drug. After taking the medicine, if PGI2/TXA2 becomes much larger than the normal level, bleeding side effects may occur. If PGI2/TXA2 decreases significantly, cardiovascular risks will be raised.

Aspirin is a strong COX-1 inhibitor and a mild COX-2 inhibitor. COX-1 is the main COX isozyme in PLT, which is responsible for the major production of TXA2 in the model. A low concentration of aspirin is reported to have an antithrombotic effect (Patrono et al, 2001). In our simulation, as aspirin strongly inhibited the production of TXA2, the value of PGI2/TXA2 was much larger than before the administration of medicine. Thus, aspirin can prevent myocardial infarction and ischemic stroke but raise the risk of bleeding. When the relative IC50(COX-1:COX-2) increases, the inhibition effect of the medicine on TXA2 production and PLT aggregation decreases when compared with their inhibition effect on PGI2 production (Sun and Li, 2000; Van Hecken et al, 2000). The bleeding risk of NSAIDs lessens following the reduced inhibition of COX-1. In our simulation, the value of PGI2/TXA2 was observed to decrease. When the relative IC50 of COX inhibitors increased above 10, we observed a strong inhibition on the production of PGI2, whereas the production of TXA2 was hardly affected. The value of PGI2/TXA2 became significantly smaller than that before the administration of medicine. Cardiovascular side effects have been found in selective COX-2 inhibitors (Rahman and Khan, 2004; Singh, 2004; Solomon et al, 2005), presumably due to the decrease in PGI2/TXA2. Indeed, in our simulation, Vioxx was correctly predicted to be a high cardiovascular risk. As COX inhibitors fail to control inflammation safely, licofelone, a dual functional inhibitor of COX-1/2 and 5-LOX, has been developed. This compound was reported to be effective in inflammation control and in cardiovascular derangement prevention (Alvaro-Gracia, 2004; Bias et al, 2004; Rotondo et al, 2006). Our simulation showed that licofelone can maintain the balance between PGI2 and TXA2, and at the same time effectively reduce PGE2 and LTB4 production.

Drug efficacy prediction of MTOI solutions

Several promising MTOI solutions were selected for further investigation. The ratio of PGI2/TXA2 was calculated as the indicator for side effects. The relative [I]/Ki values of solutions were taken from MTOI analysis. Simulation results are summarized in Table IV. Unlike the currently used drugs that inhibit only COX-1/2 (with the exception of licofelone, which also inhibits 5-LOX), MTOI solutions achieved a balanced control on the entire network. The ratio of PGI2/TXA2 was almost unchanged after taking MTOI solutions, although the production of LTB4 and PGE2 was inhibited effectively at the same time. Recently, much attention has been drawn to the two downstream drug targets: PGES and LTA4H, as their inhibitors may produce fewer side effects when compared the with upstream enzyme blockers (Fahmi, 2004; Haeggstrom, 2004). MTOI found that optimal therapeutic effects are achieved only when the two targets or one of them in combination with other targets are inhibited simultaneously; for example, the combination of PGES and LTA4H and the combination of COX-2/1 and LTA4H. Inhibiting more than one drug target is important in anti-inflammatory treatment. Another feature in MTOI solutions is that when multiple targets are inhibited simultaneously, a mild inhibition of each target is sufficient to achieve effective control of LTB4 and PGE2 production and there is a much larger therapeutic window. For example, simultaneously inhibiting COX-2/1 and LTA4H, the [I]/Ki of COX-2 should be 400 to achieve effective treatment. In the case of simultaneously inhibiting PLA2, COX-2/1 and LTA4H, the value of [I]/Ki of COX-2 needed is reduced to 80. This value is further reduced to 20 when all the six targets are inhibited. The reduced inhibition intensity may decrease the toxicity risk of the drugs. Furthermore, regulation on multiple enzymes can maintain the PGI2/TXA2 ratio more easily than single-target drugs. As discussed in the section of ‘MTOI solutions for the AAnetwork', we found that the intervention of more targets gave more robust solutions. This may explain the possible benefits of traditional Chinese medicines (TCMs), in which mild control is directed to multiple drug targets.

Table 4.

Efficacy simulation of MTOI solutions in AAnetwork

  [I]/Ki
 Inhibition of PGE2 (%) Inhibition of LTB4 (%) [PGI2]/[TXA2]
  PLA2 COX-2 PGES 5-LOX LTA4H COX-1      
Control 0 0 0 0 0 0 0 0 0.6817
1 0 400 0 0 100 56.5 97 97 0.6843
2 14 80 0 0 50 35 97 97 0.6857
3 12 60 0 60 40 13 97 97 0.6855
4 9 20 10 50 30 26 97 97 0.6823
5 0 0 20 000 0 45 0 97 95 0.5405
6 0 200 50 0 45 26.5 97 95 0.6853
7 0 200 50 60 30 32.5 97 95 0.6833
8 0 450 0 1200 0 95 97 97 0.6819
9 0 450 0 80 50 79 97 97 0.6817
10 0 200 50 1200 0 40.5 97 97 0.6824
11 250 5000 0 0 0 5000 98 95 0.6255
12 250 5000 5000 0 0 5000 98 95 0.625
13 15 190 0 90 0 190 98 95 0.6837
14 15 190 190 90 0 190 98 95 0.6832
15 15 105 105 0 25 105 98 95 0.6835
Open in a new tab

The same parameter set used is the same as in Figure 3. In the same way, the ratio of PGI2/TXA2 reflects possible side effects of the drug. After taking the medicine, if PGI2/TXA2 becomes much greater than the normal level, bleeding side effects may occur. If PGI2/TXA2 decreases significantly, cardiovascular risks will be raised.

Discussion

We have developed a systematic method (MTOI) to search for optimal interventions in a disease network. The basic concept is simple: the goals are to identify effective points of intervention and the optimal combinations of interventions that restore the network to a normal state. Quantitatively, optimization is carried out with an objective function that specifies the customer-defined requirements of what the normal state should be, including safety conditions. An MCSA algorithm is employed here to optimize the network state with perturbations on network components and/or interactions. The end results include promising drug targets and optimal solutions of their combinatorial intervention. We have applied the method to a network responsible for inflammation—the AAnetwork. We have demonstrated the utility and power of the method with the robust identification of the drug targets and the multi-target intervention solutions that are both effective and safe.

Discovering drug targets

MTOI systematically analyzes the conversion between the disease and desired states to identify potential drug targets and to find multi-target intervention solutions with user-defined efficacy and safety thresholds. Compared with the traditional drug target search methods, such as parameter sensitivity analysis (Palsson and Lee, 1993; Pant and Ghosh, 2005), MTOI emphasizes the influence of the drug target candidate's activity on the entire network state. Thus, it can be regarded as a network-state-based drug target sensitivity analysis method. Instead of relying on individual parameters for target identification, MTOI dynamically perturbs and searches the various combinations of the entire parameters of drug target candidates to accurately and robustly identify the relationship between target candidates and the network state. As a comparison, we also performed single parameter sensitivity analysis on the AAnetwork (Supplementary Table SV, see details in Supplementary information). Although the top list was consistent with the result of MTOI, the ways of invention (upregulate or downregulate) cannot be predicted from the analysis.

When applied to the AAnetwork, MTOI has succeeded in identifying some well-known anti-inflammatory drug targets, including PLA2, COX-2, 5-LOX, PGES and LTA4H. PLA2 regulates the metabolism of AA upstream in the network. Inhibition of PLA2 can effectively control both PGE2 and LTB4, but will also downregulate all the downstream AA metabolites including vasoactive eicosanoids, which has important physiological functions. COX-2 and 5-LOX have been studied intensively and became regular anti-inflammatory drug targets. Medicines against these two enzymes, respectively, such as ibuprofen and zileuton, were developed for general clinical treatment. PGES and LTA4H are recently discovered downstream enzymes. Inhibitors against PGES or LTA4H attracted much attention due to the anticipated reduction of toxicity. MTOI has also identified several important enzymes, for example, 15-LOX, CYP4F3, for which increased activity is desired for anti-inflammatory treatment. Although it is difficult to devise drugs that increase enzyme activity, this result may be useful to understand elevated disease susceptibilities or variations in drug response among individuals due to single nucleotide polymorphism (Shastry, 2005).

Finding multiple target intervention solutions

Identification of optimal multi-target intervention solutions is the core function of MTOI. The complexity of a network, due to connectedness, feedback, cross talk and so on, is exploited here to provide the researchers multiple choices for intervention solutions. Moreover, the desired network state is customer-designed by the user. This allows MTOI to be applicable in the regulation and intervention of other kinds of networks, for example, in studies of pesticides.

The efficacy of currently used NSAIDs has been correctly predicted by the AAnetwork model. Except for licofelone, these compounds were found to have side effects both clinically and in our simulation. As MTOI can correctly reproduce the known side effects of NSAIDs, one may apply it in predicting the possible side effects for new anti-inflammation drugs targeting the AAnetwork. Furthermore, MTOI study also gave several novel multi-target intervention solutions for the AAnetwork control with high efficacy and low toxicity. Although, theoretically it is better to inhibit all the six enzymes at the same time, practically, it might be difficult to design one medicine that can inhibit all the six enzymes simultaneously or to use a cocktail containing six different inhibitors. To simplify the case, we can start from the solutions with fewer enzymes. For example, we believe that there are several such solutions that are rather promising for developing anti-inflammation drugs: (1) the combination of PGES and LTA4H and the combination of COX-2/1 and LTA4H. These two solutions basically involve only two targets and should be relatively straightforward to achieve. However, care should be taken to make sure that the inhibitors should be used only in the proper dosing range. The valid [I]/Ki range is quite narrow for LTA4H in the PGES and LTA4H solution, and the ratio of inhibition for COX-1/COX-2 should be maintained in a narrow range for the COX-2/1 and LTA4H solution. (2) The combination of PLA2, 5-LOX and COX-2/1 or the combination of PLA2, COX-2/1 and LTA4H. With more targets that are inhibited, the dosing ranges for these two solutions are much larger, making them very attractive candidates for multi-target drug design.

Our MTOI study suggested that optimal solutions often involve mild but simultaneous interventions of multiple targets. This is reminiscent of TCM in which multiple targets are intervened with mild or low intensity. It would be interesting to explore the molecular mechanisms of TCM along this line. Of course, the targets of the most TCM are unknown, which presents a significant challenge.

Multi-target drug design at systems level

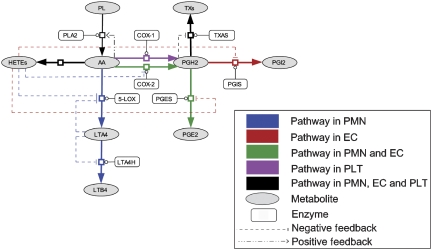
Given sufficient knowledge about the disease-related network, our results suggest that computational methods can play an important and unique role in the new era of network-based drug design. Construction of a network that is reasonably complete is the first key step. However, as almost surely the network is incomplete and with many parameters being unknown, a major challenge is to devise a robust computational algorithm that is able to extract desirable information based more on the overall structure of the network than on individual parameters. In principle, it is difficult to know when the knowledge about a network is sufficient to apply a network-based drug discovery method. One way to test this is to perturb the network and see how the solutions change. We have constructed a simplified AAnetwork model (Figure 4, parameters are summarized in Supplementary Table SIII) using partial information of the network and applied MTOI to this model. In the simplified model, only the disease-related metabolites and enzymes were included and unknown parameters were evaluated by parameter fitting (see details in Supplementary information). MTOI has identified 14 multi-target solutions in the simplified AAnetwork model (Supplementary Table SIV). All of them are among the MTOI solutions of the full model (Table II). With the fast accumulation of experimental data and more disease networks revealed, we expect an increasingly critical role for computational approaches in systems drug design.

Figure 4.

Figure 4

Open in a new tab

The simplified network of arachidonic acid metabolism in human PMN, EC and PLT. The separate AAnetworks in PMN, EC and PLT can be found in Supplementary Figure S2.

Materials and methods

Finding multi-target intervention solutions in disease network

MTOI contains two stages. MCSA is employed as the main optimization tool in both stages. The procedure of stage 1 includes the following steps:

Step 1. Define the disease and desired states. A state in the MTOI program is defined as a steady or temporal state of the network, which can be a collection of concentrations of proteins and/or metabolites, metabolic fluxes or any other relevant information, for example, the temporal behavior of the network within some time window. Generally, the disease state can be obtained by experimental data from patients or cells in abnormal conditions. The desired state is specified by researchers, which can be the normal physiological state of the network.

Step 2. Select reactions that can be controlled by drugs. Define a quantity that controls the corresponding reaction rate as the activity of the drug target candidate. For example, if the target is an enzyme, the activity is defined as Kcat [E]/Km.

Step 3. Starting from a randomly selected set of the activities of drug target candidates, perform MCSA to drive the system toward the desired state. The activities of drug target candidates are perturbed in MCSA, whereas the other parameters are maintained at the same values of the disease state. The difference between the present network and desired states is used as the objective function.

Step 4. Record as ‘acceptable' the set of the drug target candidates' activities, when the desired state is reached by MCSA. Calculate the standard deviation of the activities of each drug target candidate over all acceptable sets: 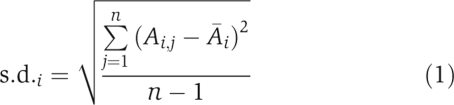Inline graphic where Ai,j is the activity of the ith drug target candidate in the jth set and 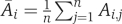Inline graphic is the average activity of the candidate over all ‘acceptable' sets.

Step 5. Calculate the m.d. of the activity of drug target candidates between the desired and disease states: 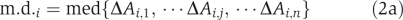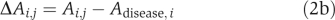Inline graphic Inline graphic where Adisease,i is the activity of the ith candidate in the disease state. Use ∣m.d.i/s.d.i∣ to determine the importance of the drug target candidate and the sign of m.d.i to decide whether inhibition or activation should be performed in the treatment.

Step 6. Repeat steps 3–5 until s.d. and m.d. converge to stable values for all drug candidates (see details in Supplementary information).

Stage 1 can be skipped if the drug targets have been identified by experiments or other methods. After identifying drug targets in the network, one starts stage 2, which includes the following steps:

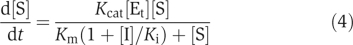Step 1. Add reactants of drugs against the selected drug targets in the network. The reactants influence the fluxes and rates of the target reactions in different ways depending on specific reaction kinetics. For example, if the target is an enzyme and the reaction has the Michaelis–Menten kinetics: Inline graphic where [S] is the concentration of the substrate, [Et] the total concentration of the enzyme, Kcat turnover number, Km Michaelis–Menten constant, a competitive reversible inhibitor I would change the equation (3) into Inline graphic where [I] is the concentration of the inhibitor and Ki the inhibition constant: 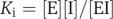Inline graphic. [I]/Ki is defined as the intensity of the drug influence against the drug target.

Step 2. Starting from the disease state and selecting a random set of intensities of drug influence against all drug targets, perform MCSA to drive the system toward the desired state. Only the intensities of drug influence are perturbed, whereas other parameters in the network are maintained at the values of the disease state. The difference between the present network and desired states is used as the objective function.

Step 3. Record as ‘acceptable' the set of the intensities of the drugs against all targets, when the desired state is reached by MCSA. This ‘acceptable' set is one multi-target intervention solution for the disease network.

Step 4. Repeat steps 2 and 3 until many solutions are found and the results are clustered in the space of intensities to find distinct solutions.

Construction of the AAnetwork model in human PMN, EC and PLT cells

The AAnetwork in human PMN, EC and PLT cells was set up based on our previous study and experimental data was published (see details in Supplementary information). As the ratio of PMN, EC and PLT depends on the size of the blood vessel, we simulated the metabolism of AA in a 1-cm long and 50-μm diameter vessel. The concentration of PMN and PLT in the model is set to the same value as in human blood, that is, 4500 and 2.5 × 105 cells/μl, respectively, so that the number of PMN and PLT in the considered region was 88 and 4908, respectively. The diameter of PMN and PLT was set to 10 and 2 μm, respectively. The number of EC depends on the size of the vessel. Only the inner layer of EC was considered and the diameter of EC was set to 50 μm, thus in the considered region the number of EC in the model was 628.

On the basis of the AAnetwork of Figure 2, a set of ODEs were constructed to describe cell behavior in inflammation. The ode15 s routine of Matlab 6.5 (The Mathworks Inc., http://www.mathworks.com) was used to integrate the ODEs. Michaelis–Menten equations (equation (3)) were used to describe enzyme catalytic reactions in the network. Equation (4) was employed if competitive reversible inhibitors were involved in the catalysis. If the inhibition is irreversible, we assumed that the enzyme would decay according to Inline graphic

When activators were involved in the catalysis, we used: 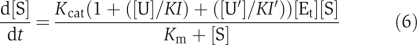Inline graphic

To describe the reaction kinetics, where [U] is the concentration of the activator and KI is a constant.

When upregulation occurred through transcription, we described its effect with the following equation: Inline graphic where [g] is the concentration of the metabolite upregulating the transcription of the enzyme, K and k are constants.

MTOI application in the AAnetwork model

The MTOI procedure described earlier was applied in the AAnetwork model to find multi-target anti-inflammatory control solutions. Stage 1 of the procedure includes:

Step 1. Define the disease and desired states. The disease state in AAnetwork was described by parameter sets derived from parameter fitting (see details in ‘Construction of the AAnetwork model in human PMN, EC and PLT cells'). The desired state was a state where the 1 h cumulative production of LTB4 and PGE2 is less than 10% of that in the disease state. The fluxes of other metabolites are not monitored.

Step 2. All the enzymes in the AAnetwork were selected as potential drug target candidates. The activity of an enzyme was defined as Inline graphic

Step 3. Perform MCSA as described earlier to find the desired state. In the process, the initial temperature was set to be 50°C, the maximum number of Monte Carlo attempts under the same temperature was 500, the constant in the exponential cooling scheme was 0.7, and the final temperature in MCSA was 5 × 10−6. The perturbed range of enzyme activity was [0.01Adisease, 100Adisease]. The objective function was 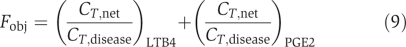Inline graphic where CT,net and CT,disease were the 1 h cumulative production of the metabolite in the present network and disease states, respectively. Equation (9) optimized the production of LTB4 and PGE2 toward zero. In the calculation, when the production of LTB4 and PGE2 was below 10% of that in the disease state, respectively, the corresponding set of enzyme activities was accepted as the desired state.

Step 4. Record as ‘acceptable' the set of activities of the drug target candidates, when the desired state is reached by MCSA. Standard deviation of enzyme activity over all accepted sets was calculated as 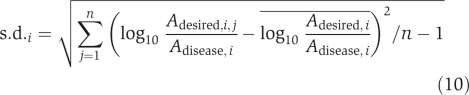Inline graphic where Adesired,i,j is the activity of the ith drug target candidate in the jth desired set. Because of the requirement of normalization, here we used 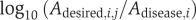Inline graphic for s.d. calculation instead of Ai,j as in equation (1). This change does not influence the result on drug targets selection.

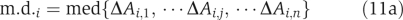
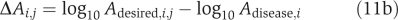
Step 5. Mead deviation of enzyme activity between the desired and disease states was calculated as Inline graphic Inline graphic

Again, we used equation (11) instead of (2) due to normalization.

Step 6. Repeat steps 3–5 until s.d. and m.d. converge.

The procedure of stage 2 was:

Step 1. Add reactants of drugs against the selected drug targets in the network. Drugs in AAnetwork were assumed to be competitive reversible inhibitors, thus [I]/Ki was defined as inhibition intensity.

Step 2. Perform MCSA to find the desired state. The high temperature, the maximum number of Monte Carlo attempts under the same temperature, the constant in the exponential cooling scheme and the final temperature in MCSA adopted the same value as those in stage 1. [I]/Ki was perturbed in a range of [0 100000]. The objective function was 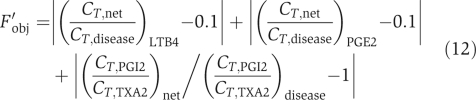Inline graphic

This objective function was set according to the following considerations: in the desired state, the production of LTB4 and PGE2 was below 10% of that of the disease state and the change of PGI2/TXA2 was less than 20%.

Step 3. Record as ‘acceptable' the set of the intensities of drug influence, when the desired state is reached by MCSA.

Step 4. Repeat the above steps until no more new solutions are found.

In the end, we also calculated the sensitivity of drugs' safety and effectiveness to [I]/Ki as 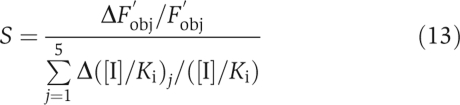Inline graphic where Fobj was calculated with equation (12). S measures how sensitive the drug effects are to small changes in the inhibition intensities.

Supplementary Material

Supplementary Figures and Tables

msb200860-s1.pdf (874.4KB, pdf)

Supplementary Information 1

msb200860-s2.xml (61.3KB, xml)

Supplementary Information 2

msb200860-s3.xml (54.4KB, xml)

Supplementary Information 3

msb200860-s4.xml (18.5KB, xml)

Acknowledgments

This research was supported, in part, by the Ministry of Science and Technology of China and the National Natural Science Foundation of China (nos. 30490245, 90403001 and 20228306). We thank Daqi Yu, Hao Chen, Zhenming Liu, Lu Wang and Ping Wei for helpful discussions.

Footnotes

The authors declare that they have no conflict of interest.

References

  1. Abbate R, Gori AM, Pinto S, Attanasio M, Paniccia R, Coppo M, Castellani S, Giusti B, Boddi M, Neri Serneri GG (1990) Cyclooxygenase and lipoxygenase metabolite synthesis by polymorphonuclear neutrophils: in vitro effect of dipyrone. Prostaglandins Leukot Essent Fatty Acids 41: 89–93 [DOI] [PubMed] [Google Scholar]
  2. Ahren B (2008) Novel combination treatment of type 2 diabetes DPP-4 inhibition + metformin. Vasc Health Risk Manag 4: 383–394 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Alvaro-Gracia JM (2004) Licofelone—clinical update on a novel LOX/COX inhibitor for the treatment of osteoarthritis. Rheumatology (Oxford) 43 (Suppl. 1): i21–i25 [DOI] [PubMed] [Google Scholar]
  4. Ambegaonkar A, Livengood K, Craig T, Day D (2004) Predicting the risk for gastrointestinal toxicity in patients taking NSAIDs: the Gastrointestinal Toxicity Survey. Adv Ther 21: 288–300 [DOI] [PubMed] [Google Scholar]
  5. Anderson MW, Crutchley DJ, Tainer BE, Eling TE (1978) Kinetic studies on the conversion of prostaglandin endoperoxide PGH2 by thromboxane synthase. Prostaglandins 16: 563–570 [DOI] [PubMed] [Google Scholar]
  6. Araujo RP, Liotta LA, Petricoin EF (2007) Proteins, drug targets and the mechanisms they control: the simple truth about complex networks. Nat Rev Drug Discov 6: 871–880 [DOI] [PubMed] [Google Scholar]
  7. Arellano FM (2005) The withdrawal of rofecoxib. Pharmacoepidemiol Drug Saf 14: 213–217 [DOI] [PubMed] [Google Scholar]
  8. Bays HE, Dujovne CA, McGovern ME, White TE, Kashyap ML, Hutcheson AG, Crouse JR (2003) Comparison of once-daily, niacin extended-release/lovastatin with standard doses of atorvastatin and simvastatin (the ADvicor Versus Other Cholesterol-Modulating Agents Trial Evaluation [ADVOCATE]). Am J Cardiol 91: 667–672 [DOI] [PubMed] [Google Scholar]
  9. Bias P, Buchner A, Klesser B, Laufer S (2004) The gastrointestinal tolerability of the LOX/COX inhibitor, licofelone, is similar to placebo and superior to naproxen therapy in healthy volunteers: results from a randomized, controlled trial. Am J Gastroenterol 99: 611–618 [DOI] [PubMed] [Google Scholar]
  10. Borisy AA, Elliott PJ, Hurst NW, Lee MS, Lehar J, Price ER, Serbedzija G, Zimmermann GR, Foley MA, Stockwell BR, Keith CT (2003) Systematic discovery of multicomponent therapeutics. Proc Natl Acad Sci USA 100: 7977–7982 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bouwmeester T, Bauch A, Ruffner H, Angrand PO, Bergamini G, Croughton K, Cruciat C, Eberhard D, Gagneur J, Ghidelli S, Hopf C, Huhse B, Mangano R, Michon AM, Schirle M, Schlegl J, Schwab M, Stein MA, Bauer A, Casari G et al. (2004) A physical and functional map of the human TNF-alpha/NF-kappa B signal transduction pathway. Nat Cell Biol 6: 97–105 [DOI] [PubMed] [Google Scholar]
  12. Brooks P (1998) Use and benefits of nonsteroidal anti-inflammatory drugs. Am J Med 104: 9S–13S; discussion 21S–22S [DOI] [PubMed] [Google Scholar]
  13. Camacho M, Lopez-Belmonte J, Vila L (1998) Rate of vasoconstrictor prostanoids released by endothelial cells depends on cyclooxygenase-2 expression and prostaglandin I synthase activity. Circ Res 83: 353–365 [DOI] [PubMed] [Google Scholar]
  14. Csermely P, Agoston V, Pongor S (2005) The efficiency of multi-target drugs: the network approach might help drug design. Trends Pharmacol Sci 26: 178–182 [DOI] [PubMed] [Google Scholar]
  15. Duarte NC, Becker SA, Jamshidi N, Thiele I, Mo ML, Vo TD, Srivas R, Palsson BO (2007) Global reconstruction of the human metabolic network based on genomic and bibliomic data. Proc Natl Acad Sci USA 104: 1777–1782 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fahmi H (2004) mPGES-1 as a novel target for arthritis. Curr Opin Rheumatol 16: 623–627 [DOI] [PubMed] [Google Scholar]
  17. Food and Drug Administration (2004) Innovation and Stagnation: Challenge and Opportunity on the Critical Path to New Medical Products. FDA White Paper (http://www.fda.gov/oc/initiatives/criticalpath/whitepaper.pdf) [Google Scholar]
  18. Frantz S (2005) Drug discovery: playing dirty. Nature 437: 942–943 [DOI] [PubMed] [Google Scholar]
  19. Ganter B, Tugendreich S, Pearson CI, Ayanoglu E, Baumhueter S, Bostian KA, Brady L, Browne LJ, Calvin JT, Day GJ, Breckenridge N, Dunlea S, Eynon BP, Furness LM, Ferng J, Fielden MR, Fujimoto SY, Gong L, Hu C, Idury R et al. (2005) Development of a large-scale chemogenomics database to improve drug candidate selection and to understand mechanisms of chemical toxicity and action. J Biotechnol 119: 219–244 [DOI] [PubMed] [Google Scholar]
  20. Gupta EK, Ito MK (2002) Lovastatin and extended-release niacin combination product: the first drug combination for the management of hyperlipidemia. Heart Dis 4: 124–137 [DOI] [PubMed] [Google Scholar]
  21. Haeggstrom JZ (2004) Leukotriene A4 hydrolase/aminopeptidase, the gatekeeper of chemotactic leukotriene B4 biosynthesis. J Biol Chem 279: 50639–50642 [DOI] [PubMed] [Google Scholar]
  22. Honn KV, Cicone B, Skoff A (1981) Prostacyclin: a potent antimetastatic agent. Science 212: 1270–1272 [DOI] [PubMed] [Google Scholar]
  23. Hopkins AL, Mason JS, Overington JP (2006) Can we rationally design promiscuous drugs? Curr Opin Struct Biol 16: 127–136 [DOI] [PubMed] [Google Scholar]
  24. Hwang WC, Zhang A, Ramanathan M (2008) Identification of information flow-modulating drug targets: a novel bridging paradigm for drug discovery. Clin Pharmacol Ther (advance online publication, 9 July 2008; doi:10.1038/clpt.2008.129) [DOI] [PubMed] [Google Scholar]
  25. Ivanov AI, Romanovsky AA (2004) Prostaglandin E2 as a mediator of fever: synthesis and catabolism. Front Biosci 9: 1977–1993 [DOI] [PubMed] [Google Scholar]
  26. Kitano H (2007) A robustness-based approach to systems-oriented drug design. Nat Rev Drug Discov 6: 202–210 [DOI] [PubMed] [Google Scholar]
  27. Kiviniemi H, Ramo J, Stahlberg M, Laitinen S, Jalovaara P, Viinikka L, Kairaluoma M (1987) Prostacyclin and thromboxane in acute hemorrhagic pancreatitis in dogs. J Surg Res 42: 232–236 [DOI] [PubMed] [Google Scholar]
  28. Kobayashi T, Tahara Y, Matsumoto M, Iguchi M, Sano H, Murayama T, Arai H, Oida H, Yurugi-Kobayashi T, Yamashita JK, Katagiri H, Majima M, Yokode M, Kita T, Narumiya S (2004) Roles of thromboxane A(2) and prostacyclin in the development of atherosclerosis in apoE-deficient mice. J Clin Invest 114: 784–794 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Korcsmaros T, Szalay MS, Bode C, Kovacs IA, Csermely P (2007) How to design multi-target drugstarget search options in cellular networks. Expert Opin Drug Discov 2: 799–808 [DOI] [PubMed] [Google Scholar]
  30. Kusmak JM (2005) COX-2 inhibitors and the risk for cardiovascular events: a re-evaluation of the data and proposed mechanisms. SDJ Med 58: 269–272 [PubMed] [Google Scholar]
  31. Kyrle PA, Minar E, Brenner B, Eichler HG, Heistinger M, Marosi L, Lechner K (1989) Thromboxane A2 and prostacyclin generation in the microvasculature of patients with atherosclerosis—effect of low-dose aspirin. Thromb Haemost 61: 374–377 [PubMed] [Google Scholar]
  32. Larder BA, Kemp SD, Harrigan PR (1995) Potential mechanism for sustained antiretroviral efficacy of AZT–3TC combination therapy. Science 269: 696–699 [DOI] [PubMed] [Google Scholar]
  33. Lehar J, Zimmermann GR, Krueger AS, Molnar RA, Ledell JT, Heilbut AM, Short GF III, Giusti LC, Nolan GP, Magid OA, Lee MS, Borisy AA, Stockwell BR, Keith CT (2007) Chemical combination effects predict connectivity in biological systems. Mol Syst Biol 3: 80 10.1038/msb4100116 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lindsay MA (2003) Target discovery. Nat Rev Drug Discov 2: 831–838 [DOI] [PubMed] [Google Scholar]
  35. Martin C, Varner MW, Branch DW, Rodgers G, Mitchell MD (1996) Dose-related effects of low dose aspirin on hemostasis parameters and prostacyclin/thromboxane ratios in late pregnancy. Prostaglandins 51: 321–330 [DOI] [PubMed] [Google Scholar]
  36. Nelson HS (2001) Advair: combination treatment with fluticasone propionate/salmeterol in the treatment of asthma. J Allergy Clin Immunol 107: 398–416 [DOI] [PubMed] [Google Scholar]
  37. Palsson BO, Lee ID (1993) Model complexity has a significant effect on the numerical value and interpretation of metabolic sensitivity coefficients. J Theor Biol 161: 299–315 [DOI] [PubMed] [Google Scholar]
  38. Pant D, Ghosh A (2005) Automated oncogene detection in complex protein networks with applications to the MAPK signal transduction pathway. Biophys Chem 113: 275–288 [DOI] [PubMed] [Google Scholar]
  39. Patrono C, Patrignani P, Garcia Rodriguez LA (2001) Cyclooxygenase-selective inhibition of prostanoid formation: transducing biochemical selectivity into clinical read-outs. J Clin Invest 108: 7–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Peri S, Navarro JD, Amanchy R, Kristiansen TZ, Jonnalagadda CK, Surendranath V, Niranjan V, Muthusamy B, Gandhi TK, Gronborg M, Ibarrola N, Deshpande N, Shanker K, Shivashankar HN, Rashmi BP, Ramya MA, Zhao Z, Chandrika KN, Padma N, Harsha HC et al. (2003) Development of human protein reference database as an initial platform for approaching systems biology in humans. Genome Res 13: 2363–2371 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Rahman SZ, Khan RA (2004) Is nimesulide safe in a cardiovascular-compromised patient. Indian J Pharmacol 36: 252–253 [Google Scholar]
  42. Rainsford KD (1993) Leukotrienes in the pathogenesis of NSAID-induced gastric and intestinal mucosal damage. Agents Actions 39 (Spec no.): C24–C26 [DOI] [PubMed] [Google Scholar]
  43. Rajasethupathy P, Vayttaden SJ, Bhalla US (2005) Systems modeling: a pathway to drug discovery. Curr Opin Chem Biol 9: 400–406 [DOI] [PubMed] [Google Scholar]
  44. Rotondo S, Dell'Elba G, Manarini S, Cerletti C, Evangelista V (2006) The lipoxygenase-cyclooxygenase inhibitor licofelone prevents thromboxane A2-mediated cardiovascular derangement triggered by the inflammatory peptide fMLP in the rabbit. Eur J Pharmacol 546: 95–101 [DOI] [PubMed] [Google Scholar]
  45. Sams-Dodd F (2005) Target-based drug discovery: is something wrong? Drug Discov Today 10: 139–147 [DOI] [PubMed] [Google Scholar]
  46. Samuelsson B, Morgenstern R, Jakobsson PJ (2007) Membrane prostaglandin E synthase-1: a novel therapeutic target. Pharmacol Rev 59: 207–224 [DOI] [PubMed] [Google Scholar]
  47. Schoeberl B, Eichler-Jonsson C, Gilles ED, Muller G (2002) Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nat Biotechnol 20: 370–375 [DOI] [PubMed] [Google Scholar]
  48. Shak S, Goldstein IM (1984) Omega-oxidation is the major pathway for the catabolism of leukotriene B4 in human polymorphonuclear leukocytes. J Biol Chem 259: 10181–10187 [PubMed] [Google Scholar]
  49. Sharom JR, Bellows DS, Tyers M (2004) From large networks to small molecules. Curr Opin Chem Biol 8: 81–90 [DOI] [PubMed] [Google Scholar]
  50. Shastry BS (2005) Genetic diversity and new therapeutic concepts. J Hum Genet 50: 321–328 [DOI] [PubMed] [Google Scholar]
  51. Simmons PM, Salmon JA, Moncada S (1983) The release of leukotriene B4 during experimental inflammation. Biochem Pharmacol 32: 1353–1359 [DOI] [PubMed] [Google Scholar]
  52. Singh D (2004) Merck withdraws arthritis drug worldwide. BMJ 329: 816. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Smith JB, Araki H, Lefer AM (1980) Thromboxane A2, prostacyclin and aspirin: effects on vascular tone and platelet aggregation. Circulation 62: V19–V25 [PubMed] [Google Scholar]
  54. Solomon SD, McMurray JJ, Pfeffer MA, Wittes J, Fowler R, Finn P, Anderson WF, Zauber A, Hawk E, Bertagnolli M (2005) Cardiovascular risk associated with celecoxib in a clinical trial for colorectal adenoma prevention. N Engl J Med 352: 1071–1080 [DOI] [PubMed] [Google Scholar]
  55. Suleyman H, Demircan B, Karagoz Y (2007) Anti-inflammatory and side effects of cyclooxygenase inhibitors. Pharmacol Rep 59: 247–258 [PubMed] [Google Scholar]
  56. Sun B, Li Z (2000) NSAID induced gastric mucosal damage and its prevention in rats. World Chin J Digest 8: 271–275 [Google Scholar]
  57. Sung MH, Simon R (2004) In silico simulation of inhibitor drug effects on nuclear factor-kappaB pathway dynamics. Mol Pharmacol 66: 70–75 [DOI] [PubMed] [Google Scholar]
  58. Van Hecken A, Schwartz JI, Depre M, De Lepeleire I, Dallob A, Tanaka W, Wynants K, Buntinx A, Arnout J, Wong PH, Ebel DL, Gertz BJ, De Schepper PJ (2000) Comparative inhibitory activity of rofecoxib, meloxicam, diclofenac, ibuprofen, and naproxen on COX-2 versus COX-1 in healthy volunteers. J Clin Pharmacol 40: 1109–1120 [PubMed] [Google Scholar]
  59. Vidal C, Gomez-Hernandez A, Sanchez-Galan E, Gonzalez A, Ortega L, Gomez-Gerique JA, Tunon J, Egido J (2007) Licofelone, a balanced inhibitor of cyclooxygenase and 5-lipoxygenase, reduces inflammation in a rabbit model of atherosclerosis. J Pharmacol Exp Ther 320: 108–116 [DOI] [PubMed] [Google Scholar]
  60. Wang D, Wang M, Cheng Y, Fitzgerald GA (2005) Cardiovascular hazard and non-steroidal anti-inflammatory drugs. Curr Opin Pharmacol 5: 204–210 [DOI] [PubMed] [Google Scholar]
  61. Xiao H, Yang CS (2008) Combination regimen with statins and NSAIDs: a promising strategy for cancer chemoprevention. Int J Cancer 123: 983–990 [DOI] [PubMed] [Google Scholar]
  62. Yang K, Ma W, Liang H, Ouyang Q, Tang C, Lai L (2007) Dynamic simulations on the arachidonic acid metabolic network. PLoS Comput Biol 3: e55. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Zimmermann GR, Lehar J, Keith CT (2007) Multi-target therapeutics: when the whole is greater than the sum of the parts. Drug Discov Today 12: 34–42 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figures and Tables

msb200860-s1.pdf (874.4KB, pdf)

Supplementary Information 1

msb200860-s2.xml (61.3KB, xml)

Supplementary Information 2

msb200860-s3.xml (54.4KB, xml)

Supplementary Information 3

msb200860-s4.xml (18.5KB, xml)

Articles from Molecular Systems Biology are provided here courtesy of Nature Publishing Group

RESOURCES