Protein structure prediction using basin-hopping

Abstract

Associative memory Hamiltonian structure prediction potentials are not overly rugged, thereby suggesting their landscapes are like those of actual proteins. In the present contribution we show how basin-hopping global optimization can identify low-lying minima for the corresponding mildly frustrated energy landscapes. For small systems the basin-hopping algorithm succeeds in locating both lower minima and conformations closer to the experimental structure than does molecular dynamics with simulated annealing. For large systems the efficiency of basin-hopping decreases for our initial implementation, where the steps consist of random perturbations to the Cartesian coordinates. We implemented umbrella sampling using basin-hopping to further confirm when the global minima are reached. We have also improved the energy surface by employing bioinformatic techniques for reducing the roughness or variance of the energy surface. Finally, the basin-hopping calculations have guided improvements in the excluded volume of the Hamiltonian, producing better structures. These results suggest a novel and transferable optimization scheme for future energy function development.

INTRODUCTION

The complexity of the physical interactions that guides the folding of biomolecules presents a significant challenge for atomistic modeling. Many current protein models use a coarse-grained approach to remove degrees of freedom, such as nonpolar hydrogens, which increases the feasible time step in molecular dynamics simulations.^{1, 2} For a more dramatic improvement of the computational efficiency, the number of solvent degrees of freedom can be reduced.³ In this case more severe approximations can prevent the model from reproducing experimental results. Another option is to reduce the number of degrees of freedom of the solute. The associative memory Hamiltonian^{4, 5, 6} (AMH) is a coarse-grained molecular mechanics potential inspired by physical models of the protein folding process, but flexibly incorporates bioinformatic data to predict protein structure. The AMH is optimized using the minimal frustration principle in terms of the T_f∕T_g ratio, which estimates the separation in energy relative to the variance for the misfolded ensemble. Along with using the energy of the native structure to estimate T_f, a random energy model⁷ estimate of the glass transition temperature T_g is used based on a set of decoy structures. T_g represents a characteristic temperature scale at which kinetic trapping in misfolded states dominates the dynamics. An improved potential is produced that uses better estimates of the T_f∕T_g ratio obtained by maximizing the normalized difference between the native state and a sampled set of misfolded decoys, which are self-consistently obtained. The resulting potential is transferable for the prediction of structures outside the training set. The ratio T_f∕T_g provides a powerful metric for the optimization of this bioinformatically informed energy function,^{8, 9} as well as other types of function incorporating only physical information.^{10, 11, 12}

The optimization¹³ of parameters using a training set of evolved proteins smooths the energy landscape from that of a random heteropolymer. However, the common problem of multiple competing minima persists, even for a reasonably accurate structure prediction potential. Simulated annealing with molecular dynamics has previously been used to search the rugged landscapes of optimized structure prediction potentials.¹⁴ While free energy profiles indicate that better structures actually are present at low temperatures, the slow kinetics of a glass-like transition during annealing has prevented these minima from being reached.¹⁵ To quantitatively investigate the origin of the sampling difficulties it is desirable to use different search strategies.

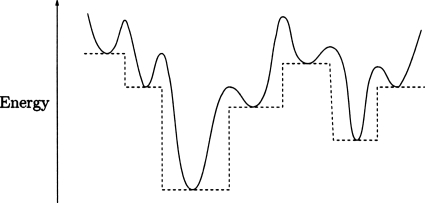
Here we implement the basin-hopping global optimization algorithm,^{16, 17, 18} which has proved capable of overcoming large energetic barriers in a wide range of systems. Basin-hopping is an algorithm where a structural perturbation is followed by energy minimization. This procedure effectively transforms the potential energy surface, by removing high barriers, as shown in Fig. 1. Moves between local minima are accepted or rejected based on a Monte Carlo criterion. Avoiding barriers by employing a numerical minimization step not only facilitates movement between local minima but also broadens their occupation probability distributions, which overlap over a wider temperature range, thereby increasing the probability of interconversion.¹⁹ Furthermore, it does not alter the nature of the local minima since the Hamiltonian itself is not changed, enabling comparison between molecular dynamics and basin-hopping generated minima. This method has previously been applied to find global minima in atomic and molecular clusters,^{20, 21} biopolymers,^{22, 23} and solids.²⁴ Since the algorithm only requires coordinates, energies, and gradients, it can be transferred between different molecular systems such as binary Lennard-Jones clusters, all-atom descriptions of biomolecules, or coarse-grained protein models, as in this study.

Figure 1.

In the basin-hopping approach the original potential energy surface (solid) is transformed into a set of plateaux (dashed). The local minima are not changed, but the transition state regions are removed.

THEORY AND COMPUTATIONAL DETAILS

The AMH energy function used in the present work has previously been optimized over a set of nonhomologous α helical proteins and consists of a backbone term E_back and an interaction term E_int, which has an additive form.^{25, 26} This model is sometimes termed the associative memory contact (AMC) model to distinguish it from the associative memory water (AMW) model, which uses nonadditive water mediated interactions.^{14, 27} Since this model has been described in detail before,^{15, 28} we will only summarize its form here. We employ a version of the coarse-grained model where the 20 letter amino acid code has been reduced to four, and the number of atoms per residue is limited to three (C_α, C_β, and O), except for glycine. The units of energy and temperature were both defined during the parameter optimization. The interaction energy ϵ was defined in terms of the native state energy excluding backbone contributions $E_{\mathrm{amc}}^{\mathrm{N}}$ via

$$ϵ=\frac{\mid E_{\mathrm{amc}}^{\mathrm{N}}\mid }{4N},$$ (1)

where N is the number of residues of the protein in question. Temperatures are quoted in terms of the reduced temperature T_AMC=k_BT∕ϵ. While E_back creates self-avoiding peptide-like stereochemistry, E_int introduces the majority of the attractive interactions that produce folding. The interactions described by E_int depend on the sequence separation ∣i−j∣. The interactions between residues less than 12 amino acids apart were defined by Eq. 2.

$$E_{\text{local}}=-\frac{ϵ}{a}\sum _{\mu =1}^{N_{\mathrm{mem}}}\sum _{j-12⩽i⩽j-3}\gamma (P_i,P_j,P_{i^{\prime }}^{\mu },P_{j^{\prime }}^{\mu },x\left(\mid i-j\mid \right))\exp [-\frac{{(r_{ij}-r_{i^{\prime }{j}^{\prime }}^{\mu })}^2}{2{\sigma }_{ij}^2}].$$ (2)

The index μ runs over all N_mem memory proteins to which the protein has previously been aligned using a sequence-structure threading algorithm.²⁹ Each i−j pair in the protein has an i^′−j^′ pair associated with it in every memory protein. If there are gaps in the alignment, and hence no i^′−j^′ pair associated with i−j for a particular memory, then this memory protein simply gives no contribution to the interaction between residues i and j. The interaction between C_α and C_β atoms is a sum of Gaussian wells centered at the separations $r_{i^{\prime }{j}^{\prime }}^{\mu }$ of the corresponding memory atoms. The widths of the Gaussians are given by σ_ij=∣i−j∣^0.15 Å. The scaling factor a is used to satisfy Eq. 1. The weights given to each well are $\gamma (P_i,P_j,P_{i^{\prime }}^{\mu },P_{j^{\prime }}^{\mu },x\left(\mid i-j\mid \right))$, which depends on the identities P_i^′ and P_j^′ of the residues to which i and j are aligned, as well as the identities P_i and P_j of i and j themselves. The self-consistent optimization calculates the γ parameter, which creates the cooperative folding in the model. A three-well contact potential [Eq. 3] is used for residues separated by more than 12 residues,

$$E_{\text{contact}}=-\frac{ϵ}{a}\sum _{i<j-12}\sum _{k=1}^3\gamma (P_i,P_j,k)c_k\left(N\right)U(r_{\min }\left(k\right),r_{\max }\left(k\right),r_{ij}).$$ (3)

The summation of k is over the three wells, which are approximately square wells between r_min(k) and r_max(k) defined by

$$U(r_{\min }\left(k\right),r_{\max }\left(k\right),r_{ij})=\frac{1}{4}\{[1+\tanh (7[r_{ij}-r_{\min }\left(k\right)]∕\AA )]+[1+\tanh (7[r_{\max }\left(k\right)-r_{ij}]∕\AA )]\}.$$ (4)

The parameters (r_min(k),r_max(k)), are (4.5,8.0 Å), (8.0,10.0 Å), and (10.0,15.0 Å) for k=1, 2, and 3, respectively. In order to approximately account for the variation of the probability distribution of pair distances with the number of residues in the protein, N, a factor c_kN has been included in E_long. It is given by c₁=1.0,c₂=1.0∕(0.0065N+0.87), and c₃=1.0∕(0.042N+0.13). The individual wells are also weighted by γ parameters, which depend on the identities of the amino acids. In contrast to the interactions between residues closer in sequence, this part of the potential does not depend on the database structures that define local-in-sequence interactions.

To pinpoint the effects of frustration caused by favorable non-native contacts, which are always present in any coarse-grained protein model, we considered a smoother energy function based on a Gō model.³⁰ Gō models are a useful tool for understanding protein folding kinetics.^{31, 32} This single structure based Hamiltonian [Eq. 5] has the same backbone terms,³³ but all the interactions E_int are defined by Gaussians with minima located at the most probable pair distribution value for the experimental structure,

$$E_{\mathrm{G}\overline{\mathrm{o}}}^{\mathrm{AM}}=-\frac{ϵ}{a_{\mathrm{G}\overline{\mathrm{o}}}}\sum _{i⩽j-3}{\gamma }_{\mathrm{G}\overline{\mathrm{o}}}\left(x\left(\mid i-j\mid \right)\right)\exp [-\frac{{(r_{ij}-r_{ij}^{\mathrm{N}})}^2}{2{\sigma }_{ij}^2}].$$ (5)

The global minimum of such an energy function should be the input structure.

Many studies have employed additional constraining potentials to characterize unsampled regions of coordinate space while using molecular dynamics.^{15, 34} To characterize the landscape sampled with basin-hopping, we also used a structure constraining potential to identify ensembles with fixed but varying fractions of native structure. Using such a potential allows the analysis of interesting configurations that are unlikely to be thermally sampled. The constraining (umbrella) potentials are centered on different values of an order parameter to sample along the collective coordinates. One of the collective coordinates is Q, an order parameter that measures the sequence-dependent structural similarity of two conformations by computing the normalized summation of C_α pairwise contact differences, as defined in Eq. 6,¹⁵

$$Q=\frac{2}{(N-1)(N-2)}\sum _{i<j-1}\exp [-\frac{{(r_{ij}-r_{ij}^N)}^2}{{\sigma }_{ij}^2}].$$ (6)

The resulting order parameter ranges from zero, where there is no similarity between structures, to one, which represents an exact overlap. The form of the potential isE(Q)=2500ϵ(Q−Q_i)⁴, where Q_i may be varied in order to sample different regions of the chosen order parameter. As in equilibrium sampling, simulations were initiated at the native state, and the Q_i parameter was reduced throughout the sampling.

We have also studied the potential energy landscape when multiple surfaces are superimposed on each other by the use of multiple homologous target proteins. This manipulation of the energy landscape has been shown to further reduce the local energetic frustration that arises from random mutations in the sequence away from the consensus optimal sequence for a given structure. By reducing the number of non-native traps, this averaging often improves the quality of structure prediction results.^{35, 36, 37, 38} As seen in Eq. 7, the form and the parameters of the energy function are maintained from Eqs. 2, 3, but the normalized summation is taken over a set of homologous sequences,

$$E_{\mathrm{AM}}=-\frac{1}{N_{\mathrm{seq}}}\sum _{k=1}^{\mathrm{seq}}\sum _{i<j}^N{E}_{\mathrm{int}}(P_i^k,P_j^k).$$ (7)

Since proteins are not random heteropolymers, the differences in the energy function for homologous proteins are randomly distributed, therefore the mean over multiple energy functions should have less energetic variation than the original function. Indeed, performing this summation is a way of incorporating optimization of the T_f∕T_g criterion into any energy function. The target sequences of the homologues can be identified using PSI-Blast with default parameters.^{39, 40} Some classes of proteins have a large number of sequence homologues, and performing a multiple sequence alignment can be impractical. Removing redundant sequences from within the set of identified homologues also removes biases that can be introduced where there are few homologues available. This procedure is performed by preventing sequences in the collection from having greater than 90% sequence identity. The remaining sequences are aligned in a multiple sequence alignment.⁴¹ Gaps within the sequence alignment can be addressed within the AMH energy function in a variety of ways. In the present work, gaps in the target sequence were removed, while gaps within homologues were completed with residues from the target protein. While this procedure may introduce small biases toward the target sequence, it is preferable to ignoring the interactions altogether.

Finally, we made several ad hoc changes to the backbone potential E_back. Eliminating some compromises necessary for rapid molecular dynamics simulations allowed the AMH potential to be adapted to basin-hopping. Preventing the overcollapse of the proteins by altering the excluded volume energy term should reduce the number of states available during minimization. The terms shown in Eq. 8 are used to reproduce the peptide-like conformations in the original molecular dynamics energy function,

$$E_{\text{back}}=E_{\mathrm{ev}}+E_{\text{harm}}+E_{\text{chain}}+E_{\mathrm{chi}}+E_{\text{Rama}}.$$ (8)

E_ev maintains a sequence specific excluded volume constraint between the C_α–C_α, C_β–C_β, O–O, and C_α–C_β atoms that are separated by less than r_ev. Previously,²⁶ we have seen that modifying E_back can produce a less frustrated energy surface when using thermal equilibrium sampling, but slow dynamics was often found to result since the local barrier heights became too large. The ability of basin-hopping to overcome such large but local, barriers allows us to consider a potential whose dynamics would otherwise be too slow for molecular dynamics. In the final part of the paper we investigate the effect of changing the excluded volume term to prevent overcollapse, as shown in Eq. 9,

$$E_{\mathrm{ev}}=ϵ{\lambda }_{\mathrm{RV}}^{\mathrm{C}}\sum _{x,y}\sum _{i<j}\theta (r_{\mathrm{ev}}^{\mathrm{C}}(j-i)-r_{{\mathrm{C}}_i^x{\mathrm{C}}_j^y}){(r_{\mathrm{ev}}^{\mathrm{C}}(j-i)-r_{{\mathrm{C}}_i^x{\mathrm{C}}_j^y})}^2+ϵ{\lambda }_{\mathrm{ev}}^{\mathrm{O}}\sum _{i<j}\theta (r_{\mathrm{ev}}^{\mathrm{O}}-r_{{\mathrm{O}}_i{\mathrm{O}}_j}){(r_{\mathrm{ev}}^{\mathrm{C}}-r_{{\mathrm{O}}_i{\mathrm{O}}_j})}^2,$$ (9)

by changing the default molecular dynamics parameters, ${\lambda }_{\mathrm{EV}}^{\mathrm{C}}=20$, ${\lambda }_{\mathrm{EV}}^{\mathrm{O}}=20$, $r_{\mathrm{ev}}^{\mathrm{C}}(j-i<5)=3.85\mathrm{\AA }$, $r_{\mathrm{ev}}^{\mathrm{C}}(j-i⩾5)=4.5\mathrm{\AA }$, and $r_{\mathrm{ev}}^{\mathrm{O}}=3.5\mathrm{\AA }$, to ${\lambda }_{\mathrm{EV}}^{\mathrm{C}}=250$, ${\lambda }_{\mathrm{EV}}^{\mathrm{O}}=250$, $r_{\mathrm{ev}}^{\mathrm{C}}(j-i<5)=3.85\mathrm{\AA }$, $r_{\mathrm{ev}}^{\mathrm{C}}(j-i⩾5)=3.85\mathrm{\AA }$, and $r_{\mathrm{ev}}^{\mathrm{O}}=3.85\mathrm{\AA }$. The force constants are over an order of magnitude larger than those used in molecular dynamics, and the radii of the C_α, C_β, and O atoms are also 10% larger than previous values. This increase in excluded volume slows the onset of chain collapse, but improves steric interactions. The other change to the backbone potential is to the terms that maintain chain connectivity. In molecular dynamics with annealing, covalent bonds are preserved using the SHAKE algorithm,⁴² which permits an increase of the molecular dynamics time step. For all basin-hopping calculations we removed the SHAKE method and replaced it with a harmonic potential E_harm between the C_α–C_α+1, C_α–C_β, C_α–O, and C_α+1–O atoms. This replacement permits the location of local minima without requiring an internal coordinate transformation and avoids discontinuous gradients. When minimized, the additional harmonic terms typically contribute only about 0.015k_BT per bond. The remaining terms of the original backbone potential are maintained. Depending on the side chain, the neighboring residues in sequence sterically limit the variety of positions the backbone atoms can occupy, as evidenced in a Ramachandran plot.⁴³ This distribution of coordinates is reinforced by a potential E_Rama with artificially low barriers to encourage rapid local exploration. The planarity of the peptide bond is ensured by a harmonic potential E_chain. The chirality of the C_α centers is maintained using the scalar triple product of the neighboring unit vectors of carbon and nitrogen bonds E_chi.

The basin-hopping algorithm is outlined in Fig. 2. Here the most important sampling parameters are the temperature used in the accept∕reject steps for local minima, T_bh, and the maximum step size for perturbations of the Cartesian coordinates, d. A higher temperature not only allows transitions to higher energy minima to be accepted but also increases the number of iterations typically required to minimize the more perturbed configurations. Too high a temperature leads to insufficient exploration of low energy regions. The temperature (T_bh) for these simulations was 10T_AMC. Lower temperatures resulted in slower escape rates from low energy traps, while higher temperatures prevented adequate exploration of low energy regions. The step size needs to be large enough to move the configuration from the basin of attraction of one local minimum to a neighboring one, but not so large that the new minimum is unrelated to the previous state. Every Cartesian coordinate was displaced up to a maximum step size (d) of 0.75 Å, the value determined from preliminary tests. Each run consisted of 2500 basin-hopping steps, saving structures every five basin-hopping steps. The convergence condition (δR_min) on the root-mean-square (RMS) of the gradient for each minimization was set to 10⁻³ϵ∕r, and the five lowest-lying minima from each run were subsequently converged more tightly (δR_final) to a RMS of the gradient of 10⁻⁵ϵ∕r. The gradient is defined by the change in the energy ϵ over distance r. It is important to note that basin-hopping does not provide equilibrium thermodynamic sampling. However, in structure prediction there is no need for the search to obey detailed balance, since the global energy minimum is the primary interest. Basin-hopping provides an efficient global optimization algorithm, but it does not provide a measure of entropy or free energy in the present form.

Figure 2.

The basin-hopping algorithm is defined by a few parameters that make it readily transferable between different systems.

In previous structure prediction studies with the AMH, low energy structures were identified using off-lattice Langevin dynamics with simulated annealing, employing a linear annealing schedule of 10 000 steps from a temperature of 2.0–0.0, starting from a random configuration.⁵ The number and length of simulations needed in both strategies were determined by the number of uncorrelated structures encountered. The current basin-hopping method with the AMH energy function encounters roughly one deep trap per run. In order to sample 100 independent structures in molecular dynamics, 20 separate runs were needed, because simulated annealing samples about five independent states before the glass transition temperature is encountered, as measured by the rapid decay of structural correlations. We compared several α helical proteins, inside and outside the training set of the AMH energy function.

RESULTS AND DISCUSSION

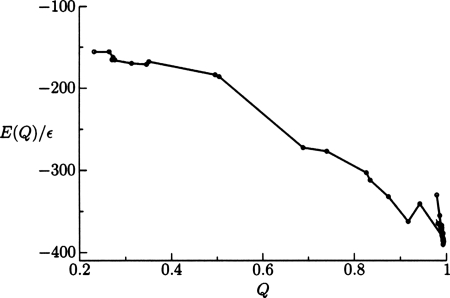
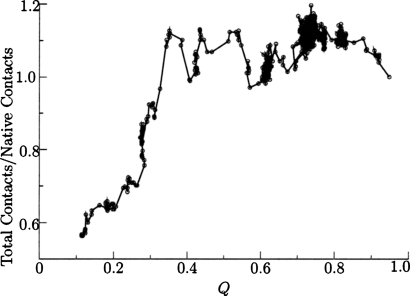
We performed initial calculations with a Gō potential for the 434 repressor (protein data bank [PDB (Ref. ⁴⁴)] ID 1r69). In Fig. 3 we show this model accurately represents the native structure. Steps where the energy increases are allowed by the sampling method and are not examples of frustration. Studies on the Gō model provide a useful benchmark for comparing the computer time required for the different global optimization strategies. Using the sampling parameters used in this report, we compared the time for initial collapse between the molecular dynamics and basin-hopping runs. The initial collapse required about 7 min for the annealing runs and 31 min for basin-hopping on a desktop computer. However, these values do not reflect the actual performance of the two approaches in locating global minima, which will depend on the move sets, step size, temperature, and convergence criteria.

Figure 3.

Variation of the energy of the current minimum as a function of Q for minima encountered in the Markov chain during a basin-hopping run using a Gō model. Steps that increase the energy are sometimes allowed by the Monte Carlo criterion, which employed a temperature of 10k_b∕ϵ.

While using the AMH structure prediction Hamiltonian, we found that basin-hopping was often able to locate lower energy structures and also identified minima that have greater structural overlap with the native state than annealing. These results were obtained for structure predictions corresponding to proteins both inside and outside the training set, as demonstrated in Table 1. The first three proteins (PDB ID 1r69, 3icb, 256b) in Table 1 are in the training set of the Hamiltonian,²⁵ while the other three are not, and therefore represent predictions. The minima located with basin-hopping show an increase in structural overlap with the native state [Eq. 6] when compared to the Langevin dynamics approach. Q scores of 0.4 for single domain proteins generally correspond to a low resolution rms deviation (RMSD) of around 5 Å or better. Q scores of 0.5 and higher have still more accurate tertiary packing and are of comparable quality to the experimentally derived models. The high quality structures obtained suggest the form of the backbone terms is appropriate, since the physically correct stereochemistry is reproduced. Lower energy structures are sampled by basin-hopping for the nontraining set proteins, but the structural overlap improvement found in these deeper minima was smaller. Larger proteins pose a greater challenge for basin-hopping with this Hamiltonian due to the random steps in Cartesian coordinates. Dihedral coordinate moves would probably be more efficient, and will be considered in future work.

Table 1.

Minima located by molecular dynamics∕annealing (MD) and basin-hopping (BH); the first three proteins are in the training set of the Hamiltonian, while the results for the second three proteins are predictions.

PDB	Length	MD				BH
		Lowest E	Q	Highest Q	E	Lowest E	Q	Highest Q	E
1r69	63	−428.92	0.39	0.53	−307.96	−435.82	0.39	0.52	−408.48
3icb	75	−536.98	0.47	0.52	−390.54	−546.57	0.40	0.49	−518.92
256b	106	−735.02	0.42	0.65	−707.51	−737.31	0.37	0.40	−716.51
1uzc	69	−457.55	0.36	0.42	−383.08	−458.09	0.37	0.45	−433.41
1bg8	76	−469.49	0.25	0.34	−465.19	−468.67	0.36	0.39	−461.50
1bqv	110	−737.91	0.21	0.27	−441.92	−764.20	0.23	0.27	−481.22

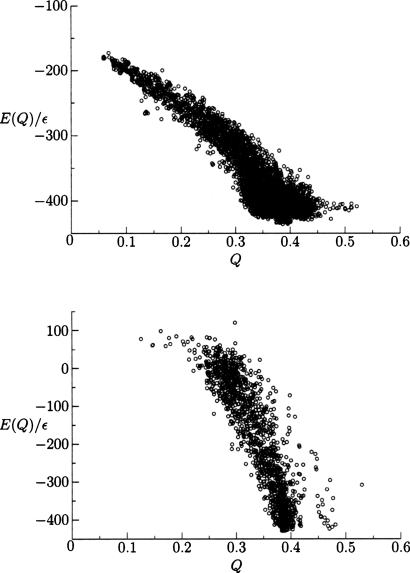
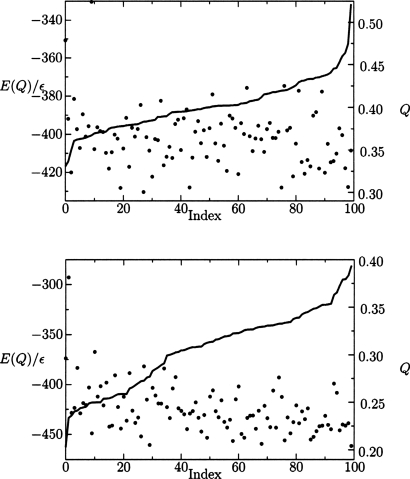
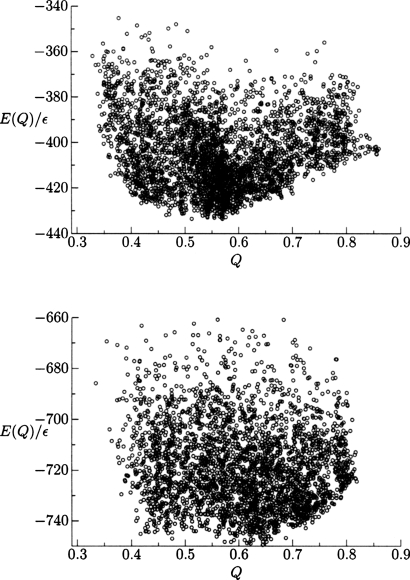
The distribution of minima encountered from multiple simulations for both search methods is shown in Fig. 4, where a greater density of high quality structures is obtained by the basin-hopping algorithm. Hence, the potential energy surface still includes significant residual frustration in the near-native basin in the form of low-lying minima separated by relatively high barriers. Without the parameter optimization to reduce frustration, folding would exhibit more pronounced glassy characteristics. Most of the cooperative folding occurs during collapse until Q values of around 0.4 are reached. While the structures from simulated annealing are accurate enough for functional determination, we see that basin-hopping can better overcome barriers that are created after collapse. The density of the high quality structures is also important for post-simulation k-means clustering analysis.⁴⁵ Another way of representing the data of a set of independent basin-hopping simulations is by selecting the lowest energy structures from each simulation of the 434 repressor (PDB ID 1r69) and HDEA (PDB ID 1bg8) proteins and ordering them with respect to their structural overlap. As shown in Fig. 5, the protein in the training set (434 repressor) produces better results than the nontraining protein, as expected.

Figure 4.

Energy as a function of Q for local minima of 434 repressor encountered during 100 independent basin-hopping optimizations (top) and 20 annealing simulations (bottom).

Figure 5.

The lowest energy structures of the training set protein, 434 repressor (top), and the blind prediction proteins, HDEA (bottom) identified from 100 independent basin-hopping simulations. Each minimum has values for energy, illustrated by dots, and structural overlap with the native state Q, represented by the continuous line. These minima are ordered with respect to their structural overlap Q with the native state (index). The data show correlations between the energy and Q, while the number of high quality structures is superior for the training protein.

We have decomposed the different energy terms in the Hamiltonian in Table 2 to examine which interactions are most effectively minimized. The AMH potential has three different distance classes in terms of sequence separation, and these are defined as short (∣i−j∣<5), medium (5⩽∣i−j∣⩽12), and long (∣i−j∣>12). Most importantly, the long range AMH interactions are successfully minimized in the basin-hopping runs due to the ability of basin-hopping to overcome large energetic barriers. This term will govern the quality of structures sampled using an approximately smooth energy landscape. The other terms that define secondary structure formation are not as well minimized. This result is due to the disruption of helices by the random Cartesian moves. These perturbations benefit favorable steric packing and therefore do well at minimizing the excluded volume energy term of the Hamiltonian. A combined minimization approach might be more efficient, where larger dihedral steps could be made early on during a run to sample a wider number of structures, followed by random Cartesian steps to optimize the steric interactions.

Table 2.

Contribution of different energy terms in local minima obtained using molecular dynamics∕annealing (MD) and basin-hopping (BH).

PDB	Method	Length	Ex vol	Rama	Short range	Medium range	Long range
1r69	MD	63	9.77	−101.64	−128.90	−84.87	−123.28
1r69	BH	63	2.65	−91.06	−125.04	−84.80	−137.57
3icb	MD	75	11.74	−127.70	−177.21	−90.11	−153.69
3icb	BH	75	4.40	−115.76	−178.47	−83.37	−173.38
1uzc	MD	69	10.10	−118.66	−134.00	−90.75	−124.24
1uzc	BH	69	2.22	−106.20	−137.95	−92.40	−123.77
1bg8	MD	76	11.68	−136.39	−173.45	−94.40	−76.94
1bg8	BH	76	2.72	−112.13	−151.95	−94.23	−113.09

Although we sampled high quality structures, we would also like to confirm that we have completely sampled the global minima of the energy surface. To access unsampled states we used umbrella potentials. When constraining a set of simulations to different values of Q, we have obtained energy minima for cytochrome c roughly 15ϵ deeper than those from unconstrained minimizations starting with a randomized structure, as shown in Fig. 6. For the 434 repressor the minima obtained from randomized states and those found with the Q constraints applied differ by only a few k_BT. This result shows that basin-hopping does indeed perform well as an unbiased global optimization method by accurately identifying the global energy minimum from multiple independent unconstrained simulations. This behavior is predictable from the choices that governed the design of the Hamiltonian. Low energy barriers between structures are desirable during a molecular dynamics simulation because they accelerate the dynamics. However, for basin-hopping these low barriers encourage tertiary contact formation before secondary structure units condense for sequences greater than 110 amino acids.

Figure 6.

Energy as a function of Q for the 434 repressor and cytochrome c proteins obtained in basin-hopping calculations with the structure prediction Hamiltonian. These runs employed an additional umbrella potential that constrains the simulation to different values of Q. The results for the 434 repressor are similar to the unconstrained basin-hopping results, but the structures for cytochrome c are 15ϵ lower in energy than those found in unconstrained basin-hopping runs.

Superposition of multiple energy landscapes

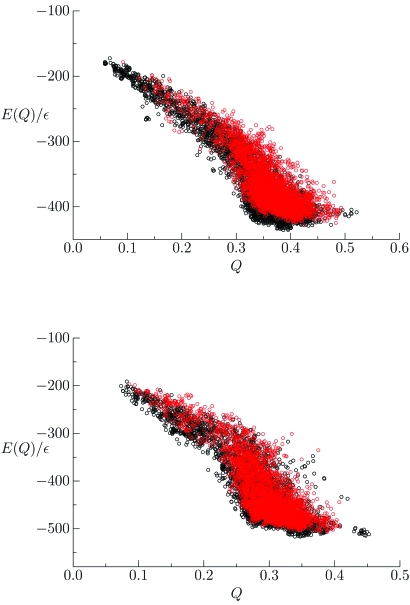
Constructing a Hamiltonian by calculating the arithmetic average of the potential over a set of homologous sequences increased the quality of predictions in both equilibrium and annealing simulations. We have found that this approach can also improve the performance in basin-hopping simulations. For two different proteins, 100 independent basin-hopping runs were performed with both the standard and sequence-averaged Hamiltonians. By the superposition of multiple energy landscapes we saw a reduction in the number of competing low energy traps around Q values of 0.3 for both the 434 repressor and uteroglobin (PDB ID 1UTG), as shown in Fig. 7. Improvement of structure prediction Hamiltonians can be statistically described by the average energy gap between the native basin and a set of unfolded structures and by the roughness of the energy surface, which corresponds to the variance of the energy. The sequence-based energy function summations limited the energetic variance of the sampled landscapes, thereby reducing the glass transition temperature. This improvement, even at the low temperatures sampled in basin-hopping, is predicted from theory, but difficult to observe in conventional equilibrium simulations due to the emergent glassy dynamics, which slows the kinetics. The energy gap improvement was smaller than the reduction of the energetic variation of the Hamiltonian. In terms of the goal of maximizing the ratio of T_f∕T_g, this increase came primarily from reducing the glass transition temperature T_g. In the low energy region we saw fewer competing states and an increased correlation between E and Q for the sequence-averaged Hamiltonian compared to the original Hamiltonian. For the 434 repressor the lowest energy structure had the highest Q value encountered.

Figure 7.

Energies of local minima obtained using basin-hopping with the original and a sequence-averaged Hamiltonian for two training proteins. Importantly for both the top graph (434 repressor) and the bottom graph (uteroglobin), fewer non-native states are seen with the sequence-averaged (red) Hamiltonian when compared to standard Hamiltonian (black).

Characterization of polymer collapse

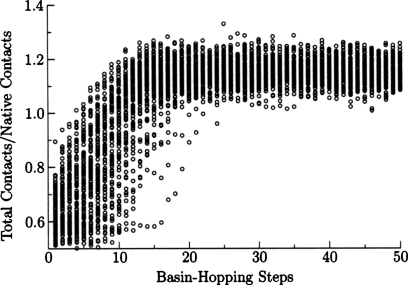
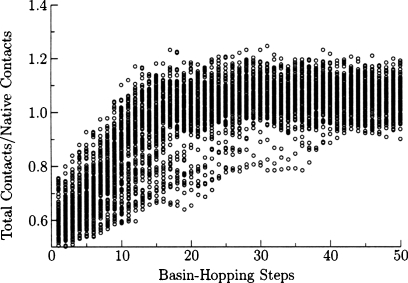
When we annealed the Hamiltonian using molecular dynamics we observed some overcollapse of the polypeptide chain, producing a smaller radius of gyration than the experimental structure. In basin-hopping runs we also found structures exhibiting a larger number of contacts than the experimental structure, as shown in Fig. 8, where a contact is defined as a C_α–C_α distance of less than 8 Å. While the low energy structures may be native-like, these structures were more compact than those observed experimentally. To investigate this behavior, we examined the backbone and interaction terms of the Hamiltonian separately using the Gō Hamiltonian in Eq. 5. Somewhat surprisingly, the Gō model also produces overcollapse, as shown in Fig. 9. Hence the interaction parameters of the structure prediction Hamiltonian were not responsible for all of the overcollapse. These minimal model-dependent frustrations were only eliminated in the final stages of minimization. The most effective technique for reducing overcollapse was to increase the force constant and the atomic radius in the excluded volume terms [Eq. 9]. The barrier crossing capabilities of basin-hopping steps produce more overcollapse than do the annealing minimizations without these parameter changes. The glass-like transition seen in simulated annealing prevents further collapse in molecular dynamics, as the rearrangement rates slow down exponentially with temperature. The improved parameter set of Fig. 10 shows more nativelike collapse, but the lowest energy structures had Q values of 0.36 and the best Q value was 0.45, which are worse than basin-hopping simulations with the original parameters.

Figure 8.

Results of 100 independent basin-hopping runs for the 434 repressor using the set of backbone parameters that was optimized for molecular dynamics. Structures were saved every 20 basin-hopping steps. The ratio of contacts to native state contacts shows that most of the structures are more compact than the native state.

Figure 9.

A Gō potential simulation for the 434 repressor shows a modest amount of overcollapse during a basin-hopping simulation, which is resolved as the structure approaches a Q value of 1.0.

Figure 10.

Results of 100 independent basin-hopping runs for the 434 repressor using the set of backbone parameters that was optimized for molecular dynamics. Structures were saved every 20 basin-hopping steps. An altered set of backbone parameters produces structures that have similar collapse behavior when compared to the native state.

CONCLUSION

In this report we have demonstrated that minima with lower energy and higher quality structures can often be located for the AMH potential using basin-hopping global optimization compared to annealing. Encouragingly, the energy contributions corresponding to long range in sequence contributions are better minimized than with simulated annealing. Umbrella sampling using basin-hopping can also show when the global minima are reached for a selected order parameter. Previous techniques for reducing the energetic variance of the energy surface in simulated annealing are also applicable to basin-hopping. Using basin-hopping also permits improvements in certain backbone terms of the Hamiltonian. These changes would make the kinetics too slow for molecular dynamics annealing runs, but larger barriers can easily be crossed using basin-hopping.

These results suggest future optimization strategies where the deep non-native traps found by basin-hopping could be used as decoys for further parameter refinement, rather than the higher-lying minima obtained by quenching with simulated annealing. This reoptimization of the potential results makes a better estimate for T_f∕T_g possible because of the efficiency of the basin-hopping algorithm at identifying low energy decoys. Another future direction would be to evaluate the equilibrium properties of low-lying structures identified by basin-hopping to calculate free energy barriers, which would be difficult to characterize via conventional simulations.