On the Adaptive Design Rules of Biochemical Networks in Evolution

Bor-Sen Chen; Wan-Shian Wu; Wei-Sheng Wu; Wen-Hsiung Li

. 2007 Feb 28;3:27–39.

On the Adaptive Design Rules of Biochemical Networks in Evolution

Bor-Sen Chen ^1,^✉, Wan-Shian Wu ¹, Wei-Sheng Wu ¹, Wen-Hsiung Li ^2,³

PMCID: PMC2674634 PMID: 19430602

Abstract

Biochemical networks are the backbones of physiological systems of organisms. Therefore, a biochemical network should be sufficiently robust (not sensitive) to tolerate genetic mutations and environmental changes in the evolutionary process. In this study, based on the robustness and sensitivity criteria of biochemical networks, the adaptive design rules are developed for natural selection in the evolutionary process. This will provide insights into the robust adaptive mechanism of biochemical networks in the evolutionary process.

We find that if a mutated biochemical network satisfies the robustness and sensitivity criteria of natural selection, there is a high probability for the biochemical network to prevail during natural selection in the evolutionary process. Since there are various mutated biochemical networks that can satisfy these criteria but have some differences in phenotype, the biochemical networks increase their diversities in the evolutionary process. The robustness of a biochemical network enables co-option so that new phenotypes can be generated in evolution. The proposed robust adaptive design rules of natural selection gain much insight into the evolutionary mechanism and provide a systematic robust biochemical circuit design method of biochemical networks for biotechnological and therapeutic purposes in the future.

Keywords: evolutionary process, adaptive design rules, robust biochemical networks and S-system

Introduction

Robustness is a ubiquitously observed property of biological systems. It is considered to be a fundamental feature of complex evolvable systems. It is pointed out that robustness facilitates evolvability and robust traits are often selected by evolution (Kitano, 2004), i.e. complex biological systems must be robust against environmental and genetic perturbations to be evolvable. Evolution often selects traits that might enhance robustness of the organism.

The central role of biochemical networks in cellular function provides a strong motivation to search for the underlying principles of adaptive evolution of biochemical networks. In this study, in order to test whether a physiological function would prevail under a new environment or not, the robustness and sensitivity criteria are developed to measure the tolerance of the metabolite concentration values of a biochemical network in the face of environmental changes. That is, we derive necessary and sufficient conditions for the metabolite network to be preserved by natural selection in the evolutionary process.

The evolutionary analysis is based on two concepts, natural selection and evolution (Freeman and Herron, 2001). In the past, most molecular biologists and biochemists assumed that variations in biochemical networks were mainly due to historical accidents and natural selection. But the design principles of biochemical networks via natural selection in evolution are still in conceptual description, not in mathematical rules. Can these mathematical natural selection principles for biochemical networks in evolution be unraveled? The investigation of design principles of biochemical networks is in its infancy and more underlying rules remain to be discovered. In fact, robustness allows change in the structure and components of the system owing to these perturbations and disturbances, but specific functions are maintained. Hence, robustness facilitates evolvability and evolution selects robust traits (Yi et al. 2000; Kitano, 2004).

In this study, the robustness criterion based on S-system is derived as a necessary adaptive design rule of a biochemical network under natural selection. In addition, to guarantee small changes of metabolite concentration values under environmental disturbances in the evolutionary process, some sensitivity criteria are proposed as the sufficient conditions for the adaptation of a biochemical network so that it can play its proper role in the corresponding physiological system. Two adaptive design schemes of robustness improvement are developed for biochemical network evolution. One scheme is to compensate the effect of parameter variations to meet the robustness criterion easily. In this way, some redundant and self-regulatory pathways are selected by natural selection to attenuate the effect of parameter variations. The other is to enhance the system structure stability of biochemical networks to tolerate larger parameter perturbations. In this way, negative feedbacks and positive feedbacks are selected to improve structure stability. These two adaptive schemes are two design methods of biochemical networks to improve their robustness and to maintain the live function against environmental changes in the evolutionary process. The biochemical networks with improved robustness can survive under natural selection. At the same time, the sensitivities of biochemical networks to environmental disturbances are also attenuated to maintain their metabolite mechanisms for normal physiology, i.e. insusceptible to environmental disturbances for species evolution or diseases such as virus infection, with immunity for individual. They are also considered in the adaptive design rules of natural selection in evolution.

Since many solutions can meet the robustness and sensitivity criteria of natural selection, a variety of biochemical networks may survive in evolution. A variety of biochemical networks with some structural differences may arise in evolution. For example, in the TCA cycles in different species, their final products are almost the same from yeast to human, but their biochemical networks have some structural differences in intermediary biochemistry reactions. Based on the adaptive design rules of biochemical networks via natural selection, one possibility of the diversity in biochemical networks in the evolutionary process is to increase the complexity of networks through successive addition of feedback and feed-forward pathways to enhance robustness against genetic mutations and environmental perturbations (Barkai and Leibler, 1997; Alon et al. 1999; West-Eberhard, 2003).

Natural selection can select only from the mutated biochemical networks that already exist in nature and cannot instantly create a new and optimal biochemical network (or phenotype) to maintain the live function. The co-option of existing biochemical networks to new networks is one of the crucial features in evolution (Kitano, 2004). Several biochemical networks are combined through positive feedback loops and negative feedback loops so that normal cellular physiology and developmental processes can be maintained. This intrinsic robustness of a biochemical network enables co-option, so that new morphologies can be generated in the evolutionary process (Freeman, 2000; Kitano, 2004). The proposed adaptive design rule via natural selection can mimic the evolution of biochemical networks by computational simulation. Simply speaking, the evolutionary way is to improve its robustness of biochemical networks to tolerate the parameter variations and environmental variations to play their proper role in the corresponding physiological systems. The proposed robust adaptive design rules of natural selection also provide a systematic robust biochemical circuit design method of biochemical networks for drug design and robust engineered synthetic biocircuit design purposes in the future. We can use computational prediction and rational design (Altamirano et al. 2000; Johannes et al. 2005; Tsuji et al. 2006), directed evolution (May et al. 2000; Wang et al. 2000; Yuan et al. 2005) and dynamic controller (Farmer and Liao, 2000; Bulter et al. 2004) to quickly create a library of variants for artificial evolution to achieve the desired property of biochemical networks. Rational design and directed evolution are to modify the catalytic or binding property of an enzyme which corresponds to the changes of kinetic parameters g_ij and h_ij in the S-System model through modulating the enzyme structure and through DNA shuffling, respectively. A dynamic controller is to construct a feedback or feedforword pathway. Finally, a computational simulation example is given to illustrate the adaptive design mechanism of a biochemical network via natural selection in evolution.

Mathematical Rules for Natural Selection

Notations

For a vector x = [x₁, …, x_n], the l₂ norm of x is defined as ${‖ x ‖}_{2} = \sqrt{x_{1}^{2} + x_{2}^{2} + \dots + x_{n}^{2}}$ . We say x ∈ l₂, if ||x||₂ < ∞. For a matrix A and y = Ax, the l₂ – induced matrix norm is defined as ||A||₂ = sup_x∈_l₂ $\frac{{‖ y ‖}_{2}}{{‖ x ‖}_{2}}$ , i.e. the gain from x to y. It has been shown that ||A||₂ = σ_max (A) = max_i $\sqrt{λ_{i} (A^{T} A)}$ where σ_max (A) denotes the largest singular value of A and λ_i(A^T A) denotes the ith eigenvalue of A^T A. ||A||₂ < 1 if and only if AA^T < I i.e. A is contractive, where I is the identity matrix (Gill et al. 1991; Weinmann, 1991).

The mathematical model, robustness and sensitivity analyses of a biochemical network under natural selection in the evolutionary process are introduced at first.

Model of a Biochemical Network

In a biochemical network, one often measures rates of reaction or influx and outflux rates of substrates, enzymes, factors or products and the rates correspond directly to changes in concentrations. The S-system model has been developed to write the reaction relationship of metabolites in differential equations in terms of their concentrations. The dynamic system of a biochemical network is described in the following S-system representation (Voit, 2000; Savageau, 2001)

\begin{array}{l} {\dot{X}}_{1} = α_{1} \prod_{j = 1}^{n + m} X_{j}^{g_{1 j}} - β_{1} \prod_{j = 1}^{n + m} X_{j}^{h_{1 j}} \\ ⋮ \\ {\dot{X}}_{i} = α_{i} \prod_{j = 1}^{n + m} X_{j}^{g_{i j}} - β_{i} \prod_{j = 1}^{n + m} X_{j}^{h_{i j}} i = 2, \dots, n - 1 \\ ⋮ \\ {\dot{X}}_{n} = α_{n} \prod_{j = 1}^{n + m} X_{j}^{g_{n j}} - β_{n} \prod_{j = 1}^{n + m} X_{j}^{h_{n j}} \end{array}

(1)

where X₁, …, X_n₊_m are metabolites, such as substrates, enzymes, factors or products of a biochemical network, in which X₁, …, X_n denote n dependent variables (intermediate metabolites and products) and X_n₊₁, …, X_n₊_m denote the independent variables (initial reactants and enzymes). Ẋ_i, the rate of change in X_i, represents concentration change of a dependent variable due to production (accumulation) or degradation (clearance). Each term is the product of the rate constant, α_i or β_i, which is positive or zero and all dependent and independent variables that affect directly the production and degradation reaction, respectively.

Each variable X_j is raised to the power of a kinetic parameter g_ij and h_ij, which represents that X_j activates (inhibits) X_i when its value is positive (negative). The rate constants α_i and β_i and kinetic parameters g_ij and h_ij are related to the characteristics of the biochemical network. The nonlinear Equation (1) describes the dynamic evolution among dependent variables. How to construct the S-system representation of a biochemical network and how to estimate its parameters from experimental data can be found in the classic textbooks (Savageau, 1976; Voit, 2000) and references therein. Recently, the nonlinear parameter estimation problem of S-systems has been efficiently solved by evolution optimization methods (Tsai and Wang, 2005; Ko et al. 2006).

Measuring directly the robustness of the nonlinear system in Equation (1) is difficult most of the time. Fortunately, the phenotype (metabolite concentration values) of a biochemical network is close to the steady state, i.e. the transient time to dynamic equilibrium is short enough in the real world and the steady state of biochemical networks can be analyzed by simple algebraic methods. Therefore, we shall focus on the robustness of a biochemical network at steady state in this paper.

Consider the steady state of biochemical network in Equation (1), i.e. the production and degradation of each dependent variable is balanced (Voit, 2000).

α_{i} \prod_{j = 1}^{n + m} X_{j}^{g_{i j}} = β_{i} \prod_{j = 1}^{n + m} X_{j}^{h_{i j}}, i = 1, 2, \dots, n

(2)

Taking the logarithm on both sides of Equation (2), we obtain

\begin{array}{l} ln α_{i} + \sum_{j = 1}^{n + m} g_{i j} ln X_{j} = ln β_{i} + \sum_{j = 1}^{n + m} h_{i j} ln X_{j}, \\ i = 1, 2, \dots, n \end{array}

(3)

After some rearrangements, we get

\begin{array}{l} \sum_{j = 1}^{n} (g_{i j} - h_{i j}) ln X_{j} = ln β_{i} - ln α_{i} \\ - \sum_{j = n + 1}^{n + m} (g_{i j} - h_{i j}) ln X_{j}, \\ i = 1, 2, \dots, n \end{array}

(4)

Introduce new variables and coefficients as follows:

y_{j} = ln X_{j}, a_{i j} = g_{i j} - h_{i j}, b_{i} - ln (\frac{β_{i}}{α_{i}})

(5)

The steady state of a biochemical system is written in n linear equations in terms of n + m variables as follows (Voit, 2000)

\begin{array}{l} a_{11} y_{1} + a_{12} y_{2} + \dots\dots + a_{1 n} y_{n} = b_{1} - a_{1, n + 1} y_{n + 1} \\ - \dots\dots - a_{1, n + m} y_{n + m} \\ a_{21} y_{1} + a_{22} y_{2} + \dots\dots + a_{2 n} y_{n} = b_{2} - a_{2, n + 1} y_{n + 1} \\ - \dots\dots - a_{2, n + m} y_{n + m} \\ a_{31} y_{1} + a_{32} y_{2} + \dots\dots + a_{3 n} y_{n} = b_{3} - a_{3, n + 1} y_{n + 1} \\ - \dots\dots - a_{3, n + m} y_{n + m} \\ ⋮ \\ a_{n 1} y_{1} + a_{n 2} y_{2} + \dots\dots + a_{n n} y_{n} = b_{n} - a_{n, n + 1} y_{n + 1} \\ - \dots\dots - a_{n, n + m} y_{n + m} \end{array}

(6)

In Equation (6), the dependent variables are separated from the independent variables. Let us denote

\begin{array}{c} Y_{D} = [\begin{array}{c} y_{1} \\ ⋮ \\ y_{n} \end{array}], b = [\begin{array}{c} b_{1} \\ ⋮ \\ b_{n} \end{array}], Y_{I} = [\begin{array}{c} y_{n + 1} \\ ⋮ \\ y_{n + m} \end{array}] \\ A_{D} = [\begin{array}{c} a_{11} & \dots & a_{1 n} \\ ⋮ & ⋱ & ⋮ \\ a_{n 1} & \dots & a_{n n} \end{array}], A_{I} = [\begin{array}{c} a_{1, n + 1} & \dots & a_{1, n + m} \\ ⋮ & ⋱ & ⋮ \\ a_{n, n + 1} & \dots & a_{n, n + m} \end{array}] \end{array}

where A_D denotes the system matrix of the catalytic interactions among dependent variables and A₁ indicates the catalytic interactions between the dependent variables Y_D and the independent variables Y₁ (i.e. environmental medium to the metabolic system). We then obtain the steady-state equation in the nominal parameter case as follows

A_{D} Y_{D} = b - A_{I} Y_{I}

(7)

Natural Selection Criteria for Biochemical Networks in Evolution

From Equation (7), if the inverse of A_D exists, then Y_D can be solved uniquely. It means that the biochemical network will result in only one steady state as long as $A_{D}^{- 1}$ exists. The assumption makes sense and agrees with the real biochemical networks. The steady state (or phenotype) of the biochemical network is solved as follows (Voit, 2000):

Y_{D} = A_{D}^{- 1} (b - A_{I} Y_{I})

(8)

Biochemical systems perform their physiological function within some local region in system parameter space in the evolutionary process. They tend to be robust to local changes in the values of the parameters that define the system in Equation (8). In the evolutionary process, suppose that some parameter variations Δα, Δβ, Δh, Δg and ΔY_I, which could be considered as design parameters in the evolutionary process owing to genetic mutations or environmental changes, alter the kinetic properties of a biochemical network in comparison with the nominal kinetic parameter case in Equation (7) as follows:

\begin{array}{l} (A_{D} + Δ A_{D}) (Y_{D} + Δ Y_{D}) = (b + Δ b) \\ - (A_{I} + Δ A_{I}) (Y_{I} + Δ Y_{I}) \end{array}

(9)

where the parameter variations of the biochemical network are defined by

\begin{array}{l} Δ A_{D} = [\begin{array}{c} Δ a_{11} & \dots & Δ a_{1 n} \\ ⋮ & Δ a_{i j} & ⋮ \\ Δ a_{n 1} & \dots & Δ a_{n n} \end{array}] \\ = [\begin{array}{c} Δ g_{11} - Δ h_{11} & \dots & Δ g_{1 n} - Δ h_{1 n} \\ ⋮ & Δ g_{i j} - Δ h_{i j} & ⋮ \\ Δ g_{n 1} - Δ h_{n 1} & \dots & Δ g_{n n} - Δ h_{n n} \end{array}], \\ Δ Y_{D} = [\begin{array}{c} Δ y_{1} \\ ⋮ \\ Δ y_{n} \end{array}] \\ Δ A_{I} = [\begin{array}{c} Δ g_{1, n + 1} - Δ h_{1, n + 1} & \dots \\ ⋮ & Δ g_{i, n + j} - Δ h_{i, n + j} \\ Δ g_{n, n + 1} - Δ h_{n, n + 1} & \dots \end{array} \\ \begin{array}{c} Δ g_{1, n + m} - Δ h_{1, n + m} \\ ⋮ \\ Δ g_{n, n + m} - Δ h_{n, n + m} \end{array}], Δ Y_{I} = [\begin{array}{c} Δ y_{n + 1} \\ ⋮ \\ Δ y_{n + m} \end{array}], \\ Δ b = [\begin{array}{c} Δ b_{1} \\ ⋮ \\ Δ b_{n} \end{array}] \end{array}

ΔA_D denotes the kinetic parameter variations owing to the kinetic parameter variations Δg_ij and Δh_ij within dependent variables; Δb denotes the parameter variations owing to rate constant variations and ΔA_I denotes the kinetic parameter variations owing to the kinetic parameter variations Δg_ij and Δh_ij between independent and dependent variables. ΔY_I denotes the concentration variations of environmental factors. ΔY_D is a perturbation effect which may lead to new steady state. Y_D+ΔY_D may own a little difference from the nominal phenotype Y_D if these variations could be tolerated by the biochemical network.

The robustness analysis of a biochemical network in this study is to check the tolerance for kinetic parameter variations with respect to the maintenance of normal physiological function of perturbed biochemical networks in the evolutionary process. First, the ΔA_D will influence the existence of the steady state. Then, the variations Δb, ΔA_I and ΔY_I will influence the sensitivity of biochemical networks to the environmental variations in the evolutionary process. The effects of these parameter variations (i.e. the design parameter space in evolution) on the biochemical network at the steady state (i.e. Ẋ_i = 0) will be discussed in the following paragraphs.

Equation (9) is equivalent to

\begin{array}{l} A_{D} (I + A_{D}^{- 1} Δ A_{D}) (Y_{D} + Δ Y_{D}) = (b + Δ b) \\ - (A_{I} + Δ A_{I}) (Y_{I} + Δ Y_{I}) \end{array}

(10)

By the similar analysis from Equation (7) to Equation (8), one can show that the condition that the system in Equation (10) can be solved uniquely is the existence of the inverse of $(I + A_{D}^{- 1} Δ A_{D})$ . It has been shown that if the following robustness criterion holds (Gill et al. 1991; Weinmann, 1991; Nobel and Daniel, 1998; Chen et al. 2005)

‖ A_{D}^{- 1} Δ A_{D} ‖_{2} < 1 o r Δ A_{D} Δ A_{D}^{T} < A_{D} A_{D}^{T}

(11)

the inverse ${(I + A_{D}^{- 1} Δ A_{D})}^{- 1}$ exists and the phenotype (steady state) of the perturbed biochemical network in Equation (10) is uniquely solved as follows

\begin{array}{l} Y_{D} + Δ Y_{D} = {(I + A_{D}^{- 1} Δ A_{D})}^{- 1} A_{D}^{- 1} [(b + Δ b) \\ - (A_{I} + Δ A_{I}) (Y_{I} + Δ Y_{I})] \end{array}

(12)

The physical meaning of Equation (11) and (12) is that if the inverse ${(I + A_{D}^{- 1} Δ A_{D})}^{- 1}$ exists, the phenotype can be preserved with some variation under this parameter variation ΔA_D, i.e. if the robustness criterion in Equation (11) is satisfied, the parameter variations ΔA_D can be tolerated by the system structure of the biochemical network A_D in the evolutionary process and the biochemical network tends to be robust to local changes in the values of parameters that define the system. Otherwise, the parameters reach a threshold beyond which the behavior of the biochemical network changes dramatically and the phenotype may cease to exist, i.e. the individuals with parameter variations (design parameters in evolution) that violate the robustness criterion in Equation (11) will be eliminated by natural selection. Therefore, the perturbed biochemical network should satisfy the robustness criterion in order to guarantee the existence of its dynamic equilibrium (for the normal physiological function) in the evolutionary process. Because the violation of Equation (11) means a lethal perturbation, it is the necessary condition to survive under natural selection. From the robustness criterion in Equation (11), natural selection favors the perturbed biochemical networks with small perturbations ΔA_D $Δ A_{D}^{T}$ or a large system structure stability matrix A_D $A_{D}^{T}$ so that the robustness criterion is not violated. A biochemical network with redundancy and self-regulation can attenuate perturbations ΔA_D and a biochemical network with adequate negative feedbacks can increase A_D $A_{D}^{T}$ to tolerate large parameter variations in the evolutionary process. These robust adaptive designs are favored by natural selection in the evolutionary process of biochemical networks. This is why there are so much redundancy due to duplicated genes, modularity, self-regulation and feedback circuits in the biochemical networks in nature (Isaacs et al. 2003; Langkjaer et al. 2003; Kellis et al. 2004; Teichman and Babu, 2004).

However, the satisfaction of the robustness criterion in Equation (11), i.e. the parameter variations ΔA_D ${ΔA}_{D}^{T}$ is bounded by the system structure matrix A_D $A_{D}^{T}$ does not always mean the perturbed biochemical network will survive in evolution because it only guarantees the existence of the steady state. But the phenotype (steady state) may be far from the nominal value for the normal physiological function. In order to play its proper role in the corresponding physiological system, its metabolite concentration values should not change too much from the nominal value. In this situation, the biochemical network should be less sensitive to the other parameter variations and environmental changes. This is the sufficient condition for natural selection for a perturbed biochemical network to survive under natural selection. In the above robust analysis, we only discussed the effect of kinetic parameter variations ΔA_D on the existence of the steady state of a biochemical network. Now, let us consider the sensitivities to the variations of the other parameters Δb, ΔA_I and the change of the environment ΔY_I in the evolutionary process.

The changes Δb, ΔY_I, and ΔA_I will influence the variations of steady states Y_D. Their effects on Y_D have been discussed by the sensitivity analysis of biochemical network (Savageau, 1971; Ni and Savageau, 1996a,b; Voit, 2000), i.e.

\frac{Δ Y_{D}}{Δ b} = A_{D}^{- 1}, \frac{Δ Y_{D}}{Δ Y_{I}} = - A_{D}^{- 1} A_{I}, \frac{Δ Y_{D}}{Δ A_{I}} = - A_{D}^{- 1} Y_{I}

(13)

In order to tolerate the variations Δb, ΔY_I and ΔA_I to preserve the phenotype of the biochemical network in the evolutionary process, the sensitivities in Equation (13) should be below some values as follows

{‖ \frac{Δ Y_{D}}{Δ b} ‖}_{2} \leq s_{1}, {‖ \frac{Δ Y_{D}}{Δ Y_{I}} ‖}_{2} \leq s_{2}, {‖ \frac{Δ Y_{D}}{Δ A_{I}} ‖}_{2} \leq s_{3}

(14)

where s₁, s₂ and s₃ are some small sensitivity values so that the phenotypes of perturbed biochemical networks would not change too much in comparison with the nominal values in Equation (13) and can be favored by natural selection, i.e. the sensitivity criterion in Equation (14) can be considered as the sufficient condition of natural selection for biochemical network evolution. In general, the sensitivities s₁, s₂ and s₃ are chosen as the sensitivities at the nominal case, because the nominal (healthy) biochemical network is less-sensitive to parameter variations and environmental changes. Based on Equation (13), Equation (14) can be written in the following equivalent form,

\begin{array}{l} I \leq s_{1}^{2} A_{D} A_{D}^{T}, A_{I} A_{I}^{T} \leq s_{2}^{2} A_{D} A_{D}^{T}, \\ Y_{I} Y_{I}^{T} \leq s_{3}^{2} A_{D} A_{D}^{T} \end{array}

(15)

That is, Equation (15) determines the ranges of the sensitivities of Y_D to parameter variations and environmental changes by natural selection in the evolutionary process. For a functional biochemical network, it should satisfy the sensitivity criteria in Equation (15) to confine the metabolite concentration values not to be changed too much. Hence, the steady state (phenotype) of a biochemical network can be preserved while exposing the parameter variations and environmental changes to natural selection in the evolutionary process. This can be considered as a sufficient condition for survival for the biochemical network.

The robustness criterion in Equation (11) and the sensitivity criterion in Equation (15) are together considered as the criteria of natural selection in evolution. If one of them is violated, it will lead to the dysfunction of the biochemical network and the perturbed biochemical network will be eliminated by natural selection. Therefore, the robustness criterion in Equation (11) and the sensitivity criterion in Equation (15) could be considered as the adaptive design rules of biochemical networks by natural selection in the evolutionary process. The specifications of sensitivities s_i, i = 1, 2, 3 in Equation (15) are species by species. In general, these sensitivities should be small in order to avoid too much influence from the environmental disturbances in the evolutionary process.

Remark 1

The equality for robustness criterion in Equation (11) can not hold because it may make $I + A_{D}^{- 1} Δ A_{D}$ singular (for example $A_{D}^{- 1}$ ΔA_D=−I) and the steady will cease to exist. However, the equality could hold in Equation (14) because we do not want the sensitivities of perturbed systems to be larger than the sensitivities of the nominal system, which has no singular problem.
Actually, the sensitivity matrices in Equation (13) hold if all the perturbations Δb, ΔY_I, ΔA_I are very small (Voit, 2000) (it was originally derived by $\frac{\partial Y_{D}}{\partial b} = A_{D}^{- 1}$ , $\frac{\partial Y_{D}}{\partial Y_{I}} = - A_{D}^{- 1} A_{I}$ , $\frac{\partial Y_{D}}{\partial A_{I}} = - A_{D}^{- 1} Y_{I}$ . For the convenience of discussion on perturbations, it was modified to the form in Equation (13)). If some perturbations are large, the equalities may be violated. One proposition of Theory of Evolution is that “Gradual evolution results from small genetic changes that are acted upon by natural selection” (Freeman and Herron, 2001). Obviously, in evolutionary process, Δb, ΔY_I, ΔA_I are all assumed to be small in every change. In this situation, the equalities in Equation (13) always hold.
The assumption that the three sensitivity inequalities in Equation (14) all hold for natural selection is based on the fact that biochemical networks are the backbones of physiological systems and can not be too sensitive to environmental changes especially for some core (conserved) biochemical networks. If some sensitivity criteria in Equation (14) are relaxed, i.e. some of inequalities in Equation (14) are violated, the phenotypes with changes to some environmental variation will also be favored by natural selection. In this situation, the phenotypes of biochemical networks are much influenced by environmental variation that they may be more adaptive to the environmental changes in the evolutionary process. In this case, new phenotypes are more easily generated to adapt the new environment. They will be discussed in the sequel.

Computational Examples

An example is given below to illustrate the mathematical adaptive design rules of biochemical networks by natural selection in the evolutionary process. Consider the following biochemical network (Savageau, 1976; Voit, 2000).

\begin{array}{l} {\dot{X}}_{1} = 10 X_{2}^{- 0.1} X_{3}^{- 0.05} X_{4} - 5 X_{1}^{0.5}, & X_{1} (0) = 0.2 \\ {\dot{X}}_{2} = 2 X_{1}^{0.5} - 1.44 X_{2}^{0.5}, & X_{2} (0) = 0.5 \\ {\dot{X}}_{3} = 3 X_{2}^{0.5} - 7.2 X_{3}^{0.5}, & X_{3} (0) = 0.1, \\ X_{4} = 0.75 \end{array}

(16)

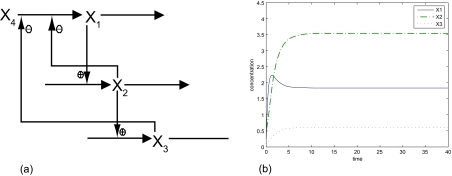
The biochemical network and its time responses are shown in Figure 1.

Suppose the biochemical network suffers the following four parameter variations due to genetic mutations in the evolutionary process.

\begin{array}{l} Δ A_{D_{1}} = [\begin{array}{c} 0 & 0 & 0 \\ 0 & 0.2826 & 0.3 \\ 0 & 0 & 0.0914 \end{array}], \\ Δ A_{D_{2}} = [\begin{array}{c} 0.3 & 0 & 0.05 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}] \end{array}

(17)

\begin{array}{l} Δ A_{D_{3}} = [\begin{array}{c} 0.04675 & 0 & 0 \\ 0 & - 0.11 & - 0.1 \\ - 0.31 & 0.06494 & 0.0914 \end{array}], \\ Δ A_{D_{4}} = [\begin{array}{c} 0 & 0 & 0 \\ 0 & 0 & - 0.43 \\ 0 & 0 & 0 \end{array}] \end{array}

(18)

The biochemical network in Equation (16) is then perturbed to the following four networks:

(I) {\begin{cases} {\dot{X}}_{1} = 10 X_{2}^{- 0.1} X_{3}^{- 0.05} X_{4} - 5 X_{1}^{0.5}, & X_{1} (0) = 0.2 \\ {\dot{X}}_{2} = 2 X_{1}^{0.5} \underline{X_{3}^{0.3}} - 1.44 X_{2}^{\underline{0.2174}}, & X_{2} (0) = 0.5 \\ {\dot{X}}_{3} = 3 X_{2}^{0.5} - 7.2 X_{3}^{\underline{0.4086}}, & X_{3} (0) = 0.1, \\ X_{4} = 0.75 \end{cases}

(19)

(I I) {\begin{cases} {\dot{X}}_{1} = 10 X_{2}^{- 0.1} X_{3}^{\underline{0}} X_{4} - 5 X_{1}^{\underline{0.2}}, & X_{1} (0) = 0.2 \\ {\dot{X}}_{2} = 2 X_{1}^{0.5} - 1.44 X_{2}^{0.5}, & X_{2} (0) = 0.5 \\ {\dot{X}}_{3} = 3 X_{2}^{0.5} - 7.2 X_{3}^{0.5}, & X_{3} (0) = 0.1, \\ X_{4} = 0.75 \end{cases}

(20)

(I I I) {\begin{cases} {\dot{X}}_{1} = 10 X_{2}^{- 0.1} X_{3}^{- 0.05} X_{4} - 5 X_{1}^{\underline{0.45325}}, \\ X_{1} (0) = 0.2 \\ {\dot{X}}_{2} = 2 X_{1}^{0.5} \underline{X_{3}^{- 0.1}} - 1.44 X_{2}^{\underline{0.61}}, \\ X_{2} (0) = 0.5 \\ {\dot{X}}_{3} = 3 X_{2}^{\underline{0.56494}} \underline{X_{1}^{- 0.31}} - 7.2 X_{3}^{\underline{0.4086}}, \\ X_{3} (0) = 0.1, X_{4} = 0.75 \end{cases}

(21)

(I V) {\begin{cases} {\dot{X}}_{1} = 10 X_{2}^{- 0.1} X_{3}^{- 0.05} X_{4} - 5 X_{1}^{0.5}, & X_{1} (0) = 0.2 \\ {\dot{X}}_{2} = 2 X_{1}^{0.5} \underline{X_{3}^{- 0.43}} - 1.44 X_{2}^{0.5}, & X_{2} (0) = 0.5 \\ {\dot{X}}_{3} = 3 X_{2}^{0.5} - 7.2 X_{3}^{0.5}, & X_{3} (0) = 0.1, \\ X_{4} = 0.75 \end{cases}

(22)

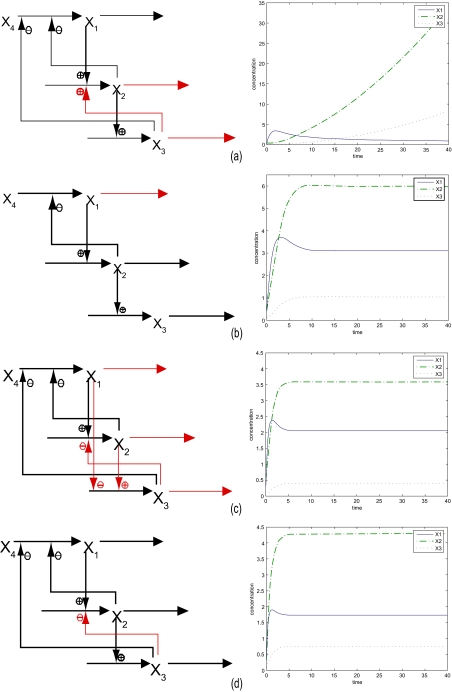
The perturbed biochemical networks and their time responses are shown in Figure 2. Suppose the sensitivity criteria s₁, s₂ and s₃ in Equation (15) are chosen as the sensitivities of the nominal biochemical network in Equation (13), i.e. $s_{1} = {‖ A_{D}^{- 1} ‖}_{2}$ , $s_{2} = {‖ A_{D}^{- 1} A_{I} ‖}_{2}$ and $s_{3} = {‖ A_{D}^{- 1} Y_{I} ‖}_{2}$ . That is to say, the perturbed networks to be selected by natural selection should have less sensitivities than the nominal biochemical network. By the adaptive design rules based on robustness and sensitivity criteria, the perturbed biochemical network (I) in Equation (19) violates the robustness criterion in Equation (11) and the parameter variations ΔA_D₁ can not be tolerated by the biochemical network. In this situation, the biochemical network (I) will be eliminated by natural selection without consideration of sensitivities. More precisely, the set of parameter variations ΔA_D₁ due to mutations is lethal. Though the biochemical network (II) in Equation (20) satisfies the robustness criterion in Equation (11), its steady state is farther from nominal value and violates sensitivity criterion in Equation (15). It means that the phenotype of biochemical network (II) is easier (more sensitive) to be destroyed while exposing to environmental disturbances, i.e. ΔA_I, Δb or ΔY_I due to environmental changes. Hence, there is a large probability that the biochemical network (II) will be eliminated by natural selection. More precisely, the parameter variations due to mutations ΔA_D_₂ are not lethal, but the biochemical network is susceptible to environmental disturbances for species evolution or diseases such as virus infection, i.e. less immunity for individuals.

From Figure 2, it is seen that the steady states, Y_D_₃ + ΔY_D_₃ and Y_D₄ + ΔY_D_₄, of biochemical network (III) in Equation (21) and biochemical network (IV) in Equation (22), respectively, are all close to the nominal values of the steady state in the nominal biochemical network of Equation (16) in Figure 1. In addition, the robustness criterion in Equation (11) and the sensitivity criterion in Equation (15) are all satisfied so that the variations ΔA_D₃ and ΔA_D₄, Δb₃ and Δb₄, ΔA_I₃ and ΔA_I₄ as well as environmental disturbances ΔY_I₃ and ΔY_I₄ do not affect the normal function of the biochemical networks too much. In other words, the biochemical networks (III) and (IV) are robust to intrinsic parameter variations and less sensitive to environmental variations, so that the two biochemical networks must be more favored by natural selection. In the next generation, the other perturbed biochemical networks will be selected by natural selection with the same procedure. This co-option of existing biochemical networks to new networks by natural selection is considered one of the crucial features in the evolutionary procedure. Several biochemical networks combined with negative and positive feedback loops are robust against parameter variations and environmental disturbances so that normal cellular physiological and developmental processes can be maintained. This intrinsic robustness and sensitivity of the biochemical network enable co-option, so that the new phenotypes can be generated by natural selection (Kitano, 2004). Therefore, the robustness criterion in Equation (11) and sensitivity criterion in Equation (15) can be viewed as the mathematical adaptive design rules of natural selection.

From Table 1, we can find that the sensitivities of biochemical network (III) and biochemical network (IV) are both smaller than the nominal one. That is, there is a high probability that the mutated biochemical networks with smaller sensitivities s₁, s₂ and s₃ can prevail under natural selection. The sensitivities of biochemical networks in Equations (16), (19), (20), (21) and (22) are listed in Table 1.

Table 1.

The sensitivities of nominal and perturbed biochemical networks.

Biochemical networks	s₁	s₂	s₃
Biochemical network in Equation (16)	3.4191	2.6647	2.5643
Biochemical network (I) in Equation (19)	217.05	140.14	162.78
Biochemical network (II) in Equation (20)	6.0274	5.7735	4.5206
Biochemical network (III) in Equation (21)	2.8203	2.3801	2.1152
Biochemical network (IV) in Equation (22)	2.276	2.1635	1.707

Open in a new tab

Diversity of Biochemical Network within Organisms or Individuals in Evolution

There are many perturbed biochemical networks that can satisfy the adaptive design rules of natural selection in Equations (11) and (15) to survive in the evolutionary process. If they are all selected by natural selection, there will be some differences in phenotype (see Equation (12)) among these selected biochemical networks. However, as the values of parameters continue to change, they reach a threshold (i.e. the robustness criterion in Equation (11) is violated) beyond which the behavior of the biochemical network changes dramatically. It may thus settle in a new local region of another steady state with a different set of behaviors, or it may become completely dysfunctional and not survive under natural selection in evolution.

After several generations in the evolutionary process, due to co-option of existing biochemical networks to new networks, diversities of biochemical networks with conserved physiological function but with different structures will be developed (Freeman, 2000). However, if the requirements on the robustness in Equations (11) and the sensitivity in Equations (15) are more strict (or more conservative), only few solutions (or structures) can be selected by the natural selection to meet these requirements. This is the reason why a conserved core biochemical network has less diversity (Kitano, 2004). For examples, in the evolutionary process of the TCA cycle, the pentosephosphate pathway and the glycolysis pathway in different species, their final products are almost the same from yeast to human. However, their biochemical networks have some differences in intermediary biochemistry reactions. From the simulation examples of perturbed biochemical networks in Equation (19), (20), (21) and (22), the perturbed biochemical networks (III) and (IV) in Equations (21) and (22), which are shown in Figure 2c and 2d, respectively, can be seen as the diversities of the biochemical network in the evolutionary process.

Remark 2

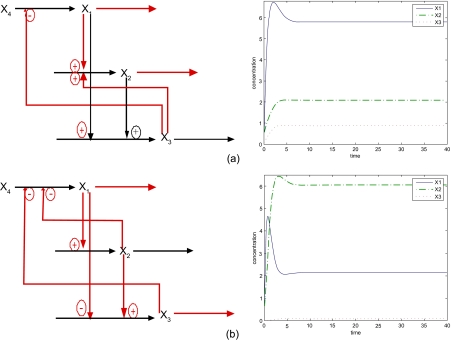
Since the violation of sensitivity criteria of natural selection in Equation (15) is not lethal, the relaxation of some sensitivity inequalities in natural selection will make biochemical networks more easily adapt to new environmental changes. For example in Figure 3a and 3b, suppose the biochemical network suffers ΔA_D_₅ and ΔA_D_₆, respectively, due to genetic mutations in the evolutionary process in Equation (23), the biochemical network in Equation (16) is then perturbed to the (V) and (VI) network in Equation(24) and (25), respectively. In the former case, the second sensitivity criterion in Equation (15) is violated. The biochemical network will adapt to the environment with large variation ΔY_I in evolution. In the latter case, the first and third sensitivity criteria are relaxed. The biochemical network will adapt to an environment with large variation in Δb and ΔA_I. The sensitivities of biochemical networks in Equation (24) and (25) are listed in Table 2.

\begin{array}{l} Δ A_{D 5} = [\begin{array}{c} 0.25 & 0.1 & - 0.2 \\ - 0.25 & - 0.5 & 0.25 \\ 0.25 & 0 & 0 \end{array}], \\ Δ A_{D 6} = [\begin{array}{c} - 0.25 & - 0.15 & - 0.2 \\ 0.25 & 0 & 0 \\ - 0.25 & - 0.25 & 0.25 \end{array}] \end{array}

(23)

(V) {\begin{cases} {\dot{X}}_{1} = 10 X_{2}^{\underline{0}} X_{3}^{\underline{- 0.25}} X_{4} - 5 X_{1}^{\underline{0.25}}, & X_{1} (0) = 0.2 \\ {\dot{X}}_{2} = 2 X_{1}^{\underline{0.25}} \underline{X_{3}^{0.25}} - 1.44 X_{2}^{\underline{1}}, & X_{2} (0) = 0.5 \\ {\dot{X}}_{3} = 3 X_{2}^{0.5} \underline{X_{1}^{0.25}} - 7.2 X_{3}^{0.5}, & X_{3} (0) = 0.1, \\ X_{4} = 0.75 \end{cases}

(24)

(V I) {\begin{cases} {\dot{X}}_{1} = 10 X_{2}^{\underline{- 0.25}} X_{3}^{\underline{- 0.25}} X_{4} - 5 X_{1}^{\underline{0.75}}, & X_{1} (0) = 0.2 \\ {\dot{X}}_{2} = 2 X_{1}^{\underline{0.75}} - 1.44 X_{2}^{0.5}, & X_{2} (0) = 0.5 \\ {\dot{X}}_{3} = 3 X_{2}^{\underline{0.25}} \underline{X_{1}^{- 0.25}} - 7.2 X_{3}^{\underline{0.25}}, & X_{3} (0) = 0.1, \\ X_{4} = 0.75 \end{cases}

(25)

Figure 3. — The perturbed biochemical networks and their time responses. (a) Biochemical network (V) in Equation (24) and its time responses. (b) Biochemical network (VI) in Equation (25) and its time responses. The biochemical network V will adapt to the environment with large variation ΔY_I in evolution. The biochemical network will adapt to an environment with large variation in Δb and ΔA_I.

Table 2.

The sensitivities of nominal and perturbed biochemical networks.

Biochemical networks	s₁	s₂	s₃
Biochemical network in Equation (16)	3.4191	2.6647	2.5643
Biochemical network in Figure 3a	3.0248	3	2.2686
Biochemical network in Figure 3b	4.1534	1.4967	3.1151

Open in a new tab

Conclusion

From the biochemical network evolution point of view, a biochemical network should be robust enough to maintain its proper role in the physiological system under parameter variations due to mutations and environmental disturbances. On the basis of stability robustness and less sensitivity to the effects of genetic mutations and environmental variations, the proposed design rules (robustness and sensitivity criteria) are developed as the underlying mathematical adaptive design principles of natural selection in the biochemical network evolution. That is, in the evolutionary process, organism enhances the structure stability by feedback or feedforward circuits to improve the robustness of a biochemical network to tolerate parameter variations or compensates the effect of external or internal perturbations. The self-regulation and redundancy are of this kind of robust design favored by natural selection in the evolutionary process (Becskei and Serrano, 2000; Issacs et al. 2003). Therefore, in the evolutionary process of biochemical networks, robustness is the maintenance of specific functionalities of the network against perturbations, and it often requires the biochemical network to change its mode of operation in a flexible way. In other words, robustness allows changes in the structure and components of the biochemical network (the so-called adaptive design) owing to parameter perturbation and environmental disturbances, but specific functions are maintained. Because there are several solutions that can meet the robustness and sensitivity criteria of the adaptive design rules by natural selection, this is the origin of diversities of the biochemical networks within organisms or individuals in evolution. These adaptive design rules incurring robustness of biochemical networks actually facilitate evolution, and evolution favors robust biochemical network. Therefore, requirements for robustness and evolvability are similar in biochemical networks. This implies that there are architectural requirements for biochemical networks to be evolvable, which essentially require biochemical network to be robust against genetic perturbation and environmental disturbance (Kitano, 2004).

In this study, a mathematical modeling is provided for the robust adaptive design mechanism of biochemical networks in evolution. As the parameter variations of biochemical networks continue to increase in some local region, they will reach a threshold (i.e. the robustness criterion of natural selection is violated) beyond which the behavior of biochemical network will change dramatically. It may then settle in a local region of another steady state (phenotype) with a different set of behaviors, or it may become dysfunctional and can not persist in evolution. Furthermore, if some sensitivity criteria of natural selection are relaxed, biochemical networks will be more susceptible to the corresponding environmental changes and turn out to be preferred in a new environment.

By using in silico examples, an adaptive design rule of a biochemical network is revealed by the S-system dynamic model to illustrate the natural selection and diversification in evolution from the robustness and sensitivity point of views. This provides much insight into the evolutionary mechanism of biochemical networks from the system perspective, and the proposed deign rules by natural selection will highlight the robust biochemical circuit design methods of biochemical networks via inserting the binding sites of transcription factors to the regulated genes (Tsai et al. 2006) for biotechnological and therapeutic purpose in future (Savageau, 2001; Hasty et al. 2002; Kitano, 2002ab; Hood et al. 2004).

Acknowledgments

The authors gratefully acknowledge the financial support from the National Science Council of Taiwan under the contract NSC95-2221-E-007-196.

Footnotes

Please note that this article may not be used for commercial purposes. For further information please refer to the copyright statement at http://www.la-press.com/copyright.htm

References

Alon U, Surette MG, Barkai N, et al. Robustness in bacterial chemotaxis. Nature. 1999;397:168–171. doi: 10.1038/16483. [DOI] [PubMed] [Google Scholar]
Altamirano MM, Blackburn JM, Aguayo C, et al. Directed evolution of new catalytic activity using the α/β-barrel scaffold. Nature. 2000;403:617–622. doi: 10.1038/35001001. [DOI] [PubMed] [Google Scholar]
Barkai N, Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–917. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]
Becskei A, Serrano L. Engineering stability in gene networks by autoregulation. Nature. 2000;405:590–593. doi: 10.1038/35014651. [DOI] [PubMed] [Google Scholar]
Bulter T, Lee SG, Wong WW, et al. Design of artificial cell-cell communication using gene and metabolic networks. Proc. Natl. Acad. Sci. U.S.A. 2004;101:2299–2304. doi: 10.1073/pnas.0306484101. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen BS, Wang YC, Wu WS, et al. A new measure of the robustness of biochemical networks. Bioinformatics. 2005;21:2698–2705. doi: 10.1093/bioinformatics/bti348. [DOI] [PubMed] [Google Scholar]
Farmer WR, Liao JC. Improving lycopene production in Escherichia coli by engineering metabolic control. Nature Biotechnology. 2000;18:533–537. doi: 10.1038/75398. [DOI] [PubMed] [Google Scholar]
Freeman S, Herron JC. Evolutionary Analysis. 2nd ed. New Jersey: Prentice-Hall; 2001. [Google Scholar]
Freeman M. Feedback control of intercellular signalling in development. Nature. 2000;408:313–319. doi: 10.1038/35042500. [DOI] [PubMed] [Google Scholar]
Gill PE, Murray W, Wright MH. Numerical Linear Algebra and Optimization. Boston: Addison-Wesley, Reading; 1991. [Google Scholar]
Hasty J, McMillen D, Collins JJ. Engineered gene circuits. Nature. 2002;420:224–230. doi: 10.1038/nature01257. [DOI] [PubMed] [Google Scholar]
Hood L, Heath JR, Phelps ME, et al. Systems biology and new technologies enable predictive and preventative medicine. Science. 2004;306:640–643. doi: 10.1126/science.1104635. [DOI] [PubMed] [Google Scholar]
Isaacs FJ, Hasty J, Cantor CR, et al. Prediction and measurement of an autoregulatory genetic module. Proc. Natl. Acad. Sci. U.S.A. 2003;100:7714–7719. doi: 10.1073/pnas.1332628100. [DOI] [PMC free article] [PubMed] [Google Scholar]
Johannes TW, Woodyer RD, Zhao H. Directed evolution of a thermostable phosphite dehydrogenase for NAD(P)H regeneration. Appl. Environ Microbiol. 2005;71:5728–5734. doi: 10.1128/AEM.71.10.5728-5734.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kitano H. Computaional systems biology. Nature. 2002a;420:206–210. doi: 10.1038/nature01254. [DOI] [PubMed] [Google Scholar]
Kitano H. Systems biology: a brief overview. Science. 2002b;295:1662–1664. doi: 10.1126/science.1069492. [DOI] [PubMed] [Google Scholar]
Kitano H. Biological robustness. Nature Reviews Genetics. 2004;5:826–837. doi: 10.1038/nrg1471. [DOI] [PubMed] [Google Scholar]
Kellis M, Birren BW, Lander ES. Proof and evolutionary analysis of ancient genome duplication in yeast Saccharomyces cerevisiae. Nature. 2004;428:617–624. doi: 10.1038/nature02424. [DOI] [PubMed] [Google Scholar]
Ko CL, Wang FS, Chao YP, et al. S-System approach to modeling recombinant Escherichia coli growth by hybrid differential evolution with data collocation. Biochemical Engineering Journal. 2006;28:10–16. [Google Scholar]
Langkjaer RB, Cliften PF, Johnston M, et al. Yeast genome duplication was followed by asynchronous differentiation of duplicated gene. Nature. 2003;421:848–852. doi: 10.1038/nature01419. [DOI] [PubMed] [Google Scholar]
May O, Nguyen PT, Arnold FH. Inverting enantioselectivity by directed evolution of hydantoinaze for improved production of L-methionine. Nat. Biotechnol. 2000;18:317–320. doi: 10.1038/73773. [DOI] [PubMed] [Google Scholar]
Ni TC, Savageau MA. Model assessment and refinement using strategies from biochemical systems theory: application to metabolism in human red blood cells. J. Theor. Biol. 1996a;179:329–368. doi: 10.1006/jtbi.1996.0072. [DOI] [PubMed] [Google Scholar]
Ni TC, Savageau MA. Application of biochemical systems theory to metabolism in human red blood cells. Signal propagation and accuracy of representation. J. Biol. Chem. 1996b;271:7927–7941. doi: 10.1074/jbc.271.14.7927. [DOI] [PubMed] [Google Scholar]
Nobel B, Daniel JW. Applied Linear Algebra. New Jersey: Prentice-Hall; Englewood Cliffs: 1988. [Google Scholar]
Savageau MA. Parameter sensitivity as a criterion for evaluating and comparing the performance of biochemical systems. Nature. 1971;229:542–544. doi: 10.1038/229542a0. [DOI] [PubMed] [Google Scholar]
Savageau MA. Biochemical Systems Analysis: a study of function and design in molecular biology. Boston: Addisson-Wesley, Reading; 1976. [Google Scholar]
Savageau MA. Design principles for elementary gene circuits: Elements, methods, and examples. Chaos. 2001;11:142–159. doi: 10.1063/1.1349892. [DOI] [PubMed] [Google Scholar]
Teichmann SA, Babu MM. Gene regulatory network growth by duplication. Nature Genet. 2004;36:492–496. doi: 10.1038/ng1340. [DOI] [PubMed] [Google Scholar]
Tsai HK, Huang TW, Lu HS, et al. Method for identifying transcription factor binding sites in yeast. Bioinformatics. 2006;22:1675–1681. doi: 10.1093/bioinformatics/btl160. [DOI] [PubMed] [Google Scholar]
Tsai KY, Wang FS. Evolutionary optimization with data collocation for reverse engineering of biological networks. Bioinformatics. 2005;21:1180–1188. doi: 10.1093/bioinformatics/bti099. [DOI] [PubMed] [Google Scholar]
Tsuji T, Onimaru M, Yanagawa H. Towards the creation of novel proteins by block shuffling. Combinatorial Chemistry and High Throughput Screening. 2006;9:259–269. doi: 10.2174/138620706776843237. [DOI] [PubMed] [Google Scholar]
Voit EO. Computational Analysis of Biochemical Systems. Cambridge: Cambridge University Press; 2000. [Google Scholar]
Wang CW, Oh MK, Liao JC. Directed evolution of metabolically engineered Escherichia coli for carotenoid production. Biotechnol. Prog. 2000;16:922–926. doi: 10.1021/bp000124f. [DOI] [PubMed] [Google Scholar]
Weinmann A. Uncertain Model and Robust Control. New York: Springer; 1991. [Google Scholar]
West-Eberhard MJ. Developmental Plasticity and Evolution. New York: Oxford University Press; 2003. [Google Scholar]
Yi TM, Huang Y, Simon MI, et al. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. U.S.A. 2000;97:4649–4653. doi: 10.1073/pnas.97.9.4649. [DOI] [PMC free article] [PubMed] [Google Scholar]
Yuan L, Kurek I, English J. Laboratory-directed protein evolution microbiol. Mol. Biol. Rev. 2005;69:373–392. doi: 10.1128/MMBR.69.3.373-392.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b1-ebo-03-27] Alon U, Surette MG, Barkai N, et al. Robustness in bacterial chemotaxis. Nature. 1999;397:168–171. doi: 10.1038/16483. [DOI] [PubMed] [Google Scholar]

[b2-ebo-03-27] Altamirano MM, Blackburn JM, Aguayo C, et al. Directed evolution of new catalytic activity using the α/β-barrel scaffold. Nature. 2000;403:617–622. doi: 10.1038/35001001. [DOI] [PubMed] [Google Scholar]

[b3-ebo-03-27] Barkai N, Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–917. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]

[b4-ebo-03-27] Becskei A, Serrano L. Engineering stability in gene networks by autoregulation. Nature. 2000;405:590–593. doi: 10.1038/35014651. [DOI] [PubMed] [Google Scholar]

[b5-ebo-03-27] Bulter T, Lee SG, Wong WW, et al. Design of artificial cell-cell communication using gene and metabolic networks. Proc. Natl. Acad. Sci. U.S.A. 2004;101:2299–2304. doi: 10.1073/pnas.0306484101. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b6-ebo-03-27] Chen BS, Wang YC, Wu WS, et al. A new measure of the robustness of biochemical networks. Bioinformatics. 2005;21:2698–2705. doi: 10.1093/bioinformatics/bti348. [DOI] [PubMed] [Google Scholar]

[b7-ebo-03-27] Farmer WR, Liao JC. Improving lycopene production in Escherichia coli by engineering metabolic control. Nature Biotechnology. 2000;18:533–537. doi: 10.1038/75398. [DOI] [PubMed] [Google Scholar]

[b8-ebo-03-27] Freeman S, Herron JC. Evolutionary Analysis. 2nd ed. New Jersey: Prentice-Hall; 2001. [Google Scholar]

[b9-ebo-03-27] Freeman M. Feedback control of intercellular signalling in development. Nature. 2000;408:313–319. doi: 10.1038/35042500. [DOI] [PubMed] [Google Scholar]

[b10-ebo-03-27] Gill PE, Murray W, Wright MH. Numerical Linear Algebra and Optimization. Boston: Addison-Wesley, Reading; 1991. [Google Scholar]

[b11-ebo-03-27] Hasty J, McMillen D, Collins JJ. Engineered gene circuits. Nature. 2002;420:224–230. doi: 10.1038/nature01257. [DOI] [PubMed] [Google Scholar]

[b12-ebo-03-27] Hood L, Heath JR, Phelps ME, et al. Systems biology and new technologies enable predictive and preventative medicine. Science. 2004;306:640–643. doi: 10.1126/science.1104635. [DOI] [PubMed] [Google Scholar]

[b13-ebo-03-27] Isaacs FJ, Hasty J, Cantor CR, et al. Prediction and measurement of an autoregulatory genetic module. Proc. Natl. Acad. Sci. U.S.A. 2003;100:7714–7719. doi: 10.1073/pnas.1332628100. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b14-ebo-03-27] Johannes TW, Woodyer RD, Zhao H. Directed evolution of a thermostable phosphite dehydrogenase for NAD(P)H regeneration. Appl. Environ Microbiol. 2005;71:5728–5734. doi: 10.1128/AEM.71.10.5728-5734.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b15-ebo-03-27] Kitano H. Computaional systems biology. Nature. 2002a;420:206–210. doi: 10.1038/nature01254. [DOI] [PubMed] [Google Scholar]

[b16-ebo-03-27] Kitano H. Systems biology: a brief overview. Science. 2002b;295:1662–1664. doi: 10.1126/science.1069492. [DOI] [PubMed] [Google Scholar]

[b17-ebo-03-27] Kitano H. Biological robustness. Nature Reviews Genetics. 2004;5:826–837. doi: 10.1038/nrg1471. [DOI] [PubMed] [Google Scholar]

[b18-ebo-03-27] Kellis M, Birren BW, Lander ES. Proof and evolutionary analysis of ancient genome duplication in yeast Saccharomyces cerevisiae. Nature. 2004;428:617–624. doi: 10.1038/nature02424. [DOI] [PubMed] [Google Scholar]

[b19-ebo-03-27] Ko CL, Wang FS, Chao YP, et al. S-System approach to modeling recombinant Escherichia coli growth by hybrid differential evolution with data collocation. Biochemical Engineering Journal. 2006;28:10–16. [Google Scholar]

[b20-ebo-03-27] Langkjaer RB, Cliften PF, Johnston M, et al. Yeast genome duplication was followed by asynchronous differentiation of duplicated gene. Nature. 2003;421:848–852. doi: 10.1038/nature01419. [DOI] [PubMed] [Google Scholar]

[b21-ebo-03-27] May O, Nguyen PT, Arnold FH. Inverting enantioselectivity by directed evolution of hydantoinaze for improved production of L-methionine. Nat. Biotechnol. 2000;18:317–320. doi: 10.1038/73773. [DOI] [PubMed] [Google Scholar]

[b22-ebo-03-27] Ni TC, Savageau MA. Model assessment and refinement using strategies from biochemical systems theory: application to metabolism in human red blood cells. J. Theor. Biol. 1996a;179:329–368. doi: 10.1006/jtbi.1996.0072. [DOI] [PubMed] [Google Scholar]

[b23-ebo-03-27] Ni TC, Savageau MA. Application of biochemical systems theory to metabolism in human red blood cells. Signal propagation and accuracy of representation. J. Biol. Chem. 1996b;271:7927–7941. doi: 10.1074/jbc.271.14.7927. [DOI] [PubMed] [Google Scholar]

[b24-ebo-03-27] Nobel B, Daniel JW. Applied Linear Algebra. New Jersey: Prentice-Hall; Englewood Cliffs: 1988. [Google Scholar]

[b25-ebo-03-27] Savageau MA. Parameter sensitivity as a criterion for evaluating and comparing the performance of biochemical systems. Nature. 1971;229:542–544. doi: 10.1038/229542a0. [DOI] [PubMed] [Google Scholar]

[b26-ebo-03-27] Savageau MA. Biochemical Systems Analysis: a study of function and design in molecular biology. Boston: Addisson-Wesley, Reading; 1976. [Google Scholar]

[b27-ebo-03-27] Savageau MA. Design principles for elementary gene circuits: Elements, methods, and examples. Chaos. 2001;11:142–159. doi: 10.1063/1.1349892. [DOI] [PubMed] [Google Scholar]

[b28-ebo-03-27] Teichmann SA, Babu MM. Gene regulatory network growth by duplication. Nature Genet. 2004;36:492–496. doi: 10.1038/ng1340. [DOI] [PubMed] [Google Scholar]

[b29-ebo-03-27] Tsai HK, Huang TW, Lu HS, et al. Method for identifying transcription factor binding sites in yeast. Bioinformatics. 2006;22:1675–1681. doi: 10.1093/bioinformatics/btl160. [DOI] [PubMed] [Google Scholar]

[b30-ebo-03-27] Tsai KY, Wang FS. Evolutionary optimization with data collocation for reverse engineering of biological networks. Bioinformatics. 2005;21:1180–1188. doi: 10.1093/bioinformatics/bti099. [DOI] [PubMed] [Google Scholar]

[b31-ebo-03-27] Tsuji T, Onimaru M, Yanagawa H. Towards the creation of novel proteins by block shuffling. Combinatorial Chemistry and High Throughput Screening. 2006;9:259–269. doi: 10.2174/138620706776843237. [DOI] [PubMed] [Google Scholar]

[b32-ebo-03-27] Voit EO. Computational Analysis of Biochemical Systems. Cambridge: Cambridge University Press; 2000. [Google Scholar]

[b33-ebo-03-27] Wang CW, Oh MK, Liao JC. Directed evolution of metabolically engineered Escherichia coli for carotenoid production. Biotechnol. Prog. 2000;16:922–926. doi: 10.1021/bp000124f. [DOI] [PubMed] [Google Scholar]

[b34-ebo-03-27] Weinmann A. Uncertain Model and Robust Control. New York: Springer; 1991. [Google Scholar]

[b35-ebo-03-27] West-Eberhard MJ. Developmental Plasticity and Evolution. New York: Oxford University Press; 2003. [Google Scholar]

[b36-ebo-03-27] Yi TM, Huang Y, Simon MI, et al. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. U.S.A. 2000;97:4649–4653. doi: 10.1073/pnas.97.9.4649. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b37-ebo-03-27] Yuan L, Kurek I, English J. Laboratory-directed protein evolution microbiol. Mol. Biol. Rev. 2005;69:373–392. doi: 10.1128/MMBR.69.3.373-392.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

On the Adaptive Design Rules of Biochemical Networks in Evolution

Bor-Sen Chen

Wan-Shian Wu

Wei-Sheng Wu

Wen-Hsiung Li

Abstract

Introduction