Abstract
Understanding nucleotide variation in natural populations has been a subject of great interest for decades. However, many taxonomic groups, especially those with atypical life history attributes remain unstudied, and Drosophila is the only arthropod genus for which DNA polymorphism data are presently abundant. As a result of the recent release of the complete genome sequence and a wide variety of new genomic resources, the Daphnia system is quickly becoming a promising new avenue for expanding our knowledge of nucleotide variation in natural populations. Here, we examine nucleotide variation in six protein-coding loci for Daphnia pulex and its congeners with particular emphasis on D. pulicaria, the closest extant relative of D. pulex. Levels of synonymous intraspecific variation, πs, averaged 0.0136 for species in the Daphnia genus, and are slightly lower than most prior estimates in invertebrates. Tests of neutrality indicated that segregating variation conforms to neutral model expectations for the loci that we examined in most species, while Ka/Ks ratios revealed strong purifying selection. Using a full maximum-likelihood coalescent-based method, the ratio of the recombination rate to the mutation rate (c/u), averaged 0.5255 for species of the Daphnia genus. Lastly, a divergence population-genetics approach was used to investigate gene flow and divergence between D. pulex and D. pulicaria.
A thorough understanding of molecular variation in natural populations is fundamental to many important evolutionary issues. Thus, the characterization of molecular variation in natural populations and the discernment of the underlying forces that shape this variation have been a central focus of evolutionary geneticists for decades (e.g., Kreitman 1983; Moriyama and Powell 1996; Schmid et al. 2005). The ability to collect vast amounts of DNA sequence data has improved greatly in recent years, and this has expanded our understanding of the mechanisms that maintain genetic variability—especially in model systems. However, many animal groups with atypical life history attributes remain unstudied, and Drosophila is the only arthropod genus for which DNA polymorphism data are presently abundant. Undoubtedly, a more complete understanding of nucleotide variation in natural populations can be obtained by examining additional taxonomic groups.
The waterflea Daphnia (Cladocera, Anomopoda) has been central to thousands of studies in many diverse areas of biology (reviewed in Peters and de Bernardi 1987). Recently, Daphnia has been recognized as a new genetic model system. As a result, the scope of Daphnia research has expanded to include gene expression, mapping, and comparative genomic studies (e.g., Watanabe et al. 2005; Cristescu et al. 2006; Omilian et al. 2006; Soetaert et al. 2006). Yet, comparatively little is known about daphniid population genetics at nuclear protein-coding loci. Past studies of genetic variation in daphniid populations mainly employed allozymes, microsatellites, and mitochondrial DNA (e.g., Hebert 1974; Mort and Wolf 1986; Crease et al. 1990; Crease et al. 1997; Weider and Hobaek 1997; Palsson 2000), and few population-genetics analyses of nuclear DNA sequences are published (Little et al. 2004; Ishida and Taylor 2007). A better understanding of Daphnia population-genetics parameters will facilitate the interpretation of the new genomic data that are derived from this organism, especially data that are interpreted in an evolutionary context.
In this study, we treat Daphnia pulex as the focal species and also report on smaller surveys of five of its congeners: D. pulicaria, D. obtusa, D. ambigua, D. magna, and D. mendotae. The latter four species are distantly related to D. pulex, being separated by millions of years of divergence (Colbourne and Hebert 1996). However, the relationship between D. pulex and D. pulicaria is less clear. Previous studies on the basis of allozymes and mitochondrial DNA have regarded D. pulicaria as a sister species to D. pulex (Hebert et al. 1993; Colbourne and Hebert 1996). However, the species barrier between North American D. pulex and D. pulicaria is tenuous; the two are nearly morphologically indistinguishable and hybridize readily in nature. Although D. pulex–D. pulicaria hybrids reproduce via obligate parthenogenesis in the wild (e.g., Hebert et al. 1993; Hebert and Finston 2001), they are capable of producing progeny via sexual reproduction in the lab (Heier and Dudycha 2009). The most obvious difference between D. pulex and D. pulicaria is their habitat: D. pulex usually reside in ephemeral fishless ponds, whereas D. pulicaria primarily inhabit lakes.
Thus, D. pulex and D. pulicaria appear to be in the process of ecological speciation, with differences between pond and lake habitats being the source of divergent selection. Divergence population genetics can be used to shed light on the divergence process between these two species. This approach is based on the premise that two nascent species share polymorphisms due to their recent divergence from a common ancestor, and as time progresses, shared polymorphisms are lost, and new mutations arise in each species. When multiple loci are examined, the variance in levels of divergence among loci is used to assess gene flow (e.g., Wang et al. 1997; Machado et al. 2002; Hey 2006). If some loci show large divergences while others do not, it may be postulated that gene flow is still occurring at some loci. Divergence in the face of gene flow implicates selection as a driving force for the divergence (Maynard-Smith 1966; Endler 1977; Rice and Hostert 1993).
Here, we investigate the evolutionary processes shaping divergence between D. pulex and D. pulicaria by examining DNA sequence polymorphism data in six nuclear protein-coding loci. In particular, we ask whether an “isolation” speciation model, in which an ancestral population splits with no subsequent gene flow between descendent populations (Wakeley and Hey 1997), or the “isolation with migration” model (Wakeley and Hey 1998) is a better fit to the data. In doing so, multiple demographic parameters are estimated that characterize the divergence between D. pulex and D. pulicaria. This article also quantifies specieswide levels of nuclear variation in several other Daphnia species, and we report for all species included in this study the following basic population-genetics information: diversity estimates, tests of neutrality, Ka/Ks ratios, and the recombination rate (c/u).
MATERIALS AND METHODS
Taxonomic sampling:
Species delimitation and nomenclature within the D. pulex complex is problematic (Mergeay et al. 2008). Thus, we present two salient issues that warrant attention for this study. The D. pulex species name is used to denote two different lineages, one that inhabits Europe (sensu Leydig 1860), and the other is primarily found in North America (sensu Hebert 1995). In the same vein, two different lineages are named D. pulicaria; European D. pulicaria (sensu Alonso 1996) are distinct from North American D. pulicaria populations (sensu Forbes 1893). Here, we refer only to North American D. pulex and D. pulicaria, and restrict our conclusions to these lineages.
Six loci were examined in D. pulex, D. pulicaria, and D. obtusa. Due to the difficulty of obtaining PCR products, two loci were analyzed for three additional species that are much more distant in their taxonomic relationship to D. pulex: D. ambigua, D. mendotae, and D. magna. For D. pulex, two individuals per collection site were sampled (36 alleles, supporting information, Table S1). Obligate parthenogens that are known to occur in D. pulex were not included in this study. For all other species, one individual from each of nine collection sites was sampled (18 alleles per species, see Table S1 for exceptions). With the exception of D. pulex, each individual sampled within a species was from a unique collection site, making it impracticable to address questions at the level of the deme. This specieswide sampling strategy from multiple demes may increase the effective population size relative to that of a single deme (Wright 1943). With multiple subdivided demes, the migration rate among demes can influence inferences regarding divergence time, relative population sizes, and phylogenetic relationships (Wakeley 2000), and the appropriateness of our sampling approach depends on how well Daphnia fit the assumptions of an island model of migration with many demes. Moreover, Daphnia are cyclic parthenogens, and asexual periods of reproduction may influence adherence to the standard coalescent, potentially influencing our analyses. Although it is beyond the scope of the present article to deal formally with this issue, we expect that the influence of selection on linked sites will be greater in a cyclically parthenogenetic population than a purely sexual population, thereby increasing the among-individual variance in reproductive success and reducing effective population size.
Because taxonomic differentiation on the basis of morphology is notoriously difficult in Daphnia, we verified the taxonomic identification of all individuals with sequence data from the 12S rDNA gene (Colbourne and Hebert 1996). Allozyme analysis for the lactate dehydrogenase (LDH) locus was used to differentiate between D. pulex and D. pulicaria (Table S1), following the conventional notion that D. pulicaria is homozygous for the F allele and D. pulex is homozygous for the S allele (Hebert et al. 1989, 1993).
It has been proposed that certain populations of D. pulex endemic to Oregon are a separate species called D. arenata (Hebert 1995). Phylogenies on the basis of mitochondrial DNA sequences show that D. pulex is paraphyletic with respect to these Oregon populations (Colbourne et al. 1998; Lynch et al. 2008), but nuclear data reveal support for D. arenata (Omilian et al. 2008). This study includes two populations from Oregon (denoted LOG and GI); one population (LOG) consists of D. arenata, while the GI population is likely to be of hybrid origin (Omilian et al. 2008). For our population-genetics analyses, we found that the D. arenata individuals were sufficiently divergent to be analyzed separately from D. pulex. The GI individuals were excluded from most analyses.
Locus information:
Loci were chosen on the basis of the presence of conserved regions for primer design in sequences present in cDNA libraries from D. pulex and D. magna (cDNA libraries provided by John Colbourne and Hajime Watanabe, see Table S2 for primer sequences). These loci appeared to be single-copy genes based on BLAST searches to the D. pulex genome (v.1.0), and data obtained from cloning did not reveal evidence for more than two alleles per individual at any locus. We examined sequences from the following loci: ATP synthase epsilon chain (atp-ep), a calcium-binding protein with an EF-hand (cbp-EF), cleavage stimulation factor (cstf), glyceraldehyde-3-phosphate dehydrogenase (g3pdh), a rab GTPase(rab4), and a protein with translation initiation factor and subtilase activity (tif).
PCR amplification, DNA sequencing, and cloning:
Specific PCR information is described in Omilian et al. (2008). Briefly, Taq polymerase with proofreading capability (Clontech) was used, and PCR products were sequenced in both directions. Because Daphnia were from natural populations, direct sequencing of PCR products revealed many heterozygous loci, that is, two overlapping peaks were observed for at least one site of the DNA sequence electropherogram. Heterozygous sites were detected with CodonCode Aligner software v1.4.3 set at the highest sensitivity and then verified by eye. Approximately 50% of our amplicons had multiple heterozygous sites and were cloned with the Invitrogen TOPO TA kit to determine the gametic phase. The QIAprep Spin miniprep kit (QIAGEN) was used for plasmid purification, and a T7 primer was used to sequence the cloned inserts. Four to 12 cloned fragments were sequenced, and the results from cloned PCR products were compared to the direct sequences of PCR products to ensure that polymorphisms were not the result of PCR or cloning-induced errors (Cronn et al. 2002).
Sequence analysis and statistical tests:
Polymorphism patterns:
Sequences were aligned with MEGA version 3.1 (Kumar et al. 2004), using the ClustalW algorithm (Thompson et al. 1994) and then manually corrected. Population-genetics parameters and tests of neutrality were calculated with DnaSP version 4.0 (Rozas et al. 2003) unless noted otherwise. Two measures of nucleotide diversity were estimated: π, the average of pairwise differences among DNA sequences (Tajima 1983), obtained using the Jukes–Cantor correction (Jukes and Cantor 1969; Lynch and Crease 1990); and θ, based on the total number of segregating mutations in the sample (Watterson 1975; Tajima 1996). Under neutrality, π and θ are expected to be equal and estimators of 4Neu, where Ne is the genetic effective population size and u is the mutation rate per site per generation. Both π and θ were estimated for the following categories of nucleotide sites/regions: total (πT, θT), nonsynonymous (πn, θn), synonymous (πs, θs), intron (πi, θi), and UTR (πU, θU).
Recombination:
A full-likelihood coalescence-based approach in LAMARC 2.0 (Kuhner 2006) was used to estimate the recombination rate, rLAMARC = c/μ, where c is the recombination rate per site per generation and μ is the neutral mutation rate per site per generation. LAMARC uses a finite-sites model and operates under the following assumptions: (1) recombination frequency is not affected by sequence divergence, (2) all recombination is homologous, (3) gene conversion and interference do not occur, (4) recombination events are selectively neutral, and (5) the recombination rate is constant across the region. We excluded loci with 10 or fewer variable sites because LAMARC requires sufficient numbers of variable sites to get reliable estimates of the parameters.
Because it was not possible to implement the best fitting model (determined by Modeltest v3.7; Posada and Crandall 1998) for most loci in LAMARC, we used the Felsenstein '84 (F84) model with empirical base frequencies (Kishino and Hasegawa 1989; Felsenstein 1993); for most loci, the F84 model is a closer fit than the other model offered by LAMARC and is computationally faster. Two categories of relative mutation rate were assigned, accounting for substitution rate differences between nonsynonymous sites and all other sites. Our sampling strategy included 20 initial chains of 1000 and 2 final chains of 50,000 genealogies with 1000 genealogies discarded per chain. Adaptive heating was used to improve the search of parameter space. The entire analysis was replicated three times and the results were combined (Geyer 1991).
Tests of neutrality and Ka/Ks ratios:
Two tests of neutrality were conducted: the Hudson–Kreitman–Aguade test (HKA, Hudson et al. 1987) and Tajima's D test (Tajima 1989). We used a multilocus version of the HKA test (Hey's HKA program; http://lifesci.rutgers.edu/∼heylab). Test statistics for both HKA and Tajima's D tests were compared with distributions generated from 10,000 coalescent simulations to determine significance. Values for Ka and Ks were calculated in MEGA using the Kumar method, which is a modification of the Pamilo–Bianchi–Li (Pamilo and Bianchi 1993; Li 1993) and Comeron (1995) methods; this method accounts for some problematic degeneracy assignments. For both Ka and Ks we subtracted the mean within-species diversity (averaged between the two species being compared) from raw estimates of divergence to get the net divergence between species. Standard errors for Ka/Ks ratios were calculated from equation A1.19b from Lynch and Walsh (1998).
Phylogenetic analyses:
We used MrBayes 3.1.2 (Huelsenbeck and Ronquist 2001) to elucidate the genealogical relationships of D. pulex, D. pulicaria, and D. arenata alleles with Bayesian inference. The six loci were concatenated in an alignment of 3160 bp for a total evidence analysis. The tree was rooted with D. obtusa, which is an uncontroversial outgroup. Large indel mutations that were likely to be the result of one insertion event, rather than several independent events, were weighted as one event (e.g., a novel intron insertion in some individuals).
We conducted an analysis without partitioning and an analysis with the sequence data partitioned by one noncoding and three codon positions (first, second, and third codon positions). Model selection for each partition was made according to the Akaike information criterion in Modeltest v3.7 (Posada and Crandall 1998). For MrBayes, default prior settings were used except for the ratepr parameter that was set to variable for the partitioned analyses, so that partitions could evolve at different rates. Branch lengths and topology were shared among partitions, but the substitution rate matrix, state frequency, and shape parameter of the γ-distribution were unlinked, allowing for separate parameter estimates. Two independent and simultaneous Markov chain Monte Carlo (MCMC) analyses of 15 heated and one cold chain were run for 6 million generations sampling from the chain every 100 generations. After determining chain convergence (average standard deviation of split frequencies <0.01), we discarded the initial 25% of trees as a burn-in. A 50% majority-rule consensus topology with posterior probability (PP) values for each node was constructed from the post-burn-in trees.
Genealogical relationships were further examined with median-joining haplotype networks using the program Network version 4.5 (Bandelt et al. 1999; http://www.fluxus-engineering.com). This method accounts for the coexistence of ancestral and descendent haplotypes, multifurcations, and reticulate relationships (Posada and Crandall 2001). We used the MP post-processing option, which removes all superfluous median vectors and links that are not contained in the shortest trees of the network.
Divergence population genetics:
A Bayesian methodology employed by the Isolation with Migration (IMa) software (Hey and Nielsen 2007) was used to generate posterior probability distributions for six parameters relevant to the divergence between D. pulex and D. pulicaria. In turn, these parameters were used to estimate the time since divergence, migration rates, and effective population sizes for D. pulex, D. pulicaria, and their ancestral population. Assuming five generations per year in Daphnia, we applied the mutation rate 2.9 × 10−8 mutations/site/year (single-nucleotide mutation rate from Haag-Liautard et al. 2007). Although this mutation rate is from a distant relative (Drosophila), it remains the most rigorously determined arthropod nuclear rate that is available. Because there is error associated with mutation-rate estimation (outlined in Haag-Liautard et al. 2007) and the application of a mutation rate from a distant relative, we also present the scaled IMa parameters.
Once appropriate prior distributions were identified (Won and Hey 2005), we used multiple runs with identical conditions except the random number seed to determine convergence. We applied the HKY mutation model (Hasegawa et al. 1985) to accommodate multiple substitutions at a single nucleotide site. Five chains with heating were used for each run. Runs of 60,000,000 steps and a burn-in period of 100,000 steps provided for effective sample sizes of at least 95.
The isolation with migration methodology is contingent upon several assumptions. First, it is assumed that variation within the dataset is selectively neutral. Second, the sampled populations, D. pulex and D. pulicaria, are assumed to be more closely related to each other than other populations, and gene flow with unsampled populations is assumed to be nonexistent. Lastly, there should be no recombination within loci and free recombination between loci (Hey and Nielsen 2004). The assumption of selective neutrality is likely to hold as neutrality tests indicated that sequences for D. pulex and D. pulicaria conform to neutral model expectations (see results). Phylogenetic analyses from previous studies reveal mixed results regarding the closest relative to D. pulex; studies on the basis of mitochondrial DNA usually reconstruct D. arenata as the closest relative to D. pulex (Colbourne et al. 1998; Mergeay et al. 2008), whereas nuclear DNA reveals that D. pulex and D. pulicaria are sister groups (Omilian et al. 2008; this study). Thus, we conducted three separate IMa analyses in which the following were compared: (1) D. pulex and D. pulicaria, (2) D. pulex and D. arenata, and (3) D. arenata and D. pulicaria. Because the assumption of no intralocus recombination is violated in our data set, we also assessed migration with a full-likelihood coalescence-based approach in LAMARC that accounts for recombination.
RESULTS
Altogether, we sequenced >280 kb representing six nuclear protein-coding loci. The aligned length for the loci ranged from 443 to 615 bp with a mean length of 519 bp. All amplified fragments contained at least 1 intron, for a total of 10 introns, with the exception of two populations (LOG and GI, both from Oregon), which were polymorphic for an intron insertion; these populations had 11 introns total. Average intron length per species ranged in size from 57 bp (D. ambigua) to 162 bp (D. pulicaria) with an average length of 82.7 bp for the Daphnia genus (see Table S3). Four loci contained UTR sequence (either 5′ or 3′) in the amplicon; in all four cases we did not get sequence data for the complete UTR.
Polymorphism patterns, tests of neutrality, and Ka/Ks ratios:
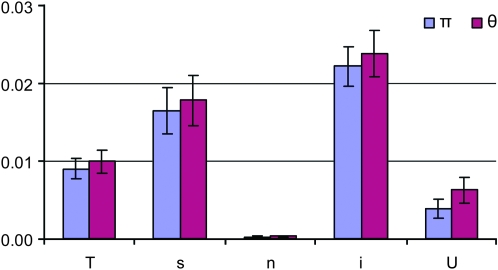
Levels of DNA polymorphism varied in Daphnia according to functional site/region, locus, and species (Table 1). Nucleotide diversity was far lower for nonsynonymous than synonymous and intron sites (P ≤ 0.0001, Figure 1). Diversity in UTRs was threefold lower than at synonymous sites or introns (P ≤ 0.002, Figure 1). Synonymous-site diversity averaged across all loci was highest in D. ambigua (πs = 0.0310), lowest in D. arenata (πs = 0.0017), and the focal species D. pulex and D. pulicaria were intermediate with values of 0.0188 and 0.0159, respectively (Table 2). Relative to the mutation rate, the overall recombination rate per site per generation (c/μ) ranged from 0.2383 to 0.7611 for Daphnia species and averaged 0.5255 for the Daphnia genus (Table 3).
TABLE 1.
Basic polymorphism statistics calculated for each species
| Species | Locus | K | H | S | πT | θT | πs | θs | πn | θn | πi | θi | πU | θU |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D. arenata | g3pdh | 1 | 0.000 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | NA | NA |
| D. pulex | 9 | 0.844 | 9 | 0.0039 | 0.0045 | 0.0111 | 0.0117 | 0.0000 | 0.0000 | 0.0133 | 0.0169 | NA | NA | |
| D. pulicaria | 3 | 0.569 | 2 | 0.0012 | 0.0011 | 0.0000 | 0.0000 | 0.0003 | 0.0009 | 0.0090 | 0.0049 | NA | NA | |
| D. obtusa | 8 | 0.890 | 6 | 0.0036 | 0.0037 | 0.0090 | 0.0086 | 0.0000 | 0.0000 | 0.0141 | 0.0155 | NA | NA | |
| D. ambigua | 4 | 0.765 | 6 | 0.0038 | 0.0034 | 0.0099 | 0.0107 | 0.0000 | 0.0000 | 0.0153 | 0.0102 | NA | NA | |
| D. magna | 3 | 0.545 | 8 | 0.0051 | 0.0051 | 0.0112 | 0.0121 | 0.0009 | 0.0010 | 0.0178 | 0.0158 | NA | NA | |
| D. mendotae | 2 | 0.366 | 1 | 0.0007 | 0.0006 | 0.0034 | 0.0027 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | NA | NA | |
| D. arenata | tif | 2 | 0.667 | 4 | 0.0055 | 0.0045 | 0.0103 | 0.0083 | 0.0000 | 0.0000 | 0.0110 | 0.0090 | NA | NA |
| D. pulex | 25 | 0.992 | 48 | 0.0200 | 0.0278 | 0.0267 | 0.0628 | 0.0000 | 0.0000 | 0.0478 | 0.0581 | NA | NA | |
| D. pulicaria | 18 | 1.000 | 32 | 0.0193 | 0.0199 | 0.0372 | 0.0309 | 0.0000 | 0.0000 | 0.0420 | 0.0423 | NA | NA | |
| D. obtusa | 8 | 0.890 | 17 | 0.0092 | 0.0111 | 0.0164 | 0.0284 | 0.0000 | 0.0000 | 0.0213 | 0.0204 | NA | NA | |
| D. ambigua | 12 | 0.941 | 22 | 0.0133 | 0.0132 | 0.0521 | 0.0441 | 0.0000 | 0.0000 | 0.0179 | 0.0191 | NA | NA | |
| D. magna | 8 | 0.900 | 14 | 0.0092 | 0.0087 | 0.0177 | 0.0136 | 0.0000 | 0.0000 | 0.0177 | 0.0174 | NA | NA | |
| D. mendotae | 6 | 0.627 | 10 | 0.0046 | 0.0059 | 0.0045 | 0.0044 | 0.0000 | 0.0000 | 0.0145 | 0.0186 | NA | NA | |
| D. arenata | atp-ep | 1 | 0.000 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| D. pulex | 16 | 0.942 | 24 | 0.0121 | 0.0154 | 0.0129 | 0.0390 | 0.0000 | 0.0000 | 0.0242 | 0.0217 | 0.0016 | 0.0057 | |
| D. pulicaria | 11 | 0.935 | 20 | 0.0164 | 0.0138 | 0.0206 | 0.0221 | 0.0016 | 0.0023 | 0.0335 | 0.0271 | 0.0000 | 0.0000 | |
| D. obtusa | 9 | 0.923 | 14 | 0.0083 | 0.0100 | 0.0000 | 0.0000 | 0.0011 | 0.0025 | 0.0189 | 0.0201 | 0.0058 | 0.0068 | |
| D. arenata | cbp-EF | 3 | 0.833 | 2 | 0.0023 | 0.0028 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0039 | 0.0050 | 0.0080 | 0.0087 |
| D. pulex | 16 | 0.942 | 22 | 0.0118 | 0.0111 | 0.0118 | 0.0108 | 0.0000 | 0.0000 | 0.0407 | 0.0336 | 0.0051 | 0.0080 | |
| D. pulicaria | 10 | 0.876 | 23 | 0.0121 | 0.0115 | 0.0240 | 0.0204 | 0.0000 | 0.0000 | 0.0353 | 0.0320 | 0.0046 | 0.0045 | |
| D. obtusa | 11 | 0.967 | 13 | 0.0062 | 0.0071 | 0.0215 | 0.0220 | 0.0000 | 0.0000 | 0.0138 | 0.0161 | 0.0023 | 0.0050 | |
| D. arenata | cstf | 1 | 0.000 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| D. pulex | 8 | 0.794 | 8 | 0.0026 | 0.0034 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0196 | 0.0235 | 0.0009 | 0.0017 | |
| D. pulicaria | 6 | 0.562 | 6 | 0.0019 | 0.0033 | 0.0021 | 0.0054 | 0.0000 | 0.0000 | 0.0142 | 0.0217 | 0.0004 | 0.0009 | |
| D. obtusa | 5 | 0.670 | 4 | 0.0015 | 0.0021 | 0.0027 | 0.0058 | 0.0000 | 0.0000 | 0.0120 | 0.0141 | 0.0000 | 0.0000 | |
| D. arenata | rab4 | 1 | 0.000 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| D. pulex | 14 | 0.944 | 29 | 0.0209 | 0.0154 | 0.0503 | 0.0300 | 0.0008 | 0.0030 | 0.0361 | 0.0246 | 0.0694 | 0.0593 | |
| D. pulicaria | 8 | 0.830 | 11 | 0.0061 | 0.0066 | 0.0113 | 0.0113 | 0.0000 | 0.0000 | 0.0135 | 0.0129 | 0.0181 | 0.0447 | |
| D. obtusa | 4 | 0.455 | 6 | 0.0024 | 0.0041 | 0.0067 | 0.0130 | 0.0000 | 0.0000 | 0.0048 | 0.0073 | 0.0000 | 0.0000 |
S, segregating sites; K, haplotypes; H, haplotype diversity, defined as the probability that two alleles randomly chosen from the population are different. π was calculated using the Jukes–Cantor correction (Jukes and Cantor 1969, Lynch and Crease 1990); θ was calculated using the total number of mutations rather than the number of segregating sites (Tajima 1996). π and θ were estimated for the following categories of nucleotide sites/regions: total (πT, θT), nonsynonymous (πn, θn), synonymous (πs, θs), intron (πi, θi), UTR (πU, θU). For loci with two introns, values for πi and θi are averages.
Figure 1.—
Estimates of π and θ for different functional regions averaged across all loci examined in the Daphnia genus. Error bars are standard errors of the mean of all loci. The following categories of nucleotide sites were examined: total (T), synonymous (s), nonsynonymous (n), intron (i), and UTR (U).
TABLE 2.
Estimates of nucleotide diversity averaged across all loci for each species of Daphnia included in this study
| πT | θT | πs | θs | πn | θn | πi | θi | πU | θU | |
|---|---|---|---|---|---|---|---|---|---|---|
| D. arenata | 0.0013 | 0.0012 | 0.0017 | 0.0014 | 0.0000 | 0.0000 | 0.0025 | 0.0023 | 0.0020 | 0.0022 |
| D. pulex | 0.0119 | 0.0129 | 0.0188 | 0.0257 | 0.0001 | 0.0005 | 0.0303 | 0.0297 | 0.0193 | 0.0187 |
| D. pulicaria | 0.0095 | 0.0094 | 0.0159 | 0.0150 | 0.0003 | 0.0005 | 0.0246 | 0.0235 | 0.0058 | 0.0125 |
| D. obtusa | 0.0052 | 0.0064 | 0.0094 | 0.0130 | 0.0002 | 0.0004 | 0.0142 | 0.0156 | 0.0020 | 0.0030 |
| D. ambigua | 0.0086 | 0.0083 | 0.0310 | 0.0274 | 0.0000 | 0.0000 | 0.0166 | 0.0147 | NA | NA |
| D. magna | 0.0072 | 0.0069 | 0.0145 | 0.0129 | 0.0005 | 0.0005 | 0.0178 | 0.0166 | NA | NA |
| D. mendotae | 0.0027 | 0.0033 | 0.0040 | 0.0036 | 0.0000 | 0.0000 | 0.0073 | 0.0093 | NA | NA |
Details regarding π and θ are described in Table 1. Six loci were examined for D. arenata, D. pulex, D. pulicaria, and D. obtusa, and two loci were examined for the remaining species.
TABLE 3.
Full-likelihood estimates of the relative recombination rate (rLAMARC = c/μ, where c is the recombination rate per site per generation and μ is the neutral mutation rate per site per generation) for Daphnia species
| Locus | rLAMARC | 95% support intervals | |
|---|---|---|---|
| D. pulexa | Overall | 0.5876 | 0.4635, 0.7355 |
| atp-ep | 0.6073 | 0.1620, 1.3777 | |
| cbp-EF | 1.8671 | 0.7719, 2.5429 | |
| rab4 | 0.2511 | 0.0356, 0.6833 | |
| tif | 1.1069 | 0.4869, 1.7404 | |
| D. pulicariaa | Overall | 0.7476 | 0.3933, 1.0892 |
| atp-ep | 0.5929 | 0.1831, 1.4095 | |
| cbp-EF | 0.2854 | 0.0408, 0.9592 | |
| rab4 | 0.2700 | 1 × 10−9, 1.4572 | |
| tif | 0.9507 | 0.4631, 1.8675 | |
| D. obtusab | Overall | 0.2383 | 0.0892, 0.5367 |
| atp-ep | 8 × 10−6 | 1 × 10−11, 0.1782 | |
| cbp-EF | 1.2634 | 0.3737, 2.9458 | |
| tif | 0.1623 | 1 × 10−9, 0.8932 | |
| D. ambiguac | tif | 0.2929 | 0.0483, 0.8701 |
| D. magnac | tif | 0.7611 | 0.1793, 2.0246 |
Ninety-five percent support intervals are shown for rLAMARC. rLAMARC could not be estimated for D. arenata or D. mendotae because all loci lacked sufficient numbers of variable sites.
The following loci were not included for LAMARC analyses because they did not have >10 variable sites:
csf and g3pdh
csf, g3pdh, and rab4
g3pdh.
We did not observe a significant departure from neutrality for any locus with the HKA test (Table 4). A significant negative mean Tajima's D was observed only for D. obtusa (Table 5). Synonymous (Ks) and nonsynonymous (Ka) divergences among D. pulex and its congeners are shown in Table 6; Ks values were higher than Ka values for all loci, and Ka/Ks ratios ranged from −0.0120 to 0.0501. D. pulex and D. pulicaria were not significantly different at silent or replacement sites (Table 6).
TABLE 4.
HKA test results
| χ2 | P | Proportion of simulations with χ2 values greater than critical value (0.05) | |
|---|---|---|---|
| D. pulex–D. arenata | 8.011 | 0.628 | 0.0007 |
| D. pulex–D. pulicaria | 7.635 | 0.664 | 0.0000 |
| D. pulex–D. obtusa | 6.493 | 0.772 | 0.0003 |
| D. pulex–D. ambigua | 1.722 | 0.423 | 0.0020 |
| D. pulex–D. magna | 3.651 | 0.161 | 0.0020 |
| D. pulex–D. mendotae | 1.561 | 0.458 | 0.0014 |
P, probability from χ2 distribution. Significance was estimated with 10,000 coalescent simulations and conventional χ2 approximation. D. arenata, D. pulex, D. pulicaria, and D. obtusa had 10 degrees of freedom. D. ambigua, D. magna, and D. mendotae had 2 degrees of freedom.
TABLE 5.
Tajima's D values for comparisons of π and θ
| Obs. mean D | Sim. mean D | Dsim < Dobs (%)a | |
|---|---|---|---|
| D. arenata | 0.202 | −0.020 | 72 |
| D. pulex | −0.286 | −0.074 | 29 |
| D. pulicaria | −0.145 | −0.071 | 43 |
| D. obtusa | −0.765 | −0.075 | 3* |
| D. ambigua | 0.141 | −0.083 | 64 |
| D. magna | 0.059 | −0.071 | 58 |
| D. mendotae | −0.172 | −0.066 | 45 |
Significance was based on 10,000 coalescent simulations. Values reported for D. arenata, D. pulex, D. pulicaria, and D. obtusa are based on six loci. Values reported for D. ambigua, D. magna, and D. mendotae are based on two loci. *Significant.
Percentage of 10,000 independent standard coalescent simulations that generated a more extreme mean Tajima's D.
TABLE 6.
Average nucleotide divergence for protein-coding genes between D. pulex and five of its congeners
| Ks | (SE) | Ka | (SE) | Ka/Ks | (SE) | |
|---|---|---|---|---|---|---|
| D. arenata | 0.00998 | 0.00345 | 0.00002 | 0.00002 | 0.0010 | 0.0016 |
| D. pulicaria | 0.00342 | 0.00380 | 0.00003 | 0.00002 | −0.0120 | 0.0080 |
| D. obtusa | 0.06338 | 0.02085 | 0.00141 | 0.00138 | 0.0163 | 0.0222 |
| D. ambigua | 0.12205 | 0.00825 | 0.00570 | 0.00570 | 0.0501 | 0.0476 |
| D. magna | 0.39928 | 0.05362 | 0.01093 | 0.01093 | 0.0316 | 0.0285 |
| D. mendotae | 0.21803 | 0.03903 | 0.00295 | 0.00295 | 0.0115 | 0.0131 |
Ka, number of nonsynonymous substitutions per nonsynonymous site; Ks, number of synonymous substitutions per synonymous site. For both Ka and Ks, mean within-species diversity (averaged between the two species being compared) was subtracted from raw estimates of divergence to get the net divergence between species.
Evolutionary relationships between D. pulex and D. pulicaria:
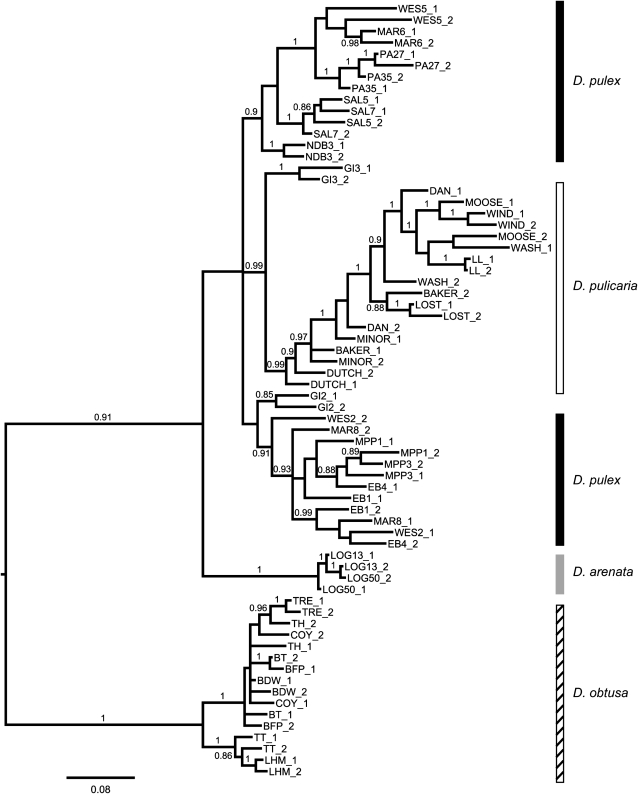
In MrBayes, the lowest average standard deviation of split frequencies was obtained with the unpartitioned data set that employed the GTR + I + Γ model of nucleotide evolution; the 50% majority-rule consensus Bayesian topology is presented from this analysis (Figure 2). The consensus tree revealed that D. pulex consists of two major monophyletic groups that are paraphyletic with respect to D. pulicaria. We find that D. pulicaria is a strongly supported monophyletic group (PP = 0.99), and D. pulex and D. pulicaria are more closely related to each other than either is to D. arenata, which is also a distinct monophyletic group (PP = 1). However, support was low for the sister relationship of D. pulex and D. pulicaria to the exclusion of D. arenata (PP = 0.65). The GI population is unique in that one of the sampled individuals groups with D. pulicaria and the other groups with D. pulex.
Figure 2.—
The 50% majority-rule consensus Bayesian genealogy from the total evidence analysis of six nuclear protein-coding loci (3160 bp) in Daphnia pulex (solid), D. pulicaria (open), and D. arenata (shaded). Numbers at nodes are posterior probabilities (PP) and are not shown if they are <0.85. The tree is rooted with the outgroup species, D. obtusa (hatched). Labels consist of the population name, followed by the individual number (if more than one individual was sampled), and the allele number (either 1 or 2). D. pulex is paraphyletic with respect to D. pulicaria, which is a monophyletic group (PP = 0.99). D. arenata is also monophyletic (PP = 1.0) and is a sister group to D. pulex + D. pulicaria; support for this branch is low (PP = 0.65).
Because a bifurcating genealogy neglects recombination within a species, we also constructed a network. Network results were consistent with those obtained from the Bayesian analysis (Figure S1).
Divergence population genetics:
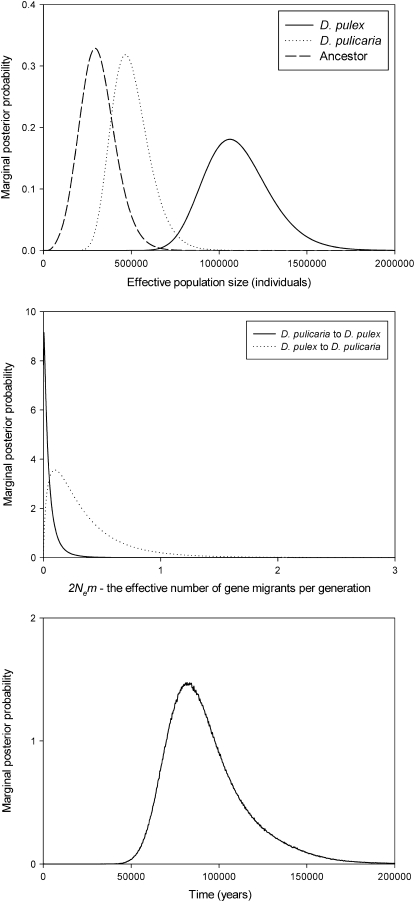
For D. pulex and D. pulicaria, multiple IMa runs with identical conditions except the starting seed revealed clear marginal posterior probability distributions of the parameters, with unimodal peaks for all curves; results are presented from a single representative run (Figure 3, Table 7). For gene flow from D. pulicaria to D. pulex, the highest probability of the posterior distribution is near zero, and the curve drops to zero at higher migration rates (Figure 3). For gene flow from D. pulex to D. pulicaria, a model of no gene flow can be rejected, but migration is low (Figure 3, Table 7). D. pulex and D. pulicaria are estimated to have diverged ∼82,000 years ago (95% HPD interval: 58,000–126,000). Population size for D. pulex is significantly larger than the ancestral population, suggesting population expansion; this is consistent with the negative mean value for Tajima's D observed in this species (Tables 5 and 7).
Figure 3.—
The marginal posterior probability distributions for effective population size, effective migration rate, and divergence time for D. pulex and D. pulicaria. Assuming five generations per year in Daphnia, model parameters were converted to demographic quantities using the mutation rate estimate 2.9 × 10−8 mutations/site/year [rate from Haag-Liautard et al. (2007), assuming five generations per year in Daphnia].
TABLE 7.
Scaled model parameters and demographic quantities from IMa analyses of nuclear protein-coding loci in D. pulex and D. pulicaria
| Scaled model parameter | High point | Lower bound | Upper bound |
|---|---|---|---|
| θpulex | 12.94 | 9.76 | 17.12 |
| θpulicaria | 5.71 | 3.88 | 8.21 |
| θancestor | 3.61 | 1.72 | 5.84 |
| t | 1.25 | 0.89 | 1.92 |
| m1 (D. pulicaria → D. pulex) | 0.03 | 0.01 | 0.16 |
| m2 (D. pulex → D. pulicaria) | 0.17 | 0.04 | 0.41 |
| Demographic quantity | |||
| Ne, effective population size for D. pulex | 1,100,000 | 801,000 | 1,404,000 |
| Ne, effective population size for D. pulicaria | 468,000 | 318,000 | 673,000 |
| Ne, common ancestor | 296,000 | 141,000 | 479,000 |
| Divergence time (years) | 82,000 | 58,000 | 126,000 |
| 2Nem, the effective number of gene migrants from D. pulicaria to D. pulex per generation | 0.16 | 0.02 | 1.37 |
| 1.71* | 1.34* | 2.14* | |
| 2Nem, the effective number of gene migrants from D. pulex to D. pulicaria per generation | 0.47 | 0.08 | 1.68 |
| 1.67* | 1.28* | 2.10* |
Estimates of migration obtained with LAMARC are also shown (indicated with asterisks). Lower and upper bounds are the estimated 90% highest posterior density, except for the LAMARC estimates, in which they represent 95% support intervals. Demographic quantity estimates were obtained using the mutation rate estimate of 2.9 × 10−8 mutations/site/year [rate from Haag-Liautard et al. (2007), assuming five generations per year in Daphnia].
Migration analyes in LAMARC, which accounts for recombination within nuclear loci, determined that migration estimates were roughly an order of magnitude higher than those obtained with IMa (Table 7). The effective number of gene migrants (2Nem) from D. pulicaria to D. pulex, per generation was 1.71 (95% support interval: 1.34–2.14), and for D. pulex to D. pulicaria, 1.67 (95% support interval: 1.28–2.10).
Despite several varied attempts, IMa runs for D. pulex and D. arenata, and D. pulicaria and D. arenata, did not have a narrow unimodal peak for the divergence-time parameter. Instead, the highest likelihood appears to have an infinitely wide range of parameter values. Thus, all parameter estimates from these runs may be invalid and are not presented. This is likely due to the low levels of variation observed in the D. arenata sequences.
DISCUSSION
Patterns of nucleotide polymorphism:
Averaged across species, daphniid nucleotide diversity (πs = 0.0136, θs = 0.0141) is lower than the average of other invertebrates (πs = 0.0265, Lynch 2006). In reference to two prominent arthropod species, synonymous diversity in Daphnia is similar to Drosophila melanogaster (πs = 0.0158, Andolfatto 2001) and lower than Anopheles gambiae (πs = 0.0235, Besansky et al. 2003; Mukabayire et al. 2001). In Daphnia, there is considerable heterogeneity in polymorphism levels for the various sites/regions and loci spanning a range from 0.0000 to 0.0694 (Table 1, Figure 1). Levels of diversity for nonsynonymous polymorphisms are far lower than for synonymous polymorphisms, reflecting purifying selection against amino acid substitutions. Mean πi and πs are significantly higher than πU (P < 0.0001 and P = 0.002, respectively), suggesting that UTRs are selectively constrained in Daphnia. These results indicate that synonymous, intron, and UTR sites should not be grouped together under the umbrella of silent sites in Daphnia and are consistent with studies that document lower levels of polymorphism in UTR regions than synonymous sites (e.g., Andolfatto 2005).
Levels of polymorphism were heterogeneous among the different species examined (Tables 1 and 2). Nucleotide diversity is notably low for D. mendotae and D. arenata, being nearly an order of magnitude lower than the other examined species for some functional sites/regions. These low diversity estimates may be due to sampling effects as only two loci were examined for D. mendotae and only four individuals were available for D. arenata. Alternatively, low estimates of nucleotide diversity could be indicative of small effective population size or lower mutation rates in these species (reviewed in Wright and Gaut 2005).
The population-genetic consequences of cyclical parthenogenesis are largely unexplored empirically. Daphnia are cyclical parthenogens that experience phases of clonal reproduction, so it is of interest if they exhibit low rates of recombination. Low recombination may cause greater vulnerability to hitchhiking effects as recombination separates independently arising mutations. The scaled recombination rate, c/μ, can be used to address this question, as recombinational activity across groups can be compared (e.g., Hudson 1987; Haddrill et al. 2005). In general, c/μ estimates are similar among Daphnia species, ranging from 0.2383 to 0.7611 (Table 3). These estimates are likely to be a lower bound on the recombination rate in Daphnia given that gene conversion may be an important factor for closely linked sites (Andolfatto and Nordborg 1998), and LAMARC does not account for gene conversion. Nevertheless, despite having phases of clonal reproduction, Daphnia appear to have recombination rates that are similar to other organisms for which estimates are available (Lynch 2007), save Drosophila, which have higher relative recombination rates than most animals (Haddrill et al. 2005; Lynch 2007).
A longstanding concern of population geneticists is quantifying how natural selection influences levels of genetic variation. The evaluation of intraspecific polymorphism and interspecific divergence can elucidate whether neutral, selective, and/or demographic forces are acting—especially when multiple loci are examined. Neutrality tests (HKA and Tajima's D) suggest that all species of Daphnia examined in this study conform to neutral model expectations, with the exception of D. obtusa, which had a significantly negative mean value for Tajima's D (Tables 4 and 5). The ratios of the number of nonsynonymous substitutions per nonsynonymous site (Ka) to the number of synonymous substitutions per synonymous site (Ks) were low for all Daphnia species, suggesting strong purifying selection (Table 6). This observation is potentially a consequence of our focus on functionally conserved genes, to maximize PCR success across a wide range of Daphnia species.
Species barrier between D. pulex and D. pulicaria:
The observation of virtually no divergence at synonymous sites (average Ks = 0.0034, standard error = 0.0038) between D. pulex and D. pulicaria suggests that the species status assigned to D. pulicaria may be inappropriate. Furthermore, previous work has shown that D. pulicaria is often paraphyletic with respect to D. pulex (e.g., Crease et al. 1989; Lehman et al. 1995; Crease et al. 1997; Dudycha 2004). Yet, for some loci/types of data, D. pulicaria does have a unique genotypic constellation to the exclusion of D. pulex (e.g., Crease et al. 1997; Colbourne et al. 1998; Černý and Hebert 1999). Our total evidence analysis of six nuclear protein-coding loci reveals that D. pulicaria and D. arenata are monophyletic groups (PP = 0.99, PP = 1, respectively; Figure 2), supporting the notion that D. pulex, D. pulicaria, and D. arenata are distinct species. Many studies report improved resolution and greater node support when data from multiple loci are combined (e.g., Remsen and Desalle 1998), perhaps explaining the paraphyly for D. pulex and D. pulicaria in earlier studies that is not observed here.
We used a divergence population-genetics approach to address whether a simple isolation model is appropriate for D. pulex and D. pulicaria. Both IMa and LAMARC analyses reveal that gene flow does occur between D. pulex and D. pulicaria, thereby ruling out a strict isolation speciation model. One migrant gene copy per generation, on average, may prevent substantial divergence at a locus (Wright 1931). Although the point estimates obtained with IMa are clearly below this, the upper bound of the 90% highest posterior density intervals exceed one, as do the migration estimates obtained with LAMARC. Despite the fact that LAMARC and IMa differ in their underlying assumptions, the confidence intervals for the estimates obtained with the different programs do overlap, with estimates obtained in LAMARC being higher (Table 7).
In contrast to IMa, LAMARC assumes migration equilibrium and accounts for intralocus recombination. Loci with unacknowledged recombination are expected to have longer gene trees, on average, than nonrecombining loci (Won and Hey 2005). Here, inferred migration events are spread over a longer time period, perhaps explaining the lower gene flow estimates obtained with the IMa program. Other studies that have used IMa with the largest nonrecombining block of sequence data vs. the full locus (with recombination) have revealed that migration estimates are not significantly affected (although in one case they did decrease); however, estimates of population size are substantially inflated when ignoring recombination (Bull et al. 2006; Strasburg and Rieseberg 2008). Thus, estimates of population size for D. pulex and D. pulicaria that were obtained in IMa should be regarded as an upper bound.
Numerous studies have outlined physiological and life history differences between North American D. pulex and D. pulicaria (e.g., Brandlova et al. 1972; Tessier and Consolatti 1991; Dudycha 2004; Weider et al. 2004). In some parts of their distribution, D. pulex and D. pulicaria switch to sexual reproduction in response to different photoperiodic cues, resulting in a prereproductive isolating barrier (Deng 1997), and they usually occupy different but geographically overlapping habitats. D. pulex typically resides in vernal ponds with leaf litter whereas D. pulicaria occupies lakes that contain fish (e.g., Hebert et al. 1993; Hebert 1995; Hebert and Finston 2001). Despite the above observations, hybrids between D. pulex and D. pulicaria do commonly occur, but are found to be obligately asexual in nature (e.g., Hebert and Crease 1983; Hebert et al. 1993; Hebert and Finston 2001). Laboratory studies, however, have revealed that these hybrids are sexual and easily backcrossed (Heier and Dudycha 2009). Our divergence population genetics approach, on the basis of nuclear loci, is consistent with the above observations—D. pulex and D. pulicaria have undergone genetic differentiation as a result of different ecological pressures, but still exchange genes at a level that may be high enough to prevent reproductive isolation.
Acknowledgments
Special thanks to John Colbourne and Mike Pfrender for assembling databases that were used for primer design. We also thank Teri Crease, Dee Denver, Jeff Dudycha, Eric Rynes, Doug Scofield, Lucian Smith, and Derek Taylor for helpful advice. Lawrence Washington, Yelena Radivojac, and Brian Molter provided excellent technical assistance. Desiree Allen, John Colbourne, Sandy Connelly, Koen De Gelas, Jeff Dudycha, John Havel, Karen Looper, Mike Pfrender, Sarah Schaack, and Emily Williams provided Daphnia specimens. Part of this work was carried out using the Computational Biology Service Unit at Cornell University, which is partially funded by Microsoft Corporation. This work was supported by a National Science Foundation IGERT fellowship (to A.R.O.), National Science Foundation grants DEB-0196450 and EF-0328516, and National Institutes of Health grant R01-GM36827 (to M.L.).
Sequence data from this article have been deposited with the EMBL/GenBank Data Libraries under accession nos. EU918429–EU918560.
Supporting information is available online at http://www.genetics.org/cgi/content/full/genetics.108.099549/DC1.
References
- Alonso, M., 1996. Crustacea, Branchiopoda, Anomopoda. Museum Nacional de Ciencias Naturales, Madrid.
- Andolfatto, P., 2001. Contrasting patterns of X-linked and autosomal nucleotide variation in Drosophila melanogaster and Drosophila simulans. Mol. Biol. Evol. 18 279–290. [DOI] [PubMed] [Google Scholar]
- Andolfatto, P., 2005. Adaptive evolution of non-coding DNA in Drosophila. Nature 437 1149–1152. [DOI] [PubMed] [Google Scholar]
- Andolfatto, P., and M. Nordborg, 1998. The effect of gene conversion on intralocus associations. Genetics 148 1397–1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandelt, H. J., P. Forster and A. Röhl, 1999. Median-joining networks for inferring intraspecific phylogenies. Mol. Biol. Evol. 16 37–48. [DOI] [PubMed] [Google Scholar]
- Besansky, N. J., J. Krzywinski, T. Lehmann, F. Simard, M. Kern et al., 2003. Semipermeable species boundaries between Anopheles gambiae and Anopheles arabiensis: evidence from multilocus DNA sequence variation. Proc. Natl. Acad. Sci. USA 100 10818–10823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandlova, J., Z. Brandl and C. H. Fernando, 1972. The Cladocera of Ontario with remarks on some species and distribution. Can. J. Zool. 50 1373–1403. [Google Scholar]
- Bull, V., M. Beltran, C. D. Jiggins, W. O. McMillan, E. Bermingham et al., 2006. Polyphyly and gene flow between non-sibling Heliconius species. BMC Biol. 4 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Černý, M., and P. D. N. Hebert, 1999. Intercontinental allozyme differentiation among four holarctic Daphnia species. Limnol. Oceanogr. 44 1381–1387. [Google Scholar]
- Colbourne, J. K., and P. D. N. Hebert, 1996. The systematics of North American Daphnia (Crustacea: Anomopoda): a molecular phylogenetic approach. Proc. R. Soc. Lond. Ser. B 351 349–360. [DOI] [PubMed] [Google Scholar]
- Colbourne, J. K., T. J. Crease, L. J. Weider, P. D. N. Hebert, F. Dufresne et al., 1998. Phylogenetics and evolution of a circumarctic species complex (Cladocera: Daphnia pulex). Biol. J. Linn. Soc. 65 347–365. [Google Scholar]
- Comeron, J. M., 1995. A method for estimating the numbers of synonymous and nonsynonymous substitutions per site. J. Mol. Evol. 41 1152–1159. [DOI] [PubMed] [Google Scholar]
- Crease, T. J., D. J. Stanton and P. D. N. Hebert, 1989. Polyphyletic origins of asexuality in Daphnia pulex. Mitochondrial DNA variation. Evolution 43 1016–1026. [DOI] [PubMed] [Google Scholar]
- Crease, T. J., M. Lynch and K. Spitze, 1990. Hierarchical analysis of isozyme and mitochondrial DNA variation in Daphnia pulex. Mol. Biol. Evol. 7 444–458. [DOI] [PubMed] [Google Scholar]
- Crease, T. J., S. K. Lee, S. L. Yu, K. Spitze, N. Lehman et al., 1997. Allozyme and mtDNA variation in populations of the Daphnia pulex complex from both sides of the Rocky Mountains. Heredity 79 242–251. [Google Scholar]
- Cristescu, M. E. A., J. K. Colbourne, Y. Radivojac and M. Lynch, 2006. A microsatellite based genetic linkage map of the waterflea, Daphnia pulex: on the prospect of crustacean genomics. Genomics 88 415–430. [DOI] [PubMed] [Google Scholar]
- Cronn, R., M. Cedroni, T. Haselkorn, C. Grover and J. F. Wendel, 2002. PCR-mediated recombination in amplification products derived from polyploid cotton. Theor. Appl. Genet. 104 482–489. [DOI] [PubMed] [Google Scholar]
- Deng, H. W., 1997. Photoperiodic response of sexual reproduction in the Daphnia pulex group is reversed in two distinct habitats. Limnol. Oceanogr. 42 609–611. [Google Scholar]
- Dudycha, J. L., 2004. Mortality dynamics of Daphnia in contrasting habitats and their role in ecological divergence. Freshw. Biol. 49 505–514. [Google Scholar]
- Endler, J. A., 1977. Geographic Variation, Speciation, and Clines. Princeton University Press, Princeton, NJ. [PubMed]
- Felsenstein, J., 1993. PHYLIP (Phylogeny Inference Package), version 3.5c. Department of Genetics, University of Washington, Seattle.
- Forbes, S. A., 1893. A preliminary report on the aquatic invertebrate fauna of the Yellowstone National Park, Wyoming, and the Flathead Region of Montana. Bull. U.S. Fish Comm. 11 207–256. [Google Scholar]
- Geyer, C. J., 1991. Estimating normalizing constants and reweighting mixtures in Markov chain Monte Carlo. Technical Report No. 568, revised 1994. School of Statistics, University of Minnesota, Minneapolis.
- Haag-Liautard, C., M. Dorris, X. Maside, S. Macaskill, D. Halligan et al., 2007. Direct estimation of per nucleotide and genomic deleterious mutation rates in Drosophila. Nature 445 82–85. [DOI] [PubMed] [Google Scholar]
- Haddrill, P. R., K. R. Thornton, B. Charlesworth and P. Andolfatto, 2005. Multilocus patterns of nucleotide variability and the demographic and selection history of Drosophila melanogaster populations. Genome Res. 15 790–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasegawa, M., H. Kishino and T. A. Yano, 1985. Dating of the human-ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 22 160–174. [DOI] [PubMed] [Google Scholar]
- Hebert, P. D. N., 1974. Enzyme variability in natural populations of Daphnia magna II. Genotypic frequencies in permanent populations. Genetics 77 323–334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hebert, P. D. N., 1995. The Daphnia of North America: An Illustrated Fauna. CD-ROM, University of Guelph, Ontario, Canada.
- Hebert, P. D. N., and T. J. Crease, 1983. Clonal diversity in populations of Daphnia pulex reproducing by obligate parthenogenesis. Heredity 51 353–369. [Google Scholar]
- Hebert, P. D. N., and T. L. Finston, 2001. Macrogeographic patterns of breeding system diversity in the Daphnia pulex group from the United States and Mexico. Heredity 87 153–161. [DOI] [PubMed] [Google Scholar]
- Hebert, P. D. N., M. J. Beaton, S. S. Schwartz and D. J. Stanton, 1989. Polyphyletic origins of asexuality in Daphnia pulex. I. Breeding system variation and levels of clonal diversity. Evolution 43 1004–1015. [DOI] [PubMed] [Google Scholar]
- Hebert, P. D. N., S. S. Schwartz, R. D. Ward and T. L. Finston, 1993. Macrogeographic patterns of breeding system diversity in the Daphnia pulex group. I. Breeding systems of Canadian populations. Heredity 70 148–161. [DOI] [PubMed] [Google Scholar]
- Heier, C. R., and J. L. Dudycha, 2009. Ecological speciation in cyclic parthenogens: sexual capability of experimental hybrids between Daphnia pulex and Daphnia pulicaria. Limnol. Oceanogr. 52 492–502. [Google Scholar]
- Hey, J., 2006. Recent advances in assessing gene flow between diverging populations and species. Curr. Opin. Genet. Dev. 16 592–596. [DOI] [PubMed] [Google Scholar]
- Hey, J., and R. Nielsen, 2004. Multilocus methods for estimating population sizes, migration rates, and divergence time, with applications to the divergence of Drosophila pseudoobscura and D. persimilis. Genetics 167 747–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey, J., and R. Nielsen, 2007. Integration within the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. Proc. Natl. Acad. Sci. USA 104 2785–2790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson, R. R., 1987. Estimating the recombination parameter of a finite population model without selection. Genet. Res. 50 245–250. [DOI] [PubMed] [Google Scholar]
- Hudson, R. R., M. Kreitman and M. Aguade, 1987. A test of neutral molecular evolution based on nucleotide data. Genetics 116 153–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huelsenbeck, J. P., and F. Ronquist, 2001. MRBAYES: Bayesian inference of phylogenetic trees. Bioinformatics 17 754–755. [DOI] [PubMed] [Google Scholar]
- Ishida, S., and D. J. Taylor, 2007. Mature habitats associated with genetic divergence despite strong dispersal ability in an arthropod. BMC Evol. Biol. 7 52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jukes, T. H., and C. R. Cantor, 1969. Evolution of protein molecules, pp. 21–132 in Mammalian Protein Metabolism, edited by H. N. Munro. Academic Press, New York.
- Kishino, H., and M. Hasegawa, 1989. Evaluation of the maximum likelihood estimate of the evolutionary tree topologies from DNA sequence data and the branching order in Hominoidea. J. Mol. Evol. 29 170–179. [DOI] [PubMed] [Google Scholar]
- Kreitman, M., 1983. Nucleotide polymorphism at the alcohol-dehydrogenase locus of Drosophila melanogaster. Nature 304 412–417. [DOI] [PubMed] [Google Scholar]
- Kuhner, M. K., 2006. LAMARC 2.0: maximum likelihood and Bayesian estimation of population parameters. Bioinformatics 22 768–770. [DOI] [PubMed] [Google Scholar]
- Kumar, S., K. Tamura and M. Nei, 2004. MEGA3: integrated software for molecular evolutionary genetics analysis and sequence alignment. Brief. Bioinformatics 5 150–163. [DOI] [PubMed] [Google Scholar]
- Lehman, N., M. E. Pfrender, P. A. Morin, T. J. Crease and M. Lynch, 1995. A hierarchical molecular phylogeny within the genus Daphnia. Mol. Phylogenet. Evol. 4 395–407. [DOI] [PubMed] [Google Scholar]
- Leydig, F., 1860. Naturgeschichte der Daphniden. Verlag der H. Laupp'shen Buchhandlung, Tübingen, Germany.
- Li, W-H., 1993. Unbiased estimation of the rates of synonymous and nonsynonymous substitution. J. Mol. Evol. 36 96–99. [DOI] [PubMed] [Google Scholar]
- Little, T. J., J. K. Colbourne and T. J. Crease, 2004. Molecular evolution of Daphnia immunity genes: polymorphism in a gram-negative binding protein gene and an alpha-2-macroglobulin gene. J. Mol. Evol. 59 498–506. [DOI] [PubMed] [Google Scholar]
- Lynch, M., 2006. The origins of eukaryotic gene structure. Mol. Biol. Evol. 23 450–468. [DOI] [PubMed] [Google Scholar]
- Lynch, M., 2007. The Origins of Genome Architecture. Sinauer Associates, Sunderland, MA.
- Lynch, M., and T. J. Crease, 1990. The analysis of population survey data on DNA sequence variation. Mol. Biol. Evol. 7 377–394. [DOI] [PubMed] [Google Scholar]
- Lynch, M., and B. Walsh, 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA).
- Lynch, M., A. Seyfert, B. Eads and E. Williams, 2008. Localization of the genetic determinants of meiosis suppression in Daphnia pulex. Genetics 180 317–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machado, C. A., R. M. Kliman, J. A. Markert and J. Hey, 2002. Inferring the history of speciation from multilocus DNA sequence data: the case of Drosophila pseudoobscura and close relatives. Mol. Biol. Evol. 19 472–488. [DOI] [PubMed] [Google Scholar]
- Maynard Smith, J., 1966. Sympatric speciation. Am. Nat. 100 637–650. [Google Scholar]
- Mergeay, J., X. Aguilera, S. Declerck, A. Petrusek, T. Huyse et al., 2008. The genetic legacy of Bolivian Daphnia: the tropical Andes as a source for the North and South American D. pulicaria complex. Mol. Ecol. 17 1789–1800. [DOI] [PubMed] [Google Scholar]
- Moriyama, E. N., and J. R. Powell, 1996. Intraspecific nuclear DNA variation in Drosophila. Mol. Biol. Evol. 13 261–277. [DOI] [PubMed] [Google Scholar]
- Mort, M. A., and H. G. Wolf, 1986. The genetic structure of large lake Daphnia populations. Evolution 40 756–766. [DOI] [PubMed] [Google Scholar]
- Mukabayire, O., J. Caridi, X. Wang, Y. T. Toure, M. Coluzzi et al., 2001. Patterns of DNA sequence variation in chromosomally recognized taxa of Anopheles gambiae: evidence from rDNA and single copy loci. Insect Mol. Biol. 10 33–46. [DOI] [PubMed] [Google Scholar]
- Omilian, A. R., M. E. A. Cristescu, J. L. Dudycha and M. Lynch, 2006. Ameiotic recombination in asexual lineages of Daphnia. Proc. Natl. Acad. Sci. USA 103 18638–18643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omilian, A. R., D. G. Scofield and M. Lynch, 2008. Intron presence-absence polymorphisms in Daphnia. Mol. Biol. Evol. 25 2129–2139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palsson, S., 2000. Microsatellite variation in Daphnia pulex from both sides of the Baltic Sea. Mol. Ecol. 9 1075–1088. [DOI] [PubMed] [Google Scholar]
- Pamilo, P., and N. O. Bianchi, 1993. Evolution of the Zfx and Zfy genes: rates and interdependence between the genes. Mol. Biol. Evol. 10 271–281. [DOI] [PubMed] [Google Scholar]
- Peters, R. H., and R. de Bernardi, 1987. Memorie dell'Istituto Italiano di Idrobiologia, Vol. 45: Daphnia. Verbania Palanza, Palanza, Italy.
- Posada, D., and K. A. Crandall, 1998. MODELTEST: testing the model of DNA substitution. Bioinformatics 14 817–818. [DOI] [PubMed] [Google Scholar]
- Posada, D., and K. A. Crandall, 2001. Intraspecific gene genealogies: trees grafting into networks. Trends Ecol. Evol. 16 37–45. [DOI] [PubMed] [Google Scholar]
- Remsen, J., and R. DeSalle, 1998. Character congruence of multiple data partitions and the origin of the Hawaiian Drosophilidae. Mol. Phylogenet. Evol. 9 225–235. [DOI] [PubMed] [Google Scholar]
- Rice, W. R., and E. F. Hostert, 1993. Laboratory experiments on speciation: what have we learned in 40 years. Int. J. Org. Evol. 47 1637–1653. [DOI] [PubMed] [Google Scholar]
- Rozas, J., J. C. Sanchez-DelBarrio, X. Messeguer and R. Rozas, 2003. DnaSP, DNA polymorphism analyses by the coalescent and other methods. Bioinformatics 19 2496–2497. [DOI] [PubMed] [Google Scholar]
- Schmid, K. J., S. Ramos-Onsins, H. Ringys-Beckstein, B. Weisshaar and T. Mitchell-Olds, 2005. A multilocus sequence survey in Arabidopsis thaliana reveals a genomewide departure from a neutral model of DNA sequence polymorphism. Genetics 169 1601–1615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soetaert, A., L. N. Moens, K. Van der Ven, K. Van Leemput, B. Naudts et al., 2006. Molecular impact of propiconazole on Daphnia magna using a reproduction-related cDNA array. Comp. Biochem. Physiol. 142 66–76. [DOI] [PubMed] [Google Scholar]
- Strasburg, J. L., and L. H. Rieseberg, 2008. Molecular demographic history of the annual sunflowers Helianthus annuus and H. petiolaris: large effective population sizes and rates of long-term gene flow. Evolution 62 1936–1950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima, F., 1983. Evolutionary relationship of DNA sequences in finite populations. Genetics 105 437–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima, F., 1989. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima, F., 1996. The amount of DNA polymorphism maintained in a finite population when the neutral mutation rate varies among sites. Genetics 143 1457–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tessier, A. J., and N. L. Consolatti, 1991. Resource quantity and offspring quality in Daphnia. Ecology 72 468–478. [Google Scholar]
- Thompson, J. D., D. G. Higgins and T. J. Gibson, 1994. ClustalW: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position specific gap penalties, and weight matrix choice. Nucleic Acids Res. 22 4673–4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakeley, J., 2000. The effects of subdivision on the genetic divergence of populations and species. Evolution 54 1092–1101. [DOI] [PubMed] [Google Scholar]
- Wakeley, J., and J. Hey, 1997. Estimating ancestral population parameters. Genetics 145 847–855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakeley, J., and J. Hey, 1998. Testing speciation models with DNA sequence data, pp. 157–175 in Molecular Approaches to Ecology and Evolution, edited by R. DeSalle and B. Schierwater. Birkhäuser Verlag, Boston.
- Wang, R. L., J. Wakeley and J. Hey, 1997. Gene flow and natural selection in the origin of Drosophila pseudoobscura and close relatives. Genetics 147 1091–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe, H., N. Tatarazako, S. Oda, H. Nishide, I. Uchiyama et al., 2005. Analysis of expressed sequence tags of the water flea Daphnia magna. Genome 48 606–609. [DOI] [PubMed] [Google Scholar]
- Watterson, G. A., 1975. Number of segregating sites in genetic models without recombination. Theor. Popul. Biol. 7 256–276. [DOI] [PubMed] [Google Scholar]
- Weider, L. J., and A. Hobaek, 1997. Postglacial dispersal, glacial refugia, and clonal structure in Russian/Siberian populations of the Arctic Daphnia pulex complex. Heredity 78 363–372. [Google Scholar]
- Weider, L. J., K. L. Glenn, M. Kyle and J. J. Elser, 2004. Associations among ribosomal (r)DNA intergenic spacer length, growth rate, and C: N: P stoichiometry in the genus Daphnia. Limnol. Oceanogr. 49 1417–1423. [Google Scholar]
- Won, Y. J., and J. Hey, 2005. Divergence population genetics of chimpanzees. Mol. Biol. Evol. 22 297–307. [DOI] [PubMed] [Google Scholar]
- Wright, S., 1931. Evolution in Mendelian populations. Genetics 16 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, S., 1943. Isolation by distance. Genetics 28 114–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, S. I., and B. S. Gaut, 2005. Molecular population genetics and the search for adaptive evolution in plants. Mol. Biol. Evol. 22 506–519. [DOI] [PubMed] [Google Scholar]