Darwinian and demographic forces affecting human protein coding genes

Abstract

Past demographic changes can produce distortions in patterns of genetic variation that can mimic the appearance of natural selection unless the demographic effects are explicitly removed. Here we fit a detailed model of human demography that incorporates divergence, migration, admixture, and changes in population size to directly sequenced data from 13,400 protein coding genes from 20 European-American and 19 African-American individuals. Based on this demographic model, we use several new and established statistical methods for identifying genes with extreme patterns of polymorphism likely to be caused by Darwinian selection, providing the first genome-wide analysis of allele frequency distributions in humans based on directly sequenced data. The tests are based on observations of excesses of high frequency–derived alleles, excesses of low frequency–derived alleles, and excesses of differences in allele frequencies between populations. We detect numerous new genes with strong evidence of selection, including a number of genes related to psychiatric and other diseases. We also show that microRNA controlled genes evolve under extremely high constraints and are more likely to undergo negative selection than other genes. Furthermore, we show that genes involved in muscle development have been subject to positive selection during recent human history. In accordance with previous studies, we find evidence for negative selection against mutations in genes associated with Mendelian disease and positive selection acting on genes associated with several complex diseases.

Complete data on DNA sequence from multiple individuals provide the gold standard for inference of population genetic factors, including the inference of Darwinian selection. It is widely hoped that by flagging genes undergoing Darwinian natural selection, it will be possible to identify genes that may affect human-specific traits or human phenotypic variation. Much interest has, for example, focused on genes that may explain the increase in brain size in humans compared with other primates (Evans et al. 2005; Mekel-Bobrov et al. 2005) or genes associated with human genetic diseases (Bustamante et al. 2005; Kelley et al. 2006). In some genome-wide studies, researchers have identified individual genes likely to have been targeted by selection using the ratio of nonsynonymous to synonymous mutations identified through comparisons between different species (Clark et al. 2003; Nielsen et al. 2005a) or using both population genetic and interspecific data (Bustamante et al. 2005). Other studies have used single nucleotide polymorphisms (SNPs) from available databases to identify regions in the human genome that may recently have been targeted by selection (Akey et al. 2002; Carlson et al. 2005; Ronald and Akey 2005; Kelley et al. 2006; Voight et al. 2006; Wang et al. 2006). Together, these studies are beginning to provide a picture of how Darwinian selection has acted to form the human genome. For example, genes involved in the immune system or in gametogenesis, certain transcription factors, apoptosis-related genes, and olfactory receptors seem more often to have been targeted by positive selection, i.e., selection favoring the fixation of new mutations. A number of individual genes that may underlie phenotypic variability or species-specific differences have also been identified (Clark et al. 2003; Voight et al. 2006; for a recent review of the literature, see Nielsen 2005; Kelley et al. 2006; Sabeti et al. 2006).

One special challenge when scanning a genome for evidence of selection is that variability in the genome is also strongly affected by demographic processes, such as population growth or bottlenecks, and by variation in the mutation and recombination processes (Simonsen et al. 1995; Nielsen 2001; Przeworski 2002). Variability in the genome has been modulated through a complex interaction of random processes, selection, mutation, and recombination. While the methods based on comparing nonsynonymous and synonymous mutations are relatively robust to these factors, methods using the frequency of alleles within populations, in one way or another, are not. Extra attention must, therefore, be paid to the effect of demographic factors and variation in the mutation and recombination rates (Nielsen 2001; Currat et al. 2006).

In this article, we present an analysis of 13,400 human genes directly sequenced in 20 European-Americans (EAs) and 19 African-Americans (AAs). Using several different computational tools and a complex demographic model to partially control for the effects of demography, we identify genes and groups of genes targeted by selection in humans currently or in the past. Most other large-scale data sets in humans have been constructed through a complicated process in which SNPs have first been identified based on a panel of just a few individuals and subsequently typed in a larger panel. This complicates the interpretation of the data, because this SNP discovery process introduces an ascertainment bias (e.g., Nielsen and Signorovitch 2003; Nielsen et al. 2004). For many large-scale SNP data sets (e.g., dbSNP and HapMap data), the ascertainment protocols vary considerably among different regions, complicating the interpretation of the data and invalidating the use of standard genomic methods for detecting selection. However, the data analyzed here have been obtained through direct sequencing and do not suffer from any of these problems.

Previous studies of this collection of directly sequenced genes have focused on detecting positive selection that increases or decreases the rate of substitution among species (Clark et al. 2003; Bustamante et al. 2005; Nielsen et al. 2005a). However, selection may also affect other properties of the data, in particular an excess or deficiency of low or high frequency polymorphisms (Gillespie 1978; Braverman et al. 1995; Przeworski 2002; Charlesworth 2006). Focusing on different aspects of the data allows us to identify loci targeted by Darwinian selection that may have, thus far, eluded detection by other approaches.

Methods for detecting selection based on allele frequency distributions include Tajima's D (Tajima 1989), Fay and Wu's H (Fay and Wu 2000), the use of F_ST (e.g., Carlson et al. 2005), the HKA test (Hudson et al. 1987), and a number of other statistics. These statistics can all be calculated as functions of the so-called two-dimensional site frequency spectrum (2D-SFS). The 2D-SFS summarizes the joint allele frequencies in the two populations in a matrix containing the number of SNPs with sample frequency i in one population and j in the other population in the (i, j)th entry of the matrix. To detect selection we devise a number of different statistics that summarize specific aspects of the 2D-SFS. This allows us to examine different aspect of the action of selection and distinguish between different types of selection.

Results

Admixture and demography

Our inference procedure has three steps. We first estimate admixture proportions between Africans and Europeans for all individuals in the sample. Then, given these admixture proportions, we estimate the parameters of a human demographic model. We then carry out tests of neutrality using the estimated demographic model (with admixture) as the null-model instead of using a standard neutral model.

The admixture proportions were estimated using a maximum likelihood approach (for details, see Methods). The estimates of the admixture proportions were 0% for all EA individuals. For AAs, we obtained estimates of 0% admixture for 15 individuals and 23%, 27%, 40%, and 42% for the remaining four individuals. The estimates of 0% admixture for most of the individuals may likely be an artifact caused by a lack of parental sample populations for these loci. We have, therefore, also repeated the analysis of significant genes using models based on other admixture assumptions.

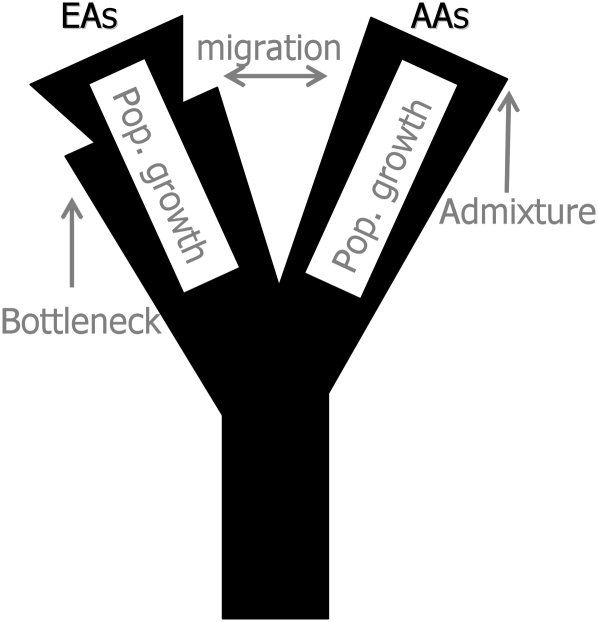
Demographic parameters were then estimated for a model that assumes divergence of the African and European populations from a common ancestral population T generations ago. Also, a model allowing a bottleneck in African did not improve upon the fit of the model. It is assumed that both populations have been expanding exponentially since the divergence event at rate α_A and α_E for Africans and Europeans, respectively (Slatkin and Hudson 1991). Gene-flow at a rate of m migrants per generation was also allowed between the two populations, and the ratio of the current African to European population sizes was set to γ. Finally, we assume that the European population went through a bottleneck 0.1 × 2N_e generations ago, which lasted 0.01 × 2N_e generations, and reduced the population size by a factor β. The reason for fixing some of these parameters' values is that the data do not allow independent estimation of all parameters (e.g., Adams and Hudson 2004; Myers et al. 2008) and that a relatively recent European bottleneck is consistent with previous efforts for estimating demographic parameters from human nuclear data (e.g., Schaffner et al. 2005). The demographic model is summarized in Figure 1.

Figure 1.

A graphical illustration of the model of the demographic history of European-Americans (EAs) and African-Americans (AAs).

The estimation procedure applied here is based on fitting the demographic model to the 2D-SFS. In brief, a coalescent simulation approach similar to the approach suggested by Nielsen (2000) was used to calculate the probability of observing a particular distribution of SNP allele frequencies. Taking a product of the probabilities of all SNPs provides a composite likelihood function, which can be optimized to provide estimates of the demographic parameters (for more details, see Methods).

Because the frequency spectrum differs between the X chromosome and the autosomes, and because migration rates and effective population sizes may differ between males and females, the models were first fitted to the autosomal data. Based on the estimates from the autosomal data of α_A, α_E, β, and γ, estimates of m and T are then subsequently obtained from X chromosome data.

The maximum likelihood estimates of the parameters based on the autosomal data were T = 0.099, α_A = 9.5, and α_E = 21.1, γ = 1.82, β = 0.018, and m = 6.67, when all parameters are scaled with the current European population size (N_e). Calibrating with the observed number of human–chimp nucleotide differences and the average number of segregating sites in the European sample and assuming 6 million years (Myr) of divergence between humans and chimpanzees, we obtain an estimate of the current effective European population size of 15,500 individuals. The estimate of the divergence time between Europeans and Africans is then 1535 generations, or about 92,000 yr, assuming a generation time of 30 yr. The estimate of the average European growth rate becomes approximately 0.07% per generation since the African–European divergence. These results are similar, but not identical to the estimates by Schaffner et al. (2005). They assumed an out-of-Africa divergence time of 3500 generations (corresponding to 105,000 yr assuming a generation time of 30) and obtained an Africa–European migration rate of 3.2 × 10⁻⁵. Our estimates of the migration rate is ∼2 × 10⁻⁴, almost an order of magnitude larger than the estimate by Schaffner et al. (2005). We are not certain what causes the discrepancy, but inadequate modeling of the admixture in AAs is one obvious explanation.

The estimate from the X chromosome data of m and T was m = 2.75 and T = 0.14. A higher estimate of T for X chromosome data is expected because of the lower effective population size of the X chromosome compared to autosomes.

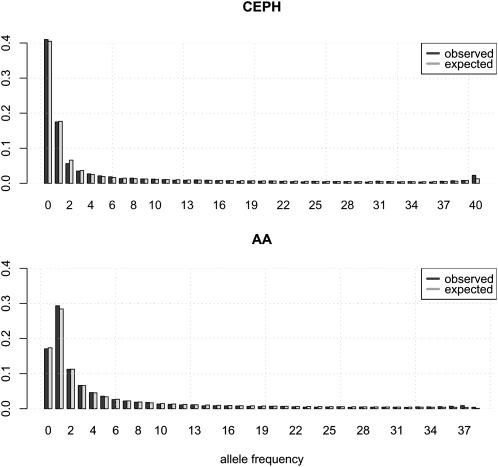
The model provided quite a good fit to the data as illustrated by the predicted and observed marginal frequency spectra (Fig. 2). The demographic model could not be rejected by a goodness-of-fit test comparing the expected and observed two-dimensional frequency spectrum (P = 0.54 and 0.18 for autosomal and X chromosome data, respectively). The goodness-of-fit test was performed using a full simulation procedure taking linkage and recombination into account (for details, see Methods).

Figure 2.

The unfolded marginal frequency spectra predicted from the best-fitting model (simulated) and the observed marginal frequency for European-Americans (top) and African-Americans (bottom) from the autosomal data. The zero category represents SNPs that are absent from one population but present in the other.

Tests of neutrality

With the exception of tests based on haplotype structure, most neutrality tests are based on statistics derived from the 2D-SFS, possibly combined with the number of fixed differences (FDs) between species. We have derived a number of new tests based on various aspects of the 2D-SFS (which in our definition includes FDs) that will help distinguish between different types of selection. The tests are described in more detail in the Methods section. The G2D test uses all of the information in the 2D-SFS data and will be sensitive to any deviations from neutrality. It measures the fit of the SNP allele frequencies and FDs in a particular gene compared with the overall pattern seen in the genome. The MWU-high and MWU-low test detect an increase in the proportion of high and low frequency polymorphisms, respectively; and F_ST detects elevated differences in allele frequencies between AAs and EAs. Significance is determined using a detailed coalescent simulation procedure that takes demography, admixture, intergenic linkage, missing data, and multiple hits into account. In brief, data are simulated for each gene to match the same number of mutations as were observed, and the distributions of the test statistics for these simulated data are compared to the observed values (see Methods section). All tests are performed on the unfolded frequency spectrum using comparisons with the chimpanzee, unless otherwise noted. The possibility of incorrect assignment of ancestral states is taken into account when assigning P-values (see Methods).

A 5% false discovery rate (FDR) set (see Methods) for the G2D test contains 737 genes out of 7911 genes with more than five polymorphisms or FDs. A Bonferroni correction gives P < 0.01 for the overall significance. For the, F_ST, MWU-high, and MWU-low, the 5% FDR set contains only two, three, and zero genes, respectively, out of 2582 genes with more than five polymorphisms. This illustrates that, after accounting for demographic effects, there is only a strong signal in very few genes. The variability found in the vast majority of genes is easily described by the demographic model. Had we instead used a standard neutral demographic model to obtain critical values, the estimate of the number of true positives would be 2458 for the F_ST-based test and 401for the MWU-low test. This illustrates the dramatic impact demographic assumptions can have on tests of neutrality.

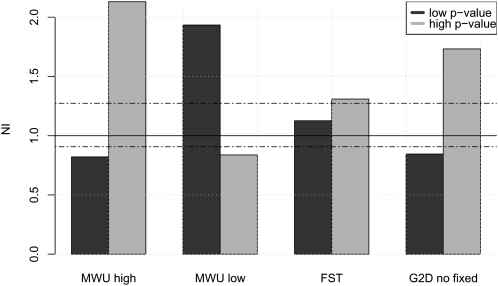
To verify that our tests in fact do detect selection among the most extreme genes, we compared our results to results based on the so-called neutrality index (NI) (Rand and Kann 1996). The NI is given by the ratio of polymorphic to fixed nonsynonymous mutations divided by the ratio of polymorphic to fixed synonymous mutations. If selection is acting recurrently, the NI ought to provide an independent check for consistency of changes imposed by selection. Under neutrality, even under complex demographic models, the expectation of the NI is independent of F_ST, MWU-low, MWU-high, and G2D (see Methods). If selection is not acting on any of the mutations, the ratio of nonsynonymous to synonymous mutations within and between species should be the same. This prediction also holds true for any category of genes that have been chosen based on allele frequency distributions. However, if selection is acting on the genes, we would expect that positive selection, which increases the rate of substitution among species, should cause NI < 1 and negative selection should result in values of NI > 1. However, it should also be noticed that certain types of selection, such as some forms of balancing selection, may have very little impact on the NI (Williamson et al. 2004).

As expected, 200 genes with the smallest P-values according to the MWU-high test have lower NI than the 200 genes with highest P-values (Fig. 3). Likewise, the test based on MWU-low show the opposite pattern of NI values. A small NI indicates positive selection increasing divergence among species or less negative selection, and a large NI indicates negative selection against new mutations or, possibly, some form of balancing selection. The results shown here demonstrate that genes with a skew toward high frequency–derived alleles, as detected by the MWU-high test, have been under positive selection in the past. The results based on G2D with no FDs suggest that this test tends to capture genes under positive selection. Somewhat surprisingly, the test based on F_ST and G2D with FDs shows no difference between NI and the 10 genes with smallest and highest P-values. The results for the G2D test may not be surprising given that this test has significant power to detect both positive and negative selection. Significant genes according to this test will, therefore, consist of a mixture of genes with high NI and with low NI. The results for F_ST may be a bit more surprising and are discussed in more detail in the Discussion section. Detailed results for each gene are provided in Supplemental material S1.

Figure 3.

The median neutrality index (NI) in the 200 genes with largest (light) and smallest (dark) P-value in the MWU-high, MWU-low, and F_ST and G2D tests without fixed differences. The dotted line indicates the global median of NI. Values above one (solid line) indicate negative selection, values below positive selection.

Most extreme allele distribution (G2D)

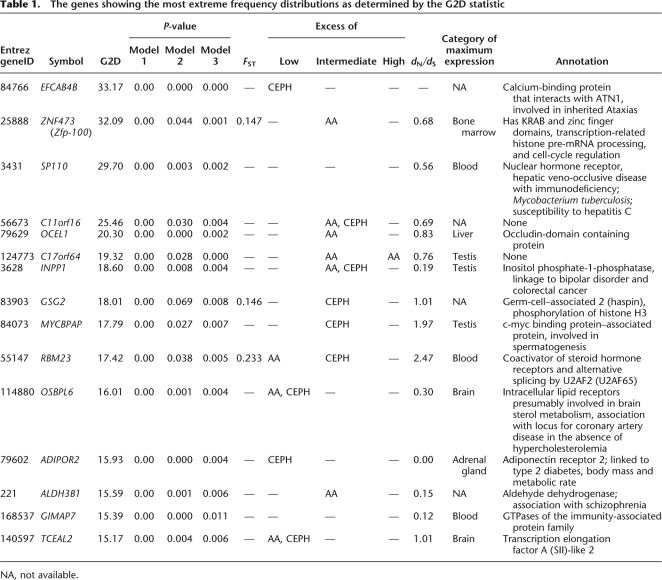
This statistic measures the difference in the distribution of SNP allele frequencies and fixed polymorphisms between the gene and the genome-wide distribution. It summarizes how surprised we should be at observing the data from a particular gene given the information regarding allele frequencies. Out of the 15 genes with smallest P-values (most unusual allele frequency distribution), 9, 5, and 1 genes have an excess of intermediate, low (≤0.2), and high (≥0.8) frequency-derived alleles, respectively, in either population or both, and three genes show significant allele frequency differences between populations (Table 1).

Table 1.

The genes showing the most extreme frequency distributions as determined by the G2D statistic

NA, not available.

The most significant gene, EFCAB4B, has an excess of low frequency alleles and contains no FDs to the chimpanzee. EFCAB4B is a calcium-signaling protein that interacts with ATN1, which has been associated with inherited ataxias (Lim et al. 2006). The excess of low frequency alleles is consistent with slightly deleterious mutations segregating in this gene. The second gene on the list is ZNF473. It shows a high level of population subdivision and has, furthermore, an excess of intermediate-frequency alleles in AAs, indicating that ZNF473 might evolve by balancing selection or is affected by an incomplete selective sweep. ZNF473 has KRAB and zinc-finger domains; this class of proteins has previously been shown to contain positively selected genes (Nielsen et al. 2005a). Surprisingly, this particular protein is involved in transcription-related histone pre-mRNA processing and cell-cycle regulation, which are highly conserved processes (Dominski et al. 2002).

To investigate if our results are likely to be influenced by the specifics of the demographic models, we also analyzed data using two other models. In model 2, we assumed that there was no migration between the populations but that the admixture rate was 20% in all AA. In model 3, we use alternative parameter estimates of T = 0.138, α_A = 10.3, and α_E = 14.1, γ = 1.91, β = 0.021, and m = 4.4. These estimates were obtained using an alternative estimation procedure and slightly different assumptions regarding admixture (see Methods). In general, the P-values using all three models were highly similar (e.g., Table 1), suggesting that our inferences regarding selection are not very sensitive to minor perturbations of the assumed demographic model.

Increased population subdivision (F_ST)

It is of some interest to examine which genes show evidence for elevated F_ST even after fitting the data to a detailed demographic model. F_ST is a measure of population subdivision that takes on large values when populations are highly differentiated genetically, and small values when the populations are genetically similar. A selective sweep that has only affected some of the analyzed populations can greatly increase F_ST (Slatkin and Wiehe 1998; Santiago and Caballero 2005). Therefore, numerous tests have been proposed that use elevated levels of F_ST to detect selection. We here compare the observed F_ST value to the distribution of F_ST values obtained in simulations under the previously estimated demographic model.

Strikingly, the second most significant gene is SLC45A2, which has previously been shown to account for part of the variation in human skin color (Graf et al. 2005, 2007). Only the allele frequencies of TRAF2 differ more between the two populations. TRAF2 forms as complex with TRAF1 to recruit apoptotic repressors. TRAF2 fulfills a wide variety of physiological roles, including from B-cell signaling and inflammatory response (for review, see Au and Yeh 2007). It seems plausible that a gene that is also involved in the defense against viruses and other pathogens will adapt quickly to new environments and therefore segregate faster.

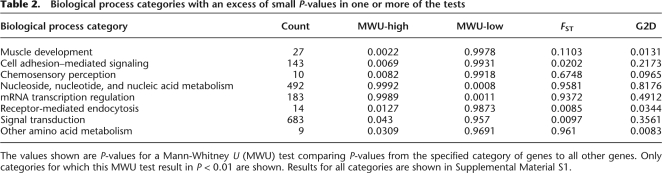
There are two biological process categories with highly significant F_ST in excess of small P-values compared with the genes in the rest of the genome. The first one is receptor-mediated endocytosis, which again suggests selection driven by host–pathogen interactions. The second category is the fairly large collection of genes involved in signal transduction, which features TRAF2 and many small GTPases (e.g., GIT2, RIT2).

Excess of high frequency–derived alleles (MWU-high)

An excess of high frequency polymorphisms is indicative of selection acting to maintain variability in the population, or possibly, the transient effect of a selective sweep as the selected allele increases in frequency in the population. All 15 genes with the smallest P-values for the MWU-high test have also highly significant P-values, if the two populations are considered separately. Furthermore, for almost all of them, the MWU-high on the folded frequency spectrum is not significant. The interpretation of this test is, therefore, fairly clear: a recent, complete or nearly complete selective sweep.

The gene with the largest excess of high frequency–derived alleles is SIGLEC10. One of the first reported physiologically relevant genetic differences between humans and chimpanzees is a deletion in CMAH, the enzyme that converts sialic acids (Chou et al. 1998). Since then multiple other genes involved in sialic acid biology have been reported to be under selection (Altheide et al. 2006). The SIGLEC genes that recognize sialic acid–coated surface proteins evolve particularly fast. This is probably because many pathogens use sialic acid sugar coats to evade recognition by the immune system. The second gene on this list is a key regulator of apoptosis NLRP1 (also known as NALP1). Multiple other apoptosis genes have previously been reported to be positively selected (Nielsen et al. 2005a).

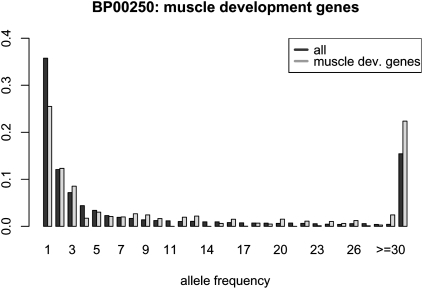
The biological process category showing the strongest evidence for selection according to this criterion (P = 0.0022) is muscle development (Fig. 4, Table 2). The two genes in this category with smallest P-values are MYOM1, a structural protein defining the M-Band of the sarcomere, and MYH1, which encodes a myosin heavy chain of skeletal muscle, and variants are associated with risk of colorectal cancer (Jenkins et al. 2006). Two further muscle-related genes are among the 15 most extreme genes: MYBPHL, which contains functional promoter differences between humans and chimpanzees (Chabot et al. 2007), and PAMR1 (also known as DKFZP586H2123), a regeneration associated muscle protease. MSTN (also known as GDF8) another muscle gene, has previously been reported to be under positive selection (Saunders et al. 2006), and MYH16 received a loss-of-function mutation on the human lineage (Stedman et al. 2004). All in all, muscle biology seems to have undergone many changes during human evolution. The next significant category is cell adhesion–mediated signaling, which is a large category incorporating diverse physiological processes.

Figure 4.

Frequency spectra of all genes combined and of genes involved in muscle development according to the PANTHER database.

Table 2.

Biological process categories with an excess of small P-values in one or more of the tests

The values shown are P-values for a Mann-Whitney U (MWU) test comparing P-values from the specified category of genes to all other genes. Only categories for which this MWU test result in P < 0.01 are shown. Results for all categories are shown in Supplemental Material S1.

The third highly significant biological process category is chemosensory perception, which is mainly due to olfactory receptor genes. These genes show evidence for positive selection using multiple other methods, including McDonald-Kreitman tests (Gilad et al. 2003; Bustamante et al. 2005) and d_N /d_S ratios between humans and chimpanzees (Nielsen et al. 2005a).

Excess of low frequency alleles (MWU-low)

An excess of low frequency polymorphisms can be caused both by the effect of a recent selective sweep and by negative selection acting on deleterious segregating mutations. The biological process categories showing the strongest evidence for an excess of low frequency polymorphisms are nucleoside, nucleotide and nucleic acid metabolism, and mRNA transcription regulation. Note that the latter group is largely a subgroup of the former. The shared significant genes include a wide variety of transcription factors, including ubiquitous ones (CNOT3) to more specialized (FOXK2, POU1F1). Because the 5% FDR was empty for this test, we will not discuss the results of this test further.

MicroRNA-regulated genes experience more negative selection

MicroRNAs are small RNAs that function as negative regulators of translation by binding to mRNAs. Most known microRNAs are highly conserved (Lagos-Quintana et al. 2003; Ibanez-Ventoso et al. 2008), and the predicted binding sites of microRNAs in the 3′ UTRs of genes show evidence of negative selection (Chen and Rajewsky 2006). Here, we show that the protein-coding regions of genes that are putatively regulated by microRNAs, as predicted by Chen and Rajewsky (2006), also experience more negative selection and are more constrained than other genes. First, the median d_N /d_S ratio in microRNA-regulated genes is 0.136, which is considerably lower than for genes that are not predicted to be regulated by microRNAs (0.268). Furthermore, microRNA-regulated genes are much less likely to have an excess of high frequency–derived alleles (MWU-high P > 0.9999) and much more likely to have an excess of low frequency alleles (MWU-low P < 0.0001), suggesting the action of ongoing negative selection on deleterious mutations. MicroRNA-regulated genes also have a marginally higher degree of population subdivision (F_ST, P = 0.03). Not only are microRNA genes highly constrained, they also show more evidence of negative selection acting on mutations segregating in the population than other genes.

Disease-related genes

As several of the tests show an apparent excess of disease-related genes, we compared the ratio of genes with P-values larger and smaller than 0.05 between genes with a morbidity annotation in the OMIM database to genes without such an annotation. The tests based on the frequency spectrum or F_ST show no significant association with morbidity status. The G2-test including FDs to the chimpanzee (P = 0.0057) shows a significant association with OMIM-morbidity. Furthermore, the NI indicates those genes contain slightly deleterious variants that are selected against. However, the OMIM-morbidity index might be a bit biased toward containing true Mendelian disorders, and hence, it is not so surprising that the evolution of those genes is dominated by negative selection. We were more interested in the evolution of genes that are involved in complex traits. We used the list of genes compiled by Hirschhorn et al. (2002). If we consider all genes in the list for which there was also information in our data (N = 157), we find a modest enrichment in genes with an excess of intermediate and a shortage of low frequency alleles (MWU-folded high P = 0.04; MWU-folded low P = 0.037). When we restrict the Hirschhorn list to the studies that have been repeated (N = 61), the MWU-test is significant for the unfolded frequency spectrum, showing that genes associated with complex disease have an excess of high and a shortage of low frequency alleles (MWU-high P = 0.0041; MWU-low P = 0.9957).

These results are in accordance with previously published results by Blekhman et al. (2008), who showed that Mendelian diseases tend to be associated with negative selection while genes associated with complex disease may be under less purifying selection or even under positive selection.

Discussion

The approach taken here avoids many of the pitfalls encountered in studies aimed at detecting selection in humans. Demography is taken into account by fitting a demographic model involving admixture, a bottleneck, divergence, and migration among populations. The tests of neutrality are based solely on the same information used to fit the demographic model. In this way, as much of the variance among loci as possible is ascribed to the demographic model. Residual variation must then be due to selection. The resulting test may be conservative because much of the effect of selection has been attributed to demographic factors, but it will, on the other hand, be unlikely to provide spurious evidence for selection. We note that there are many possible demographic models that have not been explored in this study. It is, therefore, possible that the model we have estimated does not accurately describe the demographic histories of the populations. However, the use of a more accurate demographic model, which can be shown to fit the aspects of the data used to detect selection, is necessarily an improvement over previous scans for selection in the human genome that have assumed simpler and more unrealistic demographic models or that have ignored the problem of confounding demographic effects altogether. The use of a demographic model allows us to base inferences on P-values instead of just relying on an outlier approach. Additionally, we have used correlations with the NI to demonstrate that the most extreme genes identified in this article indeed are under selection.

The sample presented here contains only 78 chromosomes. While the relatively small sample size may be cause for concern in some analyses, it should be noted that several of the tests presented here have been demonstrated to have good power, even for smaller sample sizes. For example, in a study by Nielsen et al. (2005a), the power of the MWU test was evaluated when applied to a sliding window along the chromosome of a sample of only 50 chromosomes. The selection model considered involved a single recent selective sweep, and it was found that the power was larger than 50% when 2Ns > 300, where N is the population size and s is the selection coefficient acting on the selected mutation. The power of a test similar to the G2D test was found to be even higher.

Recent surveys of natural selection in humans have been based on different methods, including analyses of d_N /d_S ratios in the human lineage (Clark et al. 2003; Nielsen et al. 2005a), comparisons between d_N /d_S ratios within and between species (Bustamante et al. 2005), the distribution of F_ST values (Akey et al. 2002), and haplotype structure (Voight et al. 2006). These analyses identify overlapping sets of genes, but sometimes that overlap is small (for reviews, see Sabeti et al. 2006; Nielsen et al. 2007). One reason is that the type of selection identified by these methods may be quite different, and the methods are sensitive to selection occurring at different time scales. For example, methods based on d_N /d_S ratios in the human lineage (Clark et al. 2003) will detect strong recurrent positive selection occurring any time during the past 5–6 Myr of human evolution. In contrast, methods based on haplotype structure (Gabriel et al. 2002; Sabeti et al. 2002; Voight et al. 2006) will tend to detect very recent ongoing selection, possibly associated with just a single selected mutation.

A complete comparison of different scans of selection in the human genome is beyond the scope of this article (but see Sabeti et al. 2006) and may, in any case, not be very informative about the efficacy or appropriateness of the methods due to the aforementioned factors. Nonetheless, it is of some interest to which degree our approach identifies genes previously implicated to be under positive selection. In general, many of the genes with the highest d_N /d_S ratios in the human lineage do not show particularly strong evidence for positive selection according to the tests employed here. For example, PRM1, the gene with the highest d_N /d_S ratios in humans, contains only two polymorphisms and has consequently very moderate P-values for the four tests ranging from 0.38–0.96. Given that this gene shows overwhelming evidence for repeated positive selection based on an excess of nonsynonymous mutations in between-species comparisons, it is possible that the low number of observed polymorphisms in this gene is caused by a recent selective sweep. However, there is also some overlap with genes shown in previous studies to be under positive selection, such as IL4R, which has P-values of 0.04 and 0.0015, according to the G2D and F_ST-based test. This gene was previously flagged as being under selection by Wu et al. (2001). Probably the most famous case of selection in the human genome, the LCT gene, shows little or no evidence for selection based on an excess of high frequency variants (MWU-high P = 0.247). Contributing factors to the relatively high P-value may be that our data set does not contain the entire LCT region but just 14 SNPs and only 39 individuals, and that the type of selection observed in LCT, a very recent incomplete selective sweep, may be hard to detect based on frequency spectrum information alone.

We compared our results to a previous genome scans aimed at detecting regions of the genome affected by selective sweeps by Williamson et al. (2007). Williamson and colleagues used genome-wide SNP data and a composite likelihood approach to detect recent completed selective sweeps. The method is similar in spirit to the current method in that it is based on comparing the frequency spectrum in a local region to the frequency spectrum observed in the rest of the genome. But it differs substantially from the current study in using genome-wide SNP data instead of exonic resequencing data and in using a statistical method that uses the spatial pattern of changes in the frequency spectrum along the sequence and an explicit population genetic model of a recently completed sweep, to detect selection. We would expect large differences between the current study and the Williamson et al. (2007) study, because the Williamson et al. study predominantly has power to detect a recently completed sweep, while the current methods may also detect incomplete selective sweeps, balancing selection, and some forms of negative selection, but may have less power to detect a recently completed sweep. In addition, we would expect the results to differ because of the differences between genome-wide SNP data, which only has few rare SNPs, and direct sequencing data from short regions. However, there is significant correlation between the results from the two studies, at least using the G2D statistic. We tested whether the test statistics calculated in this article were significantly larger among genes flagged as genes in regions under selection by Williamson et al. than among genes not flagged by Williamson et al., using a Mann-Whitney U-test, and obtained P-values of 0.039, 0.062, 1, and 0.056 for the G2D, MWU-high, MWU-low, and F_ST test, respectively. Genes identified by both the Williamson et al. (2007) study and by the G2D statistic (P < 0.05) include P4HA1, RASSF9 (also known as PAMCI), HIST1H2BE, and HIST1H2BF.

The data set analyzed here is the first comprehensive data set of variability in human protein-coding genes that is not based on SNP data, but is based on directly sequenced DNA. The problems associated with ascertainment biases in SNP data are, therefore, avoided. We cannot exclude the possibility that there are other problems with the data, such as missing singletons. However, the data have been produced through a laborious process involving manual verification of each genotype call for each individual. A considerable amount of efforts have been devoted to ensuring the high quality of the data (see Bustamante et al. 2005).

While no study can claim not to be influenced in any way by confounding factors such as demography and ascertainment biases, the current study has been designed to minimize the effect of these factors. The fact that the most extreme genes according to the tests based on allele frequency distributions also have extreme values of the NI further bolsters the confidence that the tests employed here in fact do detect natural selection.

The demographic model estimated from nuclear DNA allows for considerable amounts of migration between European and African populations, beyond what can be ascribed to admixture due to the inclusion of AAs. Interestingly, we obtain somewhat smaller estimates of migration rates for the X chromosome, possibly suggesting male driven gene-flow between populations. While we are reluctant to interpret the results too strongly because of the problems associated with the use of AAs as a population group, our results support the conclusion of previous studies (Harding et al. 1997; Wakeley 1999) that (1) divergence from an ancestral population, (2) migration among populations, and (3) changes in population size must all be included to give an adequate description of human genetic ancestry. Somewhat curiously, only four AA individuals show evidence for admixture; however, those individuals show very strong evidence of admixture. It is possible that the estimation of admixture proportions without the use of appropriate African and European reference populations will tend only to detect admixture in individuals that are very highly admixed. We have therefore also analyzed the data using a model with more admixture (see Methods) and found similar results. The fact that the model fits the data well, even though it includes less admixture in AAs than usually expected, is not surprising given that multiple different demographic models may fit the frequency spectrum equally well (Myers et al. 2008).

There are good theoretical reasons to believe F_ST should capture information regarding recent selective sweeps if selection occurred after the populations split and if the effect of migration is sufficiently weak (Slatkin and Wiehe 1998; Santiago and Caballero 2005). It is not obvious if this is the case for humans, but F_ST has previously been used to scan the genome for selected loci (e.g., Akey et al. 2002). However, F_ST showed no correlation with the NI in the data analyzed here. A contributing factor is most likely that the type of selection detected using F_ST involves a local selective sweep or other forms of population-specific selection, while the NI is sensitive to selection increasing (or decreasing) the rate of amino acid divergence among species. The lack of correlation between NI and F_ST may simply be a consequence of the fact that tests based on these two statistics may detect different forms of selection. A contributing factor may also be that selection typically is not strong enough compared to gene-flow among populations for selective sweeps to increase F_ST. Possibly, population subdivision may not be the best indicator of selection in the human genome, except if selection acts in a population-specific manner in connection to adaptations to the local environment. SLC45A2, which gave the second most significant gene for F_ST and has been shown to be responsible for variation in skin color, might be an example of adaptation to a local environment, i.e., exposure to sunlight.

The various tests applied respond to different temporal courses of natural selection, but because all are based on extant human polymorphism, all examine a relatively recent human past, extending back to perhaps 100,000 yr.

Previous genome-wide studies that have focused on positive selection and accelerated evolution have found brain-specific genes to be highly conserved and show very little evidence for positive selection. However, a lack of acceleration in the human lineage does not necessarily indicate a lack of selection on segregating variants. In this study, several tests identified numerous brain-specific genes, in particular the G2D test and the MWU-high test. The G2D test identified two genes associated with bipolar disorder and schizophrenia, respectively, and the MWU-high test identified two more associated with schizophrenia and HTR7, which has been associated with multiple neuropsychiatric disorders. Our results clearly show that selection has been acting on some genes associated with higher brain function in the recent evolutionary history of humans. Surely, there will be many such genes identified, as the association studies identify them with increasing speed and reliability.

However, the gene ontology category of biological processes showing the strongest excess of high frequency alleles is related to neither higher brain functions nor the immune system, but instead is related to muscle development. It seems plausible that muscle had to change during human evolution to keep up with changes in posture, the demand on precision movements over power, and as response to changes in dietary needs (Stedman et al. 2004). The signal of selection we report here is true for very recent human evolution. Thus, there must also have been some lifestyle changes during the last ∼100,000 yr that required adaptation in muscle development, some of which might still be ongoing (e.g., Saunders et al. 2006).

One general result we find here is that genes predicted to be regulated by microRNAs evolve under strong negative selection and experience much less positive selection than other genes. The extent of microRNA regulation in the human genome may be larger than originally thought (Friedman et al. 2009), and a possible explanation for the negative selection could be the inflated chances for pleiotropic effects of mutations propagating through microRNA-regulated networks.

Methods

Human polymorphism data

The data analyzed in this article have previously been described by Bustamante et al. (2005). It contains 13,400 protein coding genes obtained by direct sequencing from 21 EA and 19 AA individuals. There are a total of 41,151 SNPs in the data set. In tests requiring an outgroup, data from the chimpanzee (Clark et al. 2003) were used.

The human subjects, DNA sequence procedures, quality controls, and IRB approval procedures are all further described by Bustamante et al. (2005). The data have been deposited in dbSNP and can be retrieved using the Applera_GI handle. Genotype data and annotations for each gene also appear in an accessible format as Supplemental material S2.

Estimation of admixture proportions

We used a maximum likelihood approach similar to the Bayesian approach implemented in structure (Pritchard et al. 2000). In brief, the proportion of an individual's (i) genome that is from population k is q⁽ⁱ⁾_k. The n/2 by K matrix, where n/2 and K are the numbers of individuals and populations, respectively, of all values of q⁽ⁱ⁾_k, is denoted by Q. The probability that individual i has genotype jv in locus l is then

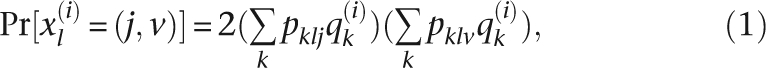where p_klj is the frequency of allele j in locus l in population k. Notice that there is an independence assumption between the two gene copies in each locus. This assumption is not well justified, as admixture proportions are truly properties of parental gene copies and not of diploid individuals. If the admixture proportion differs between the two parents, Equation 1 is not correct. Nonetheless, this is the common assumption used in the popular program structure (Pritchard et al. 2000), and because it appears to provide a useful approximation, we will also make this assumption here. The program structure (Pritchard et al. 2000) is based on a Bayesian approach for estimating admixture proportions using a Dirichlet distribution as prior for q⁽ⁱ⁾_k. We use a maximum likelihood approach for estimating q⁽ⁱ⁾_k assuming the allele frequencies in each population are equal to the observed frequencies. As in the method of Pritchard et al. (2000), the likelihood function is obtained assuming independence among loci and individuals by multiplying the value of Pr[x⁽ⁱ⁾_l = (j, v)] among all values of i and l. The likelihood function can be calculated quite easily when individuals can be assigned to populations a priori. Optimization can be done using any standard algorithms (e.g., Press 2000a). Computationally this is much faster than the Markov chain Monte Carlo (MCMC) used in structure (Pritchard et al. 2000).

Estimation of human demographic parameters

To estimate parameters of a demographic model, we apply a maximum likelihood approach assuming independence among loci. Let the demographic parameters be contained in the vector γ, and p_j(γ) be the probability of observing a SNP of type j γ. A SNP of type j is a SNP in which the mutation occurs at a frequency of j/n in the sample. When the phase of the mutations are not determined, a SNP of type j is any SNP occurring at frequency j/n or (n − j)/n. The values of p_j(γ), j = 1, 2,…, n − 1 give the site frequency spectrum, which summarizes the allele frequency distribution in the data. Note that this is the full or unfolded site frequency spectrum, where the ancestral state is inferred by parsimony using the chimpanzee as an outgroup. The likelihood function is then defined as

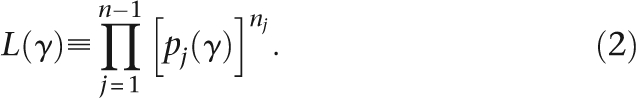Notice here the assumption of independence among SNPs. When SNPs are in linkage disequilibrium (LD), this assumption is not justified. In that case, L(γ) is a composite likelihood function. Estimators based on the composite likelihood function can be shown to be consistent under quite general assumptions (Wiuf 2006). The expected frequency of a new mutation can be found quite generally in terms of an expectation of expected coalescence times (Griffiths and Tavaré 1999). Using the notation of Nielsen (2000), the likelihood function (in the limit of small mutation rates) can be written as

where t_j is the sum of branch-lengths in the tree in which a single mutation would cause a polymorphism of size j, and T is the total tree length. Values of p_j (γ) can then be calculated (approximated) using standard coalescent simulations (Hudson 1983). B coalescent genealogies are simulated under γ. For genealogy i, the total tree length (T_i) and sum of the length of all edges in which a single mutation would cause a mutation of frequency j in the sample (t_ij) are calculated. Then p_j(γ) is approximated as

The value of γ that maximizes L(γ) can be found by repeating this scheme for many different values of γ, providing a maximum likelihood estimate of γ, or a maximum composite likelihood estimate when SNPs are not independent. Similar approaches have been used for inferences of demographic parameters in several other studies (Nielsen 2000; Wooding and Rogers 2002; Polanski and Kimmel 2003; Adams and Hudson 2004; Marth et al. 2004; Williamson et al. 2005). In many models, it is possible to evaluate Equation 3 without the use of simulations (Wooding and Rogers 2002; Williamson et al. 2005).

The likelihood was optimized by making successive optimizations on a grid of values, with each iteration zooming in on the current approximate maximum likelihood estimate. Using a grid of values, rather than using simplex bracketing, circumvents problems encountered by many algorithms caused by the simulation variance in the estimation of the likelihood values. Optimization algorithms using derivatives of the likelihood function are also not applicable in this case because of the simulation variance.

Missing data were accounted for as in the method of Nielsen et al. (2005b) by summing over all possible states of the missing data. Multiple hits were also taken into account by simulating data with multiple hits using the parameter estimates from Williamson et al. (2005), based on the method of Hwang and Green (2004).

Alternative estimation procedure

Parameters for our demographic model 3 are maximum likelihood values inferred using a method which approximates the joint frequency spectrum by numerically solving the appropriate diffusion equation (R.N. Gutenkunst, R.D. Hernandez, S.H. Williamson, and C.D. Bustamante, in prep.). In this method, the population allele frequencies in AAs are modeled as an average of those in Europeans and Africans, where the average is weighted by the admixture proportion.

Distributions of allele frequencies in the European and African populations are calculated using the demographic model of Figure 1. The derivative-based BFGS algorithm (e.g., Press 2000b) was used to optimize the demographic parameters (including the admixture proportion). Missing data were accounted for by projecting down to 28 calls per population using a hypergeometric distribution as in the method of Nielsen et al. (2005a).

Tests of neutrality

The tests of neutrality we use here are all based on summarizing the data in terms of the allele frequency distribution and number of FDs. In the most general case, we consider the 2D-SFS for individuals of EA and AA ancestry, X = (X_0,1,…, X_0,n, X_1,0, X_1,1,…, X_1,n,…, X_nm), where X_ij is the number of derived alleles of frequency i in the EA population and frequency j in the AA population. We similarly define p = (p₀₁,…, p_0n, p₁₀,…, p_1n,…, p_nn)_, where p_ij is the probability of observing a derived allele of frequency i in the first population and frequency j in the second population in a random position in the genome. Notice here that positions included are any positions with FD or with a polymorphism, but not invariable positions. Then a test statistic is formed using a composite likelihood method similar to the one used in test 1 of the method of Nielsen et al. (2005b), i.e., by comparing the X to the expected value of X calculated from all the genomic data using a likelihood ratio test statistic (the G-test statistic). The test statistic measures how well the local pattern in a gene fits the global pattern observed in the genome. Critical values for the test are obtained using coalescent simulations (Hudson 1983) under the demographic model estimated from the genome-wide data, including admixture. Recombination rates were assumed to be 7.5 × 10⁻⁴ per base pair, per generation based on the estimates of Nielsen et al. (2005b). Simulations without recombination (data not shown) were also performed, yielding similar results. Simulations are performed individually for each gene conditioned on the total number of variable sites for that gene while accounting for missing data using the method of Nielsen et al. (2005b). As for the demographic analyses, the parameter estimates of Williamson et al. (2005) are used to correct for multiple hits along the lineage leading from humans to chimpanzees. The P-values are, therefore, corrected for the effect of missing data. Five different tests have been implemented using various attributes of the information. The tests are as follows.

The G2D test

This test is the test based on the two-dimensional frequency spectrum with FDs, mentioned in the section above. The test statistic is given by

where X^(j) represents the data for the jth locus, 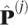is the maximum likelihood estimate of P based only on data in the jth locus, 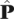is the maximum likelihood estimate of P based on the pooled data from all loci. This statistic measures how well the data in locus j fit the pattern of allele frequencies observed in the pooled data. The test is performed including the class of fixed mutations. This test was applied to all of the information in the two-dimensional frequency spectrum, while the tests discussed next uses subsets of the data. They are supposedly then sensitive to different types of selection acting on the genes.

F_ST

This test is based on the F_ST statistic (Weir and Cockerham 1984), similarly to the method employed by Akey et al. (2002). The test rejects neutrality for high values of F_ST.

MWU-low

This is a Mann-Whitney U-test comparing the frequency spectrum in the gene to the genome-wide frequency spectrum. The test rejects when there is an excess of low frequency polymorphisms. The folded frequency spectrum is used in this test.

MWU-high

This test is similar to the MWU-low, but it rejects when there is an excess of high frequency polymorphisms.

For all tests, FDR sets were constructed using the modification of the methods of Benjamini and Hochberg (1995) and Storey (2002) proposed by Williamson et al. (2007).

Correlation between NI and frequency spectrum

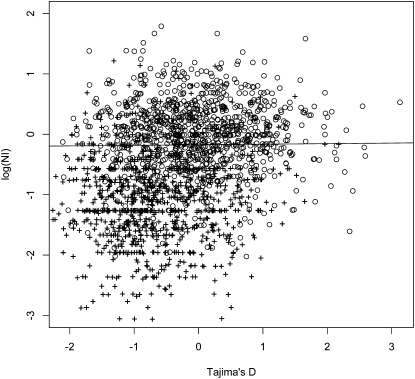
We validate inferences of selection by showing a correlation between the NI and the inferences based on the frequency spectrum. However, as the same data have been used to calculate the NI and tests statistics based on the frequency spectrum, it is not obvious that the statistics are uncorrelated under a neutral model. If the statistics are correlated under a neutral model, the NI cannot be used to validate findings of selection. We have, therefore, examined the correlation of the statistics using simulations. In Figure 5, we show an x–y plot of the joint distribution of Tajima's D, chosen as one possible summary of the frequency spectrum, and the NI. We get similar results for other functions of the frequency spectrum such as F_ST and the other statistics used in this paper. We assume a chromosomal region, mimicking a human gene, with a cumulative population scaled recombination rate of 2Nr = 0.005, θ = 4, a sample size of n = 38, and a divergence between species of 20N generations. We assume that 50% of all (nonlethal) mutations are nonsynonymous. Simulations were performed using a custom-made forward simulation program, using 2N = 400 as a proxy for a larger population size. As evident from the figure, the values of D and NI are perfectly uncorrelated. This is not surprising as the number of nonsynonymous and synonymous mutations, given the total number of mutations, are independent of the counts of the frequency spectrum. We also show results for a similar simulation performed under the same parameter settings, but assuming that 10% of all nonsynonymous mutations have a population scaled selection coefficient of 2Ns = 20. We see that the values of D and NI are both shifted toward smaller values.

Figure 5.

The distribution of values of the logarithm of the neutrality index (NI) and Tajima's D in 1000 simulations under a neutral model (○) and a model involving repeated selective sweeps (+). The parameter values and details of the simulations are described in the main text. The regression line is obtained for neutral data points only and has a slope very close to zero (−0.0093). Notice that almost all points with small values of log(NI) and small values of Tajima's D are data points simulated under the selection model.

Combining evidence in categories

Genes have been divided into categories according to expression pattern, biological process, and molecular function. A Mann-Whitney U-test is then used to test for excess of small P-values in each category compared with the rest of the data. The biological process and molecular function categorization is based on the PANTHER database (Thomas et al. 2003). Genes are allocated to a particular tissue type if they have their maximal expression in that tissue type according to the Novartis Gene Atlas (Su et al. 2002).