A Systematic Approach for Computing Zero-Point Energy, Quantum Partition Function, and Tunneling Effect Based on Kleinert’s Variational Perturbation Theory

Abstract

In this paper, we describe an automated integration-free path-integral (AIF-PI) method, based on Kleinert’s variational perturbation (KP) theory, to treat internuclear quantum-statistical effects in molecular systems. We have developed an analytical method to obtain the centroid potential as a function of the variational parameter in the KP theory, which avoids numerical difficulties in path-integral Monte Carlo or molecular dynamics simulations, especially at the limit of zero-temperature. Consequently, the variational calculations using the KP theory can be efficiently carried out beyond the first order, i.e., the Giachetti-Tognetti-Feynman-Kleinert variational approach, for realistic chemical applications. By making use of the approximation of independent instantaneous normal modes (INM), the AIF-PI method can readily be applied to many-body systems. Previously, we have shown that in the INM approximation, the AIF-PI method is accurate for computing the quantum partition function of a water molecule (3 degrees of freedom) and the quantum correction factor for the collinear H₃ reaction rate (2 degrees of freedom). In this work, the accuracy and properties of the KP theory are further investigated by using the first three order perturbations on an asymmetric double-well potential, the bond vibrations of H₂, HF, and HCl represented by the Morse potential, and a proton-transfer barrier modeled by the Eckart potential. The zero-point energy, quantum partition function, and tunneling factor for these systems have been determined and are found to be in excellent agreement with the exact quantum results. Using our new analytical results at the zero-temperature limit, we show that the minimum value of the computed centroid potential in the KP theory is in excellent agreement with the ground state energy (zero-point energy) and the position of the centroid potential minimum is the expectation value of particle position in wave mechanics. The fast convergent property of the KP theory is further examined in comparison with results from the traditional Rayleigh-Ritz variational approach and Rayleigh-Schrödinger perturbation theory in wave mechanics. The present method can be used for thermodynamic and quantum dynamic calculations, including to systematically determine the exact value of zero-point energy and to study kinetic isotope effects for chemical reactions in solution and in enzymes.

1.Introduction

Kleinert’s variational perturbation (KP) theory^1-7 for the centroid density^8-15 of Feynman path integrals^1,8,16-26 provides a complete theoretical foundation for developing non-stochastic methods²⁷ to systematically incorporate internuclear quantum-statistical effects²⁸ in condensed phase systems. Computational methods based on the KP theory complement conventional Fourier or discretized path-integral Monte-Carlo^29-39 (PIMC) and molecular dynamics^12,13,40-43 (PIMD) simulations which have been widely used in condensed phases.^44-58 Recently, we reported a computational method based on the KP theory for chemical applications.⁵⁹ In this approach which is called an automated integration-free path-integral (AIF-PI) method, the path integrals in the perturbation expansion have been analytically integrated, resulting in expressions that are free of path integrations and can be efficiently used to study quantum-statistical effects. For many-body systems, we make use of the independent instantaneous normal mode (INM) approximation such that the internuclear potential energy function along each normal mode coordinate is expanded in terms of polynomial functions.

To this end, we derived analytical expressions for the centroid effective potential up to the third order of the Kleinert perturbation (KP3).⁵⁹ The most attractive feature of the KP theory is that the perturbation series converges uniformly and exponentially.^1,60,61 We have shown that the second-order KP theory (KP2) implemented in the AIF-PI method with the INM approximation is accurate for a number of test cases, including the quantum partition function of a water molecule (3 degrees of freedom) and the rate of the collinear H₃ reaction (2 degrees of freedom), in comparison with accurate quantum results.⁵⁹ Moreover, owing to the integration-free feature, our AIF-PI method is computationally efficient such that the potential energy can be evaluated using ab initio^62-64 or density-functional theory⁶⁵ (DFT) to perform the so-called ab initio path-integral calculations.^44-50 Consequently, we used the hybrid functional B3LYP⁶⁶ to construct the potential energy function to compute kinetic isotope effects (KIE) on a series of proton transfer reactions in water with the AIF-PI method. The computed KIE results at the KP2 level are in excellent agreement with experiment.⁵⁹

A closely related theoretical approach is the variational method independently introduced by Giachetti and Tognetti,⁶⁷ and by Feynman and Kleinert⁶⁸ (hereafter labeled as GTFK), which formally corresponds to the first order approximation in the KP theory, i.e., KP1.^1,67-69 The GTFK method has been applied to a variety of systems,^1,70-79 including quantum dynamic processes in condensed phases (e.g., water and helium).^76-79 Although the original GTFK approach is among the most accurate approximate methods for estimating the path-integral centroid potential in many applications,²⁷ significant errors can exist in situations in which quantum effects are dominant, especially at low temperatures.²⁷ Our initial report⁵⁹ as well as studies by Kleinert et al. on model systems^1-7 showed that higher order perturbations of KP theory can significantly and systematically improve computational accuracy over the KP1 results.

In this article, we use the AIF-PI method to further examine the computational accuracy and properties of the KP theory, making use of a number of test cases that have been well-characterized analytically and computationally. These include an asymmetric double-well potential,²⁷ the Morse potential,⁸⁰ and the Eckart potential.⁸¹

For the double-well and Morse potentials, we focus on the quantum partition function as a function of temperature as well as the free energy at the zero-temperature limit (T = 0 K), where the minimization of the centroid potential yields two important physical quantities^1,14,15,68: the exact ground state energy, i.e., zero-point energy (ZPE), and the expectation value of the nuclear position in the ground state. Hence, the newly-derived analytical results at the limit of zero-temperature (Supporting Information) provides a convenient way to systematically compute the exact values of these two important physical quantities without solving the vibrational Schrödinger equation. At the zero-temperature limit, we demonstrate that the fast convergent property of KP theory becomes transparent by comparing the ground state energy of the Morse potential with that determined by the traditional Rayleigh-Ritz variational method^82-85 and Rayleigh-Schrödinger perturbation theory.^63,86,87 For the Eckart potential, we focus on the tunneling effect^88,89 corresponding to a proton transfer at a wide range of temperatures. Comparison of the AIF-PI method with other approximate methods, PIMC or PIMD simulations, and accurate quantum results are also given. In addition, we discuss the selection of the optimal variational parameter Ω and the temperature-dependence of zero-Ω limit which corresponds to the reference frame used in the Feynman-Hibbs variational approach.⁸

2. Kleinert’s variational perturbation theory

In this section, we briefly review Kleinert’s variational perturbation (KP) theory and its relationship to the original Giachetti-Tognetti and Feynman-Kleinert (GTFK) variational approach.^1,67-69 The path-integral (PI) representation of the canonical quantum mechanical (QM) partition function Q_QM for a single particle system can be written in terms of the centroid effective potential W as a classical configuration integral:^1,8,13-15

$$Q_{QM}=\sqrt{\frac{M{k}_{B}T}{2\pi {ħ}^2}}{\int }_{-\infty }^{\infty }{e}^{-\beta W\left(x_0\right)}d{x}_0,$$ (1)

where M is the mass of the particle, k_B is Boltzmann’s constant, T is temperature, ħ is Planck’s constant divided by 2π, β = 1/k_BT, and x₀ is a point in space. Given the centroid potential W(x₀), thermodynamic and quantum dynamic quantities can be accurately determined,^{1,8,13-15,44-50} including molecular spectroscopy of quantum fluids^76-79 and the rate constant of chemical and enzymatic reactions.^{9-13,51-58,69} The mass-dependent nature of W(x₀) is also of particular interest because kinetic isotope effects on a chemical reaction can be obtained, and it has been applied to enzymatic reactions^52,53,56-58 and carbon nanotubes.⁹⁰

The centroid potential W(x₀) in Eq. (1) is defined as follows:^1,8,13-15

$$W\left(x_0\right)=-k_{B}T\ln [\int \mathsf{ND}x\left(\tau \right)\delta (\stackrel{‒}{x}-x_0)\exp \{-\mathit{A}\left[x\left(\tau \right)\right]∕ħ\}],$$ (2)

where τ is imaginary time, x(τ) describes a path in space-time, $\int \mathsf{ND}x\left(\tau \right)\delta (\stackrel{‒}{x}-x_0)$ denotes a summation over all possible closed paths in which x̄ is equal to x₀ (i.e., a functional integration), and x̄ is the time-average position, called ‘centroid’

$$\stackrel{‒}{x}\equiv \frac{1}{\beta ħ}{\int }_0^{\beta ħ}x\left(\tau \right)d\tau .$$ (3)

In Eq. (2), $\mathit{A}$ is the quantum-statistical action:

$$\mathit{A}\left[x\left(\tau \right)\right]={\int }_0^{\beta ħ}d\tau \left\{\frac{M}{2}\stackrel{.}{x}{\left(\tau \right)}^2+V\left[x\left(\tau \right)\right]\right\},$$ (4)

where V(x) is the potential energy function of the system. Generalization of Eq. (2) to a multi-dimensional system is straightforward.^1,8

A number of computational approaches have been developed to approximately estimate the centroid potential. Feynman and Hibbs described a first-order cumulant expansion by introducing a Gaussian smearing function in a free-particle reference frame to yield an upper bound on the centroid potential.⁸ This was subsequently modified by Doll and Myers (DM) by using a Gaussian width associated with the angular frequency at the minimum of the original potential.⁹¹ The GTFK approach is another variational method that adopts a harmonic reference state by variationally optimizing the angular frequency.^67-69 Mielke and Truhlar employed a free particle reference state and approximated the sum over paths by a minimal set of paths constrained for a harmonic oscillator. The action integral is obtained by using the three-point trapezoidal rule for the potential to yield the displaced-point path integral (DPPI) centroid potential.²⁷

In Kleinert’s variational perturbation (KP) theory,^1-7 one first constructs a harmonic reference state characterized by a trial angular frequency Ω at a given centroid position x₀, and then, systematically builds up anharmonic corrections to the centroid potential of this reference system. Given the reference, or trial harmonic action:

$${\mathit{A}}_{\Omega }^{x_0}={\int }_0^{\beta ħ}d\tau \left\{\frac{M}{2}\stackrel{.}{x}{\left(\tau \right)}^2+\frac{1}{2}M{\Omega }^2{[x\left(\tau \right)-x_0]}^2\right\}.$$ (5)

the centroid potential W(x₀) in Eq. (2) can be expressed as a path integral of the harmonic action which is perturbed by the anharmonicity of the original potential:

$$e^{-\beta W\left(x_0\right)}=\int \mathsf{ND}x\left(\tau \right)\delta (\stackrel{‒}{x}-x_0)e^{-{\mathit{A}}_{\Omega }^{x_0}∕ħ}{e}^{-(\mathit{A}-{\mathit{A}}_{\Omega }^{x_0})∕ħ}=Q_{\Omega }^{x_0}{\langle e^{-(\mathit{A}-{\mathit{A}}_{\Omega }^{x_0})∕ħ}\rangle }_{\Omega }^{x_0},$$ (6)

where $Q_{\Omega }^{x_0}$ is the local harmonic partition function given as follows:

$$Q_{\Omega }^{x_0}=\int \mathsf{ND}x\left(\tau \right)\delta (\stackrel{‒}{x}-x_0)e^{-{\mathit{A}}_{\Omega }^{x_0}∕ħ}=\frac{\beta ħ\Omega ∕2}{\sinh (\beta ħ\Omega ∕2)},$$ (7)

and ${\langle \cdots \rangle }_{\Omega }^{x_0}$ is the expectation value over all closed paths of the action in Eq. (5):

$${\langle e^{-F\left[x\left(\tau \right)\right]∕ħ}\rangle }_{\Omega }^{x_0}=\frac{1}{Q_{\Omega }^{x_0}}\int \mathsf{ND}x\left(\tau \right)\delta (\stackrel{‒}{x}-x_0)e^{-F\left[x\left(\tau \right)\right]∕ħ}{e}^{-{\mathit{A}}_{\Omega }^{x_0}∕ħ},$$ (8)

In Eq. (8), F[x(τ)] denotes an arbitrary functional. It is of interest to note that Eq. (6) is the starting point of Zwanzig’s statistical-mechanical perturbation theory,⁹² which has been extensively used in free energy calculations through Monte Carlo and molecular dynamics simulations.^93,94

If we expand the exponential functional in Eq. (6) and sum up the prefactors into an exponential series of cumulants,⁹⁵ the nth-order approximation, $W_n^{\Omega }\left(x_0\right)$, to the centroid potential W(x₀) can be written as follows:^1,2

$$e^{-\beta W_n^{\Omega }\left(x_0\right)}=Q_{\Omega }^{x_0}\exp \left\{\begin{array}{c}-\frac{1}{ħ}{\int }_0^{\beta ħ}d\tau {\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\rangle }_{\Omega ,c}^{x_0}+\frac{1}{2!{ħ}^2}{\int }_0^{\beta ħ}d{\tau }_1{\int }_0^{\beta ħ}d{\tau }_2{\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_1\right)\right]{\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_2\right)\right]\rangle }_{\Omega ,c}^{x_0}\hfill \\ +\cdots +\left\{\prod _{j=1}^n{\int }_0^{\beta ħ}d{\tau }_j\right\}\frac{{(-1)}^n}{n!{ħ}^n}{\langle \prod _{k=1}^n{\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_k\right)\right]\rangle }_{\Omega ,c}^{x_0}\hfill \end{array}\right\},$$ (9)

where ${\mathit{A}}_{\mathrm{int}}^{x_0}=\mathit{A}-{\mathit{A}}_{\Omega }^{x_0}$ is the so-called inter-action, representing the perturbation to the harmonic reference state, and ${\langle \cdots \rangle }_{\Omega ,c}^{x_0}$ is a cumulant which can be written in terms of expectation values ${\langle \cdots \rangle }_{\Omega }^{x_0}$ by the cumulant expansion, e.g.,

$${\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left(\tau \right)\right]\rangle }_{\Omega ,c}^{x_0}\equiv {\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left(\tau \right)\right]\rangle }_{\Omega }^{x_0},$$ (10)

$${\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_1\right)\right]{\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_2\right)\right]\rangle }_{\Omega ,c}^{x_0}\equiv {\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_1\right)\right]{\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_2\right)\right]\rangle }_{\Omega }^{x_0}-{\left\{{\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left(\tau \right)\right]\rangle }_{\Omega }^{x_0}\right\}}^2,$$ (11)

$$\begin{array}{cc}\hfill {\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_1\right)\right]{\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_2\right)\right]{\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_3\right)\right]\rangle }_{\Omega ,c}^{x_0}& \equiv {\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_1\right)\right]{\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_2\right)\right]{\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_3\right)\right]\rangle }_{\Omega }^{x_0}\hfill \\ \hfill & -3{\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_1\right)\right]{\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_2\right)\right]\rangle }_{\Omega }^{x_0}{\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left(\tau \right)\right]\rangle }_{\Omega }^{x_0}\hfill \\ \hfill & +2{\left\{{\langle {\mathit{A}}_{\mathrm{int}}^{x_0}\left[x\left(\tau \right)\right]\rangle }_{\Omega }^{x_0}\right\}}^3,\hfill \\ \hfill & \mathrm{etc}.\hfill \end{array}$$ (12)

Furthermore, Kleinert and co-workers derived a general expression for the expectation value of the form $\left\{{\prod }_{j=1}^n{\int }_0^{\beta ħ}d{\tau }_j\right\}{\langle {\prod }_{k=1}^n{F}_k\left[x\left({\tau }_k\right)\right]\rangle }_{\Omega }^{x_0}$ in terms of Gaussian smearing convolution integrals:^5,6

$$\begin{array}{cc}\hfill \left\{\prod _{j=1}^n{\int }_0^{\beta ħ}d{\tau }_j\right\}{\langle \prod _{k=1}^n{F}_k\left[x\left({\tau }_k\right)\right]\rangle }_{\Omega }^{x_0}& =\left\{\prod _{j=1}^n{\int }_0^{\beta ħ}d{\tau }_j\right\}\left\{\prod _{k=1}^n{\int }_{-\infty }^{\infty }d{x}_k{F}_k\left(x_k\right)\right\}\hfill \\ \hfill & \times \frac{1}{\sqrt{{\left(2\pi \right)}^n\mathrm{Det}\left[a_{{\tau }_k{\tau }_{k^{\prime }}}^2\left(\Omega \right)\right]}}\exp \left\{-\frac{1}{2}\sum _{\begin{array}{c}k=1\hfill \\ k^{\prime }=1\hfill \end{array}}^n(x_k-x_0)a_{{\tau }_k{\tau }_{k^{\prime }}}^{-2}\left(\Omega \right)(x_{k^{\prime }}-x_0)\right\},\hfill \end{array}$$ (13)

where $\mathrm{Det}\left[a_{{\tau }_k{\tau }_{k^{\prime }}}^2\left(\Omega \right)\right]$ is the determinant of the n×n-matrix consisting of the Gaussian width $a_{{\tau }_k{\tau }_{k^{\prime }}}^2\left(\Omega \right)$, $a_{{\tau }_k{\tau }_{k^{\prime }}}^{-2}\left(\Omega \right)$ is an element of the inverse matrix of $a_{{\tau }_k{\tau }_{k^{\prime }}}^2\left(\Omega \right)$, and the Gaussian width is a function of the trial frequency Ω:

$$a_{\tau {\tau }^{\prime }}^2\left(\Omega \right)=\frac{1}{\beta M{\Omega }^2}\left\{\frac{\beta ħ\Omega }{2}\frac{\cosh \left[(\mid \tau -{\tau }^{\prime }\mid -\beta ħ∕2)\Omega \right]}{\sinh (\beta ħ\Omega ∕2)}-1\right\}.$$ (14)

Using these smearing potentials, the nth-order Kleinert variational perturbation (KPn) approximation, $W_n^{\Omega }\left(x_0\right)$, in Eq. (9) can be written in terms of ordinary integrations as follows:¹

$$\begin{array}{cc}\hfill W_n^{\Omega }\left(x_0\right)=& -k_{B}T\ln Q_{\Omega }^{x_0}+\frac{k_{B}T}{ħ}{\int }_0^{\beta ħ}d\tau {\langle V_{\mathrm{int}}^{x_0}\left[x\left({\tau }_1\right)\right]\rangle }_{\Omega }^{x_0}\hfill \\ \hfill & -\frac{k_{B}T}{2!{ħ}^2}{\int }_0^{\beta ħ}d{\tau }_1{\int }_0^{\beta ħ}d{\tau }_2{\langle V_{\mathrm{int}}^{x_0}\left[x\left({\tau }_1\right)\right]V_{\mathrm{int}}^{x_0}\left[x\left({\tau }_2\right)\right]\rangle }_{\Omega ,c}^{x_0}+\cdots +k_{B}T\frac{{(-1)}^{n+1}}{n!{ħ}^n}\left\{\prod _{j=1}^n{\int }_0^{\beta ħ}d{\tau }_j\right\}{\langle \prod _{k=1}^n{V}_{\mathrm{int}}^{x_0}\left[x\left({\tau }_k\right)\right]\rangle }_{\Omega ,c}^{x_0}\hfill \end{array}$$ (15)

where $V_{\mathrm{int}}^{x_0}\left[x\left(\tau \right)\right]=V\left[x\left(\tau \right)\right]-\frac{1}{2}M{\Omega }^2{[x\left(\tau \right)-x_0]}^2$. In this expression, the kinetic energy terms in Eq. (4) and (5) cancel out.

As n tends to infinity, $W_n^{\Omega }\left(x_0\right)$ approaches the exact value of the centroid potential W(x₀) in Eq. (1), which is independent of the trial Ω. But the truncated sum in Eq. (15) does depend on Ω, and the optimal choice of this trial frequency at a given order of KP expansion and at a particular centroid position x₀ is determined by the least-dependence of $W_n^{x_0}\left(\Omega \right)$ on Ω itself. This is the so-called frequency of least dependence,¹ which provides a variational approach to determine the optimal value of Ω, Ω_opt,n(x₀).

Of particular interest is the special case when n = 1, which turns out to be identical to the original GTFK variational approach.^1,67-69 An important property of KP1 or the GTFK variational approach is that there is a definite upper bound for the computed $W_1^{\Omega }\left(x_0\right)$ by virtue of the Jensen-Peierls inequality, i.e., from Eq. (6) and (9)):

$$e^{-\beta W\left(x_0\right)}=Q_{\Omega }^{x_0}{\langle \exp \left(-\frac{\mathit{A}-{\mathit{A}}_{\Omega }^{x_0}}{ħ}\right)\rangle }_{\Omega }^{x_0}\ge Q_{\Omega }^{x_0}\exp {\langle -\frac{\mathit{A}-{\mathit{A}}_{\Omega }^{x_0}}{ħ}\rangle }_{\Omega }^{x_0}=e^{-\beta W_1^{\Omega }\left(x_0\right)}.$$ (16)

Note that by choosing Ω = 0 (i.e., the reference state for a free particle), KP1 or GTFK reduces to the Feynman-Hibbs approach.⁸ For higher orders of n, unfortunately, it is not guaranteed that a minimum of $W_n^{x_0}\left(\Omega \right)$ actually exists as a function of Ω. In this case, the least dependent Ω is obtained from the condition that the next derivative of $W_n^{x_0}\left(\Omega \right)$ with respect to Ω is set to zero.^1,5,70 Consequently, Ω is considered as a variational parameter in the Kleinert perturbation theory such that $W_n^{x_0}\left[{\Omega }_{\mathrm{opt},n}\left(x_0\right)\right]$ is least-dependent on Ω.

This variational criterion relies on the uniformly and exponentially convergent property of the KP theory. Kleinert and coworkers proved that his theory exhibits this property in several strong anharmonic-coupling systems.^1,60,61 More importantly, this remarkably fast convergent property can also be observed even for computing the electronic ground state energy of a hydrogen atom (3 degrees of freedom). The ground state energy was determined by calculating the electronic centroid potential at the zero-temperature limit.⁵ The accuracies of the first three orders of the KP theory for a hydrogen atom are 85%, 95%, and 98%, respectively.

In practice, for odd n, there is typically a minimum point in Ω,^1,5,70 but due to the alternating sign of the cumulants in Eq. (15), there is usually no minimum in Ω for even n. Nevertheless, the frequency of least-dependence for an even order perturbation in n can be determined by locating the inflexion point, i.e., the zero-value of the second derivative of $W_n^{x_0}\left(\Omega \right)$ with respect to Ω.^1,5,70 Since the KP expansion is uniformly and exponentially converged, Kleinert has demonstrated that the least-dependent plateau in $W_n^{x_0}\left(\Omega \right)$, which is characterized by a minimum point for odd n or by an inflexion point for even n, grows larger and larger with increasing orders of n.¹

3. The Automated Integration-Free Path-Integral Method

A major obstacle in applying the KP theory to realistic molecular systems is the intricate n-dimensional space-time (2n degrees of freedom) smearing integrals in Eq. (13) for the KPn expansion. The complexity of the smearing integrals increases considerably for multidimensional systems, where Ω becomes a 3N×3N matrix for N nuclei.^1,5 Thus, the KP theory quickly becomes numerically intractable beyond the first order perturbation, i.e., the GTFK variational approach. To make the KP expansion feasible for many-body systems, we make use of the independent instantaneous normal mode (INM) approximation^27,43,96,97 to reduce the multidimensional potential to 3N one-body potentials. In the INM approximation, the total centroid effective potential for N nuclei is simplifed as

$$W_n^{\Omega }\left({\left\{x_0\right\}}^{3N}\right)\approx V\left({\left\{x_0\right\}}^{3N}\right)+\sum _{i=1}^{3N}{w}_{i,n}^{\Omega }\left(q_i^{x_0}\right),$$ (17)

where $w_{i,n}^{\Omega }\left(q_i^{x_0}\right)$ is the centroid potential for the INM coordinate $q_i^{x_0}$. Note that the INM coordinates are naturally decoupled through the second-order Taylor expansion. The INM approximation has also been used elsewhere.^27,43,96,97 This approximation should be especially suited for the KP expansion because the Gaussian convolution integrals in Eq. (13) exhibit the exponential decaying property from the centroid position.

For each INM, we further interpolate the potential energy along the INM coordinate in terms of an mth order polynomial function becuase we have derived the analytical results of the path integrals in Eq. (15) up to 20th order polynomials. Then, the optimal Ω_opt(x₀), is numerically located by finding the least Ω-dependent centroid potential $W_n^{x_0}\left(\Omega \right)$.⁵⁹ Hereafter, an mth order polynomial representation of the original potential energy function obtained with an interpolating step size q Å both in the forward and backward directions along the normal mode coordinate at x₀ is denoted as Pm-qA. Since the path integrals have been integrated analytically, the time-demanding Monte-Carlo or molecular dynamics samplings of Eq. (13) using different trial values of Ω to optimize the centroid potential is no longer necessary. Consequently, this essentially automated integration-free path integral (AIF-PI) approach is remarkably efficient and can be applied to chemical systems.⁵⁹ Analytical results were derived with Mathematica⁹⁸ and are available as the Supporting Material in Ref. [59].

In the INM approximation, previously we have shown that the computed values using the AIF-PI method are still very encouraging for multi-dimensional systems, even involving motions or vibrations of the lightest-nucleus hydrogen.⁵⁹ For example, we have computed the quantum partition function of a water molecule (3 degrees of freedom). At T = 200 K, the lowest temperature in which the exact partition function is available, the KP1 result is 77% of the exact, while the KP2 value is 83% which is similar to the accuracy of the second-order Rayleigh-Schrödinger perturbation theory without resonance correction (86%).⁵⁹ Moreover, we have also computed the quantum correction factor for the collinear H₃ reaction (2 degrees of freedom). The factor is defined as the ratio of the quantum rate constant to the rate constant obtained by classical transition-state theory with quantum vibrational partition function but neglect tunneling effects. In this reaction, both tunneling and vibrational quantum effects are important. At T = 200 K, again the lowest temperature in which the exact values is available, the KP1 and KP2 correction factors are 15 and 55, respectively, whereas the exact result is 46.

Although the INM approximation sacrifices some accuracy, in exchange, it makes possible analyses of specific contributions to the centroid potential W due to quantum mechanical vibration and tunneling. Positive and negative values of w_i in Eq. (17) raise (vibration) and lower (tunneling) the original potential V, respectively. In practice, positive w_i should often be found in the region in which the frequencies of the INM are real numbers (e.g., Sections 5A and 5B). By contrast, for imaginary INM, the value of w_i should often be negative (e.g., Sections 5A and 5C). To this end, we have also performed the so-called ab initio path-integral calculations^44-50 to accurately determine kinetic isotope effects for a series of proton transfer reactions in water within the INM approximation.⁵⁹ Nonetheless, we are now working on a formalism to systematically couple instantaneous normal modes in the AIF-PI method. We hope that one day this method could also be used by non-path-integral experts or experimentalist as a ‘black-box’ for any given system.

4. Computational Details

The areas of the integrations for the classical configuration integrals involving W(x₀) in Eq. (1) were chosen such that their values are converged at least up to 3 significant figures for all systems considered (Supporting Information), and the numerical integrations were performed with Mathematica.⁹⁸ To compute the centroid potential, all the original potentials were first mass-scaled in units of atomic mass unit (AMU). For the asymmetric double-well potential, we computed the eigenenergies by the Rayleigh-Ritz variational method^82-85 (Supporting Information), in which the Schrödinger equation was solved in a basis of 114 Gauss-Hermite polynomials. The partition functions calculated by summing over these eigenenergies with the Boltzmann factor are virtually identical to the quantum results reported in the Mielke-Truhlar paper.²⁷ Hence we treat them as the ‘accurate quantum’ values in Table 1 for the comparisons among all other approximate path-integral methods.

Table 1.

Classical and quantum canonical partition functions and free energies of the asymmetric double-well potential at various temperatures. Signed percent errors (%) of different theoretical methods relative to the accurate quantum results are given

	Canonical partition function
T (K)	Classical	Accurate quantum	KP1	KP2	KP3	Mielke-Truhlar†	Doll-Myers†
1000	4.03E-01	3.12E-01	0.0	0.1	0.0	0.2	-0.2
500	1.85E-01	7.09E-02	-0.3	0.4	0.0	0.7	-0.2
400	1.47E-01	3.62E-02	-0.6	0.4	0.0	0.8	0.4
300	1.10E-01	1.19E-02	-1.4	0.3	0.0	0.9	2.7
200	7.28E-02	1.30E-03	-3.5	-0.5	-0.2	-0.6	10.0
100	3.63E-02	1.69E-06	-10.4	-2.4	-1.0	-8.2	50.6
50	1.81E-02	2.85E-12	-23.2	-6.7	-2.9	--	--

	Free energy (kcal/mol)
T (K)	Classical	Accurate quantum	KP1	KP2	KP3	Mielke-Truhlar†	Doll-Myers†
1000	1.808	2.314	0.0	-0.1	0.0	-0.2	0.2
500	1.676	2.629	0.1	-0.1	0.0	-0.3	0.1
400	1.524	2.638	0.2	-0.1	0.0	-0.2	-0.1
300	1.317	2.641	0.3	-0.1	0.0	-0.2	-0.6
200	1.041	2.641	0.5	0.1	0.0	0.1	-1.4
100	0.659	2.641	0.8	0.2	0.1	0.6	-3.1
50	0.399	2.641	1.0	0.3	0.1	--	--
0	0	2.641	1.2	0.4	0.2	--	--

^†Ref. [27].

In the case of Morse potential, we have also numerically tested the sensitivity of using different orders of polynomial representation of the original potential and different interpolation steps, and we found that the results from both P10-0.02A and P20-0.08A are in excellent agreement. For example, at the equilibrium position of the original potential, their difference in the KP2 effective potential is less than 10^-8 kcal/mol at a low temperature of 50 K. For the calculations of the Rayleigh-Ritz variational method and the Rayleigh-Schrödinger perturbation theory, we interpolated the Morse potential at the equilibrium position as P10-0.02A and P10-0.04A. Both interpolating polynomials return us the same energies at least up to 10^-5 kcal/mol.

5. Results and Discussion

To illustrate the performance and accuracy of the Kleinert variational perturbation theory, we applied the AIF-PI method⁵⁹ to a number of well-studied systems, including an asymmetric double-well potential,²⁷ the Morse potential⁸⁰ corresponding to the bond vibrations of H₂,⁹⁹ HF,¹⁰⁰ and HCl,⁹⁹ and the Eckart potential⁸¹ representing a model of proton transfer reactions.^100,101

A. Asymmetric double-well potential

We first present the results for a particle of M = 1224.259 a.u. in the one-dimensional asymmetric double-well potential

$$V\left(x\right)=b_4{x}^4+b_2{x}^2+b_{1}x+b_0,$$ (18)

where the four parameters have values of 0.01, -0.02, 0.005, and 0.01514754 a.u. (atomic units), respectively. This test case has been used by Mielke and Truhlar to validate their DPPI method based on a three-point trapezoidal approximation of the potential in the free particle reference state.²⁷ Results based on the Doller-Myers approximation to the centroid potential²⁷ are also included for comparison.

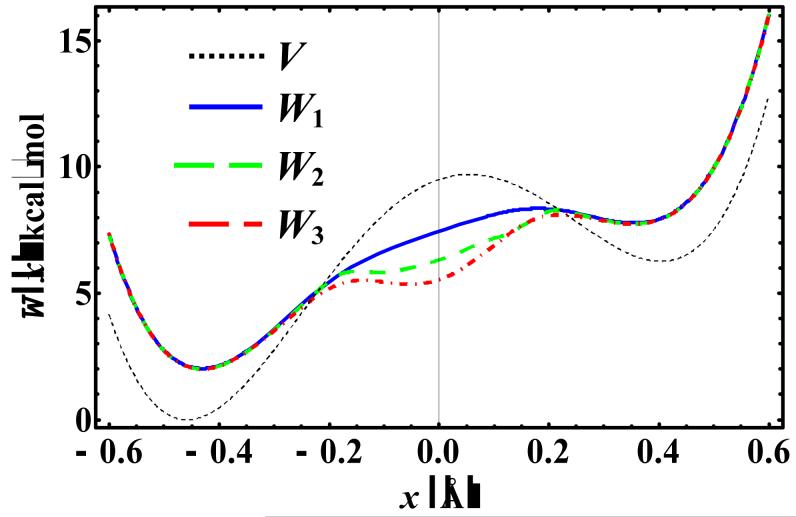
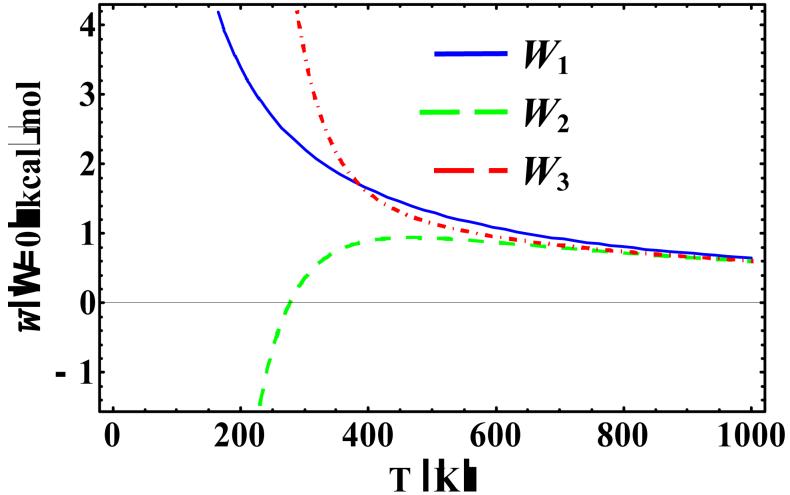
Key results are shown in Figure 1 which depicts the first three orders of KP effective potential as a function of the centroid variable x at 100 K, along with the original potential energy. It is of interest to notice that for all three perturbation levels, in the double-well regions, the path-integral centroid potential has a higher energy than the corresponding original potential energy primarily due to zero-point energy, whereas at the barrier region, the centroid potential is lowered in comparison with the original barrier, which may be attributed to tunneling effects. Furthermore, Figure 1 shows that in the double-well regions, the three perturbation results converge exceptionally well, but a noticeable progression of energy lowering effects is found at the barrier region. In fact, the original maximum point at x ≈ 0 Å, in which the frequency for the INM is imaginary, has become a local minimum at the KP3 level purely due to quantum tunneling effects. Note that for this one-dimensional case, the centroid potential is equivalent to the centroid potential of mean force along the position coordinate. Thus, if this potential of mean force is used in path-integral quantum transition state theory (PI-QTST),^{11,13,69,101,102} it seems that the lowest perturbation level at KP1 may underestimate tunneling and could lead to noticeable errors in rate calculations.

Figure 1.

Computed (mass-scaled) centroid potential at the first (W₁), second (W₂), and third (W₃) order Kleinert variational perturbation theory for an asymmetric double-well potential (V) at a temperature of 100 K.

The quantum partition function and the corresponding free energy from the Kleinert variational perturbation theory at different temperatures are summarized in Table 1, along with the results from the earlier studies.²⁷ Note that the dominant contribution to the partition function in the configuration integral is from the centroid potential near the global minimum (in which the INM frequencies are all real). This is reflected in the good agreement among all three perturbation levels (Figure 1 and Table 1). Furthermore, the absolute values of the computed partition function have greater errors in comparison with the accurate results than the corresponding free energies due to the exponential relationship between the two quantities. Consequently, the computed free energies uniformly have smaller errors than the absolute partition functions for all approximate methods. In the entire temperature range that has been considered, the KP theory, particularly at the KP2 and KP3 levels, consistently yields the most accurate results among all methods listed in Table 1. The DDPI method slightly out-performs the GTFK variational approach which is equivalent to KP1, but there are significant errors at low temperatures. In this case, the second and third order perturbation results are in excellent agreement (99%) with accurate quantum results. At 50 K, the KP1 value deteriorates significantly, whereas the results obtained using KP2 and KP3 are still in good accord with the accurate results. Interestingly, Mielke and Truhlar pointed out that although the GTFK variational approach (KP1) is the most accurate method that they have considered, the method is too expensive for computing molecular partition functions.²⁷ In the present AIF-PI method, the path integrals are determined analytically, which makes the daunting task of path-integral simulation a trivial problem, allowing the variational frequencies to be optimized quickly and efficiently.

An important property of the centroid potential is that at the limit of zero-temperature, the energy and position of the global minimum correspond to, respectively, the ground state energy and the expectation value of position in the ground state determined by wave mechanics:^1,14,15,68

$$\underset{T\to 0}{\lim }{W}_{\min }\left(x_{\min }\right)=E_0,$$ (19)

and

$$x_{\min }=\langle {\psi }_0\mid x\mid {\psi }_0\rangle ,$$ (20)

where x is the position operator, and x_min and W_min(x_min) are, respectively, the coordinate and value at the global minimum of the centroid potential. In Eq. (19) and (20), ψ₀ is the nuclear ground state wave function and E₀ the lowest eigenenvalue of the Hamiltonian, i.e., the zero-point energy. We have derived the closed-form expressions (Supporting Information) for these quantities up to KP1/P20, KP2/P20, and KP3/P6 levels of theory, which can be evaluated at no additional computational costs once the centroid potential is optimized. In contrast, it would be extremely difficult to obtain converged results at 0 K using Monte Carlo or molecular dynamics path integral simulations. In the KP theory, the quantum ground state energy and the expectation value of particle position can be obtained simply by performing centroid potential energy minimizations.

Listed in Table 2 are the calculated ground state energy and the expectation value of position for the asymmetric double-well potential from the KP theory. The estimated zero-point energies are 2.672, 2.650, and 2.645 kcal/mol at the KP1, KP2 and KP3 level of theory, respectively, which represents errors of 1.18%, 0.35%, and 0.16% from the exact value of 2.641 kcal/mol. The expectation value of the particle position is shifted away from the coordinate at the minimum of the original potential due to asymmetry of the potential. The corresponding KP results are in remarkable agreement with the accurate result, having errors only of 0.27%, 0.16% and 0.08% in comparison with the exact value of -0.52189 Å.

Table 2.

Classical and quantum ground-state energy (kcal/mol) and the expectation value of the particle position (Å) in an asymmetric double-well potential along with the minimum energy of the centroid potential and position from the first three-order of the Kleinert variational perturbation theory

Ground state	Classical	Accurate quantum	KP1	KP2	KP3
Energy	0	2.641	2.672	2.650	2.645
〈x〉	-0.55958 (xmin)	-0.52189	-0.52329	-0.52272	-0.52231

B. The Morse potential for bond vibration

The Morse potential⁸⁰ is selected to model the bond vibrations of three diatomic molecules: H₂, HF, and HCl:^99,100

$$V\left(r\right)=D_e{\left[1-\exp \left(-\frac{r-r_0}{\gamma }\right)\right]}^2,$$ (21)

where r is the bond length, r₀ is the equilibrium distance, D_e is the bond dissociation energy, and γ is a parameter related to the harmonic frequency by ${\omega }_0=\frac{1}{\gamma }\sqrt{\frac{2D_e}{\mu }}$ with μ being the reduced mass of a diatomic molecule. The parameters for the three molecules are given in Table 3.^99,100

Table 3.

The parameters of the Morse potential for hydrogen chloride, hydrogen fluoride, and hydrogen molecules

Molecule	De (kcal/mol)	r0 (Å)	γ (Å)
HCl†	106.48594	1.274577	0.535536
HF‡	136.30000	0.916600	0.452243
H2†	109.48232	0.741589	0.514992

^†Ref. [99]

^‡Ref. [100]

We first examine the temperature dependence of the quantum partition function Q_qm from the bound states for hydrogen fluoride using the KP theory. The computational results obtained by using a tenth-order polynomial with 0.02 Å interpolation steps (P10-0.02A) for the Morse potential at the KP1 and KP2 levels of theory are listed in Table 4, along with the exact results for a temperature ranging from 50 to 1000 K. Good agreement is found between results from KP1 or KP2 calculations and the exact values. Even at 50 K, the KP1 partition function is still within 75% of the exact value (-25% error), while the KP2 theory shows a remarkable 96.4% accuracy (-3.6% error). As noted above, although the absolute partition function may show greater errors due to the exponential dependence on the centroid potential, the computed free energies are less sensitive as illustrated in Table 4. For example, at the zero-temperature limit, the computed free energies using KP1 and KP2 are within 0.52% and 0.07% of the exact zero-point energy, respectively.

Table 4.

Classical and quantum canonical partition functions and free energies of the Morse potential for hydrogen fluoride at various temperatures. Signed percent errors (%) of different theoretical methods relative to the accurate quantum results are given

	Canonical bound partition function
T (K)	Classical	Quantum	KP1/P10-0.02A	KP2/P10-0.02A
1000	1.73E-01	5.61E-02	-0.2	0.0
500	8.61E-02	3.12E-03	-1.0	0.0
400	6.88E-02	7.38E-04	-1.8	0.0
300	5.16E-02	6.67E-05	-3.0	-0.1
200	3.44E-02	5.45E-07	-5.1	-0.4
100	1.72E-02	2.97E-13	-12.1	-1.3
50	8.58E-03	8.84E-26	-24.9	-3.6

	Free energy (kcal/mol)
T (K)	Classical	Quantum	KP1/P10-0.02A	KP2/P10-0.02A
1000	3.486	5.724	0.1	0.0
500	2.436	5.733	0.2	0.0
400	2.127	5.732	0.2	0.0
300	1.767	5.732	0.3	0.0
200	1.340	5.732	0.4	0.0
100	0.807	5.732	0.4	0.0
50	0.473	5.732	0.5	0.1
0	0	5.732	0.5	0.1

In Tables 5 and 6, we summarize the computed zero-point energies and bond length expectation values at the global minima of the centroid potentials from both KP1 and KP2 levels of theory, along with the exact results. In all cases, the agreement with the exact quantum data is excellent. For H₂, which is expected to have the largest quantum effects due to its small reduced mass, the error in the computed ground state energy (lowest value in the centroid potential) is only 0.15% at the KP2 level of theory. All calculated expectation values of the bond length both at KP1 and KP2 levels are within 0.0001Å of the exact quantum results.

Table 5.

Computed ground state energies (kcal/mol) for hydrogen chloride, hydrogen fluoride, and hydrogen molecules from the Morse potential using the harmonic approximation Rayleigh-Ritz (RR) variational approach, second-order Rayleigh-Schrödinger perturbation theory (RS2), and first and second orders of the Kleinert variational perturbation theory (KP1 and KP2)

Molecule	Quantum	Harmonic	RR	RS2	KP1/P10-0.02A	KP2/P10-0.02A
HCl	4.231	4.274	4.348	4.238	4.253	4.234
HF	5.732	5.793	5.899	5.742	5.762	5.736
H2	6.193	6.284	6.437	6.213	6.238	6.202

Table 6.

Computed expectation value of particle position and the minimum centroid potential coordinate (Å) for H₂, HF, and HCl using KP1 and KP2 theory. The equilibrium bond distances of the original potential are also given

Molecule	Classical	Quantum	KP1/P10-0.02A	KP2/P10-0.02A
HCl	1.274577	1.29094	1.29086	1.29089
HF	0.916600	0.93124	0.93117	0.93121
H2	0.741589	0.76423	0.76409	0.76416

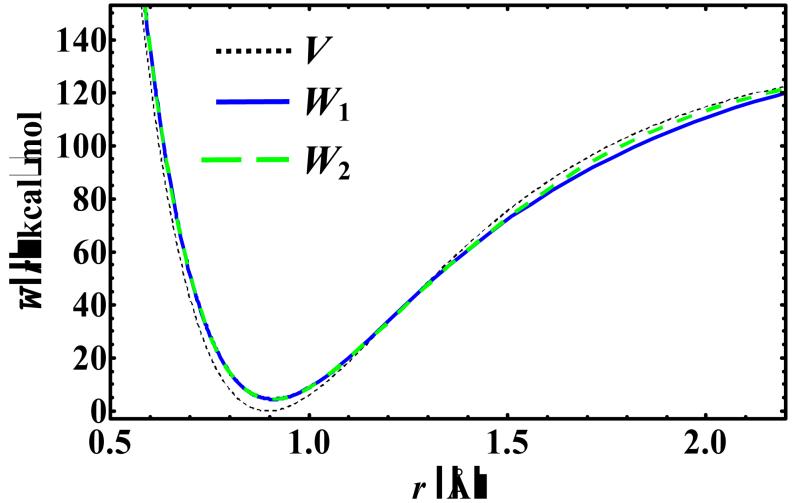
Figure 2 illustrates the KP1 and KP2 centroid potentials at 200 K. It is interesting to note that approximately before the inflexion point of the original potential (in which the INM frequencies are real), the computed centroid potentials are above the original Morse potential, dominated by zero-point vibrational effects, whereas approximately beyond the inflexion point (in which the INM frequencies are imaginary), the centroid potentials are below the Morse potential.

Figure 2.

The first and second order (mass-scaled) centroid potentials (W₁ and W₂) from the KP theory compared with the Morse potential (V) for hydrogen fluoride as a function of the centroid bond length at 200 K.

To shed light on the relationship between KP theory and the use of the harmonic frequency of the Morse potential in approximating quantum energy, as well as traditional (wave function) perturbation and variational theories, we have determined the harmonic zero-point energy (i.e., ħω₀/2), and the ground state energy using the Rayleigh-Ritz variational approach,^82-85 and the second-order Rayleigh-Schrödinger perturbation theory.^63,86,87 All results are also listed in Table 5. In the Rayleigh-Ritz method, the ground state harmonic eigenfunction centered at r₀ is variationally optimized by adjusting the Gaussian width a:

$$\tilde{\varphi }\left(r\right)=\frac{1}{{\left(2\pi a^2\right)}^{1∕4}}\exp \left[-\frac{{(r-r_0)}^2}{4a^2}\right].$$ (22)

The Rayleigh-Schrödinger perturbation was carried out up to the second order, in which the excited states are constructed by using the angular frequency $\tilde{\Omega }$ deduced from the Rayleigh-Ritz optimization:

$$E^{\left(2\right)}=\frac{ħ\tilde{\Omega }}{2}+\langle {\tilde{\varphi }}_0\mid V\left(r\right)-\frac{1}{2}\mu {\tilde{\Omega }}^2{(r-r_0)}^2\mid {\tilde{\varphi }}_0\rangle +\sum _{k\ne 0}\frac{{\mid \langle {\tilde{\varphi }}_k\mid V\left(r\right)-\frac{1}{2}\mu {\tilde{\Omega }}^2{(r-r_0)}^2\mid {\tilde{\varphi }}_0\rangle \mid }^2}{{\mathit{E}}_k-{\mathit{E}}_0},$$ (23)

where ${\tilde{\varphi }}_0$ is the wave function in Eq. (22) with the optimized Gaussian width a, $\tilde{\Omega }=ħ∕2\mu a^2$, ${\tilde{\varphi }}_k$ are the eigenfunctions for the harmonic system with the angular frequency $\tilde{\Omega }$, and ${\mathit{E}}_k$ are the eigenenergies $ħ\tilde{\Omega }(k+1∕2)$.

The zero-point energies computed using pure harmonic frequencies have errors greater than results both from the KP1 and KP2 theory, suggesting anharmonicity is indeed important for high frequency vibrations involving hydrogen atoms. Surprisingly, the Rayleigh-Ritz variational approach performs worse than the harmonic approximation, and this may be attributed to the fact that the location of the wave function is fixed at the minimum of the Morse potential energy function. If the center of the Gaussian wave function in Eq. (22) is also treated as a variational parameter along with the width, the Rayleigh-Ritz variational results reduces to the KP1 value at the zero-temperature limit. Therefore, the variationally optimized position of the Rayleigh-Ritz wave function may be interpreted as the centroid position in path integrals.^1,67-69 The deficiency without optimizing the location of the trial wave function is partially recovered by the second-order Rayleigh-Schrödinger perturbation theory (Table 5), which has an accuracy between KP1 and KP2. Although it is tempting to optimize the center of the wave functions ${\tilde{\varphi }}_k$ used in Rayleigh-Schrödinger perturbation theory, this is not possible because the perturbation theory is not a variational method. Nevertheless, for a symmetric potential, Kleinert showed that at the zero-temperature limit, the KP theory is identical to Rayleigh-Schrödinger perturbation theory, provided that the minimum point in the centroid potential is chosen as the center of the wave function.¹ In general, Kleinert’s variational perturbation theory resembles the combined features of both the Rayleigh-Ritz variational method and the Rayleigh-Schrödinger perturbation theory in wave mechanics.

C. Symmetric and asymmetric Eckart potentials

The Eckart potential^81,103 (Supporting Information) is a popular model for testing the rate theory for chemical reactions because the quantum result is known exactly. Since the reactant and product states are unbound free particles, which have identical classical and quantum partition functions, the difference between classical and quantum rate constants for the Eckart potential is entirely due to tunneling. Often, quantum tunneling effect^88,89 is expressed as the ratio of the quantum rate constant to that of classical transition state theory¹⁰⁴ (TST):

$$\kappa =\frac{k_{\mathit{qm}}}{k_{\mathit{TST}}}=\beta e^{\beta V_{\max }}{\int }_0^{\infty }{\rm Y}\left(E\right)e^{-\beta E}dE,$$ (24)

where k_qm and k_TST are the quantum and TST rate constants, and Υ(E) is the transmission probability at energy E, which can be determined exactly for the Eckart potential (Supporting Information), and V_max is the barrier height. κ is called the quantum tunneling correction factor or transmission coefficient.¹⁰³ In path-integral quantum transition state theory (PI-QTST),^{11,13,69,101,102} κ is approximated as follows (with no correction for re-crossings):

$$\kappa \approx \exp [-\beta (W_{\max }-V_{\max })],$$ (25)

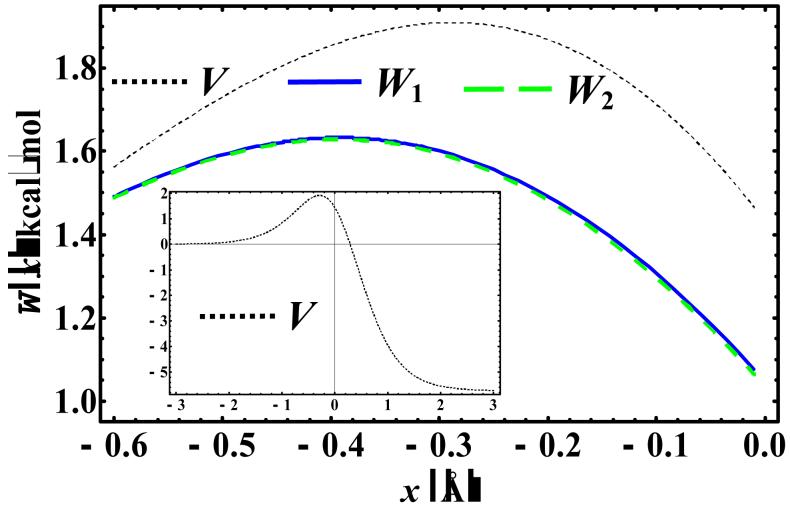
where W_max is the maximum energy of the centroid potential at the PI-QTST transition state. Note that W_max is not necessarily located at the same position as V_max (e.g., Figure 3 and Table 10), although all W_max we found are in the region where the INM frequencies are imaginary. In this study, we consider both the symmetric and asymmetric situations and compare the KP results with those from previous studies.

Figure 3.

Comparison of the mass-scaled KP1 (W₁) and KP2 (W₂) centroid potential with the corresponding Eckart potential (V) near the barrier top at 82 K..

Table 10.

Temperature dependence of x_max of the asymmetric Eckart barrier

		xmax (Å)
βħω*	T (K)	Classical	KP1/P20-0.2A	KP2/P20-0.2A
2	245	-0.28645	-0.30814	-0.30813
4	122	-0.28645	-0.33691	-0.33687
6	82	-0.28645	-0.39049	-0.39212
8	61	-0.28645	-0.48334	-0.49329

For the symmetric Eckart potential, we used a set of parameters corresponding to a protium tunneling through a barrier of V_max ≈ 5.7 kcal/mol with an angular frequency of ω* = 1047.2 cm^-1 at the top of the barrier (Supporting Information). This set of parameters has been widely used both in analytic theories and in path integral Monte Carlo (PIMC) simulations.^40,69,103 Table 7 summarizes the computed quantum correction factor κ using the present KP1 and KP2 theory, along with results obtained from a diagrammatic approach by Cao and Voth (CV),⁴⁰ and from PIMC simulations.⁶⁹ Due to symmetry, W_max is located at the same position as V_max. The theoretical approach used in the Voth-Chandler-Miller paper⁶⁹ (VCM) yields identical results as that from KP1 or the GTFK variational approach, whereas the diagrammatic method of Cao and Voth is similar to KP2 without variational optimization of the angular frequency. In our study, we have used a 20th order polynomial representation of the Eckart potential, fitted in the region of x₀ ± 2 Å. Using this interpolated polynomial potential, the KP1 results are nearly identical to those obtained by Voth at al. without using potential interpolation.⁶⁹ Hence, the computational accuracy by P20-0.2A representation is clearly reasonable in the present calculations.

Table 7.

Computed quantum transmission coefficient κ for the symmetric Eckart barrier at various temperatures

		κ
βħω*	T (K)	Exact	KP1/P20-0.2A	KP2/P20-0.2A	VCM	Cao-Voth	PIMC
2	753	1.224	1.169	1.169	1.2	--	1.2
3	502	1.525	1.419	1.420	1.4	--	1.4
4	377	2.071	1.870	1.872	1.9	--	1.9
5	301	3.102	2.696	2.708	2.7	--	2.7
6	251	5.199	4.283	4.353	4.4	4.4	4.4
8	188	21.77	14.71	16.39	15.0	17.0	17.0
10	151	161.9	74.29	112.0	73.0	110.6	105.0
12	126	1973	514.6	1484	514.0	1278.0	1240.0

^†Ref. [69].

^‡Ref. [40].

In comparison with the exact results, KP1 theory shows noticeable deviations at low temperature, while the results obtained using the KP2 theory, the CV approach, and the PIMC simulation are all very accurate even at a temperature as low as 126 K (Table 7). We list the computed kinetic isotope effects^89,105 (KIE) for protium and deuterium transfer reactions at the KP1 and KP2 levels in Table 8, which are compared with values obtained previously PIMC simulations.¹⁰⁰ A similar trend is observed in that although only KP2 theory is accurate at lower temperatures, at room temperature and above, both KP1 and KP2 perform very well in comparison with PIMC simulations and the exact data.

Table 8.

Kinetic isotope effects (KIE) on the protium and deuterium transfer over the symmetric Eckart potential at various temperatures

	KIE (protium/deuterium)
T (K)	Exact	KP1/P20-0.2A	KP2/P20-0.2A	PIMC†
500	1.232	1.186	1.186	1.19
400	1.374	1.306	1.307	1.31
350	1.511	1.421	1.423	1.43
300	1.756	1.623	1.630	1.62
250	2.283	2.036	2.068	2.08
200	3.840	3.110	3.328	3.33
150	12.17	7.206	10.29	11.10‡

^†Ref. [100].

^‡Computed in this work using the same PIMC program in Ref. [100].

We now turn our attention to the asymmetric Eckart potential (Supporting Information) which has been used by Jang et al.¹⁰¹ (ω* ≈ 340 cm^-1) to test the PI-QTST.^{11,13,69,101,102} Table 9 shows that good accord is obtained between the PI-QTST quantum correction factor from path-integral molecular dynamics (PIMD) simulations and the present perturbation result, particularly at the KP2 level of theory. It is interesting to notice that at low temperature, both the PI-QTST simulation and the KP theory overestimate tunneling effect (Table 9), whereas it is underestimated for the symmetric potential (Table 7). We attribute the difference in the asymmetric Eckart potential to the inclusion of energy E smaller than the reaction energy A in calculating the centroid potential, though there is no contribution to tunneling transmission Υ(E) for energy less than A (Supporting Information). This discrepancy may be resolved by integrating only the closed paths in which the quantum-statistical action $\mathit{A}\left[x\left(\tau \right)\right]$ is larger than or equal to A in the centroid potential calculations:

$$W\left(x_0\right)=-k_{B}T\ln [\int \mathsf{ND}x\left(\tau \right)\delta (\stackrel{‒}{x}-x_0){\mid }_{\mathit{A}\ge A}\exp \{-\mathit{A}\left[x\left(\tau \right)\right]∕ħ\}],$$ (26)

Jang et al.¹⁰¹ proposed a way to alleviate this problem by shifting the lower energy region of the asymmetric potential to match the high energy asymptotic value, i.e., by effectively using a less asymmetric potential.

Table 9.

Transmission coefficient κ for the asymmetric Eckart barrier at various temperatures

		κ
βħω*	T (K)	Exact	KP1/P20-0.2A	KP2/P20-0.2A	PIMD†
2	245	1.195	1.178	1.178	1.17
4	122	2.019	1.985	1.989	1.97
6	82	5.387	5.528	5.668	5.69
8	61	27.27	31.55	35.39	36.6

^†Ref. [101].

In Table 10, we report the x_max values, at which the centroid potential is at the maximum, at different temperatures. The x_max values correspond to the PI-QTST saddle point (or transition state), which is shifted away from the position of the original barrier. At 61 K, x_max deviates from the classical transition state by more than 0.2 Å.

D. Optimization of the Variational Frequency

Both the nth order centroid potential $W_n^{\Omega }$ and the associated optimal frequency Ω_opt,n are functions of the centroid position x₀ and temperature T. As n tends to infinity, $W_n^{x_0,T}\left(\Omega \right)$ becomes independent of Ω, and $W_{\infty }^{x_0,T}\left(\Omega \right)$ is exact. This, in fact, provides a variational procedure for determining $W_n^{\Omega }(x_0,T)$ on the basis of least dependence on Ω.¹ Thus, at a given position x₀ and temperature T, we obtain the centroid potential $W_n^{x_0,T}\left(\Omega \right)$ as a function of Ω. The optimal value Ω_opt,n(x₀,T) is at the $W_n^{x_0,T}\left(\Omega \right)$ minimum or is located at the point that $W_n^{x_0,T}\left(\Omega \right)$ has the least Ω-dependent if a minimum does not exist, i.e., the second derivative is zero. The latter corresponds to an inflexion point. In this section, we examine some features of the optimal value of the variational parameter Ω_opt,n(x₀,T) at different perturbation levels, and the dependence of the centroid potential on Ω at different temperatures. All discussions are based on the asymmetric double-well potential discussed in section 5A.

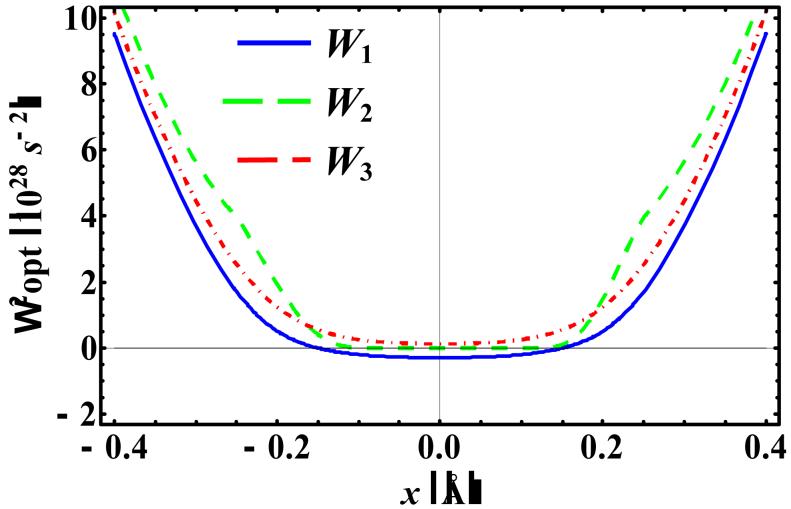
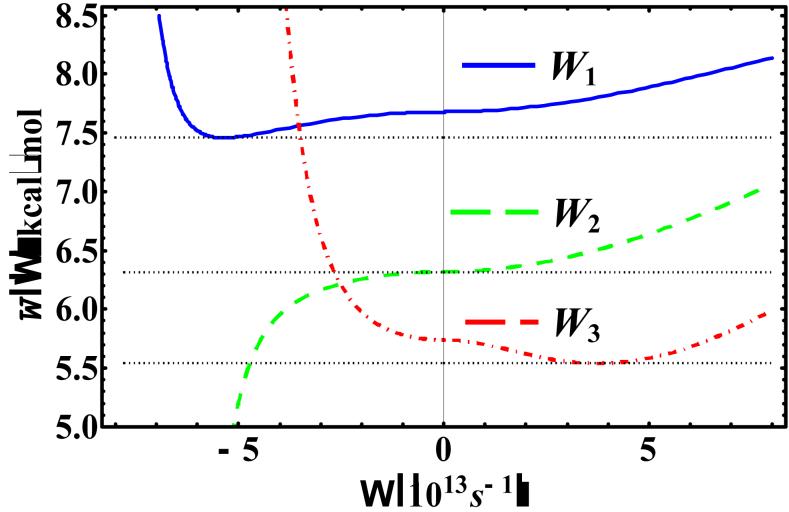
Figure 4 shows the optimal variational frequencies Ω_opt,n(x₀,T), where n = 1, 2, and 3, along the coordinate position at 100 K, which are used to determine the corresponding centroid potentials at the three perturbation levels. First, Ω_opt,n(x₀,T) can be either a real or an imaginary quantity, depending on the potential surface, the coordinate position, and temperature. For the KP1 theory, the variational frequency is imaginary in the barrier region of the double-well potential, whereas Ω_opt,3(x₀,100 K) has real values throughout. Interestingly, for an extended range around x₀ = 0, Ω_opt,2(x₀,100 K) has an optimal value of zero. In Figure 5, we focus on a given centroid position at x₀ = 0 and T = 100 K, and illustrate the dependence of the three KP centroid potentials on the variational frequency Ω. In this figure, the imaginary axis of Ω is represented by the negative axis (Note: $W_n^{x_0,T}\left(\Omega \right)$ is an even function of Ω). In this case, the optimal frequency is imaginary for W₁ with a value of 5.35694×10¹³ i s^-1, real for W₃ with a value of 3.78053×10¹³ s^-1, and zero s^-1 for W₂. For reference, the INM frequency at x₀ = 0 is imaginary, with a value of 2.36308×10¹⁴i s^-1.

Figure 4.

The Ω_opt,1(x), Ω_opt,2(x), and Ω_opt,3(x) for the mass-scaled asymmetric double-well potential at T = 100 K.

Figure 5.

$W_1^{x_0,T}\left(\Omega \right)$, $W_2^{x_0,T}\left(\Omega \right)$, and $W_3^{x_0,T}\left(\Omega \right)$ at x₀ = 0 and T = 100 K for the asymmetric double-well potential. Note that the imaginary axis of Ω is represented by the negative axis

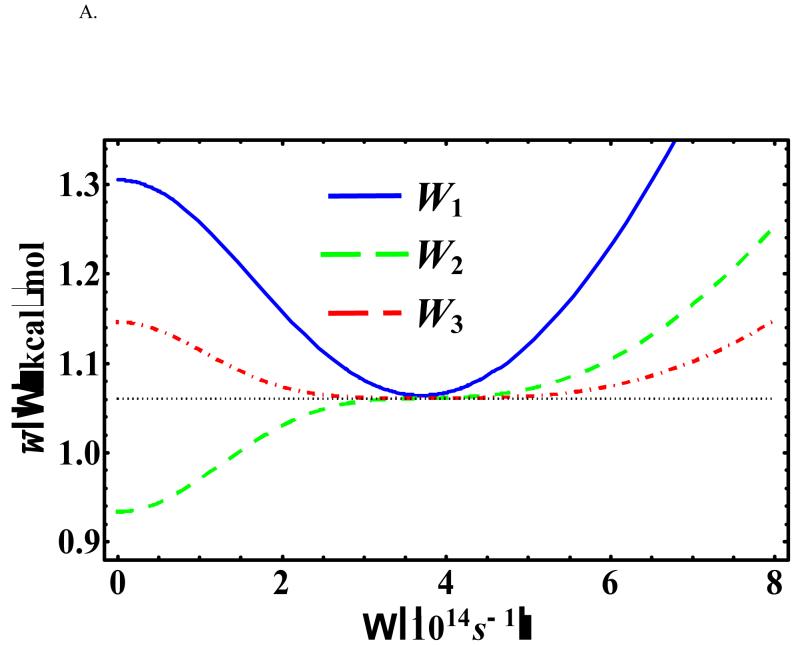
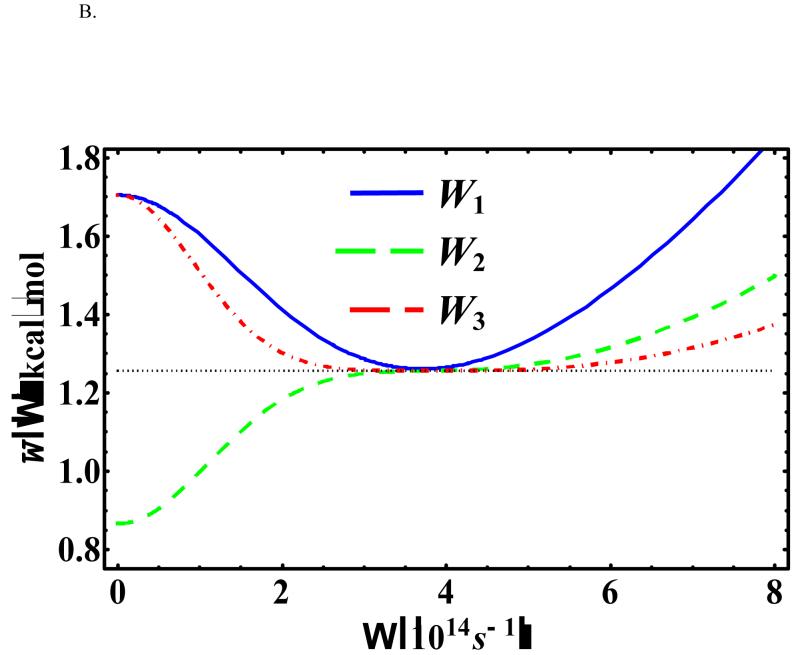
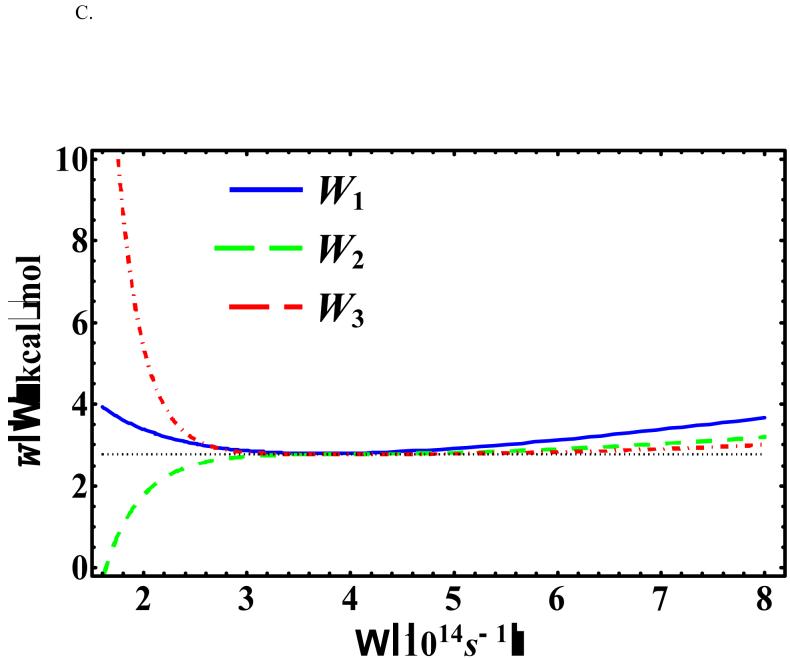
Figure 6 depicts the Ω-dependence of $W_n^{x_0,T}\left(\Omega \right)$ at x₀ = -0.55958 Å (in which the original potential [Eq. (18)] is at the global minimum) for three different temperatures: T = 500, 386, and 100 K. Under these conditions, the optimal values of the variational frequency are all real and we see that the change in the centroid potential becomes less sensitive at a higher order perturbation when Ω is large (greater than the optimal value). Furthermore, the KP2 centroid potential exhibits an inflexion point rather than a minimum as a function of Ω in all three temperatures because of the alternating signs in the cumulant expansion for even-order terms in the KP theory.^1,5,70 These observations are consistent with those described by Kleinert in Ref. [1].

Figure 6.

$W_1^{x_0,T}\left(\Omega \right)$, $W_2^{x_0,T}\left(\Omega \right)$, and $W_3^{x_0,T}\left(\Omega \right)$ at x₀ = -0.55958 Å and (a) T = 500 K, (b) T = 385.96 K, and (c) T = 200 K for the asymmetric double-well potential.

When Ω is small, at lower temperatures the centroid potential becomes more sensitive at higher order perturbations. At the limit of zero-Ω (analytical expressions are available in Supporting Information), the centroid potential corresponds to that using a free-particle reference frame, which is the frame used in the Feynman-Hibbs approach.⁸ In this limit, the perturbative inter-action in the KP theory [i.e., $V_{\mathrm{int}}^{x_0}$ in Eq. (15)] is the original potential itself. In Figure 7, the centroid potential at zero-Ω limit is shown as a function of temperature at x₀ = -0.55958 Å for the first three orders of KP theory. W₁ and W₃ coincide at temperature of 386 K. Although the results converge in the high-temperature limit, they diverge at lower temperatures. This behavior suggests that (not surprisingly) the free-particle reference state is not particularly a good choice in a general perturbation expansion.

Figure 7.

Temperature-dependence of $W_1^{x_0}(\Omega =0)$, $W_2^{x_0}(\Omega =0)$, and $W_3^{x_0}(\Omega =0)$ at x₀ = -0.55958 Å.

6. Concluding Remarks

The Kleinert variational perturbation theory is a systematic, fast convergent method for treating nuclear quantum effects in molecular systems. In the KP theory, the angular frequency Ω for a harmonic reference state at a given centroid position x₀ is variationally optimized and the exact quantum partition function is obtained by systematically incorporating anharmonic corrections to the centroid potential of this reference system. Despite the numerous attractive features of the KP theory, it has not been used in chemical applications beyond the first order perturbation, i.e., the so-called Giachetti-Tognetti-Feynman-Kleinert (GTFK) variational approach. The primarily drawback is the need to optimize the variational frequency, which becomes an n×n matrix, by path-integral calculations. The coupled path-integral effective potential optimization and evaluation of Gaussian smearing functions in the KP theory is a daunting computational task, and only until very recently, a practical procedure has been devised for condensed phase simulations at the KP1 level of theory.^77,78 Making use of the instantaneous normal mode approximation, which reduces a system of 3N degrees of freedom where N is the number of particles to 3N one-dimensional problems, we have developed an analytical method to obtain the centroid potential as a function of the variational parameter in the KP theory,⁵⁹ avoiding numerical path-integral Monte Carlo or molecular dynamics simulations. Consequently, the variational procedure in the KP theory can be efficiently carried out, and thus, higher order perturbations can be performed for realistic chemical applications. Previously, we have demonstrated that in the INM approximation, the AIF-PI method is still accurate for computing the quantum partition function of a water molecule (3 degrees of freedom) and the quantum correction factor for the reaction rate of the collinear H₃ reaction (2 degrees of freedom).

In the present study, we further test the accuracy and properties of KP theory by using the first three order perturbations to determine the zero-point energy, quantum partition function, and tunneling factor for systems including an asymmetric double-well potential, the bond vibrations of H₂, HF, and HCl represented by the Morse potential, and a hydrogen-transfer barrier modeled by the Eckart potential. The following general conclusions are drawn from these calculations:

1. Kleinert’s variational perturbation theory is an extremely accurate method for treating internuclear quantum-statistical effects and for obtaining path-integral centroid potentials. Although the lowest (first-order) level perturbation theory, KP1, which is identical to the GTFK variational method, shows noticeable deviations (by more than 25%) from the exact quantum results (including the partition function and tunneling factor), at temperatures below 100 K, the second and third order perturbations, KP2 and KP3, remain accurate, within 96% of the exact values for all systems considered;

2. Using our newly derived analytical results (Supporting Information), the minimum value of the centroid potential at the zero-temperature limit is in excellent agreement with the ground state energy (zero-point energy), and the position of the centroid-potential minimum is the expectation value of particle position in wave mechanics;

3. In comparison with Rayleigh-Ritz (RR) variational approach and Rayleigh-Schrödinger (RS) perturbation theory in wave mechanics, the results from the KP theory in path-integral quantum mechanics combine both features of RR variation (optimization of both the center and width of wave function) and RS perturbation that includes dynamic correlations. Consequently, the Kleinert perturbation theory converges exceedingly fast, and the KP2 level of theory can yield accurate results for computing kinetic isotope effects in chemical reactions;⁵⁹

4. Finally, the centroid potential obtained from the Kleinert perturbation calculations can be used in combination with path-integral quantum transition state theory (PI-QTST) to estimate the rate constant of chemical reactions and can be applied to condensed phase systems and enzymatic processes.