Abstract
A new vibrational subsystem analysis (VSA) method is presented for coupling global motion to a local subsystem while including the inertial effects of the environment. The premise of the VSA method is a partitioning of a system into a smaller region of interest and a usually larger part referred to as environment. This method allows the investigation of local-global coupling, a more accurate estimation of vibrational free energy contribution for parts of a large system, and the elimination of the “tip effect” in elastic network model calculations. Additionally, the VSA method can be used as a probe of specific degrees of freedom that may contribute to free energy differences. The VSA approach can be employed in many ways, but it will likely be most useful for estimating activation free energies in QM∕MM reaction path calculations. Four examples are presented to demonstrate the utility of this method.
INTRODUCTION
Modeling the dynamics and free energy of biomolecular systems remains a major challenge for computational biologists. Currently, minimization, molecular dynamics (MD), and harmonic analysis are the primary tools employed to examine the structure and dynamics of biomolecules. MD approaches have dominated the biosimulation community; however, the timescales required to observe global motion, which can be on the order of milliseconds to seconds, have prevented many systems from being studied.1 Although this is a particular problem for larger systems, MD is still the most commonly employed method for three main reasons. First, harmonic analysis does not account for multiple minima although newly developed course grain methodology has mitigated this problem.2, 3, 4 Second, there is often too much “noise” in large biomolecular systems which makes extracting the desired observables difficult. Third, although the computational cost of second derivative techniques is less computationally expensive than running long MD simulations the O(N3) memory requirements have been prohibitive until recently. For example, a 50 000 atom system would require a computer with over 150 Gb of memory.
Normal mode analysis (NMA) methods have been proposed and utilized to extend the range of biomolecules researchers are capable of examining.5, 6, 7, 8, 9 This ability is predicated on the theory that harmonic dynamics are sufficient for understanding the collective motions of near-native states with low frequency normal modes dominating the qualitative dynamics.7, 10, 11, 12, 13, 14 This assertion has been shown to be a good approximation by numerous groups15, 16, 17, 18, 19, 20, 21, 22, 23 and has led to the development of elastic network model (ENM) methods.2, 3, 4 These methods typically replace all-atom descriptions with Cα-centered harmonic potentials that utilize a single force constant to account for all pairwise interactions within some cutoff distance (Rc). For example, the energy of an ENM representation can be defined as
| (1) |
where dij is the distance between Cα atoms and is the reference value from experiment (i.e., crystal structure, NMR, etc.). Given the simplicity of these models, previously impossible NMA can be performed using ENM methods. This approach has been shown to to be an effective means of extracting patterns of low frequency motion.24
In the current work we present the vibrational subsystem analysis (VSA) method for coupling global motion to a local subsystem. This method is a partitioning scheme that separates (and integrates out) the motion of the environment from a user defined subsystem (see Methods section) while still allowing the environmental motion to perturb the local subsystem dynamics. It was originally applied to ENM models25 but is now generalized and extended for all-atom representations and hybrid quantum mechanical∕molecular mechanical (QM∕MM) potentials. Below is a brief list of possible uses.
-
(1)
Initially described as an ENM methodology, the VSA method is well suited to describing local-global coupling in coarse-grained macromolecular systems.26 In the current work we have extended this approach to include a mass term in the ENM-NMA procedure which allows for better coupling of timescales since the inertial terms in the environment are handled more appropriately.
-
(2)
Eliminating specific degrees of freedom without the detrimental effects of constraining the motion (i.e., making the system too rigid) or deleting part of the system (i.e., artificially increasing flexibility). A particularly useful illustration of this is in the “tip effect” (Ref. 27) which refers to small pieces of proteins that can protrude out of the main globular body (e.g., surface loops, unresolved density, etc.). Using the VSA method these problematic degrees of freedom can be integrated out of the environment while still being included as a perturbation to the subsystem of interest.
-
(3)
Elimination of noise when computing harmonic vibration free energy of large biomolecular systems. The term noise is used to depict unwanted weak coupling between degrees of freedom in the environment and degrees of freedom in the subsystem that makes it difficult to calculate properties of interest. This is particularly important when performing QM∕MM free energy calculations as the classical entropic effects from the environment can be included as a first order perturbation to the QM harmonic free energy. In addition, this can also be a very useful tool in describing how global motion of a protein can couple to the active site before and during biochemical reactions.
-
(4)
Combining VSA with simulation approaches. For example, the use of quasiharmonic analysis to generate an effective force constant matrix from a detailed simulation can allow exploration of “hidden” couplings that ENM models cannot capture. In general, the VSA approach can be combined with numerous additional normal mode treatments; such as reduced basis methods (i.e., block normal mode method) to further reduce the number of degrees of freedom treated.28
-
(5)
Inclusion of very light or mass-less particles into NMA without the need for constraints or inclusion of unwanted high frequency heat capacity. This could be particularly useful as Drude oscillator approaches become a standard classical polarization technique.
-
(6)
One of the most popular reaction path following techniques currently in use is the intrinsic reaction coordinate (IRC) method.29, 30 The IRC method, which requires knowledge of the transition state, employs internal coordinates to map the minimum energy pathway connecting reactants and products. Although this is an effective approach, IRC mapping is typically not performed on high dimensional systems (i.e., proteins) for various reasons. One benefit of the VSA approach is that by integrating out the environment, rather than fixing or deleting it, second order methods that have previously been sparingly used (i.e., IRC) will again become available. Taking this in combination with the full QM∕MM analytic second derivatives introduced in the current work QM∕MM IRC calculations on biomolecular systems could easily gain mainstream use.
In Sec. 2 (Methods) we improve the original approach for vibrational subsystem analysis26 and derive the formula for including environmental inertial effects in the VSA method in two different ways. Also described is the extension of the vibrational capabilities of CHARMM to utilize hybrid QM∕MM potentials. In Sec. 3 (Results and Discussion) we give four examples of where VSA can be applied and discuss how the results correspond to full NMA; (1) VSA is applied to a simple harmonic string of beads and computed results are compared to analytically derived results. (2) VSA is applied to the torsional potential of butane with only carbon atoms defined as the subsystem. (3) VSA is applied to the cyclohexane chair to boat conversion with only carbon atoms defined as the subsystem. (4) QM (B3LYP∕6-31G*) NMA, VSA, and block normal mode (BNM) methods are applied to a peptide radical rearrangement. Full NMA, VSA, and BNM results are compared and implications of the choice of subsystem is explored. Section 4 (Conclusions) is an overview of the VSA method with results and future directions highlighted.
METHODS
The VSA method
To specify the vibrational subsystem methodology, the entire system is first divided into two components: (1) the subsystem, which is defined as the region of interest (i.e., part of the system that controls functionality); (2) the environment, which consists of the less important remaining portions of the molecule. The main idea is to study the coupling of these two regions and how this affects the dynamics of the subsystem. To do this the potential energy of the full system is defined as
| (2) |
with xs and xe defined as the displacements of the system and environment atoms, respectively, and the full Hessian defined as
| (3) |
where Hss, Hse, and Hee are the subsystem-subsystem, subsystem-environment, and environment-environment Hessians, respectively. xe is then integrated out by setting ∂E∕∂xe=0 as a constraint, which leads to
| (4) |
which further leads to the redefinition of the potential energy using an effective Hessian
| (5) |
The fundamental approximation that is made by performing this partitioning is that the environment will be able to respond to structural changes from the subsystem by minimizing the total energy. Using this approximation and choosing an appropriate subsystem induced global changes can be predicted. Additionally, performing a standard (NMA) employing will yield the local modes that describe subsystem dynamics with a flexible environment. Following from the definition of the energy, the free energy conformational integral can also be defined and separated,
| (6) |
with xer representing the motion of environment atoms relative to the derived positions satisfying Eq. 4 (i.e.,). This also leads to a formal splitting of the vibrational free energy via
| (7) |
Since we are primarily interested in the dynamics of the subsystem (xs) we can ignore differences in Fe and focus entirely on changes in Fs. For example, in larger systems Fe is likely to be “noisy,” but may be safe to ignore whereas Fs contains subsystem data hopefully with suitable accuracy. If either of these conditions is not satisfied then repartitioning of the subsystem and environment is required and the VSA procedure needs to be repeated. More specifically, the partition of subsystem and environment should be done several times when exploring the importance of specific degrees of freedom for a reaction coordinate of interest.
To more realistically describe the system we also introduce mass into the subsystem partitioning. The addition of mass allows better timescale coupling as inertial terms in the environment are treated more consistently,
| (8) |
where Eq. 8 is the secular equation and H the full Hessian, V the eigenvectors∕normal modes, λ the eigenvalues∕frequencies squared, and M the kinetic energy matrix with mass elements along the diagonal. Eq. 8 can be written as
| (9) |
where subindex s or e refers to system or environment, respectively. Elimination of Ve from Eq. 9 gives
| (10) |
with in the limit of small λ thus leading to an expansion of a first order generalized eigenvalue problem,
| (11) |
The left side of Eq. 11 has the same effective Hessian as Eq. 5 while the right hand side of Eq. 11 has an effective kinetic energy matrix that includes the inertial effects of the motion of the environment.
Another equivalent derivation uses Lagrange multipliers. If L denotes the Lagrangian of the system, each of the constraints fk(x)=0 can be taken into account by adding a term λkfk(x) to L. Hence an additional set of variables {λk}, the Lagrange multipliers, are introduced and the Lagrangian of the constrained system becomes
| (12) |
In the case of VSA, one keeps all atoms in the environment force free, and the Lagrangian reads
| (13) |
with ne defined as the number of atoms in the environment. In order to get the harmonic oscillator approximation, the Lagrangian is expanded up to second order in the displacements of xs, xe, and λe.
| (14) |
In the unconstrained case, the Euler–Lagrange equations lead to Newton equations, which are first order. Here the VSA constraints generate 3ne extra equations for the Lagrange multipliers,
| (15) |
| (16) |
| (17) |
Eliminating xe and λe from Eqs. 15, 16, 17, the VSA eigenvalues λ and vectors V′=(Vs,Ve,Vλ) are easily found from the following eigenvalue problem for the subsystem:
| (18) |
and consequently
| (19) |
| (20) |
These equations are formally identical to those derived with perturbation theory above.
Hybrid QM∕MM analytic second derivatives
Expanding on the functionality of subsystem partitioning, we implement hybrid QM∕MM analytic second derivatives into the Q-CHEM software package and interface this with VIBRan module of CHARMM.5, 6, 7, 31, 32 Both restricted and unrestricted wave-functions are supported at the HF and DFT levels of theory, whereas previous work in this area focused only on RHF and RDFT treatments.33 We briefly review standard SCF derivative theory and illustrate how this differs from applying hybrid QM∕MM methodology.
Using Pople’s compact notation,34 where ⟨ ⟩ denotes the trace of a matrix, the SCF energy can be defined as
| (21) |
where P is the density matrix, H is the core Hamiltonian, and ∥ are the antisymmetrized two-electron integrals over spin orbitals μ, ν, λ, σ, and γ is the nuclear repulsion energy. The Fock operator is then defined as
| (22) |
and the standard SCF can be written as
| (23) |
with S defined as the overlap matrix. Now, taking the second derivative with respect to atomic perturbations the following expression is derived:
| (24) |
At this point the coupled perturbed equations (CPHF for Hartree-Fock and CPKS for DFT) need to be solved. However, in contrast to standard QM theory the Hessian matrix has four blocks: QM-QM, QM-MM, MM-QM, and MM-MM with the QM-MM and MM-QM block being equivalent. At first glance solving the CP equations would appear to be impossible for very large (thousands of atoms) systems, but given the nature of classical point charge terms involving overlap matrix derivatives (Sx,Sxy) and two-electron integral derivatives (∣∣x,∣∣xy)can be dropped (Table 1). This simplification, combined with improved techniques for solving CP equations34 lead to the case where problems that were previously impossible to examine are now feasible.
Table 1.
Overview of the integrals that can be neglected (denoted with an ×) when considering QM, QM∕MM, and MM∕MM blocks of the Hessian matrix.
| QM-QM | QM-MM∕MM-QM | MM-MM | |
|---|---|---|---|
| PHxy | √ | √ | √ |
| P∥xyP | √ | × | × |
| (PFP)Sxy | √ | × | × |
| PyHx | √ | √ | √ |
| Py∥xP | √ | √ | × |
| (PFP)ySx | √ | √ | × |
| γxy | √ | √ | √ |
Classical, quantum, and hybrid QM∕MM transition state searching
In addition to implementing QM∕MM analytic second derivatives, we also added eigenvector following routines to the Newton–Raphson minimization routines in CHARMM. This is done in a flexible manner that allows efficient minimization both in and out of a harmonic well. If the system can be approximated harmonically then standard Newton–Raphson minimization occurs making use of the energy (E), gradient of the energy (∇E) and Hessian of the energy (∇2E). However, if the system cannot be approximated as a set of harmonic oscillators then a line search is performed along the specified eigenvector(s). In addition to the three pieces of information already gathered (vide supra) two additional gradient calculations are performed along the positive and negative directions of eigenvector(s). These five pieces of information are then fit to a third order polynomial (f(x)=ax3+bx2+cx+d) and solved via a linear least squares fit procedure.
Using classical QM and QM∕MM potentials we have adapted the current minimization procedure to change the direction of eigenvector(s) searching. Typically, minimization occurs along all eigenvectors, however, in the new routines saddle points can be searched for by specifying the order of the stationary point that is desired. For example, searching for a transition state (first order saddle point) occurs by determining if the eigenvalue is below a user defined threshold. If this criteria is met then all eigenvectors except that which corresponds to the lowest eigenvalue will be minimized and the specified eigenvector will be maximized. Since eigenvalues are used to determine the mode to follow it is useful to initially perturb the structure in the direction that the desired saddle point is located. This can be done easily with coordinate fixing or restraining potentials in CHARMM or other software.
RESULTS AND DISCUSSION
In the following section the results of four test cases are reported: (1) harmonic beads on springs, (2) classical torsional barrier of butane, (3) classical chair to boat inversion of cyclohexane, and (4) quantum mechanical eclipsed-antitorsional barrier of retinol.
Harmonic beads on springs
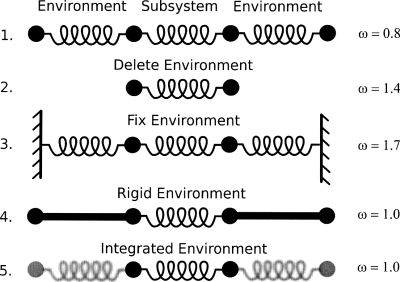
The first, and simplest, test system consists of four beads with the mass of each set to 1.0 amu. The beads are connected by springs of force constant k=1.0 kcal∕mol∕Å (Fig. 1). In this example, the subsystem (middle two beads and the spring connecting them) and the environment (the outer two beads and the springs connecting them to the subsystem) are initially defined. Five cases are constructed and examined with frequencies being computed and compared: (1) full explicit system of four beads and three springs; (2) subsystem with environment deleted; (3) full explicit system with environmental beads being fixed (i.e., their masses being set to infinity); (4) rigid environment approximation (i.e., MBH);35, 36, 37 (5) integration of environmental degrees of freedom (i.e., VSA). For each system a Hessian matrix was constructed, mass weighted, and diagonalized to yield the eigenvalues (i.e., frequencies ω).
Figure 1.
Illustration and results of harmonic beads on strings. The subsystem is defined as the middle two beads with various treatments applied to the “environment.” (1) Full treatment, (2) environment deleted, (3) environment fixed, (4) rigid environment, and (5) environment integrated out (i.e., VSA).
Results for case 1 are taken as the benchmark and determined to be ω=0.8 cm−1. Case 2, where the environment is deleted results in a near doubling of the frequency yielding ω=1.4 cm−1. Fixing the environment (case 3) enhanced the motion even further and resulted in a frequency of 1.7 cm−1. Approximating the environment as rigid rods (case 4) produced ω=1.0 cm−1 which is the same result obtained for the VSA (case 5) treatment where the environment was integrated out. It should be noted that the results (ω=1.0 cm−1) for cases 4 and 5 do not have to be the same. However, given the simplicity of the system and because the masses and springs are symmetric the results work out to be the same. For more complicated systems this will not be the case. It should also be noted that the kinetic energy matrix was included [Eq. 18] in all results and is clearly needed to account for the inertia of the environment. For example, the frequency of the VSA result would be 2.0 cm−1 if inertial effects are ignored.
Torsional barrier of butane
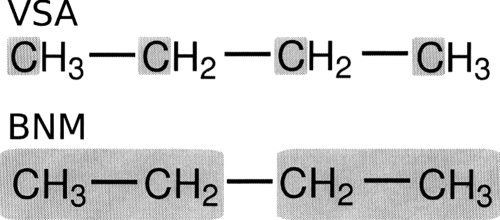
All atom and VSA NMA calculations are carried out to examine the eclipsed-antibarrier of butane. Block normal mode (BNM) calculations are also performed and compared to VSA results. The different subsystems employed for VSA and BNM calculations are illustrated in Fig. 2 and results are presented in Tables 2, 3. It should be noted that both the VSA and BNM calculations are set up to produce twelve normal modes which is approximately a 70% reduction in system size. Additionally, the newly developed saddle point optimization routines are used to locate the eclipsed transition state.
Figure 2.
Illustration of the schemes used to examine the butane anti to eclipsed rotation. The top scheme was employed with the VSA method with the bottom scheme being used with the BNM method.
Table 2.
Vibrational subsystem analysis and BNM results for butane in the global minimum (i.e., anti conformation). All frequencies are listed in cm−1.
| VSA Freq. | Full NMA Freq. (% overlap) | BNM freq. | Full NMA Freq. (% overlap) |
|---|---|---|---|
| 122 | 122 (100) | 128 | 122 (100) |
| 294 | 290 (100) | 308 | 290 (100) |
| 397 | 392 (100) | 445 | 392 (98) |
| 993 | 866 (77) | 511 | 219 (82) |
| 1107 (56) | 743 (51) | ||
| 1047 | 1012 (80) | 711 | 256 (72) |
| 985 (52) | 829 (49) | ||
| 1058 (35) | |||
| 1161 (36) | |||
| 1146 | 1036 (83) | 991 | 866 (72) |
| 1351 (45) | 1036 (34) | ||
| 1107 (58) |
Table 3.
Vibrational subsystem analysis and BNM results for butane at the highest transition state (i.e., eclipsed conformation). All frequencies are listed in cm−1.
| VSA Freq. | Full NMA Freq. (% overlap) | BNM Freq. | Full NMA Freq. (% overlap) |
|---|---|---|---|
| −165 | −175 (99) | −154 | −175 (98) |
| 314 | 310 (100) | 320 | 310 (99) |
| 516 | 501 (99) | 540 | 304 (82) |
| 684 (50) | |||
| 870 | 814 (92) | 569 | 501 (97) |
| 1093 | 968 (64) | 703 | 286 (69) |
| 1074 (65) | 1160 (40) | ||
| 1182 | 1018 (42) | 946 | 814 (81) |
| 1110 (70) | 1111 (54) |
We also compute activation free energies (ΔG298) for all atom, VSA and BNM approaches. The VSA and BNM results ΔG298=5.5 and 5.5 kcal∕mol, respectively, are in very good agreement with the all atom result, ΔG298=5.6 kcal∕mol. Although, the ΔG298 results agree well between VSA and BNM it is clear that the VSA method did a better job of reproducing high frequency motion in both the anti and eclipsed rotomers of butane. For example, the eclipsed rotomer where hydrogen bumping is known to play a much larger role in determining conformational free energies, the maximum frequency computed with VSA is 1182 cm−1 compared to 946 cm−1 with BNM (Table 3). This difference can be attributed to the inclusion of the environmental hydrogen motion in the VSA modes, whereas in the BNM procedure the internal motion within blocks is constrained.
To further examine mode mapping in the VSA and BNM approaches, mode overlap matrices are computed. This is done by taking the dot product of eigenvectors generated by the VSA and BNM methods with eigenvectors of full NMA. This analysis allows determination of which modes from the full NMA the VSA∕BNM results correspond to. Results of this analysis are listed in parentheses in Tables 2, 3.
Chair to boat inversion of cyclohexane
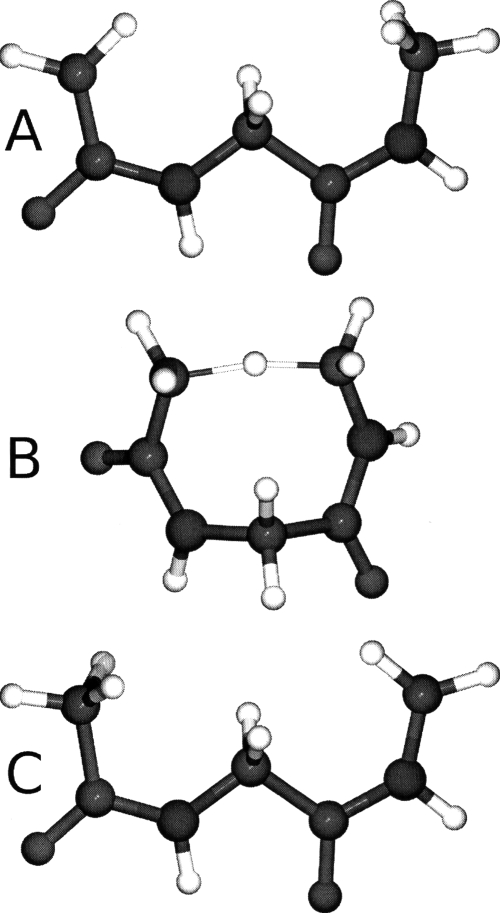
The chair to boat interconversion pathway of cyclohexane is examined using both the all atom and VSA models (Fig. 3). The subsystem employed includes only the ring carbons of cyclohexane which is a 67% reduction in system size. Additionally, we compute the ΔG298 between the four extreme points located along the pathway: (1) the global minimum chair conformer, (2) the global maximum∕transition state, (3) a local minimum twist-boat conformer, and (4) the boat conformer which is a local transition state. All transition states are located using the newly implemented saddle point finder. The free energies are defined relative to the global minimum (i.e., chair conformer) and are listed in Table 4.
Figure 3.
Illustration of the four extreme points located along the cyclohexane interconversion from the chair to the boat form. The reaction proceeds from left to right with the chair (a) being the global minimum, (b) the global transition state (i.e., reclined chair), (c) a local twist-boat minimum, and (d) the boat form (a local transition state).
Table 4.
Relative free energies for the boat to chair inversion of cyclohexane. Results are listed for both the standard NMA and VSA. All values are listed in kcal∕mol and are computed using the global minimum as the reference. See Fig. 3 for definition of states.
| Conformer | Full NMA | VSA |
|---|---|---|
| TS [chair (A) - transition state (B)] | 9.8 | 10.1 |
| Twist-boat [chair (A) - twist boat (C)] | 6.5 | 6.7 |
| boat [chair (A) - boat (D)] | 7.1 | 7.3 |
The average errors in the three ΔG298 examined is 0.25 kcal∕mol with the majority of that being contributed by the global max transition state (0.3 kcal∕mol). Using this as a guide, it is expected that hydrogen motion should be most critical at the global transition state. Further analysis and results listed in Table 5 confirm this hypothesis. For example, examining the internal coordinate derivatives shows that an important mode associated with H–C–C angle bending and H–C–C–C torsional motion does not overlap significantly with the VSA modes at the global TS. In contrast, this mode does map into VSA modes at the chair, twist-boat and boat conformers. This mode encompasses H1–C1 motion which is important because the global TS is a “reclined chair” with all but one ring carbon (C4) being approximately coplanar (Fig. 3). Therefore, the C1 carbon is associated with the major motion of a normal chair becoming a reclined chair. To further demonstrate this, we perform additional VSA calculations where the hydrogens connected to C1 were included in the subsystem and found that the average error in ΔG298 dropped from 0.25 to 0.16 kcal∕mol, which is in agreement with the error attached to the other states where the H–C–C and H–C–C–C mode is mapped correctly.
Table 5.
Cyclohexane boat to chair conversion results comparing full NMA to VSA. All frequencies are listed in cm−1 and degenerate modes are designated a and b.
| Chair | Transition state | Twist-boat | Boat | ||||
|---|---|---|---|---|---|---|---|
| VSA Freq. | Full NMA Freq. (% overlap) | VSA Freq. | Full NMA Freq. (% overlap) | VSA Freq. | Full NMA Freq. (% overlap) | VSA Freq. | Full NMA Freq. (% overlap) |
| 241a | 236a (100) | −219 | −234 (100) | 93 | 93 (100) | −88 | −88 (100) |
| 236b (0) | |||||||
| 241b | 236b (100) | 24 | 24 (100) | 253 | 243 (100) | 222 | 215 (100) |
| 236a (0) | |||||||
| 402 | 377 (100) | 327 | 313 (99) | 297 | 286 (100) | 314 | 302 (100) |
| 464a | 454a (99) | 478 | 462 (98) | 481 | 478 (100) | 481 | 478 (100) |
| 464b | 454b (99) | 480 | 473 (99) | 483 | 461 (97) | 488 | 467 (97) |
| 675 | 565 (86) | 733 | 644 (79) | 688 | 598 (87) | 689 | 596 (86) |
| 905 (51) | 893 (46) | 888 (44) | 888 (49) | ||||
| 862 | 800 (91) | 822 | 785 (89) | 854 | 797 (85) | 850 | 804 (87) |
| 1079 (38) | 839 (31) | 932 (51) | 944 (44) | ||||
| 973a | 880 (68) | 951 | 900 (90) | 962 | 906 (86) | 954 | 899 (94) |
| 938a (65) | 888 (41) | ||||||
| 938b (0) | |||||||
| 973b | 880 (68) | 972 | 883 (79) | 977 | 874 (78) | 981 | 869 (80) |
| 938a (0) | 1035 (44) | 1046 (49) | 1043 (50) | ||||
| 938b (65) | |||||||
| 1144a | 777 (35) | 1171 | 1072 (76) | 1164 | 1089 (72) | 1172 | 1093 (73) |
| 1076a (85) | 1342 (39) | 1372 (46) | 1365 (51) | ||||
| 1374a (0) | |||||||
| 1144b | 777 (35) | 1196 | 1100 (75) | 1190 | 1069 (76) | 1188 | 1070 (76) |
| 1076b (0) | 1389 (44) | 1376 (53) | 1382 (56) | ||||
| 1374b (85) | |||||||
| 1200 | 1079 (76) | 1245 | 1141 (68) | 1211 | 1114 (75) | 1214 | 1118 (74) |
| 1184 (65) | 1342 (34) | 1337 (65) | 1335 (64) | ||||
| 1352 (41) | |||||||
The VSA modes capture the important motions of ring interconversion. Specifically, in the global minimum chair state degenerate modes exist in the full NMA. These modes are correctly reproduced in the VSA results. Modes associated with the following frequencies were determined to be degenerate: 241, 464, 973, and 1144 cm−1 (Table 5). In an effort to clarify the degeneracy of these modes, we project out (via rotation) the degenerate mode and determine how the two modes overlapped with corresponding VSA modes. This is done by diagonalizing the 2×2 overlap matrix between the two degenerate full Hessian modes and the two degenerate VSA modes. This yields the linear combinations of the full Hessian modes that best overlap with the VSA modes.
Quantum mechanical peptide radical rearrangement
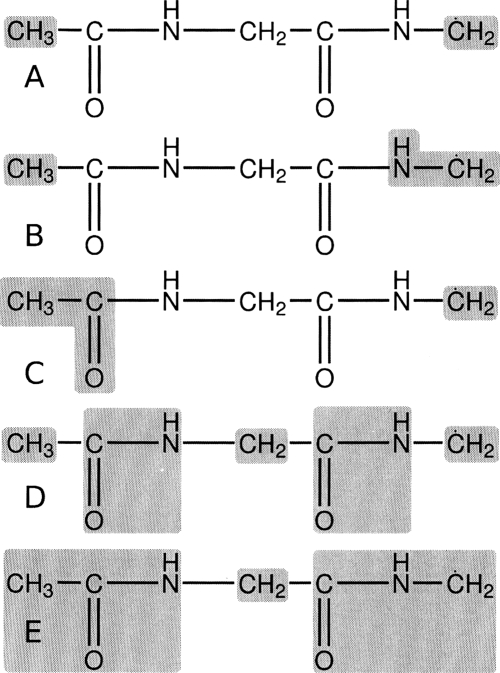
The harmonic limit free energy for intramolecular hydrogen atom transfer in a model dipeptide radical (Gly-Gly) is examined using full NMA, VSA, and BNM at the B3LYP∕6-31G(d) level of theory (Fig. 4). The definitions of the various subsystems and blocking schemes are illustrated in Fig. 5. The Gly-Gly dipeptide radical has been recently studied as a benchmark for hydrogen transfer reactions in peptides.38 In the current study, the ΔE, ΔG298, and forward and reverse ΔG‡ are reported. Moran et al. found the ΔE and barriers at the G3(MP2)-RAD level of theory to be −5.5, 18.4, and 23.9 kcal∕mol, respectively. This is in relatively good agreement with the B3LYP∕6-31G(d) results presented in Table 6 although B3LYP over stabilizes the reactant by 0.7 kcal∕mol [Fig. 4a]. The free energies are defined relative to the global minimum.
Figure 4.
Illustration of the reactant (a), transition state (b), and product (c) of the hydrogen transfer reaction in the glycine-glycine dipeptide radical.
Figure 5.
Definition of subsystem and blocking schemes used to examine the hydrogen transfer reaction in the glycine-glycine dipeptide radical. Schemes (a), (b), and (c) were applied to the vibrational subsystem analysis method while schemes (d) and (e) were employed with the BNM method. See Table 6 for results.
Table 6.
QM Full normal mode and VSA free energy results for hydrogen transfer in the glycine-glycine dipeptide radical. ΔG∕ΔE, and refer to the (free) energy of reaction, forward, and reverse (free) energy of activation. For comparison standard QM energy of reaction and barriers are listed. All calculations were performed at the B3LYP∕6-31G(d) level of theory in Q-CHEM with results reported in kcal∕mol.
The harmonic limit free energy of the full system results in a ΔG298 of −5.1 kcal∕mol and a of 20.4 kcal∕mol. We next test the VSA method using a small subsystem [Fig. 5a] consisting of only the terminal CH3 and radical CH2 groups. This yields good agreement with the results from the full NMA having a 0.7 kcal∕mol RMS error (RMS error is determined using both the free energy and free energy of activation) while reducing the system size by over 60% (i.e., reducing the number of modes from 54 down to 21). We also examine two blocking schemes and employ the BNM method. The least restrained of these [Figure 5d] consists of five blocks and keeps the transfer hydrogen completely free (total of 33 modes, a nearly 40% increase from the VSA method). The results of this BNM scheme again agree nicely, however, the RMS error increases slightly to 1.0 kcal∕mol (nearly a 20% increase over VSA results).
Moran et al. found that energetically carbon centered radicals are “more stabilized by electron donation from an adjacent N-atom lone pair than delocalization into an adjacent carbonyl group.” Using the VSA method and schemes 5(b) and 5(c) we explore the entropic contributions to this stabilization. Although both schemes 5(b) and 5(c) agree well with full NMA free energy results, there is a significant shift in relative state stabilization. For example, examining results from schemes 5(b) and 5(c) shows a reverse in stabilization of the product state [Fig. 4c] relative to the reactant [Fig. 4a]. More specifically, when the N–H group is included in the subsystem the product state is destabilized, however, the reactant state is more destabilized. This leads to a lowering for the forward and reverse barriers while ΔG298 is increased. In contrast, when the C=O group is included in the subsystem the product state is destabilized more so than the reactant state. Again, this leads to both the forward and reverse barriers being lowered, but with the ΔG298 also being decreased.
The results obtained for this model system, employing VSA coupled with quantum mechanics, are not only able to extend the understanding of radical biochemistry but also serve as an example of the powerful and accurate analysis that can be undertaken using these new techniques. For example, comparing ΔG298 for scheme 5(b) (−5.6 kcal∕mol) and scheme 5(c) (−4.8 kcal∕mol) indicates that inclusion of the N–H group in the subsystem has a stabilizing effect on the reaction whereas inclusion of the C=O group actually exerts a destabilization. This tends to confirm the assertion of Moran et al. that the N–H group is more beneficial to the stabilization of the Gly-Gly radical.
CONCLUSIONS
In the current work we presented the detailed derivation, implementation, and testing of the VSA methodology and the coupling of this with quantum mechanical and newly implemented hybrid QM∕MM analytic second derivative techniques. Four illustrative examples were presented, ranging from simply solved analytical models (the harmonic beads) to complicated isomerizations where localized hydrogen motion was analyzed and determined to be critical to complicated radical rearrangements that employed QM methods coupled with full normal mode analysis, BNM analysis, and VSA.
We reiterate that the VSA method will be useful in a variety of situations: examination of local-global motion, performing accurate NMA while eliminating unwanted degrees of freedom, eliminating excess noise from large NMA (i.e., QM∕MM), employing dynamic simulations coupled with VSA via quasi harmonic analysis, and integration of light particles during NMA (e.g., application to polarizable models).
Using the test cases designed and employed we were able to illustrate that the VSA method performs at least as well as the BNM and in many cases can outperform it while using substantially smaller subsystems (i.e., with fewer modes included). However, we feel that the primary strength of the VSA method is its use as an analysis tool. As stated previously, the VSA can be employed to study complicated local-global couplings in proteins using course grained models, but we have also shown that the VSA can be a powerful tool when analyzing complicated electronic systems. For example, using the VSA method we were able to demonstrate that carbon centered radicals in peptides are not only governed by electronic stabilization but also will be influenced by entropic factors related to motion of electronically important substituents. The VSA as an analysis tool has limitless possibilities.
ACKNOWLEDGMENTS
We thank Damian Moran from Macquarie University for helpful insight and fruitful discussions. This research was supported, in part, by the Intramural Research Program of the NIH, NHLBI. Additionally, A.G. was supported by the Fund for Scientific Research—Flanders. Y.S. and J.K. wish to acknowledge the financial support from the National Institutes of Health through SBIR Grant No. GM065617. Use of the LoBoS (www.lobos.nih.gov) supercomputer is also acknowledged and appreciated.
References
- Elber R., Curr. Opin. Struct. Biol. 10.1016/j.sbi.2005.02.004 15, 151 (2005). [DOI] [PubMed] [Google Scholar]
- Tirion M. M., Phys. Rev. Lett. 10.1103/PhysRevLett.77.1905 77, 1905 (1996). [DOI] [PubMed] [Google Scholar]
- Haliloglu T., Bahar I., and Erman B., Phys. Rev. Lett. 10.1103/PhysRevLett.79.3090 79, 3090 (1997). [DOI] [Google Scholar]
- Bahar I., Atilgan A. R., and Erman B., Folding Des. 10.1016/S1359-0278(97)00024-2 2, 173 (1997). [DOI] [PubMed] [Google Scholar]
- Brooks B. R., Janezic D., and Karplus M., J. Comput. Chem. 10.1002/jcc.540161209 16, 1522 (1995). [DOI] [Google Scholar]
- Janezic D. and Brooks B. R., J. Comput. Chem. 10.1002/jcc.540161210 16, 1543 (1995). [DOI] [Google Scholar]
- Janezic D., Venable R. M., and Brooks B. R., J. Comput. Chem. 10.1002/jcc.540161211 16, 1554 (1995). [DOI] [Google Scholar]
- Go N., Noguti T., and Nishikawa T., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.80.12.3696 80, 3696 (1983). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dykeman E. C. and Sankey O. F., Phys. Rev. Lett. 10.1103/PhysRevLett.100.028101 100, 028101 (2008). [DOI] [PubMed] [Google Scholar]
- Case D. A., Curr. Opin. Struct. Biol. 10.1016/S0959-440X(94)90321-2 4, 285 (1994). [DOI] [Google Scholar]
- Kitao A. and Go N., Curr. Opin. Struct. Biol. 10.1016/S0959-440X(99)80023-2 9, 164 (1999). [DOI] [PubMed] [Google Scholar]
- Ma J. P., Structure (London) 10.1016/j.str.2005.02.002 13, 373 (2005). [DOI] [PubMed] [Google Scholar]
- Amadei A., Linssen A. B., and Berendsen H. J., Proteins 10.1002/prot.340170408 17, 412 (1993). [DOI] [PubMed] [Google Scholar]
- Brooks B. R. and Karplus M., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.80.21.6571 80, 6571 (1983). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atilgan A. R., Durell S. R., Jernigan R. L., Demirel M. C., Keskin O., and Bahar I., Biophys. J. 10.1016/S0006-3495(01)76033-X 80, 505 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isin B., Doruker P., and Bahar I., Biophys. J. 82, 569 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keskin O., Durell S. R., Bahar I., Jernigan R. L., and Covell D. G., Biophys. J. 83, 663 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu S. and Jernigan R. L., Biophys. J. 10.1529/biophysj.103.034736 86, 3846 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tama F. and Sanejouand Y. H., Protein Eng. 10.1093/protein/14.1.1 14, 1 (2001). [DOI] [PubMed] [Google Scholar]
- Xu C., Tobi D., and Bahar I., J. Mol. Biol. 10.1016/j.jmb.2003.08.027 333, 153 (2003). [DOI] [PubMed] [Google Scholar]
- Zheng W. J. and Doniach S., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.2235686100 100, 13253 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng W. J. and Brooks B. R., J. Mol. Biol. 10.1016/j.jmb.2004.12.020 346, 745 (2005). [DOI] [PubMed] [Google Scholar]
- Delarue M. and Sanejouand Y. H., J. Mol. Biol. 10.1016/S0022-2836(02)00562-4 320, 1011 (2002). [DOI] [PubMed] [Google Scholar]
- Krebs W. G., Alexandrov V., Wilson C. A., Echols N., Yu H. Y., and Gerstein M., Proteins 10.1002/prot.10168 48, 682 (2002). [DOI] [PubMed] [Google Scholar]
- Zheng W. J. and Brooks B. R., Biophys. J. 10.1529/biophysj.104.058453 88, 3109 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng W. Z. and Brooks B. R., Biophys. J. 10.1529/biophysj.105.063305 89, 167 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu M. Y., Poon B., and Ma J. P., J. Chem. Theory Comput. 10.1021/ct050307u 2, 464 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G. H. and Cui Q., Biophys. J. 86, 743 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukui K., J. Phys. Chem. 10.1021/j100717a029 74, 4161 (1970). [DOI] [Google Scholar]
- Gonzalez C. and Schlegel H. B., J. Chem. Phys. 10.1063/1.456010 90, 2154 (1989). [DOI] [Google Scholar]
- Shao Y., Fusti-Molnar L., Jung Y., Kussmann J., Ochsenfeld C., Brown S. T., Gilbert A. T. B., Slipchenko L. V., Levchenko S. V., O’Neill D. P., Distasio R. A., Lochan R. C., Wang T., Beran G. J. O., Besley N. A., Herbert J. M., Lin C. Y., Van Voorhis T., Chien S. H., Sodt A., Steele R. P., Rassolov V. A., Maslen P. E., Korambath P. P., Adamson R. D., Austin B., Baker J., Byrd E. F. C., Daschel H., Doerksen R. J., Dreuw A., Dunietz B. D., Dutoi A. D., Furlani T. R., Gwaltney S. R., Heyden A., Hirata S., Hsu C.-P., Kedziora G., Khalliulin R. Z., Klunzinger P., Lee A. M., Lee M. S., Liang W., Lotan I., Nair N., Peters B., Proynov E. I., Pieniazek P. A., Rhee Y. M., Ritchie J., Rosta E., Sherrill D. C., Simmonett A. C., Subotnik J. E., Woodcock H. L., Zhang W., Bell A. T., Chakraborty A. K., Chipman D. M., Keil F. J., Warshel A., Hehre W. J., Schaefer H. F., Kong J., Krylov A. I., Gill P. M. W., and Head-Gordon M., Phys. Chem. Chem. Phys. 10.1039/b517914a 8, 3172 (2006). [DOI] [PubMed] [Google Scholar]
- Brooks B. R., Bruccoleri R. E., Olafson B. D., States D. J., Swaninathan S., and Karplus M., J. Comput. Chem. 10.1002/jcc.540040211 4, 187 (1983). [DOI] [Google Scholar]
- Cui Q. and Karplus M., J. Chem. Phys. 10.1063/1.480658 112, 1133 (2000). [DOI] [Google Scholar]
- Frisch M., Head-Gordon M., and Pople J., Chem. Phys. 10.1016/0301-0104(90)87055-G 141, 189 (1990). [DOI] [Google Scholar]
- Ghysels A., Van Neck D., Van Speybroeck V., Verstraelen T., and Waroquier M., J. Chem. Phys. 10.1063/1.2737444 126, 224102 (2007). [DOI] [PubMed] [Google Scholar]
- Ghysels A., Van Neck D., and Waroquier M., J. Chem. Phys. 10.1063/1.2789429 127, 164108 (2007). [DOI] [PubMed] [Google Scholar]
- Ghysels A., Van Speybroeck V., Verstraelen T., Van Neck D., and Waroquier M., J. Chem. Theory Comput. 10.1021/ct7002836 4, 614 (2008). [DOI] [PubMed] [Google Scholar]
- Moran D., Jacob R., Wood G. P. F., Coote M. L., Davies M. J., O’Hair R. A. J., Easton C. J., and Radom L., Helv. Chim. Acta 10.1002/hlca.200690210 89, 2254 (2006). [DOI] [Google Scholar]