Fragment-Based Learning of Visual Object Categories

Summary

When we perceive a visual object, we implicitly or explicitly associate it with a category we know [1-3]. It is known that the visual system can use local, informative image fragments of a given object, rather than the whole object, to classify it into a familiar category [4-8]. How we acquire informative fragments has remained unclear. Here, we show that human observers acquire informative fragments during the initial learning of categories. We created new, but naturalistic, classes of visual objects by using a novel “virtual phylogenesis” (VP) algorithm that simulates key aspects of how biological categories evolve. Subjects were trained to distinguish two of these classes by using whole exemplar objects, not fragments. We hypothesized that if the visual system learns informative object fragments during category learning, then subjects must be able to perform the newly learned categorization by using only the fragments as opposed to whole objects. We found that subjects were able to successfully perform the classification task by using each of the informative fragments by itself, but not by using any of the comparable, but uninformative, fragments. Our results not only reveal that novel categories can be learned by discovering informative fragments but also introduce and illustrate the use of VP as a versatile tool for category-learning research.

Results

Using VP to Create Shape Classes

The VP algorithm generates naturalistic object categories by emulating biological phylogenesis (see Supplemental Data available online). With VP, we created three classes of novel objects, classes A, B, and C and used 200 exemplars from each (Figure 1). Note that the three classes are very similar to each other, so that distinguishing among them is nontrivial (see below and Figure S1). Moreover, no two objects, including objects within a given category, were exactly alike, so that distinguishing among them required learning the relevant statistical properties of the objects and ignoring the irrelevant variations. Finally, note that the differences between categories arose spontaneously and randomly during VP, rather than as a result of externally imposed rules.

Figure 1. Generating Naturalistic Shape Classes by “Virtual Phylogenesis”.

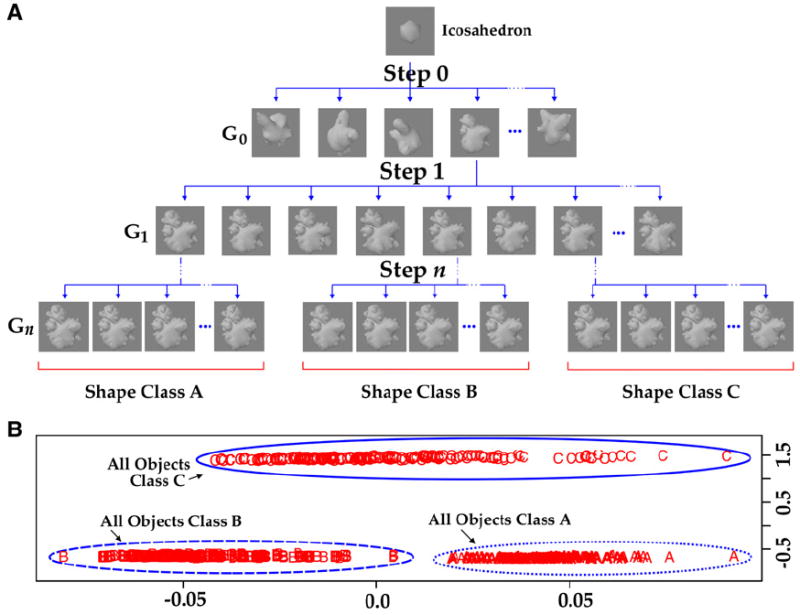
(A) The VP algorithm emulates biological evolution in that in both cases, novel objects and object classes emerge as heritable variations accumulate selectively. In the present study, we used a class of novel objects called “digital embryos,” which develop from a given parent object through simulated embryonic developmental processes [17]. At each generation G_n, selected embryos procreate, leading to generation G_n+1. The progeny inherit the shape characteristics of their parent but accrue random shape variations of their own as they develop. Thus, children of a given parent constitute a shape class. In the present study, embryos were grown for four generations with the VP algorithm, starting from a single common ancestor, an icosahedron. Three shape classes (A, B, and C) were chosen at generation n = 4, each with ~1500 “siblings.” Note that the entire object-generation process operated completely independently of the fragment-selection process or any other classification scheme. For larger images of exemplar objects from each class and for a demonstration that the categorization task is nontrivial and cannot be performed without learning the relevant classes, see Figure S1.

(B) A metric multidimensional scaling (MDS) plot of the 600 objects, 200 each from class A, B, and C, used in this study. Pixel-wise correlations of gray-level values were used as the input to MDS. Each data point represents one individual object, and the plotting symbol (A, B, or C) denotes the class to which the object belonged. MDS plots the data points so as to cluster similar data points together and disperse dissimilar data points from each other (for details, see [9, 18]). The values on either axis denote the class distance measures used by the MDS. Note that the two axes have different scales. The objects of the three classes formed three nonoverlapping clusters (ellipses), so that each cluster contained all the objects, and only the objects, of a given class.

Extracting Informative Fragments

We isolated ten fragments (“Main” fragments, Figures 2A and 2B) that were highly informative for distinguishing class A from class B (the main task in experiment 1, see Supplemental Data for details). We also isolated ten “Control” fragments (Figures 2C and 2D) and ten “IPControl” fragments (Figure S2) that were uninformative for the main task but visually comparable to the main fragments. The mutual information (MI) value of a given fragment quantifies the information it conveys about a given category. The higher the fragment’s MI, the more useful the fragment is for categorization. The MI values of all fragments used in this study are listed in Supplemental Data.

Figure 2. Informative Object Fragments.

(A) Main fragments, which are 20 × 20 pixel fragments of objects from class A that are useful for distinguishing class A from class B (main task).

(B) Location of the main fragments, overlaid on a typical object from class A. Fragment borders are outlined in yellow for clarity.

(C) Control fragments, which are fragments of objects that are not useful for the main task from class A (see Supplemental Data for details).

(D) Location of the control fragments.

Testing the Informativeness of Individual Fragments

The experiments consisted of training the subjects on whole objects and then testing them on fragments. Because only whole objects, not fragments, were used during training, subjects were not aware of the fragments or required to learn them. After the subjects were trained in the task, we tested the extent to which subjects were able to perform the classification task by using the fragments, each presented individually (see Figure 3 and Supplemental Data). We hypothesized that if the subjects learned informative object fragments during the training, then the subjects must be able to perform the categorization task by using the individual main fragments, but not the control fragments.

Figure 3. The Testing Paradigm.

A test object (center) and two sample objects, one from each class (left and right), were simultaneously shown. The test object was occluded by a translucent surface with a hole, such that only the given object fragment was visible, unoccluded, through the hole, and the location of the fragment relative to the overall object was apparent through the translucent occluder. Subjects had to classify the object into the class exemplified by the sample object on the left or right on the sole basis of the fragment visible through the hole. Subjects were informed that only the fragment, but not the darkened remainder of the test object, was useful for the task. See Supplemental Data for details. The fragment shown in this figure is the same as fragment 5 in Figures 2A and 2B.

The observed performance closely matched these predictions. Figure 4A shows the average performance of six subjects using the main fragments. Subjects performed significantly above chance with each of the fragments (binomial tests, p < 0.05 in each case). Moreover, with one exception (see below), the performance of each individual subject with each main fragment was indistinguishable from his/her performance with whole objects during the final two training sessions (binomial tests, p > 0.05, data not shown). The only exception to this was the performance of one subject with main fragment #9, for which she classified the object containing the fragment as A in only 1/16 (6.25%) of the trials (also see below). Altogether, these results indicate that the subjects were able to categorize the objects on the basis of each of the fragments alone and that the performance with the fragments was generally indistinguishable from the performance of the subjects with the whole object.

Figure 4. Classification Performance Using Fragments.

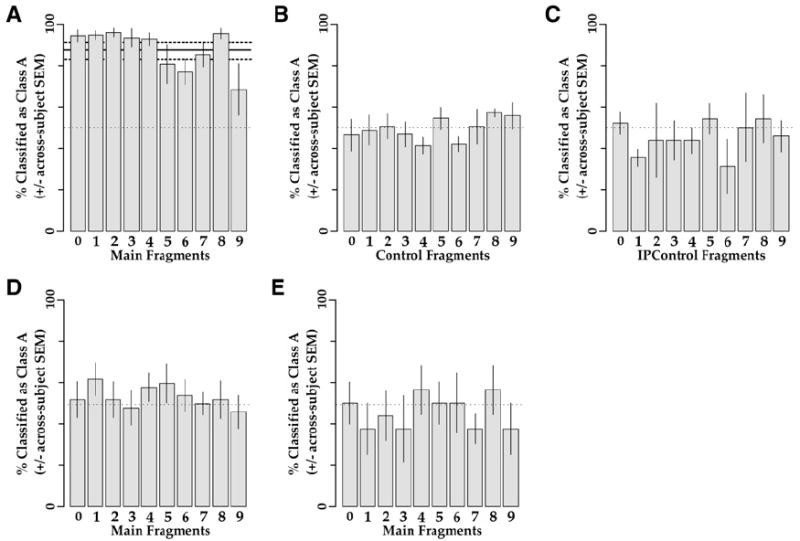
In each panel, each bar shows the average percentage (±SEM) of trials in which the subjects classified a given fragment as belonging to class A. The thin dotted line denotes 50%, or chance level performance. The thick black lines in the background in (A) denote the mean (solid line) and the SEM (dashed lines) of the subjects using whole objects during the last two sessions of training.

(A and B) Performance in experiment 1a (six subjects) with main fragments (A) and control fragments (B).

(C) Performance in experiment 1b with IPControl fragments (three of the six subjects). The IPControl fragments are shown in Figure S2. The performance with main fragments from experiment 1b is shown in Figure S3.

(D) Performance with main fragments without prior training. Subjects were tested with the same paradigm as above, but without any prior training in the categorization task. The data are averaged from six subjects.

(E) Testing with irrelevant training. Data are shown from one subject. The subject was trained in a similar, but irrelevant, categorization task and tested with the main fragments with the same paradigm as above.

By contrast, subjects were unable to perform the task above chance levels by using any of the control or IPControl fragments (Figures 4B and 4C; binomial tests, p > 0.05). That is, subjects were about equally likely to classify an object as belonging to class A or class B on the basis of a given control or IPControl fragment. Thus, although all three types of fragments belonged to class A, only the main fragments were likely to be assigned to class A.

To ensure that above results were not a function of a fortuitous designation of object classes, we performed experiment 2 in which we repeated the design of experiment 1, but with a different set of class designations, whereby the main task was to distinguish class C from class B (see Figure S4). A different set of four subjects participated in this experiment. The results of this experiment were similar to those in experiment 1 (Figure S5).

Additional analyses indicated the performance showed no improvement during the testing phase of the experiment, indicating that the subjects learned the fragments during the training phase, i.e., before the testing began (see Figure S6).

Necessity of Prior Training

In additional experiments, subjects were tested with informative fragments without having learned the categories beforehand (i.e., with the training phase omitted). Six subjects were used, five of whom also participated in experiment 1 above and one who participated in experiment 2. All subjects performed at chance levels (binomial tests, p > 0.05; Figure 4D). The performance was also indistinguishable from chance when the testing was preceded by training with similar, but task-irrelevant object categories (Figure 4E). This confirms that the categorization task required learning and in particular that the subjects could not perform the task during the testing phase by simply comparing the given fragment to the two whole objects in the display.

Learning Fragments Was Not Necessary

It is clear from the metric multidimensional scaling (MDS) plot of the three classes in Figure 1B that exemplars form three nonoverlapping clusters, each corresponding to one of the classes. The three classes are obviously linearly separable in this plot, as evident from the fact that one can draw a straight line separating any class from the other two. The fact that the projection found by MDS is linear [9] means that the original images are also linearly separable (in the pixel space). Therefore, subjects could have learned to separate the categories with complete images and did not have to learn object fragments.

Discussion

Our study is novel in two important ways. First, it reveals that informative fragments are learned during category learning. Second, it illustrates VP as a potentially powerful new tool for category-learning research.

Fragment Learning as a Part of Category Learning

Our results indicate that subjects learn informative, intermediate-complexity fragments as a matter of course when they learn new object categories, even when they were not explicitly required to learn the fragments. In other words, fragment learning was incidental to category learning. This result is significant because it straightforwardly links category learning with categorization, in that informative fragments play a role in both.

The performance of the subjects was a function of the task relevance of the fragments because subjects did not consistently associate task-irrelevant fragments to learned categories, even when the fragments were otherwise visually interesting or were informative for distinguishing the objects from another class. Together, these results reveal, for the first time, that humans selectively learn informative fragments as a part of category learning. Note that it would not have been possible to elucidate this by testing fragments from familiar categories (e.g., faces or cars; q.v. [7, 8].) because objects of these categories are frequently seen occluded, so that fragment learning could be attributed to the necessity for overcoming occlusions.

In previous studies of novel category learning, the algorithm for generating novel objects depended on the algorithm for classifying them into categories [1, 2], whereas the two were independent in our case, as they are in nature. To the extent that our stimuli and the experimental conditions reflected category learning under natural conditions, our results indicate that such incidental learning of fragments may be a common principle of learning of natural object categories (see below).

Subjects’ performance with task-relevant fragments was comparable to performance with the whole objects, suggesting that the learning of each of the fragments could, in principle, account for all or most of the category acquisition. Moreover, subjects performed close to perfect with most individual task-relevant fragments, indicating that the subjects were able to acquire most of the information conveyed by the individual task-relevant fragments (all of which had MIs at or near 1, see Supplemental Data).

Some models of perceptual learning, most notably the reverse-hierarchy theory [10], have suggested that subjects learn local features only when more global features do not suffice. In brief, reverse-hierarchy theory posits that learning takes place in spatially global-to-local fashion, such that the visual system initially learns large-scale features relevant to the task and “resorts” to finer-scale features when the large-scale features do not suffice. In our case, it was clearly not computationally necessary to learn the fragments because the tasks could be performed on the basis of whole objects (see Figure 1B). One reason why subjects nonetheless learned the fragments may be that the fragments were highly informative about the task in our case. Another, mutually nonexclusive possibility is that fragments represented the optimal spatial scale for learning in this case because the individual fragments were small enough to fit in the fovea, whereas it would have necessitated integration of information across multiple fixations to perform the task at level of the whole object. Further experiments are needed to resolve these issues.

Implications for the Mechanisms of Category Learning

Two previous studies, Harel et al. [7] and Lerner et al. [8], have examined the extent to which informative fragments support categorization of objects into familiar categories. Both showed that the ability of subjects to decide whether a given fragment was a part of a familiar object (e.g., a car or a face [7]) correlated with the MI of the fragment. Our study differed from these previous studies in several key respects, three of which are particularly worth noting. First, by using novel stimuli classes, we were able to study category learning, rather than just categorization. Second, because we controlled subject training, our fragments were extracted from the same set of images used by subjects during category learning. Third, we eliminated the possibility that the subjects might have learned the fragments out of necessity (e.g., to cope with occlusions) by ensuring that (1) the training images were completely unoccluded and (2) the classes were linearly separable, so that the categorization tasks could be performed on the basis of whole objects.

Our experiments did not test whether new categories can be learned solely from informative fragments. This is because our goal was to study learning under natural viewing conditions. In general, views strictly confined to informative fragments are highly unlikely under natural viewing conditions. Our result that subjects learned informative fragments even when presented with whole objects is therefore of greater relevance to natural vision.

Usefulness of VP in Categorization Research

Apart from the fact that the VP algorithm represents a novel method of creating object categories (c.f., “Greebles” [3, 11]), the resulting categories have several desirable features for the study of categorization and category learning. First, the categories have measurable, but randomly arising, within-class shape variations (c.f., [12, 13]). In most of the earlier studies using object categories created by compositing shape primitives, there tends to be little or no within-class variation (for reviews, see [14-16]). However, in natural scenes, two exemplars of a given category are seldom identical. Second, if necessary, both within-class variants and between-class variants in VP can be artificially selected to fit desired distributions (although we did not impose any such distributions in the present study). This means that the categories can be generated on the basis of, or independently of, an a priori classification algorithm, as desired. Third, VP can be used to generate a hierarchy of categories, directly analogous to the phylogenetic hierarchy of categories of biological objects in nature, so that VP can be a useful tool for exploring our hierarchical understanding of natural objects [1-3, 13, 16]. Finally, note that although we used “digital embryos” as the substrate for VP in the present study (Figure 1A), any virtual object, biological or otherwise, real-world or novel, can be used as a VP substrate and the algorithm can be readily modified to simulate a more complex phylogenetic process (e.g., convergent evolution, in which different taxa, such as whales and fish, come to resemble similar visual categories). Altogether, VP represents a powerful and versatile tool for generating naturalistic categories.