Model of coupled pulsation and translation of a gas bubble and rigid particle

Abstract

A model of the interaction of a spherical gas bubble and a rigid spherical particle is derived as a coupled system of second-order differential equations using Lagrangian mechanics. The model accounts for pulsation and translation of the bubble as well as translation of the particle in an infinite, incompressible liquid. The model derived here is accurate to order R⁵∕d⁵, where R is a characteristic radius and d is the separation distance between the bubble and particle. This order is the minimum accuracy required to account for the interaction of the bubble and particle. Dependence on the size and density of the particle is demonstrated through numerical integration of the dynamical equations for both the free and forced response of the system. Numerical results are presented for models accurate to orders higher than R⁵∕d⁵ to demonstrate the consequences of truncating the equations at order R⁵∕d⁵.

INTRODUCTION

Theoretical models describing the interaction of two or many gas bubbles in liquid have been in development for decades.1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 In the present work, the theoretical framework for one such model,11 previously utilized to describe bubble-bubble interaction, is applied to the interaction between a pulsating spherical bubble and a rigid spherical particle. Both the bubble and particle are free to translate.

There currently exist several models for the interaction between bubbles and immovable solid objects. Coakley and Nyborg12 derived an expression for the time-averaged force generated between a spherical bubble pulsating infinitesimally and a rigid, immovable sphere. Their expression is recovered as a special case of the present model. Theoretical, numerical, and experimental analyses of bubble behavior near rigid boundaries of infinite extent have shown that a bubble in pulsation translates toward plane, convex, and concave boundaries.13, 14, 15, 16, 17 Other investigations have focused on bubble motion near rigid and deformable, but also immovable spheres.18, 19 These latter studies have concentrated primarily on modeling the violent aspherical collapse of the bubble and have employed boundary integral or other numerical techniques. In contrast, here we present an analytical model valid for low amplitude spherical oscillations, but for which both the bubble and particle are free to translate.

The present investigation was motivated initially by a desire to account for the interaction of cavitation clusters and kidney stone fragments produced during shock wave lithotripsy.20 However, the extreme conditions of lithotripsy require consideration of liquid compressibility, cluster dynamics, and aspherical bubble deformation. While liquid compressibility corrections and dynamics of clusters containing arbitrary numbers of bubbles and particles are reported elsewhere,21 the discussion here is limited for simplicity to a system with a single bubble and single particle under conditions where the liquid may be assumed incompressible. The assumption of incompressibility is valid if the wavelength of the acoustic excitation is much larger than the characteristic separation distance between the objects. In addition, the magnitudes of the radial and translational velocities in the system must be much less than the speed of sound in the liquid. Finally, it is assumed that the bubble remains spherical, and we thus ignore shape deformation requiring spherical harmonics of higher order than monopole (pulsation) and dipole (translation).

In comparison to bubble-bubble interaction, a higher-order model is required to describe bubble-particle interaction. The model equations must be accurate to at least order R⁵∕d⁵, where R is a characteristic radius and d is the distance separating the bubble and particle. In contrast, the corresponding model equations for the coupled pulsation and translation of bubbles need only contain terms up to order R²∕d².11 In practice, when the bubble and particle are in close proximity, a model with accuracy beyond R⁵∕d⁵ is necessary to obtain numerical convergence. This issue will be addressed in detail.

This paper is structured as follows. The system energy and model equations are derived in Sec. 2, and appropriate loss mechanisms are discussed in Sec. 3. In Secs. 4, 5, the effects of size and density of the particle are investigated for both free and forced responses of the system via numerical integration of the dynamical equations.

THEORY

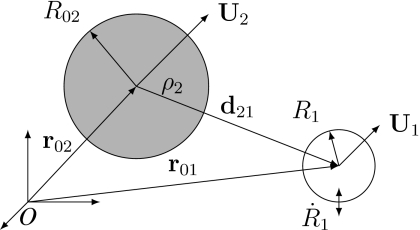
The geometry of the problem is presented in Fig. 1. Coordinates with subscript 1 correspond to the gas bubble, and coordinates with subscript 2 correspond to the rigid particle. Both objects are assumed to be spherical at all times. Their positions are defined in relation to a fixed origin by the vectors r_0i, i=1,2. The instantaneous and equilibrium radii of the bubble are given by R₁ and R₀₁, respectively, while the radius of the particle is fixed at R₀₂. Motion is described by the radial velocity of the bubble ${\dot{R}}_1$ and translational velocities ${\mathbf{U}}_i={\dot{\mathbf{r}}}_{0i}$, where dots over quantities indicate time derivatives. Lagrange’s equations describing the dynamics of the system are

$$\frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial {\dot{R}}_1}\right)=\frac{\partial \mathcal{L}}{\partial R_1},\frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial {\mathbf{U}}_i}\right)=\frac{\partial \mathcal{L}}{\partial {\mathbf{r}}_{0i}},$$ (1)

where L=K−V is the Lagrangian, K is the kinetic energy, and V is the potential energy of the system.

Figure 1.

Notation and geometry for bubble and particle with arbitrary translational motion.

Potential energy

Potential energy is stored via compression or expansion of the bubble. In differential form, it is expressed as

$$d\mathcal{V}=(P_0-P_1)d{V}_1=4\pi (P_0-P_1)R_1^{2}d{R}_1,$$

where P₀ is atmospheric pressure and $V_1=4∕3\pi R_1^3$ is the volume of the bubble. The pressure P₁ in the liquid just outside the bubble is taken to be

$$P_1=(P_0+\frac{2\sigma }{R_{01}}){\left(\frac{R_{01}}{R_1}\right)}^{3\gamma }-\frac{2\sigma }{R_1},$$ (2)

where γ is the ratio of specific heats and σ is surface tension. Additional effects that contribute to this pressure, such as heat transfer, gas diffusion, and condensation, are not considered here. Corrections for shear viscosity are discussed in Sec. 3.

Kinetic energy

The motion of the liquid, the particle, and the gas inside the bubble all contribute to the kinetic energy of the system. However, the gas density is negligible compared to the liquid density, and kinetic energy associated with the motion of the gas may be neglected. The kinetic energy due to translational motion of the particle (K_part) must be taken into account. The total kinetic energy is thus

$$\mathcal{K}={\mathcal{K}}_{\mathrm{part}}+{\mathcal{K}}_{\mathrm{liq}},$$ (3)

where K_liq is the kinetic energy of the surrounding liquid. The kinetic energy due to particle translation is simply

$${\mathcal{K}}_{\mathrm{part}}=\frac{1}{2}{m}_2{U}_2^2,$$ (4)

where m₂ is the mass of the particle.

The remaining component of the total kinetic energy, K_liq, accounts for the motion of the inviscid incompressible liquid surrounding the bubble and particle. The liquid is assumed to be irrotational, such that its motion is described by a scalar velocity potential ϕ which satisfies Laplace’s equation,

$${\nabla }^2\varphi =0.$$ (5)

The kinetic energy of the liquid is the integral

$${\mathcal{K}}_{\mathrm{liq}}=\frac{\rho }{2}{\int }_V{\mid \mathbf{\nabla }\varphi \mid }^{2}dV$$ (6)

over the volume surrounding the bubble and particle, where ρ is the liquid density. For a liquid at rest at infinity, Eq. 6 can be rewritten as22

$${\mathcal{K}}_{\mathrm{liq}}=-\frac{\rho }{2}({\int }_{S_1}\varphi \left({\mathbf{r}}_1\right)\frac{\partial \varphi \left({\mathbf{r}}_1\right)}{\partial r_1}d{S}_1+{\int }_{S_2}\varphi \left({\mathbf{r}}_2\right)\frac{\partial \varphi \left({\mathbf{r}}_2\right)}{\partial r_2}d{S}_2),$$ (7)

where the surface S_i coincides with the bubble or particle wall, and r_i=∣r_i∣ is the magnitude of the local coordinate vector r_i that defines position relative to the center of the bubble or particle.

Calculation of the kinetic energy thus requires knowledge of the velocity potential and its normal derivative on the surface of the bubble and particle. The velocity potential is expressed in the local coordinates of the bubble or particle. The normal derivative of the velocity potential on the surface of the bubble or particle is determined by the velocity boundary conditions

$${\phantom{\mid }\frac{\partial \varphi }{\partial r_1}\mid }_{S_1}={\dot{R}}_1+{\mathbf{U}}_1\cdot {\mathbf{n}}_1,$$ (8)

$${\phantom{\mid }\frac{\partial \varphi }{\partial r_2}\mid }_{S_2}={\mathbf{U}}_2\cdot {\mathbf{n}}_2,$$ (9)

where ${\dot{R}}_1$ accounts for pulsation of the bubble, U_i⋅n_i for translation, and n_i=r_i∕r_i is the unit vector in the direction of r_i. Whereas Eq. 9 for the boundary condition on the surface of the particle is exact because there can be no shape deformation of a rigid particle, Eq. 8 ignores the possibility of shape deformation of the bubble wall by the absence of spherical harmonics beyond the monopole (pulsation) and dipole (translation).

There is no known expression for ϕ that satisfies the boundary condition on each sphere exactly. However, an approximate expression can be found that satisfies the boundary conditions to a desired order of R∕d. We determine ϕ to the required accuracy by following the iterative approach used in Ref. 11. As shown in Sec. 2C, it is necessary to obtain an expression for ϕ accurate to order R⁵∕d⁵. This derivation is provided in the Appendix0.

The kinetic energy of the liquid is calculated by evaluating ϕ on the surfaces of the bubble and particle and substituting them into Eq. 7. The result of this calculation is

$${\mathcal{K}}_{\mathrm{liq}}=2\pi \rho \{R_1^3{\dot{R}}_1^2+\frac{1}{6}{R}_1^3{U}_1^2+\frac{1}{6}{R}_2^3{U}_2^2+\frac{R_2^3{R}_1^2{\dot{R}}_1}{d_{12}^2}({\mathbf{U}}_2\cdot {\mathbf{n}}_{21})+\frac{1}{2}\frac{R_1^3{R}_2^3}{d_{21}^3}[({\mathbf{U}}_1\cdot {\mathbf{U}}_2)-3({\mathbf{U}}_1\cdot {\mathbf{n}}_{21})({\mathbf{U}}_2\cdot {\mathbf{n}}_{21})]+\frac{1}{2}\frac{R_1^4{R}_2^3{\dot{R}}_1^2}{d_{21}^4}+\frac{1}{2}\frac{R_1^5{R}_2^3{\dot{R}}_1}{d_{21}^5}({\mathbf{U}}_1\cdot {\mathbf{n}}_{12})\}.$$ (10)

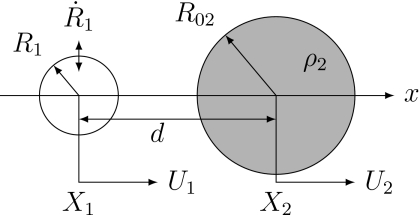
At this point it is convenient to place the bubble and particle in the orientation shown in Fig. 2. The bubble and particle lie along the x axis such that the position vectors become r₀₁=X₁n_x and r₀₂=X₂n_x, and the translational velocities are U₁=U₁n_x and U₂=U₂n_x. Note that d₁₂=n_x, d₂₁=−n_x, and d₂₁=d₁₂=d. In these coordinates, the total kinetic energy is

$$\mathcal{K}=2\pi \rho (R_1^3{\dot{R}}_1^2+\frac{1}{6}{R}_1^3{U}_1^2+\frac{1}{6}{R}_2^3{U}_2^2+\frac{R_2^3{R}_1^2}{d^2}{\dot{R}}_1{U}_2-\frac{R_1^3{R}_2^3}{d^3}{U}_1{U}_2+\frac{R_1^4{R}_2^3}{2d^4}{\dot{R}}_1^2+\frac{R_1^5{R}_2^3}{2d^5}{\dot{R}}_1{U}_1)+\frac{1}{2}{m}_2{U}_2^2.$$ (11)

Figure 2.

Notation and geometry for bubble and particle with collinear translational motion.

Equations of motion

The equations of motion are obtained by substituting Eqs. 2, 11 into Eqs. 1. The first of Eqs. 1 is the radial equation of motion for the bubble:

$$R_1{\ddot{R}}_1+\frac{3}{2}{\dot{R}}_1^2=\frac{P_1-P_0}{\rho }+\frac{1}{4}{U}_1^2+\frac{3V_{02}}{8\pi }\{\frac{{\dot{U}}_2}{d^2}-\frac{U_2}{d^3}(U_1+2U_2)-\frac{R_1}{d^4}(R_1{\ddot{R}}_1+2{\dot{R}}_1^2)-\frac{R_1^2}{d^5}[R_1{\dot{U}}_1+4{\dot{R}}_1(U_1-U_2)]\},$$ (12)

where P₁ is given by Eq. 2. The second of Eqs. 1 produces the translational equations of motion:

$${\dot{M}}_1=-F,{\dot{M}}_2=F,$$ (13)

$$M_1=\frac{1}{2}\rho V_1{U}_1-\frac{3}{2}\rho V_{02}(\frac{R_1^3}{d^3}{U}_2-\frac{R_1^5}{d^5}{\dot{R}}_1),$$ (14)

$$M_2=(\frac{1}{2}\rho +{\rho }_2)V_{02}{U}_2-\frac{3}{2}\rho V_{02}(\frac{R_1^2}{d^2}{\dot{R}}_1+\frac{R_1^3}{d^3}{U}_1),$$ (15)

$$F=3\rho V_{02}(\frac{R_1^2}{d^3}{\dot{R}}_1{U}_2+\frac{R_1^3}{d^4}{U}_1{U}_2-\frac{R_1^4}{d^5}{\dot{R}}_1^2),$$ (16)

where M₁ and M₂ are the generalized momenta of the bubble and particle and F is the translational force that acts equally and oppositely on the bubble and particle. In Eqs. 12, 13, 14, 15, 16 it proved convenient for interpretation to introduce the volumes $V_1=4∕3\pi R_1^3$ and $V_{02}=4∕3\pi R_{02}^3$ and the particle density ρ₂=m₂∕V₀₂. Except for the terms of order R⁵∕d⁵ and those containing the particle mass, Eqs. 12, 13, 14, 15, 16 coincide with the corrected order R⁴∕d⁴ equations published by Harkin et al.7 describing coupled pulsation and translation of two bubbles after setting the radial velocity of the second bubble ${\dot{R}}_2$ to zero in their equation (see footnote 17 in Ref. 11 for discussion of the corrections).

It is straightforward, albeit tedious, to obtain expressions for the velocity potential and model equations to higher orders of accuracy than R⁵∕d⁵. The steps outlined in the Appendix0 were automated with the aid of the MAXIMA computer algebra system to generate expressions for ϕ to arbitrary order in Rⁿ∕dⁿ. Harkin et al.7 used a different approach to derive the velocity potential and model equations, which we also automated to arbitrary order Rⁿ∕dⁿ to verify the present method. The results are identical. For example, to order R¹⁰∕d¹⁰ the interaction force is given by

$$F=\frac{2}{5}\pi \rho R_1^2{R}_{02}^3[\frac{10}{d^3}{U}_2{\dot{R}}_1+15\frac{R_1}{d^4}{U}_1{U}_2-10\frac{R_1^2}{d^5}{\dot{R}}_1^2-25\frac{R_1^3}{d^6}{\dot{R}}_1{U}_1-\frac{R_1}{d^7}(15R_1^3{U}_1^2+15R_{02}^3{U}_2^2+27R_1^3{\dot{R}}_1{U}_2+20R_1{\dot{R}}_1^2{R}_{02}^2)-70\frac{R_1^3{R}_{02}^4}{d^8}{\dot{R}}_1{U}_1-2\frac{R_1^2}{d^9}(15R_{02}^4{\dot{R}}_1^2+30R_1^2{R}_{02}^2{U}_1^2+30R_1{R}_{02}^3{U}_1^2-18R_1^4{\dot{R}}_1^2-20R_1{R}_{02}^3{\dot{R}}_1{U}_2)+\frac{9}{2}\frac{R_1^3}{d^{10}}{U}_1(9R_1^4{\dot{R}}_1+10R_1{R}_{02}^3{U}_2-30R_{02}^4{\dot{R}}_1)].$$ (17)

An analytic expression for the time-averaged interaction force ⟨F⟩ can be derived for infinitesimal bubble pulsation at an instant when the translational velocities of the bubble and particle are zero. At this instant M₁=M₂=0 and Eqs. 14, 15 can be rearranged to obtain

$$U_2=\frac{3\rho }{\rho +2{\rho }_2}\frac{R_1^2}{d^2}{\dot{R}}_1+O\left(\frac{R^3}{d^3}\right),$$ (18)

$$U_1=3\frac{R_{02}^3}{d^3}{U}_2=\frac{9\rho }{\rho +2{\rho }_2}\frac{R_1^2{R}_{02}^3}{d^5}{\dot{R}}_1+O\left(\frac{R^6}{d^6}\right).$$ (19)

Substitution of Eqs. 18, 19 into Eq. 17, assuming small periodic bubble pulsations with

$$R_1\left(t\right)=R_{01}+{\xi }_0\sin \omega t,{\xi }_0\ll R_{01},$$ (20)

and time-averaging over one acoustic cycle yields to leading order in ξ₀ the following contributions at fifth-, seventh-, and ninth-orders, respectively:

$$⟨F_5⟩=4\pi \rho \left(\frac{\rho -{\rho }_2}{\rho +2{\rho }_2}\right)\frac{R_{01}^4{R}_{02}^3}{d^5}{\omega }^2{\xi }_0^2,$$ (21)

$$⟨F_7⟩=-4\pi \rho \frac{R_{01}^4{R}_{02}^5}{d^7}{\omega }^2{\xi }_0^2,$$ (22)

$$⟨F_9⟩=-\frac{3}{5}\pi \rho [(15\rho -24{\rho }_2)R_{01}^4+(10\rho +20{\rho }_2)R_{02}^4]\frac{R_{01}^4{R}_{02}^3}{(\rho +2{\rho }_2)d^9}{\omega }^2{\xi }_0^2.$$ (23)

There are no time-averaged contributions from terms at first through fourth orders, or from any even-order terms in R∕d. Equation 21 is the expression derived by Coakley and Nyborg,12, 23 by an entirely different approach, for the force acting between a bubble and a rigid, stationary particle. Equation 21 indicates that, to leading order, for a particle having density greater than that of the liquid, ρ₂>ρ, the time-averaged interaction force is negative, and the bubble and particle are attracted toward one another. For a less dense particle, ρ₂<ρ, the bubble and particle repel. The result also demonstrates why it is essential to retain terms through fifth order in R∕d in the equations of motion. Despite the restrictive conditions under which Eq. 21 is derived, the same trends are predicted by numerical solutions of Eqs. 12, 13, 14, 15, 16 even for large bubble pulsations and with the particle in motion.

While it is true that the influence of terms at higher orders, proportional to Rⁿ∕dⁿ, tends to decrease with increasing order n, the higher-order contributions to the translational force may not be negligible for sufficiently small separation distances. For a neutrally buoyant particle (ρ₂=ρ) the contribution of the fifth-order terms, given by Eq. 21, vanishes. This seems to suggest that a seventh-order model is needed whenever considering neutrally buoyant particles, but we will show in Sec. 4A that the contribution of the higher-order terms is small unless the bubble and particle are extremely close. Note that the time-averaged contribution from the seventh-order force terms is always attractive, regardless of the relative particle density, while the contribution from the ninth-order terms is attractive except in the case of very dense, small particles.

SIMULATION PARAMETERS AND LOSSES

Inclusion of loss factors is guided by parameter values used for the numerical simulations. The equilibrium radius of the bubble was always taken to be R₀₁=100 μm, the parameters for the surrounding liquid to be ρ=1000 kg∕m³ and σ=0.073 N∕m, and the ambient pressure and gas constant to be P₀=101 kPa and γ=1.4, respectively, corresponding to an air bubble in water at one standard atmosphere.

The natural frequency of the bubble in the absence of viscosity, commonly called the Minnaert frequency, is 32 kHz. For all simulations the bubble is either released from a non-equilibrium radius and allowed to ring down at its natural frequency, or it is driven at its natural frequency by an acoustic excitation. In this case it is sufficient for our purposes to introduce a damping term in the radial equation of motion that provides the correct attenuation at the natural frequency. Damping of the radial motion of the bubble is modeled via introduction of the quantity $-4({\eta }_{\mathrm{eff}}∕\rho ){\dot{R}}_1∕R_1$ on the right-hand side of Eq. 12.24 Here, η_eff is an effective viscosity that is assigned the value η_eff=20η=20 mPa s, where η=1 mPa s is the viscosity of water. This choice of η_eff approximates the total damping, due to heat transfer and radiation as well as viscosity, of a 100 μm bubble that pulsates at its natural frequency.23 Harkin et al.7 used the same value in their simulations of interacting bubbles with radii on the order of 100 μm. The translational velocity of the bubble is small, and viscous drag on the translational motion was taken into account by introducing the drag force −4πηR₁U_r1 on the right-hand side of Eq. 13 for M₁, where U_ri is the translational velocity of the bubble (or particle) relative to the local velocity of the surrounding liquid.11 Viscous drag on the translational motion of the particle was taken into account by introducing the Stokes drag term −6πηR₂U_r2 on the right-hand side of Eq. 13 for M₂. Further discussion of drag is given in Ref. 11.

In the simulations that follow, the equations of motion were integrated numerically with a standard backward differentiation routine for different separation distances, acoustic excitations, and values of equilibrium radius and density of the particle. The case of free response, with no acoustic excitation, is considered first. The reason for investigating the free response is to avoid the primary Bjerknes forces produced by acoustic excitation and thus isolate the bubble-particle interaction forces, i.e., the secondary Bjerknes forces.

FREE RESPONSE

The free response of the system is investigated by setting the initial bubble radius to a non-equilibrium value R₁(0)≠R₀₁ and releasing it from rest. The particle is initially at rest in its equilibrium state. The simulations in this section were run with the higher-order extensions of Eqs. 12, 13, 14, 15, 16 that are accurate to order R⁹∕d⁹, where the numerical solution converges, as will be demonstrated in Sec. 4A.

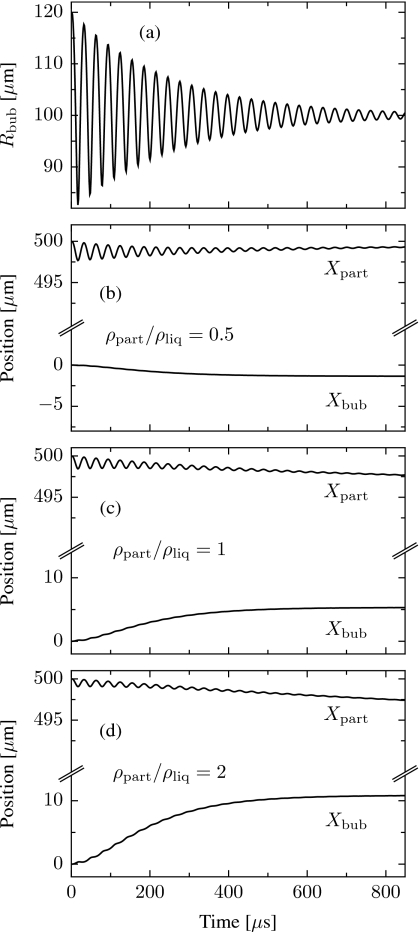
Presented in Fig. 3 are results for a particle of equilibrium radius R₀₂=2R₀₁=200 μm. Larger particles are used to emphasize interaction effects, because as seen from Eqs. 12, 16, to leading order the interaction forces are proportional to the volume of the particle. The initial positions of the bubble and particle are, respectively, X₁(0)=0 and X₂(0)=2.5R₀₂=500 μm, when the bubble is released from its initial radius R₁(0)=120 μm, a value 20% greater than its equilibrium radius. Responses are shown for three different particle densities: ρ₂=500, 1000, and 2000 kg∕m³ (ρ₂∕ρ=0.5, 1, or 2). To aid the reader, the indices i=1 and i=2 on parameters shown in the figures are replaced with the subscripts “bub” and “part,” respectively, and the density of the liquid is denoted by ρ_liq.

Figure 3.

Response of a bubble with equilibrium radius 100 μm and initial radius 120 μm with rigid particles of different densities. Bubble and particle initially separated by 500 μm. (a) Radial response of the bubble (independent of ρ_part∕ρ_liq). (b) Positions for a light particle (ρ_part∕ρ_liq=0.5). (c) Positions for a neutral particle (ρ_part∕ρ_liq=1). (d) Positions for a heavy particle (ρ_part∕ρ_liq=2).

The radial response of the bubble, which is independent of the density ratio ρ_part∕ρ_liq to within graphical resolution, is shown in Fig. 3a. Figures 3b, 3c, 3d display the positions of the bubble and particle for the three density ratios (note the split vertical axes). Consistent with the approximate analytical result for the time-averaged interaction force given by Eqs. 21, 22, 23, the bubble and particle repel for ρ_part∕ρ_liq=0.5, while they attract for ρ_part∕ρ_liq=2 and ρ_part∕ρ_liq=1, although the attractive force is less when the particle is neutrally buoyant. The attractive force in the case of a neutrally buoyant particle is due only to the inclusion of the higher-order terms which, as Eqs. 22, 23 show, are both attractive for this set of parameters. If instead the order R⁵∕d⁵ model equations were used, there would be virtually no translation in the case of a neutrally buoyant particle. Note that whereas the bubble is observed to come to rest within the time frames shown, the inertia of the particle causes it to drift for considerably longer times.

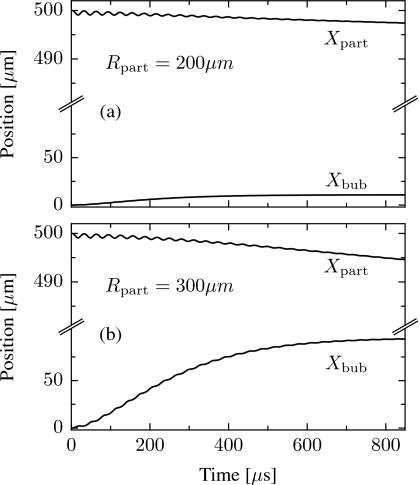
The dependence on particle size is illustrated in Fig. 4. Figure 4a is repeated from Fig. 3d (on an expanded axis), and Fig. 4b shows the effect of increasing the particle radius by 50%. Equation 16 indicates that the interaction force will increase for larger particles, although the actual increase is stronger than the $R_{02}^3$ dependence suggested by Eq. 16 because of the inclusion of the higher-order terms in the simulation model.

Figure 4.

Response of a bubble with equilibrium radius 100 μm and initial radius 120 μm with rigid heavy (ρ_part∕ρ_liq=2) particles of different radii. Bubble and particle initially separated by 500 μm. (a) Particle radius R₀₂=200 μm. (b) Particle radius R₀₂=300 μm.

Truncation error

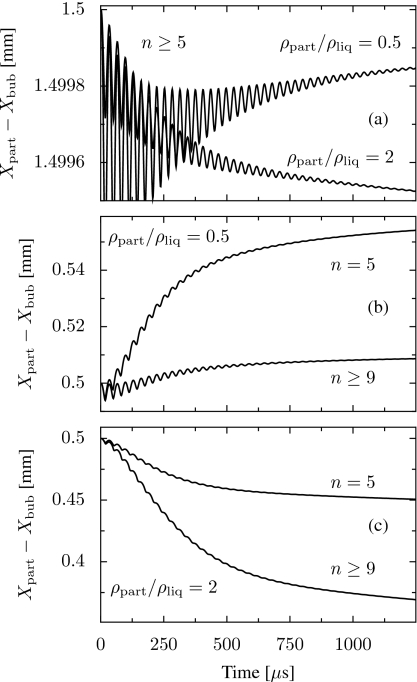
The order R⁵∕d⁵ model presented in Sec. 2C is accurate to the minimum order in R∕d required to account for the interaction force between the bubble and a rigid particle. As described previously, the steps outlined in Sec. 2 were automated with the aid of a computer algebra system to generate models of arbitrary accuracy in Rⁿ∕dⁿ for the case of two interacting spheres. Here we discuss higher-order models of a bubble interacting with a rigid particle. Equation sets accurate up to and including order R¹⁵∕d¹⁵ were solved numerically at various separation distances to determine the influence of higher-order terms on the system dynamics. Figure 5 shows cases of different initial separation distances for heavy (ρ_part∕ρ_liq=2) and light (ρ_part∕ρ_liq=0.5) rigid particles of radius R₀₂=200 μm. The bubble and particle were initially separated by d(0)=0.5 mm [Fig. 5a] or 1.5 mm [Figs. 5b, 5c] (i.e., 2.5 or 7.5 particle radii).

Figure 5.

Numerical solution of models accurate to various orders of R∕d for a bubble of equilibrium radius 100 μm and initial radius of 120 μm with rigid particles of radius 200 μm and various densities. (a) Bubble and particle initially separated by 1.5 mm for models of order R⁵∕d⁵ and higher for heavy (ρ_part∕ρ_liq=2) and light (ρ_part∕ρ_liq=0.5) particles. (b) Bubble and a light (ρ_part∕ρ_liq=0.5) particle initially separated by 0.5 mm for models accurate to order R⁵∕d⁵ or R⁹∕d⁹ and higher. (c) Bubble and a heavy (ρ_part∕ρ_liq=2) particle initially separated by 0.5 mm for models accurate to order R⁵∕d⁵ or greater than R⁹∕d⁹.

The time-averaged contributions of terms of higher order than R⁵∕d⁵ in the interaction force are attractive for these particle parameters [see Eqs. 22, 23]. Therefore, we expect the inclusion of these terms to result in greater translational motion in the case of a heavy particle [Fig. 5c], but less translation in the case of a light particle [Fig. 5b]. This prediction is confirmed by the simulations. As Fig. 5a shows, at large separation distances it is sufficient to truncate the model at n=5 [Eqs. 12, 13, 14, 15, 16]. However, as the bubble and particle move closer together the contribution of the higher-order terms becomes significant. In the cases considered here the solution converges numerically at order n=9 for both light [Fig. 5b] and heavy [Fig. 5c] particles.

FORCED RESPONSE

The system may also be driven by an acoustic source. The source was included in the model using the method of Ilinskii et al.11 To summarize, the kinetic energy due to a pulsating sphere with prescribed motion is interpreted in terms of p_src and u_src, the pressure and particle velocity of an external source. The source kinetic energy is calculated to order R⁵∕d⁵ and is thus consistent with the free-response model derived in Sec. 2. This additional kinetic energy is added to the system kinetic energy, Eq. 10. The same parameter set outlined in Sec. 4 was used, with an initial separation distance between the bubble and particle of 500 μm and a sinusoidal acoustic pressure of amplitude p₀=1 kPa and frequency of 32 kHz (equal to the natural frequency of the bubble). Because the model is spatially one-dimensional, the acoustic wave radiated by the source must be planar and propagate along the x axis. While the inclusion of source terms is an acknowledgment of finite liquid compressibility, in this case the acoustic wavelength is much larger than the separation distance between the bubble and particle. Therefore the liquid may be assumed to be locally incompressible from the standpoint of the bubble or particle.

While source interaction terms were included to order R⁵∕d⁵, terms accounting for bubble-particle interaction were included up to R⁹∕d⁹ as in Sec. 4. Simulation results for the source parameters used in the present section suggest that source interaction terms are negligible at R⁴∕d⁴, and therefore omission of the higher-order source terms will not affect the system dynamics.

Figure 6 shows the positions and separation distances between the bubble and particle for the three density ratios (ρ_part∕ρ_liq=0.5,1,2) when the source is located at −10 cm along the x axis, and Fig. 7 shows results for a source located at +10 cm. In both figures the bubble position is plotted in part (a), the particle position in part (b), and the distance separating the bubble and particle in part (c). For comparison, results for a two-bubble system (with a second bubble of radius 100 μm replacing the particle) are shown with dashed lines. Note that in both figures translation in the two-bubble system is much greater than in the bubble-particle system. This is because the secondary Bjerknes force acting between two oscillating bubbles is of order R²∕d², three orders larger than the translational force in the bubble-particle system.

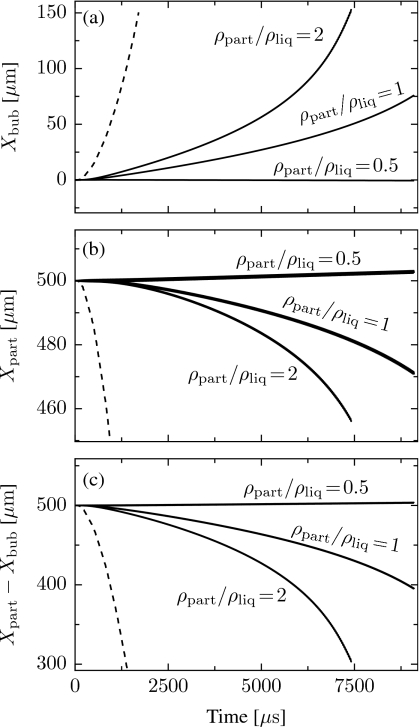
Figure 6.

Translational motion of a bubble of equilibrium radius 100 μm interacting with a second bubble of radius 100 μm (dashed line) or rigid particles of radius 200 μm (solid lines) and density ratios ρ_part∕ρ_liq=0.5, 1, and 2 excited by a sinusoidal plane wave source of amplitude 1 kPa located at −10 cm along the x axis. Initial separation distance 500 μm. (a) Bubble position. (b) Particle position. (c) Separation distance between bubble and particle.

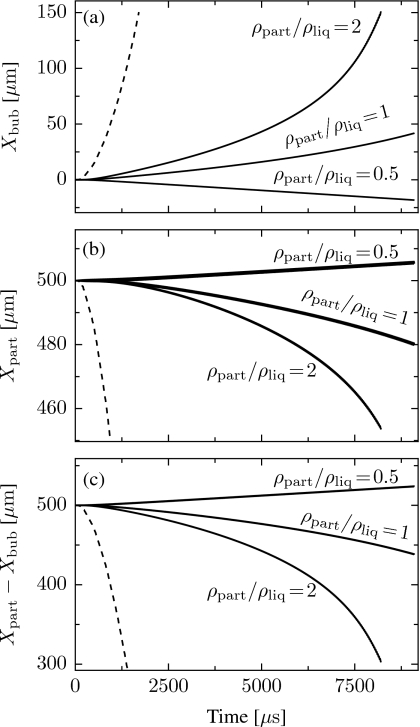
Figure 7.

Translational motion of a bubble of equilibrium radius 100 μm interacting with a second bubble of radius 100 μm (dashed line) or rigid particles (solid lines) of radius 200 μm and density ratios ρ_part∕ρ_liq=0.5, 1, and 2 excited by a sinusoidal plane wave source of amplitude of 1 kPa located at +10 cm along the x axis. Initial separation distance 500 μm. (a) Bubble position. (b) Particle position. (c) Separation distance between bubble and particle.

Notice that the direction of particle translation [Figs. 6b, 7b] is determined by the particle density [repulsive for a sufficiently light particle but attractive otherwise; recall Eqs. 21, 22, 23]. However, the radiation force (primary Bjerknes force) exerted on the bubble by the acoustic field has a non-zero time average. Therefore, the direction of bubble translation [Figs. 6a, 7a] is also influenced by the propagation direction of the acoustic excitation. In Fig. 6, with the source located at −10 cm, the radiation force tends to push the bubble toward the particle. This force, in combination with the higher-order interaction terms, causes the bubble to move toward the particle [Fig. 6a] for neutrally-buoyant and heavy particles, while in the case of a light particle the bubble remains nearly stationary. In Fig. 7, with the source located at +10 cm, the radiation force tends to push the bubble away from the particle. For the light particle its effect is sufficient to overcome the attractive force of the higher-order contributions [see Eqs. 21, 22, 23] and cause overall repulsion of the bubble and particle. However, for heavy and neutrally buoyant particles, forces due to bubble-particle interaction dominate, resulting in attraction [Fig. 7c].

These results suggest that bubble-particle interaction forces are certainly important for accurate description of free-response translational dynamics. However, in the case of a forced system the bubble-particle translational forces may be overshadowed by the primary Bjerknes forces from an acoustic source of sufficient amplitude.

SUMMARY

Lagrangian mechanics were used to derive dynamical equations describing the interaction of a gas bubble and a rigid particle in an incompressible liquid. The derivations were carried out through order R⁵∕d⁵ because this is the minimum accuracy required to account for the interaction force. Dynamical models accurate to higher orders of Rⁿ∕dⁿ were generated via a computer algebra system to illustrate consequences of truncating the model at order R⁵∕d⁵. In the case of a forced response, the presence of an external plane wave source was included to an order consistent with the model at order R⁵∕d⁵. The system dynamics exhibit dependence on the density and size of the particle as well as the direction of source propagation.

APPENDIX: DERIVATION OF THE VELOCITY POTENTIAL

Here an expression for the velocity potential, which satisfies Eq. 5 to order R⁵∕d⁵ subject to the boundary conditions [Eqs. 8, 9], is derived. The resulting expression may then be substituted into Eq. 7 to obtain an expression for the kinetic energy of the liquid. The total velocity potential is expressed as

$$\varphi \left({\mathbf{r}}_i\right)={\varphi }^r\left({\mathbf{r}}_i\right)+{\varphi }^t\left({\mathbf{r}}_i\right),$$ (A1)

where ϕ^r is the component due to radial pulsation of the bubble and ϕ^t is the component due to translation. First, an expression for the radial component of the velocity potential is obtained. Although the particle is rigid and therefore does not pulsate, for the moment we will proceed as though it pulsates radially with velocity ${\dot{R}}_2$. We then specialize the result for a rigid particle. For an isolated pulsating sphere with radius R_i and wall velocity ${\dot{R}}_i$ in an infinite liquid, the radial component of the velocity potential a distance r_i from the center of the sphere is

$${\varphi }_{0i}^r\left({\mathbf{r}}_i\right)=-\frac{R_i^2}{r_i}{\dot{R}}_i.$$ (A2)

An initial approximation of the radial velocity potential for an infinite liquid containing two pulsating spheres is the sum

$${\varphi }_0^r={\varphi }_{01}^r+{\varphi }_{02}^r.$$ (A3)

While Eq. A3 satisfies Eq. 5, it does not obey the boundary condition on either sphere. For example, let the velocity potential be expressed in terms of the coordinates of the bubble (r_i=r₁), and calculate the liquid velocity at the bubble wall for comparison with Eq. 8. The velocity potential corresponding to the particle, ${\varphi }_{02}^r\left({\mathbf{r}}_2\right)$, can be expressed in terms of r₁ by expanding ${\varphi }_{02}^r$ in a Taylor series evaluated at the bubble wall:

$${\varphi }_{02}^r\left({\mathbf{r}}_2\right)={\varphi }_{02}^r({\mathbf{d}}_{21}+{\mathbf{r}}_1)\simeq {\phantom{\mid }{\varphi }_{02}^r\left({\mathbf{d}}_{21}\right)+{\mathbf{\nabla }}_{{\mathbf{r}}_2}{\varphi }_{02}^r\left({\mathbf{r}}_2\right)\mid }_{{\mathbf{r}}_2={\mathbf{d}}_{21}}\cdot {\mathbf{r}}_1=-\frac{R_2^2}{d_{21}}{\dot{R}}_2+\frac{R_2^2}{d_{21}^2}{r}_1{\dot{R}}_2({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1),$$ (A4)

where d₂₁=r₀₁−r₀₂ is the vector pointing from the center of the particle to the center of the bubble (recall Fig. 1), d₂₁=∣d₂₁∣, and n₂₁=d₂₁∕d₂₁. In Eq. A4 and all subsequent expansions the series is truncated after the linear (dipole) term because all higher-order terms are orthogonal to the monopole and dipole terms in the integrand of Eq. 7, and therefore cannot contribute to the kinetic energy, as a result of including only monopole and dipole terms in boundary conditions [Eqs. 8, 9].

Evaluating the velocity at the bubble wall due to ${\varphi }_0^r$,

$${\phantom{\mid }\frac{\partial {\varphi }_0^r}{\partial r_1}\mid }_{S_1}={\phantom{\mid }(\frac{\partial {\varphi }_{01}^r}{\partial r_1}+\frac{\partial {\varphi }_{02}^r}{\partial r_1})\mid }_{S_1}={\dot{R}}_1+\frac{R_2^2}{d_{21}^2}{\dot{R}}_2({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1),$$ (A5)

and comparing with Eq. 8 shows that the error in satisfying the boundary condition on the radial motion is of order R²∕d² [the dipole term U_i⋅n_i in Eq. 8 will be satisfied by ϕ^t in Eq. A1]. To counteract the second term in Eq. A5 a correction ${\varphi }_1^r$ is added to ${\varphi }_0^r$ which satisfies Eq. 5 as well as

$${\phantom{\mid }\frac{\partial {\varphi }_1^r}{\partial r_1}\mid }_{S_1}{\phantom{\mid }=-\frac{\partial {\varphi }_0^r}{\partial r_1}\mid }_{S_1}+{\dot{R}}_1=-\frac{R_2^2}{d_{21}^2}{\dot{R}}_2({\mathbf{n}}_{21}+{\mathbf{n}}_1).$$ (A6)

The appropriate correction, applied to both the bubble and particle and expressed in terms of the local coordinate r₁ of the bubble, is

$${\varphi }_1^r={\varphi }_{11}^r\left({\mathbf{r}}_1\right)+{\varphi }_{12}^r({\mathbf{d}}_{21}+{\mathbf{r}}_1)\simeq {\phantom{\mid }{\varphi }_{11}^r\left({\mathbf{r}}_1\right)+{\varphi }_{12}^r\left({\mathbf{d}}_{21}\right)+{\mathbf{\nabla }}_{{\mathbf{r}}_2}{\varphi }_{12}^r\left({\mathbf{r}}_2\right)\mid }_{{\mathbf{r}}_2={\mathbf{d}}_{21}}\cdot {\mathbf{r}}_1=\frac{R_2^2{R}_1^3}{2d_{21}^2{r}_1^2}{\dot{R}}_2({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)+\frac{R_1^2{R}_2^3}{2d_{21}^4}{\dot{R}}_1+\frac{R_1^2{R}_2^3}{d_{21}^5}{r}_1{\dot{R}}_1({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1).$$ (A7)

Examining the velocity at the bubble wall due to terms ${\varphi }_0^r$ and ${\varphi }_1^r$,

$${\phantom{\mid }\frac{\partial }{\partial r_1}({\varphi }_0^r+{\varphi }_1^r)\mid }_{S_1}={\dot{R}}_1+\frac{R_1^2{R}_2^3}{d_{21}^5}{\dot{R}}_1({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1),$$ (A8)

shows that the error in satisfying the boundary condition for the radial motion is of order R⁵∕d⁵, and therefore another correction term, ${\varphi }_2^r$, must be added. The appropriate correction is

$${\varphi }_2^r={\varphi }_{21}^r\left({\mathbf{r}}_1\right)+{\varphi }_{22}^r({\mathbf{d}}_{21}+{\mathbf{r}}_1)=\frac{R_1^5{R}_2^3}{2d_{21}^5{r}_1^2}{\dot{R}}_1({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)+O\left(\frac{R^7}{d^7}\right).$$ (A9)

The velocity at the bubble wall, based on the sum of ${\varphi }_0^r$ with correction terms ${\varphi }_1^r$ and ${\varphi }_2^r$, is

$${\phantom{\mid }\frac{\partial }{\partial r_1}({\varphi }_0^r+{\varphi }_1^r+{\varphi }_2^r)\mid }_{S_1}={\dot{R}}_1+O\left(\frac{R^8}{d^8}\right).$$ (A10)

Comparison with Eq. 8 shows that the expression is accurate to the desired order R⁵∕d⁵. The final form of the velocity potential for the radial motion, expressed in the local coordinates of the bubble and consisting of terms ${\varphi }_0^r$, ${\varphi }_1^r$, and ${\varphi }_2^r$, is

$${\varphi }^r\left({\mathbf{r}}_1\right)=-\frac{R_1^2}{r_1}{\dot{R}}_1-\frac{R_2^2}{d_{21}}{\dot{R}}_2+\frac{R_2^2}{d_{21}^2}{r}_1{\dot{R}}_2({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)+\frac{R_2^2{R}_1^3}{2d_{21}^2{r}_1^2}{\dot{R}}_2({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)-\frac{R_1^2{R}_2^3}{2d_{21}^4}{\dot{R}}_1+\frac{R_1^2{R}_2^3}{d_{21}^5}{r}_1{\dot{R}}_1({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)+\frac{R_1^5{R}_2^3}{2d_{21}^5{r}_1^2}{\dot{R}}_1({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1).$$ (A11)

The corresponding expression in terms of the coordinates of the particle, r₂, is obtained simply by exchanging the subscripts 1 and 2 in all quantities. Velocity potential expressions for our specific case of a rigid particle with radius R₀₂ and zero radial velocity are then obtained from Eq. A11 by setting R₂=R₀₂ and ${\dot{R}}_2=0$.

The translational component of the velocity potential is obtained in a similar fashion. For an isolated translating sphere with radius R_i and translational velocity U_i, the velocity potential at a distance r_i from the center of the sphere is

$${\varphi }_{0i}^t\left({\mathbf{r}}_i\right)=-\frac{R_i^3}{2r_i^2}{\mathbf{U}}_i\cdot {\mathbf{n}}_i.$$ (A12)

As with the radial component, the individual contributions from each sphere are summed and then the contribution from the particle is expressed in terms of the local coordinate of the bubble:

$${\varphi }_0^t={\varphi }_{01}^t\left({\mathbf{r}}_1\right)+{\varphi }_{02}^t({\mathbf{d}}_{21}+{\mathbf{r}}_1)\simeq {\phantom{\mid }{\varphi }_{01}^t\left({\mathbf{r}}_1\right)+{\varphi }_{02}^t\left({\mathbf{d}}_{21}\right)+{\mathbf{\nabla }}_{{\mathbf{r}}_2}{\varphi }_{02}^t\left({\mathbf{r}}_2\right)\mid }_{{\mathbf{r}}_2={\mathbf{d}}_{21}}\cdot {\mathbf{r}}_1=-\frac{R_1^3}{2r_1^2}({\mathbf{U}}_1\cdot {\mathbf{n}}_1)-\frac{R_2^3}{2d_{21}^2}{\mathbf{U}}_2\cdot {\mathbf{n}}_{21}+\frac{R_2^3}{2d_{21}^3}{r}_1[3({\mathbf{U}}_2\cdot {\mathbf{n}}_{21})({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)-{\mathbf{U}}_2\cdot {\mathbf{n}}_1].$$ (A13)

Evaluating the translational velocity at the wall of the bubble,

$${\phantom{\mid }\frac{\partial {\varphi }_0^t}{\partial r_1}\mid }_{S_1}={\mathbf{U}}_1\cdot {\mathbf{n}}_1+\frac{R_2^3}{2d_{21}^3}[3({\mathbf{U}}_2\cdot {\mathbf{n}}_{21})({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)-{\mathbf{U}}_2\cdot {\mathbf{n}}_1],$$ (A14)

and comparing with Eq. 8 shows that the error is of order R³∕d³. A correction term, ${\varphi }_1^t$, which satisfies Eq. 5 as well as the condition

$${\phantom{\mid }\frac{\partial {\varphi }_1^t}{\partial r_1}\mid }_{S_1}{\phantom{\mid }=-\frac{\partial {\varphi }_0^t}{\partial r_1}\mid }_{S_1}+{\mathbf{U}}_1\cdot {\mathbf{n}}_1=-\frac{R_2^3}{2d_{21}^3}[3({\mathbf{U}}_2\cdot {\mathbf{n}}_{21})({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)-{\mathbf{U}}_2\cdot {\mathbf{n}}_1],$$ (A15)

is needed. The appropriate correction, applied to both the bubble and particle and expressed in terms of r₁, is

$${\varphi }_1^t={\varphi }_{11}^t\left({\mathbf{r}}_1\right)+{\varphi }_{12}^t({\mathbf{d}}_{21}+{\mathbf{r}}_1)\simeq {\phantom{\mid }{\varphi }_{11}^t\left({\mathbf{r}}_1\right)+{\varphi }_{12}^t\left({\mathbf{d}}_{21}\right)+{\mathbf{\nabla }}_{{\mathbf{r}}_2}{\varphi }_{12}^t\left({\mathbf{r}}_2\right)\mid }_{{\mathbf{r}}_2={\mathbf{d}}_{21}}\cdot {\mathbf{r}}_1=\frac{R_1^3{R}_2^3}{4r_1^2{d}_{21}^3}[3({\mathbf{U}}_2\cdot {\mathbf{n}}_{21})({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)-{\mathbf{U}}_2\cdot {\mathbf{n}}_1]-\frac{R_2^3{R}_1^3}{d_{21}^5}({\mathbf{U}}_1\cdot {\mathbf{n}}_{21})+O\left(\frac{R^6}{d^6}\right).$$ (A16)

Evaluating the translational velocity at the wall of the bubble yields

$${\phantom{\mid }\frac{\partial {\varphi }^t}{\partial r_1}\mid }_{S_1}={\phantom{\mid }\frac{\partial }{\partial r_1}({\varphi }_0^t+{\varphi }_1^t)\mid }_{S_1}={\mathbf{U}}_1\cdot {\mathbf{n}}_1+O\left(\frac{R^6}{d^6}\right),$$ (A17)

and therefore the expression for the translational velocity potential is accurate to the desired order of R⁵∕d⁵. The final form of the translational velocity potential, consisting of ${\varphi }_0^t$ and the correction term ${\varphi }_1^t$, is

$${\varphi }^t\left({\mathbf{r}}_1\right)=-\frac{R_1^3}{2r_1^2}({\mathbf{U}}_1\cdot {\mathbf{n}}_1)-\frac{R_2^3}{2d_{21}^2}{\mathbf{U}}_2\cdot {\mathbf{n}}_{21}+\frac{R_2^3}{2d_{21}^3}{r}_1[3({\mathbf{U}}_2\cdot {\mathbf{n}}_{21})({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)-{\mathbf{U}}_2\cdot {\mathbf{n}}_1]+\frac{R_1^3{R}_2^3}{4r_1^2{d}_{21}^3}[3({\mathbf{U}}_2\cdot {\mathbf{n}}_{21})({\mathbf{n}}_{21}\cdot {\mathbf{n}}_1)-{\mathbf{U}}_2\cdot {\mathbf{n}}_1]-\frac{R_2^3{R}_1^3}{d_{21}^5}({\mathbf{U}}_1\cdot {\mathbf{n}}_{21}).$$ (A18)

As with Eq. A11, the expression for Eq. A18 in terms of the coordinates of the particle, r₂, is obtained by exchanging the subscripts 1 and 2. The total velocity potential ϕ, the sum of Eqs. A11, A18, may now be substituted into Eq. 7 to obtain Eq. 10.