Dual synaptic plasticity in the hippocampus: Hebbian and spatiotemporal learning dynamics

Abstract

We assume that Hebbian learning dynamics (HLD) and spatiotemporal learning dynamics (SLD) are involved in the mechanism of synaptic plasticity in the hippocampal neurons. While HLD is driven by pre- and postsynaptic spike timings through the backpropagating action potential, SLD is evoked by presynaptic spike timings alone. Since the backpropagation attenuates as it nears the distal dendrites, we assume an extreme case as a neuron model where HLD exists only at proximal dendrites and SLD exists only at the distal dendrites. We examined how the synaptic weights change in response to three types of synaptic inputs in computer simulations. First, in response to a Poisson train having a constant mean frequency, the synaptic weights in HLD and SLD are qualitatively similar. Second, SLD responds more rapidly than HLD to synchronous input patterns, while each responds to them. Third, HLD responds more rapidly to more frequent inputs, while SLD shows fluctuating synaptic weights. These results suggest an encoding hypothesis in that a transient synchronous structure in spatiotemporal input patterns will be encoded into distal dendrites through SLD and that persistent synchrony or firing rate information will be encoded into proximal dendrites through HLD.

Introduction

The hippocampus is one of the most important brain areas in learning and memory (Abraham and Bear 1996; Martin et al. 2000). Regarding synaptic plasticity, long-term potentiation (LTP) and long-term depression (LTD) are well-known phenomena in response to tetanic stimuli of high and low frequencies. Since LTP and LTD in the hippocampus have time scales of hours and days, synaptic plasticity is believed to play an important role in mid-term learning and memory.

Synaptic transmission is strengthened only if the pre- and postsynaptic elements are simultaneously activated (Hebb 1949). Learning rules governing synaptic efficacy in the hippocampal area have been proposed by many researchers (LeMasson et al. 1993; Sjostrom et al. 2001; Daoudal et al. 2002). The Hebbian rule has been widely validated in various cortical areas and has been variously modified (Frey and Morris 1997; Turrigiano et al. 1998; Froemke et al. 2002).

However, several recent physiological data have shown that changes in the synaptic efficacy depend on the temporal difference between pre- and postsynaptic action potentials in the cerebral cortex and hippocampus (Markram et al. 1997; Bi and Poo 1998; Abbott and Nelson 2000). This phenomenon is termed “spike-timing-dependent plasticity (STDP).” STDP is a rule of synaptic efficacy that states that LTP occurs when a causal relationship exists between presynaptic and postsynaptic firing, and LTD or no change occurs otherwise. The firing rates of postsynaptic neurons are considered to be stabilized and maintained because of this synaptic competition. Thus, the STDP rule is thought to regulate neuronal activity levels within the optimum response band (Song et al. 2000). The action potentials of postsynaptic neurons are backpropagated into the dendrites, and this backpropagation has been considered to play a vital role in the STDP mechanism (Magee and Johnston 1997; Stuart and Hausser 2001).

The backpropagated signal attenuates as it propagates from the cell body to the dendrites. If the distance between the dendrites and the soma is great, the effect on synaptic plasticity should be correspondingly weak. However, associative LTP or LTD can also occur in the absence of postsynaptic firing. These data suggest that synaptic plasticity can be caused by local interactions at the synapse alone in absence of backpropagated signals. In fact, recent studies reported that these dendritic backpropagating action potentials are attenuated depending on the distance from the soma (Hoffman et al. 1997; Golding and Staff 2001), and LTP can occur at the synapses of the distal dendrites of the hippocampal CA1 pyramidal neurons even in the absence of postsynaptic somatic spikes (Golding et al. 2002; Aihara et al. 2005; Tsukada et al. 2005). In addition, it is suggested that the pyramidal neurons in the hippocampal CA1 area are highly sensitive to the spatiotemporal patterns of input stimuli. The stimuli that showed negative correlations in successive inter-stimulus intervals produced smaller LTPs than those that showed no correlation, while those that showed positive correlations produced larger LTPs (Tsukada et al. 1996). This led to the proposal of the “spatiotemporal learning rule,” which states that synaptic weights are modified by local spatiotemporal patterns of spikes from presynaptic neurons (Tsukada et al. 1994, 1996; Aihara et al. 1997; Tsukada and Pan 2005). These data suggest that there are two mechanisms of synaptic plasticity: one driven by pre- and postsynaptic spike timings, and another evoked by presynaptic spike timings only.

We assume that both these dynamics are involved in the mechanism of synaptic plasticity in the hippocampal neurons. To enable clear distinction between the two dynamics, we have termed these the Hebbian learning dynamics (HLD) and Spatio-temporal learning dynamics (SLD). While HLD is driven by pre- and postsynaptic spike timings, SLD is evoked by presynaptic spike timings alone. We therefore assume that synaptic efficacy depends on the total effect of these dynamics. Since the backpropagating action potential attenuates as it nears the distal dendrites, HLD may be weaker in the synapses of distal dendrites than in those of the proximal ones. To elucidate these functional differences, we assume an extreme case as a neuron model where HLD exists only at proximal dendrites and SLD exists only at the distal dendrites. In reality, we think that HLD and SLD may coexist in a single synapse.

Methods

Each pyramidal neuron in the hippocampal CA1 area receives projections via Schaffer collaterals from approximately 5,000 pyramidal neurons in the CA3 area (Amaral et al. 1990). We focused on one postsynaptic neuron (a pyramidal cell) in the CA1 area and its excitatory synapses, which were assumed to receive input spikes from CA3 neurons (Fig. 1). The dendritic area of the model neuron can be divided into two parts: proximal dendrite (PD) and distal dendrite (DD). We assume that two types of synaptic dynamics are involved in these dendrites. In the sections below, the dynamics of the neuronal membrane potential and the two types of synapses are explained.

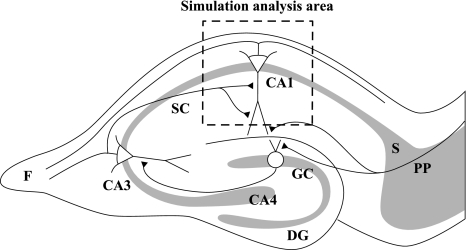
Fig. 1.

Schematic drawing of a hippocampal slice. The square delineates the area of simulation analysis in this study. DG dentate gyrus, F fimbria, GC granule cell, PP perforant path, S subiculum, SC Schaffer collateral

Dynamics of membrane potential

We adopted a leaky integrate-and-fire neuron model as a postsynaptic neuron, whose subthreshold membrane potential V(t) obeys the following equation:

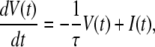1

where I(t) is the magnitude of synaptic inputs at time t, and τ is the time constant of neuronal membrane decay. When V(t) reaches the threshold θ, a spike is generated, and the membrane potential is reset to V_reset, where 0 ≤  V_reset <  θ.

The dendritic area of this model was assumed to have two parts: proximal dendrite (PD) and distal dendrite (DD). In addition, we assumed that each presynaptic neuron projects to both dendritic areas, with one synapse for each dendritic area (Figs. 1, 2). Since the number of presynaptic neurons was set to N = 100, the number of synapses was 200.

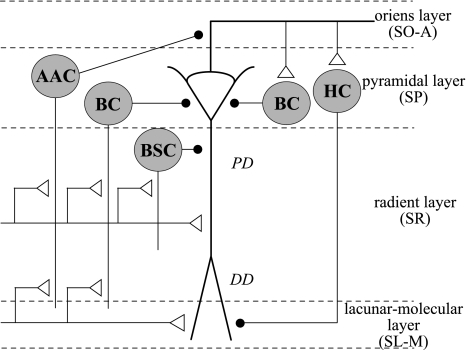
Fig. 2.

Schematic drawing of the circuitry in the hippocampal CA1 area (redrawn from Paulsen and Moser 1998). Pyramidal cells in the hippocampal CA1 area project to γ-aminobutyric acid (GABA)ergic interneurons via feed-forward and feedback circuits. GABAergic interneurons whose cell bodies are in the pyramidal cell layer (SP) of the CA1 region and are activated in a feed-forward manner include axo-axonic cells (AACs), basket cells (BCs), and bi-stratified cells (BSCs). These contact the axon initial segments and the somatic and dendritic compartments of the pyramidal cells. GABAergic feedback loops include at least one short loop involving basket interneurons and at least one long loop involving the horizontal cells (HCs) of the stratum oriens-alveus (SO-A), which project to the stratum lacunosum-molecular (SL-M). The interneurons in the hippocampus CA1 areas are merely illustrated to show the principles of organization, and this is not an exhaustive list

We assume that x_i(t) represents the firings of i-th presynaptic neuron as follows:

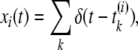2

where δ is the Dirac delta function and t⁽ⁱ⁾_k is the timing of the k-th spike of the i-th neuron. The synaptic input I(t) through the synapses in PD and DD is represented by the following equation:

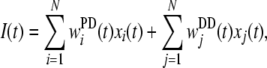3

where w^PD_i(t) represents the synaptic efficacy in the PD from the i-th neuron, and w^DD_j(t) represents the synaptic efficacy in the DD from the j-th neuron. When i = j, x_i(t) = x_j(t). However, synaptic modification rules differ between the PD and DD, in which generally w^PD_i ≠  w^DD_j.

Dynamics of synaptic modification

On the basis of our series of experiments in the hippocampal CA1 neurons (Aihara et al. 1997), we assume that the synaptic modification mechanism includes fast (10–30 ms) and slow (150–250 ms) time courses. The fast process consists of the time windows required to detect spike timings between pre- and postsynapses (termed HLD in this paper) or between pre- and presynapses (SLD), while the slow process is a temporal summation of the results of filtering by the time-window functions. The details of the time-window functions are explained in section “STDP window function.” Regarding the slow process, it has been reported that LTP depends on the amount of glutamate binding to the postsynaptic N-methyl-d-aspatate (NMDA) channel, and that the quantity of bound glutamate decays exponentially after binding (Lester et al. 1990). We assume that the quantity of glutamate can be expressed by the following equation.

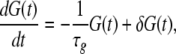4

where G(t) is the quantity of glutamate, τ_g is the time constant of exponential decay, and δG(t) is the degree of glutamate binding. Since the decay rate is essential to the sensitivity of temporal relations of spikes, the value of τ_g is one of the most important parameters. On the basis of this equation, two synaptic dynamics are formulated in the next two sections. For example, the mechanisms of glutamate binding represented by the term δG are different in the two dynamics.

In this paper, to clarify the functional differences in synaptic plasticity induced by HLD and SLD, we assumed that the synaptic modification at the PD obeys only HLD and that at the DD exclusively obeys SLD. The former depends on the timings of pre- and postsynaptic spikes, and the latter, on the timing of presynaptic spikes alone.

Spatio-temporal learning dynamics (SLD)

Spatio-temporal learning dynamics depends on the timing of the presynaptic neuronal spikes, and postsynaptic neuronal firing is not required. We assumed that the presynaptic inputs at the neighboring synapses affect the synaptic dynamics at the focused synapse #i. The quantity of glutamate G^S_i(t) and its effect on synaptic efficacy w_i(t) were calculated according to the following equations:

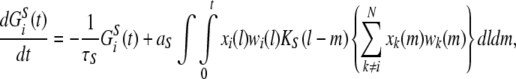5

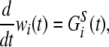6

where τ_c is the decay time constant, a_S is a proportional constant of the synaptic modification caused by a single input spike, and K_S(Δt) is the window function, which depends on the input timings of the presynaptic spikes.

In Eq. 5,

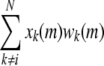indicates the coincidence factor among the presynaptic input spikes. The window function is concretely explained in section of STDP window function.

Hebbian learning dynamics (HLD)

Hebbian learning dynamics (HLD) is so named because it depends on the temporal difference in the pre- and postsynaptic neuronal spikes such as that explained by the Hebbian rule. In HLD, the dynamics of the synaptic weight w_i(t) is calculated by the following equations:

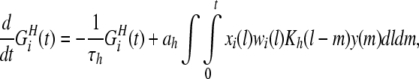7

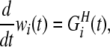8

where τ_h is the decay time constant, a_h is a proportional constant of the dendritic backpropagating action potential, w_i(t) represents the weight of synaptic efficacy from neuron i at time t, K_h(Δt) is a spike-timing window function, and y(t) is the output value (0 or 1) of the postsynaptic neuron. The time-window function is explained in the next section.

STDP window function

According to the experiments by Bi and Poo (1998), the synaptic modification rule yields temporally asymmetric plots, wherein the horizontal axis indicates the temporal differences in pre- and postsynaptic spikes, and the vertical axis indicates the change in synaptic efficacy. These data can be fitted to an exponential function as follows (Fig. 3A):

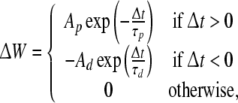9

where τ_p and τ_d are the rates of exponential decays, and A_p and A_d are the magnitudes of the changes in synaptic efficacy. Δt indicates the temporal difference between the timings of postsynaptic and presynaptic neuronal spikes, i.e, Δt = t_post − t_pre.

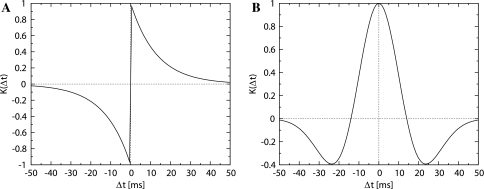
Fig. 3.

Two types of STDP window functions. (A) Equation 9, (B) Equation 10 (α = 1.0, β = 14.0, γ = 19.0)

On the basis of results of the physiological experiments that used hippocampal slices (Nishiyama et al. 2000; Tsukada et al. 2005, 2007), we assume that the symmetric window function depends on the spike timings of pre- and postsynaptic neurons. Figure 3B shows the spike-timing window function that was used for our simulations. This difference in symmetry (Fig. 3A versus B) is attributable to the experimental conditions: cells in culture and cells in sliced organization. In the hippocampal slice, more complicated local circuits, including target neurons as well as GABAergic neurons such as basket cells (BS) and horizontal cells (HC) are observed (Fig. 2). On the other hand, in cell culture, one synapse with glutamate receptors in the sparsely connected neurons is the target of observation. Thus, the feedback and feed-forward inhibitory connections in the slice may modify the asymmetric time-window plot to a symmetric time-window plot, although the mechanism underlying this modification remains yet to be elucidated. Our STDP window function is assumed to have symmetrical characteristics because the synaptic plasticity in the hippocampal circuit may effectively show the symmetry.

In our computer simulations, a Mexican hat function such as that represented below was used as the symmetrical window function.

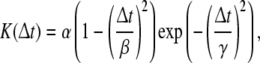10

where Δt is the difference in the firing times of the pre- and postsynaptic neurons, and α, β, and γ are the parameters which characterize the shape of the window function (Fig. 3B).

In this study, based on the results of the experiments, our assumption is that both the time-window functions in SLD and HLD are Mexican-hat type time windows.

Results

We performed three types of numerical experiments. First, to clarify the fundamental characteristics of HLD and SLD, we examined the transitions of synaptic weights in response to the frequency of input spikes. Since important information is believed to be encoded in spatiotemporal spike patterns in the hippocampus, we assume that synchronous spikes and mean firing rates are two orthogonal candidates for information representation. Therefore, in the following two experiments, when a part of the inputs is synchronous or very frequent, we would like to differentiate the responses of HLD and SLD. Unless otherwise stated, the parameter values are as follows: the membrane time constant τ is 10 ms, threshold theta is 25 mV, and V_reset is 0 mV. The initial synaptic weights are uniformly distributed in the range (0.9, 1.1). The synaptic weight has a lower limit of 0.0 and an upper limit of 2.0.

Responses to mean frequency

As a first step to elucidate the differences between HLD and SLD, we examined how the synaptic weights in each type of dynamics changed in response to inputs with a constant mean frequency. Instead of periodic trains, we employed Poisson trains in order to ignore the periodic effects of some specific temporal structures of input spikes and to focus on the effects of the input frequency. The interspike intervals (ISI) of the Poisson trains exhibit an exponential distribution. The mean ISIs of the exponential distribution for all synaptic inputs are set to be a constant and they were the same in one trial in this simulation. We observed the temporal change in the mean synaptic weights over various mean ISIs of Poisson inputs. The range of mean input frequencies is 1–100 Hz. The parameter value β is set to 1.4, so as to balance the potentiation and depression of the STDP window function.

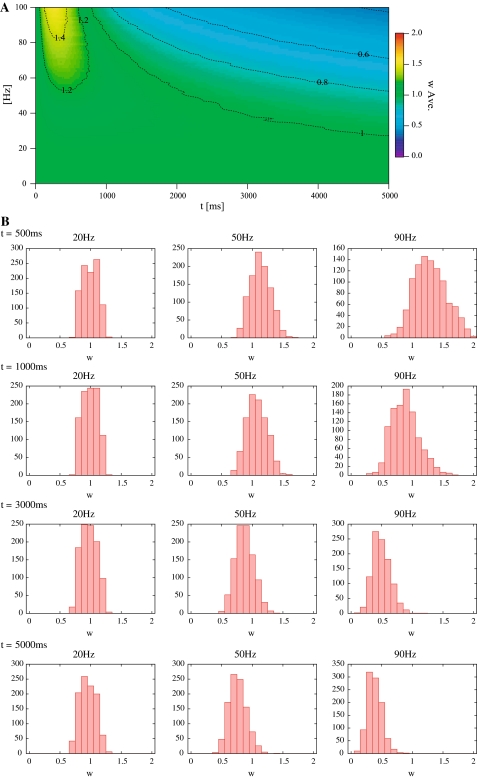
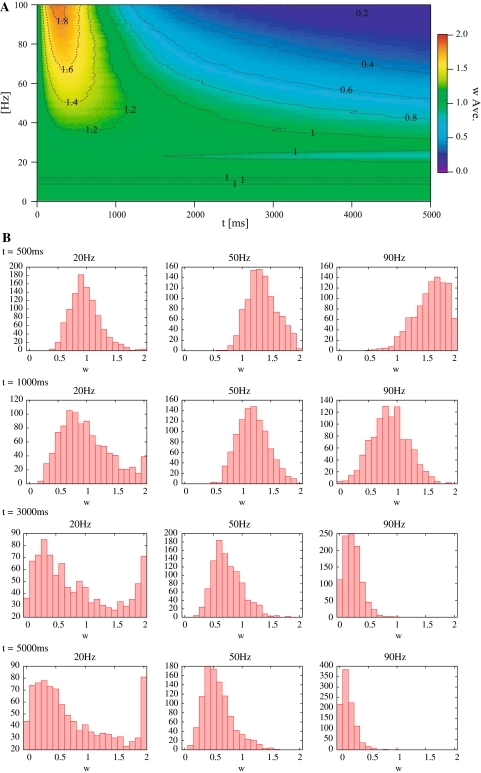
Figures 4A and 5A show the temporal change in the average synaptic weights in each type of dynamics in response to the Poisson trains. In these figures, the horizontal axis indicates time, the vertical axis indicates mean frequency of input spikes, and the density indicates an average synaptic weight. Figures 4B and 5B show histograms of the synaptic weights of each type of dynamics at several instants.

Fig. 4.

Results of responses to mean frequency in SLD. (A) The temporal change in the average synaptic weights in response to the Poisson trains. (B) Histograms of the synaptic weights of SLD at 500, 1000, 3000 and 5000 ms

Fig. 5.

Results of responses to mean frequency in HLD. (A) The temporal change in the average synaptic weights in response to the Poisson trains. (B) Histograms of the synaptic weights of HLD at 500, 1000, 3000 and 5000 ms

In both HLD and SLD, the mean synaptic weight increases rapidly within 500 ms, then decreases gradually, and finally converges to a constant value. The higher is the input frequency, the larger is the maximum value and the smaller is the convergent value of the mean synaptic weights. The convergence is due to the temporal window function (Fig. 3B). When more frequent Poisson trains are provided as input, a greater number of input spikes will be more delayed or advanced than the postsynaptic spike timings. These temporal differences eventually contribute to a reduction in G because the coverage of the depression is wider than that of the potentiation in the window function. Then, the synaptic weight decreases with some delays. This regulation function is known to be one of the characteristics of STDP (Song et al. 2000).

Most of the synaptic weights exhibit unimodal distributions (see Figs. 4B, 5B in 50 and 90 Hz). Some exceptions (bimodal distributions) are found in HLD. When the input frequency is low (or high), a group of synapses with highest (or lowest) synaptic weights emerges as the learning proceeds (Fig. 5B in 20 Hz). According to previous studies, synaptic weights with a multiplicative STDP rule driven by random inputs result in a unimodal distribution (van Rossum et al. 2000). The synapses in HLD do not exhibit a unimodal distribution despite the multiplicative STDP because the Hebbian input–output interaction affects the synaptic weights. In other words, the HLD synapse tends to drive an action potential more easily, once it has already driven it previously. On the contrary, the previous study assumes that neuron firing is uncorrelated with synaptic inputs, which leads to a unimodal distribution (van Rossum et al. 2000).

Response to temporally correlative inputs

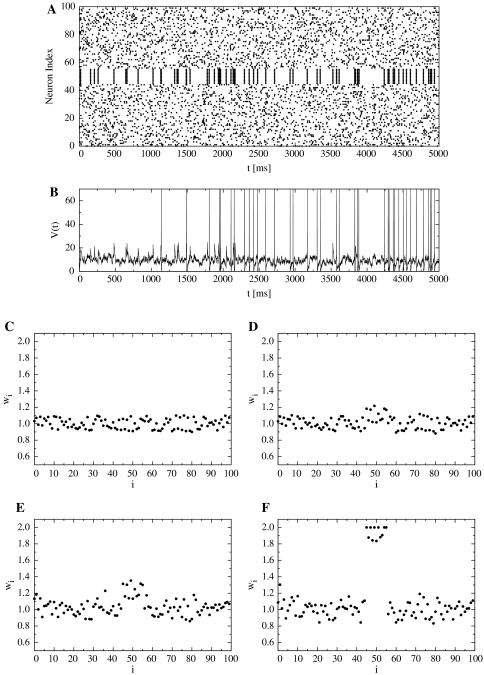
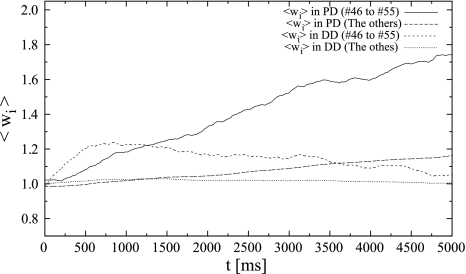
Second, we investigate the different responses of HLD and SLD when a specific part of the synaptic inputs is synchronous. We set the average frequency of each synaptic input to a lower level of 10 Hz. This is because the variances of synaptic weights on both dendrites are smaller at this frequency according to the frequency response (Figs. 4A, 5B). Synapses #46–#55 in each dendrite receive synchronous inputs whose timings follow a Poisson process, while the others receive other independent Poisson trains (see Figs. 6A).

Fig. 6.

Results of response to temporally correlative inputs. (A) Input stimulus. (B) The action potential of the postsynaptic neuron. (C) The distributions of synaptic weights on the proximal dendrite (PD) at t = 1000 ms, and (D) at t = 2000 ms. (E) The distributions of synaptic weights on the distal dendrite (DD) at t = 1000 ms, and (F) at t = 2000 ms

Figure 6B shows the action potential of the postsynaptic neuron when locally synchronous spike patterns are input. Figure 6C and D shows the distributions of synaptic weights on the proximal dendrite (PD) (t = 1000 ms, t = 2000 ms), and Fig. 6E and F shows the ones on the distal dendrite (DD).

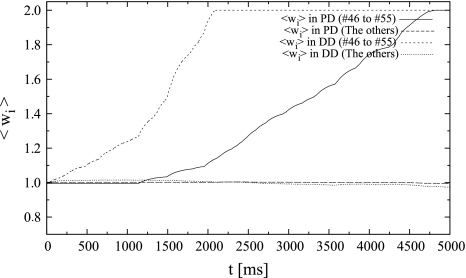
Initially, the weights of the distal synapses that received synchronous spikes increased rapidly because of the coincident detection of inputs by SLD. The weights increased until they reached the upper limit (Fig. 7). During this process, the weights potentiated by SLD enabled the neuron to fire easily. Therefore, the postsynaptic neuron began firing synchronously with the synchronous input after t = 800 ms. The weights of proximal (HLD) synapses that received synchronous spikes increased until they reached their upper limit. In fact, their weights increased by approximately 10% during t = 2000 ms. However, the weights of synapses other than synapses #46–#55 in HLD did not change significantly because of the weaker correlation between the presynaptic inputs and the postsynaptic outputs. Finally, in DD (SLD), synapses that received synchronous spikes potentiated remarkably to the upper limit, while the others fluctuated around the initial value (Fig. 6E, F). Ultimately, the synaptic weights are determined by the value of G, which is essentially an integrated value of the outputs of the window function. Assuming that the synaptic weight is an integration of the output of a stochastic process, it is analogous to the distance from the origin in a random walk process where a probability decides which way to go. The observed distribution of the synaptic weights in response to a Poisson process essentially corresponds to the Gaussian distribution observed in the case of a random walk.

Fig. 7.

The time-course of mean synaptic weights of the response to temporally correlative inputs

Response to more frequent inputs

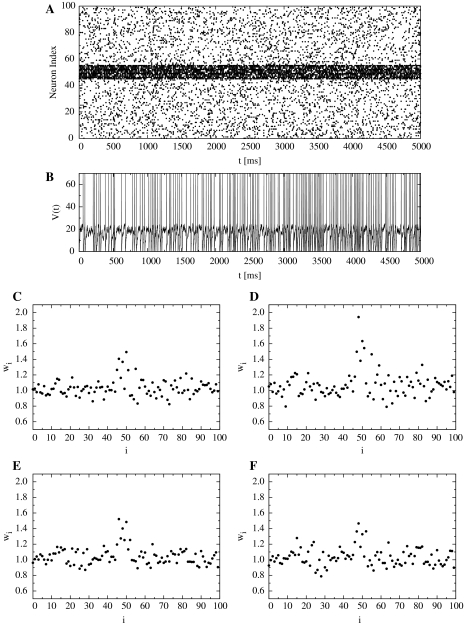
Third, we studied a case in which a specific part of the synaptic inputs had more frequent spikes. We assume that synapses #46–#55 received inputs having a higher frequency of 100 Hz, while the others received inputs having an average frequency of 10 Hz (See Fig. 8A). Each of the synaptic inputs follows an independent Poisson process.

Fig. 8.

Results of response to more frequent inputs. (A) Input stimulus. (B) The action potential of the postsynaptic neuron. (C) The distributions of synaptic weights on the proximal dendrite (PD) at t = 1000 ms, and (D) at t = 2000 ms. (E) The distributions of synaptic weights on the distal dendrite (DD) at t = 1000 ms, and (F) at t = 2000 ms

Figure 8B shows the action potential of the postsynaptic neuron when more frequent spikes are locally input. Figure 8C and D shows the distributions of synaptic weights on PD (t = 1000 ms, t = 2000 ms). With regard to the distribution of synaptic weights, only those synapses that received more frequent spikes on PD (HLD) were strengthened until they were saturated, while the other synapses on HLD and those on DD (SLD) fluctuated around the initial value (Fig. 9). In the case of multiple Poisson trains with a constant mean frequency, the rate of coincident spikes per unit time increases in proportion to the mean frequency. However, the weights of distal synapses that received inputs having a higher frequency fluctuated and were obviously not strengthened. This may be due to the regulation caused by the window function’s balance of effectively stronger depression: more frequent potentiation and much more frequent depression. This fluctuation process partly corresponds to a random walk process, as discussed in the previous section.

Fig. 9.

The time-course of mean synaptic weights of the response to more frequent inputs

Discussion

We assume that the PD of a model neuron obeys HLD and the DD obeys SLD. Both dynamics comprise two important factors: window function and temporal integration. This is because our previous studies have shown that their coincidence of input spikes and temporal summation can explain the physiological data on synaptic plasticity in the hippocampus (Aihara et al. 1997; Aihara et al. 2000; Tsukada et al. 2007). In this study, we have introduced a window function that detects the coincidence between input–input relationships (SLD) and between input–output relationships (HLD).

We examined how the synaptic weights change in response to three types of synaptic inputs: Poisson trains with (a) constant mean rates, (b) partial synchrony, and (c) partial high rates. First, the synaptic weights in HLD and SLD in response to a Poisson train having a constant mean frequency are qualitatively similar: (1) they increase rapidly and converge to a constant; (2) the higher is the input frequency, the lower is the convergent value; and (3) the synaptic weights typically exhibit a unimodal distribution. Second, SLD responds more rapidly than HLD to synchronous input patterns, while both SLD and HLD respond to them. In response to asynchronous inputs, the synaptic weights in SLD fluctuate like a Gaussian distribution. Third, HLD responds more rapidly to more frequent inputs. The synaptic weights in SLD fluctuate in response to asynchronous inputs.

These results suggest an encoding hypothesis in that a transient synchronous structure in spatiotemporal input patterns will be encoded into DD through SLD and that persistent synchrony or firing rate information will be encoded into PD through HLD. Recent physiological experiments on rat hippocampal slices show that there are two distinct inhibitory circuits: one transiently inhibits the somatic regions of pyramidal cells, while the other activated in proportion to the rate of action potentials persistently inhibits DD (Pouille and Scanziani 2004). Assuming that this recurrent inhibition acts like a filter, the rate information of action potentials is left at PD and their temporal structure is emphasized at DD, which supports our encoding hypothesis.

Although we assume two alternative types of dynamics, SLD and HLD, it is possible that they coexist in real hippocampal neurons. We will clarify the characteristics of this hybrid synaptic plasticity in future works. Our study concerns a fundamental mechanism behind encoding sensory information into distributed synaptic weights in a learning and memory system. To elucidate the learning function of the hippocampus, decoding mechanisms as well as encoding should be considered in modeling in future works.