Abstract
The molecular origin of the action of helicases is explored, starting with a model built based on the different X-ray structures of the large tumor antigen (LTag) hexameric helicase and a simplified model containing the ionized phosphate backbones of a single-strand DNA. The coupling between the protein structural changes and the translocation process is quantified using an effective electrostatic free-energy surface for the protein/DNA complex. This surface is then used in Langevin dynamics simulations of the time dependence of the translocation process. Remarkably, the simulated motion along the free-energy surface results in a vectorial translocation of the DNA, consistent with the biological process. The electrostatic energy of the system appears to reproduce the directionality of this process. Thus, we are able to provide a consistent structure-based molecular description of the energetic and dynamics of the translocation process. This analysis may have general implications for relating structural models to translocation directionality in helicases and other DNA translocases.
Keywords: DNA translocation, motor proteins, reduced models
Helicases belong to the general family of ATPase motors that couple the energy of ATP binding and hydrolysis to the cyclic conformation changes, which in turn is coupled to the DNA translocation and strand separation (reviewed in ref. 1 and the references therein). The action of helicases reflects similar principles to those that govern the action of energy transducing machines, and thus presents the same general problem of how chemical energy is converted to work.
A specific example of the helicase/translocase family is the Simian Virus 40 (SV40) large tumor antigen (LTag), an efficient hexameric molecular machine that unwinds dsDNA (2). It belongs to the AAA+ protein family and the helicase superfamily III (reviewed in ref. 1). LTag assembles into 2 hexamers (or double hexamer) at the origin of DNA replication (3). However, the C-terminal helicase domain can form a hexamer that has strong helicase activity (4).
The crystal structures of LTag hexameric helicase at various nucleotide-bound states have revealed large conformational changes triggered by ATP binding and hydrolysis, including the longitudinal movement of a β-hairpin and a loop structure along the central channel (2). These movements of the β-hairpin and the loop were suggested to play a role in DNA translocation and unwinding (2). A similar β-hairpin is also seen in central channel of the N-terminal structure of M. thermoautotrophicum MCM (mtMCM), and positively charged residues on these β-hairpins are shown to be critical for DNA binding and helicase function of mtMCM and LTag.
Despite major progress in structural studies, it is unclear at present how the ATP triggered conformational changes lead to the DNA translocation. Ref. 2 suggested a plausible structural mechanism relating the motion of the β-hairpins to the DNA translocation process, and, similarly, ref. 5 provided insight on DNA interaction, but has not provide a clear relationship between the protein structural changes and the translocation process. Other recent work (e.g., refs. 6 and 7) provides additional important structural and kinetic information. However, none of theses studies presented clear energy considerations that would allow one accept or reject a proposed mechanism.
Pioneering theoretical attempts to explore the directionality in PcrA Helicase (8, 9) provided an interesting insight into DNA translocation in a monomeric helicase system. However, the previous work did not considered the rate determining barriers (those associated with the ATPase reaction) and involved somewhat unjustified interpolation (see Discussion). Thus, the origin of the translocation directionality has not been resolved uniquely by structure-energy studies until the present study.
The present work introduces a renormalization strategy for the study of a rather complex hexameric helicase system by starting with the available structural information of LTag hexamer helicase plus model building for the internal DNA and then using a reduced model to simulate the actual translocation process and examining its molecular aspects. This is done by constructing a free-energy surface (whose nature determines the directionality) and by using Langivin dynamics to simulate the action of the LTag system. Our study provides insights about the exquisite relationship between the electrostatic energy landscape and the directionality of translocation process, and a general way for structure function correlation of translocases and the related motor proteins.
Simulating The Translocation Process
Before exploring the actual system, we present here a general analysis of the conditions for an efficient hexameric translocase. The relevant system should be able to convert the energy of ATP hydrolysis to vectorial translocation of DNA or related molecules. In the present case, we consider a system that encircles the tranlocated ssDNA in a hexameric helicase, such as LTag.
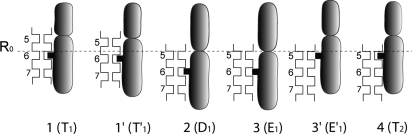
To analyze a translocation process it is useful to start with a hypothetical model system that supports such a process. This is shown in Fig. 1, in which the ssDNA is described as having equally spaced dents, representing point with strong interaction between the protein and the DNA (e.g., the phosphate groups), and the protein is described as a gray object with a dent that represents the region with the strongest interaction with the DNA. R0 is a reference point for the spatial translocation of the DNA. In the process of moving from 1 to 2 (T1 to D1), the protein position is shifted while retaining the interaction with DNA via site 6. In the 2nd and 3rd steps, the transition to E1 leads to a major reduction in the protein-DNA interaction, and the return of the protein conformation to T (3 to 4) occurs without shifting the DNA. The overall cycle results in translating the DNA from 6 to 5.
Fig. 1.
A hypothetical system that leads to DNA translocation. The figure describes a “protein” (gray and black) that has strong interaction with the DNA (nucleotide positions 5, 6, and 7 are indicated) at the indicated black protrusion. The system starts at the T state with strong bonding at site 6 of DNA, moving from T to E pushes the DNA down and then the motion to E lead to a relatively weak interaction between the protein and the DNA. The return to T leads to a strong interaction, but now with site 5 [stage 4(T2)]. Thus, the overall process pushes the DNA downward. The indexes T1 and T2 designate the same T state but with a translation step. The free-energy surface that is needed to analyze the directionality of the system is given in SI Appendix.
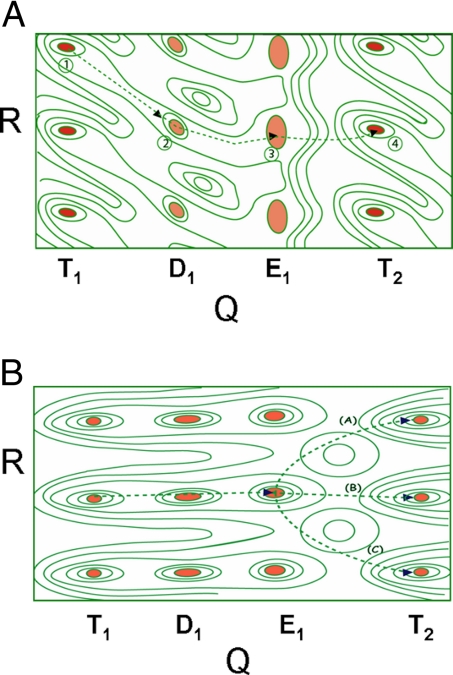
Intuitively, the system of Fig. 1 seems able to provide an effective translocation. However, the only way to really judge the corresponding efficiency is to generate an energy-structure description in terms of some generalized coordinates. This is shown in Fig. 2A, where we described the effective free energy of the hypothetical system in terms of 2 coordinates. One that moves from the ATP configuration (T) to the ADP (D) configuration and then to the empty (E) configuration. The second is the coordinate that translocates the DNA. If the energy of the system behaves like the surface in Fig. 2A, we will have a vectorial process along the path designated by 1–2-3–4. That is, in this path the system starts from the minimum at 1 and then when the protein moves from T to D the system moves to 2 and then to 3 when the system moves to E. The transition from E to T then takes the system along the least energy path to point 4 rather than back to point 1 and thus results in translocation.
Fig. 2.
Two types of free-energy maps for translocation process. (A) A map that describes the energetics of the translocation process of Fig. 1. The surface involves 2 effective coordinates; the protein structural changes (the Q axis) and the DNA translocation (the R axis). The indexes T1 and T2 designate the same T state but with a translated DNA. (B) A 2D map that describes an ineffective translocation. The surface is built in the same way as in Fig. 2A but now the motion from T to D does not involve a shift in the minimum. In this case, the system has an equal chance to move on paths A and C.
In the case considered in Fig. 2A, the current map allows one (in principle) to explore the translocation directionality by Langevin dynamics simulation or by conceptual analysis. Provided, of course, that it based on the energetic of the actual system studied.
However, if the system behaves like it does in Fig. 2B, we will have an extremely inefficient translocase because the system have equal chance to move from 6 to 7 or from 6 to 5 and even to stay at 6. Evidently, this situation will not lead to effective translocation unidirectionlity. Thus, the condition for effective action is that the minima of the surface will be shifted while moving from T to D.
The above analysis is completely hypothetical and the only way to see how the real system behaves is to generate some type of structure function correlation. Here, the best way is probably to try to generate maps of the type of Fig. 2 from the actual energetics of the system. In doing so, there is absolutely no guarantee that we will get a proper landscape that would support a unidirectional process and failing to get such a landscape would be the best evidence that the model is incomplete or simply incorrect.
Our main point is that the surface generated from a given model system does not necessarily supports a unidirectional process, and failing to get unidirectional energy valleys in the surface would be the best evidence that the model is problematic.
With the above considerations we started by focusing on generating the effective free-energy surface for the LTag system, taking advantage of the availability of the crystal structure of a viral initiator protein papillomavirus E1 in the ADP conformational state, with ssDNA bound (5) (PDB entry 2GXA). Because of the significant sequence similarity between E1 and LT SV40, the crystal structure of LTag at ADP conformation (PDB entry 1SVL) superimposes well on the E1 helicase at ADP state with ssDNA.
The monomer of LTag helicase has 3 domains: D1, D2, and D3 (4). The crystal structures of the ATP bound conformation (PDB entry 1SVO) and empty conformation (PDB entry 1SVM) of the LTag helicase were superimposed on the ADP conformation of LTag that has already been superimposed on to E1 helicase with the ssDNA in the central channel. The transformation matrices of the superposition process were generated based on the best fitting scores of the positions of all atoms in D1. The internal structures of all of the conformations were kept unchanged during the transformation process.
In the subsequent step, we generated series of intermediate conformations by taking the vectors that connect each pair of conformations. That is, starting from the crystal structure of LTag helicase with bound ATPs, we constructed 9 structures going from the crystal structure of ATP bound state to ADP bound state. This was followed by another 9 structures going from the ADP bound structure to the apo structure. Finally, 9 other structures were constructed going back from apo structure to the initial ATP bound structure. Those 30 structures were used in our calculation to represent the helicase structural changes during the ATP hydrolysis cycles.
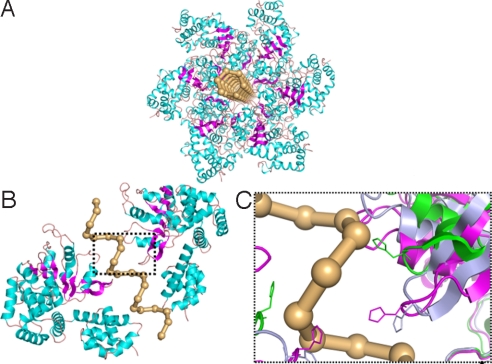
The cocrystal structure of E1 helicase-ssDNA complex contains a ssDNA with 6 nucleotides per helical turn, which corresponds to an average helical twist angel of 60° from one nucleotide to the next. The spacing along the helix axis from one nucleotide to the next is 3.4 Å. The average distance between two nucleotides is ≈6.8 Å. With this in mind, we constructed a ssDNA of 50 dT, using the twist angle and spacing parameters, and superimposing to the crystal structure of ssDNA inside the helicase channel. Focusing on the negatively charged phosphate backbone (see below), we constructed the model depicted in Fig. 3. The constructed helical ssDNA was assumed to spin while being translated so as to maximize the electrostatic interactions with the LTag residues.
Fig. 3.
A structural model of LTag hexamer in complexed with ssDNA. (A) The crystal structure of LTag protein at ATP bound conformation with a ssDNA (phosphate chain, in ball-stick model) inserted into the protein channel. (B) Side view of LTage central channel. For simplicity, only chain A and D of a hexamer are shown. (C) Critical residues in central channel of LTag proteins in different conformations. The structural changes corresponding to the ATP, ADP, and Apo states are shown in pink, light blue, and green, respectively.
In considering the energetics of the above structural information we only focused on the ionized phosphate groups of the DNA, assuming, based on physical considerations, that this should be the primary source of the protein-DNA interaction for hexameric helicases. The electrostatic energy of the protein-DNA model was evaluated using the semimacroscopic version of the protein dipole Langavin dipole model with the linear response approximation (LRA) treatment (this PDLD/S-LRA model is described in Methods and SI Appendix). Using this approach, we first mapped the free-energy surface for the protein-DNA electrostatic interaction. The resulting surface is given in SI Appendix, which indicates that the DNA-protein interaction energy is much stronger in the T sate than in the D and E states.
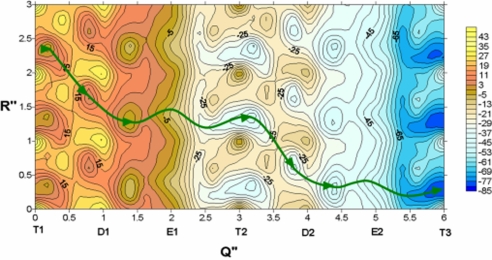
Next, we introduced a special adjustment to account for the fact that our calculated surface does not include the protein and ATP internal energy and thus the relative height of the 3 minima has to be adjusted. This adjustment involved the following considerations. The transfer from T1 to T2 (Fig. 4) involves about −8 × 6 kcal/mol change in free energy, because it reflects a change form (ATP + water) to (ADP + Pi) in aqueous solution (10, 11) for 6 ATP molecules. The transfer from T1 to D1 is assumed to involve about −1 × 6 kcal/mol contribution from the protein + the reacting system, while the transfer for D1 to E1 is assumed to involve −7 × 6 kcal/mol contribution from the reacting system. This estimate is based on the situation in F1-ATPase (10, 11), another hexameric molecular machine. We would like to clarify in this respect that our assumption is fully consistent with the fact that LTag and F1-ATPase have similar kcat (0.3 s−1 and 0.2 s−1 LTag and F1-ATPase, respectively) (10–12). The interaction with the DNA and between the subunit only changes the barrier by 1–2 kcal/mol. Furthermore, from our experience in F1-ATPase, we expect that the chemical barriers are higher or equal to the conformational barriers. At any rate, the activation barrier for transition between T and D is taken as 18 kcal/mol, and the transition from D to E as having a barrier of 17 kcal/mol. These results are based on the similar results in F1-ATPase and on the fact that our final results are not affected too much by the barriers except that the translocation rate becomes smaller if the barriers increase. We also assumed that the ΔG values for the different steps is similar to that of F1-ATPase and again our overall results are not affected by this assumption, because the real driving force is the ATP hydrolysis, which gives us a downhill gradient of ≈7 × 6 kcal/mol regardless of the nature of the ATPase. We would also like to clarify (see Discussion) that the downhill energetic is not the origin of the directionality. Now, because the barrier for a fully simultaneous hydrolysis reaction in all of the 6 subunits is estimated to be 6 × 18 kcal/mol, an energy barrier that will be overcome at room temperature in ≈1028 years, we can conclude that at least this chemical reaction step should occur in a noncorrelated or independent way. However, the finding that the chemical reactions are uncorrelated does not preclude the possibility that the conformational change can occur in a simultaneous way after the hydrolysis reactions are completed, although it is more likely that the hydrolysis reaction occurs in several subunits and cerate a spring loaded type effect on the conformational transition. At any rate, we are not trying to explore here the detailed steps in the overall conformational transition and represent them by a single coordinate. Thus, the overall drop in energy in any complete transition has to represent the effect of all of the 6 subunits. The above contributions were added to the protein −DNA electrostatic interaction to provide the overall free-energy surface. The resulting surface is shown in Fig. 4.
Fig. 4.
The PDLD/S −LRA effective free-energy surface (in kilocalories per mole) for the translocation process in LTag. This surface include the adjustment that reflects the internal energy of the LTag states (see the text in this section). The indexes T1 and T2 designate the same T state but with translated DNA. R″ represents DNA coordinates (see text for details) and Q″ (Q″ = Q/λQ, λQ = (ℏ/2)ωQδQ2) represents the protein structural changes.
Note that because in our model the ssDNA was assumed to spin-moves along the channel to maximize the electrostatic interaction, the vertical axis represents both rotation and translation. For simplicity, we use a coordinate R″ whose change by 1.0 unit represents a rotation of 60° and a vertical translocation of 3.4 Å along the channel.
Although a more complete model should have used 6 solvent (protein) coordinates (1 for each subunit), we grouped theses coordinates into 1 effective coordinate. This means that the details of the partially sequential conformational change are represented in a coarse way. Thus, the large reduction in free energy going from E to T2 should have been distributed between 6 steps, where it would provide the driving force needed to complete the overall conformational change. Neglecting this detail can result in not being able to reproduce the exact number of nucleotides transferred per ATP usage. It is quite possible that the number of nucleotides translated per ATP may be larger (or smaller) than what is predicted here once we are able to deduce the details of the conformational changes, but this improved treatment will have probably to wait until we have more information from single molecules and related experiments. However, the details are unlikely to affect the overall calculated directionality, which is the focus of this study.
As seen from Fig. 4 the least energy path forces the system to move from the minimum at R″ = 2.5 and T1 to R″ = 1.6 and D1. Then the system moves to R″ = 1.5 and E and subsequently continue to R″ = 1.2 and T2, where it completed a translocation and ready for the next cycle. As clarified in SI Appendix, this is the path needed for a vectorial process.
Now we may ask what is the basis for the shape of the translocation surface. This is done in the SI Appendix by evaluating the electrostatic group contributions for the interaction of the DNA with the protein, and taking the corresponding difference between the potential at D and T at R″ = 2.4 and the difference between the potential at D and T at R″ = 2. The calculations identify the residues that help the translocation process. Mutating these residues and examining the resulting translocation will be extremely instructive for the future studies.
Although the free-energy surfaces considered above allow one to predict the translocation direction, it is important to quantify the time dependence of the corresponding process. This is done by fitting a simplified free-energy surface (see Methods and SI Appendix) to the surface of Fig. 4 and then using Langavin dynamics (LD) simulations (see Methods and SI Appendix). The LD simulations used effective frictions and reduced masses that represented the dynamics of the complete system.
The observed translocation time has been estimated to be ≈132 nt/s for a different hexameric helicase T7 gp4 (13), which corresponds to ≈0.007 s for a motion of one nucleotide. This process cannot be simulated easily by our LD approach in a reasonable time frame [although our Monte Carlo approach (14) can do so]. Thus, we used an interpolation philosophy of scaling down the potential to values that allow direct simulation (we consider barriers up to 10 kcal/mol) and then increasing the barrier to interpolate the trend at the actual high barrier case. The results of the simulations with barriers of 4 kcal/mol are depicted in Fig. 5. More details are given in a movie provided with SI Appendix. As seen from the figure the system moves in a stochastic way in a unidirectional manner. The driving force for this process is the ATP hydrolysis reaction. The calculated translocation time for different potentials is given in Fig. S4. Using the figure we can estimate the translocation time with the full potential by interpolating to the corresponding value (see ref. 15) for a related treatment. The interpolation to a barrier of 18 kcal/mol, gave a translocation time of ≈0.004s per nucleotide in a qualitative agreement with the observed trend (0.007 s). An improved agreement may be obtained by dividing the T to D step to 6 individual steps, but this is not the purpose of the present study, which focuses on the origin of the directionality.
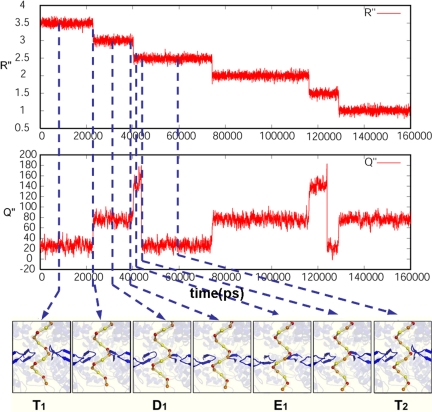
Fig. 5.
The simulated time dependence of the translocation process for a case with a low barrier. The figure displays the time dependence of the R″ and Q″ coordinates and snapshots along the translocation path. The specific simulation is done for a barrier of 4 kcal/mol for the T to D transition. Simulations with higher barriers give similar results (but, of course, with longer translocation times). See also Movie S1.
To explore the possibility that the dynamics of the translocation process is somehow non stochastic, we also changed the friction constants of the solvent and solute coordinates (γQ and γR, respectively) to see whether this can change the translocation time. We found that in cases with very low barriers (e.g., >3 kcal/mol) the values of the friction constants had significant impact on the translocation time. However, at the high barrier limit (with barriers >5 kcal/mol) the values of these constant had very little impact on the translocation time. This indicates that in the present case, when we have high barrier for the chemical steps, the translocation time is controlled by the free-energy landscape.
It should be pointed out that it is quite simple to generate movies of a translocation process, of the type presented in the SI Appendix, by arbitrary animations. However, it is quite difficult to produce such a movie as a reflection of actual simulations. It is equally hard to obtain a vectorial translocation without imposing it on the model, and obtaining such a result while considering the electrostatic interactions indicates that they dictate the physics of the system.
Discussion
The mechanism of DNA translocation by helicases is an issue of fundamental interest both in terms of the control of replication processes and the general issue of conversion of chemical energy to mechanical work. This article introduces a physically consistent energy-based analysis of the action of a hexameric helicase by developing energy diagrams that allow us to translate the structural information to translocation efficiency. Furthermore, a specialized renormalization approach allows us to explore the dynamics of the translocation process.
In this work, we used the available structural information on LTag and model building to gain an understanding of the molecular origin of the unidirectional translocation action of this system. Focusing on the electrostatic energy of the system allows us to construct energy diagrams in the 2D space of the protein structural change and the DNA translocation. The resulting diagram provided a new view of the nature of the translocation process. It appears that the electrostatic-based surface leads (without special parameterization that would force a specific directionality) to a vectorial translocation of the ssDNA.
Because the modeling of the translocation process by brute force MD simulations is impractical at present, a multiscale philosophy similar to the ones used in our studies of ion channels (16), proton translocation (14, 15), and catalytic landscape (17) was exploited in this work. Basically, we represented the system by an equivalent coarse-grained system with the relevant free-energy surface. Performing LD or related simulations of the simplified surface provides what is perhaps the most effective way of understanding the functions of complex systems. The use of langevin dynamics or related formulations in instructive studies of biological motors is not new (e.g., refs. 8 and 18); however, reproducing motor directionality with a consistent“first principle” structure function correlation has not been accomplished before this work.
It should be mentioned that previous studies (8, 9) have presented a pioneering attempt to explore the translocation directionality of ssDNA in PcrA, a monomeric helicase, which have some elements similar to the current study. However, in our view, the origin for the directionality has not been resolved by these studies. That is, a key problem in modeling directionality is the generation of a physically-based free-energy surface, which is based on the energetic of the system under consideration. Here, as also recognized in ref. 8, the attempt to draw directionality information from the so called steered molecular dynamics (SMD) is unlikely to lead at present to unique potential of mean force (PMF) in such complex systems as helicase/DNA complexes, because of enormous hysrersis and convergence problems. Thus, ref. 8 focused on the interaction between the protein and the nucleotides by using our LRA approach (19) in its powerful LIE version (20). Although this approach was validated by us in DNA polymerase (21), it does not give quantitative results for the interaction of the protein with the highly charged phosphate groups without introducing a rather large dielectric constants (21).
Perhaps the key advance in the present work relative to previous work (such ref. 8) is the construction of a free-energy surface in the complete space of the DNA protein motion, which is the key element in our study. That is, while our studies provide a complete surface that lead to directionality, figure 2 of ref. 8 gives the profile for the protein–DNA binding energy only for 2 points (the DNA binding with and without ATP) on the full surface. Interpolating these 2 points to obtain the relevant barriers is very challenging, and it is hard to justify the interpolation used in ref. 8, which seems to be equivalent to deducing the barrier between 2 bound state just based on the information at these states. Another important issue is the need to consider the dependence of the free-energy surface on the ATPase coordinates which is a key element of the present work.
Although our study reveals the origin of translocation directionality (i.e., translocation in one direction only) by focusing on the DNA main chain to construct a 2D energy diagram, resolving the issue of 3′ → 5′ or 5′ → 3′ movement will have to involve the evaluation of the interaction of the protein with the bases (the interaction with the main chain is identical in both cases). Obviously, such a study will greatly benefit from direct structural information about the complete protein-DNA complex.
Although taking into account the driving force upon the ATP to ADP transition is crucial, it does not explain the translocation directionality. That is, moving from ATP to ADP can push the DNA up or down or just leave it in its position. Obtaining the specific coupling that pushes the ssDNA down in Fig. 3 is the key outcome of our model and the basis for the directionality. This outcome is not intuitively obvious without using out 2D surfaces.
Currently, there is significant interest in whether molecular motors operate by random stochastic forces or by some type of coherent motions. The present study suggests that the translocation process may be driven by stochastic random motions, which are dictated by the free-energy landscape. This conclusion is based on the finding that the use of physically-based friction and the change of the friction by 2 orders of magnitudes has not change the translocation time, once we move to the high barrier limit (which corresponds to the actual feature of the helicases). Another interesting insight that emerged from the present energy-based analysis is that the system must operate by uncorrelated chemical hydrolysis, because otherwise it will require an infinitely long time. Nevertheless, it is still possible that the conformational change occurs after the chemical step and is completed in a somewhat simultaneous way. The exact way by which the uncorrelated or stepwise ATP hydrolysis activates the conformational changes is one of the most intriguing unsolved puzzles about this system, and its solution will require a combination of structural, single-molecule, and computational studies. Additionally, a more quantitative analysis of the directionality problem should involve a combination of the electrostatic group contribution of the type presented in SI Appendix with experimental studies of the effect of mutations on the translocation efficiency. Overall, we believe that the most significant value of our work is in introducing a new powerful way of analyzing translocation processes and thus opening the way for more systematic analysis of the emerging structural and biochemical results.
It is quite significant that the main physics of the translocation process could be simulated while considering only the electrostatic energy of the system plus the barriers for the chemical transformations. The restoring force of the electrostatic free energy reflects van der Walls repulsive energies and entropic effects, but they follow more or less the linear response approximation and establish the electrostatic reorganization energy and the effective dielectric constant. The finding that electrostatic effects can provide a powerful structure function correlation for molecular motors and other systems and is consistent with other studies (e.g., refs. 10 and 22).
Methods
To simulate the translocation process we have to generate an effective free-energy surface and to simulate the dynamics on this surface. Obviously a full macroscopic evaluation of the relevant free-energy surface is too challenging, in part in view of the absence of the full structure of the complex and in part because of extreme convergence problems. At present, we believe that the most effective strategy is to focus on the electrostatic contribution to the free energy of the system, and this is done here with the PDLD/S-LRA approach (23).
The PDLD/S-LRA method is described in ref. 22 and is summarize in SI Appendix. Here, we used this approach with a dielectric constant, εp = 20. This high value reflects the fact that we deal with a highly charged system and that our regular PDLD/S treatment considers usually charge-charge interactions macroscopically while using another dielectric (εeff) with a high value of ≈40. The nature of these dielectric constants and the justification for their values is considered extensively in other studies (22, 24). Furthermore, we used the PDLD/S-LRA treatment only for residues in a cylinder placing along the helicase channel with radius of 18 Å and then evaluated the effect of the charges on the distant residues, using macroscopic Coulombs law with εeff = 40. This type of treatment has been validated in extensive studies of mutational effects (22, 24). We also used in an initial screening a simplified treatment based on the evaluation of electrostatic group contributions (25). This approach (see SI Appendix) evaluates the electrostatic group contributions to the binding energy by scaling the electrostatic interactions with a dielectric, εx, using as εx ≈ 4 for polar residues and εx = εeff ≈ 40 for ionized residues. This approach was examined in several test cases (e.g., ref. 25) and apparently provide a reasonable result for an initial screening.
The present work has not considered van der Walls steric forces because calculations that include such interactions converge extremely slowly and would give meaningful results only after free-energy perturbation calculations that are not practical at present for the large system involved. Fortunately, however, studies in many charged systems (22, 24) have shown that after the steric effects are sampled correctly the main free-energy contribution comes from the electrostatic interactions.
The dynamics of the effective coordinates of the system was explored by introducing a LD approach similar to the one used in our studies of proton translocation processes (15). That is, to explore the time dependence that coupled protein-DNA motions, we approximate the effective surface obtained by the PDLD/S-LRA approach by a multi minima empirical valence bond (EVB)-type potential surface. In this way the system is represented by mixing potential of the form (see ref. 15 for more details)
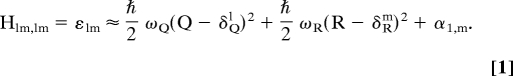 |
Where Q and R are the effective dimensionless coordinates of the protein (solvent) and the DNA, respectively R is related to the dimensional coordinate, R′, by, R = R′, whereas Q is defined by Q = − (ε2,m − ε1,m)el ℏωQδQ. Here, l = 1, 2, 3 for the ATP, ADP and empty forms, respectively, whereas m = 0, 1, 2, 3, for different positions of the DNA. Finally, αi is the difference between the minimums of the diagonal energies. The actual potential surface is obtained by diagonalizing the system Hamiltonian
The surface of Eq. 2 was fitted to the full surface as described in SI Appendix, Section III, and the resulting surface is given in SI Appendix, Fig. S3.
With the above effective surface, it is possible to run Langevin dynamics (LD) simulations and to explore the time dependence of the translocation process.
The corresponding LD equations for the solvent and solute coordinates are very similar to those used in our early work (15) and are described in the SI Appendix, where we also describe the specific frictions.
Supplementary Material
Acknowledgments.
We thank Drs. Zhen Tao Chu and Nidhi Singh for their help. This work was supported by National Science Foundation Grant MCB-0342276 and National Institutes of Health R01-AI055926. The computational work was supported by University of Southern California High Performance Computing and Communication Center (HPCC).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0900532106/DCSupplemental.
References
- 1.Singleton MR, Dillingham MS, Wigley DB. Structure and mechanism of helicases and nucleic acid translocases. Annu Rev Biochem. 2007;76:23–50. doi: 10.1146/annurev.biochem.76.052305.115300. [DOI] [PubMed] [Google Scholar]
- 2.Gai D, Zhao R, Li D, Finkielstein C, Chen X. Mechanisms of conformational change for a replicative hexameric helicase of SV40 large tumor antigen. Cell. 2004;119:47–60. doi: 10.1016/j.cell.2004.09.017. [DOI] [PubMed] [Google Scholar]
- 3.Fanning E. Simian virus 40 large T antigen: The puzzle, the pieces, and the emerging picture. J Virol. 1992;66:1289–1293. doi: 10.1128/jvi.66.3.1289-1293.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li D, et al. The structure of the replicativev helicase of the transforming protein SV40 large T-antigen. Nature. 2003;423:512–518. doi: 10.1038/nature01691. [DOI] [PubMed] [Google Scholar]
- 5.Enemark EJ, Joshua-Tor L. Mechanism of DNA translocation in a replicative hexameric helicase. Nature. 2006;442:270–275. doi: 10.1038/nature04943. [DOI] [PubMed] [Google Scholar]
- 6.Myong S, Bruno MM, Pyle AM, Ha T. Spring-loaded mechanism of DNA unwinding by hepatitis C virus NS3 helicase. Science. 2007;317:513–516. doi: 10.1126/science.1144130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chen ZC, Yang HJ, Pavletich NP. Mechanism of homologous recombination from the RecA-ssDNA/dsDNA structures. Nature. 2008;453:489–U483. doi: 10.1038/nature06971. [DOI] [PubMed] [Google Scholar]
- 8.Yu J, Ha T, Schulten K. Structure-based model of the stepping motor of PcrA helicase. Biophys J. 2006;91:2097–2114. doi: 10.1529/biophysj.106.088203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yu J, Ha T, Schulten K. How directional translocation is regulated in a DNA helicase motor. Biophys J. 2007;93:3783–3797. doi: 10.1529/biophysj.107.109546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Strajbl M, Shurki A, Warshel A. Converting conformational changes to electrostatic energy in molecular motors: The energetics of ATP synthase. P Natl Acad Sci USA. 2003;100:14834–14839. doi: 10.1073/pnas.2436328100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Weber J, Senior AE. Catalytic mechanism of F-1-ATPase. BBA Bioenerget. 1997;1319:19–58. doi: 10.1016/s0005-2728(96)00121-1. [DOI] [PubMed] [Google Scholar]
- 12.Greenleaf WB, Shen J, Gai D, Chen XS. Systematic Study of the Functions for the Residues around the Nucleotide Pocket in Simian Virus 40 AAA+ Hexameric Helicase. J Virol. 2008;82:6017–6023. doi: 10.1128/JVI.00387-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kim DE, Narayan M, Patel SS. T7 DNA helicase: A molecular motor that processively and unidirectionally translocates along single-stranded DNA. J Mol Biol. 2002;321:807–819. doi: 10.1016/s0022-2836(02)00733-7. [DOI] [PubMed] [Google Scholar]
- 14.Olsson MHM, Warshel A. Monte Carlo simulations of proton pumps: On the working principles of the biological valve that controls proton pumping in cytochrome c oxidase. P Natl Acad Sci USA. 2006;103:6500–6505. doi: 10.1073/pnas.0510860103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Braun-Sand S, Strajbl M, Warshel A. Studies of proton translocations in biological systems: Simulating proton transport in carbonic anhydrase by EVB-based models. Biophys J. 2004;87:2221–2239. doi: 10.1529/biophysj.104.043257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Burykin A, Schutz CN, Villa J, Warshel A. Simulations of ion current in realistic models of ion channels: The KcsA potassium channel. Proteins. 2002;47:265–280. doi: 10.1002/prot.10106. [DOI] [PubMed] [Google Scholar]
- 17.Roca M, Messer B, Hilvert D, Warshel A. On the relationship between folding and chemical landscapes in enzyme catalysis. P Natl Acad Sci USA. 2008;105:13877–13882. doi: 10.1073/pnas.0803405105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bustamante C, Keller D, Oster G. The physics of molecular motors. Acc Chem Res. 2001;34:412–420. doi: 10.1021/ar0001719. [DOI] [PubMed] [Google Scholar]
- 19.Lee FS, Chu ZT, Bolger MB, Warshel A. Calculations of antibody antigen interactions—Microscopic and semimicroscopic evaluation of the free-energies of binding of phosphorylcholine analogs to Mcpc603. Protein Eng. 1992;5:215–228. [Google Scholar]
- 20.Aqvist J, Luzhkov VB, Brandsdal BO. Ligand binding affinities from MD simulations. Acc Chem Res. 2002;35:358–365. doi: 10.1021/ar010014p. [DOI] [PubMed] [Google Scholar]
- 21.Xiang Y, Oelschlaeger P, Florian J, Goodman MF, Warshel A. Simulating the effect of DNA polymerase mutations on transition-state energetics and fidelity: Evaluating amino acid group contribution and allosteric coupling for ionized residues in human Polβ. Biochemistry. 2006;45:7036–7048. doi: 10.1021/bi060147o. [DOI] [PubMed] [Google Scholar]
- 22.Warshel A, Sharma PK, Kato M, Parson WW. Modeling electrostatic effects in proteins. BBA Proteins Proteom. 2006;1764:1647–1676. doi: 10.1016/j.bbapap.2006.08.007. [DOI] [PubMed] [Google Scholar]
- 23.Lee FS, Chu ZT, Warshel A. Microscopic and semimicroscopic calculations of electrostatic energies in proteins by the POLARIS and ENZYMIX programs. J Comput Chem. 1993;14:161–185. [Google Scholar]
- 24.Schutz CN, Warshel A. What axe the dielectric “constants” of proteins and how to validate electrostatic models? Proteins. 2001;44:400–417. doi: 10.1002/prot.1106. [DOI] [PubMed] [Google Scholar]
- 25.Muegge I, Tao H, Warshel A. A fast estimate of electrostatic group contributions to the free energy of protein-inhibitor binding. Protein Eng. 1997;10:1363–1372. doi: 10.1093/protein/10.12.1363. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.