Observation of strange kinetics in protein folding

Abstract

Highly nonexponential folding kinetics in aqueous solution have been observed during temperature jump-induced refolding of two proteins, yeast phosphoglycerate kinase and a ubiquitin mutant. The observations are most easily interpreted in terms of downhill folding, which posits a heterogeneous ensemble of structures en route to the folded state. The data are also reconciled with exponential kinetics measured under different experimental conditions and with titration experiments indicating cooperative folding.

Protein folding kinetics are usually explained in terms of intermediates connected by substantial thermodynamic barriers (1). This view has been complemented during the past decade by a “New View” that emphasizes the rugged appearance of the protein energy landscape and the resulting heterogeneity of the folding ensemble (Fig. 1) (2–7). The model’s predictions for two-state kinetics have been tested via rate-free energy correlations (8, 9). An experimentally untested hypothesis is the existence of fast nonexponential “downhill” folding, starting either at the transition state barrier or directly from the unfolded state (“type 0” folding) (10–12).

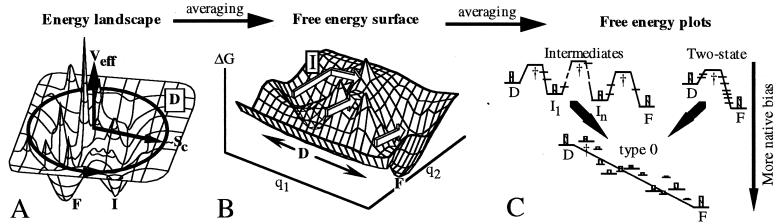
Figure 1.

(A) Protein energy landscape; the radial coordinate correlates with compactness (configurational entropy S_C); the angular coordinate symbolizes another >10³ coordinates. More compact states generally have lower contact energy E_C. The native ensemble F lies near the global minimum; there may be other deep minima I. (B) Thermally averaging the landscape over all but two reaction coordinates removes uninteresting energy spikes (e.g., because of steric hindrance) and leads to a two-dimensional free energy plot. The denatured state D is now a local minimum because of its large entropy. The arrows indicate an intermediate, two-state, and downhill pathway; not all of these necessarily appear simultaneously at constant T. Whether I is an obligatory intermediate or a trap that slows folding depends on its location, relative saddle point heights, etc. (C) Further reduction to one-dimensional pathways. The protein may switch pathways when conditions in B are changed, shifting the location and free energy of minima, maxima, and saddles. Some “nonspecial” states are shown in addition to transition states and intermediates. At weak native bias (e.g., [GuHCl] ≠ 0) a two-state or intermediate scenario results: only D, I, and F are significantly populated during folding (indicated by maximum population histograms). At strong native bias (S_C nearly compensated by E_C during folding), a type 0 scenario results. The rate is dictated by downhill folding, and I and ^† join the ranks of the “nonspecial” states, many of which are now populated. Strange kinetics (14) are not caused by thermodynamic barriers, but rather by unproductive diffusive motions “perpendicular” to the one-dimensional reaction coordinate.

Two-state or sequential intermediate models turn into type 0 folding if there is a sufficiently strong free energy bias toward the native state (Fig. 1) (10). Even when there is a thermodynamic barrier, subsequent downhill folding is a nontrivial heterogeneous process because the transition state ensemble provides a lesser structural constraint for proteins than for smaller molecules. We present submillisecond folding experiments in which proteins are tuned from exponential to nonexponential behavior by temperature adjusting the roughness, minima, and saddle points of the folding free energy surface, directly revealing the heterogeneity of protein conformations during downhill folding.

Downhill folding is a multiscale process that proceeds through an array of temporary conformations with a broad distribution of folding times (11, 12). The resulting dynamics are stretched and highly nonexponential as first observed for glasses (13) and have been called “strange kinetics” (14). At lower temperatures, the folding ensemble is more sensitive to shallow traps on the energy landscape, so the stretching should become more pronounced if the ruggedness is approximately temperature-independent (11, 12, 15). Strange kinetics have been observed experimentally in many natural phenomena (14), ranging from heme binding (16) and myoglobin structural relaxation (17) to recombination dynamics of disulfide bridges in peptides (18, 19).

We have discovered two proteins with strange folding kinetics under conditions with a relatively strong native bias: the two-domain enzyme yeast phosphoglycerate kinase (PGK) (20) and a double mutant of the small single-domain protein human ubiquitin (21). The proteins were denatured by cooling, which causes unfolding by weakening the hydrophobic interaction (22). Refolding initiated by a nanosecond temperature jump was found to be highly nonexponential over some of the temperature range and exponential over the rest. We offer a consistent explanation for these observations in terms of downhill folding, either from the barrier [human ubiquitin F45W V26G mutant (Ub*G)] or perhaps pure type 0 (PGK). The outcome of this experiment is conceptually similar to rapidly quenching a heat denatured protein toward room temperature (12), except that cooling rather than heating produces the initial unfolded state.

EXPERIMENTAL PROCEDURES

Protein Samples.

Yeast PGK from Sigma was studied in pH 6.2 aqueous buffer with 1 mM DTT and EDTA, 20 mM phosphate, 200 mM guanidinium hydrochloride (GuHCl). The protein has two tryptophans buried in the C domain and seven tyrosines (20, 23). Ub*G is a F45W V26G double mutant of human ubiquitin (21, 24, 25). Tryptophan 45 in the hydrophobic core makes the protein fluorescent, while the glycine residue destabilizes core contacts and a critical helix, making cold denaturation possible. Ub*G was constructed by site-directed mutagenesis by using an expression system provided by T. M. Handel (26) and buffered at pH 5.9 in 40 mM phosphate. Its stability was determined to be −5.9(0.8) kJ mol⁻¹ by GuHCl titration. Ub* (F45W mutant, Val26 intact) showed no cold denaturation at −7°C, the initial temperature chosen for the relaxation experiments.

Unfolded State.

Both proteins unfold cooperatively on cold denaturation in supercooled aqueous buffer. Representative characterizations of the cold denatured state are shown in Fig. 2. The PGK tryptophans are exposed to solvent (fluorescence λ_max shift from 342 nm to 355 nm between 22 and −6°C with 295 nm excitation, and over 2-fold intensity increase). A complete loss of secondary structure is observed at −18°C in 700 mM GuHCl (CD decreases from −12,500 deg⋅cm²⋅dmol⁻¹ at 20°C to −950 deg⋅cm²⋅dmol⁻¹). In 200 mM GuHCl, the cold denaturation transition is shifted down by 10°C. The light scattering radius of PGK is known to increase from 3 nm to 5 nm on cold denaturation (23). The unfolded protein is thus highly solvent exposed and expanded, but may retain fluctuating structure at the −8°C prejump temperature of our relaxation experiments.

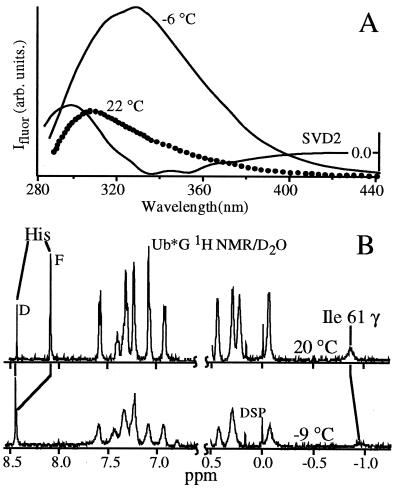
Figure 2.

Representative steady-state cold denaturation measurements. (A) Fluorescence of yeast phosphoglycerate kinase excited at 280 nm; λ_max redshifts by over 30 nm on cooling, as evidenced by the second component of a singular value decomposition of the temperature-dependent data. The tryptophan and tyrosine residues become solvent exposed. (B) ¹H NMR of Ub*G acquired in D₂O with residual water presaturation. The upfield Ile-61 peak is caused by contact with the core tryptophan 45; it disappears in the cold denatured state, indicating core solvation. Both the F and D components of the His-68 peak are resolved; the F peak rapidly decreases in intensity and shifts downfield at lower T. The chemical shift dispersion of the sample decreases toward a random coil.

Ub*G cold denaturation in supercooled solutions revealed a two-state transition toward a solvent exposed state with little tertiary interaction (¹H NMR D₂O chemical shifts dispersion decreases, Fig. 2). The Trp45 fluorescence maximum red shifts 8 nm and the lifetime increases from 1.2 to 4.7 ns between 21 and −7°C at 280 nm excitation, indicating solvent exposure of the core. The CD signature shifts toward a random coil between 25 and −18°C, with a transition midpoint near −12°C.

Fast Folding.

Within 10 ms, PGK forms a compact globular intermediate with substantial secondary structure and with several interresidue distances shorter than in the native state (formed in >10 s) (20). In stopped-flow GuHCl dilution measurements at 25°C, Ub*G has a ms folding rate to the native state (extrapolated to 0 M GuHCl in 0.4 M Na₂SO₄), with no sub-ms A_D→I amplitude and no Chevron plot turnover (21). Extrapolation to 0 M Na₂SO₄ in analogy to Ub*A (21) indicates that any intermediate is tuned to at least 16 kJ/mol above D. At 2–8°C, any intermediate is further expected to cold denature (25), raising its energy at least 22 kJ/mol above D. This puts Ub*G (2°C, 0 M sulfate) in the effective two-state limit of ref. 21. Here, the events on a <10 ms time scale are of interest. The nanosecond laser temperature jump (T-jump) apparatus used in our refolding experiments has been described previously (27, 28). Degassed and filtered aqueous PGK and Ub*G solutions were jumped from ≈−8°C to temperatures between 0 and 20°C by a 1.54 μm infrared laser pulse. A constant prejump temperature assures an identical denatured “D” state for comparison among experiments. Before and after the T-jump, integrated time-resolved protein fluorescence excited at 14 ns intervals by a UV pulse train (280–295 nm) was detected at a right angle by a photomultiplier tube and digitized with 500-ps resolution until 2 ms after the T-jump (up to 10 ms in some cases by using a “burst mode” modification of the electronics).

At time t = 0–10 ms after the T-jump, the shape of the time-resolved (t′ = 0–14 ns) fluorescence profile has changed because of refolding. As discussed in the next section, various folding scenarios are most readily distinguished by fitting the evolving fluorescence profiles to a linear combination of a profile near the beginning and one near the end of the data,

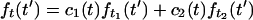1

and plotting χ₁(t) = c₁(t)[c₁(t) + c₂(t)]⁻¹ and the χ² (goodness) of the fit (Fig. 4A). t₁ and t₂>t₁ can be picked anywhere in the 0–10 ms range for which kinetic data is collected. χ₁ then indicates how the fluorescence profile evolves from the more “denatured” shape at t₁ to the more “folded” shape at t₂ (e.g., χ₁ = 1 indicates the profile still looks like the more “unfolded” profile at t₁). One advantage of the χ₁ approach, verified by numerical investigation, is that picking t₁ after refolding has already started, or picking t₂ before a quasi-steady-state is reached, underestimates any stretching of the kinetics: the analysis is therefore conservative from the point of view of detecting stretched kinetics. A further advantage of this procedure is that different folding scenarios (Fig. 1) can be distinguished no matter how complex the causes of the fluorescence are (see next section, footnote therein, and Fig. 4).

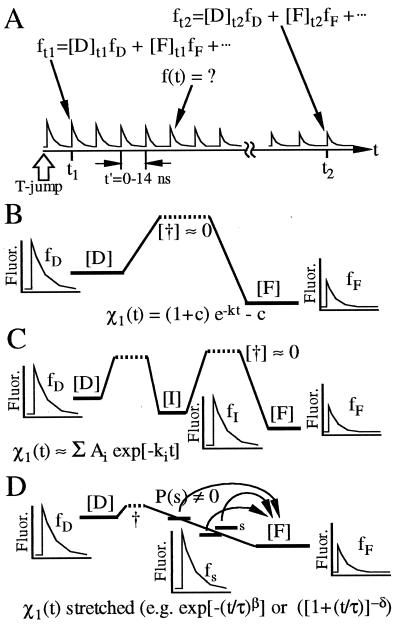
Figure 4.

(A) After a T-jump, time-resolved fluorescence transients change shape from f_t1 to f_t2 because of folding between t₁ and t₂. If only D and F are significantly populated during folding, f_t1, f_t2 and f_t are linear combinations of the denatured fluorescence signal f_D and native fluorescence signal f_F; otherwise, other populations contribute to f_t1 and f_t2. (B) Two-state model. [D]_t1 and [F]_t1 relax exponentially in time to [D]_t2 and [F]_t2 without significantly populating “^†”. f(t) is a weighted average of f_F and f_D and hence of f_t1 and f_t2. χ₁(t) therefore decreases exponentially, no matter at which time f_t1 and f_t2 are picked. The same holds true for a three-state reaction with two time scales τ₁ and τ₂, if τ₂ ≫ τ₁ and f₂ is picked at t ≪ τ₂. (C) Sequential intermediates. f_I is not necessarily well represented by a linear combination of f_t1 and f_t2. If it is, χ₁ is a linear combination of exponentials with uncorrelated lifetimes and amplitudes, some of which may be negative (e.g., if f_I ≈ f_D ≠ f_F). If it is not, χ² for the fit to Eq. 1 is greater at intermediate times than at t₁ and t₂. (D) Downhill scenario. A heterogeneous downhill folding ensemble is populated during folding because of the small transition state barrier ^†. If the subensembles {s} with different fluorescence f_s interconvert slowly, the rate laws of individual s add separately (Eq. 2), yielding a smooth nonexponential χ₁(t). The nonexponentiality can be homogeneous or inhomogeneous depending on the interconversion rates among and within subensembles (11, 12, 19).

Artifact Tests.

Our conditions were selected so tryptophan fluorescence was constant 10 ns–10 ms after the T-jump, eliminating T-jump and recooling artifacts (27). A small ≈10-μs fluorescence-quenching phase during relaxation of pH 2 PGK (which is unfolded over the entire T range) was assigned to nonspecific contraction of the polypeptide chain (Fig. 3). In T-jump experiments at a pH-favoring formation of the native state, similar 2–20 μs phases were observed to precede the PGK and Ub*G folding kinetics of interest here and assigned to “nonspecific” relaxation of the polypeptide chain. During activated folding, such relaxation occurs purely in the unfolded well and equilibrates D → D′ before the barrier crossing. In a type 0 scenario, it smoothly blends into the later stages of folding, and the distinction between “nonspecific contraction” and “folding” becomes meaningless.

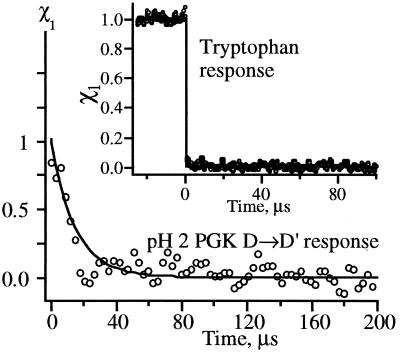
Figure 3.

PGK at pH 2 has a rapid fluorescence response attributed to relaxation of the unfolded chain (t₁ in Eq. 1 at 0.1 μs). Similar <20 μs phases are also observed preceding the folding kinetics of PGK and Ub*G at higher pH. (Inset) Tryptophan has only an “instantaneous” (<20 ns) temperature-dependent fluorescence change (t₁ at −25 μs).

Aggregation was ruled out by concentration dependence measurements. T-jumps in 18-μM PGK solutions were marginally slower (10%) than in 115 μM solution. A 10% increase in rate on 6.4-fold increase in concentration indicates that 18 μM is already near the infinite-dilution limit, eliminating aggregation after the T-jump as a major rate determinant. Aggregation before the T-jump is ruled out because the overall observed kinetics should slow down at higher concentrations because of trapping (29), opposite to what we observe. Similarly, small changes in the Ub*G signal over a 5-fold concentration range (10–50 μM) also indicate that the observed fluorescence changes are not caused by aggregation.

STRANGE KINETICS

Data.

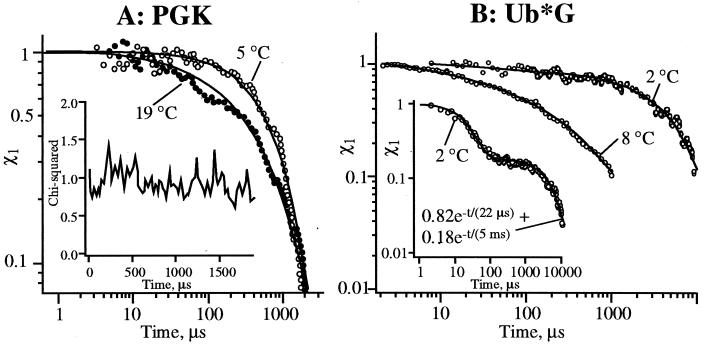
Fig. 5 A and B shows plots of χ₁ for PGK and Ub*G as a function of time after the T-jump. Kinetics at two final temperatures are shown for each protein. At low T, PGK and Ub*G exhibit biexponential kinetics with very distinct fast (2–25 μs) and slow (0.2–5 ms) phases. As T is raised toward optimum native stability, the slow phase speeds up and becomes stretched. Table 1 summarizes fits of the slow phase under various experimental conditions to stretched exponentials, power laws, and a sum of exponentials. Stretched exponentials with β ranging from ≤0.39 to ≤0.83 fitted the higher T data with the fewest adjustable parameters.

Figure 5.

Folding kinetics of PGK and Ub*G. (A) PGK folds by a slow single exponential at 5°C, a faster stretched exponential at 19°C (Table 1) (t₁≈ 8 μs, t₂ ≈ 2 ms in χ₁ fit). (Inset) χ² for the fit to Eq. 1 is approximately constant, ruling out intermediates with a fluorescence signature not represented by a linear combination of the endpoints. (B) Ub*G folds by a slow single exponential at 2°C, a stretched exponential at 8°C. (Inset) The full 2°C χ₁ trace: an ≈20 μs phase attributed to D → D′ relaxation in the unfolded well precedes slow exponential folding (τ ≈ 5 ms) over a barrier. The fast initial phase has been subtracted from the 2°C trace in the main figure (t₁ ≈ 100, 3 and 1 μs in χ₁ fit for 2°C, 8°C, and Inset, respectively).

Table 1.

Stretched exponential, powerlaw, and multiexponential fits for PGK and Ub^*G under various conditions (final temperature and excitation wavelength shown and all times in μs).

Conditions	exp[−(t/τ)β]	1/[1 + (t/τ)]δ	Σ Aiexp[−t/τi]
Ub*G (8°C, 295 nm)	β ≤ 0.39, τ = 112	δ = 0.59, τ = 32	A1 = 1 − A2 − A3, τ1 = 23 A2 = 0.51, τ2 = 261, A3 = 0.11, τ3 > 2,000
Ub*G (2°C, 295 nm)	β ≤ 1, τ = 5,000	—	See stretched exponential
PGK (19°C, 280 nm)	β ≤ 0.65, τ = 475	δ = 1, τ = 230	A1 = 1 − A2, τ1 = 56, A2 = 0.65, τ2 = 890
PGK (19°C, 295 nm)	β ≤ 0.83, τ = 3,770	δ = 1.9, τ = 5,000	A1 = 1 − A2, τ1 = 176, A2 = 0.91, τ2 = 4,250
PGK (5°C, 280 nm)	β ≤ 1, τ = 700	—	See stretched exponential
PGK (2°C, 295 nm)	β ≤ 1, τ = 2,400	—	See stretched exponential
Calculation	β = 0.6 (T/Tg ≈ 1)  to 0.8 (T/Tg ≈ 1.12)		ref. 11
Calculation	β = 0.3 (T/Tg ≈ 1)  to 0.7 (T/Tg ≈ 2)		ref. 12

Also shown are calculations based on Monte Carlo dynamics of a lattice model of protein folding. With our choice of f_t2 (Fig. 5), the β and δ values are upper limits, thus conservatively establishing the nonexponential kinetics. All multiexponential fits had positive amplitudes only. 

The Fig. 5A Inset shows that Eq. 1 fits the PGK fluorescence profiles with approximately constant χ² from 0.003–2 ms after the T-jump. This means that the intermediate time fluorescence signature is well represented by a linear combination of f_t1 and f_t2, excluding folding intermediates with a fluorescence signature substantially different from a linear combination of the kinetic endpoints. To assess the extent of folding, an f_t2 acquired in steady state at the estimated final temperature of the T-jump experiments was also used to analyze the slower phase. The PGK fluorescence lifetime shifts ≈15% from the unfolded towards the native fluorescence, as expected for the globular intermediate. The Ub*G fluorescence lifetime shifts ≈70% towards the native state, indicating that the slower phase forms the native state, in accord with ref. 21. This f_t2 yields even more stretched kinetics, but the analysis in Table 1 conservatively uses shorter time f_t2 from the same data acquisition as f_t4.

Fig. 5B Inset shows the full 2–10,000 μs kinetics of Ub*G at 2°C to illustrate the initial fast phase. A similar fast phase is measured in PGK and persists at pH 2 (Fig. 3). As discussed in the previous section, we attribute these fast phases to D → D′ contraction preceding folding. For Ub*G an intermediate cannot be ruled out. (The fast phase would then be D → I, the slow stretched phase I → F; but see Fast Folding for why D → F is effectively a two-state process below 8°C in absence of sulfate.) Either possibility is compatible with our interpretation below.

Interpretation.

Of main interest here is the slower 0.023-5 ms phase, which leads to a globular intermediate in PGK and to the native state in Ub*G. Analysis in terms of Eq. 1 allows one to make distinctions among the three scenarios in Fig. 1 (intermediates, two-state, downhill). Fig. 4 summarizes the consequences of each scenario in terms of a χ₁ analysis of the data. Activated two-state folding results in single exponential relaxation W(t) ≈ exp[−kt] of D and F, which are the only two significantly populated states. From Eq. 1 and Fig. 4A follows that χ₁ is exponential with rate k, no matter how complex the tryptophan-quenching processes or protein motions over the barrier are.‡ This possibility is compatible with the low T data, but clearly excluded by the higher T data.

The distinction between intermediates and downhill kinetics is more difficult. A scenario with n intermediates results in a sum of n + 1 exponentials with no simple relationship among the n independent amplitudes A_i and n + 1 lifetimes τ_i. Downhill folding populates a structurally continuous ensemble with a broad distribution of folding times and is expected to have smooth stretched kinetics. The important point is that when such intrinsically stretched kinetics are fitted to a sum of exponentials, the lifetimes are separated by an approximately constant factor, and all amplitudes are positive.

As a simple illustration, consider a downhill ensemble of substates {s} rapidly formed with probability P(s), which interconvert slowly and have no reverse reaction. If W(s,t) is the temporal relaxation function of each {s},

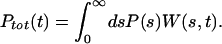2

Here s ε[0,∞] is a continuous index of subensembles. Letting P(s) = e^−s and W(s,t) = e ^−t(s/τ) corresponds to a case where the individual subensembles have simple exponential folding kinetics, a few molecules fast, most slow. Then P_tot(t) = (1 + t/τ)⁻¹ χ₁(t) equals P_tot(t) if all {s} have fluorescence identical to D, or it equals another stretched function if their fluorescence is intermediate between D and F.

Examination of Table I shows that the high T data of PGK and Ub*G are best accounted for by stretched exponentials with only two independent fitting parameters, τ and β. If fitted by a sum of exponentials, the 0.003–2-ms Ub*G data at 8°C requires three exponentials with five independent parameters to be fitted within the experimental noise. The resulting multiexponential lifetimes are separated by about a factor of 10, and the amplitudes are all positive. Although discrete intermediates can never be entirely excluded with a finite stretch of data (here 2.5 orders of magnitude), it is somewhat unlikely that a set of three intermediates would conspire to have all the necessary lifetimes and amplitudes to masquerade as a stretched exponential.

This argument is less convincing for PGK at high T with its larger β, which can be fitted by a double exponential with only one more independent parameter than the stretched exponential fit. However, an intermediate with a distinct fluorescence signature has already been ruled out by Fig. 5A. This implies that any intermediate fluorescence must either resemble f_t2 (yielding single exponential kinetics), or f_t1 (yielding an induction period fitted by a biexponential with one negative coefficient), or a linear combination of f_t1 and f_t2 (kinetics between these extremes). This does not match the observation summarized in Table 1 for PGK at 19°C. We must therefore again adapt the stretched exponential as the most viable model.

To summarize, the low T folding is best accounted for by a slow single exponential (biexponential if the fast phases correspond to intermediates rather than collapse). Closer to optimum native stability, the data is best accounted for by a “faster” stretched exponential. The exponential kinetics can be explained by activation barriers. The nonexponentiality is best explained by downhill folding: if folding is initiated near the thermodynamic barrier, or if the thermodynamic barrier is small (Fig. 6), the subsequent downhill diffusion dictates the folding kinetics. In a multidimensional landscape, there are many traps or barriers even on the downhill side. However, in a highly averaged plot of free energy vs. one reaction coordinate (Fig. 1C), this ruggedness manifests itself mainly by reducing the effective downhill diffusion constant because of unproductive motions in the “orthogonal coordinates” that have been averaged over. During this process, the folding backbones are distributed over a structurally heterogeneous folding ensemble with slowly interconverting conformations. The downhill folding times for different subensembles vary, leading to a distribution of rates and nonexponential kinetics (10).

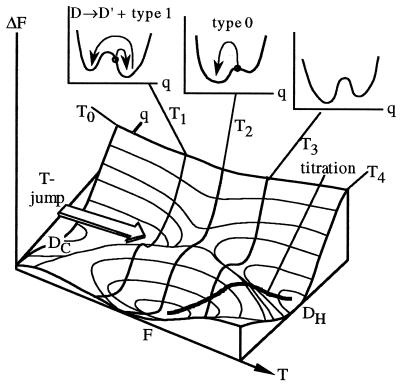
Figure 6.

Free energy as a function of T and reaction coordinate (e.g., protein compactness). At T₀, the cold denatured state D_C is most stable; at T₄, the heat denatured state. At T₂ the native state is most stable and at T₁ or T₃ the equilibrium constant is approximately 1. F is separated from D_C and D_H by barriers that always lead to cooperative temperature titrations (thick line shows average value of q during titration). A sudden small T-jump from T₀ to T₁ leaves q constant and the protein in the D well, followed by type 1 activated exponential kinetics (left Inset plot). A larger jump from T₀ to T₂ leaves the protein closer to the transition state or on a purely downhill type 0 surface if the free energy bias from D to F is too steep (middle Inset plot); the protein folds nonexponentially downhill. A jump from T₀ to T₃ would presumably result in activated kinetics again because of the onset of heat denaturation.

DISCUSSION

If downhill dynamics are adopted as an explanation for our observations, a number of questions must be addressed, such as: Are the observed β values reasonable? How inhomogeneous are the kinetics? How can downhill folding be compatible with a cooperative folding transition? Why does the observed kinetics become more exponential at lower T?

Strange kinetics have been seen in Monte Carlo lattice and off-lattice simulations of the type that have become popular within the “New View” (11, 12). In these simple protein models, a contact matrix describes the interactions between every pair of residues, whose relative motion is restricted by backbone connectivity. Such a model system can be quenched from an extended state to temperatures where the folded state is favored. Table I shows that simulated relaxation dynamics are fitted by stretched exponentials exp[−(t/τ)^β] with factors β(T) ranging from 0.3–1 (11, 14), in accord with our observations at higher T.

Ub*G has a single fluorescent probe (tryptophan 45) at an excitation wavelength of 295 nm. The nonexponentiality cannot be caused by heterogeneity among different backbone sites in the downhill ensemble.‡ On the other hand, PGK has two domains of different folding stabilities (23). The N-terminal domain is probed by excitation at 280 nm but not at 295 nm. The C-terminal domain is probed by excitation both at 280 nm and 295 nm. Although the domains are not fully formed in the 10 ms duration of our experiment (20), some of the observed nonexponentiality is caused by folding differences among domains in the downhill folding ensemble: β ≈ 0.85 at 295 nm, β ≈ 0.65 at 280 nm (Table 1). The question of how fast subensembles with different environments interconvert (homogeneity vs. inhomogeneity) (19) cannot be addressed by our present ensemble-averaged experiments with a single T-jump detection sequence.

The observed downhill folding may seem to contradict the cooperative folding transition seen during temperature titration of Ub*G, PGK, and many other proteins (20, 21). Fig. 6 shows that titration and fast relaxation experiments in fact follow different paths on a plot of free energy vs. temperature and reaction coordinate q. During titration, both T and the average q change, and a barrier between denatured and folded states always results in cooperative behavior. During T-jump, T changes suddenly while q remains constant, then q relaxes during folding while T remains constant; this process can altogether avoid the barrier (e.g., at T₂ in Fig. 6). Two such downhill cases must be distinguished: there is a barrier, but the cold denatured ensemble is promoted near its top (i.e., the state at T₀ is approximately a transition state at T₂); there is no barrier, and type 0 folding results no matter what q is in the cold denatured state (28). Ub*G is an example of the former case, because both D and N His peaks are observed at temperatures between 0 and 20°C (Fig. 2), indicating a barrier of at least several kT over the whole T range. PGK at 19°C may be an example of the latter, as we have presently no spectroscopic indications of a separately populated D state at 20°C.

The same arguments can be made for an analog of Fig. 6 with denaturant concentration replacing the T₂ to T₄ range. A downhill scenario is most likely in the case of very low denaturant concentration, whereas two-state kinetics or sequential intermediates are more likely at higher denaturant concentrations that have less native bias (Fig. 1C). Depending on how the free energy has been tuned by denaturant or T, folding intermediates and downhill kinetics are not mutually exclusive and may in fact blend smoothly into one another.

Fig. 6 also resolves an apparent conflict between our measurements and the landscape model, which in its simplest form predicts increasingly stretched kinetics as the temperature is lowered (11, 12). We measured slow exponential folding at lower T. The discrepancy is resolved by considering the two major effects of cold denaturation on the free energy plot (Fig. 6): first, cold denaturation is cooperative (D_C and F are local minima) (22); it therefore produces a double well in the free energy at some T₁ < T₂, even if the free energy is purely downhill at T₂. Because the barrier becomes more pronounced and moves to smaller q at lower T (Fig. 6), kinetics at T₁ < T₂ are likely to consist of a fast D → D′ phase followed by slow exponential folding over the barrier, as we observe for both PGK and Ub*G. The folding should also become more exponential as T is raised to T₃ > T₂ (heat denaturation), but this regime is presently not accessible in our experiments. Secondly, cold denaturation decreases the ruggedness of the energy landscape at low T by neutralizing both native and non-native hydrophobic contacts; this, after all, is the reason for unfolding at low temperature (22, 30). As a consequence, downhill folding may not continue to stretch at very low T, as observed in Fig. 5. Finally, Fig. 6 is oversimplified in that there can be intermediates at T₃ (less likely at T₁ because of cold denaturation), as compared to a simple two-state scenario (21). The experiments indicate a need for detailed calculations assessing relative changes in the ruggedness and native bias of the energy landscape with T.

Summary.

The complexity of the free energy landscape can result in nonexponential kinetics when conditions favor the native state, while two-state or intermediate kinetics are observed under conditions with a lesser native bias. Even in those folding processes where transition state barriers greater than kT dictate the folding rate, this result highlights the importance of the subsequent downhill motions of the backbone on the “flanks” of the reaction profile: the “thou must now fold” order given at the transition state is executed during downhill folding, and the execution of this order clearly involves strange kinetics.

ABBREVIATIONS

PGK

two-domain enzyme yeast phosphoglycerate kinase

GuHCl

guanidinium hydrochloride

T-jump

temperature jump

Ub*G

human ubiquitin F45W V26G mutant