Solutions of a Lagrangian system on 𝕋²

Abstract

A Lagrangian system on 𝕋² that has been studied earlier under a geometrical condition and found to possess a pair of solutions, H^±, homoclinic to periodic solutions, v^±, of a given homotopy type, is considered further. It is shown with the aid of H^± and variational arguments that, in fact, there is a much richer structure of homoclinics and heteroclinics to v^±. Indeed, the system admits chaotic solutions.

This paper studies the Lagrangian system on ℝ²:

(LS)

where the Lagrangian L is given by

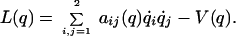Assume

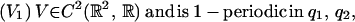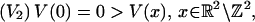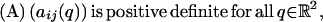and a_ij also satisfies (V₁).

Because of the periodicity of (LS) in q₁, q₂, it can be viewed as a system in ℝ² or on ℝ²/ℤ² = 𝕋². For V ≡ 0, (LS) was considered by Morse (1) and Hedlund (2). They established the existence of a pair of geodesics (for the Riemannean metric associated with L) lying between adjacent periodic geodesics in a given homotopy class on 𝕋² and heteroclinic to these periodic geodesics. When the potential V is present, the situation becomes more complicated due to the equilibrium solutions at ℤ² given via (V₂). Under further geometrical conditions, there has been some work on the existence of zero energy periodic, heteroclinic, and homoclinic solutions of (LS) in refs. 3–6. In particular in ref. 6, it was shown that a geometrical condition led to a pair of periodic solutions v⁺, v⁻ of (LS), and to homoclinics to v⁺, v⁻ lying in the region between v⁺ and v⁻. The goal of this paper is to show that, in the setting of ref. 6, there is a much richer set of homoclinic and heteroclinic solutions of (LS). Indeed there, is a full symbolic dynamics of these and other solutions. Thus, (LS) admits chaotic solutions. This will be made precise and carried out in the next section.

A Symbolic Dynamics of Solutions

To describe our results, the framework of ref. 6 must be recalled. For k ∈ ℤ²∖{0}, let

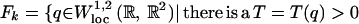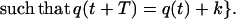Viewed on 𝕋², F_k is the class of W^1.2 curves of homotopy type k. Let

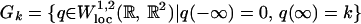The elements of G_k are candidates for heteroclinic solutions of (LS) (or homoclinics to 0 of homotopy type k viewed on 𝕋²).

For q ∈ G_k and F_k respectively, let

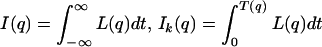and define

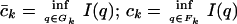It was shown in refs. 3 and 4 that, if

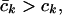1

there is a v ∈ F_k such that I_k(v) = c_k and v is a solution of (LS) (of period T(v) on 𝕋²). Moreover, there is a u ∈ G_k such that I(u) = c̄_k and u is a solution of (LS) heteroclinic to 0 and k. Let

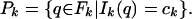The elements of P_k are only determined up to a phase shift because, if θ ∈ ℝ and τ_θq(t) ≡ q(t − θ), then I_k(q) = I_k(τ_θq) for all θ ∈ ℝ. Moreover, if p ∈ F_k, so is p + j for all j ∈ ℤ². It was shown in ref. 4 that 0 ∉ p(ℝ) for any p ∈ P_k. Therefore, 0 belongs to some component of ℝ²∖{p(ℝ)|p ∈ F_k}. This component is bounded by a pair of functions v⁺, v⁻ ∈ P_k and will be denoted by ℛ.

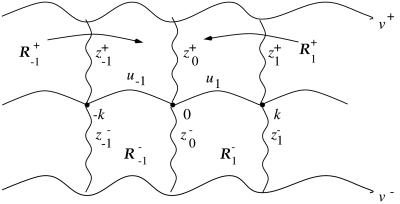
The region ℛ will be subdivided as follows. For i ∈ ℕ, set u_i = u + (i − 1)k and, for −i ∈ ℕ, set u_i = u + ik. Then, U = 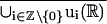divides ℛ into ℛ⁺ and ℛ⁻ with v^±(ℝ) forming a boundary component of ℛ^±. Minimizing ∫₀^∞ L(ϕ)dt over the class of W_loc^1,2 curves, ϕ, with ϕ(0) ∈ v⁺(ℝ) and ϕ(∞) = 0 yields a C² solution, z₀⁺ of (LS) in this class, joining v⁺ and U. Similarly, there is a C² solution, z₀⁻, of (LS) joining v⁻ and U with z₀⁻(0) ∈ v⁻(ℝ) and z₀⁻(∞) = 0. For k ∈ ℤ, set z_k^± = z₀^± + ik. The curves U, v^±, and z_i^± divide ℛ in a natural way into “subrectangles,” ℛ_i^±, i ∈ ℤ∖{0}. See Fig. 1. Set ℛ_i = ℛ_i⁺ ∪ ℛ_i⁻.

To continue, a stronger version of [1] is needed. Consider the class of W^1,2 curves joining v⁺([0, T(v⁺)) to v⁻([0, T(v⁻)). Minimizing ∫ L(⋅)dt over this class produces an infimum, b, of the functional. Suppose

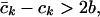2

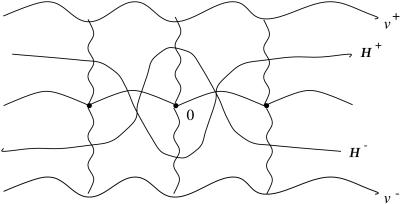
the strengthened geometrical condition. Then, there is a corresponding minimizer, ψ, of the functional that avoids ℤ². By using [2], it was shown in ref. 6 that (LS) possesses a pair of solutions, H^± with H^± homoclinic to v^±. Moreover, H^± crosses z_i^± for all i ≠ 0 and also crosses z₀^∓. In fact, H^±(0) ∈ z₀^∓(ℝ), and the curves lie in ℛ^± except for an interval in which they cross u₋₁ and z₀^∓ and reenter ℛ₁^∓ through u₁ (see Fig. 2). The functions H^± are also minimal solutions of (LS) in the homotopy class of curves that cross the curves z_i^± in the above fashion. “Minimal” means that, for all x < y, H^± minimizes ∫ L(w)dt over the class of W^1,2 curves w having the same endpoints and the same crossing (of z_i^±) properties as H^±|_x^y.

Observe that this minimality property implies that, for any i ≠ j ∈ ℤ, τ_iH⁺(ℝ) ∩ τ_jH⁻(ℝ)=φ.

With the aid of these preliminaries, H^± will be used to help construct new homotopy classes of curves and a symbolic dynamics of solutions of (LS). Let

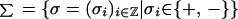A curve q : ℝ → ℛ will be said to have homotopy type σ ∈ Σ if q crosses the curves z_i^σ_i, i ∈ ℤ, in the order given by σ. Define σ^± ∈ Σ by σ_i^± = ±, i ≠ 0, and σ₀^± = ∓. Then, H^± the homotopy type σ^±.

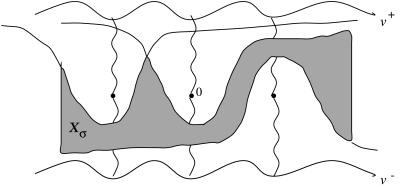
Our main result is that, for each σ ∈ Σ, (LS) has a minimal solution of homotopy type σ. To be more precise, let σ ∈ Σ and i ∈ ℤ. Consider τ_iHσ_i. It divides ℛ into two subregions. Excise the region between τ_iHσ_i and vσ_i from ℛ, calling the resulting region ℛ(τ_iHσ_i). Associate with σ the region ∩_i∈ℤℛ(τ_iHσ_i) ≡ X_σ. See Fig. 3, where σ_i = −, i ≤ 0; = +, i > 0 and X_σ is the shaded region.

Now we have

Theorem 3 If (V₁) − (V₂), (A), and [2] are satisfied, then, for each σ ∈ Σ, there exists a minimal solution Q_σ of (LS) of homotopy type σ lying in X_σ.

Theorem 3 is a consequence of a related result for a subclass of Σ. For p, r ∈ {+, −}, let

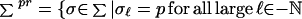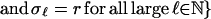Theorem 4 If (V₁) − (V₂), (A), and [2] are satisfied, then, for each σ ∈ Σ^pr and p, r ∈ {+, −}, there is a minimal solution Q_σ of (LS) of homotopy type σ lying in X_σ.

Moreover, Q_σ is heteroclinic from v^p to v^r if p ≠ r and is homoclinic to v^p if p = r.

Theorem 4 will be proved first and then Theorem 3 follows from it by an approximation argument. As in refs. 4–6, the proof of Theorem 4 involves finding Q_σ as the minimizer of an appropriately renormalized functional over a class of curves lying in X_σ. Renormalization is necessary because the natural functional is infinite on the class of curves in X_σ. The first step in the proof is to introduce an appropriate class of curves. Let σ ∈ Σ^pr and

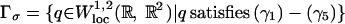where

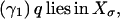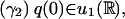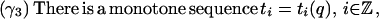Because σ ∈ Σ^pr, there is a smallest ℓ⁻, ℓ⁺ ∈ ℕ such that σ_i = p for all i ≤ −ℓ⁻ and σ_i = r for all i ≥ ℓ⁺. Define s_i = s_i(q) via q(t_i) = z_i^r(s_i(q)), i ≥ ℓ⁺ and q(t_i) = z_i^p(s_i(q)), i ≤ −ℓ⁻. Then we require that

Remark 5 The sequence (t_i(q)) need not be unique.

If (t_i) and (t̃_i) are two such sequences, by (γ₄), q(t) ∈ z_i^±(ℝ⁺) for t ∈ [t_i, t̃_i].

The renormalized functional on Γ_σ will be defined as follows. Let q ∈ Γ_σ. Set

for i ≥ 1 and

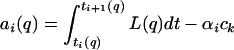for i ≤ −1 where α_i = 0 if −ℓ⁻ ≤ i ≤ ℓ⁺ and α_i = 1 otherwise. Now define

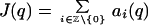Because there may be more than one possible choice of (t_i(q)), it must be shown that J(q) is independent of the choice of (t_i(q)). Thus, suppose that J(q) < ∞. Then a_i(q) → 0 as |i| → ∞, so

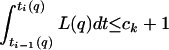6

for large |i|. By a simpler version of the proof of Proposition 3.12 of ref. 4,

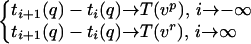7

and

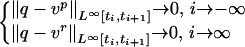8

Hence, s_i(q) → 0 as |i| → ∞. As in ref. 6, set

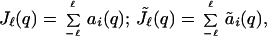where J corresponds to t_i(q)) and J̃ to (t̃_i(q)), with both (t_i(q)) and (t̃_i(q)) satisfying (γ₃). Then, [8] and s_i(q) → 0 imply

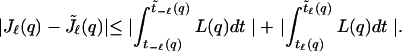9

Because q|_tℓ^t̃_ℓ lies on z_ℓ^r (ℝ⁺), [7] and [8] show |t_ℓ(q) − t̃_ℓ(q)| → 0 as ℓ → ∞ and similarly for −ℓ. Hence, [6], the right hand side of [9] → 0 as ℓ → ∞. Consequently, J(q) = J̃(q), and J is well defined.

Now define

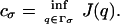10

Theorem 4 will be proved by showing there is a Q_σ ∈ Γ_σ such that J(Q_σ) = c_σ. Moreover, Q_σ is a minimal solution of (LS). Note that, by [8], Q_σ ∈ Γ_σ and J(Q_σ) < ∞ implies that Q_σ is asymptotic to v^p as t → −∞ and to v^r as t → ∞. The minimization argument is related to that of ref. 6, and, therefore, ref. 6 will be referred to for details when appropriate.

If, for example, i ≥ ℓ⁺, gluing 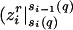−k) to 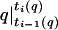produces an element of F_k. Hence, by the definition of c_k,

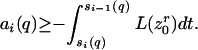11

Combining these estimates shows

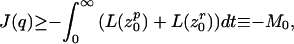12

that is, J is bounded from below on Γ_σ. An upper bound for c_σ is provided by gluing a curve in X_σ, joining v^p(−ℓ⁻T(v^p)) and v^r(ℓ⁺T(v^r)) to 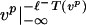and 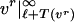, yielding H ∈ Γ_σ with c_σ ≤ J(H) < ∞.

Let (qm) be a minimizing sequence for [10]. Consider τℓ+Hr(t). Now, qm(tℓ+(qm)) lies on zℓ+r(ℝ+) between τℓ+−1Hr(tℓ+(Hr)) and τℓ+H−r(tℓ+(H−r)) and a fortiori between τℓ+(Hr(tℓ+(Hr)) and τℓ+−1Hr(tℓ+(Hr)). It can be assumed that 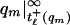lies between τℓ+−1Hr|∞tℓ+(Hr) and tℓ+Hr|tℓ+(Hr)∞. Indeed, suppose qm((x1, x2)) is outside of this region and qm(xi) = τℓ+Hr(yi), i = 1, 2. Replacing qm|x1x2 by τℓ+Hr|y1y2 yields q̂m ∈ Γσ with J(q̂m) < J(qm) via the minimality property of H±. If qm|x1∞ lies outside the region, replace Hr|y1∞ by qm|x1∞, calling the resulting function Ĥ. Because τℓ+Hr is the minimizer of J in an associated class of curves (6) (containing Ĥ), J(Ĥ) > J(τℓ+Hr), which implies

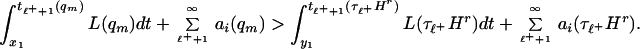13

Therefore, by [13] gluing q_m|_−∞^x₁ to τ_ℓ⁺H^r|_y1^∞ yields q̃_m ∈ Γ_σ with J(q̃_m) < J(q_m). Similar reasoning shows that q_m|_−∞^{−t_ℓ−(q_m)} lies between 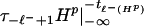and .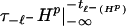

As in refs. 4–6, (q_m) is bounded in W_loc^1,2 and therefore, along a subsequence, converges weakly in W_loc^1,2 and strongly in L_loc^∞ to Q = Q_σ ∈ W_loc^1,2, with Q satisfying (γ₁) − (γ₂) as well as the constraints on (q_m) of the previous paragraph. As in ref. 6, there are numbers A_i > 0 such that

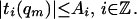14

By [14], it can be assumed that t_i(q_m) → t̃_i for all i ∈ ℤ. It remains to show that (γ₃) − (γ₅) hold for Q. The convergence already established shows for all i ∈ ℤ, as m → ∞.

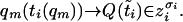15

Therefore, by [15] and (γ₃) for q_m

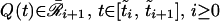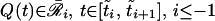16

and (γ₃) − (γ₄) holds for Q with t_i(Q) = t̃_i. Finally, as m → ∞,

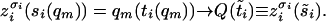17

The latter equality defines s̃_i and implies

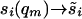18

as m → ∞. Now, (γ₅) for q_m and [18] gives (γ₅) for Q so Q ∈ Γ_σ.

Next, it must be shown that J(Q) < ∞ and J(Q) = c_σ. There is an M > 0 such that

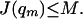19

For q = q_m, write

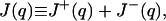20

where J⁺(q) denotes the sum over those a_i(q) such that a_i(q) ≥ 0. Note that the definition of a_i(q) implies a_i(q) < 0 is only possible when i ≥ ℓ⁺ + 1 or i ≤ −ℓ⁻ − 1. By [11] and [19],

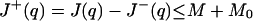21

and therefore

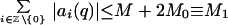22

Hence, for any n ∈ ℕ with, e.g., n > ℓ⁺ + ℓ⁻,

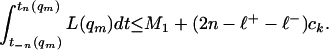23

This implies

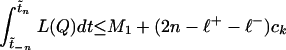or equivalently

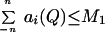24

Hence, J(Q) < ∞ via [24].

A variant of arguments from refs. 4–6 now shows J(Q) = c_σ. Indeed, let ɛ > 0. There is an m₀ = m₀(ɛ) such that m ≥ m₀,

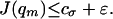25

Further, choose j = j(ɛ) so that

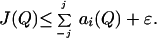26

It can also be assumed that, for m ≥ m₀,

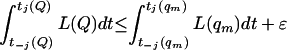27

Therefore, by [25–27] and [11],

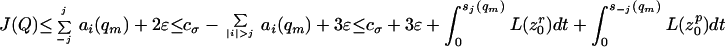28

The constraints on q_m established in the paragraph containing [13] imply

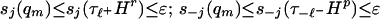29

for j sufficiently large. Now, [28–29] yield J(Q) = c_σ.

That Q is a solution of (LS) follows from simple local minimization and comparison arguments as in Proposition 5.4 of ref. 4.

Remark 30 For i ≥ ℓ⁺, s_i+1(Q) < s_i(Q); for i ≤ −ℓ⁻, s_i−1(Q) < s_i(Q).

Indeed, if equality holds in the + case, excising Q|_ti^t_i+1 from Q and gluing Q|_−∞^t_i to (Q − k)|_ti+1^∞ yields Q* ∈ Γ_σ with J(Q*) < J(Q), a contradiction, unless Q|_ti^t_i+1 coincides with v^r. But, because Q is a solution of (LS), this is impossible.

To complete the proof of Theorem 4, it must be shown that Q is a minimal solution of (LS). Suppose x < y. We claim Q|_x^y minimizes ∫ L(⋅)dt over the class of W^1,2 curves with the same end points as Q|_x^y and that cross the z_i^± in the order given by σ. Indeed, let w denote the minimizer of this variational problem. It suffices to prove that Q*, the curve obtained by replacing Q|_x^y by w, belongs to Γ_σ, for then

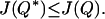31

Therefore, there must be equality in [31], and Q* is a solution of (LS). But Q and Q* coincide on an open set, so uniqueness of solutions of (LS) implies Q ≡ Q*.

To verify that Q* satisfies (γ1) − (γ5), note that the range of w lies in Xσ via the minimality properties of the boundary curves of Xσ. Hence, (γ1) holds. Parametrizing Q* appropriately gives (γ2). There is a finite set of zj± that Q|xy intersects zj±. Because w is a solution of (LS), there is a natural corresponding set of tj(w), namely tj(w) is the unique (via the minimality of zj±) value of t at which w intersects zj±. Thus, Q* satisfies (γ3), and minimality arguments imply (γ4). Suppose (γ5) fails, e.g., for i > 0. Then, si+1(Q*) > si(Q*) for some smallest i. Because sj(Q*) → 0 as j → ∞, there is a smallest j > i + 1 such that sj(Q*) ≤ si(Q*). If sj = si, excise Q*|titj(Q*)(Q*) from Q* and glue Q*|−∞ti to (Q* − k)|tj∞, obtaining Q̂ ∈ Γσ with J(Q̂) < J(Q*) ≤ J(Q), a contradiction. If sj < si, define P(t) = Q*(t) + k, t ≥ ti(Q*). Suppose for convenience that r = +. Because si+1 > si, P(ti) lies between Q*(ℝ) and v+(ℝ) while P(tj−1) lies between Q*(ℝ) and the portion of ∂Xσ given by appropriate segments of {τℓH−}. Therefore, there is a t* ∈ (ti, tj−1) such that P(t*) ∈ Q*(ℝ); i.e., Q*(t*) + k = Q(t̃). Excising Q*|t*t̃ from Q* and arguing as for sj = si yields Q such that J(Q) < J(Q*). Possibly, (γ5) still fails for Q̃, but, repeating the above argument a finite number of times yields Q ∈ Γσ such that J(Q̂) < J(Q), a contradiction. This Q is a minimal solution of (LS), and Theorem 4 is proved.

Proof of Theorem 3.

Let σ ∈ Σ. Define d_m = (d_mi)_i∈ℤ ∈ Σ as follows: d_mi = σ_i, |i| ≤ m; d_mi = σ_m, i ≥ m; d_mi = σ_−m, i ≤ − m. Then, d_m ∈ Σ^{σ_−m,σ_−m}, so, by Theorem 4, there is a minimal solution Q_m ∈ Γ_dm of (LS). The form of d_mand X_dm together with (LS) imply the functions Q_m are bounded in C_loc² and therefore converge in C_loc² to Q_σ ∈ X_σ. It readily follows that Q_σ is a minimal solution of (LS) of homotopy type σ, and the proof is complete.