Abstract
There are several classes of homogeneous Fermi systems that are characterized by the topology of the energy spectrum of fermionic quasiparticles: (i) gapless systems with a Fermi surface, (ii) systems with a gap in their spectrum, (iii) gapless systems with topologically stable point nodes (Fermi points), and (iv) gapless systems with topologically unstable lines of nodes (Fermi lines). Superfluid 3He-A and electroweak vacuum belong to the universality class 3. The fermionic quasiparticles (particles) in this class are chiral: they are left-handed or right-handed. The collective bosonic modes of systems of class 3 are the effective gauge and gravitational fields. The great advantage of superfluid 3He-A is that we can perform experiments by using this condensed matter and thereby simulate many phenomena in high energy physics, including axial anomaly, baryoproduction, and magnetogenesis. 3He-A textures induce a nontrivial effective metrics of the space, where the free quasiparticles move along geodesics. With 3He-A one can simulate event horizons, Hawking radiation, rotating vacuum, etc. High-temperature superconductors are believed to belong to class 4. They have gapless fermionic quasiparticles with a “relativistic” spectrum close to gap nodes, which allows application of ideas developed for superfluid 3He-A.
It is now well understood that the universe and its symmetry-broken ground state, the physical vacuum, may behave like a condensed matter system with a complicated and possibly degenerate ground state (1–5).
If the analogy of the quantum mechanical physical vacuum with condensed matter systems is taken seriously, the first question that arises is: which system of condensed matter reproduces most closely the properties of the quantum vacuum? Because particle physics deals with interacting Fermi and Bose quantum fields, the system should be fermionic. This requirement excludes superfluid 4He, which contains only Bose fields. In Fermi systems, such as metals, superconductors, and normal and superfluid 3He, in addition to the fermionic degrees of freedom that come from the bare fermions, electrons, and 3He-atoms, the quantum Bose fields appear as low-energy collective modes. Therefore, these systems do represent interacting Fermi and Bose quantum fields.
Which Fermi system is the best? To answer this question we first must realize that the main feature that differentiates between various Fermi systems is the topology of the quasiparticle spectrum in the low energy (infra-red) corner. I will consider only systems whose ground state is spatially homogeneous, which is one of the least disputed properties of the physical vacuum. When the topology of the quasiparticle spectrum is taken into account, the homogeneous Fermi systems can be organized into very few classes (see Fig. 1).
Figure 1.
Universality classes of the fermionic ground state (vacuum).
Systems with a Fermi Surface
The most common universality class is made of fermionic systems that have a Fermi surface (FS). Any collection of fermions with weak repulsive interactions belongs to this class. In the extreme limit of a noninteracting Fermi gas, with an energy spectrum E(p) = p2/2m − μ, where μ is the chemical potential, the FS bounds the volume in the momentum space where E(p)<0 and where the quasiparticle states all are occupied at T = 0. In this isotropic model the FS is a sphere of radius pF = 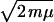 . It is remarkable that the FS survives even if interactions between particles are introduced. This stability is a topological property of the FS that is reflected in the Feynman quantum mechanical propagator G = (z − H)−1 for the particle (the one-particle Green’s function).
. It is remarkable that the FS survives even if interactions between particles are introduced. This stability is a topological property of the FS that is reflected in the Feynman quantum mechanical propagator G = (z − H)−1 for the particle (the one-particle Green’s function).
Let us write the propagator for a given momentum p and for the imaginary frequency, z = ip0 [the imaginary frequency is introduced to avoid the conventional singularity of the propagator at z = E(p)]. For noninteracting particles the propagator has the form G = (ip0 − E(p))−1. Obviously there is still a singularity. On the hypersurface (p0 = 0,p = pF) in the four-dimensional space (p0,p) the propagator is not well defined. What is important is that this singularity is stable: The phase Φ of the Green’s function G = |G|eiΦ changes by 2π around the path embracing this surface in the four-dimensional space (see Fig. 2), and the phase winding number is robust toward any perturbation. Thus the singularity of the Green’s function on the two-dimensional surface in the momentum space is preserved, even when interactions between particles are introduced.
Figure 2.
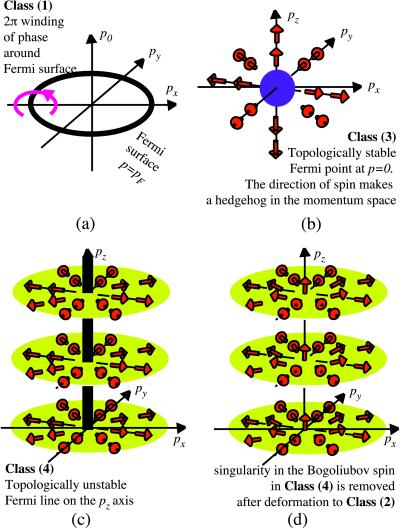
(a) Winding of the propagator phase around the FS. For simplicity the pz coordinate is hidden so that the FS is the line (p0 = 0,p = pF) in the 2+1 momentum space. This line is a singularity, which is similar to a vortex in a real three-dimensional space. The phase of the propagator G = (ip0 − (px2 + py2 − pF2)/2m)−1 changes by 2π around the line in the momentum space in the same manner as the phase of the order parameter changes by 2π around a vortex in the real space. (b) Fermi point at p = 0 in the three-dimensional momentum space (px,py,pz). At this point the particle energy E = cp is zero. A right-handed particle is considered with its spin parallel to the momentum p, i.e., s(p) = (1/2)p/p. The spin makes a hedgehog in the momentum space, which is topologically stable. (c) Fermi line, topologically unstable manifold of zeroes, is shown in the three-dimensional momentum space (px,py,pz). The (Bogoliubov) spin (arrows) is confined into the (px,py) plane and has a singularity on the pz axis. (d) This singularity can be removed by a continuous transformation. The spin escapes into a third dimension (pz) and becomes well defined on the pz axis. As a result, the quasiparticle spectrum becomes fully gapped (the relativistic fermion acquires the mass).
Exactly the same topological conservation of the winding number leads to the stability of the quantized vortex in superfluids and superconductors, the only difference being that, in the case of vortices, the phase winding occurs in the real space (see Fig. 3), instead of the momentum space. The connection between the topology in real space, and the topology in momentum space is, in fact, even deeper (see e.g., refs. 6 and 7).
Figure 3.
Dictionary.
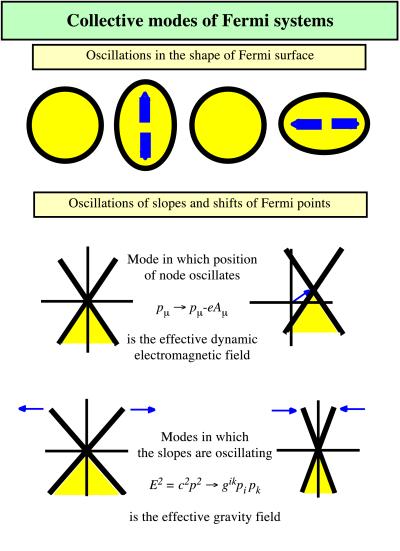
The topology of the propagator in the four-dimensional momentum space is thus essential for the Landau theory of an interacting Fermi liquid; it confirms the assumption that in Fermi liquids the spectrum of quasiparticles at low energy is similar to that of particles in a Fermi gas. The interactions do not change the topology of the fermionic spectrum, but they produce the effective field acting on a given particle by the other moving particles. Although this effective field cannot destroy the FS owing to its topological stability, it can shift its position locally. Therefore, a collective motion of the particles is seen by an individual quasiparticle as a dynamical mode of the FS. These bosonic oscillative modes are known as different harmonics of the zero sound. An example is shown in Fig. 4, Upper.
Figure 4.
Collective modes of fermionic systems.
Systems with a Fermi Point
Although the systems I have discussed above contain fermionic and bosonic quantum fields, the output is not the relativistic quantum field theory we need. There is no Lorentz invariance, and the oscillations of the Fermi surface do not resemble the gauge field even remotely. The situation is somewhat better for class 2, i.e., for fermionic systems with fully gapped spectra; examples that provide useful analogies with Dirac fermions and spontaneously broken symmetry in quantum fields are conventional superconductors (8, 9) and superfluid 3He-B (10, 11). The latter also serves as a model system for simulations of many phenomena in particle physics and cosmology (see Fig. 5), including experimental verification (12) of the Kibble mechanism describing formation of cosmic strings in the early universe (13).
Figure 5.
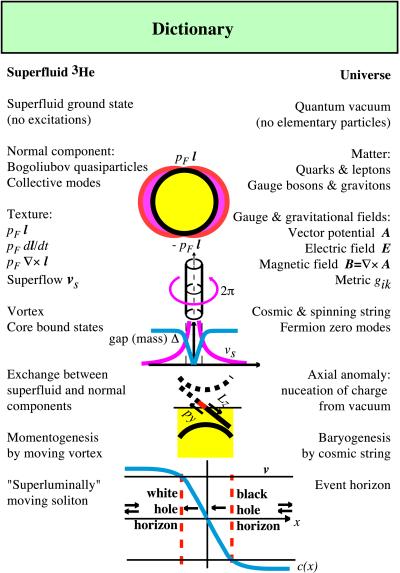
Helium-3-centric universe. Connections of superfluid 3He to other branches of physics. For each item one can find the analogous phenomenon in superfluid phases of 3He. The analogies can result from the symmetry, from topology in real space or from topology in momentum space. In many cases they are described by the same equations.
However, I proceed to class 3, which most fully exhibits the fundamental properties needed for a realization of the relativistic quantum fields, analogous to those in particle physics and gravity.
Class 3 systems, whose representatives are superfluid 3He-A and the vacuum of relativistic left-handed and right-handed chiral fermions, is characterized by points in the momentum space where the (quasi)particle energy is zero. In particle physics the energy spectrum E(p) = cp is characteristic of the massless neutrino (or any other chiral lepton or quark in the standard model of electroweak interactions) with c being the speed of light. The energy of a neutrino is zero at point p = 0 in the three-dimensional momentum space. In condensed matter systems such point nodes have been realized first in superfluid 3He-A, which I discuss later. The Hamiltonian for the neutrino, the massless spin-1/2 particle, is a 2 × 2 matrix H = ±cσ⋅p, which is expressed in terms of the Pauli spin matrices σ. The sign + is for a right-handed particle and − for a left-handed one: the spin of the particle is oriented along or opposite to its momentum, respectively.
Let us again consider the propagator of the particle G = (ip0 − H)−1 on the imaginary frequency axis, z = ip0. One can see that this propagator still has a singularity, which is now not on the surface but at point (p0 = 0,p = 0) in the four-dimensional momentum space. It is important that this Fermi point is not simply the shrinked FS, which is topologically unstable and can disappear. The discussed points control the topological stability; they cannot be destroyed by external perturbations of the system.
Such stability can be visualized if one considers the behavior of the particle spin s(p) as a function of its momentum p in the three-dimensional space p = (px,py,pz). For right-handed particles, s(p) = p/2p, whereas for left-handed ones s(p) = −p/2p. In both cases the spin distribution in the momentum space looks like a hedgehog (see Fig. 2b), whose spines are represented by spins: spines point outward for the right-handed particle and inward for the left-handed one. In the three-dimensional space the hedgehog is topologically stable. There exists an integer topological invariant, which supports the stability of the Fermi point in the same manner as the conservation of the winding number is responsible for the stability of a vortex line and the FS. This invariant can be expressed in terms of the propagator (14).
The consequence is the following: The effective fields acting on a given particle caused by interactions with other moving particles cannot destroy the Fermi point. They lead to a shift in its position in the momentum space and to a change of the slopes of the energy spectrum (see Fig. 4). This response of the class 3 systems to deformations means that the low-frequency collective modes in such Fermi liquids are the propagating collective oscillations of the positions of the Fermi point and of the slopes at the Fermi point. The former is felt by the right- or the left-handed quasiparticles as the gauge (electromagnetic) field, because the main effect of the electromagnetic field Aμ = (A0,A) is just a dynamical change in the position of zero in the energy spectrum: (E − eA0)2 = c2(p − eA)2.
The latter, i.e., the change of the slope, corresponds to a change in the speed of light, which can be different for different directions in space: cx = c + δcx, cy = c + δcy, and cz = c + δcz. In a more general consideration the energy spectrum in the perturbed state is expressed in terms of the matrix of slopes, E2 = gikpipk. In the physical sense this matrix is the metric tensor. The quasiparticles feel the inverse tensor gik as the metric of the effective space in which they move along the geodesic curves with the interval ds2 = −dt2 + gikdxidxk. Therefore, the collective modes related to the slopes play the part of the gravity field (see Fig. 4).
The most general form of the energy spectrum close to the Fermi point, i.e., at low energies, is gμv(pμ − eAμ)(pν − eAν) = 0, which describes a relativistic massless (actually chiral) particle moving in the electromagnetic and gravity fields. It is most important that this is the general form of the energy spectrum in the vicinity of any Fermi point, even if the underlying Fermi system is not Lorentz invariant; superfluid 3He-A is an example. The fermionic spectrum necessarily becomes Lorentz invariant near the Fermi point, i.e., this invariance is not fundamental but a low-energy property of any system with a Fermi point.
Another important property that results from the above equation is that the fermionic propagator near the Fermi point is gauge invariant and even invariant under general coordinate transformations (general covariance). For example, the local phase transformation of the wave function of the fermion, Ψ → Ψeieα(r,t) can be compensated by a shift of the “electromagnetic” field Aμ → Aμ + ∂μα. Such invariances usually are attributed to fundamental properties of electromagnetic (Aμ) and gravitational (gμν) fields, but here they arise spontaneously as low-energy phenomena.
What about equations for these collective bosonic modes, Aμ and gμν: Are they also gauge invariant, i.e., invariant under transformation Aμ → Aμ + ∂μα ? Also, do they obey the general covariance? In other words, do they correspond to Maxwell and Einstein equations for electromagnetic and gravitational fields, respectively? The answer to this question depends on the structure of the underlying Fermi system.
The effective Lagrangian for the collective modes is obtained by integrating over the vacuum fluctuations of the fermionic field in the presence of the collective bosonic fields. This principle was used by Sakharov (15) and Zeldovich (16) to obtain an effective gravity (15) and an effective electrodynamics (16), both arising from fluctuations of the fermionic vacuum.
Let us suppose that the main contribution to the effective action comes from the vacuum fermions whose momenta p are concentrated near the Fermi point. Because these “relativistic” fermions, moving in “gauge” and “gravity” fields, obey gauge invariance and general covariance, the result of the integration—the effective Lagrangian for the bosonic fields—is also Lorentz invariant and gauge invariant and even has a covariant form. In this case the obtained effective Lagrangian does give Maxwell equations for Aμ (16) and Einstein equations for gμν (15), so that the propagating bosonic collective modes do represent the gauge bosons and gravitons.
In the extreme limit, when the massless relativistic fermions are overdominating in vacuum, a new invariance is revealed—the conformal invariance. The conformal transformation gμν → agμν leaves the massless fermions intact, as a result the effective action for gravity becomes the conformly invariant Weyl action. Weyl gravity is a viable rival to Einstein gravity in modern cosmology (17, 18).
Thus, if two requirements are fulfilled—(i) the fermionic system has a Fermi point, and (ii) the main physics is concentrated near this Fermi point—the system acquires at low energy all the properties of modern quantum field theory: chiral fermions, quantum gauge fields, and gravity. All these of ingredients are actually low-energy (infra-red) phenomena.
As a practical realization of class 3 Fermi systems in condensed matter, let us consider excitations in 3He-A (see Fig. 3). After the transition to the superfluid state the FS disappears, a gap appears instead in the quasiparticle energy spectrum. Distinct from conventional superconductors belonging to class 2, the gap has nodes at the north and south poles of the former FS (at p = ±pF l̂, where l̂ is the direction of spontaneous angular momentum in 3He-A. Each node is a topologically stable Fermi point with left-handed quasiparticles near the north pole and right-handed quasiparticles near the south pole. Another example of the Fermi point in condensed matter has been discussed for gapless semiconductors (19).
Close to the gap nodes, i.e., at energies E ≪ Δ0, where Δ0 is the maximal value of the gap in 3He-A, playing the part of the Planck energy, the quasiparticles obey the relativistic equation gμν(pμ − eAμ)(pν − eAν) = 0. Here e = ± is the “electric charge” and simultaneously the chirality of the quasiparticles. The effective electromagnetic field is induced by the dynamical l̂-field and by the velocity vs of the superfluid quantum vacuum of 3He-A: A = pF l̂, A0 = pFvs⋅l̂. This means, e.g., that the texture of the l̂-vector is felt by quasiparticles as the magnetic field according to equation B = pF∇⃗ × l̂ (see Fig. 3). Moreover, in the low-energy limit, the Aμ field does obey Maxwell equations. The integration over the vacuum fermions is concentrated near the Fermi point because of logarithmic divergence, known in particle physics as the zero charge effect.
The metric of the effective space, where the chiral quasiparticles move along the geodesic curves, has the components: gik = c⊥2(δik − l̂il̂k)+c∥2l̂il̂k − vsivsk, g00 = −1, g0i = vsi. The quantities c∥ and c⊥—the velocities of “light” propagating along and transverse to l̂—are expressed by the “fundamental” parameters of 3He-A: c∥ = pF/m*, c⊥ = Δ0/pF, where m* and pF are the mass and Fermi momentum, respectively, of quasiparticles in the normal 3He. Because Δ0≪EF ∼ pF2/2m*, the “Einstein” and “Weyl” actions for gμν are highly contaminated by many noncovariant terms, which come from the integration over the “nonrelativistic” high-energy degrees of freedom in the region Δ0<E<EF.
In spite of the absence of general covariance in general, many different properties of the physical vacuum with a Fermi point, whose direct observation is still far from realization, can be simulated in 3He-A. One of them is the chiral anomaly, which allows the nucleation of the fermionic charge from the vacuum (20, 21) (see Figs. 3 and 5). Because the chiral anomaly is a low-energy phenomenon, the anomaly equation in 3He-A has gauge invariant and general covariant form, and thus exactly coincides with that derived by Adler (20) and Bell and Jackiw (21). This equation has been verified in several 3He experiments (22, 23). In particle physics, the only evidence of axial anomaly is related to the decay of the neutral pion π0 → 2γ, although the anomaly is much used in different cosmological scenaria, explaining an excess of matter over antimatter in the universe (see review in ref. 24).
The advantage of 3He-A for such simulations is that the theory of this superfluid is in some sense complete. At least in principle one can derive everything from the bare 3He atoms interacting via a known potential, which is why there is no cut-off problem. We know (or can calculate from first principles) what happens not only in the low-energy limit, where the fermionic spectrum is gauge invariant or covariant, but also at higher energy, where the Lorentz and gauge invariances are violated. This completeness allows us to investigate problems that require knowledge of physics beyond the Planck cut-off, e.g., the quantum effects related to the event horizon of black holes. It is also important that there is a variety of textures in superfluid 3He-A that allow us to simulate the event horizon and ergoregion when the texture moves with velocity exceeding the local speed of light (25, 26) or rotates (27) (see Figs. 3 and 5).
Systems with a Fermi Line
The high-temperature superconductors in cuprates most probably contain zeroes in their quasiparticle energy spectrum. The angle-resolved photoemission spectroscopy experiments (28) show that these are lines in the three-dimensional momentum space where the quasiparticle energy is zero or, equivalently, point zeroes in the two-dimensional CuO2 planes. The high-T superconductors thus belong to class 4 of systems with Fermi lines. The dimension D of the manifold of zeroes is 1, which is intermediate between a FS with D = 2 and a Fermi point with D = 0.
As in the other two classes, all low-energy (or infra-red) properties of cuprate superconductors are determined by zeroes. In particular, the density of the fermionic states with energy E is determined by the dimension of the zeroes: N(E) = Σpδ(E − E(p)) ∼ E2−D. Many low-temperature properties of these superconductors are obtained from a simple scaling, known in 3He-A (this represents one of the connections in Fig. 5). For example, an external magnetic field B has the dimension of E2. At finite B, the density of states is nonzero even at E = 0 and equals N(0,B) ∼ B(2−D)/2 (29). An experimental indication of such scaling with D = 1 was reported for YBa2Cu3O7 in ref. 30.
The energy spectrum of quasiparticles near each of the four gap nodes in Fig. 1 can be written as E = τ1cx(px − eAx) + τ3cy(py − eAy), where τ⃗s are the Pauli matrices in the Bogoliubov–Nambu particle-hole space. The speeds of light cx and cy are the fundamental characteristics determined by the microscopic physics of cuprates. A is the effective (not electromagnetic) field, which indicates the position of the nodal lines in the momentum space, which means that the system belongs to the same class as the 2+1 quantum electrodynamics with massless fermions.
The lines of zeroes generally have no topological stability. The singular line in the momentum space from which the spines (now the vector τ⃗) point outward (see Fig. 2c) can be eliminated by the escape of the τ⃗-vector to a third dimension. This regularization may be accomplished by an operation similar to the folding of an umbrella (see Fig. 2d).
Existence of the nodal lines can be prescribed, however, by the symmetry of the ground state. There are many nontrivial classes of superconductors, whose symmetry supports the existence of nodal lines in symmetric positions in the momentum space (31). The symmetry violating perturbations, such as impurities, an external magnetic field, etc., destroy the lines of zeroes (7). One could expect different types of transformations of these lines of zeroes that depend on the perturbation. Impurities, for example, can (i) produce the gap in the fermionic spectrum (32), thus transforming the system to class 2 (see Fig. 2d); (ii) lead to a finite density of states (33), thus transforming the system to class 1; (iii) produce zeroes of fractional dimension, which means that the exponent in the density of states N(E) ∝ E2−D is nonintegral (34) and thus corresponds to a fractional dimension D of the manifold of zeroes; and (iv) lead to localization (35). An open question is: Can the quantum fluctuations do the same; in particular, can they change the effective dimension of the zeroes?
Conclusion
The fermionic systems with topologically stable Fermi points have a remarkable property. In the low-energy corner the system exhibits an enhanced symmetry. The Lorentz invariance, general covariance, gauge invariance, and conformal invariance all appear spontaneously in this corner and bring with them chiral relativistic fermions, gauge fields, and gravity. All are low-energy phenomena, which are absent at higher energies. In particular, this analogy suggests that gravity exists only in the infrared limit, i.e., only low-energy gravitons can be quantized (36).
Distinct from the string theory, which also gives rise to gravitation, the Fermi point mechanism does not require a high dimensionality for the space-time. The topologically stable Fermi point is a property of the conventional 3+1-dimensional space-time.
There are actually two main guesses about the symmetry at high energies: (i) conventional wisdom prescribes a higher symmetry at higher energies, SO(10), supersymmetry, etc.; and (ii) a contrary conjecture is that all symmetries known in the universe disappear at higher energies when the Planck energy is approached. The latter can be applied even to the Lorentz invariance (37), whose violation at high energies can be the origin of the observed neutrino oscillations (38, 39). The condensed matter analogy with Fermi points supports the second guess.
At “very low” energies of the electroweak scale Eew ∼ 100 GeV, the chiral fermions acquire masses and become the Dirac fermions of class 2. There are also two main guesses how this happens and both can be described in terms of the Fermi points. The first is the standard model of symmetry breaking. From the point of view of momentum-space topology, it corresponds to the coalescence and mutual annihilation of Fermi points with opposite topological invariants. In the alternative theory, the mass matrix of fermions appears in the same way as the gauge field (see e.g., refs. 40–42). By using the language of the Fermi points, the gauge fields, the Higgs fields, and Yukawa interactions, all are realized as shifts of positions of Fermi points corresponding to different quarks and leptons. It is interesting that this way of unification of gauge and Higgs fields, which has been called generalized covariant derivative, is known in 3He-A, where most of effective gauge fields come from the collective modes of the order parameter, i.e., from the Higgs field.
However, at the moment it is not clear whether the Fermi point is really the true way of how all the low-energy phenomena arise in the physical vacuum. Before making a conclusion one should manage to construct a scenario of how the 45 chiral fermions of three generations (or 48 fermions, if neutrinos have a mass) and 12-gauge bosons of the SU(3) × SU(2) × U(1) group of strong and electroweak interactions can arise as effective Fermi and Bose fields from the Fermi points.
3He-A gives some hints that this scenario may be possible. The Fermi point (say, at the north pole) is actually doubly degenerate owing to the ordinary spin of the 3He atom. The double degeneracy results in the SU(2) effective gauge field, acting on quasiparticles near the Fermi point (14, 43), which means that the higher symmetry groups could be a consequence of the Fermi point degeneracy. For example, the 4-fold degeneracy could result in the four left-handed + four right-handed fermionic species and simultaneously in the SU(4) gauge group.
In this example, however, the number of bosons exceeds the number of fermions. To obtain the correct number of bosons and fermions probably would require a composite model for quarks and leptons. There is, however, another possibility how to reduce the number of the effective gauge fields. Chadha and Nielsen (37) considered the massless electrodynamics with different metrics for the left-handed and right-handed fermions; their model thus violates the Lorentz invariance. They found that the two metrics converge to a single one as the energy is lowered. Thus in the low-energy corner the Lorentz invariance becomes better and better, and at the same time the number of independent bosonic modes decreases.
The violation of all invariances at high energy imposes another problem to be solved. Why are the corrections caused by noninvariance extremely small at low energies? Actually none of the corrections have been experimentally identified so far, which means that the integration over the fermionic vacuum that produces the action for the gauge and gravity fields is very effectively concentrated near the Fermi points, where all the symmetries are present. There should be a special mechanism, such as an enhanced quasiparticle relaxation at higher energy, which effectively switches off the nonsymmetric high-energy contribution. The same mechanism could be responsible for the absence of the cosmological term in the Einstein equations.
As I already have mentioned, with given physical parameters 3He-A is not a good model for such effective cancellation. Although the Maxwell action is really dominating at low energies because of the logarithmically running coupling constant, the Einstein action is polluted by the noncovariant terms, because the contribution of the vacuum fermions far from the Fermi point becomes dominating. To remove the polluting terms, the integration must be spontaneously cut-off at energies much below the Planck scale, E ≪ Δ0. This requirement produces strong limitations on the parameters of the underlying condensed matter.
Nevertheless many phenomena related to the physical vacuum have been or could be visualized in 3He-A. There are many other connections between superfluid 3He and the rest of physics that should be exploited as well (see Fig. 5).
ABBREVIATION
- FS
Fermi surface
References
- 1.Hu B L. 3rd Asia-Pacific Conf Proc Phys. 1988;1:301–314. [Google Scholar]
- 2.Wilczek F. Int J Mod Phys A. 1998;13:863–886. [Google Scholar]
- 3.Wilczek F. Phys Today. 1998;51:11–13. [Google Scholar]
- 4.Jegerlehner F. In: Theory of Elementary Particles: Proceedings of the 31st International Symposium, Ahrenshoop, September 2–6, 1997, Buckow, Germany. Dorn H, Lüst D, Weigt G, editors. Berlin: Wiley-VCH; 1998. pp. 386–392. , e-Print Archive: hep-th/9803021. [Google Scholar]
- 5.Jackiw R. Proc Natl Acad Sci USA. 1998;95:12776–12778. doi: 10.1073/pnas.95.22.12776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Volovik G E, Mineev V P. Sov Phys JETP. 1982;56:579–586. [Google Scholar]
- 7.Grinevich P G, Volovik G E. J Low Temp Phys. 1988;72:371–380. [Google Scholar]
- 8.Nambu Y, Jona-Lasinio G. Phys Rev. 1960;122:345–358. [Google Scholar]
- 9.Nambu Y, Jona-Lasinio G. Phys Rev. 1961;124:246–254. [Google Scholar]
- 10.Alford M, Rajagopal K, Wilczek F. Phys Lett B. 1998;422:247–256. [Google Scholar]
- 11.Wilczek F. Nucl Phys A. 1998;642:1–13. [Google Scholar]
- 12.Ruutu V M H, Eltsov V B, Gill A J, Kibble T W B, Krusius M, Makhlin Yu G, Placais B, Volovik G E, Wen X. Nature (London) 1996;382:334–336. [Google Scholar]
- 13.Kibble T W B. J Phys A Gen Phys. 1976;9:1387–1398. [Google Scholar]
- 14.Volovik G E. Exotic Properties of Superfluid 3He. Singapore: World Scientific; 1992. [Google Scholar]
- 15.Sakharov A D. Sov Phys Doklady. 1968;12:1040–1041. [Google Scholar]
- 16.Zeldovich Ya B. JETP Lett. 1967;6:345–347. [Google Scholar]
- 17.Mannheim, P. D. (1998) Phys. Rev. DPart. Fields58, 103511, 1–12.
- 18.Edery A, Paranjape M B. Phys Rev D Part Fields. 1998;58:024011. , 1–8. [Google Scholar]
- 19.Abrikosov A A. Phys Rev B Condens Matter. 1998;58:2788–2794. [Google Scholar]
- 20.Adler S. Phys Rev. 1969;177:2426–2438. [Google Scholar]
- 21.Bell J S, Jackiw R. Nuovo Cim A. 1969;60:47–61. [Google Scholar]
- 22.Bevan T D C, Manninen A J, Cook J B, Hook J R, Hall H E, Vachaspati T, Volovik G E. Nature (London) 1997;386:689–692. [Google Scholar]
- 23.Volovik G E. Physica B. 1998;255:86–107. [Google Scholar]
- 24.Trodden, M. (1999) Rev. Mod. Phys., in press, e-Print Archive: hep-ph/9803479.
- 25.Jacobson T A, Volovik G E. Phys Rev D Part Fields. 1998;58:064021. , 1–7. [Google Scholar]
- 26.Jacobson T A, Volovik G E. JETP Lett. 1998;68:874–880. [Google Scholar]
- 27.Calogeracos A, Volovik G E. JETP Lett. 1999;69:281–287. [Google Scholar]
- 28.Ding H, Norman M R, Campuzano J C, Randeira M, Bellman A F, Yokoya T, Takahashi T, Mochiku T, Kadowaki K. Phys Rev B Condens Matter. 1996;54:R9678–R9681. doi: 10.1103/physrevb.54.r9678. [DOI] [PubMed] [Google Scholar]
- 29.Volovik G E. Tr J Phys. 1996;20:693–713. [Google Scholar]
- 30.Revaz B, Genoud J-Y, Junod A, Meumaier K, Erb A, Walker E. Phys Rev Lett. 1998;80:3364–3367. [Google Scholar]
- 31.Volovik G E, Gor‘kov L P. Sov Phys JETP. 1985;61:843–854. [Google Scholar]
- 32.Pokrovsky S V, Pokrovsky V L. Phys Rev Lett. 1995;75:1150–1153. doi: 10.1103/PhysRevLett.75.1150. [DOI] [PubMed] [Google Scholar]
- 33.Sun Y, Maki K. Europhys Lett. 1995;32:355–359. [Google Scholar]
- 34.Nersesyan A A, Tsvelik A M, Wenger F. Phys Rev Lett. 1994;72:2628–2631. doi: 10.1103/PhysRevLett.72.2628. [DOI] [PubMed] [Google Scholar]
- 35.Lee P. Phys Rev Lett. 1993;71:1887–1890. doi: 10.1103/PhysRevLett.71.1887. [DOI] [PubMed] [Google Scholar]
- 36.Hu, B. L. (1999) Int. J. Theor. Phys., in press, e-Print Archive: gr-qc/9902064, gr-qc/9607070.
- 37.Chadha S, Nielsen H B. Nucl Phys B. 1983;217:125–144. [Google Scholar]
- 38.Glashow S L, Halprin A, Krastev P I, Leung C N, Pantaleone J. Phys Rev. 1997;56:2433–2434. [Google Scholar]
- 39.Colladay D, Kostelecky V A. Phys Rev D Part Fields. 1998;58:116002. doi: 10.1103/physrevd.52.6224. , 1–23. [DOI] [PubMed] [Google Scholar]
- 40.Martin C P, Gracia-Bondia J M, Vrilly J S. Phys Rep. 1998;294:363–406. [Google Scholar]
- 41.Sogami I S. Prog Theor Phys. 1995;94:117–123. [Google Scholar]
- 42.Sogami I S. Prog Theor Phys. 1996;95:637–655. [Google Scholar]
- 43.Volovik G E, Vachaspati T. Int J Mod Phys B. 1996;10:471–521. [Google Scholar]