Cancellous bone lamellae strongly affect microcrack propagation and apparent mechanical properties: Separation of patients with osteoporotic fracture from normal controls using a 2D nonlinear finite element method (biomechanical stereology)

Abstract

Biomechanical stereology is proposed as a two-dimensional (2D) finite element (FE) method to estimate the ability of bone tissue to sustain damage and to separate patients with osteoporotic fracture from normal controls. Briefly, 2D nonlinear compact tension FE models were created from quantitative back scattered electron images taken of iliac crest bone specimens collected from the individuals with or without osteoporotic fracture history. The effects of bone mineral microstructure on predicted bone fracture toughness and microcrack propagation were examined. The 2D FE models were used as surrogates for the real bone tissues. The calculated microcrack propagation results and bone mechanical properties were examined as surrogates for measurements from mechanical testing of actual specimens. The results for the 2D FE simulation separated patients with osteoporotic fracture from normal controls even though only the variability in tissue mineral microstructure was used to build the models. The models were deliberately created to ignore all differences in mean mineralization. Hence, the current results support the following hypotheses: (1) that material heterogeneity is important to the separation of patients with osteoporotic fracture from normal controls and; and (2) that 2D nonlinear finite element modeling can produce surrogate mechanical parameters that separate patients with fracture from normal controls.

Introduction

At the ultrastructural level, where collagen molecules interface with mineral plates, bone is approximately a “two-phase” material [1, 2]. The distribution of mineral plates within and upon collagen fibrils very strongly determines the mechanical properties and affects microcrack propagation. Bone mineralization heterogeneity arises from the smallest level of bone structure. When bone is formed, collagenous matrix is laid down in lamellae [3] that, at least after mineralization, have differing stiffness, hardness and yield strength [4-8]. Back scattered electron microscopy (BSEM), Fourier-transformed infrared spectroscopy (FTIP) and energy dispersive X-ray (EDX) spectrometry have all been used to quantify the mineral ultrastructure of bone tissue from both human and rat [9-12]. These studies demonstrated that the details of bone mineral content and tissue material properties change during osteoporosis [11, 13, 14] which suggests that tissue mechanical properties are also changed during osteoporosis.

The microanatomy of bone lamellae is still not clear. Some researchers suggest that adjacent lamellae have roughly the same structure, but that the layers of collagen are aligned in different orientations [15]. An alternative model is that lamellae alternate between being collagen rich (dense or thin lamellae) and collagen poor (loose or thick lamellae) to create the visual appearance of lamellae [16, 17]. The measured values of the calcium and phosphorus in the collagen-poor layers (loose lamellae) was 10-15% higher than in collagen-rich layers (dense lamellae) [17]. The dense lamellae apparently have a lower wear resistance because they are more rapidly removed during polishing than were loose lamellae [18]. In the present work we are not directly examining collagen ultrastructure, but have the goal of modeling possible effects of any differences in mechanical properties between individuals caused by differences in mineral distribution. It is possible that differences between individuals in mineral distribution are caused by differences in matrix ultrastructure, but we are not considering this in the current study.

Damage in bone, as in the form of microcracks, is associated with a reduction in the mechanical properties of bone [19-21] and with increasing in bone remodeling activation [22, 23]. Microcracks accumulate in vivo with aging [19] and increase in some animal models after bisphosphonate treatment [24-26]. Bone lamellar ultrastructure greatly influences the ability of microcracks to initiate and propagate [20, 21, 27-29]. Damage due to mechanical loading can preferentially accumulate in the “thick” lamellae [30]. Microcracks might form within single lamellae, but the probability of propagating a large detrimental crack is limited by the ultrastructure of remodeling packets [31-33]. The cement line interface that bounds a region of remodeled bone has a lower mineralization than the remaining tissue, which results in a relatively ductile interface [34], and can reduce strain energy and slow crack propagation [35]. Although bone lamellar ultrastructure can slow microcrack propagation, a large crack (or detrimental crack) can still propagate through regions saturated with microcracks [36]. Despite these observations, it is not clear how the distribution of mineral and collagen determines mechanical properties and affects microcrack propagation. Development of a method to determine how a patient's bone tissue dissipates bone damage and controls microcrack propagation could be a useful tool in separating persons who have a high fracture risk from those who do not.

A two dimensional method for estimating damage tolerance: Biomechanical Stereology

Bone intrinsically has a three-dimensional (3D) structure, but due to difficulties in measuring and comparing 3D properties, 2D quantitative measurements of bone structure (also known as histomorphometric measurements) are widely used in bone research [37-42]. Mechanical testing of bone requires large efforts to prepare bone specimens and tremendous time to manually count microcracks [21]. Hence, a simple method is necessary to understand damage accumulation in bone and its effect on bone mechanical properties and fracture risk.

The finite element (FE) method provides a means to mimic bone damage behavior using computational tools. Synchrotron X-ray computed tomography (CT) can generate 3D images with spatial resolutions approaching 1 μm and better. Synchrotron images may be a sufficient data source to build a 3D finite element model for studying lamellar ultrastructure and predicting lamellar microdamage [43]. Unfortunately, such data are not widely available. We sought to develop a predictive method based on high resolution 2D images.

In this study, we present a two-dimensional finite element method to study the ability of cancellous bone tissue to sustain damage and to separate the specimens of patients with osteoporotic fracture from normal controls. We call the process biomechanical stereology (the detailed definition is in the METHODS section). The following hypotheses were tested: Hypothesis 1: Bone samples from patients with or without osteoporotic fracture history have different mineralization patterns, fracture toughness and microcrack propagation; Hypothesis 2: The fracture toughness and microcrack propagation results from biomechanical stereology measurement can separate the specimens of patients with osteoporotic fractures from normal controls.

Materials and Methods

Two-dimensional nonlinear compact tension finite element models were created from quantitative back scattered electron density images taken of iliac crest bone samples collected from individuals with or without osteoporotic fracture history. The effects of bone mineral ultrastructure on predicted bone fracture toughness and microcrack propagation were examined. Results of biomechanical stereology were used to separate the specimens of individuals with or without osteoporotic fracture history.

Definition of Biomechanical Stereology

Stereology was originally defined as “the spatial interpretation of sections” [44, 45]. It provides practical techniques for extracting quantitative information about a 3D material from measurements made on 2D planar sections of the material. Stereology is based on fundamental principles of geometry and statistics. Biomechanical stereology in our study is a new means to interpret 3D bone mechanical properties and microcrack propagation using 2D nonlinear FE models built from quantitative back scattered electron (qBSE) images of bone tissue. The specific FE model in our study mimicked a standard compact tension specimen.

Bone specimens and FE models

In total, 169 FE models were built for 47 human iliac crest cancellous bone specimens (Fig. 1a) [46, 47]. One to five FE models were built for each bone specimen. Transiliac bone biopsies, which were collected from white females, were in the control group of a subset of biopsies from a previous sodium fluoride treatment study. The transiliac bone biopsies were obtained, processed, stained, sectioned, and examined as described in the previous studies [47-49]. Briefly, the cylindrical bone biopsies were fixed in 70% ethanol, prestained using the Villanueva method, and embedded in polymethyl methacrylate [50]. The embedded blocks were cut to have bone exposed. Bone mineralization of the biopsies was studied in another previously published study [46]. The cut surfaces of the bone biopsy blocks were polished with successively finer grades of carborundum paper and polishing powders, sputter-coated with gold palladium in groups of four specimens along with the calibration standard, and scanned at 300× using an electron microscope (EM) at 30-kV excitation voltage. (The calibration standard was polished free of coating between specimen groups and was recoated with each to ensure uniform coating on the specimens and the standard to reduce artifacts caused by the coating thickness.) Twenty specimens were categorized into the fracture group (FRAC) by the donors' vertebral osteoporotic fracture history, while the other 27 were in the normal healthy group (NORM). Those in the fracture group had at least one compression fracture with loss of posterior vertebral height, or at least two non-contiguous wedge fractures. Bone formation rate per bone surface (BFR/BS) was also used to segregate the specimens with a threshold of 15 μm³/μm²/year. Twenty four specimens were above the cutoff (high BFR/BS group), while the other 23 specimens were in the low BFR/BS group.

Figure 1.

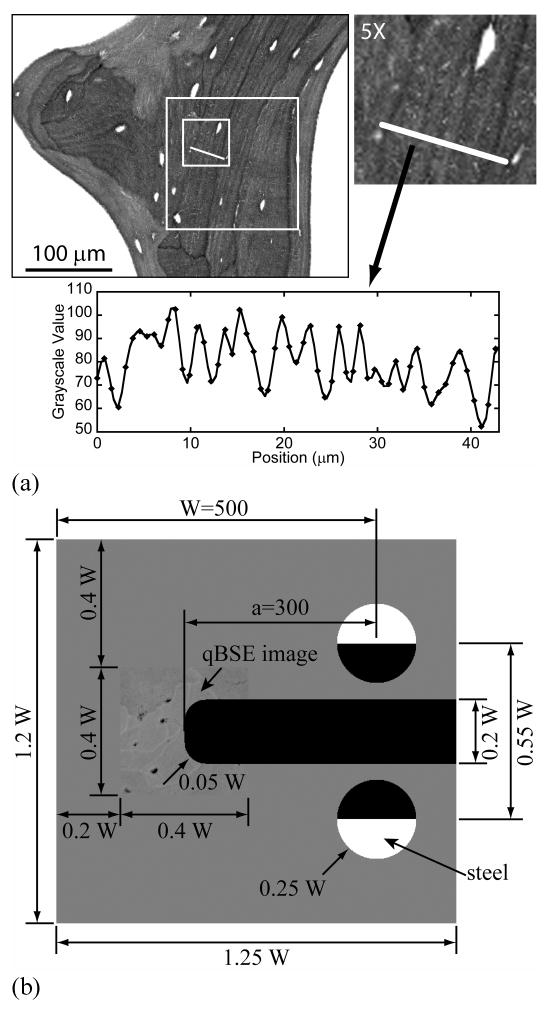
(a) A 200×200 pixel region (white box) was cut from a qBSE image of human iliac cancellous bone. The distribution of bone mineral as grayscale values is plotted below. (b) A compact tension specimen finite element model was used in biomechanical stereology. Dimensions of the compact tension FE model were plotted. Cancellous bone qBSE image was used to replace the tip regions. The unit of the image is pixel, while each pixel is equals to 0.756 mm in the finite element model.

A finite element model was built of a compact tension specimen based upon the design of Norman et al [51] with a/W=0.6 and W=500 (Fig. 1b). A 200×200 pixels (0.4W×0.4W or 200×200 pixel) qBSE 8-bit grayscale image (grayscale value: 0-255), collected from an iliac crest biopsy cancellous bone specimen [46], was placed in the notch root region before the notch was cut. The orientation of the notch was randomly selected. A single layer of 8 node brick elements was used to build the models and plane strain conditions were created by constraining all of the element nodes to planar motion. All the elements were identical in shape and dimension, which was a cube with edge length of 0.756 μ m. Loading was applied as a displacement at the midpoint of the flat faces of two semicircular steel loading pins (E=200 GPa, ν=0.3). The finite element equations were solved using the preconditioned conjugate gradient method with a convergence ratio of 1×10^-10 on the magnitude of the residual force ratio. In the region of the compact tension specimen surrounding the notch tip, where the bone qBSE image was placed, the bone element material modulus was set proportional to the naturally occurring pattern of bone tissue mineral density measured using qBSE from the iliac crest biopsies [46]. Material properties were set by assigning the mean grayscale value to 10.0 GPa and linearly interpolating the material properties as:

$$\text{E}=0.54282\times (\text{GV}-\text{mean}(\text{GV}))+10.0\text{GPa},$$ (1)

where GV is grayscale value of each pixel. Reported bone tissue moduli are roughly in the range from 5 to 25 GPa [7, 52]. An average modulus of 10 GPa was chosen to correspond to the mean grayscale value. By using the calculated modulus values from Eqn. 1, the moduli of all bone tissue in the models were in the literature range of modulus. In the figures, the dark gray maps to the smaller moduli and white to the larger. The material moduli of all peripheral elements were also set to 10.0 GPa. Hence, the grayscale value standard deviation (GVSD) of the qBSE image was the simplest parameter to represent bone mineral structural information.

A principal tensile strain of 0.005 was set to be the tissue failure criterion [53]. When the principal strain of one element reached the failure criterion, the element was marked as “failed” and the bone material modulus in the element was set to a fixed failed element material modulus (residual modulus, or E_R), which was chosen as 500 MPa for this study. For all elements, Poisson's ratio was set to 0.3 before and after failure. Each compact tension specimen model was loaded until 100 elements failed. The finite element program automatically creates a list of the failed elements with their coordinates and failure sequence for each model. A reverse rainbow color scale (violet earliest and red latest) represents the load line displacement at which a material element failed (Fig. 3). The nonlinear finite element codes were written in C++ (Microsoft Corporation, Redmond, WA), used a message passing interface protocol (MP-MPICH, University of Aachen, http://www.lfbs.rwth-aachen.de/) and ran on an specially built eight node BEOWULF architecture computer with 2.8 GHz Pentium 4 processors (Intel Corporation, Santa Clara, CA) and 16 GB main memory under Windows XP (Microsoft Corporation, Redmond, WA). The size of the models was chosen so that it took 4-5 hours to complete calculations for 100 failed elements. The total calculation time was approximately 700-900 hours for the 169 models, not counting post-processing or the “turnaround” time between the model runs.

Figure 3.

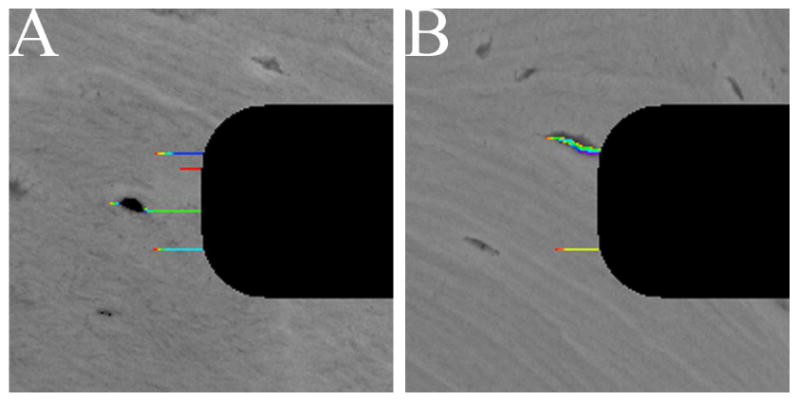
Representative microcrack propagation in the notch root regions in the specimens from the fracture group (A) and the normal group (B). The black pixels are the opened notch.

Microcrack propagation

Microcracks were identified using the list of damaged elements and custom written MATLAB codes (MATLAB 7.0, The MathWorks, Inc., Natick, MA). The MATLAB codes identified each microcrack, and its length and area. Crack number (Cr.N) was measured for each model. Crack area was calculated by multiplying the number of damaged elements in each microcrack with the area of each element, 0.571 μm². The farthest two ends of each crack were identified and the distance between the two ends was calculated as crack length. After mean crack area (Cr.Ar) and crack length (Cr.Le) were calculated within each FE model, the Cr.N, Cr.Le, and Cr.Ar from the same bone specimen were averaged within the specimen before further analysis.

Mechanical results

Deflection (D), force (F), stiffness (S) and compliance (C) of the compact tension specimen were calculated and recorded when each element failed during microcrack propagation (Table 1). The relationships between deflection, force, stiffness and compliance were

Table 1. Definitions of mechanical results.

Term		Explanation	Unit
Deflection	First	Deflection when the first element failed	mm
	Last	Deflection when the last element failed
	Minimum	Minimum deflection
	Maximum	Maximum deflection
Deflection change rate†		Deflection increase rate per unit damage (or per failed element)
Force	First	Force when the first element failed	N
	Last	Force when the last element failed
	Minimum	Minimum force
	Maximum	Maximum force
Force change rate		Force increase rate per unit damage (or per failed element)
Stiffness	First	Stiffness when the first element failed	N/mm
	Last	Stiffness when the last element failed
	Minimum	Minimum stiffness
	Maximum	Maximum stiffness
Stiffness change rate		Stiffness decrease rate per unit damage (or per failed element)
Compliance	First	Compliance when the first element failed	mm/N
	Last	Compliance when the last element failed
	Minimum	Minimum compliance
	Maximum	Maximum compliance
Compliance change rate		Compliance increase rate per unit damage (or per failed element)

^†Deflection change rate was calculated as the slope of the linear regression between deflection and numbers of failed elements. Change rate of force, stiffness and compliance were calculated similarly.

$$\text{S}=1/\text{C}=\text{F}/\text{D},$$ (2)

where S is stiffness, C is compliance, F is force and D is deflection. All the mechanical property results from the same bone specimen were averaged within the specimen before further analysis.

Since the FE simulation stopped after 100 elements failed, which is not comparable to real mechanical testing, the last deflection, force, stiffness and compliance (also the corresponding maximum deflection, maximum force, minimum stiffness and maximum compliance) were not meaningful. In all FE simulations, first deflection and compliance were equal to minimum deflection and compliance, respectively. First stiffness was always equal to maximum stiffness, therefore, first compliance was the smallest. Minimum force was proportional to the first force in all FE models (Minimum force = 0.9642×First Force+4.25×10^-6, p<0.0001, r²=0.9997). Hence, first deflection, force, stiffness and compliance were used as the important apparent mechanical properties of the compact tension model. As additional motivation for the use of these “first” values, first deflection, force, stiffness and compliance were recorded immediately after the first element failed, which is at the transition of mechanical properties of the bone specimen from elastic to inelastic behavior.

For each FE model, the rates of change in deflection, force, stiffness, and compliance with increasing number of failed elements were calculated using linear regression (Fig. 2). The slopes of the regression lines are the sensitivity of the mechanical properties to accumulated damage. The sensitivities of the different mechanical properties were examined between the study groups.

Figure 2.

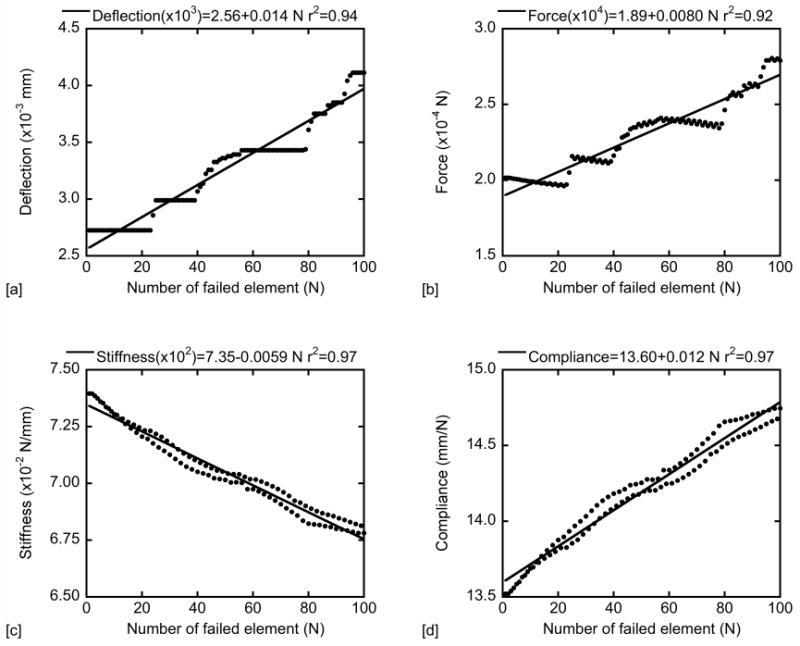
Linear regression between deflection, force, stiffness and compliance and the number of failed elements. The change rates of deflection, force, stiffness and compliance were obtained from the slopes of the linear regressions.

Statistics

Analysis of variance (ANOVA) was used to compare Cr.N, Cr.Ar and Cr.Le between the fracture and normal groups, and between the high and low BFR/BS groups (JMP 6.0, Cary, NC). Linear regression was used to study the relationship between microcrack morphometric results (Cr.N, Cr.Le and Cr.Ar) and bone mineral ultrastructure (GVSD), within all specimens, in the fracture and normal groups, and in the high and low BFR/BS groups, respectively. Mechanical results were pooled and compared between the fracture and normal groups, and between the high and low BFR/BS groups using ANOVA, respectively. The relationship between mechanical results and GVSD were also studied for all specimens using linear regression.

If statistically significant differences in the microcrack morphometric results or mechanical results were observed between groups, logistic regression and examination of receiver operating characteristic (ROC) curves were employed to identify the ability of the microcrack morphometric and mechanical results to separate the groups, for example, separating the patients with osteoporotic fracture from normal controls as a function of first stiffness. Note that ROC analysis was used as an exploratory method and that all statistical results are reported based on ANOVA or regression analysis. A ROC curve is a graphical plot of the sensitivity (True Positive) vs. (1-specificity) (False Negative) for a binary classifier system. With a ROC curve, a threshold value can be determined to optimally separate groups [54]. The ROC curve shows how well a parameter separates groups. The area under ROC curve (AUC) is the probability of separating the one group from the other [55]. The ability of separating two groups is considered perfect if AUC = 1, excellent if AUC>0.9, good if AUC is from 0.8 to 0.9, moderate if AUC is 0.6 to 0.8, and poor if AUC <0.6 [56, 57].

Results

Bone mineral ultrastructure

Bone mineralization distribution was different between the fracture and normal groups and between the high and low BFR/BS groups. The grayscale value standard deviation of bone mineral ultrastructure in the fracture group (6.64±0.46) was higher than that in the normal group (5.95±0.84) (p=0.0019, ANOVA, Table 2). GVSD in the high BFR/BS group (6.48±0.59) was also higher than in the low BFR/BS group (6.01±0.89) (p=0.036).

Table 2. Statistical analyses of microcrack morphometric results between groups.

Property	ANOVA				Logistic Regression (separate FRAC from NORM)
	NORM	FRAC	p-value	% difference compared to NORM	r2	p-value	AUC†
GVSD	5.95±0.84	6.64±0.46	0.0019	11.6	0.14	0.0024	0.72
Cr.N	4.45±0.71	5.33±0.84	0.0003	19.8	0.20	0.0003	0.79
Cr.Le (μm)	23.03±2.69	19.15±3.04	<0.0001	-16.8	0.26	<0.0001	0.83
Cr.Ar (μm2)	24.09±3.02	20.27±2.64	<0.0001	-15.9	0.27	<0.0001	0.83

^†AUC is the area under ROC curve, with a maximum value of 1.

Microcrack propagation

Predicted Cr.N was higher in the fracture group than in the normal group (p=0.0003, Table 2). Cr.Le and Cr.Ar were lower in the fracture group than in the normal group, respectively (p<0.0001). No difference in the standard deviation of Cr.Le or Cr.Ar was observed between the fracture and normal groups (p>0.79 and p>0.90). No difference in Cr.N, Cr.Le, or Cr.Ar was observed between the high and low BFR/BS group (p=0.13, p=0.12, and p=0.10).

Linear correlations were observed between Cr.N, Cr.Le, Cr.Ar and bone mineral ultrastructure (GVSD), within all specimens, in the normal group, and in the low BFR/BS group, respectively, but not in the fracture group or in the high BFR/BS group, except a positive linear correlation between Cr.N and GVSD in the high BFR/BS group (Table 3). Bone specimens with higher GVSD tended to initiate more but smaller microcracks (higher Cr.N, but lower Cr.Le and Cr.Ar). The linear correlations between Cr.N and GVSD in the high and low BFR/BS groups were not different (p=0.64, ANCOVA).

Table 3. Relationships between microcrack morphometric results and bone mineral microstructure.

Group	Cr.N vs. GVSD†	Cr.Le vs. GVSD	Cr.Ar vs. GVSD
All (N=47)	(+) p<0.0001 r2=0.36	(-) p<0.0001 r2=0.36	(-) p<0.0001 r2=0.30
FRAC (N=20)	p=0.49	p=0.50	p=0.43
NORM (N=27)	(+) p<0.0001 r2=0.48	(-) p=0.0002 r2=0.42	(-) p=0.0081 r2=0.25
High BFR/BS (N=24)	(+) p=0.034 r2=0.19	p=0.052	p=0.15
Low BFR/BS (N=23)	(+) p=0.0006 r2=0.44	(-) p=0.0004 r2=0.46	(-) p=0.0012 r2=0.40

^†(+) indicates a positive linear correlation, while (-) indicates a negative linear correlation.

Mechanical results

The rates of change in deflection, force and compliance were positive as a function of damage, while the rate of change in stiffness with damage was negative (p<0.05, Fig. 2). Significant differences were observed in FE predicted mechanical property results between the fracture and normal groups (p<0.01) (Table 4 & 5). First deflection and force right after initiation of damage were both lower in the fracture group (p<0.006) compared to those in the normal group. No significant difference was observed in any mechanical property result between the high and low BFR/BS group (p>0.05).

Table 4. Comparison of mechanical results between the fracture and normal groups.

Property†	ANOVA				Logistic Regression (separate FRAC from NORM)
	NORM	FRAC	p-value %	difference compared to NORM	r2	p-value	AUC‡
First Deflection (×10-3)	2.64±0.29	2.38±0.32	0.0064	-9.8	0.12	0.0059	0.77
First Force (×10-4)	1.96±0.22	1.77±0.24	0.0057	-9.7	0.12	0.0053	0.77
First Stiffness (×10-2)	7.44±0.05	7.40±0.05	0.0085	-0.5	0.12	0.0066	0.82
First Compliance	13.45±0.08	13.52±0.10	0.0093	0.5	0.11	0.0072	0.82

^†The real values of the mechanical results are the value in the following boxes multiplying 10^-3 or the other.

^‡AUC is the area under ROC curve, with a maximum value of 1.

Table 5. Comparison of change rates of mechanical properties between the fracture and normal groups.

Property†	ANOVA				Logistic Regression (separate FRAC from NORM)
	NORM	FRAC	p-value	% difference compared to NORM	r2	p-value	AUC‡
Deflection change rate (×10-5)	1.80±0.17	1.80±0.01	0.73	-	-	-	-
Force change rate (×10-7)	1.10±1.08	1.10±0.62	0.90	-	-	-	-
Stiffness change rate (×10-5)	-0.50±0.23	-0.60±0.35	0.0025	20	0.14	0.0023	0.75
Compliance change rate (×10-2)	1.06±0.07	1.13±0.09	0.0029	6.6	0.14	0.0028	0.75

^†The real values of the mechanical results are the value in the following boxes multiplying 10^-3 or the other.

^‡AUC is the area under ROC curve, with a maximum value of 1.

-indicates no logistic regression analysis due to no significant difference between the two groups.

The rate of change in deflection or force as a function of damage was not different between the fracture and normal groups (p>0.05, Table 5). The stiffness decrease rate per unit damage was higher in the fracture group (p=0.0025, Table 5). Linear correlations between the mechanical property results and bone mineral ultrastructure were observed, except for no correlation between force change rate and GVSD (Table 6). The first deflection, force and stiffness right after initiation of damage decreased with increasing GVSD. First stiffness also decreased with increasing GVSD.

Table 6. Relationship between mechanical results and bone mineral microstructure for all specimens.

Property vs. GVSD†	p-value	Intercept	Slope	r2
First Deflection	<0.0001	0.0040	-0.00023	0.33
Deflection change rate	0.012	0.000014	0.00000063	0.13
First Force	<0.0001	0.00030	-0.000018	0.33
Force change rate	0.056	-	-	-
First Stiffness	0.0001	0.076	-0.00033	0.28
Stiffness change rate	0.0001	-0.000042	-0.000002	0.28
First Compliance	0.0001	13.09	0.062	0.28
Compliance change rate	<0.0001	0.0074	0.00057	0.31

^†If no significant linear regression existed (p>0.05), intercept, slope or r² were not reported.

-indicates no linear correlation exists.

Logistic regression and ROC Curves

Logistic regression results were able to separate the specimens of the fracture group from those from the normal group, which in turn can be used to separate patients with osteoporotic fracture from normal controls (Table 2, 4 and 5). Both bone mineral ultrastructure (GVSD) and the microcrack morphometric results strongly separated the specimens of the fracture group from those of the normal group (p<0.002, Table 2). The AUC, indicating the probability of separating two groups, were 0.72 for GVSD and from 0.79 to 0.83 for the microcrack morphometric results, which indicated a fairly good chance of separating the two groups.

Statistically significant differences in the mechanical results (first deflection, force, stiffness and compliance) were also observed between the fracture and normal groups. The corresponding logistic regression results were significant (p<0.001, Table 4) and the AUC were from 0.77 to 0.82. Only the change rates of stiffness and compliance were different between the fracture and normal groups, and could be used to separate the two groups, both with an AUC of 0.75 (p<0.05, Table 5).

Discussion

Stereology is a methodology to extract quantitative information about a 3D material using 2D sections of the material [44, 45]. In this study, the new technique named biomechanical stereology was developed. The method used 2D nonlinear FE simulation results to probe 3D bone tissue mechanical properties and microcrack propagation behaviors. In the current study, we used high resolution qBSE images of human iliac cancellous bone as 2D surrogates of 3D bone tissue mineral ultrastructure. Not only the direct measurement of bone mineral ultrastructure (GSVD) but the computational microcrack propagation results and mechanical properties were different between the fracture and normal groups, which sustained our first hypothesis. Further study showed that both the measurement of bone mineral ultrastructure and the computational microcrack propagation results and mechanical properties separated the specimens of patients with osteoporotic fracture from normal controls. The AUC of the logistic regression for GVSD, microcrack morphometric results and mechanical property results were from 0.72-0.83, which indicates fairly good probability for separating patients with osteoporotic fracture from normal controls, hence the second hypothesis was sustained.

The ability of biomechanical stereology to separate patients with osteoporotic fracture from normal controls makes it a potential beginning for a new biomechanically based method to predict osteoporotic fracture risk. The method depends upon imaging a small section bone tissue from a biopsy suggesting that fracture risk overall might be related to differences in mineral patterning in the small scale. Additional research on this issue is necessary before any final conclusions can be made, however. The only difference in tissue morphology introduced into the FE models was the location and variability of the pixel grayscale. We set the average grayscale value (and Young's modulus) to be the same for all of the models. The relatively small differences in bone mineral ultrastructure yielded a big difference in both bone mechanical properties and microcrack propagation results in the 2D FE simulations. In actual tissue, bone tissue ultrastructure greatly influences the ability of microcracks to initiate and propagate [20, 21, 27-29]. In the models, more but smaller microcracks initiated within the bone specimens from the patients with osteoporotic fracture. If we applied the same force to the two groups of specimens, more microcracks (or more total failed elements) should initiate in the specimens in from the fracture group. The greater sensitivity of the fracture group tissue suggests a positive feedback loop where damage would accumulate more rapidly than in normal controls. Force controlled finite element simulations (as opposed to our currently used displacement controlled simulations) could demonstrate this effect pictorially and quantitatively. Such simulations could be performed at a later time, but are not within the scope of the current study. In the finite element models, the first deflection, force, stiffness and compliance revealed the transition of the mechanical properties from elastic to inelastic deformation. Higher first deflection, force and stiffness (also lower compliance) in the normal group indicated that bone tissue was stronger in the normal specimens. The negative linear correlations between first deflection, force, stiffness and GVSD (also the positive linear correlation between first compliance and GVSD) indicate that bone mineral ultrastructure is an important factor affecting bone mechanical property results.

The rates of mechanical property change with damage were quite interesting. In particular, stiffness decreased faster with accumulated damage in the fracture group. This is really quite interesting since decrease in modulus is often used as the measure of mechanical damage in a material. Thus, damage measured as stiffness loss increased more rapidly in the specimens of patients with osteoporotic fracture than in normal controls. That morphological damage (i.e., microcracks) predicts more modulus damage for the specimens of patients with osteoporotic fracture than normal controls is a partial explanation for why measurements of in vivo microcracks are not always good predictors of mechanical properties [58].

Biomechanical stereology uses 2D FE models to estimate the relative capability of bone tissue to sustain damage and to thereby separate the specimens of patients with osteoporotic fracture from normal controls. One of the advantages of the technique of stereology is that only a small number of inputs are required. Only grayscale qBSE images of the bone mineral ultrastructure were required to build the FE models. In the current study, a compact tension FE model was mimicked, in which bone tissue is mainly under tensional load. FE models of other geometric profiles, such as shear specimens, could be used.

There are some limitations to be considered when interpreting the current results. Grayscale value standard deviation of a 2D grayscale qBSE image is the simplest parameter to represent bone mineral ultrastructure. The real bone mineral ultrastructure is not revealed only by GVSD, however. Differences in bone specimen surface height following their polishing procedures might induce variation in grayscale values during qBSE measurement. However, in a pilot experiment we compared backscatter of diamond micro-milled to polished specimens, and saw the same mineralization “ripples” so we interpreted the rippling as a mineralization effect because milling makes a much flatter specimen. Hence, we believed the results of the current study resulted from bone tissue mineral differences.

The correlations between mechanical properties, microcrack propagation results and bone mineral ultrastructure were significant but weak, so it is not enough to use only GVSD to predict mechanical property results. More parameters or more complex parameter sets representing the ultrastructure might be better able to predict the mechanical results. Further, the equation used in this study to convert grayscale value to bone tissue modulus was empirical and arbitrary, and could be improved by measuring the relationship between nano-level bone tissue modulus and bone mineralization by combining nanoindentation and qBSE techniques. With the relationship between bone tissue modulus and mineralization, biomechanical stereology should be able to provide a better prediction of mechanical property and microcrack propagation results.

In summary, two-dimensional compact tension FE models were built using qBSE bone density grayscale images in the notch root. The 2D FE models were used as surrogates for 3D bone tissue properties, such as bone damage behavior, microcrack propagation and bone mechanical properties. One key point of the current study was that the 2D FE results separated the specimens of patients with osteoporotic fracture from normal controls. The models were deliberately created to ignore all differences in mean mineralization. Hence, the current results clearly support the hypothesis that material heterogeneity and resulting differences in mechanical properties are important to the separation of patients with osteoporotic fracture from normal controls.

Figure 4.

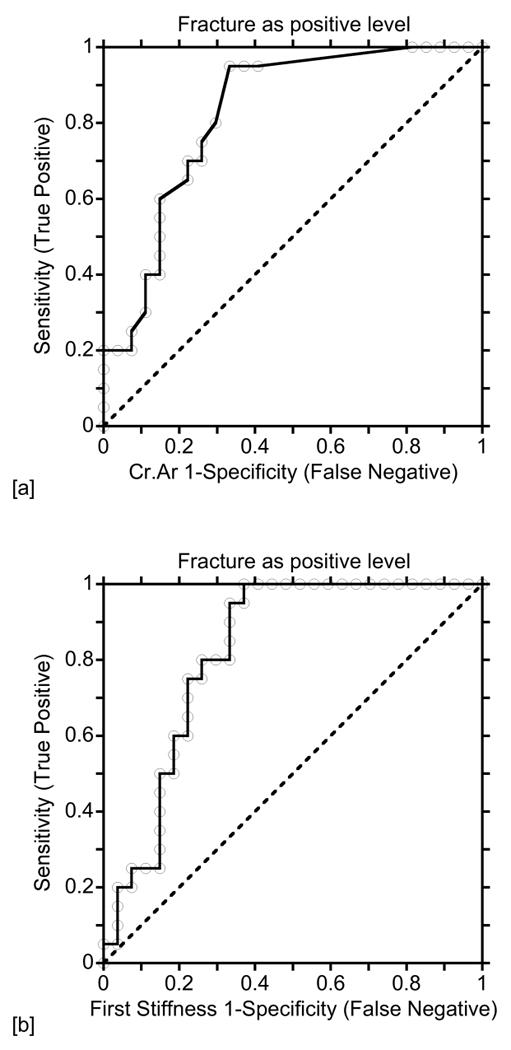
A receiver operating characteristic (ROC) curve is a graphical plot of the sensitivity (True Positive) vs. (1-specificity) (False Negative) for a binary classifier system as its discrimination threshold is varied. (a) Crack area was used to separate the specimens of patients with osteoporotic fracture from normal controls. The area under the ROC curve (AUC) was 0.83. (b) The first stiffness was used to separate the specimens of patients with osteoporotic fracture from normal controls. The AUC was 0.82.