Stretching single-domain proteins: Phase diagram and kinetics of force-induced unfolding

Abstract

Single-molecule force spectroscopy reveals unfolding of domains in titin on stretching. We provide a theoretical framework for these experiments by computing the phase diagrams for force-induced unfolding of single-domain proteins using lattice models. The results show that two-state folders (at zero force) unravel cooperatively, whereas stretching of non-two-state folders occurs through intermediates. The stretching rates of individual molecules show great variations reflecting the heterogeneity of force-induced unfolding pathways. The approach to the stretched state occurs in a stepwise “quantized” manner. Unfolding dynamics and forces required to stretch proteins depend sensitively on topology. The unfolding rates increase exponentially with force f till an optimum value, which is determined by the barrier to unfolding when f = 0. A mapping of these results to proteins shows qualitative agreement with force-induced unfolding of Ig-like domains in titin. We show that single-molecule force spectroscopy can be used to map the folding free energy landscape of proteins in the absence of denaturants.

Titin, a giant protein molecule responsible for elasticity of muscles, is comprised of a few hundred Ig and fibronectin-III repeats aligned in tandem (1–3). Recently, through nanomanipulation of single protein molecules, there has been direct evidence for sequential unfolding of individual domains on stretching (4–6). These remarkable experiments and others on DNA (7–9) have made it possible to unearth the microscopic underpinnings of the unusual elastic behavior in biological molecules. In two experiments (4, 5), individual titin molecules were tethered to a plastic bead and optical tweezers were used to stretch the molecule. Direct measurement of the forces required to stretch titin were used to infer that tension leads to unfolding of individual Ig-like domains (4, 5). Perhaps the clearest evidence for domain unraveling was presented by Rief et al. (6), who used atomic force microscopy (AFM) to pull on titin molecules adsorbed onto a gold surface. The AFM experiments, on both the model recombinant titin molecules consisting only of Ig (Ig₄ and Ig₈) domains and the native titin, showed clear sawtooth patterns in the force–extension curves, indicating sequential unfolding of domains. The constant periodicity of the sawtooth pattern (≈25 nm) is nearly coincident with the dimensions of the fully unfolded Ig domain (≈29 nm) and is very similar to the contour length inferred from fitting the force–extension curves obtained from the optical tweezer experiments (4, 5) [see also related experiments on tenascin (10)]. All the experiments conclude that sequential unraveling of the domains results on mechanically stretching titin.

Inspired by these experiments, we report the results of force-induced unfolding of single-domain proteins using simple lattice models that have been useful in the search for general principles of protein folding (11). Because the primary mechanism of stretching titin involves unraveling of individual Ig-like domains, which fold spontaneously in the absence of tension (12, 13), our calculations provide microscopic origins of force-induced unfolding. We show that the response of proteins to force depends primarily on their topology in the absence of force. By computing the phase diagram and kinetics of a number of model proteins subject to tension, we show that the folding free-energy landscape (11, 14) in the absence of force can be deciphered by using single molecule manipulation techniques.

MATERIALS AND METHODS

The polypeptide chain is modeled as a sequence of N connected beads on a cubic lattice. The energy of a conformation (given by the vectors r→_i with i = 1, 2, 3, … N) is

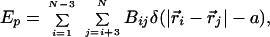1

where δ(x) is the Kronecker delta function, a is the lattice spacing, and B_ij is the contact energy between beads i and j. The set of matrix elements B_ij specifies a sequence. We use two types of contact potentials, the statistical potentials derived by Kolinski, Godzik, and Skolnick (KGS) (15) and the random bond (RB) model (16). The applied force to the terminal beads yields an additional energy

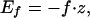2

where z = |r→₁−r→_N| is the extension. Because the polypeptide chain is on lattice, where continuous overall rotations are not possible, we assume that on stretching there is alignment of the protein along the force direction with zero torque. This is equivalent to the assumption that the relaxation time for the overall rotational degrees of freedom is much shorter than that for structural relaxation that is responsible for unfolding or folding processes. Thus we take the absolute value of z to represent the energy caused by stretching. The total energy of the chain conformation is given by the sum of Eqs. 1 and 2. We use dimensionless units for energy whose typical value is in the range (1−2) k_BT; length is measured in units of a (= 0.38 nm), and temperature is measured in units of energy/k_B. For purposes of mapping these to physical values, we use 2k_BT for energy, which means force in our simulations is measured in multiples of about 20 pN.

The thermodynamics as a function of force (f) and temperature (T) is obtained by using a variant of the multiple histogram method (17) in conjunction with standard Metropolis Monte Carlo simulations (18). When f > 0, the collection of histograms at different temperatures and zero force becomes unreliable because highly stretched conformations are almost never sampled. Such states, which have negligible Boltzmann weight in the absence of force, become thermodynamically important on stretching. It proves more convenient to collect histograms at a fixed value of T and at various values of f so that all relevant states across the entire (f, T) plane are adequately sampled.

To characterize the degree of similarity of an arbitrary sequence conformation with the native structure, we use the overlap function (19) defined as

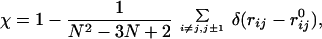3

where r_ij is the distance between the beads i and j, r_i⁰_j is the corresponding distance in the native conformation, and δ(x) is the Kronecker delta function.

The kinetic simulations of force-induced unfolding were performed at a constant temperature T_s (below T_F, the folding temperature) that satisfies the condition <χ(f = 0, T_s)> = 0.15. Starting from the native conformation, the force was suddenly increased to f_s so that at (f_s, T_s), stretched rod-like conformations are stable. The unfolding kinetics is monitored by computing the distribution of stretch times, τ_s,1i, which is the first instance a trajectory i reaches a stretched state with no contacts. Typically M = 800 trajectories have been generated for the calculation of unfolding rate. From the distribution of stretch times, the mean unfolding time and the fraction of folded molecules at time t can be calculated (16). These probes, together with the dynamics of rupture of tertiary contacts and the time dependence of extension, are used to obtain the unfolding pathways. The mean unfolding time is τ_u = 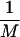 ∑_i=1^M τ_s,1i the inverse of which is taken to be the unfolding rate k_u.

To obtain the general characteristics of force-induced unfolding, we computed the phase diagram and kinetics for five sequences (four 27-mers and one 36-mer) and differing interaction potentials. We chose four 27-mer and one 36-mer sequences, whose thermodynamic and kinetic characteristics in the absence of force are documented elsewhere (16, 20), to investigate unfolding transitions caused by stretching. Three of the 27-mer and 36-mer sequences fold kinetically and thermodynamically by two-state mechanism. These sequences have small values of σ = (T_θ − T_F)/T_θ, where T_θ and T_F are the collapse and folding transition temperatures, respectively, when f = 0 (16, 20). The fourth 27-mer sequence with B_ij given by RB potentials has σ = 0.11, and its folding (thermodynamics and kinetics) reveals intermediates (16). Thus, with these sequences, we can investigate the effect of stretching for protein-like models that display distinct folding mechanisms in the absence of force. For purposes of illustration, we present results for a 36-mer sequence with the KGS potentials (σ ≈ 0) and the 27-mer RB model sequence with σ ≈ 0.11.

RESULTS

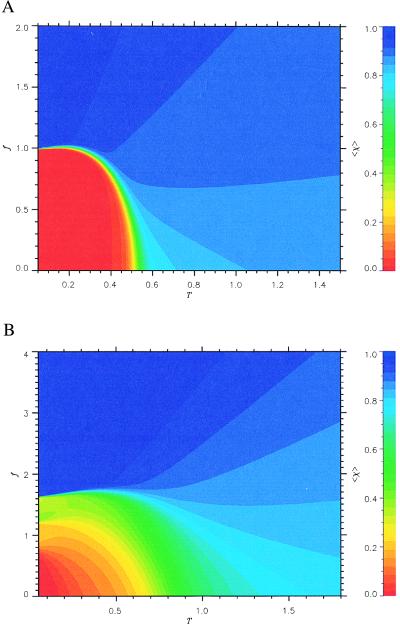
The phase diagram for the 36-mer, which exhibits two-state cooperative thermal unfolding when f = 0, is given in Fig. 1a. The states of the polypeptide chain are represented by the thermal average overlap function <χ(f, T)>, where χ gives the degree of similarity to the native state. In particular, small values of the overlap function correspond to conformations that belong to the native basin of attraction (NBA). The color codes in Fig. 1 are such that red corresponds to small <χ(f, T)> (high native content and folded states), whereas the blue region has large <χ(f, T)>, representing unfolded states. We see from Fig. 1a that the (f, T) plane divides into predominantly red (folded states) and blue (unfolded states) regions. In the red region, the overlap <χ(f, T)> ≲ 0.1, and the probability of being in the NBA is greater than 0.5 (20). In the blue region, <χ(f, T)> is typically greater than 0.8 and the probability of being in the NBA is almost zero. There is only a narrow band of the green region, which suggests that the force-induced unfolding transition for this sequence is an all-or-none process with no signature of intermediates.

Figure 1.

Phase diagrams in the (f, T) plane for (a) the 36-mer two-state KGS sequence and (b) 27-mer moderate folding RB sequence. The color code for <χ(f, T)> is given on the right. The red color corresponds to the states in the NBA, whereas the blue color indicates the unfolded states. Green areas correspond to intermediate partially folded states. For both the sequences the boundary of NBA is given by Eq. 4.

The sharp boundary between folded and unfolded states resembles that of the type I superconductors in the (H, T) plane, where H is the applied magnetic field. With this analogy, the locus of points separating the NBA and the unfolded states is given by

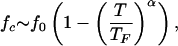4

where f_c is the critical force required to unfold the protein, f₀ is the value of f_c at T = 0, and T_F is the folding transition temperature at zero force. Both f₀ and α depend on the sequence and the native state topology. The fit using Eq. 4 gives f₀ ≃ 0.98 and α ≃ 6.0 for the 36-mer . An independent estimate for f₀ can be made by using  |F₀| ≈ f₀ΔL, where E₀ is the energy of the native state and ΔL is the gain in the end-to-end distance of the polypeptide chain on stretching to a fully extended rod state. For the 36-mer E₀ = −30.4 and ΔL ≈ 30.9 that leads to f₀ ≈ 0.98.

The phase diagram for a sequence whose folding (in the absence of force) involves intermediates is shown in Fig. 1b. Although the general appearance is similar to that shown in Fig. 1a, there are clear differences. The region of stability of the NBA (red region) is confined to low temperatures and small forces. Secondly, the boundary between the folded and unfolded states is fuzzy and contains a broad green region. This suggests that the force- (or temperature)-induced unfolding is likely to be noncooperative involving intermediates. This is reflected in the force–extension curves, which show signatures of intermediates (D.K. and D.T., unpublished observations). In contrast, for two-state folders with σ ≈ 0, the force–extension curves show that at f ≈ f₀, the chain abruptly unfolds to a stretched conformation without populating any detectable intermediates. In fact, the unfolding transition occurs in an extremely narrow interval of force, which for the 36-mer is 0.01f₀ (D.K. and D.T., unpublished observations).

We should point out that the contact interaction energies (or more precisely the potential of mean force) are dependent on temperature. It has been argued that the temperature dependence of contact interactions has to be included to reproduce certain experimental observations in proteins (21). However, we expect the qualitative features of the phase diagrams seen in Fig. 1 will be observed experimentally regardless of the details of the interaction energies.

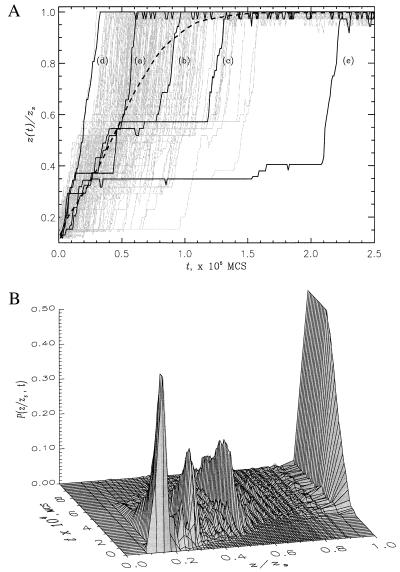
How is the completely stretched conformation kinetically reached starting from the native conformation when f exceeds f_c? For the four sequences with small σ (two-state folders in the absence of force), we find that, when averaged over an ensemble of initial molecules, unfolding occurs in a single kinetic step. However, there is a great variation in the time scales of stretching to the rod-like state. This is dramatically illustrated in Fig. 2a, in which we plot, for the 36-mer, extension z(t) as a function of t measured in Monte Carlo steps. There is a large unexpected heterogeneity in the approach to the stretched state. A striking feature in Fig. 2a is that there is a large variability in the times taken to exhibit significant stretching before reaching the rod-like conformation. Global unraveling takes place cooperatively with the disruption of local and nonlocal contacts occurring in an all-or-none manner. These features are masked in the ensemble average <z(t)>, which is shown as a dashed line in Fig. 2a. There is a remarkable similarity between the response of these protein-like models to force and that exhibited by flexible polymers subject to sudden elongational flow (22). Another interesting feature of the unfolding dynamics is that, just as in experiments, the force–extension curves show hysteresis during the stretch–release cycles (D.K. and D.T., unpublished work).

Figure 2.

(a) The time dependence of extension z(t)/z_s for 201 individual trajectories of 36-mer sequence at T_s = 0.49 and f_s = 4.0. Three generic trajectories [curves (a)−(c)], the fastest (d), and the slowest (e) trajectories are shown in black. The rest are given in grey. The average <z(t)> obtained from 400 individual trajectories is represented by a thick dashed curve. (b) The probability distribution P(z/z_s, t) for 36-mer sequence under the same unfolding conditions as in Fig. 2a. P(z/z_s, t) gives the kinetic probability of occurrence of the extension value z at the time t. In both plots the extension values are normalized by z_s = N − 1.

The time evolution of the distribution of extension values z for 400 trajectories is plotted in Fig. 2b. This plot shows that on time scales less than the mean stretch time, the chain explores a diverse manifold of states each with different z. Certain z values have significantly larger probability P(z, t) than others, which suggests that unfolding occurs in a step-wise quantized manner. Similar observations have been made by using unfolding molecular dynamics simulations of Ig-like domain (23).

Despite the large variability in the stretch times τ_s,1i, the mechanism of approaching the rod-like conformation may be qualitatively described as occurring in roughly three stages. On the time scale ≈(0.1–0.5)τ_s,1i, after the application of a sudden force there is a loss of a number of native contacts. There is a concomitant increase in the extension of the chain z(t)/z_s ≃ (0.1–0.5), where z_s = N − 1. In the second stage, the sequence searches for the equilibrium rod-like conformation. There is great variation in the time scale for this search. This stage is characterized by one or several plateaus in z(t) (see Fig. 2a). Finally, the chain explosively and cooperatively makes a transition to the rod state with z(t)/z_s ≃ 1. Naturally, there are several exceptions to this generic scenario. For example, curve (d) in Fig. 2a shows that z(t) reaches its equilibrium value monotonically in an extremely short time.

The dependence of the unfolding mechanisms on topology is illustrated by computing the dynamical evolution of all the topologically permissible contacts. We describe the results for two 27-mer RB two-state folders labeled A and B (these are the sequences 61 and 63, respectively, in ref. 16). The native state of each sequence is maximally compact. However, the key topological distinction between them is that in the native conformation for A, the terminal beads are on the same facet of the cube, whereas for B they are placed directly on opposite facets. By tracking the time evolution of the loss of the 156 topological contacts, of which 28 are native, we computed the breaking times τ_b^k for contact k. The times τ_b^k are determined by (i/N)(N − j)/N, which measures how close the contact k, formed between beads i and j, is to the sequence ends. For sequence A, we find that the time scales for the rupture of contacts are similar for groups of contacts that are close to one or the other end of the sequence. In contrast, for sequence B the disruption of contacts from the amino terminus (bead 1) occurs fast, whereas the contacts located near the carboxyl terminus break up later in the unfolding process. Thus, topology determines details of the force-induced unfolding pathways. Because in Ig-like domain the amino and carboxyl termini are at opposite ends, we expect that the underlying mechanism by which this domain unfolds may be similar to that for sequence B.

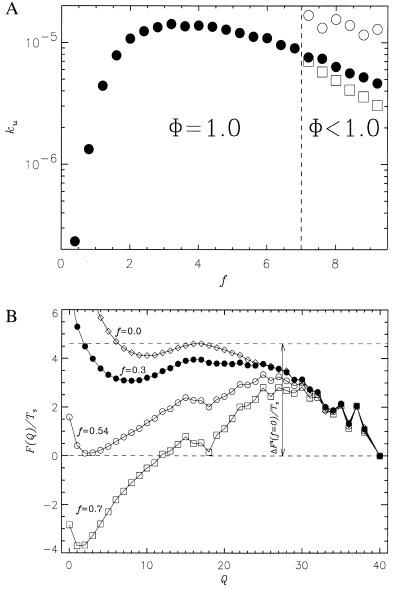
In Fig. 3a, we present the force-induced unfolding rate k_u as a function of f for the 36-mer at T_s = 0.49. Qualitatively similar results were obtained for the 27-mers as well. The unfolding rates were computed from the distribution of stretch times for 800 trajectories. It is expected that k_u should increase with increasing f because the activation- free energy is lowered upon application of force (24, 25). The free energy profiles as a function of the number of native contacts (Q), which is an approximate reaction coordinate for two-state folders (26), are given in Fig. 3b for the 36-mer at various force values. The decrease in the unfolding barrier explains the observed dependence of k_u on f for f < f_opt. The unfolding rate is well described by k_u ≃ k₀exp(fΔx/k_BT) for f < f_opt, which is given by

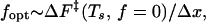5

where ΔF^‡(T_s, f = 0) is the unfolding free energy barrier at T = T_s and zero force, Δx is an approximate width of the unfolding potential, and k₀(T_s) is the unfolding rate in the absence of force. For the 36-mer, ΔF^‡ is 2.26 at T_s = 0.49 (see Fig. 3b), f_opt ≈ 3.2, and therefore Δx ≈ 0.02L, where L is the contour length of the chain. The small value of Δx implies that the transition region is quite narrow. When f ≥ f_opt, the unfolding rate starts to decrease because sudden (corresponding to large pulling speed) application of relatively large forces traps the polypeptide chain in conformations, whose unfolding requires transient shortening of the end-to-end distance. The transition from such conformations, which requires local annealing of the chain, slows down the unfolding process. For f > 7 (see Fig. 3a), there is a free energy barrier associated with the breakup of contacts in the conformations acting as transient kinetic traps. In this force regime, the fraction of molecules that are folded at a time t is best fit using a sum of two exponentials, with the slow phase signaling the onset of local trapping. It should be emphasized that the decrease in unfolding rates at large forces (see Fig. 3a) is expected to depend on the topology of the native state and pulling speeds. In the context of lattice models, it may also be caused by the move sets used in the simulations.

Figure 3.

(a) The dependence of unfolding rate k_u (filled circles) on f for the 36-mer sequence at T_s= 0.49. For values of f less than 7.0, the force-induced unfolding takes place by a two-state process. For f > 7.0, unfolding trajectories separate into a fast pool (the fraction of which is Φ) that reaches the stretch state with the rate 1/τ_s,FAST (open circles) and a slow pool trajectories characterized by the rate 1/τ_s,SLOW (open squares). At these f, the partition factor Φ < 1. (b) The free energy F(Q)/T_s for 36-mer sequence at T_s = 0.49 and f = 0.0 (diamonds), f = 0.3 (full circles), f = 0.54 (open circles), and f = 0.7 (open squares). It is seen that the free energy unfolding barrier ΔF^‡/T_s decreases as f becomes stronger: ΔF^‡/T_s = 4.6 at f = 0.0, 4.0 at f = 0.3, 3.3 at f = 0.54, and 2.8 at f = 0.7. The free energy of stability (in units of T_s) at f = 0.0 is 2.0.

Our results for unfolding triggered by force are consistent with a number of experimental observations on the unraveling of isolated Ig-like domains in titin (4–6, 10). (i) The ratio of f_c/f₀ for Ig-like domains can be computed by using Eq. 4 with T = 25°C, the folding temperature T_F ≈ 60°C (27), and α ≈ 6.0. This gives f_c/f₀ ≈ 0.49. From the phase diagram in Fig. 1a, we obtain a similar value for the 36-mer when the temperature (measured in Kelvin) is approximately 0.89T_F. Thus the general shape of the phase boundary should be useful in calibrating the experimental measurements on proteins. (ii) The typical values of the threshold force f₀ required to induce stretching in the two-state folders are in the range of (1–2.5). By translating these into physical units, we obtain f₀ ≈ (20–50) pN. Using this range for f₀, we would predict that the unfolding force f_c, which depends on the pulling speed, for Ig-like domains in titin should be around (10–25) pN. These values are not inconsistent with the experimental measurements (see Fig. 5 of ref. 6). (iii) The width of the unfolding potential Δx that is obtained by using Eq. 5 and the computed values of f_opt and the activation-free energy ΔF^‡ (see Fig. 3b) in the absence of force for the 36-mer is 0.02L. Rief et al. (6) estimated that Δx/L ≈ 0.01 using Δx = 0.3 nm and L = 31 nm. If we use the fact that the lattice constant a, which gives the distance between α-carbon atoms, is ≈0.4 nm, then the value of Δx for the 36-mer in physical units is roughly 0.3 nm. These numbers are in very good accord with the experiments.

The theoretical findings can be used to map the underlying folding free energy landscape for two-state proteins by using data from force-induced unfolding experiments. This is illustrated by applying our results for the 36-mer to Ig-like domains. An estimate of f_opt for Ig domain can be made by using the value of 3.2 for the 36-mer and by assuming that a f_opt scales linearly with N. For the 90-residue Ig-like domain, we find that f_opt ≈ 160 pN. The unfolding barrier is f_optΔx, which is approximately 12 k_BT, assuming that Δx = 0.3 nm (6). From the stability of Ig domain [ΔG ≈ 2.6 kcal/mol (12)], we predict that the refolding barrier is approximately 4.6 kcal/mol. From these, the folding and unfolding times are predicted to be 0.1 s and 400 s, respectively. These predictions are in fairly reasonable agreement with experimental estimates (12). The estimates of barriers to folding by force-induced unfolding measurements are likely to be complement to the standard method of measuring rates at finite denaturant concentration and then extrapolating to the desired values in the absence of denaturants.

CONCLUSIONS

This study has led to the following predictions: (i) The unfolding time scales should decrease exponentially with force only until an optimum value of force, whose magnitude is determined by only the unfolding barrier in the absence of force. (ii) The phase diagram, especially the boundary separating the unfolded and folded states, has the characteristic type seen in Fig. 1 and is quantitatively given by Eq. 4. (iii) The nature of force-induced unfolding depends on the proximity of the amino and carboxyl termini in the native state. These predictions are all amenable to experimental test. Because the response to force depends sensitively on the characteristics of the sequence when f is zero, it follows that the mechanisms of protein folding (presence of intermediates, the nature of the transition states, and barriers to folding) may be very directly probed by single molecule force spectroscopy.

ABBREVIATIONS

RB

random bond

NBA

native basin of attraction

KGS

statistical potentials derived by Kolinski, Godzik, and Skolnick