Shedding light on the dark and weakly fluorescent states of green fluorescent proteins

Abstract

Recent experiments on various similar green fluorescent protein (GFP) mutants at the single-molecule level and in solution provide evidence of previously unknown short- and long-lived “dark” states and of related excited-state decay channels. Here, we present quantum chemical calculations on cis-trans photoisomerization paths of neutral, anionic, and zwitterionic GFP chromophores in their ground and first singlet excited states that explain the observed behaviors from a common perspective. The results suggest that favorable radiationless decay channels can exist for the different protonation states along these isomerizations, which apparently proceed via conical intersections. These channels are suggested to rationalize the observed dramatic reduction of fluorescence in solution. The observed single-molecule fast blinking is attributed to conversions between the fluorescent anionic and the dark zwitterionic forms whereas slow switching is attributed to conversions between the anionic and the neutral forms. The predicted nonadiabatic crossings are seen to rationalize the origins of a variety of experimental observations on a common basis and may have broad implications for photobiophysical mechanisms in GFP.

Green fluorescent protein (GFP) (1) is a uniquely important member of the exciting class of photoactive proteins that includes, among others, bacteriorhodopsin (2) and the photoactive yellow protein (3–5). Wild-type GFP is a highly efficient fluorescent emitter that performs wavelength shifting in vivo by resonance energy transfer (6). The chromophore, p-hydroxybenzylideneimidazolidinone, forms autocatalytically on the nascent apoprotein backbone by cyclization and subsequent oxidation of the Ser65-Tyr66-Gly67 sequence (7). Because of its great practical and commercial interest as a cloneable reporter of gene expression (8), GFP has been studied intensively over the past few years (6–25, 39). Crystallographic studies of wild-type (11, 12) and mutant GFPs (13, 14) have revealed the cylindrical shape protecting its buried chromophore from solvent. The remarkable rigidity of the protein inferred from recent molecular dynamics simulations (39) further explains its high fluorescence efficiency. Indeed, the bare chromophore in solution is not significantly fluorescent at room temperature (10). Based on optical absorbance spectra and ultrafast time-resolved fluorescence excitation and emission measurements (15, 16), a three-state model has been suggested for wild-type GFP (15, 16). In this, the chromophore exists in either a neutral (A) or an anionic form; the latter occurs in two different protein environments, in a kinetically accessible but thermodynamically unstable (I) form and in a thermodynamically stable (B) form.

Recently, single-molecule spectroscopic measurements of fluorescence in GFP triple mutants under constant illumination have revealed on-off blinking and switching (17), a behavior that is completely obscured when a large number of molecules is observed at once. Correspondingly, dramatic reductions in fluorescence also have been observed in solution-phase studies of related GFP mutants (18, 19). The molecular origins of these phenomena are largely inexplicable on basis of the canonical three-state model. Although small alterations of the protein environment apparently influence the quantum yield of fluorescence significantly, the wild type and all of these mutants contain chemically identical chromophores (17–21). This observation prompted us to search for an underlying mechanism largely intrinsic to the photophysics of the chromophore itself.

Cis-trans photoisomerization is a well known mechanism for radiationless decay in organic molecules (26) and has been implicated in the photocycles of retinal in bacteriorhodopsin (2) and of the photoactive yellow protein chromophore (3). In the present study, we report quantum chemical calculations on three photoisomerization paths around the two central bonds of a GFP model chromophore in vacuo in three different protonation states, neutral, anionic, and the recently suggested zwitterionic form (22, 23). For reasons given below, we do not include the cation also suggested in the mentioned work (22, 23). The isomerization paths include the two separate rotations around either of the two ring-bridging bonds (ϕ and τ) and the concerted and simultaneous rotation around both bonds, the so-called hula-twist (HT) (27) motion (Fig. 1). These pathways constitute the extreme and most different from each other among all of their conceivable combinations. An illustrative molecular dynamics (MD) simulation of wild-type GFP with the neutral chromophore in the τ-rotated trans configuration has been performed to estimate the plausability of this configuration in the protein environment. However, the timescales of the conformational changes cannot be assessed quantitatively in this work. This would require a much more extensive MD sampling of the conformational barrier crossing events and is a suitable topic for a separate subsequent study.

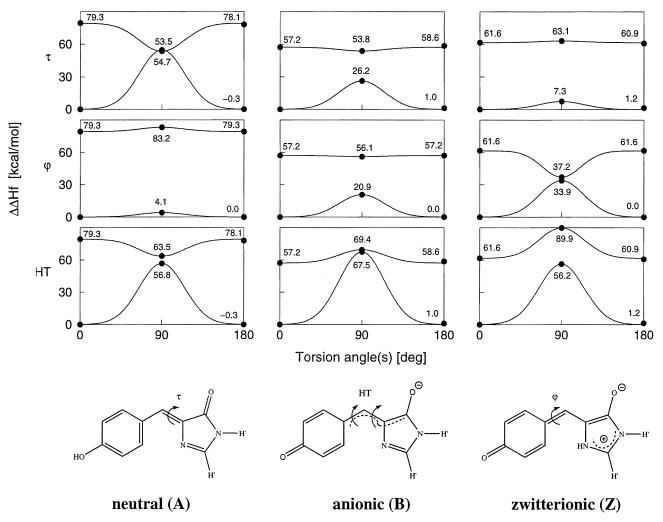
Figure 1.

Models of p-hydroxybenzylideneimidazolidinone GFP chromophore in the neutral, anionic, and zwitterionic forms used in the quantum chemical calculations, shown in those resonance structures that best represent the calculated bond orders. The covalent links with the Ser65 and Gly67 C_α atoms are replaced by hydrogen atoms (indicated as H′). The torsional degrees of freedom around the two ring-bridging bonds considered here are denoted by ϕ, τ (C—C—C—N), and HT (hula-twist (27), concerted and simultaneous motion around ϕ and τ), respectively. Rotation by 180° around ϕ leaves the structure unchanged. The configurations displayed represent τ = 0° and are referred to as cis configurations. The upper panels show OM2 (ref. 28; W.W. and W. Thiel, unpublished work)/PERTCI (29) energy profiles for rotation around the dihedral angles τ and ϕ and for the HT motion in the ground and first singlet excited states. Calculated values are marked by dots, and the Gaussian profiles are shown as visual aid. Note that, for these calculations, we fixed the dihedral angles while relaxing all other degrees of freedom.

First, we present the computational methods and the results from the in vacuo calculations of the chromophore. Then, we introduce a general model for the electronic states of GFPs, derived from our photoisomerization calculations, as the common basis on which we interpret experimental findings in the wild type and a variety of different mutants. It is convenient to group these mutants into two general classes [yellow fluorescent protein (YFP) and green fluorescent protein (GFP)]. The YFP type mutants have the mutation T203(F, Y) in common and comprise YFP1 (S65G/S72A/T203F) (17), YFP2 (S65G/S72A/T203Y) (17), YFP3 (S65G/V68L/S72A/T203Y) (18), YFP4 (S65G/V68L/S72A/H148G/T203Y) (18), and YFP5 (S65T/F64L/T203Y) (19). Whereas all YFP mutants have chemically the same chromophore as the wild type, the BFP class is characterized by mutations within the chromophore, i.e., mutations of the type Y66(H, F,W). Specifically, we discuss BFP1 (F64M/Y66H) (16), BFP2 (Y66H/Y145F) (20), BFP3 (Y66F) (9), and BFP4 (Y66W/N146I/M153T/V163A/N212K) (9).

METHODS

All quantum chemical calculations were performed with OM2, a new semiempirical NDDO (neglect of differential diatomic overlap) method that includes novel orthogonalization corrections (ref 28; W.W. and W. Thiel, unpublished work). These corrections lead to considerable improvements over the established methods MNDO, AM1, and PM3 for many properties (29), in particular for conformational properties, such as barriers of rotation around single and double bonds (ref. 28; W.W. and W. Thiel, unpublished work) and for vertical and adiabatic excitation energies (refs. 28–30; W.W. and W. Thiel, unpublished work). For example, the mean absolute error for 33 vertical excitation energies of selected organic molecules dropped from 1.20 eV with AM1 to 0.33 eV with OM2 (ref. 28; W.W. and W. Thiel, unpublished work) (1 eV = 1.602 × 10⁻¹⁹ J). The multireference configuration interaction method PERTCI (31) was used to select singly and doubly excited configurations, which were generated from the main configuration by excitations from the 12 highest occupied molecular orbitals into the 12 lowest virtual molecular orbitals. The different configurations were included in the configuration interaction matrix when their interaction with the main configuration was >0.1 eV and were treated by means of perturbation theory otherwise (31). The excited state calculations refer to the first singlet excited states of symmetries ¹A′ (C_s) and ¹A (C₁). The use of OM2/PERTCI allows one to optimize geometries in the ground and excited states and to obtain excitation energies, all at the same level of theory, which enabled us to calculate the cis-trans photoisomerization paths. This approach significantly extends previously reported INDO/S//PM3 predictions of vertical excitation energies (22, 23).

The MD simulation was performed with the amber94 forcefield and the nwchem program (32), analogously to a previous 1-ns simulation of wild-type GFP (39). After preparation, the system was simulated for 465 ps by using a 2-fs time step, at constant temperature of 300 K and at constant pressure of 1 atm (1 atm = 101.3 kPa).

RESULTS AND DISCUSSION

Energy barriers for the three rotation paths were calculated in the ground and first singlet excited states at optimized geometries. The energy profiles for the rotations around ϕ and τ and for the HT motion are shown in Fig. 1. The planar geometries at ϕ = 0° (or 180°) and τ = 0° (cis isomer) or 180° (trans isomer) are true energy minima, as was verified by force constant analyses. The cis and trans isomers of the same protonation state are similar in their heats of formation, vertical and adiabatic excitation energies, and oscillator strengths, in spite of the close proximity of the o-hydrogen of the p-hydroxy benzylidene group and the carbonyl oxygen in the trans configuration. The magnitudes of the barriers to separate rotation around the two central bonds (ϕ and τ) in the ground states can easily be rationalized in terms of their approximate bond orders. Specifically, as the bond orders in the central moiety of the chromophore change from mainly single/double to partial double/partial double to double/single for the neutral, anionic, and zwitterionic forms, respectively, the barriers increase from 4.1 to 20.9 to 33.9 kcal/mol for the ϕ rotation and decrease from 54.7 to 26.2 to 7.3 kcal/mol for the τ rotation as measured from the cis isomer. As the HT motion comprises the simultaneous rotation around both bonds, at least one double bond is involved in all three cases. This leads to very high ground-state barriers (>56 kcal/mol) with the highest for the anionic form (67.5 kcal/mol) where both bonds have partial double bond character. Rotation profiles often look distinctively different for excited states, in particular for rotations around double bonds (26). Here, this translates to considerably lower energies at the twisted 90° geometries than for the planar configurations for rotation around τ and for the HT motion in the neutral form, and for ϕ in the zwitterionic (Z) form. Our calculations show that the ground and excited state adiabatic potential surfaces come very close at these three points, suggesting the existence of so-called diabolical conical intersections (33). However, because the ground and excited states in Fig. 1 were separately optimized, their energies do not correspond to different roots of the same Hamiltonian, and we cannot prove the existence of conical intersections here. Conical intersections have been found along isomerization paths for a variety of similar molecules (26), such as butadiene, and a model compound for retinal (34). Theory shows that conical intersections can mediate facile conformational changes by nonadiabatic crossing (NAC) between different adiabatic potential surfaces, totally quenching fluorescence and other competing decay mechanisms (26, 33). A special feature is observed for the HT motion in the anionic form: The adiabatic potential surfaces approach each other in a Renner-Teller fashion (33), thus at a higher energy than for the planar geometries. For the bare chromophore, this implies a barrier to the HT-mediated NAC, which, however, may be smaller or even disappear in specific protein environments of some mutants (see below). An excited-state barrier also is found for the HT motion of the zwitterionic form whereas the other excited energy surfaces are seen to be flat (Fig. 1).

Although this work focuses on the rotation profiles rather than on achieving close quantitative agreement between experimental and calculated vertical excitation energies, we cite values of the latter for the model chromophore, 340 (neutral), 479 (anionic), and 453 nm (zwitterionic), as a point of reference. These values are in accord with the experimentally observed ordering of wild-type absorption frequencies, recognizing that vibronic structures and the effects of the protein environment would need to be incorporated to achieve a quantitative agreement between theory and experiment. Our calculated values are also similar to the previously published INDO/S energies on a slightly larger model (22, 23). OM2/PERTCI calculations for this larger model chromophore yield 334 (neutral), 444 (anionic), and 438 nm (zwitterionic), giving some indication of the sensitivity of the results to the specific chromophore structure used.

General Model.

In the following, we present a general model based on our calculations of the electronic states of the in vacuo chromophore and the previous body of experimental work. It provides the common basis for our subsequent separate discussions of wild-type and mutant GFPs. The previously suggested three-state model for the photophysics of wild-type GFP contains two thermodynamically stable forms of the protein, with the chromophore either in a neutral (A) or in an anionic ground state (B) (15, 16). Decay of A* mainly proceeds through the excited state of an intermediate (I*) that apparently contains the anionic chromophore in a nonequilibrated protein environment (12, 14). Our calculations suggest that this model should be generalized by including cis-trans photoisomerization and a third protonation state, the zwitterionic form Z (22, 23), but not the cation (22, 23) (see below), as additional degrees of freedom (Fig. 2). Although the in vacuo neutral and charged forms are very different in their absolute energies, this difference is, of course, largely balanced by the protein environment, which acts as proton acceptor and donor and stabilizes the different forms to a varying extent, favoring one or the other form of different GFP mutants. Note that the question of where the shuttled protons reside is presently unresolved because very recent Fourier transform infrared experiments on wild-type GFP have indicated a deprotonated Glu222 for both A and B (24), in variance with the earlier suggestion that it is deprotonated in A and protonated in B (12). This uncertainty does not affect our generalized model, which focuses on the electronic states of the chromophore in its presumed protonation states, at this stage without reference to the proton shuttle mechanisms.

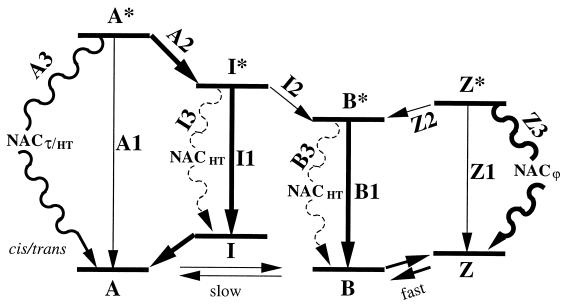
Figure 2.

Model for the photophysics of GFP as inferred from our quantum chemical calculations. Excited states are labeled by asterisks. Note that barriers may exist for processes of types 2 and 3. Excitation arrows are omitted for simplicity. The relative free energies of ground state forms A, B, I, and Z depend on the protein environment and, thus, on the specific mutant.

After vertical excitation of the neutral form A and relaxation from the Franck-Condon region, the excited A* state has three decay channels (Fig. 2): (A1) direct fluorescence to its ground state, (A2) proton release and conversion into the excited intermediate, and (A3) radiationless decay through NAC caused by τ or HT motion (A*_cis → A_cis/trans). The excited intermediate I* has three decay channels: (I1) direct fluorescence to its ground state with fast subsequent conversion into A (15), (I2) relaxation of the protein environment and conversion into B*, and (I3) radiationless decay through NAC due to HT motion (I*_cis → I_cis/trans). The excited anionic form B*, which also can be directly photoexcited, has two decay channels: (B1) direct fluorescence to the ground state and (B3) radiationless decay through NAC due to HT motion (B*_cis → B_cis/trans). Cis-trans isomerization of either of the anionic forms (I* or B*) in vacuo is unlikely because of the barrier toward the NAC (Fig. 1). Finally, the excited state of the zwitterionic form Z* has three decay channels: (Z1) direct fluorescence to the ground state, (Z2) proton release and conversion into the anionic form, and (Z3) radiationless decay through NAC by rotation around ϕ.

Application to Various GFPs.

To apply the results of Figs. 1 and 2 to the photophysics of the wild type and the various GFP mutants, the perturbing effects of the specific protein environments must be taken into account. These will affect differently (i) the populations of the various protonation states, possibly even suppressing the formation of one or the other, (ii) the energy profiles along the three isomerization paths, and, thus, (iii) the rates of the various processes. Generally, rotation around τ involves large-scale movement of the phenyl ring and leads to major steric conflicts with the rigid GFP environment, which may prevent this isomerization of the chromophore. By contrast, in certain cases, the HT motion may serve as a reasonable low-barrier mechanism because it invokes isomerization by rotating the central —CH⩵ group with respect to the two rings, leaving these relatively unchanged in space. This motion closely resembles the crystallographically observed mechanism for the very similar chromophore in the photoactive yellow protein (3, 4, 5). Finally, rotation around ϕ is expected to be only weakly perturbed by the protein surroundings because the phenyl ring is rotated around its own axis minimizing the number of atoms that move. In the nonuniform protein environment, the τ and HT profiles also will lose their almost perfect in vacuo symmetries of Fig. 1.

Accordingly, it can be inferred that the decay of A* through excited state proton transfer A2 will be faster than along A1 and A3 whereas, because I2 involves a large-scale structural rearrangement, decay of I* through I2 will be slow relative to I1 and I3. Moreover, the decay of I* and B* through I3 and B3 are expected to be likely only in specific protein environments, as is discussed further below. By contrast, for Z*, the NAC channel Z3 will be preferred to both Z1 and Z2, because Z* is much less acidic than A*, as inferred from the application of the Förster cycle to the different excitation energies of A and Z (22, 23) and because rotation around ϕ is expected to be sterically most facile. This suggests the central observation that Z* is “dark” in fluorescence. Consequently, although B and Z possibly absorb at the same absorption peak according to our vertical excitation energies, Z and the cation (22, 23) cannot be responsible for the observed bright long-wavelength and dim short-wavelength fluorescence, respectively, as has been suggested recently (22, 23). Deprotonation of the short-wavelength fluorescence form is experimentally known to lead to a form with bright fluorescence, which can be only B and not the dark Z. Therefore, the associated form must be A and cannot be the cation. Instead, as the profiles in Fig. 1 suggest, the low-energy fluorescence must be caused by the anionic form, in agreement with previous models (15, 16). The similar excitation energies also imply that the equilibrium between B and Z would be similar in the ground and excited state (Förster cycle) and may be the reason why Z and Z* have not yet been identified as such experimentally in any GFP. However, these forms may be observable in NMR and Stark spectroscopy. To account for the higher population of B, Z must be higher in energy than B, as depicted in Fig. 2, and the decay B* → Z* correspondingly unlikely.

Wild-Type GFP.

Our extended model of Fig. 2 preserves the main features of the previous models developed to explain most of the experimental findings in wild-type GFP (15, 16). Specifically, channel A2 involves a fast proton transfer (a few picoseconds) (15, 16) and dominates over both the direct fluorescence A1 and the NAC channel A3, which involves a much slower motion within the protein. This results in the previously suggested efficient cycle between A and I with weak fluorescence from A* and strong fluorescence from I* and B* (15, 16). The radiationless decay channels of I* and B* play only a very small role because of the barrier toward NAC (Fig. 1). Although no experimental findings seem to point to the zwitterionic form, unlike for the YFP class (see below), this does not rule out its existence also for the wild type.

The suggested radiationless decay channels A3 and I3/B3 on rotation are consistent with a model chromophore that is nonfluorescent in solution at room temperature because of—probably among other factors—both the NAC channels and collisional quenching but becomes fluorescent at 77 K (10). The brightening at lower temperatures of the weak A* → A fluorescence of wild-type GFP (16) may be ascribed to decreased protein flexibility, favoring the fluorescence channel A1 over the NAC channel A3. The existence of the suggested channel A3 helps also to rationalize the unexpectedly low quantum yield of I* (≈0.72–0.85) in GFP (25). From the ad hoc assumption that the excited state lifetime observed in the BFP1 mutant holds also for A* in wild-type GFP, an expected quantum yield of 0.995 was estimated (16). This difference between experiment (0.72–0.85) and estimation (0.995) points again to an existing radiationless decay process on the way between A and I, which we identify as A3 in our model.

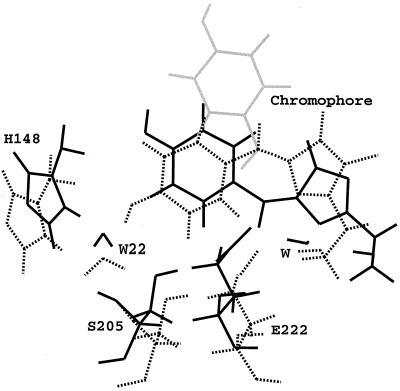
To estimate the plausability of the trans configuration, which is possible via NAC due to τ or HT motion, an illustrative 465-ps MD simulation of wild-type GFP with the neutral trans chromophore was performed. Although this simulation does not comment on the kinetics of the isomerization in the protein environment, it does clarify the thermodynamics of the trans configuration. The initial trans configuration was generated by flipping the regular cis chromophore around τ by 180°. Initially, 1,000 MD steps each were performed with very small time steps of 0.001, 0.01, and 0.1 fs to relieve close contacts between the 180° flipped chromophore and the protein. Initial and final structures are shown in Fig. 3 together with an equilibrated structure with the cis chromophore. The phenol moiety shifts back in-plane within 7 ps and superimposes nicely with the cis chromophore. Possible strain in the connections to the central α-helix is relieved after 75 ps, when the Ser65 side chain disconnects from Glu222 and swings backwards (with respect to Glu222) by ≈70°. The space previously occupied by the Ser65 hydroxyl group is immediately filled by a close water molecule (W). The hydroxyl group of the phenol ring does not find a hydrogen bonding partner throughout the simulation. W22 is coordinated by His148 instead. This structure is now stable over the remaining simulation time. Accordingly, although the trans chromophore is plausible in terms of steric constraints and is located in a very similar protein environment as the cis isomer, it is less well coordinated by surrounding protein residues. This indicates a higher energy for the trans than for the cis isomer, rationalizing why cis and not trans is found in the experimentally determined structures. The lack of structural support leaves the phenol ring quite floppy with respect to the five-membered ring, which may affect both absorption and fluorescence efficiency and wavelengths (see below).

Figure 3.

Superposition of three structures of wild-type GFP generated by molecular dynamics simulations. The dotted structure is a configuration from a previous MD simulation of GFP with a cis chromophore after 300 ps of equilibration (39). This structure was used to model a trans chromophore by rotation around τ by 180° (gray structure); 465 ps of simulation were performed starting from this configuration (32), and the structure in black is an average structure over the last 80 ps. Cis and trans configuration of the chromophore overlap well, but the trans chromophore is less well coordinated by surrounding protein residues.

YFP Mutants.

Compared with wild-type, the mutation of Thr203 into an aromatic residue results in a slight blue-shift of the high-energy absorption (≤6 nm) whereas the anionic form undergoes a substantial red-shift between 37 and 39 nm (1,17–19). The crystal structures of two mutants of this class, YFP3 and YFP4, reveal the parallel orientation of the chromophore and Tyr203 (18). Given the similar absorption and emission frequencies within this class (within 5 nm), one can expect that the five YFP mutants also show similar behaviors under various other experiments and presumably have similar three-dimensional structures.

YFP1/2 and Single-Molecule Experiments.

Our model identifies the fast time-scale blinking observed in the single molecule experiments on YFP1 and YFP2 with a conversion between the anionic and zwitterionic forms of the chromophore. We postulate this conversion to occur on the same several-second time-scale as the experimentally observed blinking, which indicates that the accompanying rearrangement of the protein environment is the rate-determining step. Constant illumination at the anionic peak will excite both B and Z. Although B* is highly fluorescent, Z* will always undergo radiationless decay through NAC due to rotation around ϕ and will appear dark in fluorescence. The zwitterionic form may be formed from the anionic form through proton transfer from nearby Glu222. This residue was shown to be hydrogen-bonded with the sp N atom of the five-membered ring in YFP3 and YFP4 (18). The proton transfer from the protein to the chromophore is postulated to induce the mentioned rearrangements in the environment. Note that the hydrogen-bond in YFP3/4 raises an interesting difference to the aforementioned very recent Fourier transform infrared experiments on wild-type GFP, which indicate a deprotonated Glu222 for both A and B (24), in variance with an earlier suggestion (12).

The observed slow time-scale switching is interpreted as conversion between the anionic and the neutral forms and thus is the single molecule equivalent of the well known macroscopic photobleaching (16). By contrast, very recent quantum control experiments on YFP2 showed that GFP bleaching may occur on the ground state (in our model of Fig. 2, this relates to the equilibrium A ⇌ B ⇌ Z) and not on the excited state (21). Once in its neutral form, the chromophore is not excited under illumination at the anionic peak wavelength. Of course, the anionic form was recovered easily in experiment by illuminating at the absorption peak of the neutral form (17).

Spectroscopy Experiments on YFP3/4/5.

After we had developed our model to explain the single-molecule experiments on YFP1/2, new spectroscopic data were published for YFP3/4/5 (18,19). These show unexpected loss of fluorescence, especially when excited at the high-energy band, corresponding to a >90% loss for YFP5 (19). Time-resolved fluorescence spectroscopy reveals a remarkably shortened lifetime of A* with rapid recovery of A compared with the wild type. Both I* and B* assigned states have slightly shortened lifetimes and decay highly nonexponentially, pointing to the existence of radiationless decay channels. Our model identifies the molecular origins of these internal conversions as the nonadiabatic crossings A3, I3, and B3 on rotation along τ, ϕ, or HT.

As indicated above, it seems very well justified to assume that the qualitative structural features found for YFP3/4 also hold for YFP1/2/5. Although one might expect the presence of the stacked Tyr203 to lead to decreased chromophore flexibility (18), we argue here that this is not necessarily so. High-level ab initio calculations have shown that T-shaped geometry of the benzene dimer is slightly more stable than the sandwich geometry (35) found for YFP3 (18). Statistical analyses of the interaction of aromatic sidechains in protein crystal structures were nonconclusive, once favoring the T-shape (36) and more recently the displaced sandwich geometry (37). These circumstances suggest that the potential energy surface is probably very flat between these two forms, allowing for an easy interchange between them. Starting from the crystal structure sandwich geometry of YFP3, both 90° rotation of the chromophore around ϕ and the HT motion to the 90°/90° position lead to the T-geometry, almost perfectly in the former and to a large extent in the latter case. In particular, for the HT motion of the anionic form, this may possibly result in an NAC at a lower energy, reducing or even removing the barrier to NAC in the protein that we found for the bare chromophore (Fig. 1). Therefore, the YFP class characteristic stacking of an aromatic residue at position 203 with the chromophore may lead to the enhanced use of the NAC decay channels, explaining the shortened lifetimes of I* and B* and their nonexponential decays.

It seems plausible to explain the red-shift in the low-energy absorption with increased polarization of the excited state because of the “π-stacked” Tyr (18). However, our calculations of the anionic form yield a larger dipole moment in the ground (7.3 D) than in the excited state (3.8 D) (1 D = 3.36 × 10⁻³⁰ cm). Therefore, one would expect that the additional polarization caused by the stacked Tyr stabilizes the ground state more than the excited state. Indeed, OM2/PERTCI calculations on a model dimer of the chromophore with p-cresol (for the Tyr) in the crystal structure geometry yield a blue-shift of 59 nm. With a relative discrepancy of almost 100 nm, the red-shift must have a different origin, requiring further clarifying studies of this feature.

BFP Mutants.

Nonexponentiality also is observed in the decay of the excited state of the double mutant BFP1, which exists only in the neutral A form under typical pH conditions (38). The nonexponentiality was tentatively explained as caused by a profound reorganization on vertical excitation, accompanied by an expected large change in dipole moment between 7 and 20 D, larger than that for the anionic form (16). However, very recent Stark data on the similar BFP2 mutant reveals that the change in dipole moment for the neutral form is only 2.5 D (20), smaller than that for B, ruling out the previous explanation. Here, the competition between channels A1 and A3 explains the nonexponentiality.

The weak fluorescence of Y66(F, H,W) chromophore mutants BFP1/2/3/4 (9) also can be explained in the framework of our model. Since deprotonation of these chromophores again does not occur at typical conditions (38) or is even impossible, the excited state only can decay via fluorescence (A1) or radiationless NAC (A3). Although the chromophore with Phe at position 66 will undergo HT motion more easily than the one with His with its two functional groups, the one with Trp will be hardest to isomerize because of its size. This sequence exactly corresponds to the observed fluorescence intensities (Phe < His < Trp) (9).

Conclusion.

A general model of the photophysics of GFP and a variety of GFP mutants is proposed (Fig. 2), based on quantum chemical calculations of the bare chromophore and empirical evidence. The model attributes a variety of experimental findings to the common basis of cis-trans photoisomerizations intrinsic to the chromophore in its various protonation states. Experimentally observed blinking and switching of single GFP mutant molecules on two different time scales is attributed to conversions between the fluorescent anionic form and the zwitterionic and neutral forms of the chromophore, respectively, the latter of which appear dark or weakly fluorescent due to nonadiabatic crossings. The quantitative timescales were not addressed here and will require much more extensive MD simulations to sample the conformational barrier crossing events. Correspondingly dramatic reductions in fluorescence quantum yields observed in similar GFP mutants also appear to correlate with accessible radiationless decay channels on rotation of the chromophore around its two central bonds. The model also helps to rationalize a number of other experimental observations, which previously were inexplicable, and provides a molecular picture that may aid the design of GFP mutants that either suppress or use the dark and weakly fluorescent states, as desired.

ABBREVIATIONS

GFP

green fluorescent protein

HT

hula-twist

MD

molecular dynamics

NAC

nonadiabatic crossing

YFP

yellow fluorescent protein

BFP

blue fluorescent protein