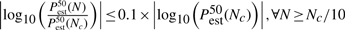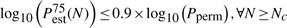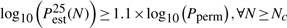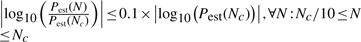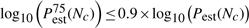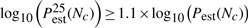Fewer permutations, more accurate P-values

Abstract

Motivation: Permutation tests have become a standard tool to assess the statistical significance of an event under investigation. The statistical significance, as expressed in a P-value, is calculated as the fraction of permutation values that are at least as extreme as the original statistic, which was derived from non-permuted data. This empirical method directly couples both the minimal obtainable P-value and the resolution of the P-value to the number of permutations. Thereby, it imposes upon itself the need for a very large number of permutations when small P-values are to be accurately estimated. This is computationally expensive and often infeasible.

Results: A method of computing P-values based on tail approximation is presented. The tail of the distribution of permutation values is approximated by a generalized Pareto distribution. A good fit and thus accurate P-value estimates can be obtained with a drastically reduced number of permutations when compared with the standard empirical way of computing P-values.

Availability: The Matlab code can be obtained from the corresponding author on request.

Contact: tknijnenburg@systemsbiology.org

Supplementary information:Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Permutation tests (also called randomization tests) are non-parametric procedures for determining statistical significance based on rearrangements of the labels of a dataset (Edgington, 1980). A test statistic, which is computed from the dataset, is compared with the distribution of permutation values. These permutation values are computed similarly to the test statistic, however, under a random rearrangement (permutation) of the labels of the dataset.

Permutation tests have become a widely used technique in bioinformatics. The non-parametric nature of these tests rationalizes their usability and popularity, since in many bioinformatics applications there is no solid evidence or sufficient data to assume a particular model for the obtained measurements of the biological events under investigation.

For example, Significance Analysis of Microarrays (SAM) (Tusher et al., 2001) and Gene Set Enrichment Analysis (GSEA) (Subramanian et al., 2005), which detect differentially expressed genes and gene sets, respectively, are two well-known techniques that use permutation tests to compute statistical significance. In these approaches, the class labels of samples from which gene expression measurements are taken, are randomly rearranged to obtain the permutation values. Besides randomization over the set of samples, permutation tests have also been performed by randomizing over the set of genes (Breitling et al., 2004; Smyth, 2004). In this case, the labels are binary indicator variables that indicate whether a gene belongs to a particular gene set or not. Efron and Tibshirani (2007) suggested to employ both permutation types to test the significance of gene sets. Other examples of permutation tests in bioinformatics include, but are not limited to: QTL detection (Doerge and Churchill, 1996), allelic association analysis (Zhao et al., 2000) and modeling ChIP sequencing (Zhang et al., 2008). In the latter case, each permutation corresponds to the simulation of a complete ChIP-seq experiment.

As in all statistical hypothesis tests, the significance of a permutation test is represented by its P-value. The P-value is the probability of obtaining a result at least as extreme as the test statistic given that the null hypothesis is true. In permutations tests, the null hypothesis is defined as: the labels assigning samples to classes are interchangeable (Edgington, 1980). Significantly, low P-values indicate that the labels are not interchangeable and that the original label configuration is relevant with respect to the data. The P-value is assessed by performing all possible permutations and computing the fraction of permutation values that are at least as extreme as the test statistic obtained from the unpermuted data.

However in practical situations, it is (by far) not feasible to perform all possible permutations. For example, class labels that represent two classes with 50 samples each can be permuted in 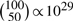different ways. Therefore, the P-value is approximated by computing a limited number of permutations, say N, and then computing the fraction of the N permutation values that are at least as extreme as the test statistic. Usually, a pseudocount is added to avoid P-values of zero, which occur when the test statistic is never surpassed by the permutation values. Theoretically, a P−value of zero is not possible in the context of permutation tests: the minimum is 1/N_all, where N_all is the number of all possible permutations. This is because one of the permuted label configurations is identical to the original one, under which the test statistic is computed.

This empirical approximation of computing P-values has two direct consequences. First, the resolution of obtainable P-values is 1/N. Second and more important, the smallest achievable P-value is 1/N. This means that a very large number of permutations is required to accurately estimate a small P-value. In general, >N permutations are required to reliably estimate a P-value of 1/N. (This is shown more extensively later in the manuscript.) Especially in bioinformatics, it is crucial to be able to accurately determine small P-values. This is due to typically huge numbers of objects [e.g. all genes, gene sets or single nucleotide polymorphism (SNPs)] that are simultaneously tested, which requires large multiple testing corrections to prevent large numbers of false positives. Clearly, other significance scores that are based on the P-values, such as the false discovery rate (FDR), will be meaningless when the P-values are not estimated correctly.

In this work, we propose to estimate the small permutation test P-values using extreme value theory (Gumbel, 1958). The set of extreme (very large or very small) permutation values that forms the tail of the distribution of permutation values is modeled as a generalized Pareto distribution (GPD). Pickands (1975) demonstrated that the GPD approximates the distribution of the extreme values of a set of independent and identically distributed (i.i.d). random variables, i.e. those values that exceed a particular (high) threshold. Applications of the GPD to model extreme values are traditionally found in climatology to model extreme weather, such as floods, and in financial risk management to model extreme losses and insurance claims. In our case, the GPD, which is fitted on the extreme permutation values, is evaluated at the value of the test statistic to estimate the P-value of the permutation test. Both theoretical probability distributions as well as gene expression datasets are employed to demonstrate that the proposed tail approximation strategy leads to an accurate estimation of the correct P-value using far fewer permutations compared with the standard empirical approach.

2 METHODS

2.1 Problem definition

Given test statistic x₀ and set X, which contains all possible permutation values, x₁^*, x₂^*,…, x_Nall^*, the permutation test P-value is defined as

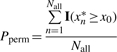(1)

where I(·) is the indicator function. The goal is to approximate P_perm using a randomly sampled subset Y (Y⊂X), which contains N permutation values, y₁^*, y₂^*,…, y_N^*. Usually, N ≪ N_all.

Note that the P-value calculation as described above corresponds to a right-tailed test. The P-value approximations discussed in this section will all correspond to a right-tailed test. Conversion to the left-tailed test and the two-tailed test is in all cases straightforward.

2.2 Empirical cumulative distribution function approximation

The standard approximation to P_perm is computed similarly to (1). Commonly, it includes a pseudocount to avoid P-values of zero:

(2)

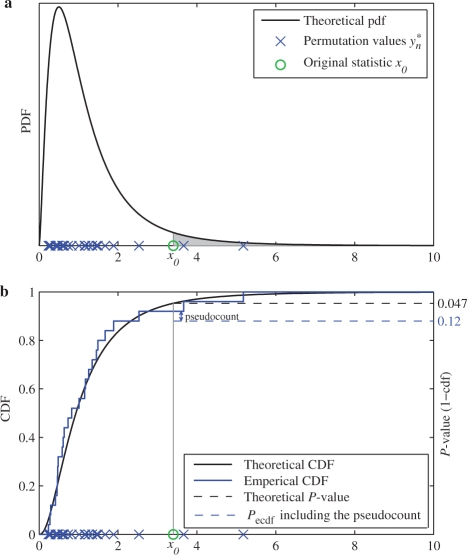
Essentially, this approach employs the permutation values in Y to build an empirical cumulative distribution function (ECDF). The ECDF is a step function that increases by 1/N at the value of each (ordered) permutation value in Y. P_ecdf is obtained as 1 minus the ECDF evaluated at x₀ and then adding the pseudocount of 1/N. Figure 1 illustrates the concept of the ECDF by approximating an F distribution using a limited number of samples randomly drawn from this distribution.

Fig. 1.

ECDF approximation of an F distribution. (a) From the PDF of the F distribution, 25 samples are randomly drawn. These samples represent the permutation values. The theoretical P-value for test statistic x₀ equals the grey area, which is 0.047. (b) The theoretical CDF is approximated by the ECDF, which is based on the 25 permutation values. Since two permutation values exceed x₀, P_ecdf is (1+2)/25=0.12 (including the pseudocount).

2.3 GPD approximation

The tail of the distribution of permutation values is modeled using the GPD. The GPD has cumulative distribution function (CDF)

(3)

and probability density function

(4)

The range of z is 0≤z<∞ for k≤0 and 0≤z≤a/k for k>0. The parameters of the GPD are a, the scale parameter, and k, the shape parameter. For the special values k=0 and 1, the GPD becomes the exponential and uniform distribution, respectively. When k<0 the GPD becomes the Pareto distribution, which has a long tail. The argument of the GPD, z, are the exceedances. In our case, these are the permutation values in Y that exceed threshold t, which then get subtracted by t to form the exceedances. Formally, if the values in Y are ordered, such that y₁^*≥y₂^*≥···≥y_N^*, we have a set Z of N_exc exceedances, z₁^*, z₂^*,…, z_Nexc^*, where z_i^*=y_i^*−t, ∀ i: y_i^*>t.

Maximum likelihood (ML) estimation is employed to estimate a and k given Z as explained in Hosking and Wallis (1987) and Grimshaw (1993). For k<1/2, Smith (1984) showed that, under certain regularity conditions, the ML estimators are asymptotically normal and asymptotically efficient. In this case, the asymptotic variance of the ML estimators can be derived, which can be used to compute confidence intervals for the estimates. When 1/2<k≤1, Smith (1984) identified the problem as non-regular, which alters the rate of convergence of the ML estimators and possibly their existence. This situation, i.e. k>1/2, however, rarely occurs in statistical applications. That notion is supported by this work, where no evidence for such cases was found in the practical applications that we analyzed. For k>1, no ML estimate exists.

Note that there exist other techniques to estimate the GPD parameters. We employed ML estimation, since this is the most commonly used technique and has overall good performance on reasonably large sample sizes as used in our application (Hosking and Wallis, 1987). The two other most widely used techniques, i.e. ‘method of moments’ and ‘probability weighted moments’, performed comparably with ML on the theoretical distributions and practical applications. See Supplementary Material.

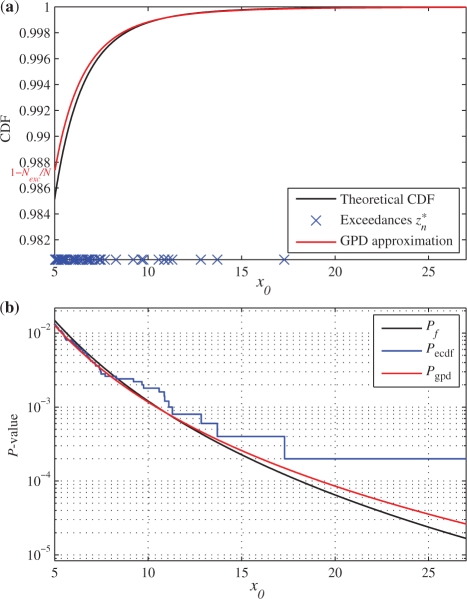
Figure 2a depicts the CDF of the GPD [F(z) in (3)] fitted to the tail of the F distribution used in Figure 1. Here, the exceedances threshold was set to five.

Fig. 2.

GPD tail approximation of an F distribution. (a) From the PDF of the F distribution (Fig. 1), 5000 samples are drawn. Samples that exceed five are defined as the exceedances and are modeled using a GPD. The GPD approximation of the tail (scaled to the interval [(1−N_exc/N), 1] is depicted alongside the theoretical CDF. (b) The theoretical P-value, which is derived from the CDF of the F distribution (P_f) is compared with the ECDF approximation (P_ecdf) and the GPD approximation (P_gpd) for values of x₀>5.

The permutation test P-value of the GPD approximation is computed as:

(5)

The factor N_exc/N compensates for the fact that F(z) is estimated only on the tail of the distribution of permutation values, which comprises a fraction of N_exc/N values of the complete distribution.

Figure 2b depicts P_gpd for different values of test statistic x₀. Also P_ecdf is depicted. The ECDF approximation is characterized by a step-wise function that has a lower bound of 1/N (2 × 10⁻⁴ in this case).

2.3.1 Exceedances threshold

There is a bias-variance trade-off in selecting the exceedances threshold. If the threshold is set too low, the distribution of exceedances may be outside of the domain of attraction of a generalized extreme value distribution. In that case, the tail does not follow a GPD. If the threshold is set too high, only few samples are available and the GPD parameter estimates will be prone to high-standard errors.

Goodness-of-fit tests can be employed to assess whether the exceedances follow a GPD. We use a goodness-of-fit test based on the Anderson–Darling statistic as described in Choulakian and Stephens (2001). The null hypothesis of this test is that the exceedances come from a GPD. Small P-values (of the goodness-of-fit test) indicate that this is not the case.

We propose to use the 250 most extreme permutation values as exceedances, i.e N_exc=250. We choose such a large number, because the GPD tail approximation is frequently used for extrapolation, i.e. the test statistic is much larger than the largest permutation value. (For example, take x₀=25 in Figure 2, where the largest permutation value is about 17.) A highly accurate estimate of the GPD parameters is required, because small deviations of the parameters can have a huge effect in the case of large extrapolation. If the 250 largest permutation values do not follow a GPD according to the goodness-of-fit test (P≤0.05), the number of exceedances is iteratively decreased by ten until a GPD good fit (i.e. P>0.05) is reached. If a good fit is never reached, the GPD cannot be used. However, this situation did not occur in any of the theoretical and practical cases described in this article.

The exceedances threshold t is set to (y_Nexc^*+y_Nexc+1^*)/2 (assuming that the values of Y are ordered from high to low as before). Thus, t is right between the smallest permutation value that is part of the exceedances, y_Nexc^*, and the one that just falls outside of the tail of extreme permutation values, y_Nexc+1^*.

2.4 Proposed algorithm

The GPD approximation can only be used when the test statistic is in the range of the extreme permutation values or when it is even larger. For example, when 50 out of the 100 permutation values exceed the test statistic, the test statistic is not in the tail of the distribution of permutation values and the GPD tail approximation is useless. Furthermore, in that case the standard empirical method to compute the P-value is adequate. Therefore, we have developed a criterion to decide when to employ P-value estimation using the GPD tail approximation.

This criterion is based on the fact that the number of permutation values that exceed the test statistic follows a binomial distribution. This is because each generated permutation value can be seen as a Bernoulli trial with probability P_perm of success, i.e. the permutation value being larger or equal to the test statistic. Let M be the number of permutation values that exceed the test statistic, i.e.

(6)

Note that [from (2)] M=NP_ecdf if we would exclude the pseudocount. Let P′_ecdf be P_ecdf excluding the pseudocount, i.e. P′_ecdf=M/N. According to the central limit theorem, if M ≥ 10 one may rely on the normal approximation to the binomial distribution:

(7)

Substituting P_perm by its estimate P′_ecdf gives us an estimate of the confidence bounds on P′_ecdf:

(8)

This procedure of determining the confidence bounds on the P-value estimate is identical to the one described in Nettleton and Doerge (2000). Note that the pseudocount can be omitted, because P-values of zero can no longer occur when M>0.

Since when M≥10 we can reliably compute P′_ecdf and its confidence bounds, we propose the following algorithm:

3 RESULTS

3.1 Theoretical distributions

Seven different distributions functions, ranging from light-tailed to heavy-tailed, were employed to test the GPD approximation. See Table 1, where distribution functions are ordered from light-tailed to heavy-tailed with the most light-tailed one on the left. Permutation values are obtained by randomly drawing samples from these distributions. The theoretical permutation test P-value can be obtained by evaluating the CDF at the value of the test statistic. Since an infinite number of samples can be generated from a distribution function, this theoretical P-value = P_perm from (1) in the limit case where N_all approaches infinity. For each distribution function, we chose a set of eight test statistics such that P_perm assumes the following set of values: 10⁻², 10⁻³, 10⁻⁴, 10⁻⁵, 10⁻⁶, 10⁻⁹, 10⁻¹² and 10⁻¹⁵. Using a range of different numbers of permutations values, i.e. N = 10…, 1 000 000, the P-value estimates P_ecdf and P_gpd were computed. This experiment was repeated 1000 times.

Table 1.

Minimum number of permutations (N_c) required for convergence to the correct P-value

The top three rows of the table state the names of distribution functions, their arguments and their ranges of the estimated scale parameter k. N_c is given for both estimators (P_ecdf and P_gpd) for a range of different P−values P_perm.

Note that P_gpd is computed according Algorithm 1, i.e. if M ≥ 10 we compute P′_ecdf in stead of P_gpd. This, however, almost never occurs in the experiments presented in this section, since we intentionally focus on the situations were the GPD approximation can be useful. These are the situations, where the test statistic is larger than (almost) all permutation values, i.e. M = 0 or very small.

3.1.1 P-value estimates as a function of N

Figure 3 displays a typical result. The ECDF approximation converges to the correct P-value linearly with the number of permutations, N. This behavior can be attributed to the effect of the pseudocount of 1/N. In general, when N <1/P_perm, P_ecdf = 1/N. If this pseudocount was omitted P_ecdf would be zero, until a sufficiently large number of permutations was performed.

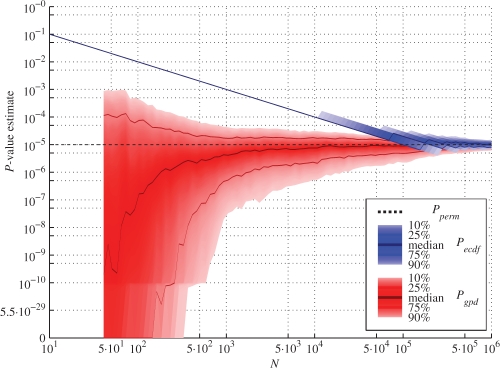
Fig. 3.

P_ecdf and P_gpd for an F distribution. Median and 10th, 25th, 75th and 90th percentile values are given for both P-value estimators as a function of N. The median and percentile values are based on 1000 repeats. The true P-value P_perm is represented by the black dashed line. The y-axis is logarithmically scaled from 10⁰ to 10⁻¹⁰; below 10⁻¹⁰, it is logarithmically scaled from 10⁻¹⁰ to the lowest non-zero P-value found in this experiment (i.e. 5.5 × 10⁻²⁹). P-value estimates of zero are set to intersect with the x-axis.

In contrast, the GPD approximation converges with far fewer permutations. In Figure 3, a decent estimate of P_perm is obtained with 10⁴ permutation values (see also Table 1). However, when N ≫ 1/P_perm, there is a lot of variability in P_gpd, illustrated by the large range that the P-value estimate assumes in this case. This range can even include P-value estimates of zero. This occurs when the range of z of the estimated GPD [in (3)] is limited, i.e. k>0, and the original statistic falls outside of this range, i.e. x₀−t>a/k. A large variance in the P-value estimate (including P-values of zero) for small N are more frequently observed for the light-tailed distributions, where, indeed, k>0. See Supplementary Material, which contains all figures (similar to Fig. 3) for the seven distribution functions and the eight values of P_perm.

3.1.2 Number of permutations required for convergence

Table 1 provides an overview of the number of permutations necessary before convergence to a reasonable estimate. This number, N_c, is computed for the different distribution functions and for different values of P_perm. Three criteria were jointly employed to assess convergence:

• 

• 

• 

where P_est^α(N) is the value of the α-th percentile of the estimated P-value P_est (either P_ecdf or P_gpd) after N permutations. The first criterion ensures that the P-value estimate has converged, i.e the median P-value estimate after N_c permutations varies <10% (on a log₁₀-scale) across the interval [N_c/10, 10⁶]; 10⁶ being the maximum number of permutations performed. The second and third criteria ensure sufficient accuracy; the 25th–75th percentile values of the P-value estimate deviate <10% from P_perm (on a log₁₀-scale). N_c is the minimum number of permutations at which these criteria are met. (Note that these criteria are heuristics and other stopping criteria could be employed.)

In all cases, tail estimation using the GPD requires fewer permutations than the standard ECDF approach. For not too small P-values, such as from 10⁻³ to 10⁻⁵, about 5 to 10 times fewer permutations are necessary. For smaller P-values, the P_ecdf did not converge within the 10⁶ permutations that were performed, but the N_c values from the P_gpd that did converge, suggest that orders of magnitude fewer permutations are sufficient for a reliable estimate. In general, the GPD approximation usually requires fewer than 1/P_perm permutations, while estimation using the ECDF always requires more than 1/P_perm permutations.

Further for the GPD approximation, we observe that the more heavy-tailed distributions (smaller values of shape parameter k) converge with fewer permutations than the light-tailed distributions. This behavior is not observed for the ECDF approximation, where N_c does not depend on the shape of the tail. Remarkably, the most heavy-tailed distribution, the Cauchy distribution (identical to the Student's t-distribution with one degrees of freedom), requires <2000 permutations for a correct and reliable estimate of a P−value of 10⁻⁹.

3.2 Application to gene expression data

3.2.1 Differential gene expression

Permutation tests are frequently employed to detect the differential expression of genes between two or more conditions or classes. In these applications, a test statistic is compared with its permutation values, which are obtained by computing the same statistic on permuted label configurations.

SAM (Tusher et al., 2001) is the most commonly used tool to incorporate this strategy. The test statistic used in SAM is a regularized T-statistic, d_i, where i is the index of a gene. We will compare d_i with its permutation values d_i1^*, d_i1^*,…, d_iN^* to estimate the permutation test P-values. (Note that the SAM procedure to compute P-values and FDRs is slightly different, because test statistics and corresponding permutation values of all genes are used simultaneously.)

The gene expression data used in this experiment consisted of 170 microarrays of yeast chemostat cultivations (Knijnenburg et al., 2009). The arrays were separated into two classes based on the employed oxygen regime, i.e. in 80 of these arrays yeast was grown aerobically; for the other 90 arrays yeast was grown anaerobically. In this experiment, we focused on the 132 genes annotated with MIPS (Mewes et al., 1997) function category ‘respiration’, since we expected to find many differentially expressed genes in this group.

It is computationally infeasible to compute P_perm from (1), since 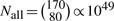. Therefore, we applied the following strategy to approximate P_perm: for each gene, we generated permutation values until M, the number of permutation values that exceeds the test statistic, was >25. Then, using (8) we can reliably estimate P_perm. For 69 of the 132 genes, M <25 even after >3 billion (N>3 × 10⁹) permutations. The other 63 genes, for which P_perm was reliably estimated, were used in the rest of the experiment.

For different values of N, we computed P_ecdf and P_gpd for the 63 genes. This experiment was repeated 200 times. Figure 4 visualizes the results for N = 10⁵. As expected, the ECDF approximation is adequate for genes with P_perm > 10⁻⁴. However, for smaller P-values, the estimate is way off and bounded by 1/N. The GPD approximation provides a better approximation for the small P-values. However, for P-values >10⁻⁶, the variance of the estimate becomes quite large and frequently P-value estimates of zero are encountered. This behavior was also observed with the light-tailed theoretical distributions. Accordingly, the range of the shape parameter k estimated on the permuted SAM statistics was [0, 0.27], similar to range of the light-tailed distributions.

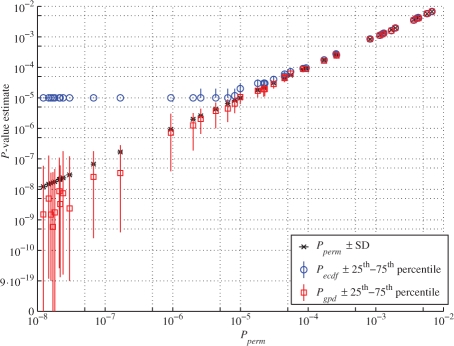
Fig. 4.

P_ecdf and P_gpd based on the SAM statistic of different genes. The median and 25th and 75th percentile values are given for both P-value estimators with N=10⁵. Each data point represents the P-value estimate (including confidence bounds) of one gene. These are compared with the true P-value P_perm. The y-axis is logarithmically scaled from 10⁻² to 10⁻¹⁰; below 10⁻¹⁰, it is logarithmically scaled from 10⁻¹⁰ to the lowest non-zero P-value found in this experiment (i.e. 9 × 10⁻¹⁹). P-value estimates of zero are set to intersect with the x-axis.

In a follow-up experiment, we aimed to transform the test statistic and its permutation values, such that k<0, i.e. the tail becomes more heavy. Basically, any strictly increasing (and thus order preserving) function can be applied to the test statistic and its permutation values without changing (the definition of) P_perm. Also, such a transformation would not influence the computation of P_ecdf. And, if the tail of the transformed permutation values still follows a GPD, which is tested using the goodness-of-fit test, they can be used to estimate P_gpd.

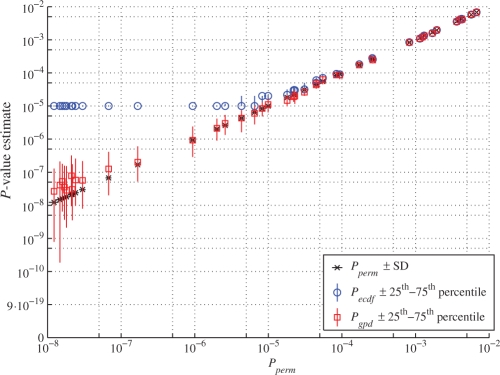
We raised all test statistics and corresponding permutation values to the power three, i.e. d′_i = (d_i)³,d′^*_in = (d_in^*)³. ∀i,n and recomputed P_gpd. After the transformation, the estimated range of the shape parameter k was [−0.6, 0]. Furthermore, P_gpd based on the transformed statistic proved to be a better estimate with much less variance (Fig. 5). Now a reasonable estimate of P-values <10⁻⁷ can be made using only 10⁵ permutations.

Fig. 5.

Similar to Figure 4, except a transformed statistic was used, i.e. the original statistic and permutation values were raised to the power three.

More discussion about transforming the permutation values will follow in Section 3.2.3.

3.2.2 Enrichment of gene sets

Another popular application of the permutation test on expression data is to uncover enriched gene sets. These are a priori defined groups of genes, e.g. functionally related genes, that show concordant differential expression across the different conditions or classes of a microarray experiment. In this case, the gene-set specific test statistic is compared with the permutation values, which are obtained by permuting the class labels and recomputing the statistic.

GSEA (Subramanian et al., 2005) is the most widely used method that follows this approach. The GSEA statistic is a weighted version of the Kolmogorov-Smirnov statistic, e_s, where s is the index of a gene set. GSEA uses the empirical way of estimating the permutation P-value based on e_s and its permutation values e_s1^*, e_s1^*,…, e_sN^*.

In comparison with SAM, GSEA is computationally very expensive, as it involves sorting all genes based on correlation with the class labels and then computing a running sum statistic. For some bioinformatics applications, dynamic programming approaches can be used to build a suitable null distribution based on the statistic (Newberg and Lawrence, 2009). One such approach has been developed for GSEA (Keller et al., 2007) in order to avoid the expensive permutations. However, this method only applies to the unweighted version of GSEA (Mootha et al., 2003), which is not the default setting of the GSEA algorithm.

We applied (default) GSEA to the (van de Vijver et al. (2002) breast cancer dataset consisting of >24 000 gene expression measurements of 295 patients, 180 with poor prognosis and 115 with good prognosis. All gene sets from gene ontology (GO) (Ashburner et al., 2000) and kyoto encyclopedia of genes and genomes (KEGG) (Kanehisa and Goto, 2000) containing >10 genes were analyzed.

P_perm was computed similarly to the previous section, i.e. for each gene set we generate permutation values until M becomes >25. Since the GSEA statistic is so computationally expensive, not more than 1 000 000 permutations (N=10⁶) were performed. We found 89 gene sets for which M>25 within the 10⁶ permutations and which had a P_perm <0.01.

In this experiment, we focused on a different aspect of the outcome of the permutation test, namely the order of the gene sets based on the estimated P-value. Often, researchers are interested in the top of the list of significant genes, gene sets, SNPs, etc., more or less regardless of the associated significance scores themselves. These objects will then be analyzed or investigated in order of significance, starting with the most significant. Here, we compare the correctly ordered list of 89 gene sets based on P_perm with the ordered lists based on P_gpd and P_ecdf. Our measure of comparison is the Spearman rank correlation. The Spearman correlation between the ordered list based on P_perm and P_gpd is denoted by C_gpd; the Spearman correlation between the ordered list based on P_perm and P_ecdf is denoted by C_ecdf. The experiment was performed for different values of N ranging from 10² to 10⁵ and was repeated 100 times.

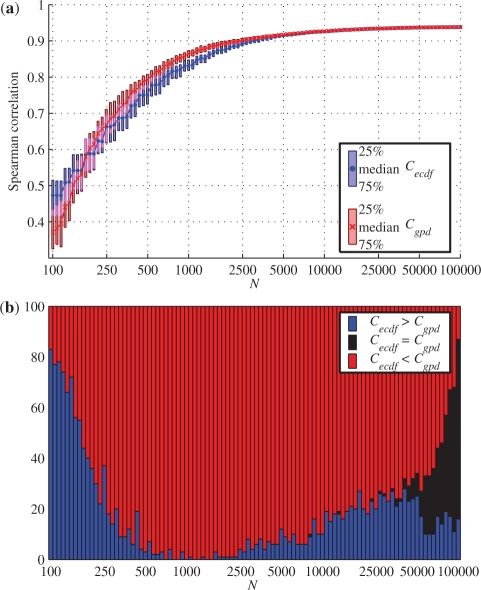
The results are visualized in Figure 6a. For values of N <250 the GPD approximation performs worse than the standard empirical approach. This could be expected, since for such small values of N, there are too few samples to accurately estimate the tail and extrapolate this to the correct P-value. However, for larger values of N, the list ordered based on P_gpd leads to a higher correlation with the optimal ordering compared with the list ordered based on P_ecdf. When N = 1000 (the standard number of permutations in GSEA), the Spearman correlation C_gpd is significantly >C_ecdf.

Fig. 6.

Comparison of C_ecdf and C_gpd for different values of N. (a) Median, 25th and 75th percentile values for C_ecdf and C_gpd for different numbers of permutations N. Overlapping intervals are illustrated in magenta. (b) Stacked bar graph indicating the number of times C_ecdf was larger or smaller than (or equal to) C_gpd out of the 100 repeats.

The difference between C_gpd and C_ecdf becomes more obvious in Figure 6b. For each of the 100 repeats, we counted how many times the one correlation was higher than the other. When N=1000, for almost all of the 100 trials, the GPD approximation led to a higher correlation, and thus to a more correctly ordered list compared with the list based on the empirical approach, which was computed on the same permutation values. When N increases, the difference between C_ecdf and C_gpd diminishes and in many cases they lead to identically ordered lists. This can be attributed to the fact that amongst the 89 genes, only few have a P_perm <10⁻⁴ and none is <2.5 × 10⁻⁵ (25/10⁶). Consequently, P_ecdf becomes a good approximation of P_perm when N approaches 10⁵.

3.2.3 Choosing N

In practical applications, P_perm is not known and no repeats are performed, i.e. only one set of permutation values is generated for a test statistic. The convergence criteria developed in Section 3.1.2 to decide when enough permutations have been performed can be slightly altered to suit practical applications:

• 

• 

• 

where P_est(N) is the estimated P-value (either P_ecdf or P_gpd) after N permutations, and P_est^α(N) is the α% confidence bound on the estimated P-value. N_c is the minimum amount of permutations at which these criteria are met. For P_ecdf it is not possible to compute confidence bounds. In that case, only the first criterion applies.

P_ecdf and P_gpd estimates (including confidence bounds) were computed for the 63 genes of Section 3.2.1 based on their SAM statistic and corresponding permutation values. The number of permutations was increased until the convergence criteria were met or when the maximum number of permutations (N=10⁶) was reached. This experiment was repeated 25 times. Table 2 displays the results for the five genes, for which P_perm was the closest to 10⁻⁴, 10⁻⁵, 10⁻⁶, 10⁻⁷ and 10⁻⁸, respectively. These genes were chosen to present results for a large range of different P_perm values.

Table 2.

The 25th and 75th percentile values of N_c and the corresponding P-value estimates (P_ecdf and P_gpd for five different genes

The power Z to which the original statistic and its permutation values were raised before GPD approximation is indicated on the left side of the table.

From the table, it is clear that fewer permutations are necessary to reach an accurate P-value estimate when employing the GPD approximation compared with the standard empirical approach. For the first two genes ∼ 5−10 times fewer permutations are necessary. For the last three genes, convergence was not reached with the empirical approach within 10⁶ permutations. However, based on the N_c values from the P_gpd estimates that did converge, we can infer that orders of magnitude fewer permutations are sufficient for a reliable estimate for these smaller P-values.

Additionally, we observed that the behavior of the confidence bounds on an individual P_gpd estimate (based on one set of permutation values) is comparable with the behavior of the confidence bounds (percentile values) based on many P_gpd estimates. That is, when too few permutations have been performed for an accurate estimate, P_gpd will tend to have large confidence bounds, and thus much uncertainty in the estimate.

With the convergence criteria, it is possible to analyze the effect of order-retaining transformations on the test statistic and its permutation values. From both the theoretical distributions and the application on gene expression data, we observed that the shape of the tail of permutation values influences the GPD estimation process. That is, for light-tailed distributions (k>0), where the GPD has a finite range, the estimate appears unstable and less accurate. Small changes in k have a huge effect on P_gpd. Especially, in the case of large extrapolation, i.e. N ≪ 1/P_perm, there is a large variance (or large confidence bounds) on the estimator and frequently P-value estimates of zero are encountered.

Order-retaining transformations can be applied to change the shape of the tail of the distribution of permutation values. While such a transformation does not affect P_perm and the computation of P_ecdf, it might provide a more robust and accurate estimate (and prevents P-values of zero) for the GPD approximation. We applied power transformations to the SAM statistic in order to reduce k. The SAM statistic, which can assume both positive and negative values, was raised to the power Z = 1 (no transformation), 3 and 5. The ranges of k for Z = 1, 3 and 5 are[0, 0.27],[−0.6, 0] and[−1.6, −0.2], respectively. Table 2 also displays the results for Z = 3 and 5.

Although the transformation is not necessary to outperform the ECDF approximation, it does lead to convergence with even fewer permutations. This gain in improvement does not continue for larger values of Z (not in the table), where N_c starts to increase again. From this analysis, we can conclude that a transformation can be useful when the shape of the tail of the distribution of permutation values is transformed from light-tailed (k>0) to heavy-tailed (k<0), where our estimator has more stable and accurate performance.

4 DISCUSSION

The non-parametric nature of the permutation test rationalizes its usability and popularity in bioinformatics applications: in most cases, there is neither solid reason nor sufficient evidence to assume a particular model for the obtained measurements of the biological events under investigation. The standard empirical method of computing the permutation test P-value is hampered by the fact that a huge number of permutations is required to correctly estimate small (and therefore interesting) P-values. In fact, the number of necessary permutations is always larger than the inverse of the actual P-value. In this work, we devised a P-value estimation scheme based on extreme value theory that uses tail approximation of the extreme permutation values. The resulting estimator requires far fewer permutations to accurately estimate small P-values.

Permutation tests are commonly performed in batches for large numbers of different test statistics, e.g. for all genes or all gene sets. In these permutation schemes, the same number of permutations is performed for each test statistic. This number is usually selected a priori (possibly based on an estimate of computational time or complexity). Such an approach can be highly inefficient, since different test statistics require different numbers of permutations. For example, if 600 of the 1000 permutation values exceed the test statistic, another 1000 permutations are not necessary, since the P-value can already be determined with great accuracy [P = 0.6±0.016 according to (8)]. However, if only one permutation value exceeds the test statistic, more permutations are necessary to accurately determine the corresponding P-value. In this work, we have shown that simple convergence criteria and confidence bounds on the estimate can be used to indicate when enough permutations have been performed to have certain statistical confidence in the P-value estimate. In most applications, only a small fraction of the test statistics will be significant, i.e. they will require a lot of permutations to reliably estimate their small P-values. The large majority of test statistics will require only a small number of permutations to reliably compute their large (and hence, insignificant) P-values. Such an approach can lead to a decrease in the total number of permutations, and thus computational time (or at least to a more sensible division of the total number of permutations), while producing more accurate P-value estimates.

In future research, we will more elaborately explore the relationship between the shape of the tail of extreme permutation values and the accuracy of the estimator. This will include investigating the possible role that transformations of the test statistic and its permutation values could play. A web interface for the proposed permutation test P-value estimation technique is under development.