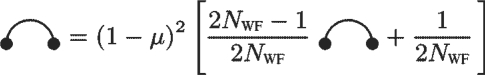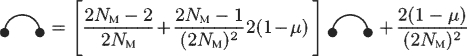Multi-locus match probability in a finite population: a fundamental difference between the Moran and Wright–Fisher models

Abstract

Motivation: A fundamental problem in population genetics, which being also of importance to forensic science, is to compute the match probability (MP) that two individuals randomly chosen from a population have identical alleles at a collection of loci. At present, 11–13 unlinked autosomal microsatellite loci are typed for forensic use. In a finite population, the genealogical relationships of individuals can create statistical non-independence of alleles at unlinked loci. However, the so-called product rule, which is used in courts in the USA, computes the MP for multiple unlinked loci by assuming statistical independence, multiplying the one-locus MPs at those loci. Analytically testing the accuracy of the product rule for more than five loci has hitherto remained an open problem.

Results: In this article, we adopt a flexible graphical framework to compute multi-locus MPs analytically. We consider two standard models of random mating, namely the Wright–Fisher (WF) and Moran models. We succeed in computing haplotypic MPs for up to 10 loci in the WF model, and up to 13 loci in the Moran model. For a finite population and a large number of loci, we show that the MPs predicted by the product rule are highly sensitive to mutation rates in the range of interest, while the true MPs computed using our graphical framework are not. Furthermore, we show that the WF and Moran models may produce drastically different MPs for a finite population, and that this difference grows with the number of loci and mutation rates. Although the two models converge to the same coalescent or diffusion limit, in which the population size approaches infinity, we demonstrate that, when multiple loci are considered, the rate of convergence in the Moran model is significantly slower than that in the WF model.

Availability: A C++ implementation of the algorithms discussed in this article is available at http://www.cs.berkeley.edu/∼yss/software.html.

Contact: yss@eecs.berkeley.edu

1 INTRODUCTION

Correlation of genealogies at different loci can cause statistical non-independence of alleles at those loci. It follows from the well-established population genetics theory that recombination breaks down this correlation and that in the case of an infinite population, the correlation between unlinked loci (say, on different chromosomes) becomes completely eliminated over time. In a finite population, however, genealogical relationships between individuals can create statistical dependence even between unlinked loci. This subtle difference between finite and infinite populations may have important implications for some practical questions of interest, a well-known example being the forensic use of DNA typing. A fundamental problem which arises in forensic science is to compute the probability that two individuals randomly chosen from a population have identical alleles at a collection of loci (Balding, 2005; Evett and Weir, 1998). We refer to this probability as multi-locus match probability (MP). In population genetics, MP corresponds to the probability of homozygosity. At present, 13 unlinked autosomal microsatellite loci, called the Combined DNA Index System loci (see http://www.fbi.gov/hq/lab/codis/index1.htm for details), are typed in the USA for forensic use, while 11 loci are used in the UK. Unlinked microsatellite data are also often used in demographic inference (e.g. see Pritchard et al. 2000), but we do not address that problem in this article.

The so-called product rule, which is used in courts, computes the MP for multiple unlinked loci by assuming statistical independence, multiplying the one-locus MPs at those loci. In light of the above discussion regarding the existence of statistical dependence between unlinked loci in a finite population, it remains debatable to date whether the product rule produces reliable results. To test the accuracy of the product rule theoretically, Laurie and Weir (2003) provided a method to compute the equilibrium MPs in an ideal finite population, assuming an infinite alleles model of mutation. Their approach was to construct a system of coupled linear recurrence equations involving MPs and then solve the system assuming stationarity. Although this method is simple in principle, setting up the system of recurrence equations becomes increasingly challenging with the number of loci. Song and Slatkin (2007) later introduced a flexible graphical method that allowed them to generalize the analysis of Laurie and Weir to cases with more loci and other models of mate choice such as monogamy. Using their framework, Song and Slatkin succeeded in computing the genotypic (i.e. two alleles per locus per individual) MP for up to three loci and the haplotypic (i.e. one allele per locus per individual) MP for up to five loci.

In this article, we employ the graphical framework of Song and Slatkin (2007) and make algorithmic improvements to carry out the MP computation for significantly more loci than what previous works could handle. For simplicity, we focus on the haplotypic MP computation. Hence, when we say MP in what follows, we mean haplotypic MP. Both Laurie and Weir (2003) and Song and Slatkin (2007) restricted their attention to the Wright–Fisher (WF) model of random mating. In our work, we consider the Moran model in addition to the WF model; the main difference between these two standard models in population genetics is that generations do not overlap in the WF model, while they do overlap in the Moran model. We are currently able to compute MPs for up to 10 loci in the WF model and up to 13 loci in the Moran model. Bear in mind that this work requires overcoming several algorithmic and engineering challenges. For example, the 13-locus case involves about 3.1 million coupled linear equations; both finding the system of linear equations and solving it are challenging tasks.

Two major findings of our work are as follows. (i) In an ideal finite population, the MPs predicted by the product rule are highly sensitive to mutation rates, while the true MPs computed using our graphical framework are not. For a range of mutation rates relevant to the observed level of homozygosity at microsatellite loci, the product rule may significantly underestimate the 13-locus MP. However, the product rule becomes more accurate if we are provided with the additional information that the individuals being compared are not close relatives. (ii) Both the WF and Moran models have been used in the population genetics community for many years, and it has been thought that the two models should produce very similar quantitative results as long as the population size and time are rescaled properly when relating one model to the other. However, our work reveals a fundamental difference between the two models which becomes transparent only when multiple loci are considered in a finite population. More precisely, we show that, for a finite population, the Moran model may produce significantly higher multi-locus MPs than that under the WF model, and that this difference grows with the number of loci and mutation rates. We show that, as expected, the two models produce the same MPs in the coalescent or the diffusion limit, in which the population size approaches infinity. We demonstrate that, when multiple loci are considered, the rate of convergence to the diffusion limit in the Moran model is significantly slower than that in the WF model.

2 MODELS OF RANDOM MATING

We adopt the same notational convention as in Song and Slatkin (2007). Throughout this article, we assume a neutral infinite-alleles model; i.e. whenever an allele mutates, it mutates to a new allele that has never been seen before. Further, we assume a single population containing 2N_WF haploid individuals in the WF model or 2N_M haploid individuals in the Moran model.

2.1 Mating schemes

The two mating schemes are detailed below.

2.1.1 The WF model

The entire population of 2N_WF haploid individuals gets replaced every generation. Individuals in the next generation are produced from those in the current generation in the following fashion: (i) Randomly sample two individuals, each with replacement. The same individual may be sampled twice under this mating scheme. A new individual is produced from the two sampled individuals as described in Section 2.2. We assume that mutations occur at locus i with probability μ_i per individual per generation, independently of other loci. (ii) Repeat the above procedure until 2N_WF new individuals are created for the next generation.

2.1.2 The Moran model

Exactly one individual gets replaced every generation as follows. (i) The same as Step (i) in the WF model. (ii) Randomly choose exactly one individual to die in the current generation; the new individual created in the previous step replaces this individual. All other individuals survive to the next generation.

2.2 Generating offspring gametes by recombination

By a gamete, we mean alleles at a collection of loci; different loci may physically reside on different chromosomes within a haploid individual. We use x_i to denote the allele at locus i in individual x.

2.2.1 Two loci

Let x₁x₂ and y₁y₂ denote the gametes of the two sampled parental individuals. Then, the inheritance pattern of the offspring is x₁x₂, y₁y₂, x₁y₂ or y₁x₂, with probability 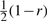, , 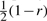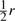or 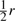, respectively. The unlinked case corresponds to r=1/2.

2.2.2 More than two loci

Let x₁x₂…x_L and y₁y₂···y_L denote the two sampled parental gametes with L loci. We focus on a set of loci that are pairwise unlinked, as was done previously by other authors (Laurie and Weir, 2003; Song and Slatkin, 2007). Hence, in the offspring gamete z₁z₂···z_L, the allele z_i at locus i is equally likely to have descended from x_i or y_i. The probability of any particular inheritance pattern is 1/2^L.

3 A GRAPHICAL APPROACH TO MP COMPUTATION

Song and Slatkin (2007) introduced a graphical framework to compute multi-locus MPs in a finite population. We employ the same framework in this article. Below, we highlight the key ideas underlying the approach.

3.1 High-level idea

In Section 2, we discussed random mating models that describe how a population evolves forward in time. In our work, we adopt a backward point of view and determine how a given MP at generation t is related to a combination of MPs at generation t−1, thus obtaining a system ℛ(t, t − 1) of recurrence equations. At stationarity, the probability of a particular match relation (e.g., the probability that two randomly chosen individuals have the same alleles at loci 1 and 4) at generation t is equal to the probability of the same match relation at generation t−1. Therefore, at stationarity ℛ(t, t − 1) becomes a closed system 𝒮 of linear equations which we can solve. In general, the recurrence equation for an L-locus MP at generation t contains k-locus MPs at generation t −1 where k≤L. Therefore, one needs to carry out the computation in the following systematic order: first solve the system of linear equations for 1 locus; then solve the system for two loci, treating 1-locus MPs as known constants; then solve the system for three loci, treating 1-locus and 2-locus MPs as known constants; so on and so forth.

Although the above procedure is simple to describe, setting up the system of recurrence equations becomes increasingly difficult with the number of loci. The key idea introduced by Song and Slatkin (2007) is to represent MPs as graphs. By performing a set of prescribed operations on a given graph at generation t, one can determine how it is related to a linear combination of graphs at generation t − 1, thus setting up the required system ℛ(t, t − 1) of recurrence equations. The graphical method makes the combinatorial structure of the problem easier to understand and it is possible to implement the method in a fully automated computer program, thus reducing the chance of human error.

3.2 From MPs to match graphs

Here, we describe the graphical framework in the case of arbitrary mutation rates μ_i at loci i=1,…, L. (As we will discuss in Section 6.1, there is a simplified representation if μ_i are the same for all i.) Let x_i ≡ y_i denote the event that alleles at locus i are identical (or match) in individuals x and y. To the probability of a particular match relation (e.g. x₁ ≡ y₁, x₂ ≡ y₂ and x₃ ≡ z₃), associate a match graph constructed as follows:

1. Create a vertex labeled x for individual x.

2. Draw an undirected edge labeled i between vertices x and y if and only if x_i ≡ y_i.

3. Remove all vertex labels.

The reason for removing all vertex labels in the last step is as follows. Any two MPs are equal under random mating if they are related by some permutation of the labels of individuals. For example, ℙ(x₁ ≡ y₁, x₂ ≡ z₂) and ℙ(x₁ ≡ y₁, y₂ ≡ z₂) are equal under random mating. In terms of our graphical representation, such an equality of MPs translates to the statement that two fully labeled graphs (in which all vertices and edges are labeled) are equivalent if they are isomorphic as edge-labeled graphs (i.e. ignoring vertex labels). An L-locus match graph has L edges, one for each locus.

Shown in Figure 1 is the match graph corresponding to ℙ(x₁ ≡ y₁,…, x_L ≡ y_L), the probability that two randomly chosen individuals have matching alleles at L loci. We use P^WF_L and P^M_L to denote this L-locus MP in the WF and Moran models, respectively. Our main objective is to compute P^WF_L and P^M_L. To solve for P^WF_L in equilibrium, we need to find a system of coupled linear equations in which P^WF_L appears as one of the unknown variables; as we will see in Section 6.1, the total number of unknown variables in such a system grows extremely fast as the number of loci increases.

Fig. 1.

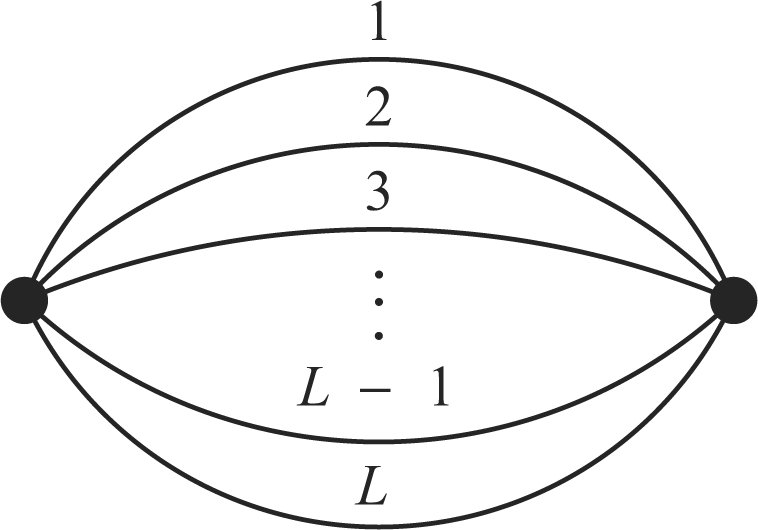
The match graph corresponding to the probability that two randomly chosen individuals have matching alleles at L loci. This probability is denoted by P^WF_L and P^M_L in the WF and Moran models, respectively.

3.3 Vertex split and merge operations

Given a number of individuals at generation t and a match relation involving them, the probability of the match relation can be written as a linear combination of MPs involving their parents. Recall that, forward in time, a reproduction event involves choosing two individuals (each with replacement) and creating a new offspring gamete from the two chosen gametes via recombination and mutation. To capture this model of reproduction, we consider the following two kinds of operations on match graphs:

3.3.1 Vertex split to represent recombination

Consider an individual x whose alleles at k > 1 loci are involved in a match relation. In the graph corresponding to that match relation, the degree of vertex x is k. If the alleles at the k loci trace back to two parental gametes as a consequence of recombination (c.f. Section 2.2), then split the vertex x into exactly two vertices v₁ and v₂, distributing the set of edges that used to be incident with x to v₁ and v₂. In the WF model, more than one vertex in the original graph may split, while in the Moran model at most one vertex may split. A graph resulting from performing a set of splits allowed in a single generation is called a split graph.

3.3.2 Vertex merge to represent sharing a common parent

Two or more gametes at generation t may trace back to a common parental gamete at generation t − 1. This sharing of a parental gamete translates to merging vertices in the split graph into a single vertex. Any isolated vertex that results from merge operations can be discarded from the resulting match graph since such a vertex is not involved in any match relation. If a graph becomes empty from discarding isolated vertices, the probability associated with it is 1.

By performing all possible split-and-merge operations on a given match graph G at generation t, we obtain a set of match graphs G′₁,…, G′_k at generation t − 1. Each split-and-merge operation has a well-defined probability associated with it, determined by the assumed model of random mating. (See Sections 4 and 5 for details.) These probabilities are used as coefficients in the equation that represents G as a linear combination of G^′₁,…, G^′_k.

4 THE GRAPHICAL FRAMEWORK FOR THE WF MODEL

In this section, we briefly review the graphical framework for the WF model, which was considered in detail by Song and Slatkin (2007). The reader should refer to that paper for a detailed explanation.

Let G be a match graph with vertex set V_G. Given a vertex v ∈ V_G, we use d(v) to denote its degree. We focus on the case with unlinked loci.

4.1 Probability associated with a vertex split

In a match graph G, consider a vertex v with degree d > 1, and suppose that edges incident with v are bijectively labeled by I={i₁, i₂,…, i_d}. Let denote a bipartition of I into two disjoint subsets. There are 2^d−1 inequivalent bipartitions of I. Each bipartition has probability 1/2^d−1 and corresponds to splitting v into two vertices, such that the edges labeled by B become incident with one vertex and the edges labeled by become incident with the other vertex.

4.2 Probability associated with a vertex merge

Suppose that a split graph G_S contains n vertices. For ease of discussion, label the vertices by [n]={1,…, n}. In the WF model, disjoint subsets of [n] may each merge into a single vertex. More generally, there exists an one-to-one correspondence between the set of all vertex merge operations on G_S and the set of all partitions of [n] into non-empty subsets, with each subset corresponding to those vertices that merge into a single vertex. A partition of [n] into k non-empty subsets defines a particular case of assigning n labeled individuals to k distinct unlabeled parents, with each parent having at least one child. Hence, the probability of a particular set of vertex merges in G_S such that k vertices remain, is given by (2N_WF)_(k)/(2N_WF)ⁿ, where z_(k) denotes the falling factorial z(z − 1)···(z − k + 1).

4.3 Probability associated with mutation

Let {x¹_i,…, x^k_i} denote a set of alleles at locus i in k individuals at time t. In the infinite-alleles model, x¹_i ≡ x²_i ≡ ··· ≡ x^k_i only if their parental alleles in generation t − 1 all match and no mutation occurs between generations t − 1 and t in the lineages relating {x¹_i,…, x^k_i} to their parents. Hence, the probability of any match relation at time t that requires x¹_i ≡ x²_i ≡ ··· ≡ x^k_i must contain an overall factor of (1 − μ_i)^k when written in terms of MPs at time t − 1. This fact translates to the following statement in our graphical representation: given a vertex v ∈ V_G, define

(1)

This is an indicator variable for whether the individual v is involved in a match relation at locus i. In an L-locus match graph, d(v)=∑_i=1^L δ_i(v). The total number of individuals involved in match relations at locus i is denoted by δ_i(G)≔∑_v∈V(G) δ_i(v). When relating G to graphs in the previous generation, we need to include an overall factor of ∏_i=1^L(1−μ_i)^δ_i(G).

5 THE GRAPHICAL FRAMEWORK FOR THE MORAN MODEL

In this section, we consider the graphical framework for the Moran model, which was not considered in Song and Slatkin (2007). We consider performing split-and-merge operations on a given match graph G with vertex set V_G, where |V_G|=k. As before, d(v) denotes the degree of a vertex v ∈ V_G and δ_i(v) is defined as in (1).

5.1 Coefficients in the recurrence equation

Below we describe the probabilities associated with vertex split-and-merge operations in the case of completely unlinked loci. In the Moran model, exactly one individual in the entire population is a newborn. This condition puts tight restrictions on the allowed split-and-merge operations. In particular, at most one vertex may undergo a split. In what follows, we list the allowed split-and-merge operations. For ease of notation, define, for v ∈ V_G,

5.1.1 No vertex splits

In this case, at most two vertices may be involved in a merge. All possible cases are as follows.

• 0 merge: G → G. The associated probability is

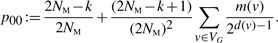
  (2)
• 1 merge: G → G′, with |V_G|=k and |V_G′|=k − 1. Let u and v denote the vertices that merge. The following probability is for that particular merge operation:

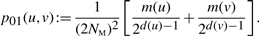
  (3)

5.1.2 Exactly one vertex splits

Let v ∈ V_G with d(v) > 1 be the vertex that splits, and let x, y denote the new vertices created by the split operation. The following probabilities are for a particular split operation at v (i.e. a particular non-trivial bipartition of the edges incident with v).

• 0 merge: G → G′, with |V_G|=k and |V_G′|=k + 1. The associated probability is

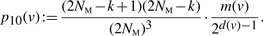
  (4)
• 1 merge:

  • ○ G → G. Here, x and y merge with each other. The associated probability is

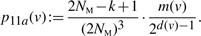
    (5)
  • ○ G → G′, with |V_G|=k and |V_G′|=k. Exactly one of x and y merges with a vertex in V_G∖{v}. The following probability is for a particular merge operation:

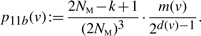
    (6)
• 2 merges: G → G′, with |V_G|=k and |V_G′|=k − 1. Here, x and y each merge with a vertex in V_G∖{v}. The following probability is for a particular set of merge operations for x and y:

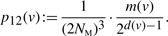
  (7)

5.2 Consistency check

The recurrence equation for a particular match graph G(t) has the following form:

(8)

where the summation is over those match graphs that can be obtained by performing vertex split-and-merge operations on G(t), and c_j(μ, N_M) are constants that depend on μ=(μ₁,…, μ_L) and N_M. For μ_i=0 for all i=1,…, L, then all MPs are identically equal to 1, thus implying ∑_j c_j(0, N_M)=1. We will now verify that the coefficients shown in (2)–(7) satisfy this consistency condition. First, define S ≔{v ∈ V_G ∣ d(v) > 1}, which denotes the set of all vertices that can undergo splits, and let k=|V_G|. Then, for μ_i=0, ∀i, the right-hand side of (8) becomes

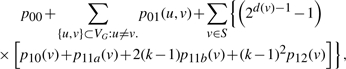where the factor [2^d(v)−1 − 1] corresponds to the total number of non-trivial bipartitions of the labeled edges incident with v. It is straightforward to show that this expression is exactly equal to 1. Hence, the probabilities in Section 5.1 are consistent.

6 SIMPLIFICATION AND EXAMPLES

Although split-and-merge operations allowed in the WF and Moran models are different, exactly the same set of inequivalent match graphs are involved in the systems of recurrence equations in the two models. In the general case, the major computational obstacle is that there are too many match graphs to consider. However, in the special case in which all loci have the same mutation rate, the computation simplifies dramatically, allowing us to compute MPs for 10 or more loci. Below we describe this simplification in detail and give a couple of examples to illustrate setting up recurrence equations.

6.1 Graph enumeration

In the case of haplotypic MPs, there is a one-to-one correspondence between the set of inequivalent match graphs with k edges and the set of inequivalent loopless multigraphs with k edges and non-isolated vertices. (Recall that a multigraph is a graph in which there may be more than one edge joining any pair of vertices.) Using this bijection, we can determine exactly how many inequivalent match graphs we need to consider. The number α(k) of inequivalent loopless multigraphs with k distinctly labeled edges is shown in Table 1 for k = 1,…, 13 (Labelle, 2000). Such edge-labeled graphs are what we need to consider if mutation rates μ_i are all distinct at different loci, and the total number of inequivalent match graphs involved in the L-locus MP computation is given by

Table 1.

The number α(k) [respectively, β(k)] of inequivalent loopless multigraphs with k labeled (respectively, unlabeled) edges and non-isolated vertices

k	α(k)	β(k)
1	1	1
2	3	3
3	16	8
4	139	23
5	1 750	66
6	29 388	212
7	624 889	686
8	16 255 738	2 389
9	504 717 929	8 682
10	18 353 177 160	33 160
11	769 917 601 384	132 277
12	36 803 030 137 203	550 835
13	1 984 024 379 014 193	2 384 411

Clearly, enumerating all such match graphs to compute the 13-locus MP is not tractable. However, if μ_i=μ, for all i=1,…, 13, then we do not need to distinguish loci, thus allowing us to remove edge labels. This property considerably reduces the total number of inequivalent graphs we need to consider, simplifying the computation significantly. Shown in Table 1 is the number β(k) of inequivalent loopless multigraphs with k unlabeled edges (Harary and Palmer, 1973). Note that β(k) grows much slower than does α(k) as k increases. If all mutation rates are equal, the number of inequivalent match graphs that we need to consider for the L-locus MP computation reduces to

(9)

In what follows, we assume that μ_i are the same across all loci; i.e. we set μ_i = μ for all i = 1,…, L.

Given a system of recurrence equations for edge-labeled graphs, a system for edge-unlabeled graphs can be obtained by summing over the coefficients of edge-labeled graphs that are equivalent as edge-unlabeled graphs.

6.2 The 1-locus recurrence equations

In the WF model, the recurrence equation for the 1-locus MP P^WF₁ is shown in Figure 2, which can be solved to yield

(10)

In the Moran model, the 1-locus MP P^M₁ satisfies the recurrence equation shown in Figure 3, which implies

(11)

Fig. 2.

1-Locus recurrence equations for the WF model.

Fig. 3.

1-Locus recurrence equations for the Moran model.

6.3 The 2-locus recurrence equations

Shown in Figure 4 is a system of recurrence equations for 2-locus MPs in the Moran model. It corresponds to the case with an arbitrary recombination rate r (c.f. Section 2.2) and mutation rates μ_i=μ for i=1, 2. Before solving this system of three coupled equations, the 1-locus MP P^M₁ should be computed first as described in Section 6.2. The system contains three unknowns and three coupled equations; P^M₂ (c.f. Fig. 1) is one of the three unknowns. The 2-locus system corresponding to the WF model is also simple to write down, but we do not show it here because of space constraint. We refer the interested reader to Figure 10 of Song and Slatkin (2007).

Fig. 4.

The system of recurrence equations for 2-locus MPs in the Moran model with an arbitrary recombination rate r and μ_i = μ for i = 1, 2.

7 IMPLEMENTATION DETAILS

Computing the MPs for more than five loci requires overcoming several algorithmic and engineering challenges. Described below are our solutions to some of these challenges. The reader only interested in results may skip to Section 8.

7.1 Algorithm for computing MPs

To compute P^WF_L in the WF model or P^M_L in the Moran model, a breadth-first search (BFS) is performed starting with the L-locus match graph shown in Figure 1. Given a match graph to explore, we perform all possible split-and-merge operations on that graph, and all newly encountered match graphs (i.e. inequivalent to the ones seen so far) get put in the BFS queue for subsequent exploration. When the BFS terminates, we would have constructed a directed, edge-weighted BFS graph defined as follows: (i) To each match graph, assign a vertex. (ii) Draw a directed edge from vertex G_i to vertex G_j if the match graph G_j can be obtained from the match graph G_i by performing vertex split-and-merge operations allowed in a single generation. We say that G_j is a neighbor of G_i. (iii) Assign the associated split–merge probability to each edge.

To avoid confusion with match graphs, we will call the above BFS graph a supergraph. This supergraph encodes a system of linear equations. A match graph with outdegree ≥1 in the supergraph can be written as linear combination of its neighbors, with the corresponding edge weights taken as coefficients in the linear combination. Since performing split-and-merge operations on a given match graph never increases the number of edges, the supergraph produced by the BFS has L strongly connected components (SCC) C₁,…, C_L, with C_k containing all k-locus match graphs (each of which has exactly k edges). Hence, the linear system for the entire supergraph is naturally decomposed into L linear systems, one for each SCC, and they can be solved sequentially from C₁ to C_L.

7.2 Graph isomorphism testing

During the BFS, when split-and-merge operations are performed on a particular match graph, it is possible to encounter a neighbor match graph which is isomorphic to one of the match graphs that has already been generated before. To avoid putting redundant match graphs into the BFS queue and to set up the system of linear equations with the correct coefficients, we therefore need an efficient way to test graph isomorphism. There is no known polynomial-time algorithm for testing graph isomorphism for arbitrary graphs, but several heuristics have been suggested that work well for most graphs. In our work, we use the nauty package (McKay, 2007) to generate a canonical permutation of the vertex labels of each graph. The canonical permutation ensures that if two graphs are isomorphic, their adjacency matrices will be identical after applying their respective canonical permutations. We hash the adjacency matrix of the canonically permuted graph and use this hash along with the adjacency matrix to store the graphs and test isomorphism.

Match graphs in our framework are multigraphs, but nauty only deals with simple graphs (i.e. graphs with at most one edge between every pair of vertices). However, nauty supports the notion of colors for partitioning vertices, which is respected by the canonical permutation of vertex labels. We take advantage of this feature to create a new colored simple graph from a match graph as follows: if vertices u and v have k > 1 edges between them, we create a new vertex w with color k and create edges {u, w} and {v, w}. The original vertices of the match graph maintain a color of 1. The canonical permutation can then be applied to this new graph for testing graph isomorphism as described before.

7.3 Order-2 truncation

In the BFS, performing all possible split-and-merge operations on a given match graph G may produce many neighbors, but a significant fraction of them might come with negligibly small edge weights (i.e. split-and-merge probabilities). To simplify the computation, we ignore all neighbors of G with edge weights of order 1/N^m where m > 2 and N is either N_WF or N_M, depending on the model. By ‘ignoring’ neighbors, we mean removing edges from G to those neighbors in the supergraph. This approximation scheme is called order-2 truncation. Song and Slatkin (2007) showed that it produces very accurate answers and we have independently verified this fact using our new implementation. In the WF (respectively, Moran) model computation, we used order-2 truncation for all match graphs corresponding to ≥2 loci (respectively, 9 loci).

7.4 Solving the linear system

In the WF model, the number of edges in the supergraph grows quadratically with the number of vertices in the supergraph. For L = 13, the supergraph contains ∼3.1 × 10⁶ vertices and at least 2 × 10¹² edges, even if the above-mentioned order-2 truncation is used. Storing the associated edge weights in 8 B double-precision data types is intractable, and therefore we pursued the WF model only up to 10 loci. This is less of a problem in the Moran model, in which the supergraph has fewer edges than that in the WF model. However, the linear system for 13 loci in the Moran model still has ∼3.1 × 10⁶ coupled equations in just as many variables, and the standard Gaussian elimination with a cubic running time is not tractable. Instead, we use the iterative Successive Over-Relaxation method to solve the linear systems up to a relative error of 10⁻⁹ for each variable.

7.5 Precomputing the supergraph structure

The algorithm described above computes the MPs for a particular mutation rate μ. This computation takes about 24 h on a 2.8 GHz Opteron PC for the 13-locus MP computation in the Moran model. Instead of repeating this expensive computation for different μ, we run the BFS procedure once and store the supergraph structure on disk without actually computing the edge weights (i.e. probabilities associated with split-and-merge operations). To compute the MPs for a specific μ, another program reads the supergraph from disk, calculates the probabilities associated with each edge of the supergraph using the specified μ and population size, and solves the linear system to determine the MPs. For the 13-locus computation in the Moran model, this program takes only about 3.5 h, of which 2 h are spent on reading the supergraph and match graphs into memory, and calculating edge weights in the supergraph.

8 RESULTS

In this section, we summarize our main results. To model a haploid population with effective population size 2N_e, we need to use N_WF=N_e in the WF model and N_M=2N_e in the Moran model (see Ewens 2004 p. 121 for explanation). In what follows, we consider a finite population with N_e=10 000, which is an approximate long-term effective population size of humans estimated from various genetic data (Harding et al., 1997; Harpending et al., 1998). Hence, we use N_WF=10 000 in the WF model and N_M=20 000 in the Moran model.

8.1 Accuracy of the product rule

We use π^WF_L to denote the L-locus MP in the WF model obtained using the product rule; note that π^WF_L=(P^WF₁)^L. Table 2 shows π^WF_L, P^WF_L and P^M_L for six different values of μ. We do not show the product rule MPs in the Moran model, since they are very close to π^WF_L for the mutation rates shown in the table. The L-locus product rule MP π^WF_L shown in the table agrees very well with Ewens' (1972) sampling formula (ESF): 1/(1+θ)^L, where θ=4N_eμ.

Table 2.

Comparison of L-locus MPs for the case with N_e=10000 and μ_i = μ for all loci i=1,…, L

L	πWFL	PML	πWFL	PWFL	PML	πWFL	PWFL	PML
	μ = 1 × 10−4			μ = 2 × 10−4			μ = 3 × 10−4
1	2.00 × 10−1	2.00 × 10−1	2.00 × 10−1	1.11 × 10−1	1.11 × 10−1	1.11 × 10−1	7.69 × 10−2	7.69 × 10−2	7.69 × 10−2
2	4.00 × 10−2	4.00 × 10−2	4.00 × 10−2	1.23 × 10−2	1.24 × 10−2	1.24 × 10−2	5.91 × 10−3	5.93 × 10−3	5.94 × 10−3
3	8.00 × 10−3	8.01 × 10−3	8.01 × 10−3	1.37 × 10−3	1.38 × 10−3	1.38 × 10−3	4.55 × 10−4	4.60 × 10−4	4.66 × 10−4
4	1.60 × 10−3	1.60 × 10−3	1.61 × 10−3	1.52 × 10−4	1.55 × 10−4	1.59 × 10−4	3.50 × 10−5	3.68 × 10−5	4.03 × 10−5
5	3.20 × 10−4	3.22 × 10−4	3.25 × 10−4	1.69 × 10−5	1.78 × 10−5	2.01 × 10−5	2.69 × 10−6	3.26 × 10−6	5.29 × 10−6
6	6.40 × 10−5	6.48 × 10−5	6.68 × 10−5	1.88 × 10−6	2.16 × 10−6	3.51 × 10−6	2.07 × 10−7	3.80 × 10−7	1.52 × 10−6
7	1.28 × 10−5	1.31 × 10−5	1.44 × 10−5	2.09 × 10−7	3.02 × 10−7	1.08 × 10−6	1.59 × 10−8	6.86 × 10−8	7.00 × 10−7
8	2.56 × 10−6	2.69 × 10−6	3.48 × 10−6	2.32 × 10−8	5.41 × 10−8	4.94 × 10−7	1.22 × 10−9	1.74 × 10−8	3.63 × 10−7
9	5.11 × 10−7	5.65 × 10−7	1.05 × 10−6	2.57 × 10−9	1.28 × 10−8	2.60 × 10−7	9.39 × 10−11	5.08 × 10−9	1.93 × 10−7
10	1.02 × 10−7	1.24 × 10−7	4.16 × 10−7	2.86 × 10−10	3.72 × 10−9	1.42 × 10−7	7.22 × 10−12	1.55 × 10−9	1.03 × 10−7
11	2.05 × 10−8		2.06 × 10−7	3.18 × 10−11		7.84 × 10−8	5.55 × 10−13		5.54 × 10−8
12	4.09 × 10−9		1.15 × 10−7	3.53 × 10−12		4.35 × 10−8	4.27 × 10−14		2.98 × 10−8
13	8.18 × 10−10		6.69 × 10−8	3.92 × 10−13		2.41 × 10−8	3.28 × 10−15		1.60 × 10-8
	μ = 5 × 10−4			μ = 1 × 10−3			μ = 5 × 10−3
1	4.76 × 10−2	4.76 × 10−2	4.76 × 10−2	2.44 × 10−2	2.44 × 10−2	2.44 × 10−2	4.94 × 10−3	4.94 × 10−3	4.95 × 10−3
2	2.26 × 10−3	2.28 × 10−3	2.29 × 10−3	5.93 × 10−4	6.09 × 10−4	6.17 × 10−4	2.44 × 10−5	4.05 × 10−5	4.88 × 10−5
3	1.08 × 10−4	1.13 × 10−4	1.18 × 10−4	1.44 × 10−5	1.87 × 10−5	2.39 × 10−5	1.20 × 10−7	3.54 × 10−6	8.53 × 10−6
4	5.13 × 10−6	6.53 × 10−6	9.74 × 10−6	3.52 × 10−7	1.42 × 10−6	4.41 × 10−6	5.95 × 10−10	8.13 × 10−7	3.59 × 10−6
5	2.44 × 10−7	6.33 × 10−7	2.43 × 10−6	8.57 × 10−9	2.88 × 10−7	1.92 × 10−6	2.94 × 10−12	2.01 × 10−7	1.67 × 10−6
6	1.16 × 10−8	1.21 × 10−7	1.10 × 10−6	2.09 × 10−10	7.45 × 10−8	9.38 × 10−7	1.45 × 10−14	5.06 × 10−8	8.08 × 10−7
7	5.52 × 10−10	3.17 × 10−8	5.57 × 10−7	5.08 × 10−12	1.99 × 10−8	4.70 × 10−7	7.16 × 10−17	1.27 × 10−8	3.98 × 10−7
8	2.63 × 10−11	8.94 × 10−9	2.88 × 10−7	1.24 × 10−13	5.36 × 10−9	2.39 × 10−7	3.54 × 10−19	3.23 × 10−9	1.98 × 10−7
9	1.25 × 10−12	2.56 × 10−9	1.49 × 10−7	3.01 × 10−15	1.45 × 10−9	1.21 × 10−7	1.75 × 10−21	8.26 × 10−10	9.82 × 10−8
10	5.95 × 10−14	7.42 × 10−10	7.79 × 10−8	7.34 × 10−17	3.98 × 10−10	6.19 × 10−8	8.62 × 10−24	2.15 × 10−10	4.91 × 10−8
11	2.83 × 10−15		4.08 × 10−8	1.79 × 10−18		3.17 × 10−8	4.26 × 10−26		2.45 × 10−8
12	1.35 × 10−16		2.13 × 10−8	4.35 × 10−20		1.62 × 10−8	2.10 × 10−28		1.23 × 10−8
13	6.41 × 10−18		1.12 × 10−8	1.06 × 10−21		8.32 × 10−9	1.04 × 10−30		6.16 × 10−9

For the mutation rates shown above, the product rule MPs under the WF and Moran models are very close, so we only show the former π^WF_L.

As Table 2 illustrates, for a give mutation rate μ, the product rule becomes less accurate as the number of loci increases. Furthermore, for a large number L of loci, a slight change in μ causes the product rule MP to decrease by a large amount; for L = 13, it decreases by a factor of about 250 000 if μ changes from 1 × 10⁻⁴ to 3 × 10⁻⁴. However, P^WF_L and P^M_L are far less sensitive to a change in μ; in particular, P^M₁₃ changes only by a factor of about 4 if μ changes from 1 × 10⁻⁴ to 3 × 10⁻⁴.

Since the accuracy of the product rule is highly sensitive to mutation rates, one important question is, ‘What range of mutation rates in the infinite alleles model is relevant to microsatellite loci?’ The observed homozygosity at the CODIS microsatellite loci typically ranges between 0.1 and 0.3, with the average over all 13 loci being about 0.2 (Budowle et al., 2001). Under the infinite alleles model with N_e=10000, ESF implies that homozygosity=0.2 corresponds to μ=10⁻⁴. For this value of μ, Table 2 shows that the product rule is reasonably accurate, especially for L ≤10 and for the WF model. But, for μ=2 × 10⁻⁴, which corresponds to homozygosity = 0.11, the product rule produces considerably less accurate MPs.

8.2 WF versus Moran

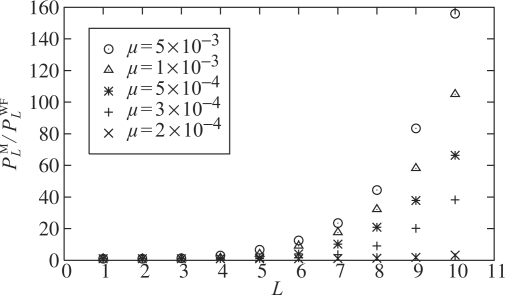
Table 2 reveals a striking difference between the WF and Moran models. The two models agree very well in the single locus case (i.e. L = 1). However, for large values of L, P^M_L in the Moran model can be orders of magnitude higher than P^WF_L in the WF model. As Figure 5 shows, for a given mutation rate μ, the ratio P^M_L/P^WF_L increases rapidly with the number L of loci. For a given L, the ratio P^M_L/P^WF_L increases with μ.

Fig. 5.

The ratio of P^M_L to P^WF_L for N_e = 10 000 and various values of μ.

As μ → 0 and N_WF → ∞ while θ=4N_eμ=4N_WFμ is held fixed, one can analytically show that P^WF₁ in (10) approaches 1/(1+θ), which agrees with the ESF mentioned in the previous section. Likewise, as μ → 0 and N_M → ∞ while θ=4N_eμ=2N_Mμ is held fixed, P^M₁ in (11) approaches 1/(1+θ). Therefore, as expected P^WF₁ and P^M₁ converge to the same value in the diffusion limit. For L > 1, we used our software to check numerically that both P^WF_L and P^M_L converge to 1/(1+θ)^L in the diffusion limit. However, for large values of L, the rate of convergence for the Moran model seems much slower than that for the WF model. Table 3 illustrates this point. For N_e=10⁹ and μ=10⁻⁸, which correspond to θ=40, P^WF_L for L ≥ 6 are much closer to 1/(1+θ)^L than are P^M_L.

Table 3.

MPs for N_e = 10⁹ and μ = 10⁻⁸, which correspond to θ = 40

L	1/(1 + θ)L	PWFL	PML
1	2.44 × 10−2	2.44 × 10−2	2.44 × 10−2
2	5.95 × 10−4	5.95 × 10−4	5.95 × 10−4
3	1.45 × 10−5	1.45 × 10−5	1.45 × 10−5
4	3.54 × 10−7	3.54 × 10−7	3.54 × 10−7
5	8.63 × 10−9	8.63 × 10−9	8.65 × 10−9
6	2.11 × 10−10	2.11 × 10−10	2.20 × 10−10
7	5.13 × 10−12	5.34 × 10−12	9.86 × 10−12
8	1.25 × 10−13	1.79 × 10−13	2.52 × 10−12
9	3.05 × 10−15	1.75 × 10−14	1.22 × 10−12

8.3 The 2-locus case with a variable recombination rate

In the case of two loci, we can symbolically solve the coupled equations in Figure 4 to obtain an analytic formula for P^M₂ for the Moran model. Likewise, we can symbolically solve the coupled equations in Figure 10 of Song and Slatkin (2007) to obtain an analytic formula for P^WF₂ for the WF model. The value r^∗ of 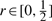for which the ratio P^M₂/P^WF₂ is maximized depends on N_e and μ. For example, with N_e fixed at 10000, r^∗≈0.129 for μ = 5 × 10⁻⁴, r^∗≈0.224 for μ = 1 × 10⁻³ and for μ = 5 × 10⁻³.

8.4 Excluding siblings

To estimate the contribution of close relatives to MPs, we want to compute MPs conditioned on the event that the two individuals being compared are neither full-sibs nor half-sibs in the WF model. This computation can be carried out as follows. Suppose that the two individuals are sampled from generation t. Then, we compute the equilibrium MPs as before and use them as MPs at generation t − 1. To compute MPs at generation t conditioned on the two individuals being non-sibs, we set up a system of restricted recurrence equations, obtained by restricting vertex merge operations to avoid generating sibling relationships. In the Moran model, it is not clear how the analogs of full-sibs and half-sibs should be defined, so the Moran model is omitted from this discussion.

Shown in Table 4 are π^WF_L and P^WF_L conditioned on the event that the two individuals being compared are non-sibs. Comparing that table with Table 2, we see that the product rule becomes much more accurate if we are provided with the additional information that the individuals being compared are not close relatives.

Table 4.

MPs between non-siblings in the WF model with N_e=10 000

L	Non-sib πWFL	Non-sib PWFL	Non-sib πWFL	Non-sib PWFL	Non-sib πWFL	Non-sib PWFL	Non-sib πWFL	Non-sib PWFL
	μ = 1 × 10−4		μ = 5 × 10−4		μ = 1 × 10−3		μ = 5 × 10−3
1	2.00 × 10−1	2.00 × 10−1	4.75 × 10−2	4.75 × 10−2	2.43 × 10−2	2.43 × 10−2	4.89 × 10−3	4.89 × 10−3
2	4.00 × 10−2	4.00 × 10−2	2.26 × 10−3	2.26 × 10−3	5.91 × 10−4	5.95 × 10−4	2.39 × 10−5	2.78 × 10−5
3	7.99 × 10−3	7.99 × 10−3	1.07 × 10−4	1.08 × 10−4	1.44 × 10−5	1.48 × 10−5	1.17 × 10−7	3.67 × 10−7
4	1.60 × 10−3	1.60 × 10−3	5.11 × 10−6	5.20 × 10−6	3.49 × 10−7	3.93 × 10−7	5.71 × 10−10	1.62 × 10−8
5	3.19 × 10−4	3.20 × 10−4	2.43 × 10−7	2.54 × 10−7	8.48 × 10−9	1.22 × 10−8	2.79 × 10−12	1.01 × 10−9
6	6.39 × 10−5	6.39 × 10−5	1.15 × 10−8	1.28 × 10−8	2.06 × 10−10	5.19 × 10−10	1.36 × 10−14	6.68 × 10−11
7	1.28 × 10−5	1.28 × 10−5	5.48 × 10−10	6.81 × 10−10	5.01 × 10−12	3.15 × 10−11	6.67 × 10−17	4.48 × 10−12
8	2.55 × 10−6	2.56 × 10−6	2.61 × 10−11	4.02 × 10−11	1.22 × 10−13	2.39 × 10−12	3.26 × 10−19	3.06 × 10−13
9	5.10 × 10−7	5.12 × 10−7	1.24 × 10−12	2.76 × 10−12	2.96 × 10−15	2.00 × 10−13	1.59 × 10−21	2.16 × 10−14
10	1.02 × 10−7	1.03 × 10−7	5.89 × 10−14	2.23 × 10−13	7.19 × 10−17	1.74 × 10−14	7.79 × 10−24	1.61 × 10−15

9 DISCUSSION

For a finite population, we have shown that the accuracy of multi-locus MPs predicted by the product rule is highly sensitive to mutation rates in the range of interest. For N_e = 10000 and μ = 10⁻⁴, the product rule provides a reasonable approximation to the true MP, but slightly increasing the mutation rate (say, to μ = 2 × 10⁻⁴) can change this conclusion dramatically. There is no doubt that the true 13-locus MP at the CODIS loci is a very small number, but it is important to find out how small it is, as the following recent work illustrates: Song et al. (2009) considered a hypothetical series of criminal cases in which a suspect is identified based only on ‘cold hit’, i.e. the DNA profile of a crime-scene sample is found to match a known profile in a DNA database. They showed that the average probability that a ‘cold hit’ in a DNA database search results in an erroneous attribution is approximately equal to twice the number of individuals in the population not in the database times the average MP. Hence, since the population size is very large, an increase by several orders of magnitude in the MP may change the above probability of erroneous attribution from being negligibly small to being non-negligible.

The reader should bear in mind that the results described here pertain to a simplified, ideal finite population. The models we consider ignore several important aspects of human genetics. In particular, monogamy is ignored for simplicity, while Song and Slatkin (2007) showed that monogamy increases the probabilities of matches at unlinked loci and that the effect of monogamy increases with the number of loci. Other relevant features that should be explored include diploidy and population structure. Another limitation of our study, which also applies to that of Laurie and Weir (2003) and Song and Slatkin (2007), is that we assume an infinite alleles model of mutation; as such, we do not allow for independent origins of the same allele, as can happen with microsatellite loci. In the infinite alleles model, identity in allelic state implies identity by descent. Our work studies the effect of shared genealogies in a finite population on the joint probability of identity by descent. Regarding this question, our work applies to other mutation models as well.

As an important by-product of our work on MP computation, we have revealed a fundamental difference between the WF and Moran models, which are two standard models widely used in population genetics. We have shown that the difference in MPs in the two models increases with the number of loci. It will be interesting to provide a genealogical interpretation of this finding. We speculate that the times to the most recent common ancestors at unlinked loci are more correlated in the Moran model than in the WF model. Given the results discussed in this article, it is tempting to suspect that other quantities, such as linkage disequilibrium, of interest to population geneticists may be fundamentally different in the two models, especially when many loci are considered. Consequently, it seems pertinent to think about which random mating model is more appropriate for humans.